La radice
Premessa
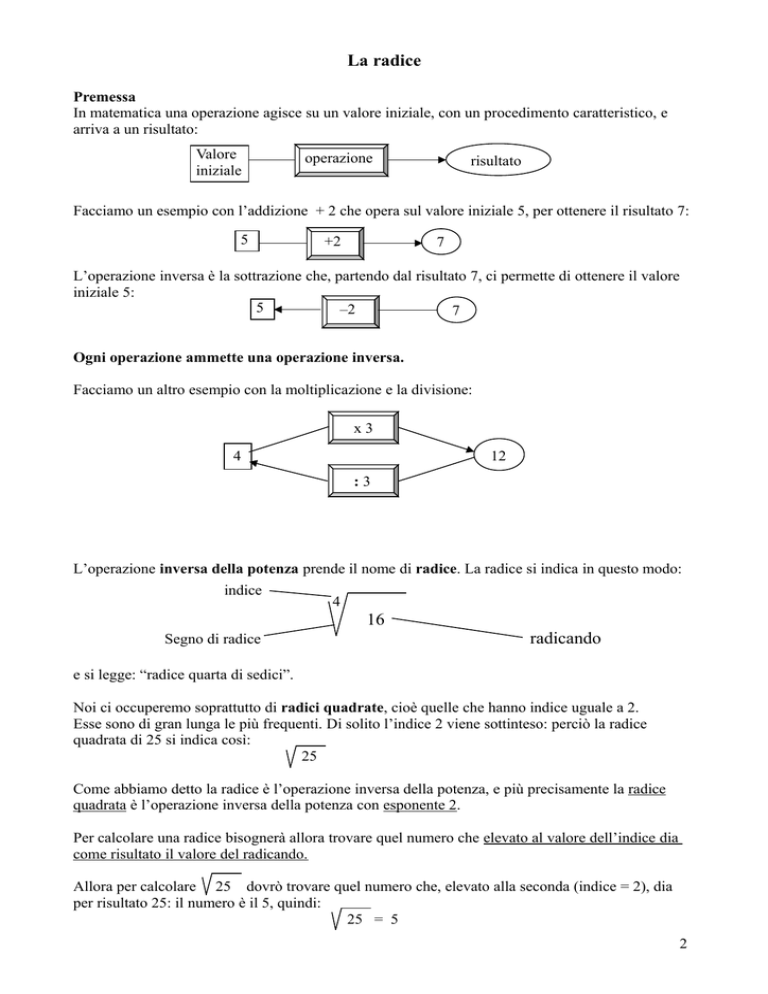
In matematica una operazione agisce su un valore iniziale, con un procedimento caratteristico, e
arriva a un risultato:
Valore
iniziale
operazione
risultato
Facciamo un esempio con l’addizione + 2 che opera sul valore iniziale 5, per ottenere il risultato 7:
5
+2
7
L’operazione inversa è la sottrazione che, partendo dal risultato 7, ci permette di ottenere il valore
iniziale 5:
5
–2
7
Ogni operazione ammette una operazione inversa.
Facciamo un altro esempio con la moltiplicazione e la divisione:
x3
12
4
:3
L’operazione inversa della potenza prende il nome di radice. La radice si indica in questo modo:
indice
4
16
Segno di radice
radicando
e si legge: “radice quarta di sedici”.
Noi ci occuperemo soprattutto di radici quadrate, cioè quelle che hanno indice uguale a 2.
Esse sono di gran lunga le più frequenti. Di solito l’indice 2 viene sottinteso: perciò la radice
quadrata di 25 si indica così:
25
Come abbiamo detto la radice è l’operazione inversa della potenza, e più precisamente la radice
quadrata è l’operazione inversa della potenza con esponente 2.
Per calcolare una radice bisognerà allora trovare quel numero che elevato al valore dell’indice dia
come risultato il valore del radicando.
Allora per calcolare 25 dovrò trovare quel numero che, elevato alla seconda (indice = 2), dia
per risultato 25: il numero è il 5, quindi:
25 = 5
2
Riprendiamo lo schema già usato:
52
25
5
25
Proviamo a calcolare altre radici quadrate
(a destra è indicata l’operazione inversa):
4
=2
22 = 4
9
=3
32 = 9
64
=8
82 = 64
100 = 10
102 = 100
49 = 7
72 = 49
81 = 9
92 = 81
È facile osservare che in tutti questi esempi il risultato della radice è un numero naturale, facilmente
calcolabile.
Tutti quei numeri la cui radice quadrata è un numero naturale si chiamano quadrati perfetti.
Nella maggior parte dei casi è però meno semplice pervenire al risultato. Prendiamo per esempio
55
=?
In questo caso il numero che elevato alla seconda è uguale a 55 sarà di certo
compreso tra 7 e 8: infatti, come abbiamo appena osservato, 72 = 49 e
2
8 = 64. In realtà il numero richiesto è
7,4161984870956629487113974408007….
cioè un numero decimale con un elevato numero di cifre dopo la virgola. I puntini finali però fanno
capire che le cifre decimali non sono state tutte indicate !!!
Questo è infatti di un tipo di numero diverso dai numeri razionali (indicati con la lettera Q), con cui
abbiamo finora lavorato: si tratta di numeri detti irrazionali (indicati con la lettera I), che sono
numeri decimali con un numero infinito di cifre decimali, che però, a differenza dei numeri
periodici, non possono essere in alcun modo previste.
Q
4,5
7, ø
I
2
3/4
N 137
13
10
30
L’unione dei numeri razionali Q e dei numeri irrazionali I costituisce l’insieme dei numeri reali, che
vengono indicati con la lettera R.
R=IUQ
(U => unione)
Per riconoscere se un numero è un quadrato perfetto, occorre scomporlo in fattori primi. Se tutti i
fattori della scomposizione hanno esponenti pari, allora il numero è un quadrato perfetto.
Vediamo qualche esempio:
144 = 24 · 32 quadrato perfetto
32 = 25
non quadrato perfetto
810 = 2 · 34 · 5
8100 = 22 · 34 · 52
non quadrato perfetto
quadrato perfetto
2
Proprietà delle radici
Se il radicando è espresso sotto forma di moltiplicazione di due o più fattori, il valore della radice si
può ottenere come moltiplicazione delle radici dei fattori
A·B·C =
Esempio:
9·4 =
9
A ·
·
B
4
·
C
= 3·2=6
Una regola analoga vale anche se sotto il segno di radice si trova una divisione:
A: B
=
A
:
Esempio:
100 : 25 =
Oppure:
64
––
4
B
100 :
25
= 10 : 5 = 2
64
8
= –––––––– = ––– = 4
4
2
Nota Bene: non vale una regola simile per la somma o la sottrazione!
16 + 9 è facilmente calcolabile come
ma se noi scrivessimo
16 + 9 =
25
16
+
=5
9
otterremmo 4 + 3 = 7 (ben diverso dal
risultato corretto che è 5!)
Una seconda importante proprietà permette di semplificare l’indice della radice con l’esponente del
radicando quando ammettono entrambi un divisore comune:
ni
i
ne
R
e
=
R
Esempi:
6
2
3
5
=
3
73 = 7
5
(la radice è calcolata!)
Combinando entrambe le proprietà delle radici e usando la scomposizione in fattori primi del
radicando, è possibile calcolare radici di numeri quadrati perfetti:
196 =
2 2 · 72 =
22 ·
72
= 2 · 7 = 14
o ridurre a calcoli più semplici radici il cui radicando non sia un quadrato perfetto:
243 =
35
=
3 · 34 =
3
· 32
=
9 · 1,732
(1,732 è il valore di 3 preso dalle tavole numeriche)
2
Esercizi
1)
2)
3)
é3ù
êë 2 úû
é3ù
êë 4 úû
1 1 5
+ - +2 =
2 6 12
éæ 3 ö 2 1 æ 1 5 ö 12 ù 8
êç - 1 ÷ : + ç + ÷ × ú : =
ëêè 2 ø 2 è 4 6 ø 13 ûú 3
Calcola (tutti i termini delle frazioni sono quadrati perfetti):
169
144
25
64
=
=
=
=
49
16
121
81
5 8ù
é13
ê 7 ; 3; 11 ; 9 ú
ë
û
4) Calcola, mediante la scomposizione in fattori primi, la radice quadrata dei seguenti
numeri (quadrati perfetti):
784
1024
1089
1764
1936
2304
11664
11025
8649
9604
7744
36100
5) Sapendo che:
2
= 1,41;
3
= 1,73;
5
9216
7056
= 2,24;
calcola, mediante la scomposizione in fattori primi, la radice quadrata dei seguenti numeri ( non
quadrati perfetti):
27; 32;
72;
432; 288; 405; 300; 500; 245; 675.
2












