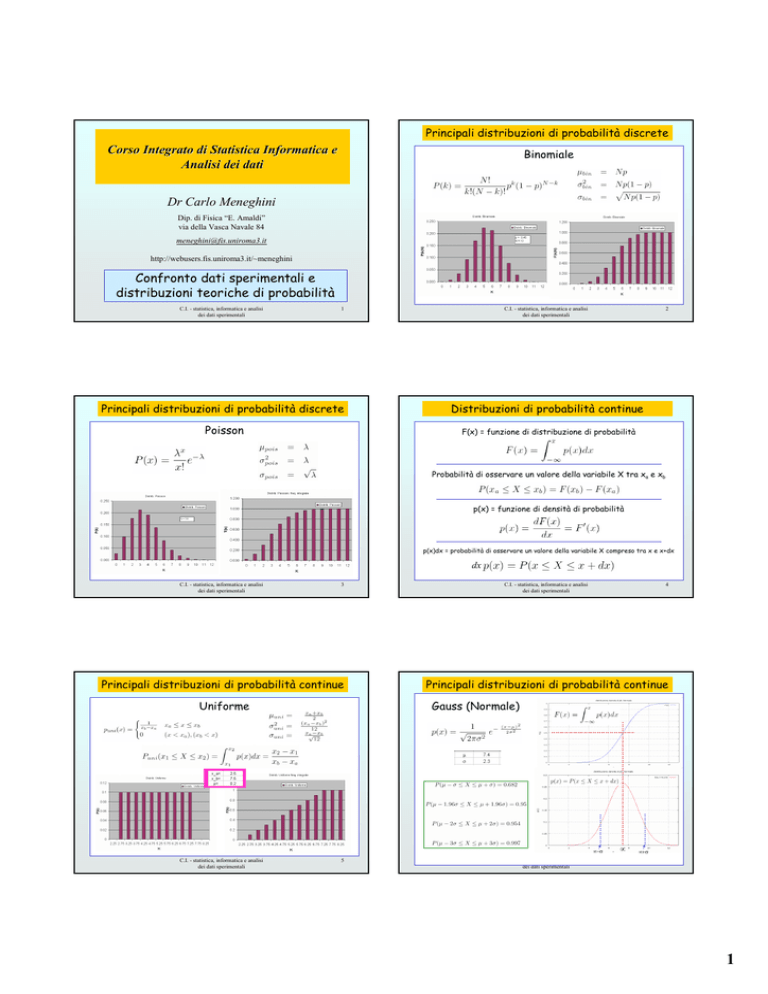
Principali distribuzioni di probabilità discrete
Corso Integrato di Statistica Informatica e
Analisi dei dati
Binomiale
Dr Carlo Meneghini
Dip. di Fisica “E. Amaldi”
via della Vasca Navale 84
[email protected]
http://webusers.fis.uniroma3.it/~meneghini
Confronto dati sperimentali e
distribuzioni teoriche di probabilità
C.I. - statistica, informatica e analisi
dei dati sperimentali
1
C.I. - statistica, informatica e analisi
dei dati sperimentali
2
Principali distribuzioni di probabilità discrete
Distribuzioni di probabilità continue
Poisson
F(x) = funzione di distribuzione di probabilità
Probabilità di osservare un valore della variabile X tra xa e xb
p(x) = funzione di densità di probabilità
p(x)dx = probabilità di osservare un valore della variabile X compreso tra x e x+dx
dx
C.I. - statistica, informatica e analisi
dei dati sperimentali
3
Principali distribuzioni di probabilità continue
Uniforme
C.I. - statistica, informatica e analisi
dei dati sperimentali
4
Principali distribuzioni di probabilità continue
Gauss (Normale)
µ−σ
C.I. - statistica, informatica e analisi
dei dati sperimentali
5
C.I. - statistica, informatica e analisi
dei dati sperimentali
µ
µ+σ
6
1
Principali distribuzioni di probabilità continue
Gauss (Normale)
Istogramma:
Right-click
L’area del rettangolo
rappresenta la frequenza
di una classe, l’altezza la
densità di frequenza.
Il centro della base
rappresenta il valore di
riferimento.
C.I. - statistica, informatica e analisi
dei dati sperimentali
7
incertezza di misura
C.I. - statistica, informatica e analisi
dei dati sperimentali
8
incertezza di misura
La funzione di distribuzione binomiale è la funzione di
distribuzione da cui provengono le frequenze di un
istogramma costruito a partire dalle misure sperimentali.
La funzione di distribuzione binomiale è la funzione di
distribuzione da cui provengono le frequenze di un
istogramma costruito a partire dalle misure sperimentali.
In questo caso
Il numero totale di prove: NT = 30
Consideriamo successo il fatto di osservare un valore
nella classe 5 e insuccesso qualunque altro valore
Il numero di volte che abbiamo osservato il valore 5 è 3
quindi, in base ai dati sperimentali la probabilità di
successo è:
p5 =3/NT = 0.1
In base ai dati sperimentali il numero di volte
che è lecito aspettarsi di trovare 5 fagioli neri
pescando NT fagioli è (valore atteso)
µ = N p5
L’incertezza è:
σ2 = N p5 (1-p5 )
E' lecito aspettarsi che, ripetendo l'esperimento, le
osservazioni sperimentali siano distribuite intorno al
valore vero e che queste siano più frequenti
nell'intervallo µ−σ, µ+σ
La deviazione standard σ è l'incertezza standard sul
valore osservato.
C.I. - statistica, informatica e analisi
dei dati sperimentali
9
L'incertezza standard sul numero di sul valore osservato in una data
classe è σi
Dati
sperimentali
Riepilogo
Statistiche
C.I. - statistica, informatica e analisi
dei dati sperimentali
µ
10
incertezza di misura
L'incertezza standard sul numero di sul valore osservato in una
data classe è σi
Istogramma di frequenze
Right-click
Ni
C.I. - statistica, informatica e analisi
dei dati sperimentali
11
C.I. - statistica, informatica e analisi
dei dati sperimentali
12
2
Confronto dati sperimentali e distribuzioni
teoriche
Confronto dati sperimentali e distribuzioni
teoriche
Distribuzioni discrete
Problema:
Confrontare la distribuzione sperimentale (N dati con distribuzione di frequenze assolute
Ni) con la distribuzione teorica di probabilità P(x). Una volta costruito l'istogramma di
frequenze sperimentali:
A
B
Calcolare la distribuzione delle frequenze
relative fexp
Calcolare l'incertezza sulle frequenze
assolute:
Calcolare l'incertezza sulle frequenze
assolute:
Calcolare le frequenze assolute teoriche:
Calcolare l'incertezza sulle frequenze
relative
NTh=piNT
Riportare sul grafico NTh e Ni con le
incertezze di misura
Riportare sul grafico P(x) e fexp
con le
C.I. - statistica, informatica e analisi
incertezze di misura
dei dati sperimentali
13
Confronto dati sperimentali e distribuzioni teoriche:
classi con più di un carattere (valore)
Dati
sperimentali
C.I. - statistica, informatica e analisi
dei dati sperimentali
14
Confronto dati sperimentali e distribuzioni teoriche:
distribuzioni continue
Riepilogo
Statistiche
Per una la classe i-esima la funzione
FREQUENZA di Excel calcola
Per una distribuzione continua la probabilità associata
ad un intervallo di valori (classe) si calcola a partire
dalla distribuzione integrata:
F(i) - F(i-1) = Ni-Ni-1
P(xa<X<xb) = F(xb) - F(xa)
Questo valore deve essere
confrontato con la Pb di osservare
il valore i-esimo oppure i-1 esimo
C.I. - statistica, informatica e analisi
Vedere
l'esempio nel file: confronto2.xls
dei dati sperimentali
15
C.I. - statistica, informatica e analisi
Vedere dei
l'esempio
nel file: confronto3.xls
dati sperimentali
16
3












