Leggi della dinamica

Leggi della dinamica
1. Se Fris=0
a=0
Definizione operativa di sistema inerziale
2.
Fx=m ax
Fris=m a
Fy=m ay
Fz=m az
Studio delle varie forze
3.
FAB= - FBA
FAB
A
B
FBA
Massa: unità di misura
Dimensioni: unità di
misura
i
f
fondamentale
d
t l
Unità di misura: [SI] kg
[CGS] g
Fattore di ragguaglio
1 kg = 1000 g
Il campo di variazione
delle masse nell’universo
kg
g
1050 _ Universo
,3 10
041
1040 _ Via Lattea ≈ 2,32
kg
1030 _ Sole ≈ 1,98 1030 kg
1020 _
Terra ≈ 5,98 10244 kg
1010 _
1
_
10-10
_
10-20
_
Uomo ≈ 70 kg
Mol. di DNA
≈10-17 kg
27 kg
P t
Protone
≈ 1,67
1 67 10-27
k
10-30 _ Elettrone ≈ 9,11 10-31 kg
Forza: unità di misura
F=m a
Dimensioni [[F]] =[L][M][T
[ ][ ][ -2]
Unità di misura: [SI] newton (N) = m.kg.s-2
[CGS] dina = cm.g.s-22
Fattore di ragguaglio
1 N = 1 kg.m.s-2 =(103g)(102 cm) s-2= 105 dine
Forza gravitazionale
F =G
Mm
r
2
M
m
= mg
Costante di gravitazione universale
G = 6,673 x 10-11 Nm2kg-2
(m3kg-1s-2)
Se m è un corpo posto sulla
superficie
fi i d
della
ll T
Terra
g =G
M
r2
= 6,673 × 10 −11 ×
x 1024 kg
M = 5,98
,
g
r = 6,374 x 106 m
5,98 × 10 24
40,628 × 1012
= 9,82 ms − 2
Quesito: Se la luna avesse una massa doppia dell’attuale ma si
muovesse
ss nella
ll stessa
st ss orbita,
bit quale
l sarebbe
s
bb il suo
s periodo
i d di
rivoluzione rispetto a quello attuale?
R: Lo stesso
Mm mv
2πr
F =G 2 =
; v=
t
r
r
2
Il giro del mondo
in 80 minuti
L’astronauta
Umberto Guidoni
all’interno della
navicella spaziale
p
Columbia.
(r = 6,374 x 106m)
h = 300 km
m = 600 kg
g
Diametro = 1.6 m
v=circa 28
28.000
000 km/h
t=circa 90 min
Forza elettrostatica
F =K
q1q 2
r
La costante K nel vuoto vale:
2
K0 =
-
+
+
+
q1
q2
1
4πε 0
= 9 × 10 9 Nm 2C − 2
ε0 costante dielettrica del
12 u. SI
vuoto=8,854
8 854 10-12
I
In un mezzo vale : K=K0/εr
εr ≥ 1 costante
t t di
dielettrica
l tt i
relativa al mezzo
Carica elettrica Dimensioni: unità di misura fondamentale
Unità di misura: [SI] coulomb (C)
La carica è quantizzata: e
e= 1,602x10-19 C
Pari alla carica dell’elettrone e del protone.
Costante dielettrica relativa p
per alcune
sostanze
Sostanza
εr
aria
1,000590
acqua
81,07
alcool
l
l etilico
tili
25 8
25,8
vetro
7,0
acetone
20,7
cloroformio
4,8
Membrana di assone
90
9,0
Esempio: Determinare la forza (in modulo, direzione e verso) che si
esercita su una carica p
positiva di intensità Q =2.10-6 C, situata al vertice
di un triangolo equilatero di lato L=10 cm, da parte di due cariche di
uguale intensità e di segno opposto (q1 = 5.10-6 C e q2 = - 5.10-6 C ) poste
negli
n
g a
altri
tr due
u vertici
rt c del tr
triangolo.
ang .
F1
Soluzione:
Q +
Scrivo |q1| = |q2| = |q|
F2
L
qQ
F1 = F2 = K 2 = 9N
L
F
θ
+
q1
qQ
F = F1 cosθ + F2 cosθ = 2K 2 cosθ = F1 = F2
L
q2
Esempio: Determinare la forza (in modulo, direzione e verso) che si
esercita su una carica positiva di intensita Q=2.10-6 C, situata al centro
di un quadrato la cui diagonale ha lunghezza L=20 cm
cm, da parte di quattro
cariche tutte di intensita q= 5.10-6 C poste ai vertici del quadrato stesso.
Si determini tale forza per le seguenti sequenze di segni delle cariche q:
(a) ++++, (b) ----, (c) +--+, (d) ++--.
Soluzione
q1 +
q1 - q2
+ q2
( )
(a)
(b)
F4
F3
F2
F1=F2=F3=F4
F1=F2=F3=F4
F1
+
R=0
R=0
+
Q
Q
F2
F1
F4
F3
+
+q
q4
q
4
q3
3
q1 +
q
+ 2
q1 +
- q2
F4
(d)
F2
(c)
Q
F1=F2=F3=F4
F1=F2=F3=F4
+
Q +
F4
F3
R
=
8F
R =0
1
F2 F1
F3
F1
+q
q3 q4
q
4
3
R
Esempio: Nei nuclei atomici i protoni si trovano a una
distanza reciproca di circa 10-15 m. Quanto valgono le
forze di repulsione elettrostatica e di attrazione
gravitazionale tra due protoni?
Soluzione: un protone ha massa m= 1,67x10-27 kg e carica
q= 1,6x10-19 C.
q
(
−19
qq
9 1,6 × 10
Fel = K 2 = 9 ×10
r
10 −30
Fg = G
mm
r2
= 6,67 × 10 −11
)
2
= 230 N .
(1,67 × 10 )
− 27 2
10 − 30
= 1,86 × 10 − 34 N .
Il rapporto tra queste due forze è
Fel
230
=
= 1,23 ×1036
−34
Fg 1,86 × 10
Quesito: Una sferetta di carbonio ha massa m= 1 g.
Q
Quanti
ti elettroni
l tt
i possiede
i d lla sferetta?
f
tt ?
Il carbonio ha massa atomica 12 e numero atomico Z = 6.
Quindi 12 g di carbonio, cioè una mole, contengono
6 02.1023 atomi,
6,02
t mi ovvero
vver 6 vvolte
lte ttanti
nti elettr
elettroni.
ni
Il numero di elettroni in 1 g di carbonio è quindi
quindi:
(
)
1
6 × 6,02 × 10 23 = 3,01× 10 23
12
Forza elastica di richiamo
F = − kx
x =0
F =0
Blocco fissato
alla molla
x
0
k costante elastica
d ll f
della
forza
x1
F
0
Es. Forze con cui un
corpo solido
sol do si
s oppone a
piccole deformazioni
x1
x
x2 negativo
F F positiva
x2
x2
x1 positivo
F negativa
g
0
x
Reazioni vincolari
y
Vincolo ≡ qualunque causa
capace di limitare il moto
R
mg+R=ma=0
m
R=mg
F+mg+R=ma
Fx=Fcosθ =ma
R-mg-Fy=0
y
Fx
θ
Fy
F
L’intensità delle reazioni vincolari è
definita dalle forze cui si oppongono.
x
mg
R
m
mg
x
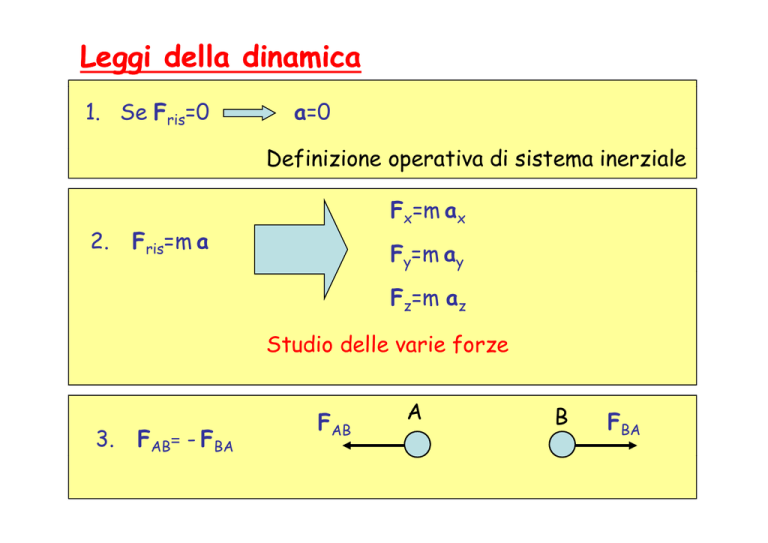
Su un blocco di ferro di massa m=30 kg appoggiato su una superficie
liscia e priva di attrito, agisce la forza F (vedi figura sottostante). Se
il blocco si muove con accelerazione costante a=10 m/s2, si calcoli
l’angolo θ che la forza F forma con l’orizzontale sapendo che la
reazione vincolare normale offerta
ff
dal p
piano è p
pari a R=500 N.
⎧ xˆ : F cos θ = ma x = ma
⎨ˆ
⎩ y : R − Fsenθ − mg = ma y = 0
ma
cos θ
ma
R−
senθ − mg = 0
cos θ
F=
R − mg
= 0.68
ma
R − mg
θ = arctg
= 34.2°
ma
tgθ =
θ
F
m
piano liscio
m
Esempio: La massa m=2 kg di un pendolo
A
viene lasciata andare dalla p
posizione A,
quando il filo è tenuto in posizione
orizzontale.
mg
T
Se il filo ha lunghezza L
L=50
50 cm, qual
qual’è
è la
tensione del filo quando la massa
raggiunge il punto più basso B, se la
velocità della massa in quel punto è di
B
3,13 m/s? (Si consideri il filo
inestensibile e di massa trascurabile)
mg
Soluzione
Le forze in gioco sono la forza di gravità e la forza di tensione del
filo:
T + mg = ma
v 2B
T − mg = ma c ⇒ T = mg + m
= 2 ⋅ 9.8
9 8 + 2 ⋅ 3.13
3 13 2 ÷ 0.5 = 58,8 N
L
Esempio: Un blocco di peso P = 200 N è
trascinato per 2 m lungo un piano inclinato di
p
all’orizzontale da una forza
30° rispetto
costante F = 150 N diretta parallelamente al
piano inclinato, Calcolare la forza di contatto
tra blocco e piano.
piano
R
F
30°
30
P
Soluzione:
R = Pcosθ =
= 200 × 0,87 =
= 174N
Esempio: Un blocco di peso P = 200 N è
per 2 m lungo
g un piano
p
inclinato di
trascinato p
30° rispetto all’orizzontale da una forza
costante F = 150 N diretta orizzontalmente.
Calcolare la forza di contatto tra blocco e
piano.
R
F
30°
30
P
Soluzione:
R = Pcosθ + Fsenθ
Esempio: Un autocarro di massa Ma=8500 kg traina un
rimorchio di massa Mr= 27000 kg,
g, lungo
g una strada
orizzontale. L’accelerazione è di 0,78 m/s2. Trascurando le
forze di attrito, calcolare a) la forza motrice F
dell’autocarro
dell
autocarro e b) il modulo della tensione nelle aste di
traino orizzontale tra il rimorchio e l’autocarro.
S l i
Soluzione:
T
T'
b) T = Mra = 27000x0,78
0 78 = 21060 N
N.
a) F= (Ma+Mr)a
F= (Ma+Mr) a = (8500+27000)x0,78 = 27690 N.
F T ‘ = Maa
FT ‘ = F - Ma a = 27690 - 8500x0,78 = 21060 N.
F
Esempio: La figura illustra un apparecchio di trazione
usato per il trattamento di una lesione
a carico di un piede. Calcolare il valore
della massa M necessaria per
T1
bilanciare la forza
φ
muscolare F.
φ
F
T2
Soluzione:
F=T1cosφ+T2cosφ=2Tcosφ=2Mgcosφ
M F/(2
M=F/(2gcosφ)
)
M