Esercizi Svolti

1
Esercizio : calcolo della conducibilita’ in un conduttore metallico.
Si consideri una striscia di metallo in un circuito integrato, con dimensioni:Lunghezza L =
2.8 [mm] , Area della sezione A = 4 [µm²] (micrometri quadri 10-6).Ai capi del conduttore
metallico viene applicata una tensione pari a: 0.1 [ V]. La corrente che scorre nel
conduttore è : 5·10ֿ³ [A],la mobilità degli elettroni a temperatura ambiente è: 500 [
cm/V·sec].Determinare la conducibilità, la concentrazione degli elettroni e la resistenza
della striscia.
Svolgimento
Sapendo che per : i=J·A=E·σ·A , moltiplico e divido denominatore e numeratore per L :
i=E·σ·A·(L/L) =(σ·A·E·L)/L
ma
(σ·A)/L = 1/R per cui i=(E·L)/R , dato che E·L=V
allora i=V/R. Inoltre : i=(A·σ·V)/L e
σ=(i·L)/(V·A) , per cui :
σ= (5·10¯³ [A] · 2.8·10¯³ [m]) / (0.1 [V] · 4·10-12 [m²]) = 0.05 [A/V] ·0.07·109 [m¯¹] =
=
3.5·10 −7 [(Ω·m)¯¹] .
Poiche’ :
n = σ / (µn· e)
3.5·10
n =
[1/(Ω·m)]
3.5·10
--------------------------------------------------------------------
500·10
=
7
−4
[m/V·sec] · 1.6·10
−19
=
[C]
0.004375·10 30 [(V·sec)/(Ω·m·m²·A·sec)]
[(Ω·m)¯¹]
----------------------------------------------------------
500·1.6·10
=
7
−23
[(m·C)/(V·sec)]
4.35·10 27 [1/m³]
=
2
2.8·10¯³ [m]
R= L/(σ·A) =
0.2· 10¯³ [m]
------------------------------------------------------------7
3.5·10 [(Ω·m)¯¹]·4·10
−12
=
[m²]
------------------------------------------------7
10 [(Ω·m)¯¹]·10
−12
=
[m²]
0.2· 10 9 [m¯¹]
=
--------------------------------
0.2·10 2 [Ω].
=
7
10 [(Ω·m)¯¹]
Esercizio : calcolo della conducibilita’ in un semiconduttore intrinseco.
Calcolare la conducibilità di un semiconduttore (ad esempio silicio) nel caso intrinseco.
Sapendo che: alla temperatura di 300 K, ni = 1.45·10 10 [cm¯³]. Inoltre la mobilità degli
elettroni , µn= 1500 [cm 2 /(V·sec)], e µp = 500 [cm 2 /(V·sec)].
Svolgimento
Se il semiconduttore e’ intrinseco :
n = p= ni
poiche’ σ = e·(µn ·n + µp· p) ne segue :
σ= e · ni· (µn + µp) .
Da cui :
σ =
1.6 ·10 −19 [C] · 1.45 ·10 10 [cm¯³] · (1500 + 500) [cm²/(V·sec)]
=
3
=
2.32·10 −7 [A·cm¯³·sec] · 2000 [cm²/(V·sec)]
=
4.64·10 −4 [(Ω·m)¯¹].
Esercizio : calcolo della conducibilita’ in un semiconduttore estrinseco
( drogaggio di tipo n)
Dato un provino di materiale semiconduttore (Silicio) con le seguenti caratteristiche :
lunghezza L = 3 [mm] , A = 50x100 [µm²], concentrazione di Drogante (donatore) ND =
5·10 14 [cm −3 ] a temperatura ambiente (300 K). Sapendo che dopo aver applicato un
campo elettrico stazionario ai capi esso e’ attraversato da una corrente i = 1 [µA], calcolare
la σ e il potenziale V relativo al campo elettrico applicato.
Nota: µn = 1500 [cm2/(V·sec)] , µp = 500 [cm2/(V·sec)].
Svolgimento
Trattandosi di drogaggio di tipo n , n ≅ ND , a temperatura ambiente, per cui:
p ≅ ni 2 / ND
(1.45· 10 10 ) 2 [cm −6 ]
p =
---------------------------------------------
=
4.2·10 5 [cm −3 ]
5·10 14 [cm −3 ]
Poiche’ : σ = (µn · n + µp · p)· e
σ = (5·10 14 [cm¯³] · 1500 [cm²/(V·sec)] + 500 [cm 2 /V·sec] · 4.2·10 5 [cm −3 ]) · 1.6·10 −19 [C]
4
Si puo’ osservare che µp·p << µn·n , per cui µp·p e’ trascurabile rispetto a µn·n :
σ = 5·10 14 [cm −3 ] · 1500 [cm 2 /(V·sec)] · 1.6·10 −19 [C]
σ = 7.5 ·1017 [(cm·V·sec)-1] · 1.6·10-19 [A·sec]
= 0.12 [(Ω·cm)¯¹]
=
=
0.12 · 10¯² [(Ω·m)¯¹].
V = R·i e R =( σ·L) / A ne segue che V = (i · L)/( A · σ) per cui :
10 −6 [A] · 3·10¯³ [m]
V =
------------------------------------------------------------------------
5000·10
V =
−12
=
0.05 [ A/Ω ]
[m²]· 0.12·10¯² [(Ω·m)¯¹]
0.05 [V].
Esercizio : calcolo della conducibilita’ in un semiconduttore estrinseco
(drogaggio di tipo p)
Dato un provino di materiale semiconduttore (Silicio) con le seguenti caratteristiche:
lunghezza L = 3 [mm], sezione A = 50x100 [µm²], concentrazione di Drogante(accettore)
NA = 7·10 16 [cm¯³], a temperatura ambiente ( 300 K). Sapendo che dopoaver applicato
5
un campo elettrico stazionario ai capi, esso è attraversato da una corrente i= 1 [µA],
calcolare σ e potenziale V relativo al campo elettrico applicato.
Nota: µn = 1500 [cm2/(V·sec)] , µp = 500 [cm2/(V·sec)].
Svolgimento
Trattandosi di drogaggio di tipo p :
p ≅ NA , a temperatura ambiente, per cui:
n ≅ ni / NA
1.45·10 10 [cm −6 ]
n
=
------------------------------------------------
=
3·10 3 [cm −3 ]
7·10 16 [cm¯³]
Poichè σ = (µn · n + µp · p) · e :
σ = (1500 [cm2/(V·sec)] · 3·103 [cm-3] + 500 [cm²/(V·sec)] · 7·1016 [cm¯³]) · 1.6·10-19 [C] =
Si può osservare che µn · n << µp · p , per cui µn·n è trascurabile se confrontato con µp·p :
σ = (500 [cm2/(V·sec)] · 7·1016 [cm-3]) · 1.6·10-19 [C] =
= 5600·10¯³ [(Ω·cm)¯¹] = 5.6 [(Ω·cm)¯¹] = 5.6·10¯² [(Ω·m)¯¹]
Sapendo che V = R·i e R = (σ· L)/ A ne segue che V = (i· L)/(A· σ)
10-6 [A] · 3·10¯³ [m]
V
=
-------------------------------------------------------------------------12
5000 · 10
[m²] · 5.6·10¯²[(Ω·m)¯¹]
=
6
3·10-9 [A·m]
=
------------------------------------------10
2.8·10
[m/Ω]
=
10.71 [V]
7
Esercizio : circuito con diodo
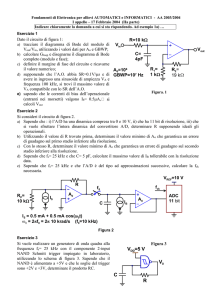
Sia dato il circuito in figura, ove
Vin(t)= 0 [V] per t < 0 [ms] e per
t > 4 [ms] e Vin(t) = K· t [V] per
0 ≤ t ≤ 4 [ms]. Si chiede di calcolare e
disegnare l’andamento temporale della
tensione V(t) ai capi del diodo, della
corrente i(t) che scorre nel diodo
nell’intervallo 0 ≤ t ≤ 5 [ms].
Determinare l’istante in cui il diodo
passa in polarizzazione inversa/diretta o
diretta/inversa.
Calcolare infine la potenza dissipata dal
diodo nell’istante t = 4[ms].
Sapendo che:
Vin(t) = K · t
VR = 1 [V]
Vγ = 0.6 [V]
Rf = 20 [Ω]
R = 180 [Ω]
K = 2 [V/ms]
8
Svolgimento
Nell’instante t0 = 0 [ms]
Suppongo che il diodo sia in polarizzazione diretta e sostituisco al diodo il
suo circuito equivalente ai grandi segnali in polarizzazione diretta:
Vin(t) = 0 da cui - i · R - Vγ - i · Rf - VR = 0
Dalla (1)
- Vγ - VR
i = ----------------------------------- da cui
(1)
i<0
R + Rf
Ma i, in polarizzazione diretta, deve essere positiva per cui il diodo nell’istante t = 0 [ms] è
polarizzato in inversa.
9
Sostituisco al diodo il circuito equivalente in polarizzazione inversa :
in t0 V(t0) = - VR
All’istante t1 il diodo passa in
polarizzazione diretta:
V (t1) = Vin(t) - VR = K · t1 - VR = Vγ
t1 =
VR + Vγ
da cui
1 [V] + 0.6 [V]
=
--------------------------
---------------------------------------
K
=
0.8 [ms] istante t1
2 [V/ms]
Per t > 0.8 [ms] il diodo è in polarizzazione diretta
Nell’intervallo : 0.8 [ms] < t < 4 [ms]
Vin (t) - i · R - Vγ - i · Rf - VR= 0
i (t) =
Vin (t) - Vγ - VR
----------------------------------------
R + Rf
=
K · t - Vγ - VR
--------------------------------------
R + Rf
Rf
Rf · Vγ
K
=
---------------
R + Rf
Rf · VR
·t -
Vγ + VR
----------------------
R + Rf
10
V (t) = Vγ + i · Rf =
-----------------
·K·t -
--------------------
R + Rf
-
R + Rf
-------------------
R + Rf
+ Vγ
K · t - Vγ - VR
VR(t) = R · i (t) = R ·
-----------------------------------------
R + Rf
Calcolo i valori di i (t) negli istanti t1 = 0.8 [ms] e t2 = 4 [ms]
2 [V/ms] · 0.8 [ms] - 0.6 [V] - 1 [V]
i (t1) =
----------------------------------------------------------------------------------
=0
180 [Ω] + 20 [Ω]
2 [V/ms] · 4 [ms] - 1.6 [V]
i (t2) = ----------------------------------------------------------------------------------- = 0.032 [ V/(V/A) ] = 0.032 [A]
200 [Ω]
Calcolo i valori di V(t) negli istanti t1 = 0.8 [ms] e t2 = 4 [ms]
V (t1) =
Vγ +
K · t - Vγ - VR
-----------------------------------
R + Rf
· Rf =
2 [V/ms] · 0.8 [ms] - 1.6 [V]
= 0.6 [V] +
-------------------------------------------------------------------
200 [Ω]
= 0.6 [V]
· 20 [Ω] =
11
2 [V/ms] · 4 [ms] - 1.6 [V]
V (t2) = 0.6 [V] +
--------------------------------------------------------------
· 20 [Ω] =
200 [Ω]
= 0.6 [V] + 0.64 [V] = 1.24 [V]
Calcolo i valori di VR (t) negli istanti t1= 0.8 [ms] e t2 = 4 [ms]
2 [V/ms] · 0.8 [ms] - 1.6 [V]
VR(t1) = 180 [Ω] ·
---------------------------------------------------------------------
= 0
200 [Ω]
2 [V/ms] · 4 [ms] - 1.6 [V]
VR(t2) = 180 [Ω] ·
---------------------------------------------------------------------
= 5.76 [V]
200 [Ω]
Nell’intervallo 0 < t < t1 :
i(t) = 0 ,
V(t) = -VR
, VR(t) = 0
Per il tempo t > 4 [ms]
i(t) = 0 ,
V(t) = -VR
,
VR(t) = 0
Calcolo la potenza dissipata dal diodo nell’istante t2 = 4 [ms]
12
P = V(t) · i(t) = 0.032 [A] · 1.24 [V] = 0.039 [W]
Grafici degli andamenti :
13
Esercizio: calcolo del circuito equivalente di Thevenin di un circuito lineare in
corrente continua.
Dato il circuito in figura, sapendo che: E1 = 10 [V] , R2 = R3 = R4 =R5 = 50
[Ω], calcolare ETH ed RTH .
Svolgimento
Dato un circuito lineare qualsiasi e considerando due nodi A e B, esso è
riconducibile a questo circuito equivalente :
Dove VAB1 = VAB2 = ETH
e RTH = VAB / Icc
14
Calcolo la tensione a circuito aperto ai nodi A e B.
R4 = R5 sono in serie.
Req4,5 e R3 sono in parallelo
Req 345 =
VCB = E1 ·
R2 · Req 345
----------------------------
=
R2 + Req 345
Req 345
---------------------------------
Req 245 + R2
------------------------------------------
=
50 [Ω] + 50 [Ω]
e
VAB = VCB ·
25 [Ω]
VCB = 10[V] · ------------------------------------------ = 2.5 [V]
50 [Ω] + 50 [Ω]
VAB = (2.5 [V] · 50 [Ω] ) / 100 [Ω] = 1.25 [V]
Calcolo la RTH
2500 [Ω2]
50 [Ω] · 50 [Ω]
-----------------------------
= 25 [Ω]
100 [Ω]
R5
--------------------
R4 + R5
= ETH
15
RTH =
VAB
---------------
Icc(corrente di corto circuito) = -
Icc
Req 34 =
VCB =
ove
R3 · R4
Req 34
------------------------------
R2 + Req 34
-----------------
R4
50 [Ω] · 50 [Ω]
-----------------------------
R3 + R4
VCB
=
----------------------------------------
= 25 [Ω]
50 [Ω] + 50 [Ω]
25 [Ω]
· E1 = 10[V] · -------------------------------------- = 0.333·10[V] = 3.333 [V]
50 [Ω] + 25 [Ω]
Sapendo che:
Icc = - VCB / R4
(il meno è necessario in quanto Icc e’ negativo per
convenzione)
16
3.333 [V]
Icc = -
-------------------------
= - 0.06 [A]
50 [Ω]
1.25 [V]
RTH =
---------------------------
0.06 [A]
=
18.75 [Ω]
17
Esercizio: stadio amplificatore con transistore nMOS
Sia dato il circuito in figura e le caratteristiche (Vds, Ids) del transistore nMOS.
Si chiede di:
a) calcolare tensioni e correnti del circuito nel punto di lavoro (trascurando V(in) e R(in),
circuito equivalente del generatore di ingresso ai piccoli segnali);
b) disegnare le rette di carico sulle caratteristiche (VDS, IDS)
c) calcolare i parametri del circuito equivalente ai piccoli segnali del transistore MOS nel
punto di lavoro.
d) determinare l’espressione del guadagno in tensione ai piccoli segnali AV = VOUT / VIN e
calcolare il valore.
Sapendo che: λ = 0 [V-1] , W/L = 1 (dove W = larghezza del canale e L = lunghezza) , K =
0.5 [mA/V2] , VTH = 1 [V] , Vcc = 10 [V] , R1 = 10 [MΩ] [ 106 Ω] , R2 = 10 [MΩ] , RD = 6 [kΩ] [
103Ω], RS = 6 [kΩ] e RIN = 1 [kΩ]
Caratteristiche del transistore: IDS - VDS e IDS -VGS :
18
a)
19
Punto di lavoro :
VG º =
Vcc · R1
---------------------------
= 10 [V] · 10·106[Ω] / 20·106 [Ω] = 5 [V]
R1 + R2
Utilizzando l’equazione di Kirchoff (KVL) ricavo l’equazione della “retta di
carico” :
VG º - VGS – IDS · RS = 0.
La retta passa per i punti A (0 , 8.3·10-4) e B (5 , 0). dove x = VGS e y = IDS .
Metto a sistema le equazioni che ho a disposizione per ricavare i valori numerici di IDS.
IDS = K · (VGS - VTH)² (1)
e
VG º - VGS - IDS · RS = 0 (2)
Dalla (2) ho : VGS = VG º - IDS · RS , vado poi a sostituire nella (1) :
IDS
=
K · (VG º - IDS · RS - VTH)²
=
K · (5 [V] – 1 [V] – IDS · RS)²
IDS
=
16 [V²] · K + IDS² · RS² ·K + 8 [V] · IDS · RS · K
=
.
Da cui :
0.5 · 10¯³ [A/V²] · 36 · 106 [Ω²] · IDS² - (8 · 0.5 · 10¯³ · 6 · 10³ [(A·Ω)/V²] + 1) · IDS +
- 0.5 · 10¯³ [A/V²] · 16 [V²] = 0 .
20
18⋅10³ [(A·Ω²)/V²]· IDS2 – (24 [(A·Ω)/V)] + 1) · IDS + 8·10¯³ [A] = 0
∆ = (25)² - 4·18·10³ · 8·10¯³ = 625 – 576 = 49
Le soluzioni dell’equazione sono:
IDS 1,2 = ( 25 +/-
49 ) / ( 2·18·10³ ) .
Ho ottenuto IDS1 = 0.89 [mA] e IDS2 = 0.5 [mA].
IDS1 = 0.89 [mA] --->
VGS = VG - VS
VS = 0.89 ·10¯³ [A] · 6·10³ [Ω] = 5.34 [V] da cui :
= 5 [V] - 5.34 [V] = - 0.34 [V]
Ma se VGS è negativa, il transistore risulterebbe così spento, per cui la soluzione IDS1 non
è accettabile
Si utilizza quindi IDS2 = 0.5 [mA] da cui : VS = 0.5·10¯³ [A] · 6·10³ [Ω] = 3 [V]
Per cui :
VGS º = 5 [V] - 3 [V] = 2 [V]
21
Utilizzando l’equazione di Kirchoff (KVL) alla maglia ABC :
VS + VDS + VRD - Vcc = 0
Nel punto di lavoro :
VDS º + IDS º · (RS + RD) = Vcc ------>
VDS º = Vcc - IDS º · (RS + RD) .
Da cui :
VDS º = 10 [V] - 0.5·10¯³ [A] · 12·10³ [Ω] = 4 [V] .
b)
Grafico della retta di carico:
c)
22
Calcolo gM
gM
= K·(W / L) · 2·(VGS – VTH)
= 1 [mA / V]
=
0.5 [mA / V2]·1·2·( 2 [V] – 1 [V]) =
= 10-3 [A / V] = 10-3 [Ω-1]
1/ RDS è calcolabile attraverso la derivata di IDS rispetto a VDS :
1/ RDS = K· (W / L)· (VGS – VTH)2 =
0.5 [mA / V2]·1·( 2 [V] – 1 [V])2 · 0.01 [V-1]
= 5·10-3 [mA /V] = 5·10-6 [A /V].
per cui:
RDS = 0.2·106 [Ω]
Calcolo VOUT
Ricavo la VG ai piccoli segnali tramite la KVL considerando che R1 // R2 :
VIN - RIN ·i - (R1 // R2)·i = 0
I(t) = VIN (t) / [RIN ·(R1 // R2)]
Applico il partitore di tensione per ricavare VG:
VG = [(R1 // R2)/ (RIN + (R1 // R2)] · VIN
Ricavata la tensione tra il Gate e la massa di segnale, calcolo VOUT sapendo che la KCL
per il nodo di Drain è IDS + IRD = 0 :
VOUT = IRD · RD
da cui sostituendo nella KCL
= - 0.5 [mA] · 6·103 [Ω] = - 3 [V]
d)
VOUT = - IDS · RD =
23
Calcolo il guadagno in tensione:
VS = RS · IDS = RS · gM· VGS
VS = RS· gM ·(VG – VS) = VS = RS ·gM·VG - RS·gM ·VS
VS = (RS ·gM·VG) / [1 + (gM· RS)]
VGS = VG· VS = VG·{1 – [gM· RS] / [1 + (RS·gM)]}
Ponendo RP = R1 // R2 :
VGS = [RP / (RIN + RP)] ·VIN· {1/ [1 + (RS· gM)]}
Dato che IDS = gM· VGS :
VOUT =
- gM · RD · RP· 1
----------------------------------------------------------------------
(RIN + RP) · [1 + (RS ·gM)]
· VIN
- 10-3 [Ω-1] ·6·103 [Ω] ·50·106 [Ω]
AV =
---------------------------------------------------------------------------------------------
(103 [Ω] + 50·106 [Ω])·[1 +(6·103 [Ω]· 10-3 [Ω-1])]
- 3·108 [Ω]
=
---------------------------------------------9
(1.05·10 [Ω]) · 6
=
- 0.4 · 10-1
=
24
Corso di Tecnologie Elettroniche 1
Prova scritta del 6 settembre 2002
Fig. 1
Soluzione
a)
Se trascuriamo, come suggerito nel testo,VIN ed RIN (che rappresentano il circuito equivalente del
generatore di ingresso per piccoli segnali), risulta che, nel punto di lavoro (quindi in corrente
continua), il sistema costituito da Vcc, R1 e R2, è un partitore di tensione ( I G = 0) per cui:
V1 = Vcc ⋅ R1 /( R1 + R2 ) = 5 V ⋅ 3 kΩ / (3 kΩ +7 kΩ) = 1.5V
V2 = Vcc – V1 = 5 V – 1.5 V = 3.5 V
I 1 = I 2 = Vcc / ( R1 + R2 ) = 5 V / (3 kΩ +7 kΩ) = 0.5mA
Per determinare tensioni e correnti nel punto di lavoro:
VGS0 = V1 = 1.5V (Nota: La resistenza fra Source e massa è nulla)
In questo modo viene fissata la curva con VGS = 1.5V nel grafico di figura 2.
La retta di carico si può tracciare dopo aver determinato due suoi punti, ad esempio:
•
per I DS = 0 VDS = Vcc = 5V
•
per VDS = 0 I DS = Vcc/ RD = 5V / 8333333 Ω = 0.6 µmA
25
Il punto di lavoro si determina, come illustrato in Fig. 2, dall’intersezione della retta di carico (in
0
= 1.5 V:
rosso), con la curva con per VGS
0
VDS
=3V
I D0 = 0.24 µmA
b)
Fig. 2
I D0
V DS0
c)
rds =
gm =
0
1 + λ ⋅ VDS
λ ⋅ I D0
2⋅ k
W 0
ID
L
= ∞Ω
=
per λ tendente a zero
2 ⋅ 0.5 ⋅ 10 −6
1
A
⋅ 1 ⋅ 0.24 ⋅ 10 −6 A =
= 0.7 ⋅ 10 −6 Ω −1
2
1.43MΩ
V
26
d)
Disegniamo il circuito equivalente ai piccoli segnali del circuito di figura 1 passivando i generatori di
tensione costante (in particolare il generatore Vcc) e sostituendo al MOSFET il suo circuito
equivalente ai piccoli segnali.
RIN
V IN
+
R2
RD
Gate
R1
VGS g m
Drain
rds
Fig. 3
Vout
Source
Il circuito di figura 3 può essere ridisegnato evidenziando meglio l’effetto del cortocircuito ottenuto
dalla passivazione di Vcc ed considerando che la resistenza rds è infinita.
Gate
V IN
RIN
+
R1
-
Drain
VGS g m
R2
RD
Fig. 4
Vout
Source
In questo modo si evidenzia meglio il parallelo di R1 ed
equivalente
che viene sostituito dalla loro resistenza
R12 :
Gate
V IN
R2
+
RIN
R12
VGS g m
Drain
RD
Fig. 5
Vout
Source
R12 = R1 ⋅ R2 / ( R1 + R2 ) = 3kΩ ⋅ 7kΩ / (3kΩ + 7kΩ) =
Ne segue quindi:
VGS = V IN ⋅ R12 /( R12 +
VIN = VGS ⋅ 1.47
2.1 kΩ
RIN ) = VIN ⋅ 2.1 kΩ / (2.1 kΩ + 1 kΩ) = VIN ⋅ 0.68
da cui:
27
Vout = −Vgs gmRout = −VG
Rin
gmRout
Rin + RG


Rin
Vout =  −
gmRout Vin

 Rin + RG


Rin
 −
gmRout Vin
Rin + RG
V
 = − Rin gmR
Av = out = 
out
Vin
Vin
Rin + RG
Vout = - VGS ⋅ g m ⋅ RD = - VIN ⋅ 0.68 ⋅ g m ⋅ RD
Vout
− VIN ⋅ 0.68 ⋅ g m ⋅ RD
AV =
VG
=
= − 0.68 ⋅ 0.7 ⋅ 10 −6 Ω −1 ⋅ 8.33 ⋅ 10 6 Ω = - 3.56
VIN
Soluzione
a)
Siccome all’inizio (t=0) il diodo è polarizzato in inversa, possiamo considerare il circuito
equivalente di figura 6 nel quale il diodo è stato sostituito con il suo “Circuito equivalente ai grandi
segnali in Inversa”. Siccome Is=0 e RrÆ∞, il circuito equivalente del diodo ai grandi segnali in
inversa è un circuito aperto.
VR
28
R
VIN(t)
+
iD
fig. 6
VD
-
Applicando KVL alla maglia e, procedendo in senso antiorario, si ottiene:
VR - VIN(t) + VD = 0
da cui risulta che, essendo nulla la corrente nella maglia, la caduta di
tensione sulla resistenza è nulla:
VD = VIN(t)
(1)
Ma il circuito equivalente è valido solo fino a che VD <
VD < 0.6 V, quindi, applicando la
VIN(t) < 0.6 V
Visto che
VIN (t)
Vγ ,
cioè sino a che:
(1), sino a che:
cresce linearmente
(VIN (t)=k t),
si può calcolare l’istante di tempo
t1
in cui
VIN( t1 ) raggiunge il valore di 0.6 V oltre al quale il diodo risulta polarizzato in diretta.
VIN ( t1 )= k t1 =0.6 V da cui:
t1 =
0 .6 ⋅ V
= 0.15 ms
V
4⋅
ms
Quindi nell’intervallo di tempo 0 < t < 0.15 ms:
ID = 0
VD = VIN(t) = kt
Quando 4ms >t > 0.15 ms, il diodo risulta polarizzato in diretta e possiamo allora sostituire al
circuito di figura 6 il seguente circuito di Fig. 7 nel quale il diodo è stato sostituito con il suo
“Circuito equivalente ai grandi segnali in diretta”.
VR
R
VIN(t)
Rf
+
iD
-
fig. 7
VR f
+
-
Vγ = 0.6
VD(t)
29
Applicando KVL alla maglia in senso antiorario otteniamo:
VR - VIN(t) + Vγ + VR f = 0
ID(t) ⋅R - VIN(t) + Vγ + iD(t) ⋅ R f = 0
iD(t) =( VIN (t) - Vγ ) / (R + R f )
V
⋅ t − 0.6V
mA
ms
= 20
iD(t) =( VIN (t) – 0.6 V) / (40 Ω + 160 Ω) = (kt – 0.6 V)/ 200 Ω =
⋅ t - 3mA
200Ω
ms
mA
VD(t) = Vγ + VR f = 0.6 V + iD(t) ⋅ 160 Ω = 0.6 V + ( 20 ⋅ t - 3 mA) ⋅ 160 Ω =
ms
V
0.12 V + 3.2
⋅t
ms
4
30
In particolare:
Per t = t1 = 0.15 ms
mA
iD(t) = 20 ⋅ 0.15ms - 3mA = 0 mA
ms
V
VD(t) = 0.12 V + 3.2 ⋅ 0.15ms = 0.6 V
ms
Per t = t 2 = 4 ms
mA
iD(t) = 20 ⋅ 4ms - 3mA = 77 mA
ms
V
VD(t) = 0.12 V + 3.2 ⋅ 4ms = 12.92 V
ms
Quando 5 ms
e quindi vale :
>t > 4 ms, risulta VIN(t)= 0 per cui il diodo è nuovamente polarizzato in inversa
Nell’intervallo di tempo 4 ms < t < 5 ms:
ID = 0
VD = VIN(t) = 0
31
Fig. 8
14
12
Vd(t) [ V ]
10
8
6
4
2
0
0
1
2
3
t [ms]
4
2
3
t [ms]
4
5
6
90
80
id(t) [ mA ]
70
60
50
40
30
20
10
0
0
Diodo in
interdizione
1
Diodo in
diretta
5
Diodo in
interdizione
6
32
Soluzione
+
Vbar
A
I bar
L
Rbar
E
-
Fig. 9
a) semiconduttore intrinseco
La conducibilità σ del semiconduttore è espressa dalla formula:
σ = ( µn ⋅ n + µp ⋅ p) ⋅ e (1)
Nel caso di semiconduttore “Intrinseco” la concentrazione di elettroni e lacune è uguale alla
concentrazione “Intrinseca” per cui:
p = n = Ni = 1.45 ⋅ 1010 cm −3 a 300 K
Quindi la (1) diventa:
σ = Ni ⋅ ( µn + µp ) ⋅ e = 1.45 ⋅ 10 cm
10
−3
(
cm 2
cm 2
1500
+ 475
Vs
Vs
)
⋅ 1.6 ⋅ 10 −19 C =
cm −1 A ⋅ s
= 4.58 10 −6 Ω −1 ⋅ cm −1
V ⋅s
b) semiconduttore intrinseco
4.58 ⋅ 10 −6
La conducibilità σ è definita dalla seguente relazione:
J = σ E dove J è la densità di corrente ed E è il campo elettrico nel semiconduttore.
La Figura 9 esprime il fatto che la barra di materiale può essere considerata equivalente ad una
resistenza Rbar se, sottoposta alla tensione Vbar ai suoi capi, è percorsa dalla corrente I bar .
Quindi:
Rbar = Vbar / I bar
33
Ma:
Vbar = E L
se supponiamo il campo E costante all’interno del provino ed L la sua lunghezza.
I bar = J A in quanto la corrente è pari al prodotto della densità di corrente J per la sezione A del
provino. Quindi si ottiene:
Rbar = Vbar / I bar =
0.5 ⋅ cm
EL
L
L
=
=ρ =
= 109 k Ω (2)
−6
JA
σA
A 4.58 ⋅ 10 cm −1Ω −1 ⋅ 1 ⋅ cm 2
a) semiconduttore drogato
Calcoliamo le concentrazioni degli elettroni n e delle lacune p.
In un materiale di tipo n la concentrazione delle lacune è approssimativamente uguale alla densità
di atomi donatori per cui:
n ≅ NA = 3 ⋅ 1015 cm −3
2
Applicando la “Legge dell’azione di massa” n p = N i risulta:
p = N i 2 / n = (1.45 ⋅ 1010 cm −3 ) 2 /( 3 ⋅ 1015 cm −3 ) = 48 ⋅ 10 3 cm −3
La conducibilità σ del semiconduttore drogato risulta ancora dalla formula (1):
σ = ( µn ⋅ n + µp ⋅ p) ⋅ e
µn ⋅ n =
µp ⋅ p =
dove:
cm 2
cm −1
⋅ 3 ⋅ 1015 cm −3 = 4500 ⋅ 1015
Vs
Vs
2
−1
cm
3
−3
3 cm
475
⋅ 48 ⋅ 10 cm = 22800 ⋅ 10
Vs
Vs
1500
Il contributo di µp ⋅ p
σ ≅ µn ⋅ n ⋅ e =
è molto inferiore a µn ⋅ n per cui lo trascuriamo. Quindi si ottiene:
4500 ⋅ 10
15
cm −1
cm −1 As
−19
⋅1.6 ⋅ 10 C = 0.72
= 0.72 cm −1Ω −1
Vs
Vs
b) semiconduttore drogato
Applicando la (2) si ottiene:
Rbar = Vbar / I bar =
0.5 ⋅ cm
EL
L
L
=
=ρ =
= 0.7 Ω
JA
σA
A 0.72 ⋅ cm −1Ω −1 ⋅ 1 ⋅ cm 2
34
V4
V2
i2
i3
i1
V1
V6
i6
i4
V3
V5
i7
V7
i5
fig. 10
i8
V8
Soluzione
a)
La grandezza incognita
V1
=
E1
V1
è:
=5V
Il circuito di cui sopra risulta equivalente al seguente circuito in cui è stata sostituita, alle resistenze
R6, R7 ed R8 in serie (i6= i7= i8 = i678), la sua resistenza equivalente R678:
R678 = R6 + R7 + R8 = 1 kΩ + 3 kΩ +2 kΩ = 6 kΩ
V2
R2
V1
i2
+
E1
-
V4
R4
V3 i3
i1
R3
i4
fig. 11
V5 i5
i6= i7= i8
R5
R678
Sostituendo alle resistenze R5 e R678 in parallelo (V5= V678= V5678) la resistenza equivalente
R5678 si ottiene il seguente circuito dove:
R5678 = R5 ⋅ R678 / (R5 + R678) = 6 kΩ ⋅ 6 kΩ / (6 kΩ + 6 kΩ ) = 3 kΩ
V2
R2
V1
i2
+
E1
-
i1
V4
R4
V3 i3
R3
i4
fig. 12
R5678
V5=V678=V5678
35
Il circuito di cui sopra risulta equivalente al seguente circuito in cui è stata sostituita, alle resistenze
R4, ed R5678 in serie(i4= i5678= i45678), la sua resistenza equivalente R45678:
R45678 = R4 + R5678 = 3 kΩ + 3 kΩ = 6 kΩ
V2
R2
fig. 13
V1
i2
+
E1
V3 i3
i1
-
R3
R45678
i4= i5678= i45678
Sostituendo alle resistenze R3 e R45678 in parallelo (V3=V45678=V345678) la resistenza equivalente
R345678 si ottiene il seguente circuito dove:
R345678 = R3 ⋅ R45678 / (R3 + R45678) = 6 kΩ ⋅ 6 kΩ / (6 kΩ + 6 kΩ ) = 3 kΩ
V2
R2
V1
i2
+
E1
i1
-
fig. 14
R345678
V3=V45678=V345678
Il circuito di cui sopra risulta equivalente al seguente circuito in cui è stata sostituita, alle resistenze
R2, ed R345678 in serie (i2= i345678= i2345678), la sua resistenza equivalente R2345678:
R2345678 = R2 + R345678 = 2 kΩ + 3 kΩ = 5 kΩ
Nodo 1
fig. 15
V1
+
E1
-
i1
R2345678
i2= i345678= i2345678
Applicando KCL al nodo 1 risulta i1 - i2 = 0 da cui
i1 = i2.
i1 = i2 = E1/R2345678 = 5V / 5 kΩ = 5 V / (5 ⋅ 103 Ω)
= 1 ⋅ 10−3 A = 1 mA
Utilizzando a ritroso i circuiti delle figure 14, 13, 12, 11, 10, si possono ricavare tutte le altre
variabili incognite come segue:
36
V2 = R2 i2 = 2kΩ ⋅ 1 A = 2 ⋅ 103 Ω ⋅ 1 ⋅ 10−3 A = 2 V (vedi fig. 14)
V3 = R2345678 ⋅ i2 = 5 kΩ ⋅ 1 mA = 5 V (vedi fig. 14)
i3 = V3 / R3 = 5 V / 6 kΩ = 5 V / (6 ⋅ 103 Ω) = 0.83 ⋅10−3 A = 0.83 mA (vedi fig. 13)
i4 = V3 / R45678 = 5 V / 6 kΩ = 5 V / (6 ⋅ 103 Ω) = 0.83 ⋅ 10−3 A = 0.83 mA (vedi fig. 13)
V4 = R4 i4 = 3 kΩ ⋅ 0.83 mA = 3 ⋅ 103 Ω ⋅ 0.83 ⋅ 10−3 A = 2.5 V (vedi fig. 12)
V5 = R5678 ⋅ i4 = 3 kΩ ⋅ 0.83 mA = 2.5 V (vedi fig. 12)
i5 = V5 / R5 = 2.5 V / 6 kΩ = 0.42 mA (vedi fig. 11)
i6 = i7 = i8 = V5 / R678 = 2.5 V / 6 kΩ = 0.42 mA (vedi fig. 11)
V6 = R6 i6 = 1 kΩ ⋅ 0.42 mA = 0.42 V (vedi fig. 10)
V7 = R7 i7 = 3 kΩ ⋅ 0.42 mA = 1.26 V (vedi fig. 10)
V8 = R8 i8 = 2 kΩ ⋅ 0.42 mA = 0.84 V (vedi fig. 10)
37
Corso di Tecnologie Elettroniche 1
Prova scritta del 17 dicembre 2001
Compito A
Soluzione
Il circuito di cui sopra risulta equivalente al seguente circuito :
R
+
E(t)
-
C
Vc(t)
dove:
‰
R è la resistenza equivalente alla serie delle due resistenze R1 ed R2 per cui:
R = R1 + R2 = 10 kΩ + 20 kΩ = 30 kΩ
‰
C è la capacità equivalente al parallelo delle due capacità C1 e C2 per cui:
C = C1 + C2 = 2 nF + 4 nF = 6 nF
τ = RC = 30 kΩ ⋅ 6 nF = 30 ⋅ 103 Ω ⋅ 6 ⋅ 10−9 F = 180 ⋅ 10 −6
= 180 ⋅ 10 −6
Cs
= 180 µs
C
Ω ⋅ F= 180 10 −6
V C
=
A V
38
Vc(t) = E (1 − e − t / RC ) = K (1 − e − t / 180 µs )
K
Vc(t)
K ⋅ 0.99
K ⋅ 0.63
τ = 180 µs
5τ = 900 µs
t
All’inizio (t = 0) il condensatore è scarico (Q=0) per cui risulta (dalla Vc = CQ) che Vc=0.
Solo dopo un tempo molto lungo (t tendente all’infinito) il condensatore risulta completamente
carico al valore di tensione finale K. In tale situazione la corrente nel circuito è nulla.
NOTA:
‰
‰
All’ istante t = τ la tensione è pari al 63% del valore finale. Questo punto si ottiene anche la
tangente alla curva della tensione Vc(t) all’istante t = 0.
All’istante t = 5τ la tensione è già superiore al 99% del valore finale.
39
fig. 1
Soluzione
a)
La grandezza incognita V1 è :
V1 = E1 = 4 V
Il circuito di cui sopra risulta equivalente al seguente circuito in cui è stata sostituita, alle due
resistenze R3 ed R4 in parallelo, la sua resistenza equivalente R34:
R34 = R3 ⋅ R4 /(R3 + R4) = 1kΩ ⋅ 1kΩ /(1kΩ + 1kΩ) = 0.5 kΩ
V2
R2
Nodo 1
V1
E1
-
fig. 2
i2
+
R34
i1
V3 = V4
Nel circuito equivalente di fig. 2 :
V3 = V4 in quanto le due resistenze R3 ed R4 sono in parallelo (o applicando KVL alla maglia R3
– R4). Inoltre : i2 – i1 = 0 per l’applicazione della KCL al nodo 1, da cui risulta i1 = i2
Sostituendo alle resistenze in serie R2 e R34 la resistenza equivalente R234 si ottiene il seguente
circuito dove:
R234 = R2 + R34 = 1kΩ + 0.5kΩ = 1.5 kΩ
R234
V1
fig. 3
+
E1
-
i1
40
Utilizzando a ritroso i circuiti equivalenti delle figure 3,2,1, si possono ricavare tutte le altre variabili
incognite come segue:
i1 = E1/R234 = 4V / 1.5 kΩ = 4 V / (1.5 ⋅ 103 Ω) = 2.66 ⋅10−3 A = 2.66 mA = i2 (vedi fig. 3)
V2 = R2 i2 = 1kΩ ⋅ 2.66 A = 1 ⋅ 103 Ω ⋅ 2.66 x 10−3 A = 2.66 V (vedi fig. 2)
V3 = V4 = R34 ⋅ i2 = 0.5kΩ ⋅ 2.66 A = 1.33 V (vedi fig. 2)
i3 = V3 / R3 = 1.33 V / 1 kΩ = 1.33 V / (1 ⋅ 103 Ω) = 1.33 ⋅ 10−3 A = 1.33 mA (vedi fig. 1)
i4 = V4 / R4 = 1.33V / 1 kΩ = 1.33 V / (1 ⋅ 103 Ω) = 1.33 ⋅ 10−3 A = 1.33 mA (vedi fig. 1)
b)
Il circuito equivalente di Thevenin vista ai nodi A e B risulta il seguente:
Rth
A
fig. 4
+
Vth
-
B
Dove Vth = VABO che è la tensione di circuito aperto (Open circuit) che risulta pari a
Quindi:
Vth = V3 = 1.33 V
V3
e
V4.
Rth = VABO/IABS dove IABS è la corrente di corto circuito (Short circuit) cioè quella che si otterrebbe ai
morsetti A e B cortocircuitandoli con il verso evidenziato in Fig.5. Cortocirquitando i morsetti A e B
si ottiene il seguente circuito:
R2
+
E1
A
Corto Circuito
R3
R4
IABS
-
fig. 5
B
Le due resistenze R3 e R4 sono in parallelo ad una resistenza nulla (cortocircuito) per cui la
resistenza è 0. R3 e R4 è come se non ci fossero in quanto tutta la corrente passa dal cortocircuito.
Quindi:
IABS = E1 / R2
=
4V / 1 kΩ = 4 V / (1 ⋅ 103 Ω) = 4 ⋅ 10−3 A = 4 mA
E quindi :
Rth = VABO / IABS = 1.33 V / 4 ⋅10−3 A = 0.33 ⋅ 103 Ω = 0.33 kΩ
41
c) Calcolo della potenza dissipata per effetto Joule nei resistori del circuito
La potenza W dissipata in un resistore R attraversato dalla corrente I è pari a:
W = RI 2
Quindi, se indichiamo con W2 la potenza dissipata da R2, con W3 quella dissipata da R3 e W4
quella dissipata da R4, la potenza totale Wtot dissipata nel circuito risulta:
Wtot = W2 + W3 + W4 = R 2 ⋅ i 2 2 + R3 ⋅ i3 2 + R 4 ⋅ i 4 2 = 1 ⋅ 103 Ω ⋅ (2.66 ⋅ 10 −3 A) 2 + 1 ⋅ 103 Ω ⋅
(1.33 ⋅ 10 −3 A) 2 +1 ⋅ 103 Ω ⋅ (1.33 ⋅ 10 −3 A) 2 =
V
2.66 ⋅ 10−3
A2 +
A
V
1.33 ⋅ 10−3
A2 +
A
V
1.33 ⋅ 10−3
A2 = 5.32 mW
A
42
Soluzione
a) Calcolo della conducibilità σ del semiconduttore drogato
Ibar
A
+
Vbar
L
E
-
Fig. 6
Rbar
Calcoliamo le concentrazioni rispettivamente degli elettroni N e delle lacune P.
In un materiale di tipo n la concentrazione di elettroni liberi è approssimativamente uguale alla
densità di atomi donatori per cui:
n ≅ ND = 5 x 1016 cm −3
2
Applicando la “Legge dell’azione di massa” np = Ni risulta:
p=Ni2/ N = (1.45 ⋅ 1010 cm −3 ) 2 /( 5 ⋅ 1016 cm −3 ) = 4.2 ⋅ 10 3 cm −3
La conducibilità σ del semiconduttore drogato risulta dalla formula:
σ = ( µn x N + µp x P) x e
da cui, trascurando il contributo di µp x P che è molto inferiore a µn x
N, si ottiene:
σ ≅ µn ⋅ n ⋅ e =
12
1500
cm 2
⋅ 5 ⋅ 1016 cm −3 ⋅ 1.6 ⋅ 10 −19 C =
Vs
cm −1 As
= 12 cm −1Ω −1
Vs
43
b)
La conducibilità σ è definita dalla seguente relazione:
J = σ E dove J è la densità di corrente ed E è il campo elettrico nel semiconduttore.
La Figura 6 esprime il fatto che la barra di materiale può essere considerata equivalente ad
una resistenza
Rbar se, sottoposta alla stessa tensione Vbar ai suoi capi, assorbe una stessa
corrente Ibar. Quindi:
Rbar = Vbar / Ibar
Ma:
Vbar = E L
se supponiamo il campo E costante all’interno del provino ed L la sua lunghezza.
Ibar = J A in quanto la corrente pari al prodotto della densità di corrente
provino. Quindi si ottiene:
Rbar = Vbar / Ibar =
J per la sezione A del
3mm
3mm ⋅ 10mm ⋅ Ω
EL
L
=
=
=
= 0.025 Ω
−1 −1
2
JA
σA 12cm Ω 100mm
12 ⋅ 100mm 2
44
Vd
fig. 7
Soluzione
a)
Supponiamo che all’inizio (t=0) il diodo sia polarizzato in inversa. Possiamo considerare circuito
equivalente di figura 8 nel quale il diodo è stato sostituito a sua volta con il suo “Circuito
Equivalente ai grandi Segnali in Inversa” (in questo caso un circuito aperto).
Siccome Is=0 e
aperto.
Vin(t)
+
RrÆ∞, il circuito equivalente del diodo ai grandi segnali in inversa è un circuito
VR1
Vd
R1
id
R2
fig. 8
VR2
+
-
-
Vout(t)
VR
Applicando KVL alla maglia e procedendo in senso antiorario si ottiene:
VR + VR2 + Vd + VR1 - Vin(t) = 0
da cui risulta, considerando che, essendo nulla la corrente
nella maglia, le cadute di tensione sulle resistenze sono nulle:
Vd = Vin(t) - VR = Vin(t) – 1.4 V
(1)
Ma il circuito equivalente è valido solo fino a che :Vd < Vv.
Vd < 0.6 V. quindi, applicando la (1) sino a che:
Vin(t) – 1.4 V < 0.6 V cioè:Vin(t) < 2 V
cioè sino a che:
45
Visto che
Vin(t)
cresce linearmente
(Vin(t)=k t),
si può calcolare l’istante di tempo
t1
in cui
Vin(t1) raggiunge il valore limite di 0.2 V oltre al quale il diodo risulta polarizzato in diretta:
Vin(t1)= k t1 = 2 V da cui:
t1 = 2 V / k = 2 V / (2 V/ms) = 1 ms
Nell’intervallo di tempo 0 < t <
t1,
la
Vout(t) risulta pari a VR, in quanto la caduta su R2 è
nulla, per cui:
Vout(t) = VR = 1.4 V
b)
Quando t > t1,
il diodo risulta polarizzato in diretta e possiamo allora sostituire al circuito di figura
7 il seguente circuito (vedi Fig. 9) nel quale il diodo è stato sostituito con il suo “Circuito
equivalente ai grandi segnali in diretta”.
Siccome Rf = 0, il circuito equivalente del diodo ai grandi segnali in diretta si riduce ad un
generatore di tensione con una tensione pari a Vδ = 0.6 V.
VR1
Vδ=0.6V
-
+
R1
Vin(t)
+
id
R2
+
-
fig. 9
VR2
-
VR
Vout(t)
Applicando KVL alla maglia in senso antiorario otteniamo:
VR + VR2 + Vd + VR1 - Vin(t) = 0
VR + idxR2 + Vd + idxR1- Vin(t) = 0
Id(t) =( Vin(t) - Vd -VR) / (R1+ R2)
Id(t) =( Vin(t) – 2 V) / 300 Ω da cui risulta:
Vin(t ) − 2V
⋅ 100Ω = 0.74 V + 0.33 x Vin(t) =
300Ω
V
0.74 V + 0.33 x k t = 0.74 V + 0.33 x 2
⋅t =
ms
Vout(t) = VR + id x R2 = 1.4 V +
In particolare:
V
⋅1 ⋅ ms = 1.4 V
ms
V
Æ Vout(t) = 0.74 V + 0.33 ⋅ 2
⋅ 4 ⋅ ms = 3.38 V
ms
Per t = t1 = 1 ms Æ Vout(t) = 0.74 V + 0.33 ⋅ 2
Per t = 4 ms
46
Fig. 10 Andamento tensioni di Input/Output
9
8
Tensioni (v)
7
6
5
Vin
Vout
4
3
2
1
0
0
1
2
3
t (ms)
Diodo in
Interdizione
Diodo in
diretta
4
47
Fig. 11
Soluzione
a)
Se trascuriamo, come suggerito nel testo,VG ed RG (che rappresentano il circuito equivalente del
generatore di ingresso per piccoli segnali), risulta che nel punto di lavoro (quindi in corrente
continua) il sistema costituito da Vcc, R1 e R2, è un partitore di tensione (IG = 0) per cui:
V1 = Vcc ⋅ R1/(R1+R2) = 5 V ⋅ 2 kΩ / (2 kΩ +3 kΩ) = 2V
V2 = Vcc – V1 = 5 V – 2 V = 3 V
I1 = I2 = Vcc / (R1 + R2) = 5 V / (2 kΩ +3 kΩ) = 1mA
Per determinare tensioni e correnti nel punto di lavoro
In questo modo viene fissata la curva con VGS = 2V nel grafico di Fig. 11
V0GS = V1 = 2V
La retta di carico si può tracciare dopo aver determinato due sui punti, ad esempio :
•
•
per IDS = 0 VDS = Vcc = 5V .
per VDS = 0 IDS = Vcc/ RD = 5V / 2 kΩ = 2.5 mA .
48
Il punto di lavoro che si determina, come illustrato in fig. 12, dall’intersezione della retta di carico (in
rosso), con la curva valida per VGS = 2 V, risulta il seguente:
VDS 0= 3 V
ID 0= 1 mA
b)
Fig. 12
IDQ
VDSQ
c)
r =
ds
gm =
1 + λ ⋅ VDSQ
λ ⋅ IDQ
2⋅ k
W
IDQ
L
1 + 0.01 ⋅ V −1 ⋅ 3 ⋅ V
= 103 KΩ
0.01 ⋅ V −1 ⋅ 1 ⋅ 10 −3 A
1
A
= 2 ⋅ 10-3Ω-1
2 ⋅ 10 −3 2 ⋅ 1 ⋅ 10 −3 A =
0.5kΩ
V
=
=
49
d)
Disegniamo il circuito equivalente ai piccoli segnali del circuito di figura 11 passivando constanti (in
particolare il generatore Vcc) e sostituendo al MOSFET il suo circuito equivalente ai piccoli segnali.
R2
RG
VG
+
RD
Gate
Drain
R1 VGs gm
r
Vout
ds
Fig. 13
Source
Il circuito di figura 13 può essere ridisegnato evidenziando meglio l’effetto del cortocircuito ottenuto
dalla passivazione di Vcc.
RG
VG
+
VGs
R1
-
Drain
Gate
gm
R2
R
ds
RD
Vout
Fig. 14
Source
In questo modo si evidenziano meglio il parallelo di R1 II R2 ed rds II RD che vengono sostituiti dalle
loro resistenze equivalenti:
RG
VG
Gate
+
-
Vgs gm
Drain
Rout
Rin
Vout
Source
Rin = R1 ⋅ R2 / (R1 + R2) = 2 kΩ ⋅ 3 kΩ / (2 kΩ + 3 kΩ) = 1.2 kΩ
Rout = rds ⋅ RD / (rds + RD) = 103 kΩ ⋅ 2 kΩ / (103 kΩ + 2 kΩ) = 1.96 kΩ
Ne segue quindi:
VGS = VG ⋅ Rin /( Rin + RG) = VG ⋅ 1.2 kΩ / (1.2 kΩ + 0.1 kΩ) = VG ⋅ 0.92 da cui:
VG = Vgs ⋅ 1.086
Fig. 15
50
Vout = −Vgs gmRout = −VG
Rin
gmRout
Rin + RG


Rin
Vout =  −
gmRout Vin
 Rin + RG



Rin
 −
gmRout Vin
Rin + RG
V
 = − Rin gmR
Av = out = 
out
Vin
Vin
Rin + RG
Vout
=
Vgs ⋅ gm ⋅ Rout = Vgs ⋅ gm ⋅ Rout = Vgs
Av = Vout/VG =
Vgs ⋅ 3.92
= 3.60
Vgs ⋅ 1.086
1
⋅ 1.96 kΩm = Vgs ⋅ 3.92 V
0.5kΩ
51
Corso di Tecnologie Elettroniche 1
Prova scritta del 17 dicembre 2001
Compito B
Soluzione
Il circuito di cui sopra risulta equivalente al seguente circuito:
R
+
E(t)
-
C
V (t )
c
dove:
‰
R è la resistenza equivalente al parallelo delle due resistenze
R = R1 ⋅ R2 /( R1 +
‰
ed
R2 :
R2 )= 1 kΩ ⋅ 3 kΩ /(1 kΩ + 3 kΩ) = 0.75 kΩ
C è la capacità equivalente alla serie delle due capacità
C=
R1
C1 e C 2 :
C1 ⋅ C 2 /( C1 + C 2 ) = 8 nF ⋅ 16 nF/(8 nF + 16 nF) = 5.33 nF
τ = RC = 0.75 kΩ ⋅ 5.33 nF = 0.75 ⋅ 103 Ω ⋅ 5.33 ⋅ 10−9 F = 4 ⋅ 10 −6 Ω ⋅ F= 4 ⋅
= 4 ⋅ 10 −6 ⋅
Cs
= 4 µs
C
10 −6 ⋅
V C
=
A V
52
Vc (t ) = E (1 − e − t / RC ) = K (1 − e − t / 4 µs )
V c (t )
K
K ⋅ 0.99
K ⋅ 0.63
t=
τ = 4 µs
t = 5τ = 20 µs
t
All’inizio (t = 0) il condensatore è scarico per cui Vc (0) =0.
Solo dopo un tempo molto lungo (t tendente all’infinito) il condensatore risulta completamente
carico al valore di tensione finale K. In tale situazione la corrente nel circuito è nulla.
Nota
‰
‰
All’istante t = τ la tensione è pari al 63% del valore finale. Questo punto si ottiene anche
tracciando la tangente alla curva della tensione Vc (t ) all’istante t = 0.
All’istante t = 5τ la tensione è già superiore al 99% del valore finale.
53
fig. 1
Soluzione
a)
La grandezza incognita
V1
=
E1
V1
è:
=8V
Il circuito di cui sopra risulta equivalente al seguente circuito in cui è stata sostituita, alle due
resistenze R3 ed R4 in parallelo, la sua resistenza equivalente R34:
R34 = R3 ⋅ R4 /(R3 + R4) = 2kΩ ⋅ 2kΩ /(2kΩ + 2kΩ) = 1 kΩ
V2
R2
Nodo 1
V1
E1
-
fig. 2
i2
+
R34
i1
V3 = V4
Nel circuito equivalente di fig. 2 :
V3 = V4 in quanto le due resistenze R3 ed R4 sono in parallelo (o applicando KVL alla maglia R3
– R4). Inoltre i2 – i1 = 0 per l’applicazione della KCL al nodo 1, da cui risulta i1 = i2
Sostituendo alle resistenze in serie R2 e R34 la resistenza equivalente R234 si ottiene il seguente
circuito dove:
R234 = R2 + R34 = 2kΩ + 1kΩ = 3 kΩ
R234
V1
fig. 3
+
E1
-
i1
54
Utilizzando a ritroso i circuiti equivalenti delle figure 3,2,1, si possono ricavare tutte le altre variabili
incognite come segue:
i1 = E1/R234 = 8V / 3 kΩ = 8 V / (3 ⋅ 103 Ω) = 2.66 ⋅10−3 A = 2.66 mA = i2 (vedi fig. 3)
V2 = R2 i2 = 2kΩ ⋅ 2.66 A = 2 ⋅ 103 Ω ⋅ 2.66 ⋅ 10−3 A = 5.32 V (vedi fig. 2)
V3 = V4 = R34 ⋅ i2 = 1kΩ ⋅ 2.66 mA = 2.66 V (vedi fig. 2)
i3 = V3 / R3 = 2.66 V / 2 kΩ = 1.33 V / (1 ⋅ 103 Ω) = 1.33 ⋅10−3 A = 1.33 mA (vedi fig. 1)
i4 = V4 / R4 = 2.66 V / 2 kΩ = 1.33 V / (1 ⋅ 103 Ω) = 1.33 ⋅ 10−3 A = 1.33 mA (vedi fig. 1)
b)
Il circuito equivalente di Norton visto ai nodi A e B risulta il seguente:
A
+
In
fig. 4
Rn
-
B
Calcoliamo VABO che è tensione di circuito aperto (Open circuit) che risulta pari a
Quindi:
VABO = V3 = 2.66 V
V3
e
V4.
Calcoliamo IABS che è la corrente di corto circuito (Short circuit) cioè quella che si otterrebbe ai
morsetti A e B cortocircuitandoli (il verso positivo di IABS è quello evidenziato in Fig. 5).
Cortocircuitando i morsetti A e B si ottiene il seguente circuito:
R2
+
E1
A
R3
Corto Circuito
R4
IABS
-
fig. 5
B
Le due resistenze R3 e R4 sono in parallelo ad una resistenza nulla (corto circuito) per cui la
resistenza equivalente è nulla. Quindi R3 e R4 è come se non ci fossero in quanto tutta la corrente
passa nel corto circuito. Quindi:
IABS = E1 / R2
=
8V / 2 kΩ = 4 V / (1 ⋅ 103 Ω) = 4 ⋅ 10−3 A = 4 mA
Gli elementi del circuito equivalente di Norton di Fig. 4 si ottengono come segue:
In = IABS = 4 mA
Rn = VABO / IABS = 2.66 V / 4 ⋅ 10−3 A = 0.66 ⋅ 103 Ω = 0.66 kΩ
55
c) Calcolo della potenza dissipata per effetto Joule nel circuito
La potenza W dissipata in un resistore R attraversato dalla corrente I è pari a:
W = RI 2
Quindi, se indichiamo con
W2
la potenza dissipata da
R2 ,
con
W3 quella
dissipata da
W4 quella dissipata da R4 , la potenza totale Wtot dissipata nel circuito risulta:
Wtot = W2 + W3 + W4 = R2 ⋅ i2 2 + R3 ⋅ i3 2 + R4 ⋅ i4 2 =
2 ⋅ 103 Ω ⋅ (2.66 ⋅ 10 −3 A) 2 + 2 ⋅ 103 Ω ⋅ (1.33 ⋅ 10 −3 A) 2 + 2 ⋅ 103 Ω ⋅ (1.33 ⋅ 10 −3 A) 2 =
14.15 ⋅ 10−3
V
V
V
A2 + 3.54 ⋅ 10−3
A2 + 3.54 ⋅ 10−3
A2 = 21.23 mW
A
A
A
R3 e
56
Soluzione
a)
Vbar
A
I bar
+
L
E
-
Rbar
Fig. 6
Calcoliamo le concentrazioni degli elettroni n e delle lacune p.
In un materiale di tipo p la concentrazione delle lacune è approssimativamente uguale alla densità
di atomi donatori per cui:
p ≅ NA = 5 ⋅ 1016 cm −3
2
Applicando la “Legge dell’azione di massa” n p = N i risulta:
n = N i 2 / p = (1.45 ⋅ 1010 cm −3 ) 2 /( 5 ⋅ 1016 cm −3 ) = 4.2 ⋅ 10 3 cm −3
La conducibilità σ del semiconduttore drogato risulta dalla formula:
σ = ( µn ⋅ n + µp ⋅ p) ⋅ e
µn ⋅ n =
µp ⋅ p =
−1
cm 2
3
−3
3 cm
1500
⋅ 4.2 ⋅ 10 cm = 6300 ⋅10
Vs
Vs
2
−1
cm
cm
475
⋅ 5 ⋅ 1016 cm −3 = 2375 ⋅ 1016
Vs
Vs
Il contributo di µn ⋅ n è molto inferiore a µp ⋅ p per cui lo trascuriamo. Quindi si ottiene:
σ ≅ µp ⋅ p ⋅ e =
475
cm 2
cm −1 As
⋅ 5 ⋅ 1016 cm −3 ⋅ 1.6 ⋅ 10 −19 C = 3.8
= 3.8 cm −1Ω −1
Vs
Vs
57
b)
La conducibilità σ è definita dalla seguente relazione:
J = σ E dove J è la densità di corrente ed E è il campo elettrico nel semiconduttore.
La Figura 6 esprime il fatto che la barra di materiale può essere considerata equivalente ad
una resistenza Rbar se, sottoposta alla tensione Vbar ai suoi capi, è percorsa dalla corrente
I bar .
Quindi:
Rbar = Vbar / I bar
Ma:
Vbar = E L
se supponiamo il campo E costante all’interno del provino ed L la sua lunghezza.
I bar = J A in quanto la corrente è pari al prodotto della densità di corrente J per la sezione A
del provino. Quindi si ottiene:
Rbar = Vbar / I bar =
3mm
3mm ⋅ 10mm ⋅ Ω
EL
L
L
=
=ρ =
=
= 0.079 Ω
−1 −1
2
JA
σA
A 3.8cm Ω 100mm
3.8 ⋅ 100mm 2
58
fig. 7
Soluzione
a)
Supponiamo che all’inizio (t=0) il diodo sia polarizzato in inversa. Possiamo considerare il circuito
equivalente di figura 8 nel quale il diodo è stato sostituito a sua volta con il suo “Circuito
equivalente ai grandi segnali in Inversa”. Siccome Is=0 e RrÆ∞, il circuito equivalente del diodo ai
grandi segnali in inversa è un circuito aperto.
Vin(t)
+
VR1
Vd
R1
id
R2
+
-
fig. 8
VR2
-
VR
Vout(t)
Applicando KVL alla maglia e, procedendo in senso antiorario, si ottiene:
VR + VR2 + Vd + VR1 - Vin(t) = 0 da cui risulta che, essendo nulla la corrente nella maglia, le
cadute di tensione sulle resistenze sono nulle:
Vd = Vin(t) - VR = Vin(t) – 2.4 V
(1)
Ma il circuito equivalente è valido solo fino a che Vd < Vγ, cioè sino a che:
Vd < 0.6 V, quindi, applicando la (1), sino a che:
Vin(t) – 2.4 V < 0.6 V cioè:
Vin(t) < 3 V
59
Visto che
Vin(t)
cresce linearmente
(Vin(t)=k t),
si può calcolare l’istante di tempo
t1
in cui
Vin( t1 ) raggiunge il valore di 3 V oltre al quale il diodo risulta polarizzato in diretta.
Vin( t1 )= k t1 = 3 V da cui:
t1 = 3 V / k = 3 V / (3 V/ms) = 1 ms
Nell’intervallo di tempo 0 < t <
t1 ,
Vout(t) risulta pari a VR, in quanto la caduta su R2
la
è nulla,
per cui:
Vout(t) = VR = 2.4 V
b)
Quando t > t1 , il diodo risulta polarizzato in diretta e possiamo allora sostituire al circuito di figura
7 il seguente circuito di Fig. 9 nel quale il diodo è stato sostituito con il suo “Circuito equivalente ai
grandi segnali in diretta”.
Siccome R f = 0, il circuito equivalente del diodo ai grandi segnali in diretta si riduce ad un
generatore di tensione con una tensione pari a
VR1
Vin(t)
+
= 0.6 V.
Vγ = 0.6
-
+
R1
Vγ
id
-
R2
fig. 9
VR 2
+
-
VR
Vout(t)
Applicando KVL alla maglia in senso antiorario otteniamo:
VR + VR 2 + Vd + VR1 - Vin(t) = 0
VR + id⋅ R2 + Vd + id⋅ R1 - Vin(t) = 0
id(t) =( Vin(t) - Vd -VR) / ( R1 + R2 )
id(t) =( Vin(t) – 3 V) / 300 Ω da cui risulta:
Vin(t ) − 3V
⋅ 100Ω = 0.9 V + 0.5 ⋅ Vin(t) =
200Ω
V
V
⋅ t = 0.9 V + 1.5 ⋅
⋅t
0.9 V + 0.5 ⋅ k t = 0.9 V + 0.5 ⋅ 3
ms
ms
Vout(t) = VR + id(t) ⋅ R2 = 2.4 V +
In particolare:
V
⋅ 1 ⋅ ms = 2.4 V
ms
V
Per t = t 2 = 4 ms, Vout( t 2 ) = 0.9 V + 1.5
⋅ 4 ⋅ ms = 6.9 V
ms
Per t = t1 = 1 ms, Vout( t1 ) = 0.9 V + 1.5
60
Fig. 10
14
Vin(t), Vout(t) [ V ]
12
10
Vin
Vout
8
6
4
2
0
0
1
2
t [ms]
3
4
0
1
2
3
4
1
0.5
Vd(t) [ V ]
0
-0.5
-1
-1.5
-2
-2.5
-3
t [ms]
50
45
id(t) [ mA ]
40
35
30
25
20
15
10
5
0
0
1
Diodo in
interdizione
2
t [ms]
Diodo in
diretta
3
4
61
fig. 11
Soluzione
a)
Se trascuriamo, come suggerito nel testo,VG ed RG (che rappresentano il circuito equivalente del
generatore di ingresso per piccoli segnali), risulta che, nel punto di lavoro (quindi in corrente
continua), il sistema costituito da Vcc, R1 e R2, è un partitore di tensione ( I G = 0) per cui:
V1 = Vcc ⋅ R1 /( R1 + R2 ) = 4 V ⋅ 1 kΩ / (1 kΩ +1 kΩ) = 2V
V2 = Vcc – V1 = 4 V – 2 V = 2 V
I 1 = I 2 = Vcc / ( R1 + R2 ) = 4 V / (1 kΩ +1 kΩ) = 2mA
Per determinare tensioni e correnti nel punto di lavoro:
VGS0 = V1 = 2V (Nota: La resistenza fra Source e massa è nulla)
In questo modo viene fissata la curva con VGS = 2V nel grafico di figura 12.
La retta di carico si può tracciare dopo aver determinato due suoi punti, ad esempio:
•
per I DS = 0 VDS = Vcc = 4V
•
per VDS = 0 I DS = Vcc/ RD = 4V / 2 kΩ = 2 mA
62
Il punto di lavoro si determina, come illustrato in Fig. 12, dall’intersezione della retta di carico (in
0
= 2 V:
rosso), con la curva con per VGS
0
VDS
=2V
I D0 = 1 mA
b)
Fig. 12
I D0
V DS0
c)
rds =
gm =
0
1 + λ ⋅ VDS
λ ⋅ I D0
2⋅ k
W 0
ID
L
=
=
1 + 0.01 ⋅ V −1 ⋅ 2 ⋅ V
= 102 KΩ
0.01 ⋅ V −1 ⋅ 1 ⋅ 10 −3 A
2 ⋅ 10 −3
1
A
⋅ 1 ⋅ 10 −3 A =
= 2 ⋅ 10 −3 Ω −1
2
0.5kΩ
V
63
d)
Disegniamo il circuito equivalente ai piccoli segnali del circuito di figura 11 passivando i generatori
di tensione costante (in particolare il generatore Vcc) e sostituendo al MOSFET il suo circuito
equivalente ai piccoli segnali.
RG
VG
+
R2
RD
Gate
R1
VGS g m
Drain
rds
Fig. 13
Vout
Source
Il circuito di figura 13 può essere ridisegnato evidenziando meglio l’effetto del cortocircuito ottenuto
dalla passivazione di Vcc.
Gate
VG
+
R1
-
VGS g m
R2
rds
RD
Fig. 14
Vout
Source
In questo modo si evidenziano meglio il parallelo di R1 ed
dalle loro resistenze equivalenti:
RG
VG
+
Gate
Rin
VGS g m
R2
ed
rds e RD
che vengono sostituiti
Drain
Rout
Vout
Source
Rin = R1 ⋅ R2 / ( R1 + R2 ) = 1 kΩ ⋅ 1 kΩ / (1 kΩ + 1 kΩ) = 0.5 kΩ
Rout = rds ⋅ RD / ( rds + RD ) = 102 kΩ ⋅ 2 kΩ / (102 kΩ + 2 kΩ) = 1.96 kΩ
Ne segue quindi:
VGS = VG ⋅ Rin /( Rin + RG ) = VG ⋅ 0.5 kΩ / (0.5 kΩ + 0.1 kΩ) = VG ⋅ 0.83
VG = VGS ⋅ 1.2
da cui:
Fig. 15
64
Vout = −Vgs gmRout = −VG
Rin
gmRout
Rin + RG


Rin
Vout =  −
gmRout Vin
 Rin + RG



Rin
 −
gmRout Vin
Rin + RG
V
 = − Rin gmR
Av = out = 
out
Vin
Vin
Rin + RG
Vout = - VGS ⋅ g m ⋅ Rout = - VG ⋅ 0.83 ⋅ g m ⋅ Rout
Vout
− VG ⋅ 0.83 ⋅ g m ⋅ Rout
AV =
VG
=
VG
= − 0.83 ⋅ 2 ⋅ 10 −3 Ω −1 ⋅ 1.96 ⋅ 10 3 Ω = - 3.25
65
Corso di Tecnologie Elettroniche 1
Prova scritta del 09 gennaio 2003
Compito A
Esercizio n. 1 [punti 4/30]
Sia dato il circuito RC illustrato in Figura. Si chiede di calcolarne la costante di tempo τ (nota: si
proceda all’inizio alla riduzione serie/parallelo dei resistori e dei condensatori).
Domanda facoltativa: si chiede di indicare l’espressione matematica della tensione Vc(t) per t ≥ 0
nel caso in cui il generatore
Vin(t) = 1 (t) 3 [V] (si suppongano i condensatori scarichi per t ≤ 0
s).
R1 = 10 kΩ, R2 = 20 kΩ, C1 = 2 nF, C2 = 4 nF (Nota: k = 103, n = 10-9).
Esercizio n. 2 [punti 4/30]
Sia dato il seguente circuito. Si chiede di: a) risolvere il circuito; b) determinare il circuito
equivalente di Thevenin ai nodi A e B.
Domanda facoltativa: si chiede di calcolare la potenza dissipata per effetto Joule sui resistori del circuito.
R2 = R3 = R4 = 1 kΩ, E1 = 4V
Esercizio n. 3 [punti 4/30]
Sia dato un provino di materiale semiconduttore (Silicio) di sezione rettangolare di area A pari a A=100 mm2 e
di lunghezza L = 3 mm. Si supponga di drogare il provino con atomi pentavalenti (drogaggio di tipo n) di
concentrazione ND = 5 10 16 cm –3. Alla temperatura di 300 K si chiede di: a) calcolare la conducibilitá σ del
semiconduttore cosí drogato; b) la resistenza R del provino di semiconduttore drogato.
cm2
µ n = 1500
Vs
66
µ p = 475
Nota: a 300 K la mobilitá di elettroni e lacune é la seguente:
mentre la concentrazione intrinseca é:
e la carica dell’elettrone è: e = 1.6 10–16 C
ni = 145
. ⋅ 1010 cm−3
cm2
Vs
67
Corso di Tecnologie Elettroniche 1
Prova scritta del 09 gennaio 2003
Compito A
Esercizio n. 4 [punti 10/30]
Sia dato il seguente circuito, ove VIN(t) = 0 [V] per t < 0 [ms] e t > 4 [ms] e VIN(t) = -2 [V/ms] t [ms] + 8 [V], per 0
≤ t ≤ 4 [ms]. Si chiede di calcolare e disegnare l’andamento temporale di VOUT (t) per 0 ≤ t ≤ 5 [ms].
k = 2 [V/ms], VR= 1.4 V, R1 = 200Ω, R2 = 100Ω, Vγ = 0.6 V, Rf = 0 Ω, Is = 0 A, Rr →∞.
Esercizio n. 5 [punti 12/30]
Sia dato il seguente circuito e la caratteristica del transistore nMOS del foglio allegato. Si chiede di: a)
calcolare tensioni e correnti del circuito nel punto di lavoro (non considerando quindi Vin e RI, circuito equivalente del
generatore di di segnale di ingresso); b) disegnare la retta di carico sul grafico (Vds,Ids); c) calcolare i parametri del
circuito equivalente ai piccoli segnali del transistore MOS nel punto di lavoro; d) calcolare il guadagno in
tensione ai piccoli segnali: AV = vout/vin.
Vcc=5V, VTH = 0.9 V, RD = 6250 Ω, R1 = 340 Ω, R2 = 660 Ω, Rin = 100 Ω, W/L = 1, k = 10–3 A/V2, λ = 0.01 V1.
68
Tecnologie Elettroniche 1
Prova scritta del 09/01/2003
69