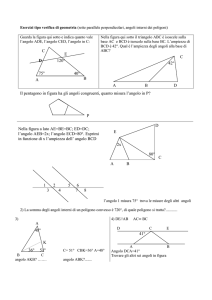
XX.1 – COSA E’ UN ANGOLO
Tra i moltissimi argomenti che la Geometria piana ci propone,
gli angoli hanno certamente un ruolo di principale importanza non
soltanto per le innumerevoli conseguenze matematiche, ma anche
pratiche.
Vediamo
se
le
tue
conoscenze acquisite nel
percorso
di
Scuola
Primaria ti aiutano a
svolgere questo esercizio:
osserva attentamente la
seguente foto (fig.1) e
metti un cerchietto sugli
oggetti, o sulla parte che
interessa di un oggetto,
che indica un angolo.
Confrontati, dopo, con i
tuoi compagni e discutine
con il tuo insegnante.
Figura 1: Foto del giardino in Via delle orchidee
La parola “angolo” nel linguaggio comune
Guarda l’immagine e scrivi la frase di uso comune in cui compare la
parola angolo:
………….
………….
………….
………….
………….
………….
………….
Cerchiamo ora di dare una
definizione geometrica di angolo e
quindi sul tuo quaderno svolgi
O
questa attività:
disegna un piano e traccia su di
esso due semirette aventi la stessa
origine (fig.2).
Osserverai, quindi, che il piano Figura 2: Semirette con origine in comune
resta diviso in due regioni:
colorando le due regioni in modo diverso avrai così evidenziato i due
angoli.
Si chiama angolo ciascuna delle parti in cui un piano è
diviso da due semirette che hanno la stessa origine.
Le due semirette si chiamano lati dell'angolo, l'origine
comune O delle due semirette si chiama vertice dell'angolo.
In fig.3 sono evidenziate le varie parti dell’angolo.
lato
vertice
O
lato
X.1.1 – Costruzione e definizione
Gli angoli si possono anche indicare con le lettere dell’alfabeto (fig.4):
una per indicare il vertice, e altre due per indicare i rispettivi lati
dell’angolo.
Quindi si scrivono le tre lettere di seguito
e la lettera che indica il vertice deve
essere sempre al centro: !!!
Quando non ci sono motivi di equivoco,
per semplicità, si scrive solo la lettera del
vertice: !
Figura 4: Angolo indicato con tre lettere
dell'alfabeto
Figura 3: Le parti dell'angolo
X.1.2 – Angoli concavi e convessi
Come facciamo a distinguere i due angoli disegnati?
Se prolunghiamo le due semirette dalla parte dell'origine
comune (fig.5), diremo che si chiama concavo l'angolo che
contiene i prolungamenti
e convesso l'angolo che
non li contiene.
angolo
angolo convesso
O
Guardiamo
un
momento
concavo
l'immagine: ci accorgiamo subito
che il prolungamento dei lati si
trova nella regione di piano di
colore rosa, di conseguenza essa Figura 5: Angolo concavo e convesso
rappresenta un angolo concavo, la parte celeste invece indica un angolo
convesso.
Un angolo si dice
- convesso quando al suo interno non contiene il
prolungamento dei suoi lati.
- concavo quando contiene il prolungamento dei suoi lati.
RICORDA CHE UN ANGOLO NON E’
L’ARCHETTO CHE SI USA PER
INDICARLO, NE’ IL SUO VERTICE,
ma una parte di piano!
X.1.3 - Prova TU
1. Indica i seguenti angoli usando le tre lettere:
………………
……
………………
……
………………
……
………………
……
2. Per ciascun angolo indica se è concavo o convesso (prova a tracciare i
prolungamenti dei lati)
………………
……
………………
……
………………
……
………………
……
XX.2 – ANGOLI A CONFRONTO
Confrontare significa…
“Confrontare” in Geometria è un’azione che coinvolge sia la forma
degli oggetti matematici che le loro misure. Il confronto porta a
stabilire se i due oggetti considerati hanno la stessa ampiezza o se uno
è maggiore o minore dell'altro.
Per fare questo, bisogna sovrapporre i due angoli facendo coincidere i
rispettivi vertici e un lato.
Per sovrapporre i due angoli è necessario trasportare un
angolo sull'altro. Per eseguire questa operazione possiamo
ricalcare l'angolo su di un foglio di carta trasparente e
spostare la carta sull’altro angolo sovrapponendoli.
H.2.1 – Angoli congruenti e non
CASO n.1:
sovrapponendo il vertice A al vertice B (fig.6), un lato del primo angolo
con un lato del secondo,
vediamo che anche gli altri
due lati coincidono: i due
angoli sono congruenti e si
scrive
!≡!
Figura 6: Angoli congruenti
CASO n.2:
sovrapponendo il vertice A al vertice B (fig.7), un lato del primo angolo
con un lato del secondo, vediamo che il secondo lato dell’angolo A cade
all’esterno dell’angolo B, quindi
i due angoli non sono
congruenti e si scrive,
!>!
Figura 7: Angolo rosso maggiore di angolo verde
ovvero l’angolo ! è maggiore
dell’angolo !.
CASO n.3:
Figura 8: Angolo arancione minore di angolo rosso.
sovrapponendo il vertice A al
vertice B (fig.8), un lato del
primo angolo con un lato del
secondo, vediamo che il secondo lato dell’angolo A cade all’interno
dell’angolo B, quindi i due angoli non sono congruenti e si scrive,
!<!
ovvero l’angolo ! è minore dell’angolo !.
X.2.2 – Angoli consecutivi e adiacenti
L’aggettivo “consecutivi” fa pensare a un angolo che “segue” un altro.
Pertanto
Due angoli si dicono consecutivi (fig.9) quando hanno il
vertice e un lato in comune, mentre gli altri due lati si trovano
da parti opposte rispetto al lato comune.
O
O
Figura 10: Angoli consecutivi
Figura 9: Angoli adiacenti
O
L’aggettivo “adiacenti” fa pensare a un angolo “vicino” ad un altro.
Pertanto
Due angoli si dicono adiacenti (fig.10) se sono consecutivi e i
lati non comuni sono semirette opposte, cioè sono l’uno sul
prolungamento dell’altro.
Se proviamo a tracciare due rette incidenti (fig.11), osserviamo che si
individuano
quattro
angoli: quelli dello stesso
colore sono congruenti
O
fra loro.
Figura 11: Rette incidenti che individuano 4 angoli
Due angoli si dicono opposti al vertice quando i lati
dell’uno sono sul prolungamento dell’altro.
X.2.3 – Operazioni con gli angoli
Le operazioni che hai finora imparato a svolgere con i numeri, si
possono eseguire anche con gli angoli. Vediamo come.
L’addizione
Per addizionare due angoli (fig.12) bisogna disporli l’uno
consecutivo all’altro, magari trasportandone uno; l’angolo
somma è l’angolo che ha per lati quelli non comuni degli
angoli dati e che contiene il lato comune, ovvero:
!!! + !!! = !!!
B
B
+
O
A
A≡D
D
O
=
O
C
C
Figura 12: Somma di due angoli
Per addizionare tre (fig.13) o più angoli, si addizionano i primi due, poi
si addiziona il terzo all’angolo ottenuto e così via.
+
Figura 13: Somma di tre angoli
+
=
La sottrazione
Per sottrarre due angoli (fig.14) si trasporta il secondo sul
primo facendo coincidere un lato e il vertice e in modo che gli
altri due lati si trovino dalla stessa parte rispetto a tale lato. Il
lato del secondo angolo cadrà all’interno del primo angolo e si
scriverà:
!!! + !!! = !!!
Figura 14: Differenza tra due angoli
Multipli e sottomultipli
Un angolo che è la somma di 2, 3, 4, … angoli congruenti all’angolo
!!! si dice multiplo di !!! secondo 2, 3, 4, …
Riferendoci alla fig.15, scriveremo:
!!! = !!!!
D
cioè l’angolo !!! è
B
multiplo dell’angolo
!!! secondo
il
O
numero 3.
O
C
A
Figura 15: Multiplo di un angolo
C
Un angolo che è la metà, la terza parte, ecc … di un altro angolo, si dice
che è sottomultiplo di quell’angolo secondo 2, 3, ecc, …
Riferendoci
alla
figura
seguente, scriveremo:
D
B
O
A
Figura 16: Sottomultiplo di un angolo
O
!
!!!
!
cioè
l’angolo !!! è
sottomultiplo
dell’angolo
!!! =
C
!!! secondo il numero 3.
Dall’angolo multiplo alla bisettrice
Consideriamo ora l’angolo !!! secondo e la semiretta OC (fig.17). Si
dice che OC è bisettrice
B
dell’angolo !!! perché lo
B
C
divide
in
due
parti
traccia la
semoretta OC
congruenti.
Equivalentemente potremo
dire che l’angolo
O
O
A
Figura 17: Bisettrice di un angolo
A
!!!=!!!!!
ovvero !!! è multiplo di !!!.
Si chiama bisettrice di un angolo la semiretta che ha l’origine
nel vertice dell’angolo e che lo divide in due parti congruenti.
• Per aiutarti a ricordare la nuova
terminologia,
RICORDA
CHE
BISETTRICE
DERIVA
DA
“BISECARE”
che
letteralmente
significa “DIVIDERE IN DUE”.
• CIASCUN
ANGOLO
INDIVIDUATO
DALLA
BISETTRICE POTRA’ ESSERE ULTERIORMENTE
DIVISO DA UN’ALTRA BISETTRICE…e così via!
XX.3 – LA MISURA DEGLI ANGOLI
Quale grandezza misuriamo in un angolo?
Non certo una lunghezza come per i segmenti, ma…l’ampiezza
dell’angolo. Potremmo chiederci (fig.18): a che angolo suona la sveglia? E la
seconda ora? A che
angolo
suona
la
ricreazione? A che
angolo
incontrerò
Antonello?
Per rispondere a
queste
domande
abbiamo bisogno di:
! unità di misura;
! strumento
di
misura.
Figura 18: Angoli da misurare
X.3.1 – Unità di misura
L’unità di misura degli angoli è il grado.
Un grado, ovvero 1°, è la 360-esima parte di un angolo giro.
Il simbolo per indicarlo è un piccolo cerchietto scritto come apice.
I sottomultipli del grado sono: primi e secondi.
Un primo, ovvero 1’, è la 60-esima parte di un grado.
Il simbolo per indicarlo è un piccolo apice.
Un secondo, ovvero 1’’, è la 60-esima parte di un primo, o
equivalentemente la 3600-esima parte del grado.
Il simbolo per indicarlo è un doppio apice.
Esplicitiamo la misura
La misura di un angolo può essere espressa in:
GRADI° PRIMI′ SECONDI″
Dove GRADI° è un numero intero, PRIMI′ è un numero intero
compreso tra 0 e 59, mentre SECONDI″ deve essere un numero (non
necessariamente intero) minore o al più uguale a 59.
ESEMPI
" Angolo espresso in forma normale:
123° 42′ 36″
perché rispetta le condizioni che dette prima.
" Angolo espresso in forma non normale:
97° 72′ 85″
perché i numeri che indicano, rispettivamente, i primi e i secondi
non sono più piccoli di 60. Che facciamo in questo caso?
Riduzione a forma normale
# Riduciamo a forma normale l’angolo 97° 72′ 85″
Partiamo dai secondi: 85'' è un numero maggiore di 59.
Calcoliamo la divisione intera per 60, in questo modo calcoleremo
quanti primi ci sono in 85''.
85'' 60
60″ 1′
25″
Il resto 25″ va sostituito al posto di 85″. Il quoziente 1 è il numero
di primi e va invece sommato ai primi della traccia, ottenendo:
97° 72′+ 1′ 25″ = 97° 73′ 25″
RICORDA CHE SE I SECONDI
SUPERANO IL VALORE DI 59’’
ALLORA
SI
EFFETTUA
LA
DIVISIONE PER 60. IL QUOZIENTE
DELLA DIVISIONE VA SOMMATO
AI PRIMI, MENTRE IL RESTO E’ IL
NUOVO VALORE DEI SECONDI.
In questo esempio anche i primi superano 59, allora possiamo
pensare di ripetere il ragionamento che abbiamo utilizzato per i
secondi. Dividiamo per 60 i primi così da determinare quanti gradi ci
sono in 72′.
73' 60
60′ 1°
13′
Il quoziente è il numero che andrà sommato ai gradi, mentre il resto
è il valore da sostituire ai primi:
97° + 1° 73′ 25″ = 98° 73′ 25″
SE I PRIMI SUPERANO IL VALORE 59'
ALLORA SI EFFETTUA LA DIVISIONE
PER 60. IL QUOZIENTE DELLA
DIVISIONE VA SOMMATO AI GRADI,
MENTRE IL RESTO È IL NUOVO
VALORE DEI PRIMI
# Ora vogliamo scrivere in forma normale 5716″. Naturalmente i
secondi hanno un valore molto più grande di 59 e quindi dividiamo
per 60.
5716″ 60
540 95′
316
300
16″
Il quoziente intero è 95, mentre il resto è 16, di
conseguenza:
5716″ = 95′ 16″
Dobbiamo, ora, scrivere in forma normale i primi.
Dividiamo 95′ per 60 e otteniamo 1 come quoziente
e 35 come resto, cioè
95′ = 1° 35′
in definitiva:
5716″ = 1° 35′ 16″
ESEMPI
Scriviamo in forma normale l'ampiezza dell'angolo: 68,235°
La parte intera, cioè 68, rappresenta i gradi della forma normale, la
parte decimale, 0,235, la moltiplichiamo per 60 e otteniamo così i
primi: 0,235 × 60 = 14,1′
68,235 = 68° 14,1′
Dobbiamo trasformare anche i primi seguendo lo stesso
procedimento: 0,1 × 60 = 6″,
14,1′ = 14′ 6″
In definitiva: 68,235° = 68° 14′ 6″
SE I GRADI SONO NUMERI DECIMALI
ALLORA SI PRENDE PER GRADO LA
PARTE INTERA, LA PARTE DECIMALE
INVECE VERRÀ MOLTIPLICATA PER 60.
Otterremo così un nuovo numero, la sua parte
intera sarà il valore da associare ai primi,
l'eventuale parte decimale invece verrà moltiplicata per 60 ed
il risultato saranno i secondi della misura dell'angolo
espresso in forma normale.
X.3.2 - Prova TU
Riduci in forma normale le seguenti ampiezze di angoli.
43,245°
87° 84′ 96″
98,342°
231° 156′ 125″
128,276°
64° 257′ 145″
56,98°
56° 98′ 220″
X.3.3 – Strumento di misura
Per misurare gli angoli si usa il goniometro (fig.19).
Come si usa?
! si fa coincidere il
vertice dell’angolo con il
centro del goniometro;
! si fa coincidere il
bordo rettilineo con una
semiretta dell’angolo;
! si legge la misura
dell’angolo sulla scala
graduata,
in
corrispondenza
della
seconda
semiretta
Figura 19: Il goniometro per misurare gli angoli
dell’angolo. Nel nostro
caso: !!!=50°; !!!=130°.
X.3.3 – Angoli particolari
Un angolo si dice piatto se i suoi lati sono l’uno sul prolungamento
dell’altro. Esso misura 180°.
angolo piatto
O
Se la semiretta OA ruota intorno
all’origine O di un giro completo, allora
descrive un angolo costituito da tutti i
punti del piano che viene detto angolo
giro. Esso misura 360°.
angolo giro
A
O
angolo nullo
Se la semiretta OA non compie nessuna
rotazione intorno all’origine O, allora si ottiene
l’angolo nullo. Esso misura 0°.
angolo retto
A
O
Se si traccia la bisettrice di un angolo
piatto, si ottengono due angoli
congruenti che si chiamano angoli retti.
Quindi, l’angolo retto è la metà di un
angolo piatto e misura 90°.
Un angolo di riferimento
L’angolo retto oltre a rappresentare l’angolo che più frequentemente
incontriamo nella realtà, è anche usato per
B
fare la distinzione tra angolo acuto e ottuso.
Un angolo si dice acuto se è minore di un
angolo retto, ovvero !!!<90°.
angolo acuto
O
D
angolo ottuso
O
C
A
Un angolo si dice ottuso se è
maggiore dell’angolo retto, ovvero
!!!>90°, e minore di un angolo
piatto, ovvero !!!<180°.
RICORDA CHE PER STIMARE LA
MISURA DI UN ANGOLO QUANDO NON
HAI LA POSSIBILITA’ DI MISURARLO
PRECISAMENTE,
DEVI
RIFERIRTI
AGLI ANGOLI NOTI!
X.3.4 - Prova TU
Completa la tabella:
angolo
Acuto
Ottuso
Retto
Piatto
Giro
Concavo Convesso
Angoli complementari, supplementari, esplementari
Gli “angoli particolari” e le operazioni sugli angoli ci servono per
definire altre tre tipologie:
" complementari se la loro somma è un angolo
retto, ovvero
α+β=90°
" supplementari se la loro somma è un
angolo piatto, ovvero
α+β=180°
" esplementari se la loro somma è un angolo
giro, ovvero
α+β=360°
angoli complementari
α
β
α
angoli supplementari
β
angoli esplementari
α
β
XX.3.5 - Mettiamo in pratica
1. Segna la V o la F, secondo che l’affermazione sia “vera” o “falsa” e
rappresenta graficamente ciascuna situazione
a. La somma di due angoli complementari è un angolo
piatto
b. Due angoli ottusi possono essere supplementari
V
F
V
F
c. Un angolo concavo ed uno convesso possono essere
esplementari
d. Un angolo acuto e uno ottuso possono essere
complementari
e. La somma di due angoli supplementari è un angolo
piatto
f. Due angoli piatti non sempre sono asplementari
V
F
V
F
V
F
V
F
g. Due angoli retti sono sempre complementari
V
F
2. Disegna una coppia di angoli complementari, una di angoli
supplementari e una di angoli esplementari. Per ciascuna coppia
scrivi la relazione che lega entrambi gli angoli.