Simulazione Anatomica di Muscoli Facciali per Volti Virtuali Generici

Università degli studi di Roma La Sapienza
Facoltà di Ingegneria
Tesi di Laurea in
Ingegneria Informatica
Simulazione Anatomica di Muscoli
Facciali per Volti Virtuali Generici
Relatore
Candidato
Prof. Marco Schaerf
Francesco Iannucci
Correlatore
Ing. Marco Fratarcangeli
Anno Accademico 2005/2006
Università degli studi di Roma La Sapienza
Facoltà di Ingegneria
Tesi di Laurea in
Ingegneria Informatica
Simulazione Anatomica di Muscoli
Facciali per Volti Virtuali Generici
Relatore
Candidato
Prof. Marco Schaerf
Francesco Iannucci
Correlatore
Ing. Marco Fratarcangeli
Anno Accademico 2005/2006
Alla mia famiglia
Sommario
Il volto è il canale più rilevante della comunicazione non verbale. Le espressioni del volto cambiano rapidamente e hanno una funzione fondamentale
nell’interazione sociale; esse sono attentamente controllate dallo sguardo rivolto al viso.
In questa tesi è stata sviluppata un’applicazione chiamata Anatomical Facial Muscle Simulator (afms) che è in grado di generare automaticamente
le mappe complete dei muscoli mimici di un volto virtuale, a partire dal
modello vrml della faccia 3D e da alcuni punti situati in posizioni particolari del volto come occhi, zigomi, bocca che deﬁniscono completamente le
caratteristiche del viso rappresentato.
La pelle del volto è stata realizzata introducendo un sistema di masse e molle
che ne simulano le proprietà elastiche. I muscoli mimici sono stati costruiti
attraverso l’aggregazione di segmenti muscolari di base.
Tutti i muscoli generati da afms sono controllabili singolarmente attraverso
i relativi slider posti nel pannello di controllo dell’applicazione, in questo
modo possono essere realizzate molteplici espressioni facciali.
afms è stato concepito per essere applicato prevalentemente a volti umani,
in quanto tutto lo studio anatomico e ﬁsiologico è stato fatto in relazione
all’uomo, tuttavia, come è stato veriﬁcato, è possibile anche un suo utilizzo
per modelli umanoidi più generali.
3
Indice
1 Introduzione
6
2 Background
2.1 Related Works . . . . . . . . . . .
2.2 MPEG-4 . . . . . . . . . . . . . . .
2.3 Implementazione . . . . . . . . . .
2.3.1 Ambiente di sviluppo . . .
2.3.2 Microsoft Foundation Class
2.3.3 OpenGL . . . . . . . . . . .
2.3.4 Il modello VRML . . . . . .
2.3.5 visage|SDK . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9
9
10
13
13
14
15
16
19
3 Anatomia del volto umano
3.1 Osteologia del cranio . . . . . . . . . . .
3.1.1 Neurocranio . . . . . . . . . . . .
3.1.2 Splancnocranio . . . . . . . . . .
3.2 Miologia del cranio . . . . . . . . . . . .
3.2.1 Muscoli scheletrici (Masticatori)
3.2.2 Muscoli mimici (Pellicciai) . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
20
20
21
23
24
24
.
.
.
.
.
.
.
.
.
32
32
34
35
37
39
39
42
42
42
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Modello della pelle
4.1 Anatomia della pelle umana . . . . . . . . . . . . . . . . .
4.2 Biomeccanica della pelle umana . . . . . . . . . . . . . . .
4.3 Mass-Spring System . . . . . . . . . . . . . . . . . . . . .
4.4 Forze vincolari di compenetrazione del cranio . . . . . . .
4.5 Integrazione numerica . . . . . . . . . . . . . . . . . . . .
4.5.1 Equazioni che regolano la deformazione della pelle
4.6 Strutture dati nel mass-spring system . . . . . . . . . . .
4.6.1 Struttura dati del nodo-massa . . . . . . . . . . . .
4.6.2 Struttura dati della molla . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
5 Modello muscolare
44
5.1 Struttura anatomica reale del muscolo . . . . . . . . . . . . . 44
5.2 Modello muscolare virtuale . . . . . . . . . . . . . . . . . . . 50
4
5.3
5.2.1 Il modello muscolare di Kähler . . . . . . . . . . . . .
5.2.2 Il modello muscolare realizzato . . . . . . . . . . . . .
La mappa muscolare . . . . . . . . . . . . . . . . . . . . . . .
6 Analisi dei risultati
50
55
59
63
7 Conclusioni
73
7.1 Prospettive future . . . . . . . . . . . . . . . . . . . . . . . . 74
A Guida all’interfaccia utente
79
5
Capitolo 1
Introduzione
Il volto umano è uno dei più importanti e complessi mezzi espressivi con il
quale l’uomo può comunicare. È proprio attraverso il viso che si riesce a
trasmettere un particolare sentimento o stato d’animo. La complessità e il
numero di espressioni che si riescono a produrre ha attratto l’attenzione di
importanti discipline quali la psicologia, la computer vision e non ultima la
computer graphics.
Infatti il riuscire a riprodurre nel miglior modo possibile le espressioni del
volto umano è uno degli obbiettivi che ci si è posti nell’ambito dell’informatica graﬁca, in quanto sono sempre maggiormente richieste applicazioni
riguardanti l’intrattenimento (eﬀetti speciali per il cinema, videogames), comunicazione tra dispositivi mobili con poca banda disponibile (videoconferenze, videofonia), applicazioni mediche e realtà virtuale.
In questa tesi ci si è posti come obbiettivo principale la simulazione delle
espressioni del viso attraverso un’attenta realizzazione dei muscoli facciali,
nel modo più anatomicamente corretto possibile. Sono infatti i muscoli che
guidano l’animazione deformando la pelle e non viceversa.
È stato creato quindi un tool applicativo che genera automaticamente su
un modello di volto virtuale 3D i suoi muscoli mimici attraverso i quali è
possibile generare tutte le espressioni facciali umane.
La pelle è stata simulata realizzando una complessa rete di masse e molle
che ne emulano le proprietà elastiche mentre per realizzare i muscoli facciali,
si è deciso di implementare il modello muscolare introdotto da Kähler, Haber e Seidel [1] (che a sua volta è stato sviluppato partendo dal modello di
Lee, Terzopoulos e Waters [2]), in cui sia i muscoli lineari che quelli circolari vengono costruiti essenzialmente come un’unica aggregazione di segmenti
muscolari di base.
La contrazione isotonica del muscolo si ottiene attraverso la contrazione di
ciascun singolo segmento che lo costituisce rispetto al suo punto di inserzione, se il muscolo è di tipo lineare, come per esempio il muscolo zigomatico
maggiore che ha origine nella faccia laterale dell’osso zigomatico e si inseri-
6
sce sulla faccia profonda della cute e della mucosa labiale, in corrispondenza
della commessura labiale (vedi ﬁg. 5.9a par. 5.2.2).
Se invece il muscolo è di tipo circolare, come per esempio il muscolo orbicolare dell’occhio che ha la forma di un anello ellittico che si dispone intorno
alla rima palpebrale, la contrazione avviene rispetto ad un punto, che normalmente è interno al muscolo stesso (vedi ﬁg. 5.9b par. 5.2.2).
In questo modo è possibile realizzare qualsiasi tipo di muscolo che compare
nel volto umano cosı̀ da ottenere un’animazione quanto più realistica possibile e soprattutto rispondente ai vincoli anatomici reali.
A partire da un modello vrml (Virtual Reality Modeling Language) che rappresenta un volto umano e attraverso gli 84 fdp (Facial Deﬁnition Points)
deﬁniti dallo standard mpeg-4, viene ricostruita automaticamente l’intera
mappa dei muscoli facciali. Gli fdp sono utilizzati per deﬁnire la forma
di un modello di viso proprietario [3], sono disposti in gruppi, ognuno corrispondente ad una diversa zona del viso (occhi, naso, bocca, ecc.). La
localizzazione degli fdp deve essere conosciuta per ogni modello facciale.
L’applicazione realizzata in questa tesi, Anatomical Facial Muscle Simulator
(afms), è interattiva, cioè permette all’utente di azionare i muscoli mimici
e di vederne in tempo reale il loro movimento, che genera, a sua volta, la
relativa deformazione della pelle del modello virtuale.
afms ancora non supporta il movimento simultaneo di più muscoli contemporaneamente, l’espressione facciale desiderata deve essere quindi composta
agendo su un muscolo alla volta.
Nel Capitolo 2 verrà introdotto l’ambiente di sviluppo, gli strumenti softR
Foundation Class, visage|SDK [3]) e
ware (MPEG-4, OpenGL, Microsoft
gli algoritmi (Kähler, Haber e Seidel [1]) che sono alla base della realizzazione di questo lavoro.
Nel Capitolo 3 verrà dato un breve accenno all’anatomia reale del volto
umano, analizzando sia la sua struttura ossea che quella muscolare, focalizzando però prevalentemente l’attenzione sui muscoli mimici, il loro posizionamento e la loro attività.
Il Capitolo 4 descrive il modo in cui è stato realizzato il modello che simula
le proprietà della pelle e come vengono visualizzati gli eﬀetti prodotti dall’attività muscolare; la realizzazione di un buon modello di pelle è un passaggio
fondamentale per una buona simulazione. Vengono inoltre descritti i metodi
matematici e ﬁsici utilizzati per ottenere la simulazione, ponendo particolare
attenzione al mantenimento di un buon compromesso tra prestazioni e costi
computazionali.
Il Capitolo 5 è il cuore di questa tesi, qui infatti viene descritto in modo molto accurato il modello muscolare implementato, il posizionamento
7
anatomico dei muscoli sul volto e il modo in cui i muscoli agiscono sulla
deformazione della pelle.
Il Capitolo 6 è la sezione dedicata all’analisi dei risultati ottenuti e in particolare, facendo riferimento alle espressioni facciali reali fornite da [4], viene
presentata una serie di immagini delle espressioni facciali dei volti virtuali
con cui è stata testata l’applicazione realizzata nel corso di questo studio.
Inﬁne, nel Capitolo 7, viene presentata una breve digressione sulle possibili
applicazioni dello studio eﬀettuato e sulle sue prospettive future.
8
Capitolo 2
Background
2.1
Related Works
Sono passati ormai più di venti anni da quando, agli inizi degli anni Ottanta,
prima Platt e Badler [5] nel 1981 e poi Parke [6] nel 1982 iniziarono a lavorare all’animazione facciale; all’inizio l’animazione era ottenuta attraverso il
morphing tra due maschere calcolate a priori e salvate in una libreria [7],
poi però, per eliminare la necessità di possedere un database completo dei
modelli usati, furono introdotti i modelli parametrici che permettevano all’animatore di creare un’espressione facciale speciﬁcando un insieme di valori
per i parametri di controllo.
In seguito, per applicazioni multimediali con un basso bit rate, la ricerca
si focalizzò sullo standard mpeg-4 che deﬁnisce 68 diversi faps(Facial Animation Parameters), attraverso i quali è possibile controllare l’animazione
facciale.
Sono stati anche sviluppati dei modelli chiamati physics-based, che simulano
le proprietà elastiche della pelle attraverso un sistema di masse e molle. Un
modello di questo tipo è stato realizzato da Lee, Terzopoulos e Waters [2],
in cui il viso è costituito principalmente da solo due strati (derma + strato grasso e muscoli), connessi attraverso delle molle al teschio, che viene a
sua volta stimato a partire dalla superﬁcie del volto. Il sistema di masse
e molle utilizzato in questo approccio preserva il volume del volto in modo
tale da non essere deformato in modo non opportuno.
Un lavoro molto importante è stato quello realizzato da N. I. Badler , C.
Pelachaud e M. Steedman [8] sull’animazione facciale di alta qualità con il
movimento della testa in accordo con il parlato, che include anche l’intonazione della voce.
Ci sono stati degli sviluppi anche in ambito medico, come negli articoli di E.
Gladilin, S.Zachow, P. Deuﬂhard, H.C. Hege [9] [10] che, simulando i muscoli e la pelle del volto, hanno cercato di prevedere i risultati post-operatori
sulla mimica facciale dopo un intervento di chirurgia cranio-facciale.
9
2.2
MPEG-4
L’mpeg-4 [11] è uno standard iso/iec sviluppato dall’mpeg (Moving Picture Experts Group) lo stesso comitato che ha sviluppato l’mpeg-1 e l’mpeg-2.
L’mpeg-4 è il risultato di uno sforzo che ha coinvolto centinaia di ricercatori
e di ingegneri di tutto il mondo, la sua deﬁnizione formale è iso/iec 14496,
ultimato nell’Ottobre del 1998 e diventato un’International Standard agli
inizi del 1999.
L’mpeg-4 è stato costruito a partire dal successo acclarato di tre campi: la
Digital television, l’Interactive graphics applications e l’Interactive multimedia; l’mpeg-4 fornisce gli elementi tecnologici standard per la produzione,
la distribuzione e l’accesso al contenuto dei paradigmi di questi tre campi.
L’interesse verso questo standard in questo progetto è legato al fatto che
l’mpeg-4 supporta la face animation e la body animation.
La face animation viene usata per eﬀettuare il rendering di un volto animato virtuale, la forma, l’espressione e le texture sono controllate dai Facial
Deﬁnition Points (fdps) e/o dai Facial Animation Parameters (faps ). A
partire da un volto che ha un’espressione generica neutra, con la ricezione
dei fap viene prodotta l’animazione del volto (espressione, parlato, ecc.).
La speciﬁca dell’mpeg-4 deﬁnisce 84 punti di deﬁnizione facciale chiamati
Facial Deﬁnition Points (fdp) o anche Feature Points (fp) e 68 Facial Animation Parameters (faps ).
Gli fdp (vedi ﬁg. 2.1) vengono usati per deﬁnire le caratteristiche principali
di un volto e per fornire le giuste corrispondenze spaziali ai fap. Gli fdp
sono raggruppati in base alla loro diversa posizione sul volto (occhi, bocca,
naso, ecc.), la loro posizione deve essere nota a priori per ogni modello facciale, aﬃnché afms funzioni correttamente. Per i modelli utilizzati in afms,
gli fdp sono stati calcolati con l’ausilio del pacchetto software visage|life.
I fap speciﬁcano di quanto può essere mosso un particolare fdp, modiﬁcando cosı̀ il modello facciale generico di input. I fap si basano sullo studio delle
azioni facciali minimali e sono strettamente correlati alle azioni muscolari.
Rappresentano un insieme completo di espressioni facciali.
Tutti i fap sono espressi in termini di Face Animation Parameter Units
(fapus ) (ﬁg. 2.2), che sono deﬁniti per permettere l’interpretazione dei fap
su ogni modello facciale in modo consistente, producendo risultati ragionevoli in termini di espressioni e di parlato. Per ogni fap si conosce su quale
fdp agisce, in quale direzione si muove e quale fapu è usato come unità per
il movimento.
La speciﬁca deﬁnisce anche una Face Animation Tables (fats ), che permette di speciﬁcare, per ogni fap, l’esatto movimento dei vertici nel modello
3D.
10
Fig. 2.1: Facial Deﬁnition Points (fdp)
11
Fig. 2.2: Face Animation Parameter Units (fapu)
IRIS Diameter
Eye Separation
Eye - Nose Separation
Mouth - Nose Separation
Mouth - Width Separation
Angular Unit
IRISD = IRISD0 /1024
ES = ES0 / 1024
ENS = ENS0 / 1024
MNS = MNS0 / 1024
MW = MW0 / 1024
AU = 10−5 rad
La divisione per 1024 è stata introdotta per avere unità suﬃcientemente
piccole in modo che i fap possano essere rappresentati con i numeri interi.
12
2.3
Implementazione
2.3.1
Ambiente di sviluppo
L’applicazione è stata sviluppata su un personal computer con processoR
Centrino 1.4 GHz e 512 MB ddr sdram con sistema operativo
re Intel
R
R
ViWindows XP con SP2. L’implementazione è avvenuta con Microsoft
sual C++ 6.0 con il supporto fondamentale del pacchetto di sviluppo visage|SDK (C++ Software Development Kit for Virtual Character animation)
prodotto dalla Visage Technologies AB [3] e la libreria graﬁca OpenGL.
R
Foundation Class.
L’interfaccia graﬁca è stata realizzata con le Microsoft
A partire da un modello vrml raﬃgurante un volto umano e dai relativi
fdp (che devono essere noti), Anatomical Facial Muscle Simulator (afms),
genera automaticamente la mappa anatomica dei muscoli mimici, inoltre
Fig. 2.3: Esempio di Anatomical Facial Muscle Simulator (afms)
attraverso i relativi slider situati sul pannello a sinistra, si può regolare la
contrazione di ciascun muscolo, ﬁno ad ottenere l’espressione facciale voluta.
La forza che ciascun muscolo esercita sulla pelle viene letta dal relativo ﬁle
.mfo (Muscle FOrce), nel caso in cui però non si ha a disposizione il suddetto ﬁle, verranno caricate delle forze muscolari di default.
Attraverso il mouse è possibile eﬀettuare lo spostamento, la rotazione e lo
zoom del modello all’interno della ﬁnestra OpenGL, inoltre attraverso il menu a tendina sono disponibili varie operazioni da poter eﬀettuare sul modello.
Per ulteriori informazioni circa l’utilizzo di afms, si consiglia la lettura
dell’Appendice A (Guida all’interfaccia utente).
13
2.3.2
Microsoft Foundation Class
Come detto in precedenza, il progetto afms è stato interamente sviluppato con Microsoft Visual C++ 6.0 avvalendosi dell’utilizzo delle Microsoft
Foundation Class (MFC), infatti uno degli sforzi più importanti che è stato
compiuto per realizzare questa applicazione è stato proprio quello di imparare ad usare le MFC in modo corretto, cosa tutt’altro che banale.
Microsoft Foundation Class, meglio conosciuta con l’acronimo MFC, è una
libreria di classi C++ prodotta da Microsoft con lo scopo di incapsulare le
Windows API; è un application-framework, fornisce infatti tutto il codice
necessario per la gestione di ﬁnestre, menu e dialog box.
MFC è stata introdotta nel 1992 per essere usata con le versioni a 16 bit di
Windows ed è stata progettata per essere una sorta di rassegna delle potenzialità del linguaggio di programmazione C++.
Da un punto di vista pratico, lo sviluppo di programmi Windows con MFC
risulta molto più rapido e sempliﬁcato rispetto all’uso diretto delle Windows
API, anche se la loro conoscenza è quasi indispensabile per un programmatore MFC per via della poca astrazione introdotta dalla libreria di classi.
Uno dei vantaggi maggiori deriva dal fatto che gli handle degli oggetti vengono gestiti automaticamente dalla libreria e chiusi quando gli oggetti vengono
distrutti.
Quando un’applicazione gira su Microsoft Windows, l’utente interagisce con
documenti che sono visualizzati in frame window. MFC deﬁnisce due tipi
di document frame window : Single Document Interface (SDI) e Multiple
Document Interface (MDI).
Le applicazioni di tipo SDI permettono di aprire un solo document frame
window alla volta, mentre quelle di tipo MDI permettono di aprire più document frame window contemporaneamente. Un document frame window
è costituito principalmente da due componenti: il frame e il contenuto del
frame, questi sono visualizzati e gestiti da due diverse classi in MFC. Una
Fig. 2.4: Relazione tra frame window e view in SDI - MFC
14
frame-window class gestisce il frame e una view class gestisce il contenuto.
La view window è una sottoﬁnestra della frame window e tutto quello che
riguarda l’interazione con l’utente viene eﬀettuato nella window’s client area
(Fig. 2.4). Il frame window fornisce un frame visibile attorno ad una view
completa della caption bar e di tutti i controlli standard di Windows (menu,
bottoni per minimizzare e massimizzare la ﬁnestra e i controlli per eﬀettuare
il resizing della ﬁnestra).
afms è stato realizzato a partire da un progetto SDI standard.
2.3.3
OpenGL
OpenGL (Open Graphics Library) è una speciﬁca che deﬁnisce una API
per più linguaggi e per più piattaforme per scrivere applicazioni che producono computer graﬁca 2D e 3D. L’interfaccia consiste in circa 250 diverse
chiamate di funzione che si possono usare per disegnare complesse scene tridimensionali a partire da semplici primitive (punti, linee e poligoni). È usato
nell’industria dei videogiochi, per applicazioni di tipo CAD e realtà virtuale.
La speciﬁca di OpenGL è supervisionata dall’OpenGL Architecture Review
Fig. 2.5: Logo di OpenGL
Board (ARB), che si è formato nel 1992. L’ARB consiste in un insieme di
aziende interessate a creare un’API coerente e ampiamente disponibile.
OpenGL è un’evoluzione di (ed ha uno stile molto simile a) IRIS GL, l’interfaccia 3D di SGI (Silicon Graphics). Una delle restrizioni di IRIS GL
era che forniva accesso solamente alle caratteristiche supportate dall’hardware soggiacente. Se l’hardware graﬁco non supportava una caratteristica,
allora l’applicazione non poteva usarla. OpenGL ha superato questo problema fornendo supporto via software per le caratteristiche non supportate
dall’hardware, permettendo alle applicazioni di usare della graﬁca avanzata
su sistemi di potenza relativamente bassa.
OpenGL è stato progettato per essere di solo output: fornisce solamente
funzioni di rendering. L’API di base non contempla la gestione di ﬁnestre, l’audio, la stampa, la tastiera, il mouse, né altri dispositivi di input.
Per quanto questo può sembrare restrittivo, permette al codice di rendering
di essere completamente indipendente dal sistema operativo su cui funziona,
permettendo lo sviluppo di codice indipendente dalla piattaforma. Tuttavia,
per consentire un’interazione con il sistema ospitante, è necessario integrare
il software con il sistema a ﬁnestre nativo. OpenGL è una rendering library
e lavora in immediate mode, cioè la deﬁnizione di un oggetto causa immedia15
Fig. 2.6: Librerie basate su OpenGL
tamente il suo disegno, OpenGL però non scrive direttamente sullo schermo
ma accede ad un framebuﬀer ; inoltre OpenGL è una state-machine per cui
sono le variabili di stato che guidano il rendering. Per costruire e modiﬁcare
oggetti complessi si usano librerie costruite sopra OpenGL (ﬁg.2.6).
2.3.4
Il modello VRML
Il vrml (Virtual Reality Modeling Language) è un linguaggio di programmazione che consente la simulazione di mondi virtuali tridimensionali. Mediante il vrml è possibile cioè descrivere ambienti virtuali contenenti oggetti,
sorgenti luminose, immagini, suoni e ﬁlmati. Questi mondi, inoltre, possono
essere animati e presentare caratteristiche anche complesse di interattività.
Inﬁne, allo stesso modo di qualsiasi documento ipertestuale, il vrml prevede
l’impiego di link a url remoti e naturalmente a qualunque altro ﬁle di tipo
.wrl (questo è il formato dei ﬁles vrml).
Per una corretta pronuncia della sigla vrml occorre sillabare le singole lettere dell’alfabeto inglese: ViErEmEl. In gergo vrml viene anche denominato,
più semplicemente, “vermel”. Per quanto riguarda il signiﬁcato, in un pri-
Fig. 2.7: Logo vrml97
mo periodo vrml veniva tradotto in Virtual Reality Markup Language (in
analogia con html e i linguaggi che fanno uso dei cosiddetti “marcatori” o
contrassegni); in seguito la parola Markup è stata sostituita con Modeling
per meglio rappresentare le proprietà di modellazione graﬁca del linguaggio.
Il motivo fondamentale per cui si è deciso di usare il vrml per importare i
volti virtuali sta nel fatto che il vrml costituisce un formato standard per
descrivere scene tridimensionali, contrariamente ai formati proprietari dei
16
numerosi tools che si trovano in circolazione.
Ciò signiﬁca che un ﬁle vrml è accessibile da qualsiasi macchina indipendentemente dalla piattaforma, come per i documenti html che possono essere
visualizzati sostanzialmente allo stesso modo su macchine Windows, Mac,
Unix, Linux, ecc.
Il vrml consente all’utilizzatore di interagire con il modello, spostarlo, ruotarlo e osservarlo da diversi punti di vista.
Un ﬁle .wrl, è un semplice ﬁle di testo che utilizza caratteri ascii (come
l’html ad esempio) che contiene al suo interno tutti i comandi necessari a
descrivere una scena tridimensionale. I principali componenti [12] contenuti
nel ﬁle vrml sono: header, scene graph, i prototypes e gli event routing:
• header - per una semplice identiﬁcazione del ﬁle vrml, ogni ﬁle vrml
inizia con: #VRML V2.0.
• scene graph - lo scene graph contiene i nodi che descrivono gli oggetti
e le loro proprietà, i componenti sono raggruppati gerarchicamente
per fornire una rappresentazione audio/video dell’oggetto. È un grafo
diretto aciclico, se c’è un arco tra un nodo A e un nodo B, signiﬁca
che nel nodo A c’è un campo nel quale viene direttamente speciﬁcato
il nodo B.
• prototypes - i prototypes permettono all’utente di estendere l’insieme
dei tipi dei nodi vrml.
• event routing - alcuni nodi vrml possono generare eventi in risposta
ai cambiamenti del mondo rappresentato oppure a causa dell’interazione con l’utente. L’event routing fornisce all’autore del modello un
meccanismo per separare la scena visualizzata dallo scene graph attraverso il quale gli eventi si propagano, generando cambiamenti in altri
nodi. Una volta generati, gli eventi vengono inviati sequenzialmente
e processati dai nodi cui sono destinati. Questo processamento può
cambiare lo stato di un nodo, può generare eventi addizionali oppure
cambiare la struttura dello scene graph.
Il processamento, l’esecuzione e la presentazione di un ﬁle vrml tipicamente
fanno parte di un meccanismo che prende il nome di browser, che visualizza
gli oggetti contenuti dallo scene graph.
Il browser mostrato in ﬁg. 2.8 raﬃgura un’applicazione che prende come
input il ﬁle contenente il modello vrml e gli input di manipolazione e navigazione che arrivano dall’utente. I tre principali componenti del browser
sono: il parser, lo scene graph e l’audio/visual presentation.
Il parser legge il ﬁle vrml e genera lo scene graph. Lo scene graph è costituito dalla Transformation Hierarchy (i nodi) e dal Route Graph; include
anche l’Execution Engine che processa gli eventi, legge e edita il Route Graph ed eﬀettua i cambiamenti nella Transformation Hierarchy. Lo user input
17
Fig. 2.8: Modello concettuale di un browser vrml
riguarda i sensori e la navigazione, è strettamente collegato al Route Graph (i sensori) e all’Audio/Visual Presentation. L’Audio/Visual Presentation
esegue sia il rendering graﬁco che quello audio della Transformation Hierarchy che viene ripresentato all’utente.
In afms, il modello che viene fornito come input per l’applicazione deve
soddisfare dei prerequisiti fondamentali, più speciﬁcatamente, il modello deve essere compatibile con la deﬁnizione di volto neutro data dallo standard
mpeg-4, e cioè:
lo sguardo deve essere rivolto nella direzione dell’asse z, tutti i muscoli devono essere rilassati, le palpebre devono essere tangenti all’iride, il diametro
della pupilla deve essere 1/3 di quello dell’iride, il labbro superiore e quello
inferiore si toccano in modo tale che la bocca sia chiusa, i denti dell’arcata
superiore si toccano con quelli dell’arcata inferiore.
Inﬁne, al modello di input vengono resettate tutte le trasformazioni presenti
(traslazioni, rotazioni e scalamenti), in modo tale da rappresentarlo in coordinate del mondo anzichè in coordinate locali. Il fatto di avere il modello
rappresentato in coordinate del mondo è necessario per la costruzione della
mappa muscolare del volto e per deformare la pelle agendo direttamente
sulla mesh vrml.
18
2.3.5
visage|SDK
visage|SDK C++ Software Development Kit for Virtual Character animation, è
un pacchetto software completamente dedicato all’animazione di personaggi
virtuali, è basato sullo standard mpeg-4 fba (Face and Body Animation)
e contiene i supporti necessari sia all’interattività che all’animazione oﬀ-line
dei modelli virtuali (vrml).
Il visage|SDK-SE è un insieme di librerie per lo sviluppo dell’animazione facciale utilizzabili sia con Microsoft Visual C++ 6.0 che con Microsoft Visual
Studio .NET 2003, il loro utilizzo è stato fondamentale per l’implementazione di afms, in quanto mettono a disposizione dello sviluppatore tutti gli
strumenti necessari per l’animazione dei volti virtuali, come per esempio la
possibilità di gestire i modelli vrml con i relativi fdp e di interagire con
essi attraverso mouse e tastiera.
Del pacchetto software messo a disposizione dalla Visage Technologies AB [3]
di particolare aiuto è stato visage|life con il quale è stato possibile visualizzare ed editare gli fdp dei modelli vrml.
Fig. 2.9: Esempio di visage|life
19
Capitolo 3
Anatomia del volto umano
3.1
Osteologia del cranio
Lo scheletro del cranio è distinto in due porzioni: la scatola cranica (neurocranio) ed il massiccio facciale (splancnocranio).
3.1.1
Neurocranio
Le ossa del neurocranio si distinguono in impari e pari.
Le ossa impari sono rappresentate dal frontale, l’etmoide, lo sfenoide, l’occipitale; quelle pari sono il temporale e il parietale.
Il frontale è un osso mediano, che contribuisce a delimitare la fossa cranica,
con la sua porzione verticale, e la cavità orbitaria, con la sua porzione orizzontale.
L’etmoide è un osso mediano, costituito da due lamine e due masse laterali.
La sua lamina perpendicolare contribuisce alla costituzione del setto nasale.
Le masse laterali contribuiscono a formare l’orbita, mentre la faccia mediale
compone in parte le cavità nasali.
L’osso sfenoide è anch’esso mediano; insieme ad altre ossa, compone la base
cranica, le cavità orbitarie e nasali.
Esso presenta un corpo centrale, dalle cui facce laterali originano le cosiddette ali dello sfenoide: due piccole ali anteriori e due grandi ali posteriori.
Inferiormente, sono presenti i processi pterigoidei.
L’occipitale, osso mediano, occupa la porzione postero-inferiore della scatola
cranica. È costituito da una squama posteriore, da due porzioni laterali e
da una anteriore o basilare. Tali porzioni delimitano il foro occipitale.
Il temporale è un osso pari. Contribuisce alla costituzione della base cranica
e delle pareti laterali della volta. È composto da più parti: la petromastoidea, la squamosa, la timpanica e la stiloidea. Notevole importanza è
rivestita dalla porzione petrosa, costituita dalla piramide o rocca, contenente l’organo dell’udito.
Il parietale è un osso quadrilatero, pari e simmetrico, che contribuisce a de20
limitare la volta cranica, nella sua porzione postero-superiore.
3.1.2
Splancnocranio
Lo splancnocranio, o massiccio facciale, è rappresentato dalle quattordici
ossa della porzione antero-inferiore del cranio.
Le ossa pari del massiccio facciale sono: il mascellare, il nasale, il lacrimale,
l’osso palatino, il cornetto inferiore e lo zigomatico; le ossa impari sono il
vomere e la mandibola. Solo quest’ultima gode di mobilità, articolandosi
con i condili dell’osso temporale (articolazione temporo-mandibolare).
Il mascellare è un osso pari, che contribuisce a delimitare la cavità orbitaria,
boccale e nasale. È costituito da un corpo e da quattro processi: frontale,
zigomatico, palatino ed alveolare. Nel corpo è disposta un’ampia cavità,
detta seno mascellare, comunicante con le cavità nasali.
Le ossa nasali sono piccole lamine quadrilatere, che costituiscono la volta
della piramide nasale.
L’osso lacrimale è un osso pari e simmetrico, che contribuisce a delimitare
parte della cavità orbitaria.
L’osso palatino, anch’esso pari, è costituito da due lamine: verticale ed orizzontale. Quest’ultima forma, insieme al processo palatino del mascellare, la
volta del palato e, quindi, la base delle cavità nasali.
Lo zigomatico è un osso quadrilatero pari. È articolato anteriormente con il
mascellare, posteriormente con il temporale e superiormente con il frontale.
Il vomere è un osso impari, che partecipa alla costituzione del setto nasale,
insieme all’etmoide.
La mandibola è un osso impari e mediano, costituito da una parte centrale, detta corpo, e da due porzioni laterali, dette branche montanti. Nella
porzione superiore di queste ultime si trova una profonda incisura, che si articola con l’osso temporale per formare l’articolazione temporo-mandibolare,
per mezzo della quale è possibile compiere movimenti di apertura e chiusura della bocca, nonché di spostamento anteriore, posteriore e laterale della
mandibola stessa.
[13]
21
Fig. 3.1: Vista frontale del cranio. Legenda: 1- Tubercolo mentale. 2Corpo della mandibola. 3- Ramo della mandibola. 4- Spina nasale anteriore.
5- Fossa canina. 6- Foro infraorbitario. 7- Foro zigomatico. 8- Superﬁcie
orbitaria del mascellare. 9- Fossa temporale. 10- Superﬁcie laterale dell’etmoide. 11- Fessura orbitaria superiore. 12- Osso lacrimale. 13- Foro ottico.
14- Forame etmoidale. 15- Linea temporale. 16- Solco sopraorbitario. 17Glabella. 18- Tuberosità frontale. 19- Arco sopraccigliare. 20- Osso parietale. 21- Sutura naso frontale. 22- Pterion. 23- Grande ala dello sfenoide. 24Superﬁcie orbitaria della grande ala dello sfenoide. 25- Parte squamosa del
temporale. 26- Osso nasale sinistro. 27- Osso zigomatico. 28- Fessura orbitaria inferiore. 29- Arco zigomatico. 30- Apertura piriforme. 31- Processo
mastoideo. 32- Fossa incisiva. 33- Angolo della mandibola. 34- Forame
mentale. 35- Sinﬁsi mentoniera.
22
3.2
Miologia del cranio
Al cranio fanno capo vari gruppi muscolari, che possono essere distinti in
estrinseci ed intrinseci.
I muscoli estrinseci hanno origine in parti diverse dal cranio (collo, tronco)
e prendono inserzione su di esso.
I muscoli intrinseci sono invece completamente alloggiati nella testa, dove
trovano sia origine che terminazione.
La muscolatura intrinseca del cranio è costituita da muscoli scheletrici (o
masticatori) e muscoli mimici (o pellicciai).
Oltre ad essi, si trovano nella testa altri muscoli, come quelli del padiglione
auricolare, del globo oculare, dell’orecchio medio, della lingua etc., che non
saranno però oggetto della presente trattazione.
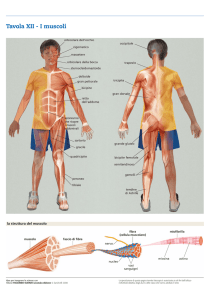
Fig. 3.2: Muscoli mimici visti anteriormente [14]
23
3.2.1
Muscoli scheletrici (Masticatori)
I muscoli masticatori collegano la scatola cranica alla mandibola, determinando i movimenti di quest’ultima: abbassamento ed elevazione, proiezione
anteriore e posteriore, lateralità.
I muscoli agenti sull’articolazione temporo-mandibolare sono il temporale,
il massetere ed i muscoli pterigoidei esterno ed interno.
Il muscolo temporale ha una forma triangolare ed è alloggiato nella fossa
temporale. Esso origina dalla linea temporale inferiore dell’osso parietale e,
anteriormente, dall’osso frontale. I suoi fasci si ﬁssano, tramite un robusto
tendine, sul processo coronoideo della mandibola. La contrazione di tale
muscolo determina l’elevazione e lo spostamento posteriore della mandibola.
Il muscolo massetere è un muscolo di forma quadrilatera, disposto sulla
branca montante della mandibola. È formato da una porzione superﬁciale
e una profonda. Esso origina dall’arcata zigomatica e si porta in basso per
raggiungere il margine posteriore, l’angolo e il margine inferiore della mandibola. L’azione del muscolo massetere determina, unitamente a quella del
temporale, l’elevazione della mandibola.
Il muscolo pterigoideo esterno origina dal processo pterigoideo e dalla grande
ala dello sfenoide e si porta lateralmente al collo del condilo della mandibola.
Tale muscolo agisce spostando la mandibola in avanti e lateralmente.
Il muscolo pterigoideo interno ha forma quadrilatera ed è situato sulla faccia mediale del ramo della mandibola. Origina dalla fossa pterigoidea e si
inserisce sulla faccia mediale dell’angolo della mandibola. L’azione di tale
muscolo determina l’elevazione mandibolare.
3.2.2
Muscoli mimici (Pellicciai)
I muscoli mimici sono per lo più formati da esili fasci muscolari, spesso privi
di aponeurosi. Essi prendono inserzione, con almeno uno dei due capi, sulla
faccia profonda della cute e sono determinanti nell’espressione ﬁsionomica.
Tali muscoli intrinseci, per la prevalente funzione che svolgono, sono particolarmente sviluppati nel massiccio facciale, mentre si presentano più ridotti in
corrispondenza del neurocranio. Lo strato muscolare mimico è posizionato
profondamente allo strato del tessuto connettivo sottocutaneo.
I muscoli mimici sono numerosi e collocati in diversi strati, tuttavia la descrizione seguente considera unicamente i muscoli implementati nel presente
progetto.
Per comodità espositiva, è possibile seguire un criterio topograﬁco e suddividere le regioni del cranio in: epicranica, orbitaria, nasale e buccale, considerandone i relativi muscoli. Non sarà menzionata la regione auricolare,
della quale non è stato implementato alcun muscolo, essendo questa dotata,
24
nell’umano, di scarsissima possibilità di movimento.
Regione epicranica
Di essa fanno parte il muscolo frontale e il muscolo procero (porzioni del
muscolo epicranico, che occupa l’intera regione).
Il muscolo frontale è rappresentato dalla porzione anteriore del muscolo epicranico, che si presenta come una sottile formazione muscoloaponeurotica,
distesa sulla volta cranica. Il frontale è un muscolo pari, appiattito e di forma quadrilatera; origina dal margine anteriore della galea capitis (porzione
intermedia aponeurotica del muscolo epicranico) e si porta anteriormente e
in basso per inserirsi nella faccia profonda della cute, in corrispondenza del
sopracciglio, della glabella e della parte superiore del dorso del naso; i suoi
fasci più mediali sono indicati con il termine di muscolo procero. Il muscolo
frontale, contraendosi, sposta in avanti il cuoio capelluto e corruga la fronte
(vedi ﬁg. 3.3).
Fig. 3.3: Muscolo frontale e muscolo procero in afms.
Regione orbitaria
Di tale regione fanno parte due muscoli: il corrugatore del sopracciglio e
l’orbicolare dell’occhio.
Il muscolo corrugatore è una sottile lamella carnosa, a concavità inferiore,
situata nel sopracciglio.
Origina dall’estremità mediale dell’arcata sopraccigliare e si inserisce sul
derma del sopracciglio in corrispondenza del foro sovraorbitario. È posto
25
profondamente al muscolo frontale e alla parte orbitaria del muscolo orbicolare. Contraendosi, porta medialmente e in basso la cute del sopracciglio.
Il muscolo orbicolare dell’occhio ha la forma di un anello ellittico, che si
dispone intorno alla rima palpebrale. Vi si distinguono una parte orbitaria,
una parte palpebrale e una parte lacrimale.
La porzione orbitaria è la più sviluppata ed è posta eccentricamente rispetto
alla palpebra. Essa origina dal margine superiore del legamento palpebrale
mediale e dal terzo mediale del margine sovraorbitario; si inserisce sul margine inferiore del legamento palpebrale mediale, sul terzo mediale del margine
infraorbitario e sul sacco lacrimale. Essa costituisce dunque un anello quasi
completo intorno alle palpebre, che si interrompe soltanto medialmente, tra
l’origine e l’inserzione. In corrispondenza dell’angolo laterale dell’occhio, alcuni fascetti abbandonano la parte orbitaria, scendendo nella guancia, dove
entrano nella compagine del muscolo zigomatico.
La porzione palpebrale è contenuta nello spessore della palpebra superiore
ed inferiore. Le sue ﬁbre originano dal legamento palpebrale mediale e si
portano esternamente per inserirsi al rafe palpebrale laterale.
La porzione lacrimale è situata profondamente. Prende origine dalla cresta
lacrimale posteriore, dietro al sacco lacrimale, e si dirige anteriormente e
in fuori, ﬁno alla commessura palpebrale mediale dove si divide in due fasci, rispettivamente per la palpebra superiore e inferiore, che conﬂuiscono
nella parte palpebrale del muscolo. La contrazione del muscolo orbicolare
dell’occhio determina la chiusura della rima palpebrale, convoglia le lacrime
verso l’angolo interno dell’occhio e ne facilita il deﬂusso, dilatando il sacco
lacrimale (vedi ﬁg. 3.4).
Fig. 3.4: Muscolo corrugatore del sopracciglio e muscolo orbicolare
dell’occhio in afms.
26
Regione nasale
I muscoli considerati, per questa regione, sono il nasale e il trasverso nasale
(porzione del precedente).
Il muscolo nasale è formato da una parte trasversa (muscolo trasverso del
naso) e da una parte alare (muscolo mirtiforme).
L’origine delle due parti è comune, dai gioghi alveolari dei denti incisivi e
canini superiori e dalla fossetta incisiva.
La parte trasversa, che ha origine più lateralmente, ricopre la parte posteriore dell’ala del naso e si ﬁssa al dorso del naso mediante un’aponeurosi che
si unisce a quella del lato opposto.
La parte alare si porta alla cute dell’estremità posteriore del setto mobile e
della narice. Contraendosi, il muscolo nasale comprime la parete leterale del
naso, restringendo la narice e il vestibolo (vedi ﬁg. 3.5).
Fig. 3.5: Muscolo nasale e muscolo trasverso nasale in afms.
Regione buccale
Le labbra presentano grande mobilità e sono pertanto fornite di un ricco
corredo muscolare, del quale sono stati presi in considerazione il muscolo elevatore del labbro superiore, zigomatico maggiore e minore, orbicolare
della bocca, risorio, depressore dell’angolo della bocca e mentale.
Il muscolo elevatore del labbro superiore origina dal margine infraorbitario,
al di sopra del foro infraorbitario, e si inserisce alla cute del labbro superiore,
medialmente alla terminazione dello zigomatico minore. La contrazione di
tale muscolo determina il sollevamento del labbro superiore (vedi ﬁg. 3.6).
Il muscolo zigomatico maggiore origina dalla faccia laterale dell’osso zigomatico e si inserisce sulla faccia profonda della cute e della mucosa labiale,
in corrispondenza della commessura, dove invia anche ﬁbre nella compagine
del muscolo orbicolare della bocca. Con la sua azione, sposta la commessura
labiale in alto e indietro (vedi ﬁg. 3.7).
27
Fig. 3.6: Muscolo elevatore del labbro superiore in afms.
Fig. 3.7: Muscolo zigomatico maggiore in afms.
Il muscolo zigomatico minore origina dalla faccia laterale dell’osso zigomatico, anteriormente allo zigomatico maggiore, e si inserisce alla cute del labbro
superiore, al di sopra della commessura. La contrazione di tale muscolo consente il sollevamento del labbro superiore (vedi ﬁg. 3.8).
Il muscolo orbicolare della bocca partecipa largamente alla costituzione delle labbra e si presenta come un anello ellittico disposto intorno alla rima
buccale; si estende dal margine libero delle labbra alla base del naso, in alto,
e al solco mentolabiale, in basso. Vi si considerano una parte esterna e una
parte interna. La parte esterna è periferica e comprende fasci che provengono da vari muscoli mimici (canino, buccinatore, triangolare, incisivi); tali
fasci formano due semicerchi che hanno il loro centro in corrispondenza della
commessura e la loro estremità sulla linea mediana del labbro superiore e inferiore. Alcuni fasci della porzione esterna si inseriscono alla faccia profonda
della cute labiale, in vicinanza della linea mediana e della cute che riveste il
contorno posteriore della narice e la parte posteriore del setto membranoso
(muscolo depressore del setto). La parte interna del muscolo orbicolare è
formata da una anello posto in vicinanza del margine libero delle labbra.
Tale anello è costituito da una parte superiore (labbro superiore) e da una
28
Fig. 3.8: Muscolo zigomatico minore in afms.
parte inferiore (labbro inferiore), che si incrociano a livello delle commessure, inserendosi alla faccia profonda della cute e della mucosa.
In vicinanza del margine libero delle labbra, si trovano poi fasci che si dirigono sagittalmente dalla faccia profonda della cute alla faccia profonda della
mucosa. Con la sua azione, il muscolo orbicolare della bocca restringe o
chiude la rima buccale; consente inoltre di sporgere in avanti le labbra (vedi
ﬁg. 3.9).
Fig. 3.9: Muscolo orbicolare della bocca in afms.
Il muscolo risorio ha forma triangolare, con la base posteriore e l’apice anteriore. Prende origine dalla fascia parotidea e si porta anteriormente, decor29
rendo sulla fascia masseterina, per raggiungere la commessura labiale, dove
si inserisce profondamente alla cute. Contraendosi, il risorio sposta indietro
la commessura labiale (vedi ﬁg. 3.10).
Fig. 3.10: Muscolo risorio in afms.
Il muscolo depressore dell’angolo della bocca (o muscolo triangolare delle
labbra) si trova al di sotto della commessura labiale, con la base in basso e l’apice in alto. Origina dalla faccia esterna del corpo della manibola,
in vicinanza della base; i suoi fasci si portano in alto, inserendosi in parte
sulla cute della commessura e in parte risalendo nel labbro superiore, dove
entrano a far parte del muscolo orbicolare. La contrazione del depressore
dell’angolo sposta in basso la commessura labiale (vedi ﬁg. 3.11).
Fig. 3.11: Muscolo depressore dell’angolo della bocca in afms.
Il muscolo mentale si trova in corrispondenza della sinﬁsi del mento. Origina dal giogo alveolare del dente incisivo mediale inferiore e si porta in basso
inserendosi alla cute del mento. Con la sua azione, solleva e corruga la cute
del mento (vedi ﬁg. 3.12).
[13] [14] [15]
30
Fig. 3.12: Muscolo mentale in afms.
31
Capitolo 4
Modello della pelle
4.1
Anatomia della pelle umana
La pelle umana è l’organo più grande di tutto il corpo, la sua superﬁcie, in
una persona adulta, è di circa 2 metri quadri e svolge innumerevoli funzioni,
tutte di grandissima importanza e utilità: ci protegge dai virus e dai batteri che ci attaccano dal mondo esterno, regola la temperatura corporea e
immagazzina acqua, grasso e sangue. La sua importanza può essere meglio
percepita con l’aiuto di qualche dato signiﬁcativo:
• la pelle di una persona adulta costituisce circa il 15–20% dell’intero
peso corporeo
• ogni centimetro quadrato di pelle ha circa 6.000.000 di cellule, 5.000
recettori sensoriali, 100 ghiandole sudoripare e 15 ghiandole sebacee.
La pelle viene continuamente rigenerata. Una cellula nasce nel livello più
basso chiamato derma, fornita di vasi sanguigni e terminazioni nervose, quindi migra verso l’alto per circa due settimane, ﬁno a quando raggiunge il livello più esterno, chiamato epidermide. La cellula passa altre due settimane
nell’epidermide, appiattendosi gradualmente, poi muore e viene cambiata.
Ogni giorno vengono cambiate circa 2-3 miliardi di cellule, la pelle si rinnova completamente ogni mese e questo accade perché è la nostra prima
linea difensiva contro la disidratazione, le infezioni, le ferite e le temperature
estreme.
L’epidermide
L’epidermide è la zona più esterna della pelle, ha uno spessore compreso tra
0.5 - 1 mm, ed è costituita da tre tipi di cellule: cheratinociti, melanociti e
cellule di Langerhans.
Le cellule cheratinociti sono quelle che producono la cheratina e rappresentano la maggior parte delle cellule dell’epidermide, man mano che maturano
32
perdono acqua e si appiattiscono, muovendosi verso lo strato più esterno,
chiamato stratum corneum, formato anche da proteine indurite e da lipidi,
generando cosı̀ una crosta protettiva.
I melanociti invece, producono la melanina, che è il pigmento responsabile
del tono e del colore della pelle.
Inﬁne ci sono le cellule di Langerhans che costituiscono il primo livello del
sistema immuntario, queste prevengono l’assorbimento da parte della pelle
di sostanze dannose.
Il derma
Il derma è lo strato interno della pelle. In esso sono presenti le ghiandole
sudoripare, i bulbi piliferi e le terminazioni nervose, mentre alla sua base si
trova il pannicolo adiposo, che prende il nome di ipoderma. Il ruolo del derma
è fondamentale in quanto provvede al nutrimento e all’ossigenazione della
soprastante epidermide, sprovvista di vasi. L’interfaccia tra epidermide e
derma è costituita da centinaia di estroﬂessioni di entrambi i tessuti (papille
e creste) il cui ﬁne è quello di aumentare esponenzialmente l’area di contatto
in modo da ottimizzare l’adesione e gli scambi.
L’ipoderma
È lo strato più interno della pelle, si trova al di sotto del derma ed è costituito
essenzialmente di grasso. Il grasso subcutaneo assorbe gli urti e funge da
isolante termico, proteggendo i tessuti sottostanti dal freddo e dai traumi.
Fig. 4.1: Sezione trasversa della pelle umana
33
4.2
Biomeccanica della pelle umana
La biomeccanica studia il comportamento meccanico dei materiali biologici
sotto particolari condizioni (pressione, trazione, vibrazione, frattura, ecc.).
Nel caso particolare di questo studio sull’animazione facciale, la biomeccanica spiega bene il comportamento della pelle del volto quando questa viene
deformata da forze esterne, che possono essere indotte dalla contrazione muscolare e/o dal movimento della mandibola.
Tipicamente in biomeccanica, la forza applicata ad un materiale è misurata
in relazione della grandezza del campione. Questa relazione è espressa dalla
seguente formula:
f
σ=
S
N
m2
(4.1)
dove σ è lo sforzo, f è la forza applicata e S è la sezione su cui è stata
applicata la forza.
Se invece si tratta di qualcosa di abbastanza semplice, come per esempio una
molla, lo sforzo e dovuto al cambiamento della sua lunghezza l, a partire da
una lunghezza a riposo lr si può calcolare come:
e=
l − lr
lr
(4.2)
Purtroppo, però, il comportamento della pelle, come quello di altri tessuti
organici, non può essere propriamente descritto da queste formule.
Risultati sperimentali hanno mostrato che la pelle ha un andamento viscoelastico non lineare [16] (vedi ﬁg. 4.2). Sottoposta ad un piccolo sforzo, la
Fig. 4.2: Relazione stress-strain del tessuto facciale
cute oﬀre una piccola resistenza alla forza, a causa delle ﬁbre di collagene
che si tendono. Se però la deformazione è maggiore, le ﬁbre di collagene si
34
tendono ancora di più, ﬁno ad allinearsi con la deformazione, aumentando
la resistenza.
Si può vedere infatti che la relazione stress-strain durante la fase di deformazione (loading) è diversa da quella durante la fase di rilascio (unloading),
formando un ciclo. Ciascuna parte di questo ciclo (loading e unloading) può
essere descritta da una funzione pseudo-elastica non lineare, poiché però, la
diﬀerenza tra le due non è signiﬁcativa, è possibile approssimare tutta la
relazione con una curva bifasica.
La pelle mostra delle evidenti proprietà viscoelastiche, infatti si comporta
in parte come un solido elastico e in parte come un ﬂuido viscoso.
La simulazione delle complesse proprietà della pelle è un obiettivo molto difﬁcile da perseguire, anche se si hanno a disposizione PC sempre più potenti
e performanti.
In afms, per simulare in maniera realistica la cute umana, si è deciso di
usare un modello ﬁsico che si basa principalmente sul concetto di masse e di
molle (mass-spring system), che permette di simulare l’elasticità non lineare
con uno sforzo computazionale abbastanza contenuto.
4.3
Mass-Spring System
Nella computer graphics il sistema masse-molle (mass-spring system) viene
utilizzato spesso per simulare oggetti deformabili, come per esempio la stoﬀa
e gli oggetti soﬃci. In questo caso viene utilizzato un sistema di masse-molle
per simulare la cute umana. Come è stato già detto, afms prende come
input un modello vrml che raﬃgura un volto umano, il modello è costituito
da un insieme di mesh triangolari (vedi ﬁg. 4.3). In pratica, simulare l’elasticità della pelle vuol dire deformare le mesh del modello vrml quando i
muscoli facciali vengono azionati.
A questo scopo l’intero sistema di mesh che costitutisce il modello viene convertito in un sistema di masse e molle, in cui a ciascun vertice del triangolo
Modello
VRML
beta
joakim
john
kevin
king
reana
yoda
Vertici
2197
909
736
498
757
6420
853
Poligoni
4118
1752
1341
956
1468
12524
1622
Molle
12634
5324
4156
2908
4452
37864
4954
Tabella 4.1: Questa tabella mostra, per ciascun modello, il numero di
vertici, di poligoni e di molle.
35
Fig. 4.3: (a) Modello facciale con textures (b) Modello facciale wire frame
viene fatta corrispondere una massa m e a ciascun lato viene fatta corrispondere una molla.
La deformazione è generata dall’applicazione delle forze muscolari sui nodimassa, il movimento di questi nodi induce delle forze interne che a loro volta
fanno muovere i nodi-massa a loro adiacenti, questo processo continua ﬁno a
quando non si raggiunge un nuovo punto di equilibrio in cui le forze interne
ed esterne si annullano.
La forza esercitata da una molla [17] sui nodi-massa a e b che vi sono
attaccati è:
l̇ · l l
Fa = − ks (|l| − r) + kd
|l| |l|
(4.3)
Fb = −Fa
(4.4)
dove con Fa e Fb è stata indicata la forza esercitata rispettivamente sul
nodo a e b, l è la lunghezza della molla deformata, r è la lunghezza della
molla a riposo, ks è la costante di rigidità, kd è la costante di smorzamento
e l̇ è la derivata nel tempo di l, cioè la diﬀerenza tra le velocità dei due nodi
a e b (va − vb ).
Nell’equazione 4.3 l’intensità della forza è proporzionale alla diﬀerenza tra
36
Fig. 4.4: (a) Disposizione delle molle sulla superﬁcie del modello (b) Le
unità di base che costituiscono la molla nel sistema di coordinate 3D. Il
triangolo grigio rappresenta lo smorzamento (damper).
la lunghezza attuale della molla e quella a riposo, mentre l’intensità della
forza di smorzamento è proporzionale alla diﬀerenza delle velocità dei nodi a
e b. Forze uguali ed opposte agiscono su ogni nodo, lungo l’asse che li unisce.
Come è stato detto nel par.4.1, la pelle umana è essenzialmente costituita
da tre strati; in afms la pelle viene simulata come un unico strato, questo
per ottenere una simulazione più veloce, in quanto si riduce sensibilmente il
numero di molle. Nonostante questa sempliﬁcazione, la simulazione continua ad essere molto relistica.
Può però accadere che l’intero sistema di masse e molle diventi instabile quando il movimento delle molle diventa estremamente grande e rapido
(questo può accadere quando c’è un movimento facciale molto veloce), in
questo caso quindi, l’intero sistema entra in risonanza e collassa. A volte
nemmeno aumentare la costante di smorzamento può servire. Per cercare di
rendere l’intero sistema il più stabile possibile, si cerca di calibrare bene la
costante di elasticità e il timestep della simulazione.
4.4
Forze vincolari di compenetrazione del cranio
Per riuscire ad ottenere una buona simulazione bisogna tener conto anche di
un altro componente fondamentale del volto: il cranio. A causa infatti della
presenza del teschio [2], la pelle, durante la creazione di un’espressione, deve
poter scivolare sulla parte ossea.
Se cosı̀ non fosse, durante la simulazione, a causa delle forze imposte sul modello dai muscoli mimici, si potrebbero avere degli eﬀetti indesiderati come
per esempio quello della perdita della forma e del volume corretti del volto.
Per ovviare a questo problema, è stata aggiunta oltre alle varie forze (musco37
lari ed elastiche) anche una forza vincolare di non penetrazione del teschio,
applicata a tutti i nodi interessati dal movimento, che permette a tutti i
nodi della pelle di scivolare sul cranio.
In afms viene preso come superﬁcie di riferimento per il teschio il modello
vrml stesso.
La forza vincolare di non penetrazione del volto Fskull (xi ), applicata a ciascun nodo xi del modello vrml è calcolata come:
Fskull (xi ) =
−(Fnet (xi ) · ni ) ni se Fnet (xi ) · ni < 0
0
altrimenti
(4.5)
dove Fnet (xi ) è la forza totale (elastica, di smorzamento e muscolare) dell’intera rete di nodi del modello vrml agente sul nodo xi e ni è la normale
al nodo xi . Quindi, aﬃnchè la pelle scivoli sul cranio (vedi ﬁg. 4.5), alla
Fnet (xi ) viene sommata la Fskull (xi ), ottenendo come risultato la F net (xi ).
Fig. 4.5: Forza vincolare di non penetrazione del cranio Fskull (xi )
38
4.5
Integrazione numerica
Durante lo sviluppo di afms, è stata posta particolare attenzione sull’utilizzo da parte di questa applicazione delle risorse di memoria e di tempo, si è
cercato infatti di riuscire ad ottenere un buon compromesso tra prestazioni
e accuratezza dell’animazione.
Uno dei punti chiave è stato quello di realizzare correttamente il comportamento dell’intero sistema di masse e molle, dell’azione muscolare e del
vincolo imposto dal cranio, attraverso un’integrazione numerica che fosse la
meno dispendiosa possibile dal punto di vista delle risorse computazionali.
4.5.1
Equazioni che regolano la deformazione della pelle
Le equazioni che regolano la deformazione del volto virtuale costituito dal
sistema di masse e molle, dai muscoli mimici e dal vincolo di non compenetrazione del cranio, sono equazioni diﬀerenziali del secondo ordine e possono
essere espresse [18] attraverso vettori tridimensionali, del tipo:
M
dx(t)
d2 x(t)
+ Kx(t) = Fmus (x(t)) + Fskull (x(t))
+D
2
dt
dt
(4.6)
dove M è la massa del nodo, D è il fattore di smorzamento, K è il coeﬃciente di elasticità, Fmus è la forza esercitata dai muscoli e inﬁne Fskull è la
forza vincolare di non compenetrazione del cranio.
Se si ha un sistema formato da n nodi, allora x è un vettore di dimensione
3n mentre M, D e K sono matrici diagonali 3n × 3n.
Kx(t) è la forza elastica, quindi si può introdurre Fela che può essere espressa come:
Fela (x(t), K) = Kx(t)
(4.7)
sostituendo la 4.7 nell’equazione 4.6 e riordinando si ottiene:
M
dx(t)
d2 x(t)
= Fmus (x(t)) + Fskull (x(t)) − Fela (x(t), K)
+D
2
dt
dt
(4.8)
Fmus , Fskull e Fela sono vettori di dimensione 3n.
La soluzione completa per l’intero sistema si ottiene processando iterativamente tutti i punti-massa e per ognuno di essi bisogna risolvere l’equazione 4.8.
39
Si prenda, per semplicità, in considerazione un singolo punto-massa mi e
per esso verrà risolta l’equazione 4.8. Per comprendere meglio come cercare
la soluzione di questa equazione diﬀerenziale del secondo ordine, la si divide
in un sistema di due equazioni diﬀerenziali del primo ordine, introducendo
la funzione della velocità vi (t).
⎧ dx (t)
i
⎪
⎨ dt = vi (t)
⎪
⎩ dvi (t)
dt
=
Fmus (xi (t))+Fskull (xi (t))−Fela (xi (t),K)−Dv i (t)
mi
(4.9)
Se al tempo t0 i valori iniziali sono:
x0i = xi (t0 )
vi0 = vi (t0 )
data la posizione xni = xi (tn ) e la velocità vin = vi (tn ) al tempo tn , l’obiettie vin+1 del time step successivo
vo è quello di calcolare rispettivamente xn+1
i
tn+1 .
È stato dimostrato [17] che i metodi di integrazione implicita sono migliori rispetto a quelli espliciti nel caso in cui si ha a che fare con sistemi di
equazioni rigidi. In questo modo, un soﬁsticato metodo implicito consente
di poter usare time step abbastanza grandi per risolvere le equazioni indicate sopra. L’attenzione verrà ora focalizzata su un semplice metodo che
garantisce un’alta velocità di aggiornamento per l’animazione.
e vin+1 al tempo tn+1 a partire
Si usa il metodo implicito per calcolare xn+1
i
dagli stati correnti xni e vin al tempo tn .
⎧
Fmus (xn+1
)+Fskull (xn+1
)−Fela (xn+1
,K)−Dvn+1
i
i
i
i
⎪
⎨ vin+1 = vin + Δt
mi
⎪
⎩
xn+1
i
=
xni
+
(4.10)
Δtvin+1
Come è possibile notare, la seconda equazione del sistema 4.10 dipende solamente dalla variabile vin+1 ; ma nella prima equazione, la funzione della
forza muscolare, la funzione della forza vincolare di non compenetrazione
del cranio e la forza elastica del sistema masse-molle, dipendono a loro volta
.
ancora da xn+1
i
ad ogni
Per sempliﬁcare la risoluzione del sistema, anzichè estrarre xn+1
i
viene
stimato
usando
il
metodo
di
Eulero
esplicito,
ottenentime-step, xn+1
i
do:
= xni + Δtvin
(4.11)
xn+1
i
appena calcolato con la 4.11 nella prima
Quindi, inserendo il valore di xn+1
i
equazione del sistema 4.10, si ottiene la vin+1 .
Il metodo di Eulero viene utilizzato per una gran quantità di applicazioni,
come per esempio i videogames. In afms è stata introdotta un’ulteriore
40
sempliﬁcazione nel metodo di Eulero (Semi-Implicit Backward Euler), che
permette una maggiore stabilità dell’applicazione, infatti viene dapprima
calcolata in maniera esplicita la vin+1 come:
Fmus (xn+1
) + Fskull (xn+1
) − Fela (xn+1
, K) − Dvn+1
i
i
i
i
mi
(4.12)
come:
e poi viene calcolata in maniera implicita la xn+1
i
vin+1 = vin + Δt
= xni +
xn+1
i
Δt n
(v + vin+1 )
2 i
(4.13)
Per assicurare che il sistema sia stabile, bisogna che valga sempre la seguente
relazione:
mi
(4.14)
Δt < 2
K
il che in pratica vuole dire che il time step Δt e la costante di rigidità K non
devono essere troppo grandi, mentre la massa mi non deve essere troppo
piccola.
41
4.6
Strutture dati nel mass-spring system
Al ﬁne di ottenere una simulazione realistica degli eﬀetti dei muscoli mimici
sulla pelle del volto, si è resa necessaria la disponibilità di alcuni dati per
ciascun nodo-massa e per ciascuna molla.
In fase di progettazione di afms, si è deciso di dedicare una classe per la
rappresentazione del singolo nodo e una classe per la rappresentazione della
molla.
4.6.1
Struttura dati del nodo-massa
L’oggetto “nodo” è composto dai seguenti campi:
• Massa: la massa del nodo, tutti i nodi hanno la medesima massa.
• Posizione iniziale: la posizione iniziale del nodo all’istante t0 .
• Posizione corrente: la posizione corrente del nodo all’istante ti .
• Prossima posizione corrente: la posizione del nodo all’istante ti+1 .
• Velocità corrente: la velocità corrente del nodo all’istante ti .
• Prossima velocità corrente: la velocità del nodo all’istante ti+1 .
• Forza della rete: la somma di tutte le forze agenti sul nodo.
• Normale: la normale ni del nodo.
• Nodi vicini: il vettore contenente gli indici dei nodi vicini.
• Numero dei nodi vicini: il numero dei nodi vicini.
• Facce: il vettore contenente gli indici delle facce dei poligoni a cui il
nodo appartiene.
• Vettore delle molle di connessione: il vettore contenente tutte le
molle che collegano il nodo xi ai suoi vicini.
• Numero delle molle di connessione: il numero delle molle che
connettono il nodo xi ai nodi vicini.
4.6.2
Struttura dati della molla
L’oggetto “molla” è composto dai seguenti campi:
• Lunghezza di riposo: è la lunghezza della molla quando su di essa
non agisce alcuna forza.
42
Fig. 4.6: Modello strutturale della molla. s è la componente elastica, d è
lo smorzamento
• Costante di rigidità: (stiﬀness) la costante di rigidità della molla
gioca un ruolo fondamentale nella simulazione, infatti attraverso di
essa si riesce a regolare la “durezza” della molla, controllandone quindi
l’andamento oscillatorio.
• Fattore di smorzamento: (damping factor ) è il fattore di smorzamento che regola per l’appunto lo smorzamento della molla. Vale la
pena ricordare che il modello di molla utilizzato in questo progetto
è quello costituito da una componente elastica e dallo smorzamento
(vedi ﬁg. 4.6).
• Gli estremi: vengono speciﬁcati i nodi-massa che si trovano agli estremi della molla; degli estremi si conosce l’indice che fa riferimento ai
vertici del modello vrml e la posizione attuale assunta dai nodi-massa
al tempo ti .
43
Capitolo 5
Modello muscolare
5.1
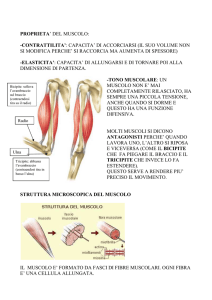
Struttura anatomica reale del muscolo
Ogni muscolo risulta composto da ﬁbre muscolari, il cui numero dipende
dalla grandezza del diametro trasverso del muscolo e dal troﬁsmo1 di ogni
singola ﬁbra, nonché dall’orientamento delle ﬁbre stesse.
Vi sono diverse fasce connettivali che avvolgono il muscolo e le sue ﬁbre, in
maniera tale da dividere la sua struttura globale in gruppi e sottogruppi.
La fascia più esterna è quella che avvolge l’intero muscolo e prende il nome
di epimisio. Le successive fasce sono il perimisio (che avvolge i fasci di ﬁbre
muscolari) e l’endomisio (che avvolge le singole ﬁbre).
Ogni ﬁbra ha un diametro da 10 a 100 μm ed è costituita dalla membrana che
la avvolge, l’endomisio, da un contenuto indiﬀerenziato detto sarcoplasma
(il citoplasma delle cellule muscolari) e da un certo numero di mioﬁbrille, il
cui diametro varia da 1 a 2 μm. A sua volta la mioﬁbrilla, avvolta da una
membrana detta sarcolemma, è costituita da mioﬁlamenti fra loro contigui
o a contatto, in base alla funzione che stanno esplicando, detti actina e
miosina.
Funzione contrattile ultramicroscopica
La funzione contrattile è desumibile dal movimento dei ﬁlamenti di actina e
miosina (proteine contrattili). Tali ﬁlamenti, siti all’interno delle mioﬁbrille,
si allineano parallelamente lungo l’asse maggiore del muscolo.
I ﬁlamenti di miosina sono più grossi e dotati di espansioni peduncolate,
dette ponti trasversali. Durante la contrazione, i ponti trasversali vengono
a contatto con i ﬁlamenti di actina, in particolari punti detti siti attivi; successivamente essi modiﬁcano la loro angolazione, spostando actina e miosina
l’una rispetto all’altra; quando un ponte perde il contatto con un sito dell’actina, viene ripreso dal sito attivo successivo, e cosı̀ via ﬁno al termine della
1
Grado di “nutrizione” di un tessuto. Per le fibre muscolari ci si riferisce al loro spessore.
44
contrazione. I ﬁlamenti non variano dunque la loro lunghezza, ma scorrono
gli uni sugli altri, determinando macroscopicamente un complessivo accorciamento muscolare.
Anatomicamente, le striature visibili nelle sezioni longitudinali del muscolo
sono dovute al particolare allineamento dei ﬁlamenti actinici e miosinici. Si
distinguono, infatti, bande chiare e scure.
Le bande chiare sono deﬁnite bande o zone I (isotrope), quelle scure sono
deﬁnite bande o zone A (anisotrope). All’interno di ogni zona A è visibile
una parte più chiara detta zona H. La linea verticale che divide a metà la
zona I è detta linea Z.
L’unità funzionale contrattile del muscolo è denominata sarcomero. Tale segmento è compreso tra due linee Z, dunque risulta composto da una banda
scura A e due semibande chiare I. Le mioﬁbrille possono essere considerate
come una successione di sarcomeri.
La contrazione muscolare determina un avvicinamento di due linee Z successive e, dunque, l’accorciamento di ogni singolo sarcomero.
Fig. 5.1: Struttura muscolare
45
Modello meccanico muscolare
Oltre alla speciﬁca azione contrattile svolta dalle mioﬁbrille, il muscolo è
dotato anche di strutture elastiche.
Le strutture elastiche sono costituenti del tessuto connettivo e si dividono
in strutture elastiche in serie e in parallelo.
Le strutture elastiche in serie (Es) sono rappresentate dal tendine e dai suoi
prolungamenti all’interno del muscolo: la loro funzione, durante l’attività
contrattile, è quella di “ammortizzare” le sollecitazioni prodotte sia dagli allungamenti che dalle contrazioni.
Le strutture elastiche in parallelo (Ep), rappresentate dal sarcolemma (membrana connettivale della mioﬁbrilla), da altre membrane connettivali e dal
tessuto connettivo interposto, “smorzano” soltanto le sollecitazioni prodotte dagli allungamenti, riducendo le resistenze. Dalla ﬁg. 5.2 che mostra il
Fig. 5.2: Modello meccanico muscolare
modello meccanico muscolare, dove C sono gli elementi contrattili (ﬁbre),
Es ed Ep rispettivamente gli elementi elastici in serie e in parallelo, si può
constatare che se C si accorcia, solo gli Es si allungano, viceversa se il muscolo viene allungato, sia gli Es che gli Ep vengono allungati. Se, infatti,
nella linea del modello meccanico rappresentato da C e da Es ci fosse solo
C, dopo lo stiramento tutto il percorso necessario per la contrazione sarebbe
eﬀettuato solo in maniera attiva, richiedendo quindi energia supplementare.
È necessario inoltre considerare la funzione di protezione interna, oltre che
esterna, di tali elementi connettivali: infatti, alla trazione e contrazione a
cui la parte contrattile partecipa in prima persona, contribuiscono con il
loro apporto di resistenza gli Es e gli Ep. Da sottolineare nuovamente, il
contributo in allungamento dato dagli Es, che consentono inoltre, nella fase
di ritorno elastico del muscolo, un risparmio di energia contrattile.
Forma e diametro dei muscoli
I muscoli del corpo umano presentano forme e dimensioni diverse, che dipendono in gran parte dalla qualità e dalla quantità di lavoro che devono
compiere. Ovviamente, quante più ﬁbre muscolari sono comprese in un muscolo, tanta più forza esso potrà esprimere.
46
Per valutare la forza potenziale esprimibile da un muscolo, si considera la sezione trasversa anatomica del muscolo nel punto medio in cui, normalmente,
il diametro presenta la sua maggior ampiezza. Ciò è possibile soprattutto nei
muscoli fusiformi, che presentano la particolarità funzionale di poter esprimere un maggior grado di accorciamento e di allungamento.
Quando, tuttavia, si ha a che fare con muscoli penniformi, l’obliquità delle
loro inserzioni non consente con un’unica misura di veriﬁcare il diametro
trasverso; si fa, pertanto, ricorso alla misurazione della loro sezione trasversa ﬁsiologica, cosı̀ detta in quanto non si tratta di una vera e propria sezione
trasversale.
Va osservato che l’obliquità delle ﬁbre di un muscolo pennato consente di
potervene immagazzinare una maggior quantità e, quindi, di essere potenzialmente più forte. Viceversa, i muscoli fusiformi hanno, proporzionalmente, minor forza, ma, come già ricordato, possono esprimere una maggior
escursione dei loro ﬁlamenti contrattili, dunque una maggior ampiezza di
movimento.
Contrazione, allungamento e velocità di contrazione
Ricerche di ﬁsiologia, eﬀettuate con preparazioni muscolari confermate da
ricerche in vivo, hanno consentito, soprattutto attraverso la costruzione della
curva tensione/lunghezza (T/L) e tensione/velocità (T/V), di determinare
una serie di dati uili alla comprensione di alcune importanti proprietà e limiti del tessuto muscolare.
Si tratta, innanzitutto, delle modalità con cui si realizzano contrazioni e allungamenti nelle ﬁbre muscolari e, poi, delle particolari modiﬁcazioni ﬁsiche
che possono aver luogo a loro carico in presenza di variazioni della velocità
di contrazione o di allungamento.
Occorre infatti precisare che, per eﬀetto di un identico impulso nervoso,
quindi con eguale scarica di potenziali d’azione, si possono avere eﬀetti meccanici diversi. Ciò è dovuto al fatto che la forza espressa dal muscolo non
dipende solo da fattori nervosi, ma anche dallo stato in cui esso si trova nel
momento in cui viene raggiunto dallo stimolo elettrico.
Oltre alla funzione elastica delle strutture passive del muscolo (Ep, Es) e alla funzione contrattile delle strutture attive (ﬁlamenti di actina e miosina),
occorre aggiungere che il muscolo presenta le seguenti proprietà meccaniche
durante la funzione contrattile:
- la stiﬀness;
- la viscosità.
Si intende per stiﬀness (“durezza”, “rigidità”) il rapporto esistente fra l’aumento della tensione muscolare e l’allungamento che la ﬁbra muscolare subisce. In pratica, la stiﬀness rappresenta la reazione del muscolo a seguito
47
del suo stesso allungamento; tale reazione è direttamente proporzionale all’entità dell’allungamento ed è dovuta soprattutto all’impiego delle strutture
attive (ﬁbre muscolari), ma anche di quelle passive, ossia delle strutture elastiche in serie (Es).
Si intende per viscosità la reazione meccanica presente nel muscolo soprattutto a causa della velocità con la quale si compiono contrazione e allungamento. Si tratta di un fenomeno che porta a dissipazione di parte dell’energia
utilizzata per l’azione muscolare. Vi è proporzionalità diretta con la velocità
di contrazione per quanto riguarda attriti modesti dovuti agli Es. Gli attriti
principali, però, sono quelli presenti nei ﬁlamenti di actina e miosina, per i
quali tale principio di proporzionalità non è valido.
La curva tensione/lunghezza (ﬁg. 5.3) manifesta che, in seguito all’allunga-
Fig. 5.3: Curva Tensione/Lunghezza
mento di un muscolo, la tensione inizia alla lunghezza di riposo (Ldr) del
muscolo stesso e l’allungamento può arrivare ﬁno a circa il 90% in più della
sua Ldr; superato tale livello, il muscolo si rompe.
La produzione di tensione può iniziare anche a metà della Ldr, ma non a misure inferiori a questa, poiché il muscolo perderebbe la capacità di contrarsi.
Dal 50% della Ldr ﬁno al 100%, la tensione è tutta a carico delle strutture
contrattili, successivamente intervengono anche le strutture elastiche.
Strutture elastiche e contrattili lavorano insieme ﬁno a circa il 120–130%
della Ldr, successivamente si ha una rapida riduzione e scomparsa del contributo delle strutture contrattili e, ﬁno al limite di rottura, la tensione
rimane a carico delle sole strutture elastiche. Si è potuto, cosı̀, stabilire che
le condizioni di allungamento ottimali del muscolo che determinano la migliore risposta muscolare allo stimolo nervoso sono, all’incirca, il 120-130%
48
della sua Ldr. Lunghezze maggiori o minori riducono la tensione esistente
nel muscolo e quindi la validità della sua contrazione.
Dal punto di vista ultramicroscopico, si veriﬁcano i seguenti fenomeni: il
sarcomero si allunga con una certa proporzionalità ﬁno ad un massimo che
corrisponde all’apice della curva T/L, corrispondente al 120–130% della Ldr.
Qui le capacità contrattili sono favorite da un massimo numero di ponti fra
actina e miosina. All’inizio dell’allungamento (dal 50% della Ldr), è presente
una grande sovrapposizione dei ponti actomiosinici, cosa che li rende meno
eﬃcienti.
Al contrario, dopo la fase ottimale (120–130% della Ldr) inizia un allontanamento eccessivo dei ﬁlamenti di miosina rispetto a quelli di actina. Si
hanno, pertanto, sempre meno ponti: ciò porta a minor contrazione e al
vicariamento della tensione a carico dei soli elementi elastici in serie; vi è
caduta di tensione e l’allungamento diminuisce. È stato inoltre dimostrato
che occorre uno stimolo nervoso di intensità minore per ottenere lo stesso
tipo di contrazione se il muscolo è preventivamente allungato.
La forza esprimibile varia a seconda dello stato di allungamento delle ﬁbre,
riferito alla Ldr, nel momento in cui il muscolo viene stimolato. Riassumendo, un allungamento del 120%, rispetto al 100% della Ldr di una ﬁbra
muscolare, è quello che consente di ottenere il massimo della forza, a parità
di altre condizioni, mentre la minor forza si ha partendo da una lunghezza
della ﬁbra muscolare pari al 50% della sua Ldr. La curva tensione/velocità
(ﬁg. 5.4) mostra il rapporto esistente tra le variazioni di forza (tensione)
Fig. 5.4: Curva Tensione/Velocità
espresse dal muscolo e gli incrementi di velocità della contrazione.
A sinistra del graﬁco, si può constatare che, con l’aumento della velocità,
una contrazione isotonica eccentrica (in allungamento), tende ad aumentare
49
la tensione, ﬁno ad un punto in cui essa si stabilizza. A destra del graﬁco è illustrata la relazione T/V nella contrazione isotonica concentrica, che
provoca accorciamento delle ﬁbre ﬁno alla ﬁne del movimento articolare. In
essa si può notare che quanto più aumenta la velocità, tanto più il muscolo
diminuisce la propria tensione, ﬁno ad una massima velocità, in cui la tensione si riduce a zero. Ciò si veriﬁca per eﬀetto della “viscosità”, che risulta
soprattutto a carico dello scorrimento dei ﬁlamenti di actina e miosina.
Dai due graﬁci T/L e T/V si evince che la massima potenza muscolare in
condizioni ergonomiche, ossia di massima funzionalità con minimo dispendio
energetico, si ottiene a velocità e accorciamenti non elevati, ma intermedi.
[19]
5.2
Modello muscolare virtuale
afms prende come input un modello vrml che raﬃgura un volto umano e,
a partire da questo e dagli fdp (che devono essere necessariamente noti),
vengono generati automaticamente tutti i muscoli mimici del volto, realizzando cosı̀ l’intera mappa muscolare.
In afms, i muscoli mimici possono essere suddivisi in due gruppi distinti: i
muscoli lineari (frontale, nasale, zigomatico, ecc.) e i muscoli circolari (muscoli degli occhi e della bocca).
Per realizzare i muscoli, si è deciso di implementare il modello proposto da
Kähler [1], nel quale, sia i muscoli lineari che quelli circolari vengono deﬁniti
come un’aggregazione di segmenti.
5.2.1
Il modello muscolare di Kähler
In questo modello [1] il muscolo viene rappresentato come un insieme di
ﬁbre, ognuna delle quali ha una struttura di controllo costituita da un poligono lineare formato da segmenti.
La contrazione isotonica di un muscolo viene controllata da un parametro
numerico, che causa l’accorciamento e la deformazione della geometria del
muscolo.
La sempliﬁcazione sta nel fatto che tutte le contrazioni del muscolo vengono visualizzate istantaneamente, in modo che possono essere trascurate le
dinamiche interne e la dipendenza dal tempo.
I modelli muscolari basati sulle ﬁbre sono molto comuni nell’ambito dell’animazione facciale, queste ﬁbre possono essere combinate tra di loro in fasci
paralleli, in modo da formare piani muscolari di larghezza arbitraria. La superﬁcie del muscolo è il risultato dell’unione di forme geometriche (poligoni
rettangolari) che sono attaccate ai segmenti che lo costitiuscono.
Il modello supporta due tipi di contrazioni: il muscolo lineare si contrae
lungo la sua estensione nella direzione del suo punto di origine mentre il
50
muscolo circolare, si contrae nella direzione di un punto centrale, tipicamente in modo ortogonale alla direzione delle ﬁbre.
Entrambi i tipi di muscoli sono descritti essenzialmente dallo stesso tipo di
poligono di controllo, anche se la rappresentazione del muscolo circolare necessita dell’identiﬁcazione del suo centro di contrazione.
Poligono di controllo del muscolo
Una ﬁbra muscolare è costituita da N control points pi ∈ R3 (i = 0, . . . , N − 1)
formando un poligono di controllo P. Un muscolo lineare si contrae sempre nella direzione di po (il punto di origine del muscolo lineare), invece il
muscolo circolare necessita di un ulteriore centro di contrazione p∗ verso il
quale si muovono tutti i suoi control points.
Per riprodurre la sporgenza e la contrazione delle labbra, non è suﬃciente
un unico centro di contrazione statico, bensı̀ p∗ può muoversi lungo un asse
centrale a0 a1 , fornendo al muscolo un parametro addizionale a ∈ [0, 1] che
descrive la posizione del centro di contrazione corrente tra i due estremi a0
e a1 dell’asse:
p∗ = (1 − a)a0 + aa1 .
(5.1)
Fig. 5.5: Esempio di ﬁbre muscolari lineari con i relativi poligoni di controllo
P = {pi }. (a) un muscolo lineare; (b) un muscolo circolare con il centro di
contrazione sull’asse centrale. Le frecce indicano la direzione generale della
contrazione.
Forma dei segmenti muscolari
Ciascun segmento del muscolo ha le proprie coordinate del mondo, che deﬁniscono la sua orientazione, lunghezza, altezza e spessore. Gli assi del
51
Fig. 5.6: Geometria del segmento muscolare. (a) Fibre muscolari stilizzate
(b) Alle ﬁbre muscolari sono stati aggiunti dei parallelepipedi per migliorarne
la rappresentazione.
segmento sono deﬁniti dalla sua direzione, che è data dalla connessione dei
control points, in più c’è un ulteriore vettore che punta nella direzione della pelle. La deformazione del muscolo modiﬁca i segmenti del poligono di
controllo e le molle che sono attaccate ai nodi della mesh vengono mossi in
accordo con la nuova posizione che hanno assunto.
Il fatto importante è che il cambiamento delle coordinate locali dei segmenti
durante la deformazione del muscolo, deﬁnisce completamente la forza esercitata da quest’ultimo sulla pelle del volto, non è quindi necessaria nessuna
informazione aggiuntiva circa la geometria complessiva del muscolo.
Tipicamente, un muscolo è formato da un fascio di ﬁbre che lavorano in
parallelo, però, per facilitare la gestione delle connessioni dei segmenti (del
poligono di controllo) che formano ciascun muscolo e le connessioni del muscolo con la pelle, è stata introdotta una sempliﬁcazione: ciascun muscolo
viene rappresentato come un’unica ﬁbra.
Deformazione del muscolo
Per ogni frame di animazione, la contrazione corrente di ciascun muscolo è
speciﬁcata da uno scalare c ∈ [0, 1], dove c = 0 signiﬁca che non c’è contrazione e c = 1 signiﬁca invece che c’è contrazione. Deve essere inoltre
speciﬁcato il parametro a ∈ [0, 1] introdotto per il muscolo circolare, che
muove il centro di contrazione del muscolo.
Sono sempre i muscoli che guidano la deformazione della pelle, al contrario,
la pelle non muove i muscoli.
Il processo che implica la traduzione dei parametri di contrazione di un muscolo nella deformazione vera e propria e nel conseguente spostamento dei
nodi-massa della mesh vrml viene eﬀettuato per stadi successivi.
Per un muscolo lineare, dato il valore di contrazione c, viene calcolato un
−1
N −1
nuovo poligono di controllo Q = {qi }N
i=0 a partire da P = {pi }i=0 , a ciascun control point pi ∈ P è assegnato un parametro t ∈ [0, 1] che descrive
52
Fig. 5.7: Contrazione (c = 12 ) di un muscolo lineare (a) e circolare (b). I
control points {pi } e {qi } rappresentano rispettivamente il muscolo rilassato
e contratto [1].
la posizione del punto nel poligono:
⎧
⎪
⎨ 0
i
||pj −pj−1 ||
ti =
j=1
⎪
N−1
⎩
j=1
||pj −pj−1 ||
, se i = 0
, altrimenti.
(5.2)
I parametri ti vengono scalati dal fattore di contrazione (1 − c) e quindi
limitati nell’intervallo [0.01, 1] per evitare di contrarre troppo il segmento:
t̃i = max{(1 − c)ti , 0.01}
(5.3)
Successivamente, ogni parametro t̃i è mappato nell’indice ki ∈ {0, . . . , N −2}
del punto di origine del segmento che contiene t̃i :
ki =
0
, se i = 0
j : tj < t̃i ≤ tj+1 , altrimenti.
(5.4)
Inﬁne i nuovi control points qi sono calcolati per interpolazione lineare:
qi = pki + (pki +1 − pki )
t̃i − tki
tki +1 − tki
(5.5)
In questo modo si ottiene un accorciamento della ﬁbra pari ad un fattore c,
in cui tutti i control points del muscolo si muovono lungo il percorso descritto
dal poligono di controllo di partenza, come mostrato nella ﬁgura 5.7(a).
53
Per il muscolo circolare, i segmenti vengono semplicemente contratti nella direzione del centro di contrazione corrente p∗ ∈ R3 (vedi ﬁg. 5.7(b)).
qi = p∗ + (1 − c)(pi − p∗ )
(5.6)
Per migliorare la contrazione non omogenea del muscolo orbicolare della
bocca, alle ﬁbre viene data la possibilità di sporgere di una quantità diversa
per la parte superiore rispetto a quella inferiore.
La parte più esterna del muscolo orbicolare della bocca (quella subito sotto
il naso) sporge molto poco, poiché questa parte del volto è strettamente vincolata da altri muscoli e dall’attaccamento al cranio del tessuto circostante.
Al contrario, la parte più interna del labbro può muoversi molto liberamente, questo eﬀetto viene realizzato variando il centro di contrazione per ogni
ﬁbra.
I punti che si trovano nella parte più esterna di una ﬁbra si contraggono
nella direzione del punto p⊥ , calcolato come:
p⊥ = a0 +
a · (pi − a0 )
a
||a||2
(5.7)
I punti che invece si trovano nella parte più interna della ﬁbra usano p∗ .
Per quei muscoli formati da f > 1 ﬁbre che lavorano in parallelo, le ﬁbre
sono numerate da 0 a f − 1, a partire dalla ﬁbra più esterna. Il centro di
contrazione p∗j usato dai punti sulla ﬁbra j viene calcolato per interpolazione
lineare tra gli estremi:
p∗j
j
j
p∗ + 1 −
=
p⊥
f −1
f −1
54
(5.8)
5.2.2
Il modello muscolare realizzato
In questa sezione viene presentato il modello muscolare implementato in
afms e, con l’ausilio di una serie di immagini, viene fatto il parallelo con
quello deﬁnito da Kähler, che è stato descritto nella sezione precedente.
I muscoli facciali si suddividono in: muscoli lineari e muscoli circolari.
Fig. 5.8: (a) Muscolo lineare: “muscolo elevatore del labbro superiore”. (b)
Muscolo circolare: “muscolo orbicolare della bocca”
I muscoli lineari presenti nella mappa muscolare facciale di afms sono: frontale, procero, corrugatore, nasale, trasverso nasale, elevatore del labbro superiore, zigomatico minore, zigomatico maggiore, labbro superiore, risorio,
depressore e mentale.
I muscoli circolari invece sono: l’orbicolare dell’occhio e l’orbicolare della
bocca.
Fig. 5.9: (a) Elementi costitutivi di un muscolo lineare. (b) Elementi
costitutivi di un muscolo circolare.
Per ciascun muscolo lineare si ha un punto di origine, un punto di inserzione
55
nella cute e inoltre il muscolo è suddiviso, come accade in realtà, in tanti
sarcomeri, che ne rappresentano le unità di costituzione di base (a livello
microscopico).
Per il muscolo circolare, invece, non c’è né origine e né inserzione, ma c’è il
centro di contrazione, inoltre anch’esso è suddiviso in tanti sarcomeri.
Poligono di controllo del muscolo
Come descritto dal modello muscolare di Kähler [1], per ciascun muscolo
viene deﬁnito un poligono di controllo P = {pi }; allo stesso modo, in afms
il comportamento di un muscolo viene regolato dal suo poligono di controllo.
Fig. 5.10: (a) Poligono di controllo di un muscolo lineare (zigomatico maggiore). (b) Oltre al poligono di controllo viene mostrato anche il perimetro
delimitatore.
La ﬁgura 5.10(a) mostra il poligono di controllo del muscolo zigomatico maggiore che, come si può vedere, è formato dai suoi control points {p0 , . . . , p5 },
mentre la ﬁgura 5.10(b) mostra anche il perimetro delimitatore del muscolo.
Allo stesso modo la ﬁgura 5.11(a) mostra il poligono di controllo del muscolo
orbicolare dell’occhio, che è un muscolo circolare, formato dai control points
{p0 , . . . , p7 }; la ﬁgura 5.11(b) mostra inoltre il suo perimetro delimitatore.
56
Fig. 5.11: (a) Poligono di controllo di un muscolo circolare (orbicolare dell’occhio). (b) Oltre al poligono di controllo viene mostrato anche il perimetro
delimitatore.
57
Contrazione del muscolo
In afms ciascun muscolo viene deformato, in base a quanto descritto dall’algoritmo di Kähler, agendo progressivamente sul suo poligono di controllo
(e quindi anche sui suoi control points).
Fig. 5.12: (a) Muscolo zigomatico maggiore rilassato. (b) Muscolo zigomatico maggiore contratto. (c - d) Esempio di azione dei muscoli orbicolari
degli occhi.
58
5.3
La mappa muscolare
Come è stato già detto in precedenza, afms, a partire da un modello vrml
rappresentante un volto umano e dai suoi fdp, ricostruisce in modo automatico la mappa dei muscoli facciali.
In questo studio è stata posta particolare attenzione all’aspetto anatomico, infatti si è cercato di ricreare e posizionare ciascun muscolo in modo
anatomicamente corretto, seguendo fedelmente le indicazioni dei manuali di
anatomia clinica e umana [13] [14] [15] e di quello di cinesiologia [19].
Ciascun muscolo è stato posizionato sul volto traducendo le indicazioni anatomiche nella sua localizzazione virtuale, che è funzione degli fdp.
Ovviamente il risultato che si ottiene dipende molto dalla deﬁnizione del
modello vrml fornito in input (che può essere espressa in base al numero
dei vertici che lo costituiscono); ma ancora di più dall’accuratezza con cui
sono stati editati (con l’aiuto di visage|life) gli fdp.
La tabella seguente mostra la corrispondenza tra gli fdp e i punti di origine
e inserzione dei muscoli lineari. Vale la pena ricordare che i punti di origine
e inserzione deﬁniscono completamente il muscolo lineare e la sua posizione
sul volto.
Muscolo Lineare
Frontale Interno
destro
sinistro
Frontale Maggiore
destro
sinistro
Frontale Esterno
destro
sinistro
Corrugatore del
destro
sopracciglio
sinistro
Procero
destro
sinistro
Nasale
destro
sinistro
Trasverso
destro
Nasale
sinistro
Labbro
destro
superiore
sinistro
Elevatore del
destro
labbro superiore
sinistro
Punto di
origine
(11.2 − 11.1) 16 + 11.1
(11.3 − 11.1) 16 + 11.1
(11.2 − 11.1) 13 + 11.1
(11.3 − 11.1) 13 + 11.1
(11.2 − 11.1) 23 + 11.1
(11.3 − 11.1) 23 + 11.1
4.4
4.3
(11.2 − 11.1) 16 + 11.1
(11.3 − 11.1) 16 + 11.1
9.6
9.7
9.12
9.12
(9.15 − 9.4) 12 + 9.4
(9.15 − 9.5) 12 + 9.5
3.10
3.9
Punto di
inserzione
4.2
4.1
4.4
4.3
4.6
4.5
(4.2 − 4.4) + 4.4
(4.1 − 4.3) + 4.3
(4.2 − 4.4) 43 + 4.4
(4.1 − 4.3) 32 + 4.3
9.2
9.1
(9.3 − 9.2) 12 + 9.2
(9.3 − 9.1) 12 + 9.1
8.9
8.10
(9.15 − 9.3) 12 + 9.2
(9.15 − 9.1) 12 + 9.1
Tabella 5.1: (1-2) Tabella delle corrispondenze dei punti di origine e di
inserzione di un muscolo lineare con gli fdp del modello.
59
Muscolo Lineare
Zigomatico
destro
minore
sinistro
Zigomatico
destro
maggiore
sinistro
Risorio
destro
sinistro
Depressore del
destro
labbro inferiore
sinistro
Mentale
destro
sinistro
Punto di
origine
3.10
3.9
5.4
5.3
5.2
5.1
(8.4 − 9.2) + 8.4
(8.3 − 9.1) + 8.3
(2.1 − 8.3) · 2 + 9.1
(2.1 − 8.4) · 2 + 9.2
Punto di
inserzione
(2.7 − 8.6) 12 + 8.6
(2.6 − 8.5) 12 + 8.5
8.4
8.3
8.4
8.3
8.4
8.3
2.9
2.8
Tabella 5.2: (2-2) Tabella delle corrispondenze dei punti di origine e di
inserzione di un muscolo lineare con gli fdp del modello.
Come per i muscoli lineari, anche il posizionamento dei muscoli circolari è
stato eﬀettuato a partire dagli fdp. Come descritto dal modello di Kähler,
la contrazione del muscolo circolare è deﬁnita a partire dal centro di contrazione p∗ verso il quale tendono tutti i punti del poligono di controllo. In
afms il poligono di controllo del muscolo circolare viene calcolato a partire
dai punti che si trovano rispettivamente a nord, sud, est e ovest (Np, Sp, Ep,
Wp) di p∗ e che appartengono al contorno dell’occhio o della bocca (vedi
ﬁg. 5.13).
Fig. 5.13: I punti che deﬁniscono completamente il muscolo circolare. p∗
è il centro di contrazione; Np, Sp, Ep, Wp sono i punti attraverso i quali
viene realizzato il poligono di controllo del muscolo.
60
La tabella 5.3 mostra per ciascun muscolo circolare il centro di contrazione
p∗ e i quattro punti Np, Sp, Ep e Wp.
Muscolo Circolare
Orbicolare
destro
dell’occhio
sinistro
Orbicolare della bocca
p∗
3.6
3.5
2.3
Np
3.14
3.13
8.1
Sp
3.10
3.9
8.2
Ep
3.8
3.7
2.4
Wp
3.12
3.11
2.5
Tabella 5.3: Tabella delle corrispondenze tra i punti p∗ , Np, Sp, Ep, Wp
e i relativi fdp.
La ﬁgura 5.14 mostra il risultato ﬁnale ottenuto da afms, confrontato con la
mappa dei muscoli facciali reali [14]. Come si può vedere, a ciascun muscolo
del volto umano corrisponde il relativo muscolo sul volto virtuale.
Fig. 5.14: Corrispondenza tra i muscoli facciali reali (a) e quelli virtuali
generati automaticamente da afms (b).
61
Fig. 5.15: (a) Mappa muscolare completa stilizzata, sono visibili tutti i
muscoli con i loro poligoni di controllo. (b) Mappa muscolare completa wire
frame, per ciascun muscolo sono ben visibili i suoi sarcomeri.
Fig. 5.16: Esempio di due espressioni facciali realizzate con afms. (a)
Felicità (yoda). (b) Collera (john).
62
Capitolo 6
Analisi dei risultati
Come è stato già detto nel Capitolo 1, il volto è il canale più rilevante della
comunicazione non verbale [4].
Gli individui sono in grado di assumere, a piacere, un gran numero di espressioni facciali diverse, ma i decodiﬁcatori riescono a discernere solo fra più
ampi raggruppamenti di espressioni. Le diverse ricerche condotte sull’argomento, concordano che tutte le espressioni emozionali possono essere suddivise in sei grandi gruppi: felicità, tristezza, sorpresa, collera, paura e disgusto/disprezzo.
Con afms è possibile riprodurre tutte le espressioni appena citate sopra ed
eventualmente anche altre, che però potrebbero non riferirsi propriamente
ad emozioni, come per esempio interesse, vergogna, dolore, perplessità, stupore, ecc.
Verranno di seguito mostrati alcuni dei risultati ottenuti con afms; dapprima verranno mostrate per vari modelli facciali le mappe muscolari generate
automaticamente, si ricorda che la maggiore aderenza della mappa virtuale
con la muscolatura facciale reale dipende dal modello vrml, dal numero
dei suoi vertici e da quanto sono accurate le posizioni degli fdp del volto.
Quindi verranno mostrate le principali espressioni facciali realizzate per vari
modelli vrml.
Alla ﬁne ci sono anche le tabelle 6.1 e 6.2 nelle quali vengono dati i parametri
ﬁsici con cui sono state realizzate le suddette espressioni facciali e il tempo
impiegato da afms per realizzare l’intera rete di masse-molle e la mappa
muscolare.
I risultati riportati di seguito sono stati ottenuti con un personal computer
R
Centrino 1.4 GHz e 512 mb ddr sdram con sistema
con processore Intel
R
operativo Windows XP con SP2.
63
Fig. 6.1: I modelli vrml di riferimento utilizzati durante losviluppo di
afms. (a) beta. (b) john. (c) kevin. (d) yoda. (e) king. (f) reana.
64
Fig. 6.2: Esempi dei poligoni di controllo dei muscoli facciali. (a) beta. (b)
john. (c) kevin. (d) yoda. (e) king. (f) reana.
65
Fig. 6.3: Esempi di mappe muscolari con textures generate automaticamente da afms. (a) beta. (b) john. (c) kevin. (d) yoda. (e) king. (f)
reana.
66
Fig. 6.4: Espressioni facciali di beta. (a) Felicità. (b) Tristezza. (c)
Sorpresa. (d) Collera. (e) Paura. (f) Disgusto/Disprezzo.
67
Fig. 6.5: Espressioni facciali di john. (a) Felicità. (b) Tristezza. (c)
Sorpresa. (d) Collera. (e) Paura. (f) Disgusto/Disprezzo.
68
Fig. 6.6: Espressioni facciali di kevin. (a) Felicità. (b) Tristezza. (c)
Sorpresa. (d) Collera. (e) Paura. (f) Disgusto/Disprezzo.
69
Fig. 6.7: Esempio di espressioni realizzate da afms per un volto non umano:
yoda.
70
Fig. 6.8: Espressioni varie di king.
71
beta
john
kevin
king
reana
yoda
Stiﬀness
2.8
10
2.8
10
10
20
Damping factor
30
30
30
30
30
30
Massa (g)
0.30
0.30
0.30
0.30
0.30
0.30
Tabella 6.1: I valori della stiﬀness, del damping factor e della massa dei
nodi usati in afms per ottenere le espressioni riportate in precedenza.
beta
john
kevin
king
reana
yoda
Rete
masse-molle (sec)
1.362
0.671
1.052
1.342
10.445
0.471
Mappa
muscolare (sec)
0.02
0.01
0.01
0.01
0.06
0.01
Tempo
totale (sec)
1.382
0.681
1.062
1.352
10.505
0.481
Tabella 6.2: Tempi impiegati (in secondi) da afms per costruire la rete di
masse-molle e per generare la mappa muscolare.
72
Capitolo 7
Conclusioni
Il percorso logico concettuale che è stato seguito ﬁn qui è stato realizzato
in modo tale da spiegare nella maniera più accurata possibile tutte le scelte
implementative e tutti i problemi incontrati e risolti durante la realizzazione
di afms.
Tutto è nato dalla volontà di realizzare qualcosa che potesse in qualche
modo avere delle applicazioni reali, soprattutto nell’ambito della multimedialità e, più speciﬁcatamente, nell’informatica graﬁca.
Il fatto di implementare un’applicazione che realizzasse i muscoli mimici per
modelli virtuali e, conseguentemente le relative espressioni facciali, è sembrato l’argomento ideale che più si coniuga con l’obiettivo appena dichiarato.
Come è stato già accennato in precedenza, il volto umano può essere considerato senza alcun dubbio uno dei più potenti mezzi espressivi e di comunicazione esistenti; infatti tutti noi siamo capaci di interpretare il pensiero e
lo stato d’animo della persona con cui stiamo interagendo solamente osservando con attenzione l’espressione del suo viso.
Innanzitutto si è cercato di individuare il modello muscolare che fosse il
più “anatomicamente” adatto e quello proposto da Kähler nel suo articolo:
“Geometry-based Muscle Modeling for Facial Animation” [1] è quello che più
di altri simula il reale comportamento delle ﬁbre muscolari umane.
Si è passati poi alla progettazione e all’implementazione dell’applicazione,
sfruttando principalmente le librerie graﬁche contenute nel pacchetto software visage|SDK, messe a disposizione dalla Visage Technologies AB[3].
Durante lo sviluppo è stata posta particolare attenzione all’utilizzo delle
risorse computazionali di tempo e di memoria, quindi si è cercato di raggiungere un livello di simulazione che fosse il più reale possibile. Infatti,
oltre ad usare modelli di volti umani, afms è stato applicato anche ad un
volto non umano, yoda, riuscendo comunque ad ottenere dei buoni risultati
(le immagini di afms applicato a yoda si trovano nel capitolo 6 ﬁg. 6.7).
73
afms è un’applicazione eﬃciente e robusta, soprattutto grazie all’utilizzo
del metodo di Eulero (Semi-Implicit Backward Euler) per la realizzazione
del movimento ﬁsico delle molle.
Tutti i parametri della simulazione sono stati calibrati in modo tale da rendere l’applicazione più robusta possibile, cercando di ridurre al minimo i
casi di oscillazione dell’intero sistema masse-molle durante la simulazione.
Le oscillazioni rendono infatti il sistema molto instabile e talvolta possono
danneggiare irreparabilmente il modello 3D.
Per di più afms è un’applicazione interattiva, il che complica non poco le
cose, in quanto c’è un utente che interviene direttamente sulla simulazione,
che si ricorda avviene in tempo reale.
Tuttavia, la forte dipendenza della simulazione dalla topologia del modello
(disposizione e numero dei vertici e la precisione degli fdp sul volto), va a
scapito dell’accuratezza.
Nonostante tutto, in afms si è cercato di arrivare ad un buon compromesso tra eﬃcienza e robustezza, e i risultati che ne derivano sono certamente
molto credibili.
7.1
Prospettive future
Ovviamente, lo sviluppo di afms potrà continuare cercando da una parte di
migliorarne alcuni aspetti e dall’altra di estendere questa applicazione per
un più ampio utilizzo. afms potrebbe infatti essere preso come punto di
partenza nell’ambito di eventuali progetti di animazione facciale.
In questo senso, infatti, afms può essere l’inizio dell’animazione di personaggi virtuali 3D.
Per esempio: con afms si può realizzare la mappa dei muscoli mimici del
volto di un personaggio virtuale che poi potrà essere usata per simulare in
maniera opportuna le sue espressioni facciali nell’ambito della sua animazione globale.
Le future applicazioni di questo progetto potranno coinvolgere vari campi,
come ad esempio le telecomunicazioni, la realtà virtuale, l’insegnamento e
l’apprendimento, l’intrattenimento.
• Telecomunicazioni: nell’ambito delle telecomunicazioni si può pensare ad applicazioni tipo le videoconferenze online, infatti anziché trasmettere i frames con i volti reali, si potrebbe realizzare il modello
virtuale 3D dell’interlocultore, memorizzarlo su tutti i dispositivi connessi e quindi trasmettere soltanto i parametri di animazione del volto. In questo modo si potrebbe risparmiare moltissima banda, il che
avrebbe come diretta conseguenza la possibilità di realizzare videoconferenze anche con apparecchi che hanno una limitata disponibilità di
74
banda per la connessione, come ad esempio i telefoni cellulari di ultima
generazione.
• Realtà virtuale: moltissime sono le possibilità di utilizzo di afms
nella realtà virtuale, come per esempio la realizzazione di pagine web,
di tools per il training in ambito medico, centri informazioni, simulatori
di vario tipo, ecc.
• Insegnamento e apprendimento: si possono realizzare applicazioni
per impartire i primissimi insegnamenti ai bambini nella prima età scolare, per far apprendere le persone disabili oppure anche per realizzare
strumenti multimediali in grado di aiutare eventuali utenti nell’utilizzo
di un particolare pc o macchinario nell’ambiente lavorativo.
• Intrattenimento: non ultime sono le possibilità di applicazione nell’ambito dell’intrattenimento, quali la creazione di eﬀetti speciali per
il cinema, cartoni animati in 3D che ormai sono sempre più diﬀusi e i
videogiochi che, nell’ultimo decennio, grazie alla possibilità di sfruttare
le risorse di computer sempre più potenti, sono diventati cosı̀ curati in
ogni loro dettaglio che sembra quasi di essere realmente i protagonisti
delle avventure vissute sullo schermo.
75
Bibliografia
[1] K. Kähler, J. Haber, H. P. Seidel. Geometry-based Muscle Modeling for Facial Animation. Max-Planck-Institut für Informatik,
Stuhlsatzenhausweg, Germany.
[2] Y. Lee, D. Terzopoulos, K. Waters. Realistic Modeling for Facial
Animation. Computer Graphics (SIGGRAPH ’95 Conf.Proc.), pages
55–62, August 1995.
[3] Visage Technologies AB. URL: www.visagetechnologies.com, October,
2006.
[4] M. Argyle. Il corpo e il suo linguaggio, studio sulla comunicazione non
verbale. Zanichelli 2 Ed.
[5] S. M. Platt, N. I. Badler. Animating Facial Expressions. Computer
Graphics (SIGGRAPH ’81 Conf. Proc.), pages 245–252, August 1981.
[6] F. I. Parke. Parameterized Models for Facial Animation. IEEE
Computer Graphics and Applications, pages 61–68, November 1982.
[7] F. I. Parke. Computer generated animation of faces. Master’s thesis,
University of Utah, Salt Lake City, June 1972.
[8] C. Pelachaud, N. I. Badler, M. Steedman. Generating Facial Expressions for Speech. Department of Computer and Information Science,
University of Pennsylvania, Philadelphia.
[9] E. Gladilin, S. Zachow, P. Deuﬂhard, H.C. Hege. Towards a Realistic
Simulation of Individual Facial Mimics. In Proc. of Vision, Modeling
and Visualisation 2001 (VMV), Stuttgart, Germany:129–133, 2001.
[10] E. Gladilin, S.Zachow, P. Deuﬂhard, H.C. Hege. A nonlinear soft tissue model for craniofacial surgery simulations. In Proc. of Modeling
and Simulation for Computer-aided Medicine and Surgery (MS4CMS),
12:61–66, INRIA, Paris, France 2002.
[11] ISO/IEC 14496. MPGEG-4 Standard.
76
[12] ISO/IEC 14772. VRML97 - The Virtual Reality Modeling Language,
1997.
[13] G. Marinozzi, E. Gaudio, M. Ripani. Anatomia clinica. Antonio Delﬁno
Editore, Roma, 1993.
[14] F. H. Netter. Atlante di anatomia umana. Novartis Edizioni.
[15] G. Balboni, A. Bastianini, P. Motta et al. Anatomia umana. Edi-Ermes.
[16] Y. Zhang, E. Sung, E. C. Prakash. 3D Modeling of Dynamic Facial
Expressions for Face Image Analysis and Synthesis.
[17] A. Witkin, D. Baraﬀ. Physically Based Modeling: Principles and
Practice. School of Computer Science Carnegie Mellon University,
SIGGRAPH ’97.
[18] Y. Zhang, E. Sung, E. C. Prakash. Real-time Facial Expression
Animation on An Individualized Face Using Adaptive Simulation
Algorithm.
[19] V. Pirola.
Cinesiologia - Il movimento umano applicato alla
rieducazione e alle attività sportive. Edi-Ermes, February 1999.
[20] M. Fratarcangeli. Physically Based Synthesis of Animatable Face Models. Workshop On Virtual Reality Interaction and Physical Simulation,
F. Ganovelli and C. Mendoza (Editors) 2005.
[21] L. P. Nedel, D. Thalmann. Real Time Muscle Deformation Using
Mass-Spring Systems. Swiss Federal Institute of Technology, Lausanne,
Switzerland.
[22] Microsoft Developers Network MSDN. URL: www.msdn.microsoft.com,
October, 2006.
[23] D. Terzopoulos, K. Waters. Physically-Based Facial Modeling, Analysis
and Animation. University of Toronto, Toronto, Ontario.
[24] D. Baraﬀ, A. Witkin. Large Steps in Cloth Simulation.
Institute Carnegie Mellon University.
Robotics
[25] Foley, Van Dam, Feiner, Hughes, Phillips. Introduction to Computer
Graphics. Addison-Wesley, 1994.
[26] P. Ekman.
Program.
Psychology Emotion and Facial Recognition Training
[27] M. Cadoli, M. Lenzerini, P. Naggar, A. Schaerf. Fondamenti della progettazione dei programmi, principi tecniche e loro applicazioni in C++.
Città Studi Edizioni.
77
[28] J. Neider, T. Davis, M. Woo. OpenGL Programming Guide - The red
book. Addison-Wesley, First Printing, 1993.
[29] M. Fratarcangeli, M. Schaerf. Realistic Modeling of Animatable Faces
in MPEG-4. Departement of Computer System Science - University of
Rome ”La Sapienza”.
78
Appendice A
Guida all’interfaccia utente
Questa appendice è stata realizzata per guidare gli utenti ad un corretR
Vito utilizzo di afms. afms è un’applicazione realizzata con Microsoft
sual C++ 6.0 e gira su macchine con sistema operativo Windows XP.
Fig. A.1: Come si presenta afms al suo avvio.
Si presenta come una ﬁnestra suddivisa in due parti: la parte destra è costituita dalla ﬁnestra OpenGL nella quale viene visualizzato il modello vrml
del volto, mentre la parte sinistra è costituita da un pannello nel quale è
possibile trovare tutti i controlli necessari per la creazione dell’espressione
facciale, agendo direttamente su ciascun singolo muscolo.
79
Nella parte superiore della ﬁnestra c’è un menu di tipo standard, attraverso
il quale si può caricare il ﬁle .wrl ed eﬀettuare alcune operazioni di visualizzazione sul modello.
Di seguito è stata riportata una tabella che spiega la funzione svolta da ciascun item del menu.
Open WRL...
File
Exit
View
Face FDP
Face Vertex
Simple
Map
Polygon
Map
Texture
Map
Muscle
Muscle
Muscle
Muscle
Single Muscle
Apre il ﬁle .wrl contenente il
modello del volto
Termina l’applicazione e chiude la
ﬁnestra di afms
Mostra gli fdp del modello caricato
Mostra tutti i vertici del modello che
costituiscono la pelle del viso
Mostra l’intera mappa muscolare in
maniera stilizzata (linee e punti)
Mostra l’intera mappa muscolare
realizzata con i poligoni
Mostra l’intera mappa muscolare
realizzata con le textures
Frontalis
Visualizza solo il
muscolo frontale
Procerus
Visualizza solo il
muscolo procero
Corrugator Visualizza solo il
muscolo corrugatore
Orbicularis Visualizza solo il
Oculi
muscolo orbicolare
dell’occhio
Nasalis
Visualizza solo il
muscolo nasale
Transversus Visualizza solo il
Nasalis
muscolo trasverso
nasale
Upper Lip Visualizza solo il
Elevator
muscolo elevatore
del labbro superiore
Tabella A.1: (1-2) Tabella esplicativa degli elementi del menu di afms
80
Muscle
?
Single Muscle
Legenda
About...
Zygomaticus Visualizza solo il
Minor
muscolo zigomatico
minore
Zygomaticus Visualizza solo il
Major
muscolo zigomatico
maggiore
Upper Lip
Visualizza solo il
muscolo del labbro
superiore
Orbicularis Visualizza solo il
Oris
muscolo orbicolare
della bocca
Risorius
Visualizza solo il
muscolo risorio
Depressor
Visualizza solo il
Anguli
muscolo depressore
della bocca
Mentalis
Visualizza solo il
muscolo mentale
Mostra una ﬁnestra con una semplice legenda delle abbreviazioni usate
per etichettare i vari slider
Mostra una ﬁnestra con le informaziioni relative ad afms
Tabella A.2: (2-2) Tabella esplicativa degli elementi del menu di afms.
Comando
tasto sx mouse
tasto dx mouse
Ctrl + tasto sx mouse
F1
F2
F11
Azione
Il modello viene traslato
Il modello viene ruotato
Zoom
Visualizzazione wireframe
Visualizzazione solid con textures
Riposizionamento del modello al centro
della ﬁnestra
Tabella A.3: Questa tabella mostra l’azione svolta da ciascun comando.
81
È possibile anche interagire con il modello visualizzato nella ﬁnestra
OpenGL attraverso una combinazione di comandi impartiti con il mouse
e la tastiera, la tabella A.3 mostra l’azione svolta da ciascun comando.
Attraverso il menu a tendina “Single Muscle” è possibile visualizzare uno
o più muscoli generati da afms, come è possibile vedere nella ﬁgura A.3a.
Ciascun muscolo è costituito da più parti ed è possibile agire su ognuna
di esse muovendo il relativo slider, tutti gli slider relativi ad uno stesso muscolo sono stati raggruppati all’interno di un “group box ” (vedi ﬁg. A.3b).
Ogni slider inoltre, all’interno del suo group box, viene identiﬁcato attraverso un’etichetta che è l’acronimo del muscolo che muove; per esempio,
osservando la ﬁg. A.3b lo slider indicato con l’etichetta LFI muove il muscolo frontale interno sinistro (Left Frontalis Inner).
Sul pannello di controllo si trova anche un group box chiamato “Eye z-Adjust”
(ﬁg. A.2), all’interno del quale si trovano due campi editabili etichettati con
L e R. Il valore inserito in ciascuno dei due campi indica l’entità dello spiazzamento sull’asse z tale che, quando l’occhio si chiude, non accade che la
palpebra compenetri il bulbo oculare. I valori di default sono 1 e 4 ma possono essere cambiati solamente dopo che è stato caricato il modello vrml.
Una volta inseriti i valori desiderati, bisogna premere il pulsante “Apply”
aﬃnché i cambiamenti vengano memorizzati.
All’interno di questo group box si trova anche un check button anch’esso
usato per aggiustare il movimento della chiusura dell’occhio, si può attivare
soltanto prima che il modello vrml sia caricato e fa sı̀ che durante la chiusura dell’occhio venga eliminato uno spiazzamento lungo l’asse x inserito per
default.
Normalmente il setup iniziale che si trova quando l’applicazione viene avviata, è quello che, nella maggior parte dei casi, funziona meglio.
Fig. A.2: Eye z-Adjust group box.
82
Fig. A.3: (a) Esempio dell’utilizzo del menu a tendina “Single Muscle”. (b)
Etichetta del muscolo frontale interno sinistro (LFI = Left Frontalis Inner).
83
Continuando a scorrere il pannello di controllo si trova un group box di
fondamentale importanza: “Stiﬀness” (ﬁg. A.4).
Attraverso questo group box è possibile modiﬁcare il valore della stiﬀness
per il modello, il nuovo valore deve essere inserito prima che il modello venga
caricato. In pratica, modiﬁcando questo valore si agisce sulla durezza delle
molle che formano l’intero sistema di masse-molle attraverso il quale viene
simulata l’elasticità della pelle.
Come in precedenza, una volta inserito il nuovo valore, aﬃnchè questo venga
memorizzato, bisogna premere il bottone “Apply”.
Fig. A.4: Il group box per la regolazione della stiﬀness.
Di seguito vengono riportate alcune ﬁgure sull’utilizzo di afms, di come
agiscono i comandi del menu sul modello e l’azione della forza muscolare
regolata dagli slider.
Fig. A.5: Questa ﬁgura mostra come, attraverso il menu View → Face FDP,
vengono visualizzati sul modello i suoi fdp.
84
Fig. A.6: Questa ﬁgura mostra come, attraverso il menu View → Face Vertex, vengono visualizzati sul modello tutti i vertici della mesh della
pelle.
Fig. A.7: Esempio di applicazione della forza muscolare.
85
86
Abbreviazioni e simboli
AFMS
:
Anatomical Facial Muscle Simulator
API
:
Application Program Interface
CAD
:
Computer Aided Design
FAPs
:
Facial Animation Parameters
FAPUs
:
Face Animation Parameter Units
FATs
:
Face Animation Tables
FDP
:
Facial Deﬁnition Points
Ldr
:
Lunghezza di riposo
MDI
:
Multiple Document Interface
MPEG
:
Moving Picture Experts Group
OpenGL
:
Open Graphics Library
SDI
:
Single Document Interface
VRML
:
Virtual Reality Modeling Language
P
:
Insieme dei punti del poligono di controllo di un muscolo rilassato
Q
:
Insieme dei punti del poligono di controllo di un muscolo contratto
87
Ringraziamenti
Vorrei ringraziare tutti coloro che mi sono stati vicini durante il mio percorso
universitario a partire dalla mia famiglia, i miei amici e soprattutto Nadia.
Ringrazio il prof. Marco Schaerf che mi ha dato la possibilità di svolgere
questo lavoro e in particolare l’Ing. Marco Fratarcangeli, che mi ha seguito
durante tutto lo svolgimento di questa tesi per i suoi consigli fondamentali,
la sua grande disponibilità e pazienza.
Un ringraziamento sentito va ai miei cari amici Carmine e Luigi con i quali
ho condiviso tutta la mia avventura universitaria.
88
Questo documento è stato realizzato in LATEX.
89