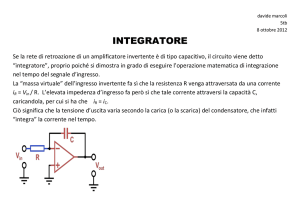
Derivatore invertente
Il circuito derivatore invertente è un dispositivo che dà in uscita un segnale
proporzionale alla derivata del segnale d’ingresso; ossia la forma d’onda d'uscita è la
derivata della forma d’onda d’ingresso.
Un circuito derivatore è quello riportato in figura.
Calcolo della funzione d’uscita per un generico segnale d'ingresso
Si calcola la funzione d'uscita. Tenendo conto dell'equipotenzialità degli ingressi
(V− = V+ = 0) , e che gli ingressi non assorbono corrente, si ha:
I C (t ) = I R (t ) ⇒ C ⋅
d(Vi − V− ) V− − Vo
=
dt
R
⇒ Vo = − RC ⋅
dVi
dt
La tensione d'uscita è proporzionale alla derivata del segnale d’ingresso.
Calcolo della funzione d’uscita in notazione simbolica con ingresso sinusoidale.
L'amplificatore operazionale sé in configurazione di amplificatore invertente, per cui:
Vo = −
ZR
ZC
⋅ Vi = −
R
⋅ V i = − jωRC ⋅ V i
− jX C
L'uscita risulta sfasata in ritardo di 90° rispetto all'ingresso. Nel piano complesso si ha:
Im
Vi
Re
Vo
Si scrive la funzione di trasferimento e se ne calcola modulo e fase:
1
G (jω) =
G (jω) = ωRC = 2πfRC
Vo
Vi
= − jωRC
ϕ=−
π
→ −90°
2
π
. L’ampiezza invece dipende da ω .
2
Amplificazione e frequenza sono direttamente proporzionali, quindi all’aumentare della
frequenza aumenta l’amplificazione, e viceversa.
La fase non dipende da ω ed è sempre −
-
Se ω → 0
⇒
G (jω) → 0
-
Se ω → ∞
⇒
G (jω) → ∞
Il problema si presenta alle alte frequenze, alle quali l'amplificazione tende ad assumere
il suo massimo valore. Sovrapposti la segnale d'ingresso sono presenti le tensioni di
rumore, tensioni di ampiezza molto piccola ed elevata frequenza, che vengono derivate,
insieme al segnale d'ingresso, con la massima amplificazione, portando l'uscita in zone
di funzionamento non lineari rendendo problematico il corretto funzionamento del
circuito.
L'elevato valore dell'amplificazione alle alte frequenze è dovuto alla capacità la cui
reattanza è inversamente proporzionale alla frequenza, ossia alle alte frequenze la
capacità tende ad assumere le caratteristiche di un corto circuito (reattanza di valore
praticamente nullo). Per impedire che il ramo contenente la capacità presenti
un'impedenza troppo bassa, ossia per limitare l'amplificazione alle alte frequenze, si
mette in serie alla capacità una resistenza di opportuno valore, come riportato in figura.
Derivatore invertente reale
Alle alte frequenze la reattanza capacitiva X C diminuisce e aumenta l’amplificazione.
Bisogna, quindi, impedire che il ramo contenente la capacità diventi un cortocircuito
inserendo in serie alla capacità una resistenza R, così che l'impedenza del ramo
contenente la capacità avrà in ogni caso un valore finito, limitando l'amplificazione alle
alte frequenze.
2
La funzione d'uscita è:
Vo = −
R
R
Vi = −
⋅
R 1 − jX C
R1
1
X
1− j C
R1
⋅ Vi = −
R
⋅
R1
1
1
1− j
ωR 1 C
⋅ Vi
La funzione di trasferimento è:
G (jω) =
G ( jω) = −
R
⋅
R1
R
⋅
R1
1
1− j
1
ωR 1 C
1
⎛ 1 ⎞
⎟⎟
1 + ⎜⎜
⎝ ωR 1 C ⎠
2
⎛
1
1 ⎞
⎟⎟ = π + arctg
ϕ = π − arctg⎜⎜ −
ωR 1 C
⎝ ωR 1 C ⎠
Al variare della frequenza, si ha:
⎛ 1 ⎞
1
⎟⎟
>> 1 ⇒ 1 è trascurabile rispetto a ⎜⎜
Se ω → 0 ⇒
ωR 1 C
⎝ ωR 1 C ⎠
⇒ G (jω) = ωRC e ϕ = 3
Se ω → ∞ ⇒
2
⇒
π
π
si c om porta da derivatore invertene
=−
2
2
1
1
<< 1 ⇒
è trascurabile rispetto a 1 ⇒
ωR 1 C
ωR 1 C
⇒ G (jω) =
R
e ϕ = π si c om porta da amplificatore invertene
R1
Il circuito presenta una frequenza di taglio f t , ossia quella frequenza alla quale il
modulo della funzione di trasferimento si riduce di un fattore 2 rispetto al suo
massimo valore.
La pulsazione di taglio si ottiene imponendo che il modulo della funzione di
R 1
trasferimento, a tale pulsazione, sia
⋅
:
R1
2
R
⋅
R1
1
⎛
1 ⎞⎟
1 + ⎜⎜
⎟
⎝ ω t R 1C ⎠
2
=
R 1
⋅
R1
2
⇒
1
⎛ 1 ⎞
⎟⎟
1 + ⎜⎜
⎝ ω t R 1C ⎠
3
2
=
1
2
⇒
2
⇒
⎛ 1 ⎞
⎜⎜
⎟⎟ = 1
ω
R
C
⎝ t 1 ⎠
⇒
ω t R 1C = 1
⇒
A tale frequenza la fase subisce una variazione di
ϕ = π + arctg
ωt =
1
R 1C
⇒
ft =
1
2πR 1C
π
:
4
1
π
π
1
= π + arctg
= π+ =5
1
ω t R 1C
4
4
⋅ R 1C
R 1C
La frequenza a guadagno unitario è quella frequenza alla quale il guadagno (il modulo
della funzione di trasferimento alle basse frequenze) vale 1:
1
1
⇒ f1 =
RC
2πRC
ω1 RC = 1 ⇒ ω1 =
Le condizioni di progetto, se non ci sono particolare richieste, sono:
RC = T
;
R = 10R 1
dove T è il periodo del segnale d'ingresso.
π
3
2
π
5
4
G ( jω) dB
20 log
R1
R
f1
ft
log f
ϕ
π
0 0,1f t
diagramma di Bode del modulo
ft
10f t
log f
diagramma della fase
Risposta del circuito all’onda triangolare
Se in ingresso mettiamo un segnale ad onda triangolare otteniamo in uscita un segnale
ad onda quadra.
⎧ 4ViM
(t − kT) − ViM
⎪
⎪⎪ T
v i (t ) = ⎨
⎪ 4V
T
⎪− iM ⎛⎜ t − − kT ⎞⎟ + ViM
⎪⎩
T ⎝
2
⎠
4
per
per
kT ≤ t <
T
+ kT
2
T
+ kT ≤ t < T + kT
2
Vi
ViM
t
− ViM
Vo
VoM
t
− VoM
Risposta alla rampa in salita, per 0 ≤ t <
Vo (t ) = − RC
dVi (t )
4RCViM
d ⎛ 4V
⎞
= − VoM
= − RC ⎜ iM t − ViM ⎟ = −
dt
dt ⎝ T
T
⎠
Risposta alla rampa in discesa, per
Vo (t ) = − RC
T
2
T
≤t<T
2
dVi (t )
⎤ 4RCViM
d ⎡ 4V ⎛
T⎞
= − RC ⎢ − iM ⎜ t − ⎟ + ViM ⎥ =
= VoM
dt
dt ⎣
T ⎝
2⎠
T
⎦
Riassumendo
⎧ 4RCViM
⎪−
T
⎪
v o (t ) = ⎨
⎪ 4RCV
iM
⎪
T
⎩
per
per
kT ≤ t <
T
+ kT
2
T
+ kT ≤ t < T + kT
2
Risposta del circuito all’onda quadra
⎧
⎪ ViM
⎪
v i (t ) = ⎨
⎪
⎪− ViM
⎩
kT ≤ t <
per
T
+ kT
2
T
+ kT ≤ t < T + kT
2
per
5
Vi
ViM
t
− ViM
Vo
VoM
t
− VoM
L’uscita, durante il tempo in cui Vi è costante, è nulla. Si ha, invece, un transitorio
d’uscita negli istanti in cui la tensione d’ingresso commuta da livello alto a livello
basso, e viceversa. In tali istanti si ha una variazione della tensione d’ingresso
∆V i = ±2ViM . Non potendo la tensione ai capi della capacità variare istantaneamente,
tale variazione ∆Vi si avrà sulla resistenza R 1 , con conseguente variazione della
∆Vi
corrente i C (t ) di una quantità ∆i C =
. Poiché istante per istante i C (t ) = i R (t ) ,
R1
analoga variazione di corrente si dovrà avere per i R (t ) , ∆i C = ∆i R , con conseguente
variazione istantanea della tensione Vo (t ) di una quantità pari a
∆Vo = − R∆i C = −
R
R
∆Vi = m
2ViM .
R1
R1
La capacità, attraverso R 1 , si carica, partendo dal valore m ViM , alla tensione ± ViM ,
secondo l’equazione.
v C (t ) = ± ViM + (m ViM m ViM )e
−
t
R 1C
= ± ViM m 2ViM e
−
t
R 1C
t
−
⎛
⎞
R 1C ⎟
⎜
d ± ViM m 2ViM e
t
⎜
⎟
dv C (t )
2ViM − R1C
⎝
⎠
=C
Quindi: i C (t ) = i R (t ) = C
=m
e
⇒
dt
dt
R1
t
−
R
⇒ v o (t ) = − R ⋅ i R (t ) = m
2ViM e R1C ,
R1
R
2ViM , che decresce
R1
esponenzialmente. In particolare si avrà un impulso positivo in corrispondenza dei
fronti di discesa, e un impulso negativo in corrispondenza dei fronti di salita del segnale
d’ingresso.
in uscita si avrà una forma d’onda impulsiva di ampiezza m
6