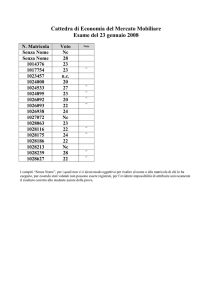
Logica Matematica
Prova Scritta - 13 febbraio 2013
Tempo a disposizione: 90 minuti.
Nome: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matricola: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Stabilire se ∃x(S(x) ∧ Q(f (f (a)))) è conseguenza logica dell’insieme di formule:
• ∀x(Q(a) → S(x))
• ∀x(Q(x) → Q(f (x)))
• ∀x(Q(a))
Suggerimento: usare metodo di risoluzione.
2. Discutere la soddisfacibilità della formula:
(¬p1 ∨ ¬p2 ∨ p3 ) ∧ (p3 ) ∧ (p1 ) ∧ (¬p1 ∨ p2 ) ∧ (¬p3 ∨ ¬p1 ).
3. Discutere la soddisfacibilità di (p → G) → q assumendo che la formula G sia
una contraddizione.
4. Unificare, se possibile, P (g(x), f (a), g(x, y)), P (g(c), y, g(h(a), y)), e P (g(c), u, g(h(u), u)).
5. Chiudere in forma normale prenessa la formula ben formata:
∀x(P (f (x)) ∨ P (g(x))) ↔ ∀yP (y).