2011-12 Semiconduttori 4TA

17/10/2011
ITIS OMAR 4 TA‐TB 2011‐2012
1904
tubo a vuoto
l’evoluzione dell’elettronica 1968
circuito integrato
1947
transistor
1980
integrati VLSI
oggi
integrati ULSI
1971 Microprocessore
(Intel 4004 – Federico
Faggin)
1
17/10/2011
diodi
transistor
2
17/10/2011
grafici,
tabelle,
schemi
applicativi
3
17/10/2011
semiconduttori
4
17/10/2011
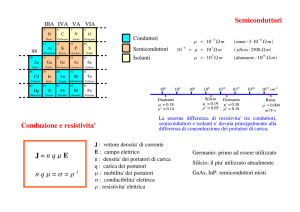
Che cosa sono i semiconduttori?
sono materiali di tipo semi-isolante
nei quali la struttura atomica e i legami chimici li
rendono particolari dal punto di vista
termico,
meccanico, ecc.
termic magnetico,
ma netic ottico,
ttic meccanic
ecc
quarzo
SiO2
Sili i
Silicio
Semiconduttori:
Silicio (Si)
Germanio (Ge)
Arseniuro di Gallio (GaAs)
e altri (GaAlAs, AlP, AlAs, GaP, AlSb, GaSb, InP, InAs,
I Sb SiC,
InSb,
SiC ZnO,
Z O CdS,
CdS CdSe,
CdS CdTe,
CdT PbS
PbS, PbT
PbTe, PbS
PbSe, GaN,
G N ecc.))
questi materiali sono perfetti isolanti solo a basse temperature,
solo ad elevata purezza, se monocristallini, al buio
e in assenza di radiazione
nelle altre condizioni divengono in parte conduttori,
soprattutto ad alta temperatura e se contengono elementi estranei
ISOLANTI
CONDUTTORI
SEMICONDUTTORI
5
17/10/2011
struttura elettronica del Silicio
Si14 = 1s2 + 2s2 + 2p6 + 3s2 + 3p2
Ne10 = Neon
3p6
elettroni di valenza
energia potenziale
energia di legame
rappresentazione nel diagramma dell’energia
6
17/10/2011
energia
termica
a temperatura ambiente (o in presenza di altre forme di energia), vengono rotti
alcuni legami covalenti, e alcuni elettroni passano in banda di conduzione
7
17/10/2011
a temperatura ambiente il semiconduttore è in parte conduttore
il numero ni di legami covalenti rotti dall’agitazione termica è dato da:
ni = A ·T3/2 ·e -Eg/2KT
essa indica all’incirca il raddoppio ogni 10°C
ni = concentrazione difetti (o
concentrazione intrinseca)
A = costante del semiconduttore
T = temperatura assoluta [°K]
E = energy gap
Eg
K = costante di Boltzmann= 1,38 ∙ 10−23 J K−1
=8,617 ∙ 10−5 eV K−1
questa formula fornisce quindi il numero delle coppie elettroneelettrone-lacuna libere
presenti nel semiconduttore, che possono quindi dar luogo alla conduzione
a causa del diverso Energy-gap dei vari semiconduttori, a 25°C si ha che:
semic.
Eg (eV) ni (cm-3)
Ge
0.7
2·1013
Si
1.2
1010
GaAs
1.4
106
anche la conducibilità
varia di conseguenza
conducibilità intrinseca = ni · q · (µe + µp)
8
17/10/2011
Un semiconduttore composto è un semiconduttore composto da elementi
provenienti da due o più diversi gruppi della tavola periodica. Questi elementi
appartengono ai gruppi 13-15 (vecchi gruppi III-VI), ad esempio gli elementi
del gruppo 13 (ex gruppo III) Boro, Alluminio, Gallio, Indio e del gruppo 15
((ex g
pp V)) Azoto,, Fosforo,, Arsenico,, Antimonio,, Bismuto.
gruppo
La gamma delle possibili combinazioni è piuttosto ampia, perché questi
elementi possono formare leghe binarie (due elementi, ad esempio, Arseniuro
di Gallio (GaAs)), ternarie (tre elementi, ad esempio, arseniuro di Gallio-Indio
(InGaAs)) e quaternarie (quattro elementi, ad esempio, fosfuro di Indio-GallioAlluminio (AlInGaP)).
9
17/10/2011
Composto III‐IV
Energy Gap [eV]
Mobilità elettroni
n [cm2/V*s]
Composto II‐IV
Energy Gap [eV]
AlP
3.0
‐‐‐
ZnO
3.3
AlAs
2.3
23
‐‐‐
CdS
45
2.45
GaP
2.25
450
CdSe
1.8
AlSb
1.52
1400
CdTe
1.45
GaAs
1.34 (1.43)
8500
PbS
0.37
InP
1.27
6000
PbTe
0.33
G Sb
GaSb
0.70
5000
PbSe
0 27
0.27
InAs
0.33
23000
InSb
0.18
80000
Transistor al silicio INTEL
Miniaturizzazione molto costosa sotto i 50 nm
Si poco adatto ad “elettronica veloce” (TeraHz)
Si limitato nei dispositivi fotonici
GaAs
Vantaggi dei dispositivi a semiconduttori composti
•Tecniche di fabbricazione molto potenti
•Ricchezza di fenomeni fisici (soprattutto quantistici) sfruttabili
•Grande flessibilità di caratteristiche funzionali
•Regolazione su misura delle caratteristiche del dispositivo
•Dimensioni ridottissime (transistor fino a 20 nm per particolari applicazioni)
•Possibilità di integrazione in un unico circuito di elementi sia ottici che elettronici
10
17/10/2011
a bassa temperatura
vi sono poche coppie
elettrone-lacuna libere,
e il semiconduttore
è un buon isolante
a ‐100°C il Silicio presenta una resistività simile a quella del vetro
+200°C
gamma di
temperatura
di utilizzo
-55°C
all’aumentare della temperatura
le coppie elettrone-lacuna aumentano,
e il semiconduttore
cessa di essere un buon isolante
11
17/10/2011
ad alta temperatura
il notevole aumento
delle coppie elettrone-lacuna
fa sì che il semiconduttore
diventi un conduttore
a 400°C il Silicio presenta una conducibilità simile a quella del carbone
25°C
La variazione della conducibilità con la temperatura è enorme:
il Silicio passa da un ni di 107 a -55°C a 1014 a + 200°C,
il che significa un aumento di 10 milioni di volte!!
12
17/10/2011
al fine di limitare
questa enorme variazione della conducibilità con la temperatura,
si introducono nel semiconduttore delle impurezze,
(piccole tracce di elementi chimici)
che vengono definite “materiali droganti”
La conducibilità  passa
così
da “intrinseca” (Silicio puro)
(sigma) = ni ∙ q ∙ µ
(dove ni = 1010cm‐3)
ma raddoppia ogni 10 °C
(sigma) = ND∙ q ∙ µ
a “estrinseca”
controllata solo dal tenore di droganti
dove ND = 1015... 1021 atomi/cm3 e indipendente dalla temperatura
si noti che il “tenore” delle impurezze introdotte è bassissimo:
si va infatti da 1 atomo ogni 108 fino ad un massimo dello 0.1%
13
17/10/2011
variazione della conducibilità a seconda delle impurezze
Conduttori
Semiconduttori
Isolanti
Materiale
Rame
Oro
Tungsteno
Acciaio
Silicio
Germanio
Mica
Conduttori:
• elettroni liberi
• moto elettronico facile
Resistività @ 20
20°C
C
1.7 µcm
2.2 µcm
5.6 µcm
11 µcm
100 µcm  100 cm
100 µcm  10 cm
1014 cm
Isolanti:
• elettroni legati agli atomi
• impossibilità di movimento
14
17/10/2011
impurezze droganti di tipo N:
Fosforo 5+
P
Arsenico 5+
As
Antimonio 5+ Sb
Silicio
impurezze droganti di tipo P:
Boro 3+
B
Alluminio 3+
Al
Nichelio 2+
Ni
Rame 2+
Cu
Oro 1+
Au
inserendo queste sostanze
la conducibilità
del semiconduttore aumenta
da 100 mila volte
fino a 100 miliardi di volte !
Silicio in presenza di atomi estranei (impurezze sostituzionali)
Boro 3+
lacuna
Fosforo 5+
elettrone
l
drogante di tipo P
drogante di tipo N
15
17/10/2011
Una striscia conduttiva su un chip di un circuito integrato è lunga 2,8 mm ed
ha una sezione rettangolare di 1μm x 4μm. Una corrente di 5mA produce
una caduta di tensione di 100mV ai capi della striscia.
Calcolare la concentrazione di elettroni liberi sapendo che la mobilità degli
elettroni vale 500 cm2/(Vs).
Dati
Specificazioni
I=5mA
Corrente nella striscia
A= 1*10-6m x 4*10-6m=4*10-12 m2=
=4*10-12 * ((10+2 cm))2= 4*10-8 cm2
Sezione della striscia ortogonale al
flusso della corrente I
L= 2,8 mm= 0,28 cm
Lunghezza della striscia e quindi del
percorso della corrente I
V = 100 mV
Caduta di tensione ai capi della striscia
μn = 500 cm2/(Vs)
Mobilità degli elettroni
Convertire i dati dimensionali in cm (m
in 100 cm; mm in 0.1 cm ecc…)
Incognita
n
Specificazioni
Unità di misura
Concentrazione elettroni liberi
cm‐3
I = J * A
Calcolo conduttività 
Nota la corrente I ; la sezione
A; la caduta di tensione V e la
lunghezza L si può calcolare 
(corrente= densità di corrente * superficie attraversata)
J =  * E
A
(densità di corrente = conducibilità * campo elettrico)
(Sezione ortogonale all’attraversamento della corrente)
= J / E
J = I / A
E = V / L (campo elettrico agli estremi = tensione ai capi estremi della barretta/ distanza tra i due estremi) E = V / L
Buon conduttore (metallo, ferro)
 = I * L /(A * V)

5 *10 3 * 2.8 *10 1
 3.5 *105 ( * cm) 1
0.1* 4 *10 8
16
17/10/2011
D’altra parte la conduttività ,
nel caso sia presente un solo
portatore di carica, si può anche
calcolare come:
 = q * n * μ
(conducibilità = carica elementare * concentrazione volumica dei portatori * mobilità dei portatori)
Da cui si ricava n:
n =  / (q * μ)
q = 1.602*10-19 C
(carica elementare
dell’elettrone)
n
3.5 *105
 4.37 *10 21 cm 3
1.602 *10 19 * 500
Esercizio 2
Una barretta di Silicio intrinseco è lunga L= 3 mm ed ha una sezione A rettangolare di 50 µm x 100 µm. A 300 °K trovare il campo elettrico E nella barretta e la tensione Vbar ai capi della stessa quando viene attraversata da una corrente I di 1 µA.
attraversata da una corrente I di 1 µA
[ ρ (@ 300°K) = 2.30 * 105 Ω cm resistività del Silicio a 300°K]
SVOLGIMENTO
17
17/10/2011
Esercizio 2 – Calcolo campo elettrico
SVOLGIMENTO
Per cui il campo elettrico sarà:
E
1*106 A
* 2.30 *105 *102   m  4.60 *105V / m  4.60 *103V / cm
6
6 2
50 *10 *100 *10 m
Esercizio 2 – Calcolo tensione
SVOLGIMENTO
Mentre la tensione ai capi della barretta sarà:
Vbar  E * L  4.60 *10 5 (V / m ) * 3 *10 3 m  1380V
18
17/10/2011
Un campione di Silicio n è lungo 3 mm ed ha una sezione
rettangolare di 50μm x 100μm. La concentrazione dei “donori”
a 300 °K è pari a 5x1014 cm-3 e corrisponde ad un atomo di
impurità ogni 108 (100 milioni) atomi di Silicio
Silicio. Una corrente di
1 μA attraversa la barretta.
N.B.: stessa barretta e stessa corrente di cui all’esercizio 2
Trovare la concentrazione di elettroni liberi e lacune, la conduttività e la
tensione ai capi della barretta.
Dati
Specificazioni
I=1 μA
Corrente nella barretta
A= 50*10-6m x 100*10-6m=5*10-9 m2=
=5*10-9 * (10+2 cm)2= 5*10-5 cm2
Sezione della striscia ortogonale al
flusso della corrente I
L= 3 mm= 0,3 cm
Lunghezza della striscia e quindi del
percorso della corrente I
μn = 1500 cm2/(Vs)
Mobilità degli elettroni nel Silicio
ND=5*1014
concentrazione di atomi “donori”
cm-3
Convertire i dati dimensionali in cm (m
in 100 cm; mm in 0.1 cm ecc…)
Incognita
Specificazioni
Unità di misura
n
Concentrazione elettroni liberi
cm‐3
p
Concentrazione lacune
cm‐3

d i ià
conduttività
(Ω*cm)) ‐1
(Ω*
Tensione ai capi della barretta
V
Vbar
Altri dati
Specificazioni
U.m.
ni =1.45*1010
Concentrazione intrinseca del Silicio a 300°K
cm‐3
q=1.602*10‐19
Carica dell’elettrone
C
19
17/10/2011
Formule
n*p=ni2
ND+p=NA+n
Specificazioni
Note
Legge dell’azione di massa
n = concentrazione di elettroni liberi
p = concentrazione di lacune
Legge di neutralità della carica
ND= concentrazione di atomi “donori”
NA=concentrazione di atomi accettori
RICHIAMI TEORICI
Per ionizzare le impurità (gli atomi droganti) è necessaria solo una piccola
energia.
Ad esempio nel Silicio il quinto elettrone dell’atomo “donore” necessità di
circa 0.05 eV per staccarsi ed essere libero (n.b.: l ’ a t o m o d o n o r e s i
i o n i z z a ! ).
) Tale energia è molto più bassa di quella necessaria a rompere
il legame covalente del Silicio (1.12 eV).
A TEMPERATURE > 200°K L’ENERGIA TERMICA E’ SUFFICIENTE A
IONIZZARE TUTTE LE IMPURITA’!
RICHIAMI TEORICI
Legge gg
azione di massa
L’ipotesi di completa ionizzazione
ci porta alla formulazione della
Legge di neutralità della carica
che, insieme alla legge dell’azione
di massa,
massa ci permettono di trovare
la concentrazione di cariche libere
in qualsiasi semiconduttore
Ipotesi completa ionizzazi
one
Legge di neutralità della carica
20
17/10/2011
In un semiconduttore tipo n:
NA=0
Dalla legge di neutralità della carica
n ≈ ND
In un semiconduttore tipo n:
n>>p
n  N D  5 *1014 cm 3
Nota la concentrazione n
degli elettroni liberi in un
semiconduttore tipo n
Dalla legge di azione di massa
p = ni2 / n
(1.45 *1010 ) 2
p
 4.2 *105 cm 3
14
5 *10
21
17/10/2011
Nota la concentrazione n
degli elettroni liberi
 = q*(n*μn+p*μp)
Allora si può ricavare la conduttività
Nota la concentrazione p
delle lacune
Poiché n>>p di un rapporto
pari a 1014/105=109 ossia di
1 milione di volte allora si
può trascurare μp
  q * n *  n  1.60 *10 19 * 5 *1014 *1.5 *103  0.12 (  cm) 1

1

 100 / 12  8.33   cm
I = J * A
Calcolo Vbar
(corrente= densità di corrente * superficie attraversata)
Nota la corrente I ; la sezione
A; la conducibilità  e la
lunghezza L si può calcolare la
caduta di tensione Vbar
J =  * E
A
(densità di corrente = conducibilità * campo elettrico)
(Sezione ortogonale all’attraversamento della corrente)
E = V / L (campo elettrico agli estremi = tensione ai capi estremi della barretta/ distanza tra i due estremi) = J / E
J = I / A
Contro i 1380V dell esercizio 2 !
dell’esercizio 2 !
E = V / L
Vbar = I * L /(A * )
Vbar 
10 6 * 0.3
 0.05 V
5 *10 3 *10  2 * 0.12
22
17/10/2011
Silicio con 1018 atomi/cm3 di Boro
semiconduttore di tipo P
il tenore di lacune
(portatori maggioritari)
è controllato dal drogaggio,
mentre quello degli elettroni
(portatori minoritari)
è funzione della temperatura
Silicio con 1018 atomi/cm3 di Fosforo
semiconduttore di tipo N
il tenore di elettroni
(portatori maggioritari)
è controllato dal drogaggio,
mentre quello delle lacune
(portatori minoritari)
è funzione della temperatura
conducibilità estrinseca = ND ∙ q ∙ µ = 1018∙q∙µ
conducibilità intrinseca = ni ∙ q ∙ µ = 1010∙q∙µ
23
17/10/2011
 Barretta drogata non in equilibrio termodinamico: p
,
p
modifica della concentrazione dei portatori, tempo di vita medio, lunghezza di diffusione, profilo delle concentrazioni nel tempo e lungo la barretta…………….
giunzione P-N
Silicio di tipo P
Silicio di tipo N
i
di carica
i spaziale,
i l
zona di iinversione,
di svuotamento o “depletion layer”
(la giunzione P‐N deve essere realizzata in un unico monocristallo)
24
17/10/2011
Silicio di tipo P
Silicio di tipo N
BANDA DI CONDUZIONE
BANDA DI CONDUZIONE
livelli donatori
livelli accettori
BANDA DI VALENZA
i droganti di tipo P
inducono la formazione di
“livelli accettori”
poco al di sopra della banda
di valenza
BANDA DI VALENZA
i droganti di tipo N
inducono la formazione di
“livelli donatori”
poco al di sotto della banda
di conduzione
quando materiale P ed N vengono a contatto, si equilibrano i
livelli donatori e accettori, il che provoca lo spostamento delle
posizioni energetiche delle bande di valenza e di conduzione
L’energia E da superare per avere la conduzione è proporzionale a Eg
25
17/10/2011
polarizzazione inversa
polarizzazione diretta
progressività dei parametri legati a Eg
parametro
Energy gap Eg a 300 °K
concentraz,, ni a 300 °K
mobilità elettronica µe
mobilità delle lacune µh
resist. intrinseca a 300 °K
densità atomica
rigidità dielettrica Emax
punto di fusione Tf
conducibilità termica Kth
peso specifico
Ge
Si
GaAs
unità
0,66
13
2,4·10
,
3900
1900
47
4·1022
10
937
0,64
5,3
1,12
10
1,6·10
,
1500
600
2E5
5·1022
34
1420
1,45
2,3
1,43
7
1,1·10
,
8500
400
1E7
2·1022
38
1238
0,46
5,3
eV
-cm2/V·sec
cm2/V·sec
ohm·cm
cm-3
V/µm
°C
W/cm·°C
g/cm3
incremento di Eg
26
17/10/2011
confronto fra Silicio e semiconduttori composti
parametro
Energy gap a 300 °K (Eg)
1,12
costante dielettrica relativa (r)
11,9
rigidità dielettrica (Ec)
300
mobilità elettronica (µn)
1500
mobilità delle lacune (µp)
600
1,5
conducibilità termica (
velocità drift elettroni sat.(vsat)
1
unità
1,43
13,1
400
8500
400
0,46
1
3,03
9,66
2500
500
100
3,9
2
3,26
10,1
2200
1000
115
3,9
2
3,45
9
2000
1250
850
1,3
2,2
eV
-KV/cm
cm2/V·sec
cm2/V·sec
W/cm·°C
107 cm/sec
27