1
Prof. Luigi Cai
Anno scolastico 2015/2016
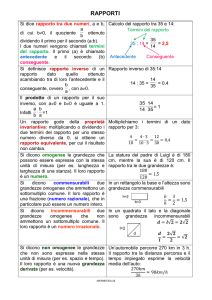
CLASSE DI GRANDEZZE OMOGENEE
E’ un insieme di grandezze geometriche per le quali è possibile stabilire:
a) un criterio di confronto;
b) un’operazione di somma.
Valgono inoltre i seguenti postulati:
- Postulato di Archimede: date due grandezze diverse, esiste un multiplo della più piccola che
supera la maggiore.
- Postulato di divisibilità: è sempre possibile dividere una grandezza in n parti congruenti.
MISURA DELLE GRANDEZZE
La misura di una grandezza è quel numero (razionale o irrazionale) che esprime quante volte l’unità
di misura U è contenuta nella grandezza da misurare; questo numero insieme all'unità di misura U
permetterà di ricostruire la grandezza iniziale.
Se la misura è un numero razionale si dice che le due grandezze sono commensurabili, cioè che
ammettono uno stesso sottomultiplo comune oppure che il rapporto tra le due grandezze è un numero
razionale; pertanto si possono avere le situazioni:
1) A è un multiplo di U secondo un numero intero
U
A
A=3U
quindi la misura di A rispetto ad U è un numero n intero positivo e si scrive: A = n U , cioè U è
contenuto n volte in A
2) A un multiplo di U secondo un numero razionale positivo (cioè una frazione o un numero periodico)
U
B
B = 7 U/2 ===> B = 7/2 U
quindi la misura di A rispetto ad U è un numero razionale positivo m/n e si scrive: A = m/n U
cioè U è contenuto m/n volte in A.
Se la misura è un numero irrazionale si dice che le due grandezze sono incommensurabili, cioè che
non ammettono uno stesso sottomultiplo comune oppure che il rapporto tra le due grandezze non è un
numero razionale.
Un esempio di coppia di grandezze incommensurabili è rappresentato dalla diagonale e dal lato di un
quadrato, come evidenzia il seguente teorema:
Teorema
La diagonale e il lato di un quadrato sono grandezze incommensurabili.
Dimostrazione
Supponiamo per assurdo che la diagonale AC e il lato AB del quadrato in figura abbiano uno stesso
sottomultiplo comune U, cioè che esistano due numeri naturali n e m primi fra loro tali che AB= n U e
AC = m U . Applicando il teorema di Pitagora al triangolo ABC si ha:
1
2
A
B
D
C
AB² + BC² = AC²
(nU)²+ (nU)²= (mU)²
2 n² = m²
tale relazione è assurda, perché se m è pari, m² risulterebbe divisibile per 4, mentre 2n² risulterebbe
divisibile per 2 ( infatti n è dispari, poiché n e m sono primi fra loro, quindi 2n² è divisibile per 2).
c.v.d.
La definizione di misura comporta anche la possibilità di ricostruire la grandezza conoscendo la sua
misura e l'unità di misura. Infatti si possono presentare tre casi (per semplicità si considerano i
segmenti):
a) misura = 3
l’unità di misura U
allora il segmento si ottiene prendendo tre volte l'unità di misura
b) misura = 2/3
l’unità di misura
U
allora per costruire il segmento si divide l'unità di misura in tre parti e se ne prendono due
c) misura =
2
l’unità di misura U
il problema è più complesso, perché 2 è definito dalla sezione (A1,A2), dove A1 contiene le
approssimazioni per difetto e A2 quelle per eccesso:
A1: 1 1.4 1.41 1.414 . . . . .
2
A2: 2 1.5 1.42 1.413 . . . . .
Basta riportare su una semiretta di origine O i punti A, B, C, .. in modo tale che i segmenti OA, OB,
OC , .. rappresentino le misure per difetto della classe A1, e i punti A', B', C', .. in modo che i segmenti
OA', OB', OC',.. rappresentino le misure per eccesso della classe A2.
O
A B C P
A' B' C'
In base al postulato di continuità esisterà un segmento OP che fa da elemento di separazione delle due
classi e la cui misura è 2 .
Postulato di continuità
Due classi di grandezze omogenee separate ( ogni grandezza della prima classe è minore di ogni
grandezza della seconda classe) e contigue ( la differenza tra una grandezza della seconda classe e una
grandezza della prima diventa sempre più piccola) ammettono un’unica grandezza di separazione delle
due classi.
2