Esercitazione 5

Esercitazione 5 del 20/03/2017
Dott.ssa Sabrina Pedrini
Domande a risposta multipla
1) Se produco 40 unità di prodotto ho un costo totale pari a 80 euro, se ne produco 50 il costo totale
è 110 euro. Quindi, nell’intervallo produttivo considerato, ho
a) Economie di scala
b) Diseconomie di scala
c) Rendimenti costanti di scala
d) Prodotto marginale decrescente
e) Nessuna delle risposte indicate è corretta
2) Nel lungo periodo, un’impresa perfettamente concorrenziale che ottiene profitti economici nulli:
a. uscirà dal mercato cercando un uso più redditizio delle proprie risorse.
b. ottiene un tasso di rendimento normale sui propri investimenti.
c. opera male e dovrebbe uscire dal mercato.
d. sono vere entrambe le risposte a e c.
3) Se la funzione di costo totale per un’impresa perfettamente concorrenziale è CT=50+10q+q2e il
prezzo di mercato è €130, quale è il ricavo totale e quale il profitto ? (Suggerimento: con
C'=10+2q, ricordare che il profitto è massimo quando p=C', trovare i ricavi, trovare i profitti come
differenza tra ricavi e costi)
a. €2.600; €83
b. €1.300; €917
c. non vi sono informazioni sufficienti per determinare il livello di produzione che massimizza il
profitto.
d. €7.800; €3.550
4) Un’impresa potrebbe decidere di chiudere nel breve periodo:
a. se la massimizzazione del profitto si verifica a un livello di produzione a cui il prezzo è minore
del costo totale medio ma maggiore del costo variabile medio.
b. se la massimizzazione del profitto si verifica a un livello di produzione a cui il prezzo è minore
del costo totale medio.
c. se la massimizzazione del profitto si verifica a un livello di produzione a cui il prezzo è
minore del costo variabile medio.
d. se la massimizzazione del profitto si verifica a un livello di produzione a cui il prezzo è uguale al
costo totale medio e l’impresa non prevede cambiamenti del prezzo di mercato nel futuro.
5) La curva di domanda specifica di un’impresa perfettamente concorrenziale:
a. è inclinata verso il basso poiché la quantità domandata aumenta al diminuire dei prezzi praticati
dall’impresa.
b. è una curva di domanda orizzontale, perfettamente elastica al prezzo di mercato.
c. è una retta inclinata verso il basso elastica rispetto al prezzo a prezzi più alti e anelastica quando
il prezzo scende e si avvicina a zero.
d. sono vere entrambe le risposte b e c.
Esercizio 1
Un’impresa utilizza una tecnologia descritta dalla seguente funzione di produzione:
i prezzi dei fattori lavoro e capitale sono rispettivamente
e
. Determinare la
combinazione ottima di fattori nel caso in cui l’impresa possa sostenere una spesa massima per
l’acquisto dei fattori pari a 1200;
Svolgimento
La scelta ottimale dei fattori può essere ottenuta risolvendo il problema di massimizzazione
dell’output sotto un vincolo di costo, imponendo che l’impresa possa sostenere una spesa massima
per l’acquisto dei fattori pari a 1200. Il sistema da risolvere in questo caso è:
da cui si ottiene
e
. A cui corrisponde una produzione di:
Esercizio 2
Un’impresa produce palloni usando i fattori di produzione K e L seguendo la funzione di
produzione q(L;K)=min[2L;5K]. Il costo unitario del lavoro è w=6 e quello del capitale è r=3.
L’impresa non ha un vincolo sulla quantità da produrre, ma è limitata nella sua liquidità. In
particolare, il budget per acquistare i fattori di produzione è pari a 600 e non è possibile spendere di
più.
1) Che relazione intercorre tra lavoro e capitale? Ovvero di quale tipologia di fattori di
produzione stiamo parlando?
2) Disegnate la mappa degli isoquanti.
3) Rappresentate in un grafico la retta di isocosto CT=600 evidenziandone pendenza, intercetta
orizzontale e verticale.
4) Calcolate la combinazione ottimale dei fattori produttivi quando CT=600 e il corrispondente
livello di output q.
5) Con riferimento alla funzione di produzione, cosa si può dire relativamente ai rendimenti di
scala?
Svolgimento
1) La funzione di produzione mostra una coppia di fattori produttivi che l’impresa considera
come perfettamente complementari: i due input sono utilizzati in proporzioni sempre fisse e
non sono sostituibili tra loro o con altri fattori.
2) Gli isoquanti di questa funzione sono ad angolo retto e i vertici si trovano tutti lungo la
semiretta che passa dall’origine e che ha funzione 2L=5K, ossia K=2L/5. Definiamo tale
semiretta “retta dei vertici” perché essa passa per tutti i vertici degli isoquanti ad L
caratteristici di questa funzione di produzione.
3) La retta di isocosto la otteniamo partendo dalla generica funzione di costo totale CT=wL+rK
e andando a sostituire a questa i valori forniti nel testo. Otteniamo quindi 600= 6L+3K, che
espresso in funzione di K (fattore di produzione indicato sull’asse verticale del nostro
grafico) diventa K=200-2L. L’isocosto è dunque una funzione lineare negativamente
inclinata, la cui pendenza è -2. L’ intercetta verticale è 200 e l’intercetta orizzontale 100.
Graficamente:
4) Quando il vincolo è un dato budget, e non il livello di q, per calcolare la combinazione ottimale
dei fattori si deve risolvere il sistema a due equazioni e due incognite (L,K) composto dalla retta di
isocosto e dalla la retta dei vertici.
Per ottenere, infine, il livello di output q, associato a questa combinazione di fattori di produzione è
sufficiente sostituire il valore del livello ottimo dei fattori all’interno della funzione di produzione:
q(K*;L*)= min[2(250/3);5(100/3)] = 500/3
5) I rendimenti di scala dell’impresa sono costanti. Se ad esempio, L=K=1, q=2; raddoppiando gli
input e sostituendo nella funzione L=K=2, si ottiene il raddoppio dell’output, ossia q=4.
Esercizio 3
Svolgimento
Punto 1
In regime di concorrenza perfetta, l'impresa massimizza il profitto producendo là dove p=C'. In
questo caso p=2+q. Esplicitando tale espressione rispetto a q si ottiene quindi la funzione di offerta
della singola impresa qs=qs(p):
qs=p-2
L'impresa continuerà a produrre finchè il livello del prezzo dei suoi prodotti rimane al di sopra del
costo medio variabile. Nel nostro caso, il costo medio variavile (=CV/q) è pari a
CMV= [2q+(1/2)q2]/q=2+(1/2)q
Con C'=2+q avremo che C'>CMV e quindi che p=C'>CMV per ogni valore di q
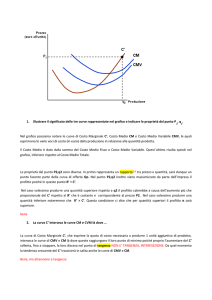
Rappresentiamo graficamente le funzioni di costo:
C'
CMV
p*
2
q*
q
Punto 2
La curva di offerta di un mercato perfettamente concorrenziale che presenta 50 imprese identiche si
ottiene come somma orizzontale delle 50 curve di offerta individuali::
Qs= nqsi
dove i indica la generica impresa i sul mercato, i= 1,…, 50
s
s
Q = 50. q i =50(p-2)= 50p-100
L’equilibrio di mercato si ottiene eguagliando domanda e offerta di mercato: QD=QS, ossia
200-10p=50p-100
da cui p*=5, Q*=150 e qi=3
I profitti si calcolano facendo riferimento alla singola impresa, come differenza tra i ricavi che
riesce ad ottenere proponendo il suo prodotto al prezzo di mercato e i costi che deve sostenere per
produrre.
Π=p*.qi*- CT= 2,5 (>0)
Punto 3
Il surplus individuale del consumatore è la differenza positiva fra il prezzo che un individuo è
disposto a pagare per ricevere un determinato bene o servizio e il prezzo di mercato dello stesso
bene. Il massimo che un consumatore è disposto a pagare viene detto "prezzo di riserva".
Geometricamente, si ottiene calcolando l’area compresa tra la curva individuale di domanda e la
linea del prezzo fino alla quantità acquistata q dal consumatore. Il surplus aggregato del
consumatore è la somma dei surplus individuali dei consumatori partecipanti ad un mercato ed è
sempre pari all’area compresa tra la curva di domanda di mercato e la linea del prezzo fino alla
quantità scambiata in equilibrio. In questo caso, essa è pari all’area del triangolo rettangolo
compresa tra i punti 20 (prezzo massimo che il consumatore è disposto a pagare), 5 (prezzo di
mercato) e 150 (quantità scambiata).
Il surplus individuale del produttore o sovrappiù del produttore è la differenza positiva tra il
prezzo di un dato bene pagato al produttore ed il prezzo minimo che il produttore sarebbe
disposto ad accettare per produrre quell’unità di bene in più, ossia il suo costo marginale.
Geometricamente è l’area compresa tra la linea del prezzo e la curva di costo marginale fino alla
quantità q prodotta dall’impresa. In generale, nel breve periodo tale surplus del produttore è pari al
profitto economico più i costi fissi (o in altre parole, è pari alò profitto variabile). Il surplus
aggregato del produttore è la somma dei surplus individuali ed è sempre pari all’area sotto la linea
di prezzo e sopra la curva di offerta fino alla quantità scambiata in equilibrio (si noti infatti come la
curva di offerta non sia altro che la somma orizzontale delle curve di costo marginale dei produttori
di un particolare mercato). Nel nostro caso l’area del triangolo compreso tra i punti 5 (prezzo di
scambio), 2 (prezzo minimo che può essere accettato dal venditore) e 150 (quantità scambiata).
p
20
O
5
2
D
150
200
q
SC=[(20-5)150]/2=1125
SP=[(5-2)]150/2=225
Punto 4
Come risulta dal punto 2 in questo mercato le imprese realizzano dei profitti positivi nel breve
periodo. Questo rende profittevole il mercato per nuove imprese che, in assenza di barriere
all’entrata, possono scegliere di cominciare a produrre per questo mercato.
Questi aggiustamenti sposteranno progressivamente la curva di offerta di mercato verso destra,
abbassando gradualmente il prezzo di equilibrio che ogni singola impresa prende poi come un dato.
Tale processo continuerà fino a che il prezzo di equilibrio diventa pari al valore minimo della curva
del costo medio di lungo periodo e il profitto economico è nullo per tutte le imprese. In tale punto di
minimo della curva di costo medio, quest’ultima è attraversata dalla curva di costo marginale, e tale
informazione può essere utilizzata per calcolare il livello di produzione di lungo periodo, dato che la
singola impresa massimizza comunque il profitto là dove p=C’. Uguagliando CMT=C', nel nostro
caso si ottiene
(2/q)+2+(1/2)q=2+q da cui q=2
Il prezzo di scambio nel lungo periodo deve eguagliare il punto di minimo della funzione di costo
medio totale. Il punto lo troviamo andando a sostituire q=2 all'interno della funzione di costo medio
totale, ottenendo un valore per il prezzo pari a 4.
In corrispondenza di un prezzo di scambio, per il lungo periodo, pari a 2 avremo
Qd= 200-10(4)=160 come quantità totale scambiata sul mercato. Data la quantità proposta dalle
singole imprese, 2, facilmente otteniamo il numero di imprese presenti sul mercato, nel lungo
periodo, come rapporto tra la quantità totale e quella individuale: N=Qd/qi=160/2=80.