M.Balconi e R.Fontana, Dispense di Economia:
10) Note sul monopolio
Note sul monopolio
1) Il monopolista fronteggia la domanda del mercato: diventa cruciale il concetto di ricavo
marginale
In monopolio esiste una sola impresa che perciò fronteggia tutta la domanda di mercato.
A differenza di un mercato in concorrenza perfetta, la curva di domanda che fronteggia la
singola impresa è decrescente. Questo significa che ogni unità aggiuntiva di bene è venduta
ad un prezzo più basso.
Data questa situazione, il monopolista può prendere in considerazione l’idea di
aumentare i propri ricavi aumentando la quantità prodotta, ma deve tenere conto del fatto che
la vendita di un’unità aggiuntiva farà diminuire il prezzo di mercato anche per le unità che
erano vendute in precedenza. Questo farà diminuire i ricavi.
E’ interessante analizzare, data questa situazione, quale effetto ha la vendita di un’unità
aggiuntiva sul ricavo totale. La variazione del ricavo in corrispondenza della vendita di
un’unità aggiuntiva si chiama ricavo marginale (MR).
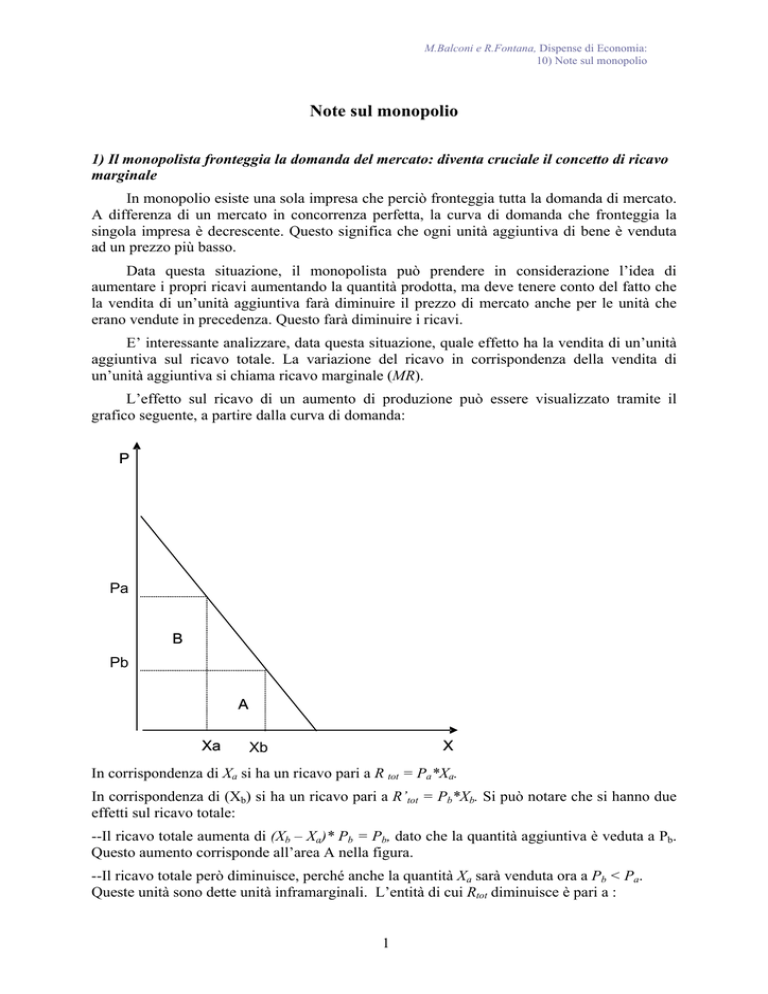
L’effetto sul ricavo di un aumento di produzione può essere visualizzato tramite il
grafico seguente, a partire dalla curva di domanda:
P
Pa
B
Pb
A
Xa
X
Xb
In corrispondenza di Xa si ha un ricavo pari a R tot = Pa*Xa.
In corrispondenza di (Xb) si ha un ricavo pari a R’tot = Pb*Xb. Si può notare che si hanno due
effetti sul ricavo totale:
--Il ricavo totale aumenta di (Xb – Xa)* Pb = Pb, dato che la quantità aggiuntiva è veduta a Pb.
Questo aumento corrisponde all’area A nella figura.
--Il ricavo totale però diminuisce, perché anche la quantità Xa sarà venduta ora a Pb < Pa.
Queste unità sono dette unità inframarginali. L’entità di cui Rtot diminuisce è pari a :
1
M.Balconi e R.Fontana, Dispense di Economia:
10) Note sul monopolio
(Pa – Pb)*Xa. Questa diminuzione corrisponde all’area B nella figura.
Tenendo conto di entrambi gli effetti, la variazione del ricavo sarà data da ΔR = A – B,
ovvero ΔR = Pb * ΔX - Xa * ΔP
Dividendo per ΔX si ottiene la variazione dei ricavi per una variazione unitaria dell’output,
ossia il ricavo marginale:
ΔP
MR = P −
*X
b ΔX
a
Il ricavo marginale starà quindi sempre al di sotto della curva di domanda per ogni X > 0, in
quanto MR < P. Per X = 0 si avrà che MR = P.
P
D
MR
X
In termini infinitesimali, il ricavo marginale è la derivata del ricavo totale:
d(PX)
dP
= P+
X
dX
dX
(1)
In generale sussiste una precisa relazione tra ricavo marginale ed elasticità della
domanda.
dX P
Ricordiamo che l'elasticità della domanda in funzione del prezzo (ε) è:
e quindi
dP X
dP X
1
=
dX P
ε
Raccogliendo P, il ricavo marginale viene espresso in termini di elasticità della domanda:
1
ε
MR = P (1+ )
Tenendo conto del segno negativo dell'elasticità, posso scrivere:
1
MR = P (1- )
(2)
ε
2
M.Balconi e R.Fontana, Dispense di Economia:
10) Note sul monopolio
Solo per valori dell’elasticità maggiori di 1, il ricavo marginale ha un valore positivo.
Allorché ε = 1, MR = 0. Al livello di produzione in corrispondenza del quale MR = 0, i
ricavi totali dell’impresa raggiungono il massimo valore e per produzioni superiori i ricavi
decrescono (infatti MR < 0).
P
ε =∞
ε =1
MR
ε =0
Domanda
X
Vediamo ora di ricavare analiticamente la relazione tra curva di domanda e di ricavo
marginale nel caso di una domanda lineare:
P(X) = a – bX
abbiamo che:
RTOT = P * X = (a − bX )X = aX − bX 2
MR =
dRTOT
= a − 2bX
dX
Si può notare che le due curve hanno la stessa intercetta verticale (a) ma la pendenza di MR è
doppia rispetto a quella della curva domanda ( −2b invece di –b).
Sappiamo inoltre (si vedano le dispense precedenti sull’elasticità e la pendenza della curva di
X 1
1
domanda) che per questa curva − b
= e quindi se MR = P (1+ ), avremo che
P ε
ε
X
MR = (a - bX) (1- b
) = a – bX – bX = a-2bX,
(a − bX )
come effettivamente si è visto sopra.
Ricordiamo infine che nel caso della concorrenza perfetta la curva di domanda per la singola
impresa price taker è orizzontale, ossia abbiamo che:
P(X) = a
3
M.Balconi e R.Fontana, Dispense di Economia:
10) Note sul monopolio
Il ricavo totale sarà quindi:
RTOT = a X
E il ricavo marginale Æ MR = a risulta quindi uguale al prezzo.
2) Determinazione dell’equilibrio di monopolio
Nel caso di un monopolista, la quantità X1 da produrre che massimizza il profitto si determina
nel punto in cui MR = MC (costo marginale). Il prezzo di equilibrio P1 invece si determina
sulla curva di domanda in corrispondenza della quantità X1.
In generale, dato che P > MR si avrà che P > MC. Dunque il monopolista pratica un prezzo
maggiore di quello di un’impresa che opera in concorrenza perfetta (CP). Inoltre si avrà che
Xm* < X*cp. Dunque il monopolista produce una quantità inferiore a quella che producono nel
loro insieme le imprese operanti in concorrenza perfetta. Graficamente:
P
MC
P1
E
D
MR
X
X1
Il livello dei profitti per unità di prodotto è dato dalla distanza tra P1 e AC (dove AC è il costo
medio totale). Nella figura sotto si vede che in corrispondenza di X1 l’impresa fa un profitto
positivo pari a (P1 - AC)X1. Inoltre il monopolista rimane in attività se P ≥ AC
4
M.Balconi e R.Fontana, Dispense di Economia:
10) Note sul monopolio
P
MC
AC
E
P1
Π
D
MR
X
X1
Abbiamo parlato generalmente di equilibrio senza distinguere tra breve e lungo periodo.
Questo perché, a differenza del caso in CP, in monopolio le condizioni di accesso al mercato
non cambiano nel lungo periodo, in quanto non c’è libertà di entrata. In monopolio si ha
quindi un profitto positivo anche nel lungo periodo. Se i costi medi tuttavia a livello delle
quantità che massimizzano i profitti fossero maggiori del prezzo, il monopolista non potrebbe
sopravvivere. E’ la relazione tra la domanda e i costi che determina le possibilità del
monopolista di realizzare profitti massimi positivi nonché il loro ammontare.
Tornando alla relazione tra ricavo marginale ed elasticità della domanda - si riveda la (2) - in
equilibrio avremo che
1
P
) ⇒ C=Pε
ε
P−C 1
=
P
ε
C = P (1-
(3)
P−C
è chiamato indice di Lerner del grado di monopolio. La distanza tra
P
P e C è il margine di profitto, che viene rapportato al prezzo. Si vede che il margine di
profitto sul prezzo varia inversamente rispetto ad ε .
dove il rapporto
Quando ε = ∞ e MR = P, in equilibrio P = C , come in concorrenza perfetta.
5
M.Balconi e R.Fontana, Dispense di Economia:
10) Note sul monopolio
Il caso rilevante per il monopolio è quello che si ha quando 1< ε < ∞ e quindi MR < P e
inoltre ha valore positivo. Infatti, poiché il costo marginale è sempre maggiore di zero,
l'uguaglianza tra MR e CM comporta di considerare solo i valori positivi di MR.
Vediamo ora la determinazione della soluzione di equilibrio per il monopolista nel caso della
curva di domanda lineare P = a - bX e di una funzione di costo totale del tipo CTOT = CX . Il
monopolista massimizzerà il suo profitto producendo la quantità in corrispondenza della quale
MR = MC. Facendo i calcoli si ottiene:
RTOT = PX = (a − bX )X = aX − bX 2
MR = a − 2bX
MC = C
max π se MR = MC
a −C
2b
X* è la quantità di equilibrio. Sostituendo tale valore all’interno della funzione di domanda si
ottiene il corrispondente prezzo di equilibrio:
a − 2bX = C ⇒ 2bX = a − C ⇒ X* =
P*= a-bX*= a – b
2a − a + C a + C
a −C
=
=
2b
2
2
Il profitto che il monopolista realizzerà sarà dato da:
π * = P* X* − C X*
π *= (P*− C) X*
π *= (
a −C
a+C
- C) (
2
2b
a −C
π =(
2
*
) ( a −C
2b
6
)
(a − C ) 2
)=
.
4b