POLIGONI: PROPRIETÀ E FORMULE PER IL CALCOLO DI PERIMETRO E AREA
NOME E FIGURA
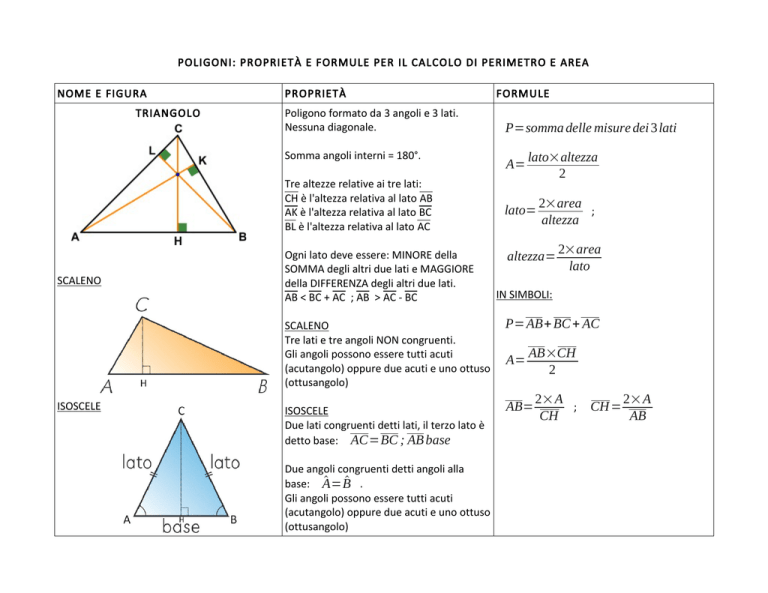
TRIANGOLO
PROPRIETÀ
Poligono formato da 3 angoli e 3 lati.
Nessuna diagonale.
Somma angoli interni = 180°.
Tre altezze relative ai tre lati:
CH è l'altezza relativa al lato AB
AK è l'altezza relativa al lato BC
BL è l'altezza relativa al lato AC
SCALENO
ISOSCELE
Ogni lato deve essere: MINORE della
SOMMA degli altri due lati e MAGGIORE
della DIFFERENZA degli altri due lati.
AB < BC + AC ; AB > AC - BC
FORMULE
P=somma delle misure dei 3lati
A=
lato×altezza
2
lato=
2×area
;
altezza
altezza=
2×area
lato
IN SIMBOLI:
SCALENO
Tre lati e tre angoli NON congruenti.
Gli angoli possono essere tutti acuti
(acutangolo) oppure due acuti e uno ottuso
(ottusangolo)
P= AB+ BC + AC
ISOSCELE
Due lati congruenti detti lati, il terzo lato è
detto base: AC=BC ; AB base
AB=
Due angoli congruenti detti angoli alla
̂ B̂ .
base: A=
Gli angoli possono essere tutti acuti
(acutangolo) oppure due acuti e uno ottuso
(ottusangolo)
A=
AB×CH
2
2× A
;
CH
CH =
2× A
AB
EQUILATERO
EQUILATERO
Tre lati e tre angoli congruenti:
AB=BC =CA
∘
∘
̂
̂ B=
̂ C=180
A=
:3=60
I tre angoli congruenti misurano 60° quindi
è un triangolo acutangolo.
RETTANGOLO - SCALENO
RETTANGOLO
∘
̂
Un angolo retto C=90
.
I due lati perpendicolari si dicono cateti e il
lato opposto si chiama ipotenusa.
AC e BC cateti ; AB ipotenusa
Gli altri due angoli sono acuti e
∘
̂ B=90
̂
complementari: A+
Gli angoli acuti possono essere:
- diversi → il triangolo è scaleno.
RETTANGOLO - ISOSCELE
- congruenti → ognuno misura 45° , il
triangolo è isoscele e i due cateti sono
∘
̂ B=45
̂
congruenti: A=
; AC=CB
PARALLELOGRAMMO
Quadrilatero ( 4 angoli e 4 lati).
I lati opposti sono paralleli e congruenti.
AB // CD ; AB=CD
BC // AD ; BC = AD
Il lato AB è detto anche base e il lato BC è
detto anche lato obliquo.
Gli angoli opposti sono congruenti:
̂ ; B=
̂ C
̂ D
̂ .
A=
Gli angoli adiacenti allo stesso lato sono
supplementari:
∘
∘
̂
̂ D=180
̂
̂ C=180
A+
; B+
Somma degli angoli interni = 360°.
Due diagonali AC e BD che si tangliano a
metà: AO=OC ;BO=OD
P=somma delle misure dei 4lati
A=lato×altezza
lato=
A
;
altezza
altezza=
A
lato
IN SIMBOLI:
P= AB+ BC +CD+ DA=
=2× AB+2×BC=2×( AB+ BC)
A= AB× DH
AB=
A
A
; DH =
DH
AB
Due altezze relative a base e lato obliquo:
DH è l'altezza relativa al lato AB
DK è l'altezza relativa al lato BC
RETTANGOLO
Quadrilatero (4 angoli e 4 lati).
Il rettangolo è un parallelogrammo con 4
angoli congruenti e quindi retti.
I lati opposti sono paralleli e congruenti.
AB // CD ; AB=CD
BC // AD ; BC = AD
P=somma delle misure dei 4lati
A=lato×lato=base×altezza
base=
A
A
; altezza=
altezza
base
I quattro angoli interni sono congruenti e IN SIMBOLI:
la loro somma vale 360° quindi ognuno
misura 90° : angolo interno = 360° : 4 = 90° P= AB+ BC +CD+ DA=
I lati consecutivi sono perpendicolari tra
loro → Le altezze coincidono con i lati.
AB è detto anche base e BC è detto anche
altezza. La base e l'altezza si dicono anche
dimensioni.
=2× AB+2×BC=2×( AB+ BC)
A= AB×BC
AB=
A
A
; BC=
BC
AB
Le due diagonali sono congruenti e si
tangliano a metà:
AC=BD ; AO=OC ; BO=OD
ROMBO
Quadrilatero (4 angoli e 4 lati).
Il rombo è un parallelogrammo con 4 lati
congruenti.
I lati sono congruenti e i lati opposti
paralleli.
AB // CD ; BC // DA
AB=BC =CD=DA
Gli angoli opposti sono congruenti:
̂ ; B=
̂ C
̂ D
̂
A=
Gli angoli adiacenti allo stesso lato sono
supplementari:
∘
∘
̂
̂ D=180
̂
̂ C=180
A+
; B+
Somma degli angoli interni = 360°
P=somma delle misure dei 4lati
lato=
P
4
Considerando il rombo come un
parallelogrammo:
A=lato×altezza
lato=
A
A
; altezza=
altezza
base
Considerando la proprietà delle diagonali
perpendicolari:
Le diagonali AC e BD si tagliano a metà,
sono perpendicolari e sono le bisettrici
degli angoli interni.
AO=OC ;BO=OD
AC ⊥ BD
̂D
̂ C=C A
̂ B=B Ĉ A= A C
DA
̂ B=B D
̂ C= A B
̂ D=B D
̂C
AD
Le due altezze sono congruenti: DH = DK
DH è l'altezza relativa al lato AB
DK è l'altezza relativa al lato BC
A=
diagonale maggiore×diagonale minore
2
diagonale maggiore=
diagonale minore=
2× A
diagonale minore
2× A
diagonale maggiore
IN SIMBOLI:
P= AB+ BC +CD+ DA=4× AB
AB=
P
4
Considerando il rombo come un
parallelogrammo:
A= AB× DH
AB=
A
A
; DH =
DH
AB
Considerando la proprietà delle diagonali
perpendicolari:
A=
AC ×BD
2
AC=
2× A
;
BD
BD=
2× A
AC
QUADRATO
Quadrilatero (4 angoli e 4 lati).
P=somma delle misure dei 4lati
→ Il quadrato è un parallelogrammo con 4
lati e 4 angoli congruenti e quindi retti.
P
lato=
Oppure, ricordando il rettangolo:
4
→ il quadrato è un rettangolo con 4 lati
congruenti.
Considerando il quadrato come un
Oppure, ricordando il rombo:
parallelogrammo:
→ il quadrato è un rombo con 4 angoli
A=lato×lato=lato 2 ; lato= √ A
congruenti e quindi retti.
I lati sono congruenti e i lati opposti sono
paralleli: AB // CD ; BC // DA
AB=BC =CD=DA
Considerando il quadrato come un rombo:
diagonale×diagonale diagonale 2
A=
=
2
2
diagonale= √ 2× A
Gli angoli interni sono congruenti e
la loro somma vale 360° quindi ognugno
IN SIMBOLI:
misura 90°: angolo interno = 360° : 4 = 90°
P= AB+ BC +CD+ DA=4× AB
I lati consecutivi sono perpendicolari tra
loro → Le altezze coincidono con i lati.
AB=
P
4
Le diagonali AC e BD sono congruenti, si
tangliano a metà, sono perpendicolari tra Considerando il quadrato come un
loro e sono le bisettrici degli angoli interni: parallelogrammo:
A= AB× AB= AB2 ; AB= √ A
AC=BD e AC ⊥ BD
AO=OC ;BO=OD
̂ D=45∘
̂ C=C A
̂ B=B Ĉ A= A C
DA
̂ B=B D
̂ C= A B
̂ D=B D
̂C
AD
Le diagonali dividono il quadrato in 4
triangoli rettangoli isosceli congruenti.
Considerando il quadrato come un rombo:
A=
AC ×BD AC 2
=
2
2
AC= √ 2× A
TRAPEZIO
Quadrilatero (4 angoli e 4 lati).
Due lati opposti paralleli chiamati base
maggiore e base minore: AB // CD
AB base maggiore, simbolo “B”
CD base minore, simbolo “b”
Somma degli angoli interni = 360°.
Gli angoli adiacenti allo stesso lato obliquo
sono supplementari:
̂
̂ D=180
̂
̂ C=180
A+
; B+
∘
∘
Due diagonali AC e BD e una altezza
(distanza tra le basi): DH = CK = altezza
AH e KB sono le proiezioni dei lati obliqui
sulla base maggiore mentre HK è la
proiezione della base minore: HK = CD
SCALENO
SCALENO
I lati obliqui, gli angoli interni, le diagonali e
le proiezioni dei lati obliqui NON sono
congruenti.
P=somma delle misure dei 4lati
A=
(base maggiore +base minore)×altezza
2
altezza=
2× A
base maggiore +base minore
base maggiore +base minore=
2× A
altezza
IN SIMBOLI:
P= AB+ BC +CD+ DA
A=
( AB+CD)×CH
2
CH =
2× A
2× A
; AC +CD=
AB+CD
CH
ISOSCELE
ISOSCELE
I lati obliqui sono congruenti AD=BC .
Gli angoli adiacenti a ciascuna base sono
̂ D
̂ B̂ ; C=
̂ .
congruenti: A=
Le diagonali sono congruenti
AC=BD
Le proiezioni dei lati obliqui sulla base sono
congruenti: AH =KB .
Quindi in questo caso vale:
AH =KB=
RETTANGOLO
AB−CD
2
Un lato obliquo è perpendicolare alle due
basi e quindi coincide con l'altezza.
AD ⊥ AB e AD ⊥ DC
AD=CH
Due angoli interni sono retti.
∘
̂ D=90
̂
A=
In questo caso vale:
KB= AB−CD












