Microeconomia

Microeconomia
Indice
Introduzione …………………………………………………………………………………………..pag. 3
Domanda e Offerta …………………………………………………………………………………..pag. 10
La curva di offerta …………………………………………………………………………pag. 11
La curva di domanda
………………………………………………………………...….pag. 14
Meccanismo di mercato ………………………………………………………………………...….pag. 17
Variazioni dell’equilibrio di mercato ………..………………………………………...….pag. 19
Teoria del consumatore ………………………………………………………………………...….pag. 22
Vincolo di bilancio
……………………………………………………………...….pag. 23
Preferenze del consumatore
……………………………………………………...….pag. 29
Curve d’indifferenza: beni sostituti e beni complementari
…………………...….pag. 36
Scelta ottima del consumatore
………………………………………………...….pag. 38
Curva di Engel
..………………………………………………………………...….pag. 42
Costruzione della curva di domanda …………………………………………………...….pag. 46
Effetto di sostituzione ed effetto reddito per un bene inferiore ………………...….pag. 52
Effetto di sostituzione ed effetto reddito per un bene di Giffen ………………...….pag. 53
Surplus del consumatore ………………………………………………………………...….pag. 55
Elasticità della domanda
……………………………………………………………………...….pag. 57
Elasticità della domanda rispetto al prezzo
…………………………………...….pag. 57
Elasticità della domanda rispetto al reddito
…….…………………………………...….pag. 62
Elasticità della domanda rispetto ad altri beni o incrociata
……………………...….pag. 65
Teoria della produzione: l’Impresa …………………………………………………………...….pag. 66
La funzione di produzione
…………………………………………………...….pag. 67
L’analisi
…………………………………………………………………...….pag. 71
La funzione di produzione di lungo periodo
……………………………………...….pag. 76
Gli Isoquanti ……………………………………………………………………...….pag. 77
Gli Isocosti ……………………………………………………………………...….pag. 82
Combinazione ottima di capitale e lavoro ……………………………………...….pag. 85
La funzione di costo di breve periodo
…………………………………...….pag. 88
I Costi Fissi di produzione ……………………………………………………...….pag. 89
I Costi Variabili ………………………………………………………………...….pag. 90
I Costi Totali …………………………………………………………………...….pag. 92
Costi Fissi Medi
…………………………………………………………...…....pag. 94
Costi Variabili Medi ……………………………………………………………….pag. 95
Costi Totali Medi …………………………………………………………………..pag. 97
Costi Marginali .………………………………………………………………...….pag. 98
Concorrenza Perfetta
………………………………………………………………...….pag. 100
Metodo dei costi marginali ...…………………………………………………...….pag. 107
Monopolio …….……………………………………………………………………...….pag. 111
Oligopolio ….…………………………………………………………………………...….pag. 112
Concorrenza monopolistica …………………………………………………………...….pag. 115
INTRODUZIONE
L’Economia Politica è una scienza che studia l’attività dell’uomo rivolta al
soddisfacimento dei propri bisogni. Essa si suddivide in due branche,
Microeconomia
e
Macroeconomia,
che
studiano
rispettivamente
il
comportamento dei singoli individui e quello delle c.d. “grandezze
aggregate”.
Questo studio avviene attraverso l’utilizzo di mezzi matematici e
geometrici, pertanto risulta necessario effettuare alcuni richiami di analisi
matematica.
Cominciamo con il concetto di funzione.
Dicesi funzione ogni regola matematica che permette di calcolare il valore
di una variabile (dipendente), partendo dal valore di una o più variabili
(indipendenti) e si scrive:
y= f(x)
con x variabile indipendente (y variabile dipendente)
In questo caso, la variabile y varia a seconda della funzione e a seconda
dei valori arbitrari dati alla variabile x.
Consideriamo ora la legge:
y= f(x1,x2)
due variabili indipendenti x1 e x2 (y variabile dipendente)
In questo caso, per ogni valore di x1 e x2 (scelti a piacere), la variabile y
assume un valore calcolabile a seconda della funzione considerata.
Le funzioni sono rappresentabili sul piano cartesiano mediante un grafico, il
quale permette di evidenziare la relazione causale esistente tra due
variabili (una dipendente e l’altra indipendente).
La relazione esistente tra due variabili può essere:
- lineare quando è rappresentabile come una linea retta;
- non lineare quando è rappresentabile come una curva.
Inoltre, d’ora in avanti diremo che due variabili sono legate da una
relazione diretta se aumentano proporzionalmente (ad esempio offerta e
ricavo totale); viceversa diremo che esse sono legate da una relazione
inversa se all’aumentare dell’una, l’altra diminuisce proporzionalmente
(come accade ad esempio per la domanda all’aumentare del prezzo di
mercato).
Introduciamo ora il concetto di pendenza di una funzione, ovvero di
coefficiente angolare di una curva: la pendenza di una funzione misura
la sua inclinazione e indica il grado di reattività della variabile y rispetto alla
variabile x. La pendenza si misura facendo il rapporto tra la distanza delle
ordinate (Δy) e la distanza delle ascisse (Δx):
Pendenza (coefficiente angolare) : Δy/ Δx
Se la relazione è diretta (funzione crescente), la pendenza sarà positiva,
mentre se la relazione è inversa (funzione decrescente), essa sarà
negativa.
Infine, quando avremo a che fare con funzioni lineari (rappresentate da una
retta), riscontreremo una pendenza costante pari a k (coefficiente angolare
della retta); viceversa, utilizzando funzioni curvilinee, riscontreremo una
pendenza diversa a seconda del punto in cui viene calcolata (In particolare,
di volta in volta, andremo a calcolare la pendenza della retta tangente nel
punto della curva considerato).
Nel caso delle funzioni curvilinee, a seconda dell’aumento o della
diminuzione del
coefficiente angolare
all’aumentare della variabile
indipendente, essa sarà rispettivamente concava o convessa.
4
Introduciamo ora il concetto di vincolo di bilancio e una relazione
generale che consentirà di calcolarlo in tutti i casi.
Il vincolo di bilancio rappresenta l’insieme dei beni che un
consumatore può acquistare spendendo tutto il suo reddito. Esso
dipende da due variabili: reddito e prezzo dei beni.
Analizziamo ad esempio la spesa per acquistare i beni y1 e y2 :
10y1 + 20y2= 200
Essa non può superare i 200 euro (Reddito).
Quindi:
Spesa ≡ Ricavo
Questa è la relazione generale de vincolo di bilancio. Nella formula del
vincolo compaiono:
1. due variabili: le quantità dei beni y1 e y2
2. tre dati: i due prezzi e il reddito
Per i tre dati usiamo i seguenti simboli:
1. P1 e P2 per i prezzi
2. M per il reddito
Vediamo quindi la forma implicita e quella esplicita della relazione del
vincolo:
P1y1 + P2y2
y2 = M _
P2
forma implicita
P1 y1
forma esplicita
P2
5
In questo caso, il coefficiente angolare è _ P1, mentre il termine noto è M
P2
P2
La formula del vincolo sarà:
y2 = M _ (P1) y1
P2
P2
Ed è del tipo: y = a + bx
Dove a è il termine noto e b il coefficiente angolare.
A seconda del valore di b, si avrà un andamento diverso della funzione.
Primo caso: b>0
 a misura l’intercetta ovvero l’intersezione del vincolo con l’asse delle
ordinate;
 b misura l’inclinazione della retta. Se essa aumenta, la retta ruota
verso l’alto; se invece diminuisce, la retta ruota verso il basso.
36
Secondo caso: b<0
Se ora consideriamo la formula del vincolo si ha:
a = M b = (P1)
P2
P2
E graficamente sarà:
 b è la pendenza della retta ed ha un valore negativo
7
Consideriamo ora il concetto di variazione, indicata col simbolo Δ: una
variazione sull’asse delle ascisse è indicata come Δx = x2-x1; una
variazione sull’asse delle ordinate è indicata come Δy = y2 – y1. Quindi la
variazione viene calcolata facendo la differenza tra valore finale e iniziale
della variabile considerata.
Se consideriamo un coefficiente angolare b=2, quando Δx = 1 si avrà
sempre Δy = 2. Questo perchè qualunque sia il valore di Δx, si ottiene
sempre:
Δy = b Δx, ovvero stando all’esempio: Δy = 2 Δx
Infatti, come abbiamo già visto il coefficiente angolare è sempre uguale al
rapporto Δy .
Δx
Introduciamo il concetto di variazione percentuale.
Se indichiamo con xn (n inteso come nuovo) il valore finale e con xv (v
inteso come vecchio) il valore finale, Δx sarà: Δx = xn-xv
La variazione percentuale sarà la variazione diviso per il livello di
partenza ed il risultato sarà successivamente moltiplicato per 100.
Consideriamo un esempio:
pv = 20
pn = 22
Δp = pn – pv = 2
Δp = 2 = 0,1 = 10%
pv
Variazione
Variazione percentuale
8
Per meglio comprendere come misurare l’inclinazione di una curva,
consideriamo la distribuzione di Gauss-Giordan
 l’inclinazione varia da punto a punto;
 in ogni punto è misurata dal coefficiente angolare della retta tangente
al punto;
 ha sempre lo stesso valore Δy/ Δx solo se il valore di Δx è
infinitesimo.
Ritornando al vincolo di bilancio, la forma implicita risulta comoda per
costruire il grafico del vincolo:
9
 si pone y2 (Quantità desiderata bene 2) = 0 e si trova subito la
quantità che si acquisterebbe se si decidesse di spendere l’intero
reddito nel bene 1, cioè y1 = M
P1
 Allo stesso modo si pone y1 (Quantità desiderata bene 1) = 0 e si
trova subito y2 = M
P2
Verifichiamo cosa succede se aumenta P1
Se P1 aumenta, il paniere M si sposta a sinistra e la retta ruota verso il
P1
Basso, quindi sarà possibile acquistare una quantità inferiore del bene 1
per mantenere lo stesso vincolo di bilancio
10
Analizziamo infine il saggio marginale di sostituzione:
Questa è la curva di indifferenza e rappresenta l’insieme dei beni che
garantiscono al consumatore lo stesso livello di utilità. La sua inclinazione
ci è data dal coefficiente angolare della retta tangente al punto.
L’inclinazione della curva si chiama SAGGIO MARGINALE DI
SOSTITUZIONE (S.M.S.), e rappresenta graficamente la quantità di bene
a cui si è disposti a rinunciare per ottenere una unità aggiuntiva di un altro
bene, mantenendo lo stesso livello di utilità. E’ dato dal valore assoluto del
coefficiente angolare della retta tangente al punto.
Quando l’inclinazione, in valore assoluto, lungo una curva di indifferenza
tende a diminuire, come nella figura, la curva è convessa.
Nel caso molto usuale di preferenze convesse del consumatore il saggio
marginale di sostituzione è decrescente, quindi la quantità di bene a cui si
è disposti a rinunciare per avere una unità aggiuntiva di un altro bene
tende a diminuire.
11
DOMANDA E OFFERTA
La ragione per cui noi studiamo la microeconomia è legata al fatto che le
risorse naturali presenti sul nostro pianeta sono scarse e dunque occorre
allocarle in modo tale da soddisfare le esigenze del maggior numero di
individui. D’altro canto, se per assurdo, il reddito fosse illimitato, non ci
sarebbe il problema della povertà, se l’aria che respiriamo fosse illimitata
non ci sarebbe neanche il problema dell’inquinamento e neppure la
disoccupazione sarebbe un problema se ci fosse un numero di posti di
lavoro sufficiente a soddisfare le esigenze di ciascun individuo. Tuttavia,
dato che ciò non avviene, la microeconomia si preoccupa di come allocare
in modo efficiente queste risorse scarse.
Per fare ciò, essa ipotizza un “mercato di beni”, ovvero, un luogo fisico o
virtuale dove interagiscono due tipologie di agenti:
1. il CONSUMATORE: che domanda beni e servizi
2. il PRODUTTORE:
che offre beni e servizi
Essi, avendo entrambi il problema della scarsità delle risorse, interagiscono
nel mercato e, grazie al “meccanismo dei prezzi”, raggiungono l’equilibrio
di mercato, ovvero una condizione in cui entrambi scambiano le quantità
desiderate ai prezzi desiderati.
A tal proposito, è opportuno sottolineare come tale equilibrio, nella realtà
rappresenti più un punto di riferimento a cui tendere che un obiettivo
pienamente raggiungibile. Inoltre dobbiamo precisare che il meccanismo
dei prezzi, benché imperfetto, risulta assai più efficiente quando lo Stato
non interviene nel mercato, ma lascia quella che Adam Smith chiamava la
“mano invisibile”, libera di agire. (es. l’Equocanone: quando lo Stato è
intervenuto per contenere i prezzi degli affitti sul mercato, ha ottenuto un
12
effetto esattamente opposto, incentivando inoltre la pratica degli affitti in
nero).
Per questo la microeconomia, auspica quasi sempre il non-intervento dello
Stato nel mercato(laissez-faire, laissez-passaire), in modo da favorire la
libera interazione di consumatori e produttori che, rappresentano
rispettivamente la domanda e l’offerta.
CURVA DI OFFERTA
La curva di offerta rappresenta graficamente il comportamento dei
produttori al variare dei prezzi sul mercato, ovvero la quantità di prodotto
che i produttori sono disposti a vendere a quei prezzi, ipotizzando che
rimangano costanti tutti gli altri fattori che influiscono sulla quantità offerta
(ceteris paribus).
Tale relazione prezzo-quantità può essere descritta dalla seguente
equazione:
QS = QS (P) Quantità offerta in funzione del prezzo.
Come si evince dal grafico, la curva di offerta è positivamente inclinata e
ciò implica che all’aumentare dei prezzi di mercato, i produttori saranno
disposti a produrre una quantità maggiore dello stesso bene. Tuttavia è
opportuno precisare che, anche se ciò si verifica nella quasi totalità dei
casi, esistono delle eccezioni, ovvero casi in cui l’offerta non aumenta
all’aumentare dei prezzi, bensì rimane costante perché la quantità che può
essere prodotta è fissa, invariabile. Ad esempio il numero delle lezioni
all’università in un semestre è prestabilito e anche se uno studente fosse
disposto a pagare una retta più elevata, esso non potrebbe aumentare. Lo
stesso vale per i quadri d’autore, infatti, anche se il prezzo che i suoi
estimatori sono disposti a pagare aumentasse a dismisura, il numero dei
quadri non potrebbe aumentare (perché ad esempio l’autore non è più in
vita).
Per questo motivo è più corretto parlare di teoria dell’offerta e non di
legge dell’offerta.
Una seconda precisazione poi va fatta in relazione al fatto che, benché i
nostri grafici siano per comodità bidimensionali e dunque diano
l’impressione che la quantità offerta dipende solo dal livello dei prezzi di
mercato, in realtà essa è influenzata anche da altre variabili:
- COSTI DI PRODUZIONE:
 Lavoro
 Capitale
 Materie prime
- TECNOLOGIA;
- CONDIZIONE CLIMATICHE (fondamentali, ad esempio, per le aziende
agricole)
In relazione alla curva dell’offerta sopra riportata si precisa che:
 una variazione del prezzo determina degli spostamenti sulla curva
di offerta;
 una variazione di un’altra delle variabili elencate determina una
traslazione della curva di offerta.
Esempio: CADUTA DEI COSTI DI PRODUZIONE
Se si riducono i costi di produzione, il produttore ha un maggiore incentivo
a produrre e, dunque, a vendere una quantità superiore del bene, e ciò
graficamente si traduce in una traslazione verso destra della curva di
offerta. Il risultato sarà che, in corrispondenza dello stesso prezzo di
mercato, la quantità offerta sarà maggiore se diminuiscono i costi di
produzione.
Una situazione analoga (traslazione verso destra della curva di offerta) si
verificherà anche in caso di:
- miglioramento della tecnologia di produzione;
- aumento del numero di produttori sul mercato;
- diminuzione delle tasse.
Viceversa, la curva di offerta traslerà verso sinistra (con conseguente
diminuzione della quantità offerta a parità di prezzi) in caso di:
- peggioramento della tecnologia;
- diminuzione del numero dei produttori sul mercato;
- aumento delle tasse.
CURVA DI DOMANDA
Rappresenta graficamente il comportamento del consumatore al
variare del prezzo sul mercato, ovvero quanto i consumatori di un
bene sono disposti a comprarne, quando il prezzo unitario cambia, se
rimangono costanti tutte le altre variabili che influenzano la domanda
(ceteris paribus).
Tale relazione prezzo-quantità può essere definita dalla seguente
equazione:
QD = QD (P)
quantità domandata in funzione del prezzo
Come si evince dal grafico, la pendenza della curva di domanda è
negativa e ciò implica che i consumatori saranno disposti a comprare
una quantità maggiore di un bene quando il suo prezzo diminuisce.
A tal proposito è opportuno sottolineare che tale relazione, a differenza
della funzione di offerta E’ UNA LEGGE.
Anche la domanda come l’offerta, è influenzata da altre variabili:
- REDDITO;
- PREFERENZE DEI CONSUMATORI;
- PREZZI DEI BENI COLLEGATI;
 Sostituti
 Complementari
- NUMERO DEI CONSUMATORI.
Naturalmente, anche in questo caso, è necessario fare un’importante
distinzione in relazione al grafico della curva di domanda. In
particolare è opportuno precisare che:
 in seguito a variazioni del prezzo saranno registrati spostamenti
lungo la curva di domanda;
 in seguito a variazioni di un’altra delle variabili elencate si
verificherà una traslazione della curva di domanda
Esempio: AUMENTO DEL REDDITO DEL CONSUMATORE
Se il reddito del consumatore aumenta, esso avrà una maggiore
propensione al consumo, ovvero, in corrispondenza di un prezzo
uguale a quello precedente, egli sarà disposto ad acquistare una
quantità maggiore del bene. Ciò graficamente si traduce in una
traslazione verso destra della curva di domanda.
Una situazione analoga (traslazione verso destra della curva di
domanda) si verificherà anche in caso di:
- aumento del numero di consumatori;
- aumento del prezzo dei beni sostituti;
- diminuzione del prezzo dei beni complementari;
- aumento della preferenza dei consumatori per il bene in
questione.
Al contrario, si verificherà una traslazione della curva verso sinistra in
caso di:
- diminuzione del numero di consumatori,
- diminuzione del prezzo dei beni sostituti,
- aumento del prezzo dei beni complementari,
- diminuzione della preferenza dei consumatori per il bene in
questione.
IL MECCANISMO DI MERCATO
Se rappresentiamo la curva di offerta e la curva di domanda in un
unico grafico, otteniamo il seguente risultato:
Il punto E, nel quale la curva di offerta e quella di domanda si
incontrano, è detto EQUILIBRIO DI MERCATO (o market clearing
price). Quando esso si verifica, si realizzano la seguenti condizioni:
 Quantità domandata uguale alla quantità offerta (QD = QS)
 Nessuna carenza di domanda
 Nessun eccesso di offerta
 Nessuna pressione verso cambiamenti di prezzo
Quest’ultima caratteristica, è legata al fatto che quello trovato, è un
equilibrio PARETO-EFFICIENTE, ovvero una situazione di mercato
in cui risulta impossibile migliorare la condizione di una parte senza
peggiorare la condizione dell’altra. Tale condizione rende l’equilibrio
stabile. Naturalmente, esso rappresenta una situazione ideale,
difficilmente raggiungibile in una realtà come la nostra, spesso
caratterizzata dalle cosiddette “inefficienze del mercato” (informazione
asimmetrica e azzardo morale). Esso, comunque, dovrebbe sempre
essere considerato un punto di riferimento verso il quale convergere,
almeno nel lungo periodo. Difficilmente infatti, l’equilibrio è presente
sin dall’inizio (ad esempio, al momento del lancio sul mercato di un
nuovo prodotto). Vediamo dunque cosa accade in una situazione di
equilibrio. A tal proposito presentiamo due possibili alternative:
non-
1. Prezzo di mercato maggiore del prezzo di equilibrio
In questa situazione registreremo un “eccesso di offerta” (Q S >Q D )
ovvero un SURPLUS, che indurrà i produttori a diminuire i prezzi di
mercato. Ciò inevitabilmente provocherà una diminuzione della
quantità offerta ed un aumento di quella domandata, con la
conseguente traslazione delle rispettive curve e con l’individuazione di
un nuovo punto di equilibrio:
2. Prezzo di mercato minore del prezzo di equilibrio
Questa volta registreremo una CARENZA di offerta, perché i produttori
non saranno disposti a soddisfare la domanda a queste condizioni e di
conseguenza alzeranno il prezzo inducendo una diminuzi one della
quantità domandata e un aumento della quantità offerta, fino a quando
non si giungerà nel punto di equilibrio.
VARIAZIONI DELL’EQUILIBRIO DI MERCATO
Benché l’equilibrio di mercato sia Pareto - efficiente esso può andare
incontro a variazioni, se cambia una delle variabili “ ceteris paribus” ,
che solitamente consideriamo costanti, relative alle funzioni di
domanda e/o di offerta. Vediamo alcuni esempi:
Es.1: CADUTA DEI PREZZI DELLE MATERIE PRIME
Questa
variazione incide sulla curva di offerta, perché i produttori
(essendo diminuiti i “costi di produzione) avranno interesse a offrire
una quantità maggiore per un livello di prezzo pari al precedente;
la -curva di offerta traslerà verso destra, creando una situazione di
“eccesso di offerta” (B);
i produttori
saranno così costretti ad abbassare i prezzi fino a
giungere nel nuovo punto di equilibrio (C);
la caduta
dei prezzi delle materie prime ha creato un nuovo equilibrio
in cui il prezzo è minore e la quantità scambiata è maggiore
Es.2: AUMENTO DEL REDDITO DEL CONSUMATORE
- Questa variazione incide sulla curva di domanda, perché il
consumatore, avendo un reddito più alto, sarà disposto ad acquistare
una maggiore quantità del bene ad un livello di prezzo pari al
precedente;
- la curva di domanda traslerà verso destra creando una situazione di
CARENZA DI OFFERTA;
- i produttori di conseguenza aumenteranno i prezzi fino a che non si
giungerà nel nuovo punto di equilibrio;
- l’aumento del reddito del consumatore ha creato un nuovo equilibrio
in cui il prezzo è maggiore e anche la quantità scambiata è
maggiore
Es.3: AUMENTO DEL REDDITO e CADUTA DEI PREZZI DELLE
MATERIE PRIME
- Sia la curva di offerta che la curva di domanda trasleranno verso
destra;
- questa volta tuttavia, la posizione del nuovo equilibrio rispetto al
precedente non può essere definita a priori, poiché non risulterà
essere sempre la stessa, bensì dipenderà da quale sarà la variazione
maggiore fra l’aumento del reddito (che trasla verso destra la curva di
domanda) e la caduta dei prezzi delle materie prime (che trasla verso
destra la curva di offerta)
- Se ad esempio, ipotizziamo che l’aumento in D sia maggiore
dell’aumento in S otteniamo la seguente situazione:
Nel nuovo equilibrio si registrano
prezzi e quantità più alte
Se invece avessimo ipotizzato un aumento in D minore dell’aumento in
S avremmo ottenuto una situazione diversa, giungendo ad un nuovo
punto di equilibrio in cui il prezzo sarebbe stato minore e la quantità
maggiore.
LA TEORIA DEL CONSUMATORE
La teoria del consumatore ha come obiettivo principale quello di
comprendere il comportamento del consumatore che,
è stato rappresentato tramite la curva di domanda individuale.
Essendo il nostro sistema caratterizzato dalla scarsità di risorse il
consumatore non è libero nelle sue scelte, bensì vincolato dal suo
reddito (se questo fosse infinito infatti non ci porremmo il problema
della scelta del consumatore).
Si pone dunque un problema di “massimizzazione vincolata”, ovvero di
massimizzazione della soddisfazione del consumatore, sotto due
vincoli:
1) vincolo di bilancio (vincolo oggettivo)
2) curve di indifferenza (vincolo soggettivo)
Il vincolo di bilancio è detto “vincolo oggettivo” perché non cambia a
seconda dei soggetti presi in esame. Infatti, posto un certo reddito, la
quantità acquistabile è uguale per tutti i consumatori. Tale oggettività
scaturisce dal fatto che esso dipende da due variabili esogene alla
volontà del consumatore:
 reddito
 prezzo dei beni
Nei nostri modelli, ipotizzeremo per comodità, l’esistenza di due soli
beni
nel
mercato,
ma
è
facilmente
dimostrabile
come,
le
considerazioni che faremo, possano essere estese a un mercato con
un numero superiore di beni.
Non è detto che tutti i consumatori decidano di ripartire il loro reddito
nelle stesse proporzioni, ovvero che decidano di acquistare la stessa
quantità del bene 1 e la stessa quantità del bene 2. Detta decisione
dipenderà, infatti, dalle “preferenze dei consumatori”, che ovviamente,
differiscono a seconda dei soggetti.
Per questo si parla di “vincolo soggettivo” che viene rappresentato
graficamente
attraverso
le
“curve
di
indifferenza”,
costituite
dall’insieme di combinazioni dei due beni che assicurano al
consumatore la stessa utilità.
Quindi, la teoria del consumatore ci aiuta a capire quale sia, posto
un certo reddito e un dato livello dei prezzi, la combinazione dei
due beni che, in base alle proprie personali preferenze, rende
massima l’utilità del consumatore.
A tal fine si dovrà procedere all’esame ed allo studio integrato del
“vincolo di bilancio” derivante dalla condizioni poste (reddito e prezzo
dei beni) e delle “curve di indifferenza” relative al consumatore preso
in considerazione.
Passiamo
dunque
a
formalizzare
nonché
a
rappresentare
graficamente quanto detto finora.
1) VINCOLO DI BILANCIO
Esso rappresenta le varie combinazioni di beni ( dette anche “panieri
di consumo”) che il consumatore può permettersi dato il suo reddito e
il prezzo dei beni.
Se lo rappresentiamo, infatti, in un sistema di assi cartesiani, esso
disegna una retta in cui ogni punto indica una possibile combinazione
dei due beni che il consumatore può acquistare. Ogni combinazione è
detta paniere1.
Vediamo dunque come si costruisce gr
aficamente il vincolo di bilancio:
- Si parte raccogliendo informazioni in merito al reddito del
consumatore, al prezzo del bene x e al prezzo del bene y;
Si
- calcolano le intercette, ovvero le intersezioni del vincolo con gli
assi cartesiani. Otterremo così un’intercetta verticale (R/Py) ed una
orizzontale (R/Px);
- Si uniscono le intercette con una retta e si ottiene il vincolo di
bilancio che risulterà essere sempre una retta .
Esempio:
- Se il consumatore decide di spendere tutto il reddito per il bene x :
egli è in grado di acquistare R/Px unità;
- Se il consumatore decide di spendere tutto il reddito per il bene y
egli è in grado di acquistare R/Py unità;
- Se il consumatore decide di acquistare entrambi i beni sceglierà
uno dei panieri compresi nella retta congiungente le intercette
1
Il più noto paniere, è quello che ogni anno prende in considerazione l’ISTAT, per
calcolare l’inflazione: un insieme d
i beni che sono ritenuti essere i più utilizzati
dagli italiani, del quale si stimano le variazioni dei prezzi rispetto all’anno
precedente)
(maggiore sarà la quantità acquistata di un bene , minore sarà la
quantità acquistata dell’altro bene );
Qualunque paniere sceglierà fra quelli presenti sul vincolo di bilancio,
avrà un costo complessivo pari al proprio reddito R .
Esempio:
- Nel punto C avremo la seguente spesa:
spesa bene x:
50*5= 250
spesa bene y:
250*1= 250
totale spesa: 250+250= 500
R
- Il punto E rappresenta un paniere che dato il nostro reddito e i
prezzi del mercato, il consumat
- Il punto D è una scelta
senso tenere un cer
ore non può permettersi;
inefficiente. In economia, infatti, non ha
to ammontare di denaro da parte, in quanto il
denaro va speso in beni
di consumo oppure va investito. D non è un
punto in cui si realizza un risp
inefficiente allocazione de
speso solo in parte
.
armio, bensì una situazione di
l reddito, in quanto quest’ultimo viene
Formalizziamo ora il vincolo di bilancio:
Equazione del vincolo di bilancio (forma implicita):
R= Px*X + Py*Y
Esplicitando l’equazione rispetto al termine in ordinata abbiamo
l’equazione del vincolo di bilancio in forma esplicita:
Y= (-Px/Py)*X + R/Py
- La pendenza del vincolo di bilancio sarà pari a -Px/Py;
- L’intercetta con l’asse delle ordinate sarà R/Py;
- L’intercetta con l’asse delle ascisse sarà R/Px;
Dall’equazione del vincolo di bilancio deduciamo anche che
la sua
pendenza sarà sempre negativa.
L’interpretazione
economica
di
detta
considerazione
è
che,
naturalmente, essendo il reddito limitato, all’aumentare della quantità
acquistata di un bene, corrisponderà una diminuzione proporzionale
della quantità acquistata dell’altro (relazione inversa tra le quantità
acquistabili dei due beni).
Tuttavia d’ora in avanti , dando per assodato che la pendenza del
vincolo di bilancio sia sempre negativa, considereremo sempre il suo
valore assoluto, in modo da avere un valore positivo.
SPOSTAMENTI DEL VINCOLO DI BILANCIO DOVUTI AD UNA
VARIAZIONE DEI PREZZI O AD UNA VARIAZIONE DEL REDDITO
DEL COSUMATORE
Come già stato detto, il vincolo di bilancio dipende da una serie di
variabili, al variare delle quali il vincolo cambierà. In particolare, esso
subirà una variazione in due casi:
a) variazione del prezzo dei beni
b) variazione del reddito del consumatore
a) Variazione del prezzo dei beni
La variazione del prezzo di uno dei due beni determina sempre una
variazione della pendenza del vincolo di bilancio.
Esempio: aumento del prezzo del bene x (Px ↑)
Se il prezzo del bene rappresentato sulle ascisse aumenta
il vincolo di
bilancio diventa più ripido, infatti, l’intercetta orizzontale si sposta verso
sinistra mentre l’intercetta verticale, rimanendo Py
costante, non varia.
Di conseguenza il vincolo di bilancio ruoterà in senso orario
all’intercetta verticale che fungerà da perno.
intorno
È facilmente dimostrabile che, se invece aumenta il prezzo del bene y,
l’intercetta orizzontale rimarrà la stessa, mentre l’ intercetta verticale si
sposterà verso il basso facendo ruotare il vincolo di bilancio in senso
antiorario.
Ricapitolando:
 Variazione di Px :
- Aumento: rotazione oraria del vincolo di bilancio
- Diminuzione: rotazione antioraria del vincolo di bilancio
 Variazione di Py:
- Aumento: rotazione antioraria del vincolo di bilancio
- Diminuzione: rotazione oraria del vincolo di bilancio
b) Variazione del reddito del consumatore
Come è facilmente intuibile se il reddito del consumatore varia
potrà permettersi di acquistare una quantità
egli
diversa di entrambi i beni.
Ciò graficamente si tradurrà in una traslazione del vincolo di bilancio
In particolare, se il reddito aumenterà il consumatore potrà acquistare
una maggiore quantità di beni ed assisteremo ad una traslazione
verso destra del vincolo di bilancio. Viceversa, se il reddito diminuirà
assisteremo ad una traslazione verso sinistra.
Esempio: riduzione del reddito del consumatore
.
Nel nostro esempio, i beni continuano ad essere scambiati allo stesso
trade-off perché i prezzi dei beni non sono cambiati (graficamente ciò
è riscontrabile dal fatto che il nuovo vincolo è parallelo al precedente),
tuttavia le possibilità de consumatore si sono ridotte.
Allo stesso modo si può dimostrare che:
- se raddoppia il reddito e raddoppiano entrambi i prezzi, le due
variazioni si compensano e si annullano, lasciando la situazione
inalterata;
- se il reddito raddoppia e i prezzi si dimezzando, la capacità di
acquisto del consumatore aumenta di 4 volte.
2) PREFERENZE DEL CONSUMATORE
Finora abbiamo parlato di un vincolo oggettivo, uguale per tutti i
consumatori, i quali non possono intervenire sulle sue variabili (reddito
e prezzo dei beni).
Abbiamo, però, già accennato al fatto che esiste un secondo vincolo,
stavolta soggettivo, da ricondurre alle personali preferenze di ogni
singolo consumatore, il quale, dato il vincolo di bilancio, sceglierà la
combinazione di beni (paniere) che massimizza la sua utilità.
A tal proposito è interessante notare come ogni individuo abbia
preferenze diverse per ogni bene, ovvero attribuisce ad ognuno di essi
un’importanza diversa dagli altri individui in base a quello che è il suo
ordinamento delle preferenze. Esso permette al consumatore di
classificare i diversi panieri in base alla loro desiderabilità.
Pertanto è opportuno sottolineare come gli economisti non facciano
valutazioni di merito sulle preferenze dell’individuo (de gustibus non
disputandum est), tuttavia stabiliscono su di essi delle proprietà
generali.
Proprietà (assiomi) delle preferenze:
- Completezza: il consumatore sa sempre scegliere tra panieri
diversi. In altre parole gli economisti assumono che il consumatore
sia sempre in grado di decidere quale paniere preferisce, senza
indecisioni.
- Transitività: se il consumatore preferisce A a B e B a C, allora
preferirà A a C.
- Non sazietà: il consumatore preferisce sempre avere la quantità
massima di tutti i beni.
- Convessità delle preferenze: Il Saggio Marginale di Sostituzione
(SMS) è decrescente, quindi le curve di indifferenza hanno forma
convessa.
Ricapitolando, dunque, il vincolo di bilancio indica cosa il consumatore
può permettersi di comprare mentre le preferenze indicano cosa il
consumatore vorrebbe comprare.
Naturalmente anche le preferenze , come il vincolo di bilancio, sono
rappresentabili graficamente. Il metodo utilizzato in microeconomia è
quello inventato da Pareto nel 1906: la Mappa delle Curve di
Indifferenza (CdI).
Una Curva di Indifferenza è il luogo geometrico di tutti i panieri di
consumo per i quali il consumatore trae la medesima utilità (è
indifferente).
Nel piano cartesiano esistono infinite CdI, una per ogni livello di
soddisfazione che il consumatore può raggiungere consumando i due
beni. Ciascuna CdI comprende un numero infinito di panieri che danno
al consumatore il medesimo livello di soddisfazione.
La rappresentazione grafica della CdI è la seguente:
Il paniere C contiene molta più birra, il paniere A contiene invece una
quantità maggiore di pizza, ma entrambi garantiscono lo stesso livello
di soddisfazione.
Le CdI ci danno informazioni sulla quantità di un bene a cui il
consumatore è disposto a rinunciare per ricevere una unità in più
dell’altro bene. Questa informazione
definita Saggio Marginale di
Sostituzione (SMS) che pari alla pendenza della curva di indifferenza
in un determinato punto. Esso infatti misura il saggio (rapporto) a cui il
consumatore è disposto a scambiare un bene con un altro, stavolta
non in base ai prezzi del mercato ma in base alle proprie preferenze.
Dunque esso non va confuso col rapporto tra i prezzi che invece
misura il saggio oggettivo a cui è possibile scambiare i beni sul
mercato.
Naturalmente essendo il SMS la pendenza di una curva ( che per
definizione, ha un coefficiente angolare variabile), esso sarà differente
per ogni punto della CdI.
Tuttavia il metodo per calcolarlo è sempre lo stesso e dipende dalla
differenza delle coordinate dei due panieri:
SMS = ∆y / ∆x
(differenza in ordinata) / (differenza in ascissa)
Esso, in definitiva, indica la compensazione psicologica in termini del
bene x richiesta in caso di riduzione del bene y per restare sulla stessa
CdI.
Esempio: i punti di invalidità
Proprietà delle Curve di Indifferenza
Esse non vanno confuse con gli assiomi delle preferenze, benché
come vedremo, abbiamo una relazione diretta con essi.
1. Il consumatore preferisce sempre CdI più alte.
2. Le curve d indifferenza hanno sempre pendenza negativa.
3. Le curve di indifferenza non si intersecano mai.
4. Le curve di indifferenza hanno pendenza via via decrescente.
Procediamo ora con la dimostrazione di suddette proprietà.
1. Il consumatore preferisce sempre CdI più alte
Tale proprietà scaturisce direttamente dall’assioma di non sazietà
delle preferenze, secondo il quale il consumatore, potendolo fare,
sceglie sempre una maggiore quantità di beni perché ciò gli garantisce
un maggiore livello di soddisfazione.
2. Le curve di indifferenza hanno sempre pendenza negativa
Per dimostrare detta proprietà dobbiamo illustrare come si costruisce
una curva di indifferenza. Per fare ciò consideriamo in un asse
cartesiano un paniere A e tracciamo per esso perpendicolari agli
assi,formando cosi 4 nuovi quadranti aventi il punto A come origine.
Ora, se consideriamo il quadrante a Nord-Est tra cui è compreso
anche il paniere B, notiamo che esso contiene tutti i panieri migliori di
A. Viceversa, il quadrante a Sud-Ovest, che comprende il paniere C,
contiene i panieri peggiori di A.
Se congiungiamo B e C (paniere migliore di A e paniere peggiore di A)
ci accorgiamo subito che i panieri che si trovano a Sud- Est sono
indifferenti ad A.
Con un ragionamento analogo si può facilmente verificare , tenendo
conto di paniere E ed F che, anche i panieri che si trovano a NordOvest sono indifferenti ad A. Dunque ricapitolando: se consideriamo A
come origine di un secondo asse cartesiano troviamo:
- Quadrante Nord-Est: insieme di panieri migliori di A;
- Quadrante Sud-Ovest: insieme dei panieri peggiore di A;
- Quadrante Sud-Est
Insieme dei panieri indifferenti ad A.
- Quadrante Nord-Ovest
Dunque la curva di indifferenza dovrà passare obbligatoriamente da
quadrante
Nord-Ovest
al
quadrante
Sud-Est
e
dunque
avrà
sicuramente pendenza negativa.
3. Le curve di indifferenza non si intersecano mai
Per dimostrare ciò, ragioniamo per assurdo e ipotizziamo che due
curve di indifferenza possano intersecarsi:
- A è indifferente a B;
- B è indifferente a C;
- Per l’assioma della transitività ciò implicherebbe che A è
indifferente a C, ma dato che i due punti giacciono su due curve di
indifferenza diverse, tale relazione è inammissibile. Dunque non
esiste alcuna possibilità che due curve di indifferenza si possano
intersecare in un punto.
4. Le curve di indifferenza hanno pendenza via via decrescente
Detta proprietà scaturisce direttamente dall’assioma di convessità
delle preferenze, secondo il quale il SMS è sempre decrescente.
Iniziamo la dimostrazione affrontando la questione graficamente:
Come si evince dal grafico il Saggio Marginale di Sostituzione è
decrescente perché la compensazione desiderata per la rinuncia ad
una unità di un certo bene diminuisce al crescere della dotazione
iniziale di quel bene.
In altre parole, se il consumatore ha un quantitativo eccessivo di birre,
rinuncerà volentieri ad una grande quantità delle stesse per ricevere
una pizza in più. Viceversa se la quantità di birre è esigua, egli non
sarà disposto a cederne una grande quantità per ricevere un’altra
unità di un bene, la pizza, di cui già possiede una grande quantità.
Tale comportamento spiegabile dal fatto che quasi tutti i consumatori,
indipendentemente dalle loro preferenze personali, propendono per la
varietà, ovvero preferiscono a prescindere dai gusti personali avere
una certa quantità di ogni bene, piuttosto che un’eccessiva quantità di
uno solo (naturalmente c’è chi avrà una particolare preferenza per un
bene e sarà portato ad acquistare un quantitativo maggiore della
media, ma si doterà sempre di una certa quantità degli altri beni).
CURVE
DI
INDIFFERENZA:
BENI
SOSTITUTI
E
BENI
COMPLEMENTARI
Sono state presentate le proprietà della curva di
indifferenza ed in particolare ci siamo soffermati sulla quarta, secondo la
quale il Saggio Marginale di Sostituzione è sempre decrescente.
In realtà, a tal proposito è opportuno precisare che, benché ciò sia vero
nella quasi totalità dei casi, esistono due casi speciali:
- Beni sostituti perfetti
- Beni complementari perfetti
Due beni si dicono sostituti perfetti quando soddisfano alternativamente
lo stesso bisogno, ovvero si scambiano nelle preferenza dell’individuo
sempre nella stessa proporzione. Ciò implica che, in questo caso il Saggio
Marginale di Sostituzione risulterà costante.
 Esempio:
Considerando ricariche telefoniche da 25 € e da 50 €, il rapporto di
scambio sarà sempre lo stesso. Essi sono perfetti sostituti, dunque le
curve di indifferenza saranno questa volta delle rette.
Sul mercato esistono anche dei sostituti imperfetti, ovvero beni il cui
rapporto di scambio è molto spesso il medesimo, tranne in alcun casi dove
si discosta leggermente.
 Esempio:
Un soggetto può essere solito scambiare una tazza di caffè con due tè.
Tuttavia ciò non esclude che qualche volta detto rapporto possa mutare. In
questo caso dunque le CdI saranno una via di mezzo tra una retta e una
curva.
Due beni saranno invece definiti complementari perfetti se vengono
consumati sempre
nelle medesime proporzioni,
al
punto
che il
consumatore trae un’utilità maggiore solo se aumentano entrambi.
Viceversa, se uno dei due rimane nelle stesse quantità, anche un aumento
cospicuo dell’altro non migliora la soddisfazione del consumatore.
 Esempio:
Questa volta in relazione al SMS, registreremo la seguente situazione:
- Sul tratto verticale della curva:
SMS = ∆y/∆x = ∞
il consumatore è disposto a rinunciare a infinite quantità del bene y per
avere un’unità aggiuntiva del bene x.
- Sul tratto orizzontale della curva:
SMS = ∆y/∆x = 0
il consumatore non è disposto a rinunciare a nessuna unità del bene y per
avere un’unità aggiuntiva del bene x perché non ne trarrebbe alcuna utilità.
- Nel punto di cuspide (l’angolo) il SMS è invece indefinito.
SCELTA OTTIMA DEL CONSUMATORE
Come è gia stato detto, premettendo che il consumatore vorrebbe sempre
più di quello che può permettersi, egli nella scelta del paniere ottimo, deve
tenere conto delle sue possibilità di acquisto.
Si pone dunque un problema di massimizzazione delle preferenze nel
rispetto del vincolo di bilancio. In tal senso è opportuno precisare che la
scelta ottima (first best) è una ed una sola e pertanto non ne è ammessa
un’altra (second best). Tale considerazione, analiticamente impone non
una condizione di intersezione (che genererebbe due soluzioni), bensì una
condizione di tangenza tra le curve di indifferenza ed il vincolo di
bilancio1, ovvero:
1
-
SMS = -P1/P2
A tal proposito va ricordato che, in letteratura, esistono 3 metodi per trovare il paniere ottimo:
metodo di sostituzione; - metodo di tangenza; -metodo di Lagrange.
In corrispondenza del paniere ottimo dunque il rapporto tra i prezzi
(pendenza del vincolo di bilancio) è pari al SMS (pendenza delle CdI).
Affrontiamo ora la questione dal punto di vista grafico:
- L’ottimo del consumatore coincide con il punto di tangenza tra il vincolo
di bilancio e le curve di indifferenza;
- Il paniere A darebbe una maggiore soddisfazione, ma non rientra nelle
possibilità di acquisto del consumatore;
- Il paniere B non rappresenta un punto di ottimo (di fatti solo i panieri sul
vincolo di bilancio sono efficienti);
- Il paniere C pur giacendo sul vincolo di bilancio non rappresenta un
punto di ottimo perché si trova su una curva di indifferenza più bassa.
L’unico paniere che rappresenta un punto di ottimo è dunque quello nel
quale la valutazione soggettiva del consumatore coincide con la
valutazione oggettiva del mercato.
Detto ciò, è tuttavia opportuno sottolineare che un paniere che si trova su
una curva di indifferenza più elevata, come il paniere A, potrebbe diventare
acquistabile qualora si modificasse la situazione di mercato, ovvero se
avvenissero delle variazioni di:
- Reddito
- Prezzo di mercato
Effetto di una variazione del reddito
Per valutare l’impatto di una variazione del reddito procediamo attraverso
la statica comparata. Essa permette di evidenziare come, un aumento del
reddito del consumatore faccia traslare il vincolo di bilancio verso destra
senza mutare la sua pendenza.
Ciò chiaramente consentirà al consumatore di scegliere un paniere che
giace su una CdI più elevata. Tuttavia a questo punto è importante fare
una netta precisazione. Quando il reddito del consumatore aumenta,
infatti, non è detto che egli decida sempre di acquistare di più di entrambi i
beni.
Potrebbe succedere infatti che, trovandosi in una migliore situazione
economica, il consumatore decida di comprare una quantità maggiore di
alcuni beni e di ridurre invece le quantità di altri.
Occorre dunque distinguere tra:
- Beni normali: se il reddito aumenta, il consumo aumenta;
- Beni inferiori: se il reddito aumenta, il consumo diminuisce.
Esempio:
Un consumatore nell’arco di un mese utilizza un certo numero di volte
l’auto e un certo numero di volte i mezzi pubblici. Se il suo reddito
aumenta, egli molto probabilmente utilizzerà molto di più l’auto, ma
diminuirà altresì il ricorso ai mezzi pubblici.
A tal proposito è opportuno poi precisare che la maggior parte dei beni
sono normali, tuttavia è impossibile che, in un determinato contesto tutti i
beni che consuma l’individuo siano inferiori ovvero che, aumentando il
reddito, il consumatore diminuisca tutte le quantità.
Detto ciò, possiamo analizzare separatamente i vari casi.
1. Effetto della variazione del reddito in presenza di beni normali
All’aumentare del reddito è aumentato il consumo di entrambi i beni.
A questo punto, introduciamo un nuovo strumento in grado di evidenziare
le varie combinazioni di ottimo al variare del reddito e, dunque, anche di
farci capire con esattezza se siamo in presenza di un bene normale o
inferiore: la Curva di Engel.
Prima però di tracciare il grafico della curva di Engel è interessante
rappresentare i vari livelli di ottimo al variare del reddito. Congiungendo
questi punti si ottiene il Sentiero di Espansione del Reddito:
LA CURVA DI ENGEL
Possiamo notare come in questo caso (due beni normali), il sentiero di
espansione del reddito sia inclinato positivamente. Possiamo ora
rappresentare la Curva di Engel, cioè il luogo geometrico delle
combinazioni di ottimo ottenute facendo variare il reddito, in un grafico
nel quale sulle ascisse consideriamo le quantità di birra e sulle ordinate il la
quantità di benzina:
Osservazioni:
- Il sentiero di espansione del reddito ha la stessa inclinazione della
Curva di Engel;
- Il bene birra è un bene normale e la curva di Engel è inclinata
positivamente;
- La relazione suddetta può essere estesa alle generalità dei casi: se la
curva di Engel ha inclinazione positiva, il bene in ascissa è un bene
nomale;
- Nel nostro esempio, la curva è una retta, ma ciò è dovuto al fatto che
abbiamo preso in considerazione solo due punti di ottimo (per due punti
l’unica rappresentazione attendibile è una retta). Aumentando i punti di
ottimo, avremmo ottenuto molto probabilmente una curva.
2. Effetto della variazione del reddito in presenza di un bene inferiore
Ipotizziamo che il consumatore per i suoi spostamenti giornalieri possa
scegliere di optare per l’auto (la cui frequenza di utilizzo è misurata dal
consumo di benzina) o per l’autobus. Empiricamente si può dimostrare che
all’aumentare del reddito, la quantità di benzina utilizzata aumenta, mentre
il numero dei viaggi in autobus diminuisce.
Anche in questo caso dunque, analizziamo la relazione alla luce della
Curva di Engel.
Propedeuticamente costruiamo quindi il sentiero di espansione del reddito.
Passiamo dunque alla realizzazione della curva di Engel per il bene viaggi
in autobus:
Osservazioni:
- Questa volta, essendo i viaggi in autobus un bene inferiore, il sentiero di
espansione del reddito e la curva di Engel sono inclinate negativamente;
- Generalizzando la suddetta relazione: Se la Curva di Engel ha
un’inclinazione negativa, il bene in ascissa è un bene inferiore.
- Un bene normale potrebbe, laddove il reddito aumentasse in modo
rilevante, diventare un bene inferiore. In questo caso probabilmente la
curva di Engel potrebbe presentare prima un tratto positivo e
successivamente, un tratto negativo.
3. Effetto di una variazione del prezzo (del bene in ascissa)
Stavolta non assisteremo a una traslazione del vincolo di bilancio, bensì ad
una rotazione:
- Verso l’esterno, se il prezzo si riduce (ampliamento delle possibilità di
consumo);
- Verso l’interno, se il prezzo aumenta (riduzione delle possibilità di
consumo).
A questo punto anche l’ottimo varierà.
Esempio: Riduzione del 50% del prezzo della birra
Osservazioni:
- In E’ rispetto ad E la quantità del bene birra (il cui prezzo è diminuito) è
aumentata mentre la quantità del bene pizza è leggermente diminuita;
- La variazione della quantità acquistata dell’altro bene dipende dal
cosiddetto “effetto sostituzione”, infatti al variare dei prezzi di uno dei
beni varierà anche la proporzione tra le quantità acquistate dei due beni;
- Stavolta non possiamo realizzare la Curva di Engel poiché essa ha un
senso solo in presenza di variazione del reddito;
- Non potendo costruire la curva di Engel non abbiamo nessuna
informazione in merito al fatto che i due beni siano normali o inferiori;
- In questo caso però, essendoci una variazione dei prezzi possiamo
costruire la curva di domanda (obiettivo che ci eravamo posti quando
abbiamo introdotto la teoria del consumatore).
Costruzione della curva di domanda
Come è stato più volte ripetuto, essa evidenzia la quantità domandata di un
certo bene al variare del prezzo. In questo senso può essere considerata
l’insieme delle scelte ottimali del consumatore ottenute facendo variare il
prezzo di un bene.
A questo punto abbiamo tutti gli strumenti necessari per capire come si può
costruire una curva di domanda. La costruzione si articola su 3 step.
Esempio: riduzione del prezzo della birra
Step 1: rappresentiamo graficamente le scelte ottime al diminuire del
prezzo della birra.
Il vincolo di bilancio ruota perché il prezzo della birra passa da 2 € a 1€.
Step 2: raccogliamo i dati relativi al prezzo e alla quantità di birra nei
diversi punti di ottimo in una scheda di domanda:
Step 3: tramite le informazioni costruite nella scheda, costruiamo la curva
di domanda:
Osservazioni:
- In questo esempio la curva di domanda è una retta perché abbiamo
raccolto informazioni in merito a due soli punti di ottimo, altrimenti molto
probabilmente avremmo ottenuto una curva;
- La funzione di domanda può essere dunque considerata il risultato delle
scelte ottimali del consumatore al variare dei prezzi (naturalmente
ceteris paribus, ovvero assumendo che tutte le altre variabili che
influenzano la domanda rimangano costanti);
- Il fatto che, al diminuire del prezzo del bene la quantità acquistata dal
consumatore aumenti, in realtà è dovuto all’azione combinata di due
effetti:
1. effetto di sostituzione: dovuto al fatto che il bene il cui prezzo è
diminuito diventa meno caro rispetto ad altri e ciò modifica il prezzo
relativo dei due beni;
2. effetto di reddito: dovuto al fatto che, la diminuzione di prezzo fa
aumentare il reddito reale e con esso il potere di acquisto del
consumatore.
Quindi l’effetto totale sulle scelte del consumatore sarà dato dalla somma
tra l’effetto di sostituzione e l’effetto di reddito.
A tal proposito è interessante separare i 2 effetti per vederne la rispettiva
entità di volta in volta. Tuttavia è opportuno precisare che essi avranno
segno diverso a seconda del bene oggetto di analisi. Per questo
studieremo l’influenza dei due effetti in 3 differenti casi:
- Beni normali;
- Beni inferiori;
- Beni di Giffen.
1. Effetto di sostituzione ed effetto di reddito in caso di beni normali
Partendo da una situazione di ottimo (B), ipotizziamo una riduzione del
prezzo del bene x. Essa farà ruotare il vincolo di bilancio in senso
antiorario intorno all’intercetta con l’asse delle ascisse provocando il
raggiungimento di un nuovo punto di equilibrio (E):
L’effetto
di
sostituzione
e
l’effetto
di
reddito
si
manifestano
contemporaneamente.
Per separarli dobbiamo procedere nel seguente modo:
- siccome l’effetto di sostituzione è dovuto alla variazione del prezzo
relativo dei due beni, per isolarlo, utilizziamo un artificio grafico in grado
di far variare soltanto il prezzo relativo tenendo fermo il reddito reale;
- per isolare l’effetto di reddito, procediamo, invece, in senso opposto,
dato che esso è dovuto esclusivamente alla variazione del reddito reale
e non anche alla variazione del prezzo relativo.
Graficamente quanto detto finora si traduce nella costruzione, sul grafico
precedente, di un vincolo di bilancio ipotetico (B’), parallelo al secondo
vincolo di bilancio (B1) e tangente alla prima curva di indifferenza (quella
passante per il punto b).
In questo modo si costruisce una situazione in cui il potere di acquisto del
consumatore è pari a quello iniziale, annullando l’effetto reddito, dato che ci
troviamo sempre sulla prima CdI, ma è variato il prezzo relativo tra i due
beni.
Naturalmente, individuato l’effetto di sostituzione, che ci porta nel punto T,
bisogna valutare l’effetto di reddito.
In particolare, la riduzione del prezzo del bene x darà luogo ad un aumento
del reddito reale che comporterà lo spostamento del punto di equilibrio (E)
nel punto di tangenza tra una Curva di Indifferenza più elevata (che
conterrà più beni della prima e nelle proporzioni determinate dall’effetto
sostituzione) ed il nuovo vincolo di bilancio (B1).
Ricapitolando, l’effetto totale ha due componenti:
- da B e T la variazione dipende dall’effetto di sostituzione;
- da T a E la variazione dipende dall’effetto di reddito.
Quindi, per separare graficamente l’effetto di sostituzione e l’effetto di
reddito che, congiuntamente, fanno variare l’ottimo del consumatore a
seguito di una diminuzione del prezzo del bene x, occorre procedere nel
seguente modo:
1) determinare la soluzione ottima di partenza (B);
2) determinare la soluzione ottima dopo la variazione del prezzo (E);
3) costruire un “vincolo di bilancio ipotetico” (B’), parallelo al secondo e
tangente alla prima curva di indifferenza. Si isola così l’effetto di
sostituzione, facendo variare solo il prezzo relativo dei due beni
(infatti la pendenza del vincolo di bilancio ipotetico è differente da
quella del vincolo iniziale) e mantenendo fermo il reddito (infatti ci
troviamo ancora sulla CdI di partenza);
4) il punto di tangenza fra il vincolo ipotetico e l’iniziale curva di
indifferenza (T), separa l’effetto di sostituzione (alla sua sinistra)
dall’effetto di reddito (alla sua destra).
Nel grafico l’effetto di sostituzione risulta essere maggiore di quello di
reddito.
Questa è la situazione più frequente nella realtà, poiché per ogni bene
esistono molti beni sostituti e i consumatori si ripartiscono fra di essi;
quando il prezzo di uno di questi diminuisce esso viene acquistato anche
da chi comprava i sostituti, proprio in virtù dell’effetto di sostituzione.
Inoltre è importante sottolineare come la situazione descritta si riferisca a
dei beni normali, infatti abbiamo un effetto di reddito positivo.
In conclusione occorre precisare che:
 l’effetto di reddito, nel caso di beni normali opera sempre in
direzione opposta rispetto alla variazione del prezzo; mentre nel caso
di beni inferiori, opera nella stessa direzione della variazione del
prezzo;
 l’effetto di sostituzione agisce sempre in senso opposto rispetto alla
variazione del prezzo.
EFFETTO DI SOSTITUZIONE ED EFFETTO DI REDDITO PER UN BENE
INFERIORE
Anche questa volta, partendo da una situazione di ottimo, ipotizziamo una
riduzione del prezzo del bene X. Determiniamo dunque il nuovo punto di
ottimo e costruiamo il vincolo di bilancio ipotetico per separare l’effetto di
sostituzione dall’effetto di reddito:
Px
: Effetto di sostituzione Q
Q
Effetto di reddito
Q
Osservazioni:
- Questa volta, considerando un bene inferiore, l’effetto di reddito opera
nella stessa direzione della variazione di prezzo, mentre l’effetto di
sostituzione in direzione opposta;
- L’effetto totale tuttavia è ancora positivo. Ciò dipende dal fatto che,
anche nel caso di beni inferiori, l’effetto di sostituzione è superiore
rispetto all’effetto di reddito;
- Anche per i beni inferiori, la funzione di domanda, benché più piatta, è
inclinata negativamente.
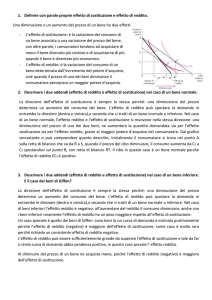
EFFETTO DI SOSTITUZIONE
ED EFFETTO DI REDDITO PER UN
BENE DI GIFFEN
Come abbiamo più volte ripetuto, la funzione di domanda è legge. Tuttavia
in letteratura esiste un’eccezione, seppur non riconosciuta dalla dottrina,
ovvero i “beni di Giffen”, dal nome dell’economista che li propose.
Secondo Giffen infatti, esistono particolari tipi di beni inferiori per i quali la
quantità domandata aumenta all’aumentare del prezzo e viceversa.
Partendo dal presupposto che esso rappresenta più un paradosso che si
verifica raramente nella realtà1 e che non tutti i beni inferiori sono beni di
Giffen è interessante comunque analizzare come agiscono in questo caso
l’effetto di reddito e l’effetto di sostituzione.
Analizziamo la diminuzione del prezzo di un bene di Giffen:
1
Sono considerati Beni di Giffen, alcuni beni di lusso come i gioielli o le auto da
collezione che vengono in genere acquistati da consumatori molto abbienti, i quali
rivestono un certo status nella società. Per questo target di consumatori spesso i
suddetti beni sono considerati tanto più ambiti quanto maggiore è il loro valore sul
mercato.
Px
: Effetto di sostituzione Q
Q
Effetto di reddito
Q
Osservazioni:
- Nei beni di Giffen, a differenza degli altri beni inferiori, l’effetto di
sostituzione, seppur positivo, è minore dell’effetto di reddito, che in
questo caso è negativo;
- Interessante sul piano teorico, il paradosso dei beni di Giffen si verifica
raramente nella realtà, data la presenza di numerosi succedanei
adeguati, i quali rendono remota l’ipotesi che l’effetto di sostituzione sia
più piccolo dell’effetto di reddito;
- E’ opportuno rimarcare il fatto che, anche se i beni di Giffen sono beni
inferiori, non tutti i beni inferiori sono beni di Giffen, infatti:
 Beni inferiori:
effetto di reddito < effetto di sostituzione
Curva di domanda inclinata negativamente
 Beni di Giffen:
effetto di reddito > effetto di sostituzione
Curva di domanda inclinata positivamente
SURPLUS DEL CONSUMATORE
Rappresenta la differenza tra ciò che il consumatore sarebbe disposto a
pagare (prezzo di riserva) e ciò che realmente paga.
Esso scaturisce dal fatto che, essendo il nostro un mercato caratterizzato
da una “informazione asimmetrica”, il produttore non conosce la curva di
domanda del consumatore.
Non sapendo, dunque, la disponibilità a pagare del consumatore per ogni
singola unità, egli non è in grado di effettuare alcuna discriminazione di
prezzo.
In questa situazione, il consumatore paga per ogni unità del bene solo ciò
che è disposto a pagare per l’ultima unità, anche se per le unità precedenti
sarebbe disposto a pagare un prezzo più elevato in virtù della sua curva di
domanda. Egli in pratica, realizza un surplus, che è pari alla differenza tra
la funzione di domanda e il prezzo di equilibrio:
Il consumatore nel punto E paga 2€ per 4 unità
2€ * 4= 8€
In realtà egli sarebbe disposto a pagare:
- per la prima unità
5€
- per la seconda unità
4€
- per la terza unità
3€
- per la quarta unità
2€
TOT.
14 €
(14 – 8) € = 6 €
SURPLUS DEL
CONSUMATORE
Dunque il surplus è dato dalla differenza tra il prezzo che egli sarebbe
disposto a pagare per ogni unità e il prezzo che effettivamente paga:
Prezzo di riserva
Prezzo pagato
Surplus
Prima unità
5
2
3
Seconda unità
4
2
2
Terza unità
3
2
1
Quarta unità
2
2
TOT. 6
ELASTICITA’ DELLA DOMANDA
Abbiamo visto come la funzione di domanda esprima la quantità di un bene
che viene domandata da parte di un individuo, ai vari prezzi di mercato, in un
determinato periodo di tempo.
In base alla correlazione esistente tra reddito e quantità domandata, abbiamo
poi fatto la distinzione tra beni normali, se c’è una correlazione positiva; beni
inferiori, se c’è una correlazione negativa. Mentre in base alla variazione del
prezzo di un bene e della quantità domandata di un altro bene, abbiamo beni
sostituti, qualora ad una variazione negativa del prezzo di un bene,
corrisponde una variazione negativa della quantità di un altro bene; beni
complementari se ad una variazione negativa del prezzo di un bene,
corrisponde una variazione positiva della quantità di un altro bene.
Adesso vediamo come l’elasticità della domanda e il coefficiente di elasticità
influenzino le specificità dei beni e per fare ciò bisogna effettuare un’analisi
quantitativa degli effetti dei movimenti della domanda.
Pertanto analizzeremo:
1. Elasticità della domanda rispetto a prezzo;
2. Elasticità della domanda rispetto al reddito;
3. Elasticità della domanda rispetto ad altri beni o incrociata.
1. ELASTICITA’ DELLA DOMANDA RISPETTO AL PREZZO
Misura la reattività della quantità domandata di un bene rispetto a variazioni
del prezzo dello stesso bene.
Definiamo ora il coefficiente di elasticità come la misura della variazione
percentuale della quantità domandata di un bene determinata da una
variazione percentuale del prezzo di quel bene, in un determinato periodo di
tempo.
Il coefficiente di elasticità, in questo caso, è un valore negativo, ma viene
nella maggior parte delle situazioni espresso in termini di valore assoluto
(quindi positivo).
Arriviamo adesso alla formula del coefficiente di elasticità:
∆Q
= variazione della quantità domandata
∆Q/ Q
= variazione relativa della quantità domandata
∆Q/ Q % = variazione percentuale della quantità domandata
∆P
= variazione del prezzo
∆P/ P
= variazione relativa del prezzo
∆P/P % = variazione percentuale del prezzo
da cui:
εp = (∆Q%)/(∆P%)
εp = (∆Q/Q)/(∆P/P)
εp = (∆Q/∆P)*(P/Q)
dove ∆Q/∆P è l’inverso del coefficiente angolare (pendenza) della curva di
domanda.
In base al valore del coefficiente di elasticità εp avremo:
- Domanda elastica: quando il valore dell’elasticità è maggiore di 1 (εp>1).
Ovvero quando la variazione percentuale della quantità domandata è
maggiore della variazione percentuale del prezzo.
- Domanda anelastica: quando il valore dell’elasticità è compreso tra 0 e 1
(0<εp<1). Ovvero quando la variazione percentuale della quantità
domandata è minore della variazione percentuale del prezzo.
- Domanda con elasticità unitaria : quando il valore dell’elasticità è pari a 1
(εp=1). Ovvero quando la variazione percentuale della quantità domandata
è pari alla variazione percentuale del prezzo.
OSSERVAZIONI:
 Se considero l’intercetta verticale, avremo un’elasticità ∞, mentre
nell’intercetta orizzontale, avremo un’elasticità nulla. Quindi per εp = 0 la
domanda sarà completamente inelastica, mentre per εp = ∞ la domanda
sarà infinitamente elastica. Entrambi sono casi prettamente teorici.
 Nel punto in cui εp = 1 la domanda è evidentemente a elasticità unitaria.
 Tra l’intercetta orizzontale (εp = 0) e l’intercetta mediana (εp = 1) la
domanda è anelastica (εp < 1).
 Tra l’intercetta mediana e l’intercetta verticale (εp = ∞), la domanda è
elastica (εp > 1).
 Se un ipotetico produttore fosse a conoscenza del valore dell’elasticità in
ogni punto della curva di domanda, potrebbe di volta in volta scegliere la
strategia di mercato a lui più favorevole, in particolare:
1. Aumenterebbe il prezzo nel tratto in cui la domanda è rigida (in
modo che il prezzo aumenta, ma la quantità non diminuisce
eccessivamente. Ciò gli consente di aumentare i suoi ricavi:
P
Q
RICAVI
2. Diminuirebbe il prezzo nel tratto in cui la domanda è elastica. Così
facendo, anche in questo caso incrementerebbe i suoi ricavi, poichè
a fronte di una piccola diminuzione di prezzo, riuscirebbe a vendere
una quantità maggiore:
P
Q
RICAVI
Vediamo ora i cosiddetti casi teorici :
 Domanda perfettamente elastica:
E’ un caso teorico che ritroveremo nello studio del mercato in una condizione
di concorrenza perfetta, ed è altresì un caso teorico al quale tutte le forme di
mercato tendono ad arrivare.
 Domanda perfettamente inelastica:
Consideriamo ora due esempi e vediamo in quale caso la domanda è più
elastica:
In base a quanto abbiamo finora detto, la seconda domanda è più elastica,
in quanto essendo più piatta della prima, la stessa variazione del prezzo
registra una maggiore variazione della domanda.
Quindi quanto più la funzione di domanda è inclinata (coefficiente angolare
tendente a ∞), tanto più la domanda è rigida; viceversa quanto più la
funzione di domanda è orizzontale (coefficiente angolare tendente a 0),
tanto più la domanda è elastica.
Da cosa dipende quindi l’elasticità della domanda?
 Dalla facilità con cui i consumatori possono sostituire i beni.
 Dal tempo: nel breve periodo, non tutti i consumatori sono al corrente
delle variazioni di mercato; mentre nel lungo periodo i consumatori
possono variare le proprie modalità di acquisto.
Pertanto la domanda tende ad essere:
 Più elastica nel lungo periodo.
 Meno elastica nel breve periodo.
2. ELASTICITA’ DELLA DOMANDA RISPETTO AL REDDITO
Misura la reattività della quantità domandata rispetto alle variazioni di
reddito.
Il coefficiente di elasticità, in questo caso, misura la variazione
percentuale della quantità domandata del bene per effetto della variazione
percentuale del reddito. Esso può essere positivo o negativo.
εr = (ΔQ%) / (ΔP%)
εr = (ΔQ/Q) / (ΔR/R)
εr = (ΔQ/ΔR)*(R/Q)
Si noti come stavolta nella formula compaia il reciproco del coefficiente
angolare della curva di Engel. Occorre inoltre sottolineare come stavolta il
coefficiente di elasticità possa essere sia negativo che positivo (a seconda
che il bene sia normale o inferiore). Non si può dunque usare il valore
assoluto.
Vediamo cosa succede nel caso di:
 Beni normali:
- εr > 0
(positiva)
- un aumento del reddito comporta un aumento della quantità
domandata (esempio: alimentari, abbigliamento …);
 Beni inferiori:
- εr < 0
(negativa)
- un aumento del reddito comporta una diminuzione della quantità
domandata ( esempio: patate, carbone, mezzi di trasporto
pubblici …)
Per quanto riguarda i beni normali, dobbiamo fare una distinzione:
 Beni di prima necessità:
- 0 < εr < 1
- la quota di spesa per questi beni aumenta meno che
proporzionalmente all’aumentare del reddito (esempio: alimentari,
vestiario …);
 Beni di lusso:
- εr > 1
- la
quota
di
spesa
per
questi
beni
aumenta
più
che
proporzionalmente all’aumentare del reddito (esempio: cellulari,
viaggi …);
Graficamente, per un aumento di reddito, ecco cosa succede alla curva di
domanda nel caso di un bene normale e di un bene inferiore:
 Bene normale
 Bene inferiore
3. ELASTICITA’ DELLA DOMANDA RISPETTO AD ALTRI BENI O
INCROCIATA
Misura la reattività della quantità domandata di un bene x rispetto alla
variazione di prezzo di un bene y.
Il coefficiente di elasticità incrociata misura la variazione percentuale della
quantità domandata di bene x rispetto alla variazione percentuale del prezzo
del bene y. Esso può essere sia positivo che negativo.
εxy =(ΔQx%)/ (ΔPy%)
εxy =( ΔQx/Qx)/ (ΔPy/Py)
εxy =( ΔQx/ ΔPy)/(Py/Qx)
In questo caso di elasticità della domanda incrociata, avremo che:
 un bene è sostituto se:
- εxy > 0 (aumenta il prezzo del bene y, aumenta anche la quantità
del bene x; ad esempio thè, caffè …);
 un bene è complementare se:
- εxy = 0
(non c’è relazione tra i beni).
TEORIA DELLA PRODUZIONE
1. L’IMPRESA
L’impresa è l’operatore economico il cui ruolo è quello di produrre beni e
servizi. Essa trasforma i fattori della produzione (input) in beni e servizi
(output). Ogni impresa cerca in genere di massimizzare i profitti.
Gli elementi fondamentali da analizzare nello studio dell’impresa sono:
 fattori produttivi: non sono gratuiti, ma hanno dei costi (terra
lavoro
salario; capitale
organizzazione
rendita;
tasso d’interesse;
profitto dell’imprenditore);
 funzione di produzione;
 produttività;
 ottimo del produttore.
Per quanto riguarda la produttività dell’impresa, dobbiamo analizzare due
concetti differenti:
 produttività media: rappresenta il rapporto tra la quantità ottenuta con
un fattore e la quantità impiegata del fattore stesso. In questo caso non
si va a valutare la produttività del singolo fattore, ma si fa una
valutazione su tutti i fattori che generano produzione all’impresa:
quantità di produzione
produttività
quantità del fattore produttivo impiegato
 produttività marginale: rappresenta l’incremento di prodotto dovuto ad
una dose aggiuntiva di fattore produttivo. La produttività marginale ci
fornisce un dato più rilevante rispetto a quella media perché fa
riferimento al singolo fattore, invece che alla media di tutti.
Variazione della quantità prodotta
produttività marginale
Variazione del fattore produttivo
Nello studio dell’attività dell’impresa, è molto importante il periodo di tempo
che si prende in considerazione, pertanto si parla di:
 breve periodo:
- l’impianto non può essere variato in questo periodo;
- si decide solo il grado di utilizzazione dell’impianto;
- alcuni dei fattori sono fissi;
 lungo periodo:
- l’impianto può essere considerato variabile;
- si decide quanto deve essere grande l’impianto in base a quanto
è in grado di produrre;
- i fattori sono tutti variabili;
2. FUNZIONE DI PRODUZIONE
Nel breve periodo essa è una funzione di tipo tecnico ed esprime una
relazione tra la quantità di prodotto ottenuto e la quantità dei fattori impiegati:
Y = f(L, K*, T)
Dove:
- L è il lavoro (variabile)
- K* è il capitale (fisso)
- T è la terra (variabile)
- Y è il livello di produzione
Notiamo come le variabili del lavoro e della terra sono evidentemente
variabili, mentre il capitale è un valore fisso e rispetto ad esso c’è variazione
della produzione.
Facciamo ora un esempio per far capire la differenza fra produttività media e
produttività marginale.
Ipotizziamo che un imprenditore possieda una sartoria con due stanze e
debba decidere di assumere un certo numero di sarti in grado di garantire
una certa produzione. A tal proposito consideriamo una situazione iniziale in
cui c’è solo un sarto e poi aumentano il numero di sarti di una unità alla volta
per capire cosa succede alla quantità prodotta.
Analizziamo dunque la situazione alla luce dei concetti di produttività media e
di produttività marginale.
Quantità fattore
Quantità
Produttività
Produttività
produttivo
prodotta
media
marginale
1
10
10
10
2
18
9
8
3
24
8
6
4
28
7
4
5
30
6
2
6
30
5
0
(n°sarti)
Osservazioni:
 Naturalmente all’aumentare dei sarti impiegati nelle due stanze, la
produzione è aumentata. Tuttavia è immediato rendersi conto che, ad
esempio raddoppiando il numero dei sarti, la quantità prodotta non è
affatto raddoppiata.
 Cercando di analizzare la situazione alla luce della produttività media ci
rendiamo conto che:
- il primo sarto da solo produce 10 unità di prodotto;
- quando i sarti diventando due la media è di 9 unità di prodotto
ciascuno;
- quando i sarti diventando sei, la media è di 5 unità di prodotto
ciascuno.
Tuttavia, pur intuendo una situazione di rendimento decrescente, non
riusciamo a capire la produttività di ogni singolo lavoratore.
 Analizzando dunque la produttività marginale ci rendiamo conto
finalmente che:
-
il primo sarto da solo produce 10 unità di prodotto;
-
il secondo sarto da solo produce 8 unità di prodotto;
-
il sesto sarto è totalmente inefficiente perché non produce alcuna
unità di prodotto aggiuntiva.
Grazie dunque al “tasso di crescita” della produzione misurato dalla
produttività marginale, abbiamo capito che la sartoria versa in una
situazione patologica fin dall’inizio poiché ogni sarto aggiunto produce una
quantità minore del sarto precedente pur percependo il medesimo salario.
 La situazione illustrata è dunque descrivibile graficamente da una
funzione di produzione.
In particolare visto che all’aumentare del fattore produttivo:
- il prodotto totale aumenta, quindi la funzione di produzione sarà
inclinata positivamente;
- il prodotto totale aumenta in maniera meno che proporzionale
all’aumentare dei fattori di produzione, quindi la funzione di
produzione sarà rappresentata da un “sigmoide” con la concavità
maggiore rivolta verso il basso.
Y
Fattore Produzione
In conclusione dunque possiamo affermare che la produttività media non
è stata molto significativa nell’analisi realizzata. Viceversa la produttività
marginale ci ha fatto capire che l’impiego già del secondo sarto è
inefficiente e che quindi se proprio l’imprenditore avesse esigenza di
produrre un quantitativo maggiore farebbe meglio ad ampliare la struttura,
aumentando ad esempio il numero delle stanze (per evitare l’affollamento
delle uniche due stanze).
TEORIA DELLA PRODUZIONE: L'ANALISI
Abbiamo introdotto la Teoria della Produzione con la
quale si studia il comportamento dell’impresa sul mercato. A tal proposito è
opportuno ricordare che l’obiettivo dell’impresa è quello di massimizzare il
profitto almeno nel lungo periodo. Ciò infatti non sempre è possibile nel breve
periodo, per questo in esso si cerca almeno di mantenere una buona
immagine pubblica o di aumentare la quota di mercato, fermo restando che
se l’impresa non realizza un profitto neanche nel lungo periodo, sarà costretta
ad uscire dal mercato.
Inoltre è poi necessario precisare che non esiste in realtà un criterio distintivo
oggettivo in grado di individuare una netta linea di separazione tra breve e
lungo periodo.
Prima di entrare nel merito della situazione già descritta, ricordiamo che non
esiste un’unica funzione di produzione per tutte le imprese, ma tutto dipende
dalla produttività media e dalla produttività marginale della specifica impresa.
Esistono infatti imprese efficienti ed imprese meno efficienti.
Il caso trattato precedentemente è un esempio di impresa inefficiente
sin dall’inizio poiché già il secondo sarto ha una produttività marginale
inferiore al primo.
Cerchiamo dunque di capire in questo caso specifico quale sarà l’andamento
della funzione di produzione:
 fino al 5° lavoratore la quantità prodotta aumenta, dunque la funzione di
produzione all’inizio sarà inclinata positivamente. Dopo il 6°lavoratore la
quantità prodotta potrebbe addirittura diminuire e dunque la funzione di
produzione diventerà inclinata negativamente;
 siccome il tasso di crescita è sempre decrescente, la funzione di
produzione sarà concava.
Tale funzione di produzione è dovuta al fatto che l’impresa esaminata versa
in una situazione di inefficienza sin dall’inizio e dunque la produttività
marginale è sempre decrescente.
Tuttavia come abbiamo già detto, non esiste un’unica funzione di produzione
in grado di descrivere la generalità dei casi. Essa, infatti, è differente a
seconda della specifica situazione in cui versa l’impresa. Per dimostrare ciò
analizziamo il secondo caso:
Q. fatt. prod.
Q. prodotta
Prod. media
Prod. marginale
1
10
10
10
2
22
11
12
3
36
12
14
4
46
11,5
10
5
52
10,4
6
6
54
9
2
Analisi:
 la quantità prodotta è sempre crescente, dunque la funzione di
produzione sarà inclinata positivamente;
 fino al terzo sarto all’aumentare del fattore produttivo, la produzione
aumenta in modo più che proporzionale. A partire dal quarto sarto
l’impresa non è più efficiente poiché all’aumentare del fattore produttivo
la produzione aumenta in modo meno che proporzionale.
Dunque:
 fino al terzo sarto la funzione di produzione è convessa;
 dal quarto sarto la funzione di produzione è concava.
La situazione descritta è tipica delle nuove imprese che sorgono nel mercato.
Esse infatti vanno incontro inizialmente ad una situazione in cui il tasso è
crescente (all’aumentare del fattore produttivo, la produzione cresce più che
proporzionalmente). Successivamente quando il mercato è saturo la funzione
di produzione benché ancora inclinata positivamente, registra un tasso
decrescente (all’aumentare del fattore produttivo, la produzione cresce meno
che proporzionalmente).
Ciò è dovuto al fatto che, solo nel breve periodo vige una legge sempre
valida, detta legge dei RENDIMENTI DECRESCENTI.
Essa afferma che se aggiungiamo ulteriori unità di fattori variabili, l’output
aumenta ma ad un tasso decrescente.
Ciò dipende dal fatto che nel breve periodo, la maggior parte dei fattori
produttivi è fissa, dunque l’aumento dei soli fattori variabili crea problemi di
congestionamento, che pongono un freno alla produttività dell’azienda.
Pensiamo, ad esempio, ad un ufficio in cui il numero dei computer è fisso, ma
si decide di aumentare comunque il numero degli impiegati (fattore variabile).
All’aumentare degli impiegati, non essendoci un computer per ogni impiegato,
la produttività non potrà aumentare più che proporzionalmente. Anzi
verosimilmente si creeranno degli attriti fra gli impiegati su questioni
riguardanti l’utilizzo dei pochi computer e ciò naturalmente andrà a scapito
della produttività.
Volendo descrivere questa situazione graficamente:
Dunque nel breve periodo si registrano rendimenti decrescenti, ovvero il
rendimento dei fattori produttivi manifesta una tendenza a decrescere
all’aumentare delle unità immesse nella produzione. Ciò può verificarsi:
 sin dall’inizio (imprese inefficiente in partenza) come nel primo caso;
 a partire da un certo quantitativo immesso nella produzione come nel
secondo caso descritto.
FUNZIONE DI PRODUZIONE DI LUNGO PERIODO, COSTI
DELL’IMPRESA ED EQUILIBRIO DEL PRODUTTORE
Finora abbiamo rappresentato delle possibili situazioni in un orizzonte
temporale di breve periodo, nel quale alcuni fattori produttivi, come ad
esempio il capitale, sono fissi. Passiamo ora ad analizzare un contesto di
lungo periodo. In particolare:
 presenteremo una funzione di produzione di lungo periodo (dove i
fattori di produzione sono tutti variabili). Essa graficamente sarà
rappresentata tramite gli ISOQUANTI;
 analizzeremo
poi
i
costi
dell’impresa
rappresentandoli
graficamente tramite la retta di ISOCOSTO;
 infine combineremo i due concetti per illustrare la decisione di
lungo periodo dell’impresa su quanto capitale (K) impiegare e
quanto lavoro (L) utilizzare.
FUNZIONE DI PRODUZIONE DI LUNGO PERIODO
In un contesto di breve periodo abbiamo rappresentato la funzione di
produzione in un grafico in cui vi era un unico fattore della produzione poiché
gli altri, essendo fissi, erano considerati delle costanti.
Nel lungo periodo, invece, i due fattori della produzione che consideriamo nei
nostri modelli, ovvero capitale e lavoro, sono entrambi variabili. Nasce
dunque l’esigenza di rappresentarli graficamente entrambi, anche alla luce
del fatto che diverse combinazioni di capitale e lavoro generano diversi livelli
di produzione.
Tutto ciò può essere rappresentato graficamente tramite gli ISOQUANTI:
Un ISOQUANTO rappresenta tutte le combinazioni di capitale e lavoro
che permettono di ottenere il medesimo livello di produzione. Essi
dunque costituiscono per il produttore ciò che le curve di indifferenza
costituiscono per il consumatore, con la differenza che mentre queste ultime
seguivano un indice ordinale, gli isoquanti rispettano un ordine cardinale.
Naturalmente come accadeva per le CdI , anche gli isoquanti sono
teoricamente infiniti e ogni curva superiore rappresenta una situazione in
cui il livello di produzione è maggiore del precedente, poiché si utilizzano
maggiori quantitativi di entrambi i fattori della produzione.
La funzione di produzione di lungo periodo di un’impresa può essere
rappresentata, quindi, a partire da una molteplicità di isoquanti, ciascuno
corrispondente ad un diverso livello di produzione.
E’ importante poi sottolineare come , a differenza delle CdI, gli isoquanti non
siano caratterizzati da preferenze soggettive. Essi costituiscono l’insieme dei
panieri dei fattori produttivi (capitale e lavoro) che l’impresa combina secondo
una data tecnologia (rappresentabile matematicamente tramite una funzione
a due variabili) per ottenere un certo livello di produzione.
Analogamente a quanto fatto per le CdI, passiamo ora ad analizzare le
caratteristiche degli isoquanti. A tal proposito anticipiamo già il fatto che
essi di fatto godono delle medesime proprietà delle curve di indifferenza:
1. Gli isoquanti hanno pendenza negativa
La produzione lungo tutto l’isoquanto deve essere sempre la stessa, pertanto,
affinchè il livello di produzione resti inalterato lungo tutta la curva, se
l’impresa vuole aumentare la quantità di capitale, deve necessariamente
ridurre la quantità di lavoro e viceversa.
Anche in questo caso, come per le CdI, il coefficiente angolare ci da il
rapporto di scambio tra le due variabili. In questo caso esso prende il nome di
SAGGIO MARGINALE DI SOSTITUZIONE TEORICA:
SMST = ΔL / ΔK
Esso indica in quale misura l’impresa è in grado di sostituire capitale e lavoro
lungo l’isoquanto.
2. Isoquanti distanti dall’origine si associano a livelli di produzione
maggiori
Di fatti se l’impresa può permettersi di usare di più di entrambi i fattori sarà in
grado di produrre una quantità maggiore di output.
3. Due isoquanti non possono mai intersecarsi
Ogni isoquanto rappresenta possibili combinazioni che generano il medesimo
livello di produzione. Se due isoquanti, per assurdo, si intersecassero, ciò
implicherebbe che una stessa combinazione con una stessa tecnologia
permette di generare due diversi livelli di produzione. Ciò naturalmente è
impossibile.
4. SMST decrescente (convessità degli isoquanti)
Osservando il grafico è possibile notare come la pendenza dell’isoquanto
cambi muovendosi lungo la curva: a sinistra, in prossimità dell’asse delle
ordinate, la curva ha pendenza elevata, poi la pendenza diminuisce. Ciò è
dovuto al fatto che i fattori della produzione hanno RENDIMENTI
DECRESCENTI. Ad esempio, se scelgo sempre di aumentare il livello del
capitale a scapito del lavoro, esso avrà un rendimento via via decrescente, in
quanto
se
aumentano
i
macchinari
e
la
manodopera
diminuisce,
inevitabilmente l’incidenza sulla produzione sarà via via sempre minore.
Seguendo ancora una volta un discorso parallelo a quello fatto per le CdI,
analizziamo ora due casi particolari di isoquanti:
a. Fattori produttivi complementari perfetti
In questo caso i due fattori di produzione vanno utilizzati necessariamente in
modo congiunto in un rapporto 1:1. Pertanto un tosaerba aggiuntivo, senza
un corrispondente incremento della forza lavoro, non aumenterà il livello di
produzione.
Questo particolare si traduce graficamente in isoquanti a forma di “L”.
In questa situazione:
 Tratto verticale :
SMST = ∞
 Tratto orizzontale: SMST = 0
 Cuspide:
SMST indefinito
b. Fattori produttivi sostitutivi perfetti
In questo caso i due fattori produttivi sono perfettamente sostituibili, dunque
utilizzare l’uno o l’altro per il produttore è indifferente. Se prendiamo ad
esempio la produzione di pan di spagna, uova bianche e uova scure sono
perfetti sostituti nel rapporto 1:1. Ne consegue che in una situazione del
genere gli isoquanti saranno delle rette e il SMST risulterà costante lungo
tutto l’isoquanto:
RETTA DI ISOCOSTO
Finora abbiamo visto le possibili combinazioni dei due fattori della produzione
(capitale e lavoro) che il produttore può scegliere per produrre il medesimo
livello di output (rappresentato attraverso gli isoquanti). Tuttavia la scelta
relativa a quale combinazione utilizzare e, soprattutto, in merito a quale livello
di produzione potersi permettere, non dipende solo dalla strategia del
produttore ma anche dai COSTI DEI DUE FATTORI PRODUTTIVI.
Nasce dunque l’esigenza di rappresentare graficamente i costi associati
ai due fattori in modo da poter individuare un punto in cui si possa produrre
la quantità massima possibile cercando di minimizzare i costi.
Si introduce, pertanto il CONCETTO DI ISOCOSTO: luogo geometrico di
tutte le possibili combinazioni dei due fattori produttivi che l’impresa
può acquistare ad un dato costo totale.
Quanto sopra si traduce matematicamente nella seguente funzione:
CT = wL + rK
FORMA IMPLICITA RETTA DI ISOCOSTO
Dove:
 wL indica il costo del lavoro, con w = salario e L = n. lavoratori;
 rK indica il costo del capitale, con r = tasso di interesse e K = capitale.
Analogamente a quanto fatto per il vincolo di bilancio nella teoria del
consumatore, esplicitiamo l’equazione rispetto al n. lavoratori L (valore delle
ordinate). Otteniamo così:
L = CT/w – (r/w)K
FORMA ESPLICITA RETTA DI ISOCOSTO
OSSERVAZIONI:
 CT/w
rappresenta l’INTERCETTA VERTICALE con l’asse delle
ordinate della retta di isocosto. Essa economicamente indica il massimo
numero di lavoratori che l’impresa può assumere se decidesse di
impiegare tutto il suo budget nel fattore lavoro senza utilizzare il fattore
capitale;
 -(r/w) rappresenta il coefficiente angolare, ovvero la pendenza della
retta di isocosto. Da essa deduciamo che la retta di isocosto è sempre
INCLINATA NEGATIVAMENTE. Economicamente esso rappresenta il
rapporto tra i prezzi dei fattori produttivi, ovvero la quantità di lavoro che
il mercato impone di sacrificare, dati i prezzi di mercato, per poter
acquisire un’unità aggiuntiva di capitale.
Graficamente:
Qualsiasi combinazione dei due fattori al di sotto della retta risulterà
inefficiente. Viceversa tutte le combinazioni sopra la curva rappresentano
panieri che il produttore non può permettersi, in quanto considerati i costi
dei fattori produttivi, hanno un costo superiore al costo totale sostenibile
dell’impresa.
Analogamente a quanto fatto per il vincolo di bilancio, analizziamo le due
possibili variazioni della retta di isocosto:
a) VARIAZIONE DEL COSTO TOTALE
In questo caso assisteremo ad una traslazione della retta di isocosto,
verso destra se il costo totale aumenta, verso sinistra se il costo totale
diminuisce. Detta variazione non modifica invece il coefficiente angolare
della retta.
b) VARIAZIONE DEI PREZZI
In questo caso cambierà la pendenza della retta di isocosto ed
assisteremo ad una rotazione.
Esempio: aumento del salario (w)
Un aumento del salario economicamente implica un aumento del costo di
lavoro e dunque una riduzione del rapporto tra i prezzi dei fattori produttivi
(r/w). Ne consegue che, nella nuova situazione, per impiegare un’unità di
capitale aggiuntivo, saranno licenziati meni lavoratori.
COMBINAZIONE OTTIMA DI CAPITALE E LAVORO
Anche in questo caso, come già visto nella teoria del consumatore, la
combinazione ottima di capitale e lavoro si avrà in corrispondenza del
punto di tangenza tra la funzione di produzione di lungo periodo
(rappresentata da isoquanti) e la retta di isocosto.
Matematicamente ciò implica l’uguaglianza di rispettivi coefficienti angolari:
L’isoquanto tangente alla retta di isocosto sarà il più efficiente (il più in alto)
possibile.
Le combinazioni B, A, C sono tutte possibili, tuttavia il punto di ottimo è uno
solo: il punto A, il quale consente un livello di produzione maggiore di B e C.
Economicamente possiamo dunque concludere che il punto di ottimo è quello
in corrispondenza del quale ciò a cui il produttore rinuncia in termini di unità di
lavoro per un’unità aggiuntiva di capitale (SMST) è esattamente uguale a
quanto il mercato può richiedere di sacrificare in termini di lavoro per avere
un’unità aggiuntiva di capitale (r/w).
Concludiamo ora la trattazione analizzando la combinazione ottima nei due
casi particolari:
a) COMBINAZIONE
OTTIMA:
FATTORI
COMPLEMENTARI
PERFETTI
Siccome in questo caso gli isoquanti hanno la cosiddetta forma ad L,
l’unico punto di tangenza con la retta di isocosto e la cuspide, poiché
altrimenti otterremo sempre l’intersezione, mentre il punto di ottimo deve
essere unico per definizione.
A tal proposito rammentiamo che il punto di cuspide rappresenta una
combinazione in cui i due fattori produttivi sono impiegati nella stessa
proporzione.
b) COMBINAZIONE OTTIMA: FATTORI SOSTITUTI PERFETTI
In questo caso gli isoquanti sono delle rette (coefficiente angolare
costante).
Anche stavolta la combinazione ottima si trova in corrispondenza del punto
in cui la retta di isocosto tange l’isoquanto più elevato possibile. Ne
consegue che il punto di ottimo coincide con l’intercetta verticale
della retta di isocosto, poiché in quel punto essa tange un isoquanto più
elevato.
LE FUNZIONI DI COSTO DI BREVE PERIODO DELL’IMPRESA
La retta di isocosto che è una funzione di lungo periodo.
Analizziamo ora una funzione di costo di breve periodo attraverso la quale
cercheremo di individuare i costi minimi che l’impresa deve sostenere per
produrre i vari livelli di output. Ci occuperemo dei costi minimi poiché lo scopo
di ogni impresa è quello di massimizzare la produzione minimizzando i costi.
Iniziamo, dunque, la nostra trattazione distinguendo i costi in espliciti ed
impliciti, in privati e sociali.
Sono COSTI ESPLICITI tutte le spese sostenute dal produttore per
acquistare o affittare gli input necessari alla produzione di output: salari per i
lavoratori assunti, interessi sul capitale di prestito, affitto dei terreni , spese
per materie prime o semilavorate. I costi espliciti sono gli unici considerati
dagli aziendalisti a fini contabili.
Tuttavia, gli economisti che si occupano delle dinamiche micro e
macroeconomiche, nelle loro analisi, prendono in considerazione anche i
cosiddetti COSTI IMPLICITI. Essi si riferiscono al valore degli input stimato
facendo riferimento a ciò che essi potrebbero rendere ove fossero impiegati
nel miglior uso alternativo anziché essere utilizzato nella produzione.
In altre parole essi comprendono:
 la massima retribuzione che l’imprenditore percepirebbe se, anziché
gestire la propria attività, lavorasse presso un’altra impresa;
 il maggior ricavo che l’impresa potrebbe ottenere se investisse altrove il
suo capitale.
I costi impliciti, dunque, misurano il costo delle rinunce a impiegare i fattori
della produzione in altre attività anziché utilizzarli nel processo produttivo.
Nei modelli microeconomici che analizzeremo, noi assumeremo sempre che
nei costi totali siano compresi sia i costi impliciti che i costi espliciti.
Per COSTI PRIVATI, invece, intendiamo i costi sostenuti dall’impresa. Essi
sono presentati in contrapposizione ai COSTI SOCIALI, ovvero ai costi
sostenuti dalla collettività.
Se, ad esempio, consideriamo un’impresa che nella sua attività produce
ingenti quantità di rifiuti, possiamo notare come essa sosterrà dei costi privati
per lo smaltimento degli stessi. Tuttavia, se l’impresa opta, invece, per
scaricare i rifiuti in mare, essa non sosterrà costi privati, e la collettività subirà
un danno ambientale che rappresenta un costo sociale.
COSTI FISSI DI PRODUZIONE (CF)
Sono ascrivibili a questa categoria tutti i costi che l’impresa deve
sostenere per poter essere presente sul mercato e condurre la sua attività
indipendentemente dal livello di produzione che essa intende realizzare.
In qualsiasi impresa, infatti, qualunque sia il livello di output da essa prodotto,
ci sono delle spese fisse che il produttore deve sostenere, come, ad esempio,
l’affitto di impianti e macchinari, l’assicurazione furto e incendio sui beni
dell’impresa ecc.
Come
è facilmente intuibile dunque, i costi fissi attengono all’uso del
capitale, mentre il lavoro solitamente
è considerato un costo variabile.
Dunque i costi fissi sono quelli che l’impresa sostiene indipendentemente
dall’output prodotto.
Quanto detto analiticamente si traduce nella seguente funzione:
CF = rK
Dove r = tasso di interesse
K = capitale
La cui rappresentazione grafica è la seguente:
Otteniamo dunque una retta parallela all’asse delle ascisse e ciò
economicamente implica che, indipendentemente dal livello di produzione, il
livello dei costi fissi è sempre costante.
COSTI VARIABILI (CV)
In contrapposizione a quanto detto per i costi fissi, i costi variabili sono
quelli che l’impresa sostiene in relazione all’output prodotto. Essi,
dunque, aumenteranno all’aumentare del livello di produzione, mentre
saranno pari a zero quando la produzione è nulla. Come già detto, essi sono
in genere riconducibili al fattore lavoro. Ne consegue che la loro forma
funzionale sarà:
CV = wL
Dove w = salario
L = n. lavoratori
In questo caso tuttavia la rappresentazione grafica non è una retta, ma segue
la legge dei rendimenti decrescenti. Di conseguenza i costi saranno:
 all’inizio decrescenti, dando vita ad un primo tratto concavo;
 successivamente crescenti, facendo diventare la funzione convessa.
Graficamente:
All’inizio il costo cresce, ma ad un tasso decrescente, poi però interviene la
legge dei rendimenti decrescenti ed il costo cresce ad un tasso crescente.
A tal proposito è opportuno precisare che, al pari di quanto detto per la
funzione di produzione, anche la funzione dei costi variabili non è unica,
bensì vari a seconda del gradi di efficienza della specifica impresa.
COSTI TOTALI (CT)
Naturalmente, nell’analisi dei costi di un’impresa, dopo aver valutato le
singole voci, è opportuno unificarle e otteniamo così i costi totali:
CT = CF + CV
I costi totali graficamente avranno la stessa forma dei costi variabili, ma
traslati verso l’altro data la presenza dei costi fissi.
Forniamo dunque una rappresentazione grafica presentando nello stesso
riferimento cartesiano CF, CV e CT:
OSSERVAZIONI:
 l’intercetta dei costi totali è la stessa dei costi fissi;
 data la presenza dei costi fissi, anche in corrispondenza di un livello di
produzione nulla, registreremo dei costi totali di una certa entità;
6
 CT e CV sono funzioni parallele;
 i costi variabili non hanno lo stesso andamento in ogni situazione, ma
dipendono dal livello di efficienza dell’impresa, ovvero dalla sua
funzione di produzione di breve periodo.
COSTI FISSI MEDI
Introducendo i costi fissi abbiamo detto che essi sono quella quota di spesa
che l’impresa deve comunque realizzare per iniziare la sua attività. Essi
dunque non dipendono dal livello di produzione. Tuttavia se consideriamo il
costo di una singola unità di output, essa avrà un certo costo variabile al
quale andrà aggiunta una quota di costi fissi da imputare alla singola unità,
poiché i costi fissi si ripartiscono e pertanto si “ spalmano” diminuendo
all’aumentare dell’output prodotto.
Ne consegue che i costi fissi medi risulteranno sempre decrescenti
poiché all’aumentare delle unità prodotte si ripartiranno su ogni singola
quantità prodotta in quote sempre più piccole.
Graficamente:
Per capire meglio il concetto su esposto, ipotizziamo di dover fare un viaggio
in auto per il quale sosteniamo un costo fisso per il carburante pari a 100€.
Naturalmente questo costo fisso diminuirà se aumenteranno il numero dei
passeggeri, poiché sarà ripartito fra più unità:
CF = 100€
 1 passeggero  CFM = 100€
 2 passeggeri  CFM = 50€
 3 passeggeri  CFM = 33€ circa
 4 passeggeri  CFM = 25€
Come notiamo, i costi fissi medi sono decrescenti all’aumentare delle unità
sulle quali essi sono ripartiti.
COSTI VARIABILI MEDI (CVM)
Analogamente a quanto visto per i Costi Fissi Medi partendo dai Costi
Variabili Totali definiamo ora i Costi Variabili Medi:
CVM = CVT / Q
Ricordando che CVT = wL e che il rapporto Q/L è definito PRODOTTO
MEDIO DEL LAVORO (PML) :
CVM = CVT / Q = wL / Q = w/ PML
Dunque i Costi Variabili Medi dipendono dal salario pagato ai lavoratori, il
quale può essere considerato costante, e dal PML, che in virtù della LEGGE
DEI RENDIMENTI DECRESCENTI inizialmente cresce, raggiunge un
massimo e poi diminuisce.
Tuttavia come si può notare il PML è al denominatore. Ne consegue che la
curva dei Costi Variabili Medi avrà un andamento speculare rispetto
all’andamento della curva del PML:
 inizialmente PML
quindi
w/PML
= CVM
(Costi Variabili Medi
decrescenti);
 successivamente a causa della legge dei rendimenti decrescenti PML ,
quindi w/PML = CVM
(Costi Variabili Medi crescenti).
Come per la funzione di produzione, anche la curva dei costi variabili medi
non è uguale per tutte le imprese. L’ampiezza della parabola su tracciata
dipende, infatti, dall’efficienza dei lavoratori dell’impresa:
 se i lavoratori sono efficienti per un lungo periodo, la parabola sarà più
ampia;
 se già dopo i primi aumenti di output i lavoratori risultano inefficienti, la
parabola sarà più stretta.
COSTI TOTALI MEDI (CTM)
CTM = CFM + CVM
La curva dei Costi Totali Medi pur presentando, al pari della curva dei Costi
Variabili Medi, una forma ad U, si distingue da quest’ultima a causa della
presenza dei Costi Fissi Medi (CFM).
A tal proposito è opportuno precisare che l’incidenza dei Costi Fissi Medi non
è uguale per ogni livello di output. Essi infatti sono decrescenti perché,
all’aumentare dell’output prodotto, essi si spalmano su più unità e, dunque,
tendono quasi ad annullarsi per Q che tende a ∞.
Pertanto:
 per Q
0 i Costi Fissi Medi sono molto alti;
 per Q
∞ i Costi Fissi Medi sono quasi nulli.
La curva dei Costi Totali Medi risente di questo andamento e, per questo
motivo, si differenzia dalla curva dei Costi Variabili Medi. Infatti:
 la curva dei CTM è decrescente inizialmente e raggiunge il punto di
minimo in corrispondenza di un livello di output maggiore rispetto alla
curva dei CVM.
 all’aumentare della quantità prodotta i Costi Fissi Medi tendono a
diminuire. Ne consegue che la loro incidenza sui Costi Totali Medi
tende via via a diminuire e ciò provoca una graduale convergenza fra i
Costi Variabili Medi e i Costi Totali Medi;
 Teoricamente la curva dei CVM e dei CTM, per Q che tende a ∞,
tenderanno a convergere, poiché i CFM tenderanno a 0. Quindi le due
curve non sono parallele poiché l’incidenza dei costi fissi è via via
decrescente.
COSTI MARGINALI
Rappresentano la variazione del costo totale all’aumentare di una unità di
output.
La variazione interesserà elusivamente i costi variabili ed avremo:
CMa = ( ΔCVT / ΔQ) * ( ΔwL / ΔQ)
Definendo ΔQ/ΔL il PRODOTTO MARGINALE DEL LAVORO (PML)
abbiamo:
CMa = w/ PML
Anche in questo caso, in virtù della legge dei rendimenti decrescenti, avremo
una rappresentazione grafica a forma di U:
OSSERVAZIONI:
 la funzione del Costo Marginale è speculare a quella del Prodotto
Marginale del Lavoro (PML). Ciò è dovuto al fatto che esso compare al
denominatore nella funzione del Costo Marginale;
 la funzione del Costo Marginale interseca le curve dei CVM e dei CTM
nei rispettivi punti di minimo che, come già detto, non coincidono;
 anche la funzione dei Costi Marginali presenta, dunque, un tratto
decrescente e poi uno crescente. Tuttavia d’ora in avanti ci
occuperemo solo del tratto crescente. Infatti la microeconomia si
preoccupa dei problemi di un’impresa quando i costi sono crescenti e
non quando sono decrescenti.
 Tutte le varie funzioni di costo fin qui presentare ci serviranno per
studiare le varie forme di mercato che possono verificarsi.
Analizzeremo in tal senso quattro possibili situazioni:
 CONCORRENZA PERFETTA
 MONOPOLIO
 OLOGOPOLIO
 CONCORRENZA MONOPOLISTICA
CONCORRENZA PERFETTA
Situazione teorica e ideale del mercato, nella quale si scambiano le quantità
ottimali ai prezzi ottimali. Essa è una situazione teorica perché richiede il
verificarsi di quattro condizioni:
1. numerosi compratori e venditori di un bene, ciascuno dei quali è troppo
piccolo per influenzare il prezzo di mercato;
2. tutti i beni presenti sul mercato sono omogenei;
3. vi è una perfetta mobilità delle risorse;
4. vi è informazione perfetta delle condizioni di mercato.
Analizziamo ora in dettaglio le suddette condizioni:
1°CONDIZIONE: ELEVATO NUMERO DI PRODUTTORI E CONSUMATORI
In concorrenza perfetta vi sono tantissimi venditori che offrono il medesimo
bene. Ne consegue che nessuno di essi esercita sul mercato un potere tale
da influenzare il prezzo. Le imprese, dunque, debbono accettare il prezzo
come dato e in corrispondenza di esso vendere qualsiasi quantità ne venga
richiesta (offerta infinitamente elastica).
OSSERVAZIONI:
 la curva di offerta S è verticale poiché nel breve periodo la quantità che
essa può offrire è fissa. Pertanto il prezzo è determinato dalla
domanda;
 non vi è alcun interesse da parte delle singole imprese a modificare il
prezzo di equilibrio perché automaticamente si verificherebbe un
surplus o una carenza;
 tutto ciò implica che stabilito il prezzo come nel primo grafico, l’offerta
deve essere pari a qualsiasi quantità richiesta, come illustrato nel
secondo grafico.
2°CONDIZIONE: BENE OMOGENEO
In concorrenza perfetta si assume che i beni venduti siano omogenei, identici,
ovvero perfettamente standardizzati. Ciò implica che l’output di ciascun
produttore non è distinguibile dall’output degli altri produttori, pertanto i
consumatori sono “indifferenti” nell’acquisto del bene dai vari produttori.
3°CONDIZIONE: PERFETTA MOBILITA’ DELLE RISORSE
Si assume che vi sia perfetta mobilità delle risorse e che dunque in una
situazione di breve periodo in cui nel mercato si realizzano profitti, nuove
imprese siano in grado di entrare facilmente in concorrenza con quelle già
presenti. Naturalmente la perfetta mobilità implica anche che, in un mercato
in cui si registrano delle perdite nel breve periodo, le imprese siano libere di
uscire senza avere particolari vincoli.
Una situazione di questo tipo si realizza quando in un mercato non vi sono
barriere all’entrata (concessioni, licenze, brevetti), né barriere all’uscita
(elevati costi di dismissione dell’attività) che impediscono alle imprese di
entrare e uscire liberamente dal mercato stesso.
Assumendo come vera questa condizione, è opportuno precisare che ciò
implicherà un mercato in cui nel lungo periodo i profitti sono uguali a zero.
Poiché, se nel breve periodo si realizzano profitti, nuove imprese si
affacceranno sul mercato riducendo i possibili proventi fino ad annullarli.
Viceversa se nel breve periodo vi è una situazione di perdita, molte imprese
usciranno dal mercato fino a che il profitto non sarà uguale a zero.
A tal proposito va precisato che una situazione in cui il profitto è uguale a
zero, in microeconomia non è una situazione negativa. I profitti infatti non
sono altro che la differenza fra ricavi e costi. Tuttavia gli economisti, a
differenza degli aziendalisti, nella nozione di costi non considerano solo quelli
espliciti ma anche quelli impliciti. Pertanto una situazione di π = 0 è
comunque positiva, perché permette di remunerare tutti i fattori della
produzione compresa l’attività dell’imprenditore e la remunerazione per il
rischio d’impresa.
4°CONDIZIONE: PERFETTA INFORMAZIONE
Tale condizione implica che nel mercato non vi siano informazioni
appannaggio solo di alcuni individui e che ogni cambiamento di prezzo sia
immediatamente noto a tutti gli agenti. Ne consegue che consumatori e
produttori hanno perfetta conoscenza di quelli che sono i prezzi di vendita
del bene. Ciò assicura che lo stesso prezzo prevalga in ogni parte del
mercato.
Tuttavia è opportuno precisare che, benché le condizioni suddette si
verifichino molto raramente, la perfetta informazione sia una condizione quasi
impossibile.
A tal proposito va, infatti, sottolineato come la concorrenza perfetta sia più un
caso teorico da tenere come riferimento che una situazione realmente
possibile. E’ quasi impossibile che le quattro condizioni descritte possano
verificarsi contemporaneamente. Le uniche eccezioni studiate in letteratura
sono il mercato del grano invernale ed il mercato telematico delle azioni.
Nonostante ciò, la concorrenza perfetta è stata ampiamente studiata in
microeconomia, perché rappresenta un importante paradigma di riferimento,
fondamentale per studiare le inefficienze delle altre forme di mercato.
In concorrenza perfetta i consumatori possono acquistare un quantitativo
superiore del bene a un prezzo più basso; essi sono ampliamente tutelati ,
cosa che non accade in altre forme di mercato.
Assumendo, dunque, che la concorrenza perfetta sia la forma di mercato più
efficiente, le altre possibili situazioni sono ad essa rapportate per valutare il
livello di inefficienza.
Premesso ciò, cerchiamo dunque di comprendere cosa accade in un mercato
perfettamente concorrenziale e qual è l’equilibrio che in esso di determina.
MASSIMIZZAZIONE DEL PROFITTO
Gli economisti tradizionalmente assumono che in qualunque mercato
l’obiettivo principale di tutte le imprese sia quello di massimizzare il profitto. A
tal proposito va evidenziato che il profitto contabile è differente dal profitto
economico:
PROFITTO CONTABILE = RICAVI – COSTI ESPLICITI
PROFITTO ECONOMICO = RICAVI–(COSTI ESPLICITI + COSTI IMPLICITI)
Ne consegue che un profitto pari a zero a livello economico non implica un
profitto uguale a zero a livello contabile.
Passiamo ora ad analizzare cosa accade in concorrenza perfetta.
In microeconomia vi sono due metodi per determinare il profitto:
a. METODO DEI COSTI TOTALI
b. METODO DEI COSTI MARGINALI
a. METODO DEI COSTI TOTALI
Assumendo π = PROFITTO
P = PREZZO
RT = RICAVI TOTALI
q = QUANTITA’
CT = COSTI TOTALI
c = COSTI
In base a quanto detto finora, sappiamo che
π = RT – CT
dove RT = P*q
Poiché il prezzo P è costante, la funzione del ricavo totale sarà una retta, la
cui inclinazione, detta RICAVO MARGINALE, sarà sempre uguale al prezzo:
PREZZO = RICAVO MARGINALE (RMa)
È molto importante sottolineare che quella appena descritta sia una
condizione esclusiva della concorrenza perfetta, l’unica forma di mercato in
cui nessun agente del mercato ha il potere di modificare il prezzo del bene,
che pertanto viene assunto come costante.
La pendenza della retta del ricavo totale è detta dunque RICAVO
MARGINALE (RMa). Essa misura la variazione del ricavo totale quando
l’impresa vende una unità in più di output. Solo ed esclusivamente in
concorrenza perfetta il ricavo marginale è uguale al prezzo.
 COSTI TOTALI (CT) = C*q
Come già visto precedentemente, la sua forma è speculare a quelle
della funzione di produzione di breve periodo. Ne consegue che , in virtù della
legge dei rendimenti decrescenti, la funzione del Costo Totale sarà prima
concava e poi convessa.
Come abbiamo già detto, obiettivo di ogni impresa presente sul mercato è
quello di massimizzare il suo profitto. Occorre, pertanto, individuare la
quantità di output che consente all’impresa di massimizzare i suoi profitti.
Ragionando in termini di funzioni di Ricavo Totale e Costo Totale e
ricordando che il profitto è pari alla differenza fra le due curve, possiamo
concludere che il massimo profitto per l’impresa si realizza nel punto di
massima distanza tra le due curve:
Tuttavia questo metodo è poco utilizzato in microeconomia perché consente
di distinguere solo due situazioni tecnicamente agli antipodi:
 perdita: l’impresa uscirà dal mercato
 profitto: l’impresa resterà nel mercato
In un mercato perfettamente concorrenziale le situazioni in cui può venirsi a
trovare un’impresa non sono soltanto queste due. Esistono situazioni
intermedie in cui un’impresa, pur essendo in perdita, potrebbe decidere di
rimanere comunque sul mercato con l’obiettivo di MINIMIZZARE LE
PERDITE.
Le ragioni di questa scelta, che alla luce del metodo sopra descritto potrebbe
apparire priva di giustificazioni, risiedono nella presenza dei costi sostenuti
dall’impresa per iniziare la sua attività, che l’hanno costretta ad indebitarsi e a
dover pagare delle rate periodiche. Perciò un’impresa, pur realizzando delle
perdite, potrebbe essere costretta a rimanere sul mercato per pagare delle
infrastrutture e dei macchinari necessari ad entrare nel mercato. Ecco che il
metodo dei costi totali si rivela inadatto ad evidenziare situazioni di questo
tipo in cui l’impresa pur realizzano una perdita deve valutare la possibilità di
restare sul mercato. Occorre infatti un’analisi più approfondita che si
concretizza in due opzioni:
 perdita rimanendo sul mercato > perdita uscendo dal mercato:
l’impresa uscirà dal mercato
 perdita rimanendo sul mercato < perdita uscendo dal mercato:
l’impresa resterà sul mercato
Per poter, quindi, valutare situazioni intermedie a quella sopra descritta, è
necessario utilizzare un altro metodo di determinazione del profitto: il
METODO DEI COSTI MARGINALI che illustreremo nella prossimamente.
METODO DEI COSTI MARGINALI
Spesso per ottenere la massimizzazione dei profitti, al metodo dei costi totali
viene in aiuto il METODO DEI COSTI MARGINALI o APPROCCIO
MARGINALISTICO, che considera ricavi e costi marginali in situazioni reali e
non idealistiche. Attraverso il metodo dei costi totali, siamo giunti alla
conclusione che la massimizzazione del profitto nel breve periodo si ha
dove c’è la massima distanza tra le curve dei Ricavi Totali e dei Costi
Totali e si ottiene nel punto in cui la retta tangente alla curva dei CT è
parallela alla retta dei RT.
Ciò significa che le due rette hanno lo stesso coefficiente angolare: la
pendenza della retta dei RT prende il nome di RICAVO MARGINALE (MR),
mentre la pendenza della curva del costo totale CT prende il nome di COSTO
MARGINALE (MC).
Partendo da ciò, abbiamo visto che se:
MR = MC
MAX PROFITTO
(in tutti i mercati)
In una condizione di mercato di concorrenza perfetta, inoltre, il massimo
profitto si ha quando il coefficiente angolare è uguale al prezzo di mercato
(P):
MR = MC = P
Partiamo dal grafico:
Come notiamo dal grafico, la curva dei Costi Marginali (MC) e la retta dei
Ricavi Marginali (MR) s’intersecano in due punti (A, B). L’ottimo si ha dove la
funzione dei costi è crescente, ovvero nel punto B (P = MR): qui si ha la
massima capacità produttiva dell’impresa, ovvero per :
P = MR = 20 €
Q = 80
otteniamo: RT = 80 * 20 = 1600 €.
Se andiamo a verificare il valore dei Costi Totali, rappresentati dalla curva
ATC, in corrispondenza di Q = 80, avremo che CT = 80 * 12 = 960 €.
Da qui ricaviamo il profitto:
π = RT – CT = 1600 – 960 = 640 €/sett.
Quindi la zona graficamente evidenziata, compresa tra 20 € e 12 €
rappresenta la ZONA DI PROFITTO per l’impresa.
Inoltre, graficamente è stata rappresentata anche la curva dei Costi Variabili
Medi (AVC): essa ci consente di valutare l’entità del profitto ed i casi in cui il
profitto è nullo o si ha una perdita:
 PROFITTO NULLO
Se la curva dei Costi Variabili Medi (AVC) dovesse avere un andamento tale
da intercettare nel punto A la retta dei ricavi marginali (MR) e dei costi
marginali (MC), allora il punto A sarà un punto di profitto nullo. In questa
condizione l’impresa dovrà necessariamente continuare a produrre.
 PERDITA
Se la curva dei Costi Variabili Medi (AVC) dovesse avere un andamento tale
da intercettare nel punto A solo la retta dei Costi Medi (MC), rimanendo al di
sopra della retta dei Ricavi Marginali (MR), allora il punto A sarà un punto di
perdita per l’impresa.
Per valutare la convenienza (o meno) di continuare a produrre bisogna
sottrarre ai costi medi totali CMT = CT /Q (ATC), i costi variabili medi (AVC),
ottenendo cosi i Costi Fissi Medi: se questo valore ottenuto è inferiore ai costi
fissi, allora per l’impresa conviene non continuare a produrre.
MONOPOLIO
In una situazione di mercato monopolistica vi è un’ UNICA IMPRESA
OPERANTE. Essa ha potere di mercato e, pertanto, può determinare il
prezzo del bene (tenendo ovviamente conto della domanda di mercato).
Per il bene prodotto dall’impresa monopolistica NON ESISTONO BUONI
SOSTITUTI , in quanto, se esistessero essa non potrebbe essere
effettivamente libera di fissare il prezzo, dato che i consumatori potrebbero
rivolgersi ad altre imprese.
L’impresa è l’unica perché ESISTONO BARRIERE ALL’ENTRATA, cioè altre
imprese non possono entrare sul mercato e diventare concorrenti per i
seguenti motivi:
1. l’impresa detiene una risorsa fondamentale;
2. lo Stato concede un diritto esclusivo di produrre un bene (MONOPOLIO
LEGALE) come nel caso dei brevetti e dei diritti d’autore, cioè i diritti di
proprietà intellettuale. L’idea di fondo è che concedendo un monopolio
viene incentivata l’attività di produzione di proprietà intellettuale;
3. la struttura dei costi rende la singola impresa più efficiente di una
molteplicità di imprese (MONOPOLIO NATURALE).
In monopolio, come già accennato, le imprese possono influire sul prezzo. La
CURVA DI DOMANDA DEL MONOPOLISTA COINCIDE CON LA
DOMANDA DI MERCATO. ESSA E’ INCLINATA NEGATIVAMENTE. E’ per
questo motivo che il monopolista non può scegliere qualsiasi prezzo, poiché
se aumenta il prezzo, la quantità venduta si riduce: se egli decidesse di
praticare un prezzo più elevato, questo lo porterebbe a vendere quantità
inferiori.
Anche per il monopolista, l’obiettivo è MASSIMIZZARE IL PROFITTO (MC =
MR).
In monopolio il prezzo è maggiore del ricavo marginale, mentre in
concorrenza perfetta, come detto, il prezzo è uguale al ricavo marginale
(MC=MR=P).
Partendo dal fatto che il prezzo è maggiore del ricavo marginale: P > Rma,
vediamo come la curva sia inclinata negativamente, cioè per
vendere
un’unità del bene, l’impresa deve ridurre il prezzo.
Ma questo nuovo prezzo, se praticato, si applica anche alle unità che
vengono vendute in precedenza. Per questo motivo, la variazione del ricavo
totale (cioè il ricavo marginale) è inferiore al prezzo del bene (cioè ricavo
medio).
Se si fosse mantenuto lo stesso prezzo vendendo un’unità aggiuntiva, allora il
ricavo marginale sarebbe uguale al ricavo medio e la curva del RM sarebbe
uguale alla curva di domanda.
Per quanto riguarda il costo del monopolio in termini di BENESSERE, è
possibile affermare che, dato che il prezzo di vendita è superiore al Costo
Marginale, per il consumatore questa rappresenta una situazione
peggiore rispetto a quella di concorrenza. Infatti in monopolio, il profitto è
massimizzato, ma c’è una PERDITA SECCA in termini di benessere; pertanto
il monopolio è una situazione di mercato altamente INEFFICIENTE.
OLIGOPOLIO
L’oligopolio è una situazione di mercato nella quale POCHI VENDITORI
offrono prodotti molto simili, se non identici, tra loro. Un esempio è quello del
petrolio greggio per il quale pochi paesi del Medio Oriente controllano la
maggior parte delle riserve petrolifere mondiali.
E’ la forma più diffusa di mercato per chi vale la REGOLA DI 10 (inteso come
10 produttori).
Le CONDIZIONI PER L’OLIGOPOLIO sono:
1. numero limitato di imprese;
2. prodotti molto simili, quasi identici;
3. forte contraddizione tra cooperazione e interesse proprio. Questo
perché se ci fosse accordo, ci sarebbe una situazione simile al
monopolio con vendita a prezzo superiore al costo marginale. Ma in
effetti, invece, ogni oligopolista cerca di ottenere il massimo profitto
personale anche a dispetto degli altri produttori.
La forma più semplice di oligopolio è il DUOPOLIO, in cui le imprese sono
soltanto due. In concorrenza perfetta il prezzo è uguale al costo marginale,
mentre in monopolio il prezzo è maggiore del costo marginale; in duopolio,
invece, le imprese tendono ad accordarsi sulla quantità da produrre e sul
prezzo da applicare.
In particolare, si parla di:
 COLLUSIONE:
accordo tra imprese, nello stesso mercato, sulla
quantità o sul prezzo da applicare.
 CARTELLO: gruppo di imprese che agiscono coordinatamente.
I cartelli nascono per godere di profitti monopolistici, ma non sempre sono
realizzabili perché le normativa antitrust vieta gli accordi espliciti oppure
perché c’è disaccordo sulla spartizione delle quote di mercato.
Di conseguenza i duopolisti, perseguendo individualmente i propri interessi,
finiscono per produrre una quantità superiore a quella che massimizza il
profitto per il monopolista, la vendono ad un prezzo inferiore e alla fine
realizzano un profitto inferiore rispetto a questo. Quindi non c’è vantaggio a
perseguire il proprio interesse in duopolio.
Ecco perché si cerca di raggiungere una situazione di equilibrio, detto
EQUILIBRIO DI NASH , attraverso interazione reciproca in modo da
scegliere la strategia ottimale. Di conseguenza il prezzo di oligopolio è
inferiore a quello di monopolio, ma superiore a quello in concorrenza
perfetta. Se aumentano le imprese dell’oligopolio, allora l’ OLIGOPOLIO
TENDE ALLA CONCORRENZA PERFETTA.
Se invece le imprese sono davvero poche, allora la collusione è certa, anche
se dal punto di vista sociale è una situazione indesiderabile perché la
produzione sarebbe troppo bassa ed il prezzo troppo elevato.
Quindi la migliore condizione sociale è quella che induce alla
competizione tra imprese.
Per ridurre la collusione ci sono leggi antitrust che censurano i contratti tra le
imprese che svolgono le stesse attività.
Ci sono alcuni indizi per ravvisare l’esistenza di un accordo tra imprese:
1. vendite a pacchetto (del tipo due al prezzo di uno);
2. prezzi predatori, cioè decisamente inferiori al quelli di mercato;
3. prezzo
di
vendita
a
dettaglio
che
apparentemente
riduce
la
concorrenza, ma che in realtà è assolutamente legittimo, perché, ad
esempio, può essere imposto dalle stesse imprese produttrici per
assicurare ai venditori un servizio inappuntabile, limitando i problemi di
free-rider.
CONCORRENZA MONOPOLISTICA
La concorrenza monopolistica è una struttura di mercato con MOLTI
VENDITORI CHE OFFRONO UN PRODOTTO SIMILE MA NON IDENTICO.
Dal punto di vista dei venditori, essa tende alla concorrenza perfetta, mentre
dal punto di vista del prodotto tende al monopolio.
Le caratteristiche di un mercato in concorrenza perfetta sono:
1. molteplicità di venditori;
2. differenziazione
del
prodotto:
ogni
impresa
produce
un
bene
leggermente differente rispetto alle altre e, dunque, si confrontano con
una curva di domanda a pendenza negativa;
3. liberta di entrata e di uscita.
Esempi di mercati in concorrenza monopolistica sono quelli dei libri, dei film,
dei videogame ecc.