2- 1
IN MATLAB – distribuzione di frequenza
2- 2
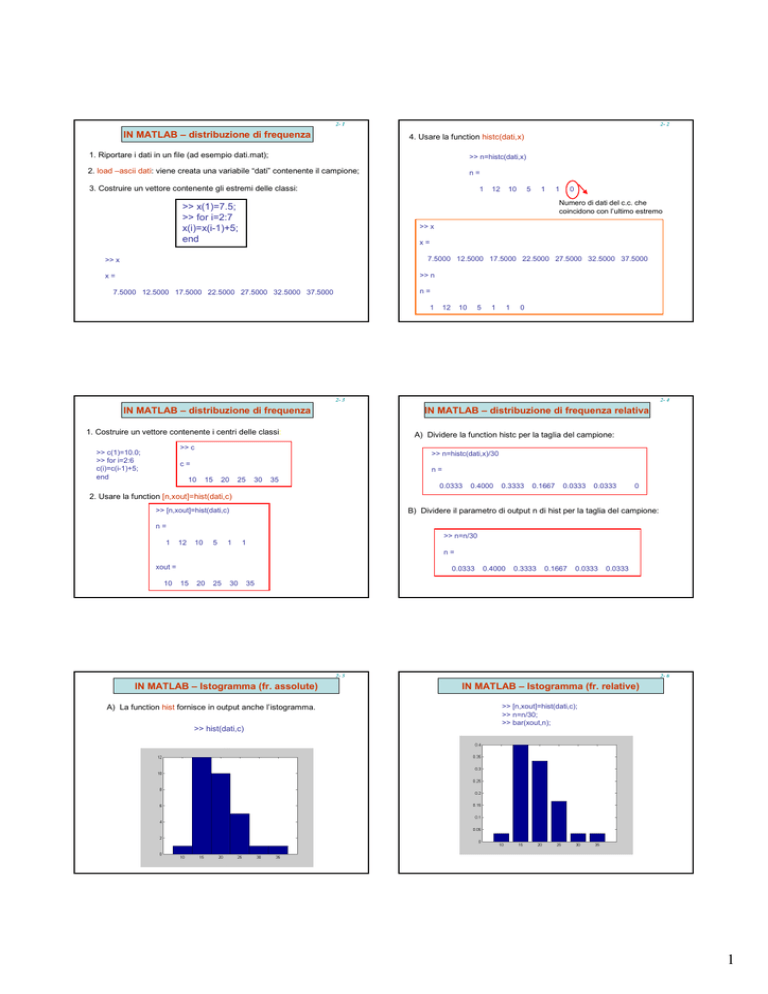
4. Usare la function histc(dati,x)
1. Riportare i dati in un file (ad esempio dati.mat);
>> n=histc(dati,x)
2. load –ascii dati: viene creata una variabile “dati” contenente il campione;
n=
3. Costruire un vettore contenente gli estremi delle classi:
1
12
10
5
1
1
0
Numero di dati del c.c. che
coincidono con l’ultimo estremo
>> x(1)=7.5;
>> for i=2:7
x(i)=x(i-1)+5;
end
>> x
x=
7.5000 12.5000 17.5000 22.5000 27.5000 32.5000 37.5000
>> x
>> n
x=
n=
7.5000 12.5000 17.5000 22.5000 27.5000 32.5000 37.5000
1
12
10
5
1
1
0
2- 3
IN MATLAB – distribuzione di frequenza
1. Costruire un vettore contenente i centri delle classi:
A) Dividere la function histc per la taglia del campione:
>> c
>> c(1)=10.0;
>> for i=2:6
c(i)=c(i-1)+5;
end
2- 4
IN MATLAB – distribuzione di frequenza relativa
>> n=histc(dati,x)/30
c=
n=
10
15
20
25
30
35
0.0333
0.4000
0.3333
0.1667
0.0333
0.0333
0
2. Usare la function [n,xout]=hist(dati,c)
>> [n,xout]=hist(dati,c)
B) Dividere il parametro di output n di hist per la taglia del campione:
n=
>> n=n/30
1
12
10
5
1
1
n=
xout =
10
0.0333
15
20
25
30
0.4000
0.3333
0.1667
0.0333
0.0333
35
2- 5
IN MATLAB – Istogramma (fr. assolute)
A) La function hist fornisce in output anche l’istogramma.
>> hist(dati,c)
2- 6
IN MATLAB – Istogramma (fr. relative)
>> [n,xout]=hist(dati,c);
>> n=n/30;
>> bar(xout,n);
1
2- 7
IN MATLAB – Qualche didascalia…
2- 8
IN MATLAB – Istogramma (fr. assolute)
E’ possibile costruire l’istogramma anche con la function histc:
>> title('frequenze relative');
>> xlabel('ore trascorse a studiare');
>> text(30,0.35,'Istogramma');
>> [n,xout]=hist(dati,c);
>> bar(xout,n)
2- 9
IN MATLAB – Istogramma (fr. relative)
2- 10
IN MATLAB – Le function bar
>> bar(xout,n/30,1)
Le barre si toccano
>> [n,xout]=hist(dati,c);
>> bar(xout,n/30)
>> barh(xout,n/30)
Barre orizzontali
>> bar3(xout,n,1,’r’)
Grafici 3-D
>> bar3h(xout,n,1)
2- 11
IN MATLAB – Poligono di frequenza
>> plot(c,n,'--rs')
2- 12
IN MATLAB – Distribuzione cumulativa
E’ possibile usare la funzione cdfplot:
>> cdfplot(dati)
2
2- 13
IN MATLAB – Q-Q plot
2- 14
IN MATLAB – Calcolo dei percentili
>>x=[96, 92, 91, 88, 86, 85, 84, 83, 82, 79, 78, 69];
>>prctile(x,25)
ans =
E’ possibile usare la funzione normplot:
>> normplot(dati)
80.5000
>>prctile(x,75)
>> prctile(x,50)
ans =
84.5000
ans =
89.5000
2- 15
IN MATLAB – Grafico del box-plot
2- 16
OUTLIERS
7. Box Plot
>> boxplot(es3)
>> boxplot(x)
>> [max(es3),min(es3)]
ans =
4.6191 0.0117
2- 17
2- 18
• Distribuzione uniforme discreta
In Matlab
>>c=[1,2,3,4,5,6]; dat=unidpdf(c,6); bar(c,dat)
• Distribuzione di Bernoulli
>> p=…; q=1-p; c=[0,1]; dat=[q,p]; bar(c,dat)
3
2- 19
• Distribuzione uniforme discreta (funzione cumulativa)
2- 20
• Distribuzione binomiale
>>dat1=unidcdf(c,6);
>> x=0:10;
>> y=binopdf(x,10,0.5);
>> bar(x,y)
>>stairs(c,dat1)
2- 21
• Distribuzione binomiale
>> x=0:10;
>> y=binopdf(x,10,0.01);
>> bar(x,y)
• Binocdf
• Binoinv
• Binornd
• Binostat
• Distribuzione binomiale (funzione di ripartizione)
2- 22
>> x=0:10;
>> y=binocdf(x,10,0.5);
>> y1=binocdf(x,10,0.1);
>> stairs(x,y,’r’);
hold on;
stairs(x,y1,’g’)
>> legend(‘0.5’,’0.1’)
2- 23
2- 24
• Distribuzione geometrica
DISTRIB.BINOM: restituisce la distribuzione binomiale per il numero di successi scelto.
Sintassi: DISTRIB.BINOM(num_successi;prove;probabilità_s;cumulativo)
Num_successi è il numero di successi nelle prove, (ossia x=0,1,…prove).
>> x=1:10;
>> y=geopdf(x,0.5);
>> bar(x,y)
Prove è il numero di prove indipendenti, ossia n.
Probabilità_s è la probabilità di successo per ciascuna prova, ossia p.
Cumulativo è un valore logico che determina la forma assunta dalla funzione. Se il
valore cumulativo è VERO, DISTRIB.BINOM restituirà la funzione di ripartizione, ovvero
la probabilità che venga restituito un numero massimo di successi pari al valore di
num_successi. Se il valore cumulativo è FALSO, verrà restituita la funzione massa di
probabilità, ovvero la probabilità che venga restituito un numero massimo di successi
pari al valore di num_successi.
4
2- 25
• Distribuzione geometrica
2- 26
• Distribuzione Poisson
>> x=0:20;
>> y=poisspdf(x,2);
>> bar(x,y)
>> x=1:10;
>> y=geocdf(x,0.5);
>> x=0:20;
>> y=poisspdf(x,5);
>> bar(x,y)
>> y1=geocdf(x,0.1);
>> stairs(x,y,’r’);
hold on;
stairs(x,y1,’g’)
>> legend(‘0.5’,’0.1’)
>> [media,var]=geostat(0.5)
>> [media,var]=poisstat(2)
2- 27
>> x=0:20;
>> y=poisspdf(x,10);
>> bar(x,y)
• Distribuzione Normale
>>x=0:20;
>> y1=binopdf(x,50,1/5);
>> bar(x,y1)
2- 29
2- 28
>> x=0:100;
>> y=poisspdf(x,50);
>> bar(x,y)
• Distribuzione Normale
[media,var]=binostat(500,0.1)
>>x=0:50;
>> y1=binopdf(x,500,1/10);
>> bar(x,y1)
2- 30
[media,var]=binostat(10,0.5)
media=50, var=45
>> x=0:0.1:100;
>> y=normpdf(x,50,sqrt(45));
>> plot(x,y)
>> [media,var]=poisstat(5)
media=5, var=2.5
>> x=0:0.01:10;
>> y=normpdf(x,5,sqrt(2.5));
>> plot(x,y)
5
2- 31
2- 32
DISTRIB.NORM: restituisce la distribuzione normale per la media e la distribuzione
standard specificate.
P POISSON: restituisce la distribuzione di probabilità di Poisson.
Sintassi: POISSON(x;media;cumulativo)
Sintassi DISTRIB.NORM(x;media;dev_standard;cumulativo)
X è il numero degli eventi.
X è il valore per il quale si desidera la distribuzione.
Media è la media aritmetica della distribuzione.
Dev_standard è la deviazione standard della distribuzione.
Cumulativo è un valore logico che determina la forma assunta dalla funzione.
Se cumulativo è VERO, DISTRIB.NORM restituirà la funzione di ripartizione, se è
FALSO restituirà la funzione densità di probabilità.
Media è il valore numerico previsto.
Cumulativo è un valore logico che determina la forma per la distribuzione
di probabilità. Se cumulativo è VERO, POISSON restituirà la funzione di ripartizione di Poisson indicante la probabilità che il numero degli eventi casuali sia
compreso tra zero e x inclusi. Se cumulativo è FALSO, verrà restituita la funzione massa di probabilità di Poisson indicante la probabilità che il numero di
eventi sia esattamente uguale a x.
•
DISTRIB.NORM.ST: restituisce la funzione di ripartizione normale standard
cumulativa. La distribuzione ha una media uguale a 0 (zero) e una deviazione
standard uguale a uno.
Sintassi: DISTRIB.NORM.ST(z)
Z è il valore per il quale si desidera la distribuzione.
2- 33
INV.NORM: restituisce il quantile associato alla coda sinistra della distribuzione
normale con media e varianza specificate.
2- 34
• Distribuzione Ipergeometrica
p = hygepdf(0:10,100,20,10)
Sintassi: INV.NORM(probabilità;media; gradi_libertà)
Probabilità è la probabilità della coda destra sotto la densità chi-quadrato.
Media è la media aritmetica della distribuzione.
Dev_standard è la deviazione standard della distribuzione.
•
Taglia popolazione
Taglia campione
successi
INV.NORM.ST: restituisce il quantile associato alla coda sinistra della
distribuzione normale standard.
>> bar(0:10,p)
Sintassi: INV.NORM(probabilità)
Probabilità è la probabilità della coda destra sotto la densità
2- 35
2- 36
DISTRIB.IPERGEOM: restituisce la distribuzione di probabilità di una variabile
aleatoria ipergeometrica.
Ipergeometrica
Sintassi:
DISTRIB.IPERGEOM(successi_camp;num_campione;successi_pop;num_popolazione)
Successi_camp è il numero di successi nel campione, ossia x.
Num_campione è la dimensione del campione, ossia n.
Successi_pop è il numero di successi nella popolazione, ossia K.
Num_popolazione è la dimensione della popolazione, ossia N.
Binomiale
>>y=binopdf(0:10,10,2/10)
>>bar(0:10,10,2/10)
6
2- 37
Il test di K-S misura la distanza media tra la funzione di ripartizione
Empirica e quella ipotizzata. Se tale distanza risulta maggiore di un
prefissato quantile, il test K-S rigetta l’ipotesi che la popolazione ha
distribuzione di probabilità prefissata.
2- 38
Kstest(x)
Confronta la funzione di ripartizione
empirica del campione x con la funzione
di ripartizione di una gaussiana standard
Se il campione casuale di dati non ha media nulla
e varianza unitaria?
I dati vanno standardizzati.
>> x=(Weight-mu)/sigma;
>> [H,P,KSSTAT,CV]=KSTEST(X)
E se il campione casuale ha legge diversa
da quella gaussiana standard?
>> x=rand(100,1);
>> ccf(:,1)=x;
>> ccf(:,2)=x;
>> [H,P,KSSTAT,CV]=KSTEST(x,ccf,0.05,0)
2- 39
>> [h,p,ksstat,cv]=kstest(x)
h=
2- 40
H = 0 => Do not reject the null hypothesis
at significance level ALPHA.
H = 1 => Reject the null hypothesis at
significance level ALPHA.
0
p=
0.7172
ksstat =
0.0687
KSTEST(...) also returns the K-S test statistic KSSTAT
defined above for the test type indicated by TAIL.
cv =
0.1340
>>
KSTEST(...) also returns the asymptotic P-value P.
KSTEST(...) returns the critical value of the test CV.
Null Hypothesis: F(x) equal to CDF for all x.
For TAIL = 0 (2-sided test), alternative: F(x) not equal to CDF.
For TAIL = 1 (1-sided test), alternative: F(x) greater than CDF.
For TAIL = -1 (1-sided test), alternative: F(x) less than CDF.
2- 41
2- 42
7
2- 43
2- 45
2- 44
2- 46
Test T sulla differenza tra medie – popolazioni normali – varianze incognite =
2- 47
2- 48
Esempio: Da una serie di rilevazioni sulla quantità di specie presenti in alcuni
Ambienti, sono stati rilevati I seguenti 20 valori di biodiversità (vedi tabella). Si
Valuti se la tendenza centrale di questa serie è significativamente differente da
6.5, valore centrale dell’area in studi precedenti.
2,5
2,7
2,9
2,9
3,1
3,1
3,1
3,8
3,9
4,2
4,5
4,9
5,3
6,5
6,5
8,9
9,7
11,7
15,7
18,9
0
0
+
+
+
+
+
N = 18, r − = 13, r + = 5
0,096252
8
2- 49
2- 50
2- 51
2- 52
2- 53
2- 54
Nel grafico, ogni media del livello viene rappresentata da un tondino che è situato al
centro di un intervallo. L’intervallo non ha alcun significato statistico. Due medie sono
differenti in modo significativo se i corrispettivi intervalli sono disgiunti (in rosso). Due
medie non sono differenti in modo significativo se i rispettivi intervalli non sono disgiunti
(in grigio). La frase sotto il grafico segnala le medie dei livelli diverse.
9
2- 55
2- 56
Si può usare il mouse per selezionare un gruppo. Il grafico mette in evidenza
gli altri gruppi (in rosso) che sono differenti significativamente dal livello esaminato.
2- 57
2- 58
2- 59
2- 60
10
2- 61
11












