PROPOSIZIONI 1 E 3 DELLA MISURA DEL CERCHIO
“Qual è ‘l geometra che tutto s’affigge
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond’elli indige,
tal era io a quella vista nova:
veder volea come si convenne
l’imago al cerchio e come vi s’indova”
Dante (Paradiso,XXXIII, 133 – 138)
IL METODO DI ESAUSTIONE
Il metodo di esaustione è una tecnica di calcolo, che anticipa di secoli i moderni metodi di
calcolo infinitesimale, usata per calcolare un’area attraverso la somma di superfici di figure
più semplici in modo che quest’ultima si avvicini il più possibile all’area cercata. Fu
inventato da Eudosso di Cnido (407-355 a.C), grande matematico e astronomo, e poi
utilizzato dai matematici dell’antichità, tra i quali Euclide e soprattutto Archimede. Ma nelle
dimostrazioni archimedee, rispetto a quelle di Euclide e di Eudosso, questo procedimento
viene sfruttato per rendere rigorose le dimostrazioni di proprietà inizialmente intuite; pur
essendo dunque un procedimento rigoroso presuppone sostanzialmente la conoscenza
del risultato.
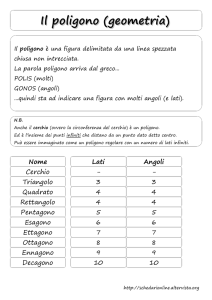
Nell’antichità questo metodo veniva usato soprattutto in geometria e consisteva nel
“riempire” con figure note sempre più piccole uno spazio a disposizione fino a che questo
venisse “esaurito” (e proprio da questo deriva il nome del procedimento). In questo modo
la somma delle aree di tali figure note approssimava l’area cercata; il metodo di
esaustione non comprendeva però alla fine alcun passaggio al limite e si arrivava invece a
dimostrare la tesi attraverso un ragionamento per assurdo. Ai giorni nostri sostituiamo le
idee di “riempire” con grandezze note l’area cercata e la finale “reductio ad absurdum”
con la costruzione di due successioni convergenti e il calcolo del loro limite comune.
Archimede usò il metodo di esaustione come base per risolvere alcuni quesiti da lui
proposti, come il problema del confronto delle superfici di figure curvilinee e rettilinee, e il
problema della quadratura del cerchio.
Tutte le dimostrazioni di Archimede con questo metodo presentano le seguenti
caratteristiche:
Per verificare che due grandezze A e B siano uguali, si opera con il procedimento di
riduzione all’assurdo.
Inizialmente si presuppone che A>B e si prende in considerazione
una
successione di grandezze omogenee, di cui fanno parte anche A e B. Due o più
grandezze si dicono omogenee se si possono confrontare, ovvero se le loro
intensità possono essere comparate, sommate o sottratte (di conseguenza devono
poter essere espresse con la stessa unità di misura). La successione deve avere le
seguenti condizioni:
1. deve essere sempre prolungabile
2. i suoi termini devono essere minori di A e B
3. si deve avvicinare progressivamente al valore della grandezza posta
maggiore
Se la grandezza A è maggiore della B (A>B), la differenza tra le due è D = A - B. La
condizione 3 ci permette di trovare un elemento T della successione, tale che la
sua differenza da A sia minore di D ( A – T<D). Di conseguenza T risulta compreso
tra A e B e in particolare maggiore di B (infatti sostituendo D nella disuguaglianza
precedente si ha: A-T<D=A-B da cui si ottiene T>B). Ma per la condizione 2 quanto
appena affermato è impossibile. Allo stesso modo si dimostra che è assurdo A<B.
In conclusione poiché non può esistere differenza tra A e B, le due grandezze sono
uguali.
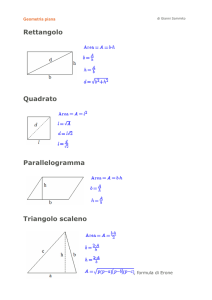
PROPOSIZIONE 1
Ogni cerchio è uguale ad un triangolo se ha il raggio uguale ad un cateto [del
triangolo] e la circonferenza uguale alla base [uguale all’altro cateto].
Il metodo di esaustione trova applicazione nella dimostrazione di questo primo teorema
del Metodo del cerchio, secondo cui l’area di ogni cerchio è uguale a quella di un triangolo
rettangolo, avente un cateto uguale al raggio del cerchio e l’altro uguale alla sua
circonferenza. Seguiamo i ragionamenti di Archimede pur utilizzando il linguaggio e il
simbolismo moderno.
c
N
R
R
C
Si consideri una circonferenza con centro N, raggio R e indichiamo con C la misura della
circonferenza, e un triangolo rettangolo con base C e altezza R. Indichiamo con A l’area
del cerchio e E l’area del triangolo rettangolo.
IPOTESI 1: supponiamo che A>E:
Inscriviamo nel cerchio un quadrato ABCD, dividiamo poi gli archi AB, BC, CD, DA in due
parti uguali e continuiamo la divisione fino a che i lati del poligono inscritto, i cui vertici
sono i punti di divisione, sottendono segmenti circolari la cui somma Σ è minore
dell’eccesso di cui il cerchio supera il triangolo, ossia Σ<A-E.
Questa disuguaglianza implica che E<A-Σ; ma A-Σ rappresenta l’area P del poligono
inscritto; per cui risulta che l’area P del poligono è maggiore di quella E del triangolo: P>E.
A
D
B
C
Tiriamo ora la perpendicolare ON al lato AM, a partire dal centro N; per cui ON, che è
l’apotema del poligono inscritto, è sicuramente minore del raggio R del cerchio. Ma poiché
, risulta:
Inoltre il perimetro del poligono inscritto è sicuramente minore della circonferenza C, e
poiché
, risulta:
Ricordando che ogni poligono regolare è equivalente ad un triangolo che ha la base
congruente al suo perimetro e l’altezza congruente alla sua apotema, dalle disuguaglianze
precedenti si può dedurre che l’area P del poligono è minore dell’area T del triangolo:
(
)
Ma ciò è impossibile, perché la disuguaglianza P<E è incongruente con la disuguaglianza
precedentemente trovata P>E. Quindi era assurdo ipotizzare A>E
A
B
O
M
N
D
IPOTESI 2: supponiamo che
C
:
Circoscriviamo al cerchio un quadrato e consideriamo i punti medi dei quattro archi
individuati dai punti di tangenza. Conduciamo da tali punti le rette le rette tangenti alla
circonferenza. Con riferimento alla figura riportata sia A il punto medio di uno di tali archi
FM e siano Q e R i punti in cui la retta tangente in A alla circonferenza incontra i lati del
quadrato circoscritto. L’angolo ̂ è retto (la retta tangente è perpendicolare al raggio
passante per il punto A di tangenza: Euclide III,18). Essendo PR e AR rispettivamente
l’ipotenusa e un cateto del triangolo rettangolo PAR, risulta
.
P
R
M
A AA A
Q
F
F
F
N
Ricordiamo che se si conducono dal punto R le tangenti RA e RM alla circonferenza di
centro M, i triangoli rettangoli RNA e RNM sono congruenti, avendo l’ipotenusa RN in
comune e i cateti AN=RN=r, per cui anche gli altri cateti AR e RM sono congruenti,
ossia
. Di conseguenza risulta
. I triangoli PAR e RAM hanno basi
diseguali e uguale altezza h (che è la distanza di A dal lato PM), per cui
(
)
(
(
)
ossia l’area del triangolo
(
)
(
)
)
(
)
(
(
)
(
)
)
è maggiore della metà dell’area della figura
(
)
(
)
Allo stesso modo, se dividiamo l’arco AM in due parti congruenti e tracciamo la tangente
per il punto S di divisione, il triangolo che questa individua con le precedenti tangenti ha
un’area maggiore della metà della figura RASM.
Quindi se al quadrato togliamo i quattro triangoli analoghi a PQR, ottenendo così
l’ottagono circoscritto al cerchio dato, si possono inscrivere dei triangoli nei segmenti
residui e ogni volta l’area di tali triangoli è maggiore della metà dei segmenti
corrispondenti.
Continuando questo processo, togliendo di volta in volta i triangoli individuati dalle
tangenti, si toglie ogni volta una grandezza che è maggiore della metà del residuo; si
ottiene così una serie di poligoni circoscritti P’ tali che la differenza Σ tra la loro area e
l’area del cerchio sarà minore della ipotizzata differenza tra l’area E del triangolo e l’area
A del cerchio: Σ<E-A. Questa disuguaglianza implica che E>A+Σ; ma A+Σ rappresenta
l’area P’ del poligono circoscritto; per cui risulta che l’area P’ del poligono circoscritto è
minore di quella E del triangolo: A+Σ=P’<E.
Ma il poligono regolare circoscritto è equivalente ad un triangolo che ha la base
congruente al suo perimetro e l’altezza congruente alla sua apotema AN che è uguale al
raggio R della circonferenza; inoltre il perimetro del poligono circoscritto è maggiore della
circonferenza C (è una conseguenza del Postulato 2 del Primo libro della Sfera e del
Cilindro)
Per cui l’area P’ del poligono circoscritto è maggiore dell’area E del triangolo:
(
)
Ma ciò è impossibile, perché questa disuguaglianza P’>E è incongruente con la
disuguaglianza precedentemente trovata P’<E. Quindi era assurdo ipotizzare A<E.
Poiché entrambe le ipotesi precedenti A<E e A>E sono assurde, deve necessariamente
essere A=E.
PROPOSIZIONE 3
La circonferenza di ogni cerchio è tripla del diametro e lo supera ancora di meno di
un settimo del diametro, e di più di dieci settantunesimi.
(
)
(
)
Da cui si deduce la nota approssimazione di pigreco: (
)
(
)
Archimede determina due approssimazioni, una per eccesso e una per difetto, per la
lunghezza di una circonferenza, considerando rispettivamente i poligoni regolari circoscritti
e quelli inscritti alla circonferenza stessa. Egli parte dall’esagono regolare e raddoppia
successivamente il numero dei lati fino a giungere ai poligoni regolari, circoscritti e inscritti,
di 96 lati e calcola con essi le approssimazioni cercate.
Nella dimostrazione Archimede utilizza spesso la Proposizine 3 contenuta nel Libro VI
degli Elementi di Euclide (che noi conosciamo come il Teorema della bisettrice di un
angolo interno ad un triangolo), anche se poi sviluppa una procedura sostanzialmente
algebrica per calcolare i perimetri dei poligoni inscritti e circoscritti. La novità del
procedimento seguito da Archimede, rispetto alle diverse approssimazioni di pigreco fatte
dai suoi predecessori babilonesi, egiziani o cinesi, è che il suo è un procedimento iterativo,
per cui si possono ottenere approssimazioni sempre migliori ripetendo sempre lo stesso
processo; tanto più grande è il numero dei lati dei poligoni considerati, tanto migliori
saranno le approssimazioni ottenute.
Nelle sue spiegazioni Archimede non sempre è stato molto chiaro o ha saltato molti
passaggi. Ripercorriamo i procedimenti archimedei, utilizzando però il linguaggio e il
simbolismo moderno.
PRIMA LIMITAZIONE:
(
)
Consideriamo un esagono regolare di lato FB circoscritto alla circonferenza di diametro
AC e centro E.
poiché metà di un lato di un esagono regolare
raggio della circonferenza
̂
Conduco la bisettrice EG dell’angolo al centro
dodecaedro regolare circoscritto alla
circonferenza data.
; perciò GC è metà di un lato di un
Per il teorema della bisettrice applicato
al triangolo CEF (in ogni triangolo, la
bisettrice di un angolo divide il lato
opposto in parti proporzionali agli altri
due lati, Euclide VI, 3), risulta:
Sommando:
(
)
(
(
)
)
Scambiando i medi con gli estremi:
(
)
Da cui si ottiene:
̂
Essendo
, allora
√
Ed inoltre
e quindi :
√( )
√
√
√
Perciò
Archimede utilizza un valore approssimativo per √ ponendo: √
Di conseguenza:
√
Quindi il rapporto tra il raggio della circonferenza inscritta nell’esagono (r crf inscr) e metà
di un lato del dodecaedro circoscritto alla circonferenza (½ l12) è maggiore del rapporto tra
571 e 153:
Archimede poi pensa giustamente che una relazione analoga possa valere anche nel
rapporto che la bisettrice EG dell’angolo α considerato ha con la metà del lato del
dodecaedro circoscritto a quella circonferenza. Infatti, se applichiamo il Teorema di
Pitagora al triangolo ECG, risulta:
( )
( )
ossia:
(
)
√(
)
(
)
Archimede prosegue i suoi calcoli in modo analogo, considerando il poligono regolare di
24 lati, circoscritto alla circonferenza data. Tracciamo quindi anche noi la bisettrice EH
dell’angolo ̂ ;
è pari a metà del lato del poligono di 24 lati circoscritto alla
circonferenza data.
Per il teorema della bisettrice applicato al triangolo CEG, si ottiene:
Sommiamo:
(
)
(
(
)
)
Scambiando i medi con gli estremi:
(
Da cui si ottiene:
)
(
)
Ma per la dimostrazione precedente:
e
Perciò:
Per cui:
Tracciamo quindi la bisettrice EK dell’angolo ̂ , ottenendo il segmento KC che è la
metà del lato del poligono regolare di 48 lati circoscritto alla circonferenza di partenza.
Continuando con lo stesso procedimento usato anche da Archimede, otteniamo il rapporto
tra il raggio della circonferenza inscritta e KC:
Infine, tracciamo la bisettrice EL dell’angolo ̂ , ottenendo il segmento LC che è la metà
del lato del poligono regolare di 96 lati circoscritto alla circonferenza iniziale. Seguendo gli
stessi procedimenti usati nelle dimostrazioni precedenti, si ritrova il rapporto calcolato
anche da Archimede:
“ ….e poiché dunque è stato dimostrato che la EC ha rispetto alla LC rapporto maggiore di
quello che 4673+1/2 ha rispetto a 153, ma AC è doppia di EC ed LM è doppia della CL,
anche la AC ha dunque rispetto al perimetro del poligono di 96 lati rapporto maggiore di
quello che 4673+1/2 ha rispetto a 14688. E 14688 è triplo di 4673+1/2 con l’avanzo di
667+1/2, avanzo che è minore della settima parte di 4673+1/2: sicchè il perimetro del
poligono circoscritto al cerchio è minore del triplo e un settimo del diametro… .”.(cit.
Misura del cerchio, da Opere di Archimede a cura di Attilio Frajese).
Così Archimede avrebbe spiegato i calcoli finali della prima limitazione. Ma vediamoli nel
dettaglio. Consideriamo l’ultima disuguaglianza scritta:
Poichè EC rappresenta il raggio della circonferenza inscritta nel poligono regolare di 96 lati
e CL è la metà del lato di tale poligono, la disuguaglianza rimane invariata se
consideriamo il rapporto tra il diametro della circonferenza, che è doppio del raggio, e il
lato della figura di 96 lati, che è il doppio di LC.
Per ottenere il perimetro della figura di 96 lati, moltiplichiamo entrambi i denominatori per il
numero di lati, cioè per 96:
(
)
(
)
Ma siccome
(
) (
)e
(
), otteniamo che il
rapporto tra il perimetro della figura di 96 lati e il diametro della circonferenza in esso
inscritta risulta essere:
(
(
)
) (
(
)
)
(
)
(
)
(
(
)
)
Ma il perimetro di un poligono circoscritto ad una circonferenza è sempre maggiore della
circonferenza stessa, di conseguenza:
che è la prima parte della Proposizione 3.
Se poi esplicitiamo la circonferenza e il diametro in funzione del raggio otteniamo:
, ossia:
SECONDA LIMITAZIONE:
Disegniamo il lato CB di un esagono regolare inscritto nella circonferenza di diametro
AC=2r; l’angolo al centro ̂
e quindi quello alla circonferenza sarà ̂
. Consideriamo il triangolo rettangolo ABC; poiché i suoi angoli sono ̂
e
̂
, risulta:
√
√
√
√ .
Archimede un altro valore approssimato per √ ponendo: √
̂
Tracciamo la bisettrice AG dell’angolo ̂ ; allora: ̂
dodecaedro regolare inscritto nella circonferenza data.
Inoltre poiché l’angolo ̂ insiste sull’arco GB risulta anche ̂
e GC è il lato del
Sia F il punto di intersezione tra la bisettrice AG e il lato dell’esagono BC.
Considero i triangoli AGC e CGF:
̂
(
)
){ ̂
(
̂
̂
̂
̂
̂
Poiché i due triangoli sono simili (per il I Criterio di Similitudine), possiamo dire che:
Per il teorema della bisettrice applicato al triangolo ABC (in ogni triangolo la bisettrice di un
angolo divide il lato opposto in parti proporzionali agli altri due lati):
Sommiamo i membri:
(
)
(
(
)
)
Scambiamo gli estremi tra loro:
(
)
Ma per la similitudine iniziale:
(
)
√
Ricordando che
(
e quindi possiamo scrivere:
)
√
ma √
Ma noi dobbiamo trovare il rapporto tra il diametro della circonferenza, AC, e il lato del
dodecaedro inscritto ad essa, GC. Quindi ( tenendo conto della disuguaglianza appena
trovata):
(
)
(
)
(
(
)
)
(
)
Estraiamo la radice quadrata:
√
(
)
Perciò si ottiene che:
Archimede prosegue i suoi calcoli considerando poligoni regolari inscritti con un numero
sempre maggiore di lati.
Consideriamo dapprima il poligono regolare inscritto di 24 lati. Tracciamo la bisettrice AH
relativa all’angolo ̂ ; di conseguenza CH è un lato del poligono di 24 lati inscritto nella
circonferenza di partenza.
̂
̂
Osserviamo che ̂
; inoltre poiché l’angolo ̂ insiste sull’arco GH
̂
risulta anche ̂
.
Sia S il punto di intersezione tra la bisettrice AH appena disegnata e il lato CG del
dodecaedro inscritto nella stessa circonferenza.
Consideriamo i triangoli CAH e CHS. Essi sono simili perché hanno gli angoli uguali.
̂
(
)
){ ̂
(
̂
̂
̂
̂
Possiamo quindi dire che:
Per il teorema della bisettrice applicato al triangolo AGC, risulta:
Sommiamo i membri:
(
)
(
(
)
)
Scambiamo gli estremi:
(
)
Per la similitudine iniziale
e quindi possiamo scrivere:
̂
(
(
)
ossia
)
Per le dimostrazioni precedenti:
e
e quindi:
Calcoliamo ora il rapporto tra il diametro AC e il lato CH del poligono regolare inscritto di
24 lati.
( )
(
)
(
)
(
(
)
)
(
)
Estraendo la radice quadrata, otteniamo:
√
(
)
Giungiamo quindi alla conclusione di Archimede:
Tracciamo ora la bisettrice AK dell’angolo ̂ ; perciò CK è il lato del poligono regolare di
48 lati inscritto nella circonferenza data. Anche in questo caso, seguendo gli stessi
procedimenti usati finora, si ottiene il risultato trovato da Archimede:
Se infine tracciamo la bisettrice AL relativa all’angolo ̂ ; di conseguenza CL è il lato del
poligono regolare di 96 lati inscritto nella circonferenza data. Mediante gli stessi calcoli,
otteniamo il rapporto tra il raggio della circonferenza e il lato di tale poligono.
“….Invertendo si ha dunque che il perimetro del poligono ha rispetto al diametro rapporto
maggiore di quello che 6336 ha rispetto a 2017+1/4. Ma 6336 è maggiore del triplo e
10/71 di 2017+1/4: dunque il perimetro del poligono di 96 lati inscritto nel cerchio è
maggiore del triplo e 10/71 del diametro, cosicchè il cerchio a più forte ragione è maggiore
del triplo e 10/71 del diametro. Dunque la circonferenza del cerchio è maggiore del triplo
del diametro ed eccede il triplo per meno di 1/7 e per più di 10/71….”.(cit. Misura del
cerchio,da Opere di Archimede a cura di Attilio Frajese).
Archimede avrebbe spiegato in questo modo i suoi calcoli, ma vediamoli con più
precisione. Dalle dimostrazioni precedenti abbiamo ottenuto il rapporto tra il diametro della
circonferenza e il lato del poligono di 96 lati inscritto in essa; la disequazione non cambia
se rapportiamo il diametro al perimetro della figura (moltiplicando entrambi i denominatori
della disuguaglianza sopra scitta per 96, che è il numero dei lati del poligono)
(
)
(
)
Semplificando rimane:
Ma la lunghezza della circonferenza circoscritta ad un poligono è sempre maggiore del
perimetro di quest’ultimo. Quindi possiamo scrivere:
che è la seconda parte della Proposizione 3
Se poi esplicitiamo la circonferenza e il diametro in funzione di r, otteniamo:
Semplifichiamo e otteniamo la seconda limitazione individuata anche da Archimede:
Quindi il valore di
risulta essere:
, secondo i calcoli appena svolti seguendo le indicazioni di Archimede,