(RIPASSO ED APPROFONDIMENTO)
IL METODO DELLE LINEE DI FORZA DI FARADAY
Una delle intuizioni geniali di Faraday, che gli valsero molto scherno e che oggi gli valgono molta
ammirazione, fu quella di rappresentare un campo elettrico o un campo magnetico attraverso quelle
che oggi chiamiamo linee di flusso o linee di forza. Si tratta di una rappresentazione, di un modo
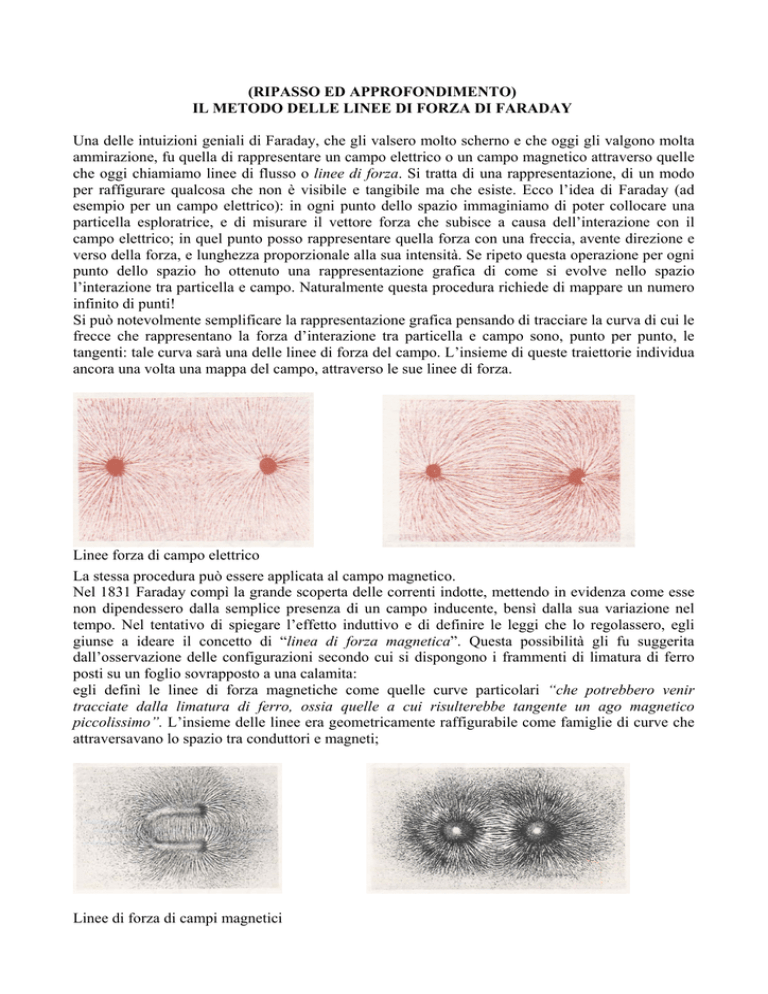
per raffigurare qualcosa che non è visibile e tangibile ma che esiste. Ecco l’idea di Faraday (ad
esempio per un campo elettrico): in ogni punto dello spazio immaginiamo di poter collocare una
particella esploratrice, e di misurare il vettore forza che subisce a causa dell’interazione con il
campo elettrico; in quel punto posso rappresentare quella forza con una freccia, avente direzione e
verso della forza, e lunghezza proporzionale alla sua intensità. Se ripeto questa operazione per ogni
punto dello spazio ho ottenuto una rappresentazione grafica di come si evolve nello spazio
l’interazione tra particella e campo. Naturalmente questa procedura richiede di mappare un numero
infinito di punti!
Si può notevolmente semplificare la rappresentazione grafica pensando di tracciare la curva di cui le
frecce che rappresentano la forza d’interazione tra particella e campo sono, punto per punto, le
tangenti: tale curva sarà una delle linee di forza del campo. L’insieme di queste traiettorie individua
ancora una volta una mappa del campo, attraverso le sue linee di forza.
Linee forza di campo elettrico
La stessa procedura può essere applicata al campo magnetico.
Nel 1831 Faraday compì la grande scoperta delle correnti indotte, mettendo in evidenza come esse
non dipendessero dalla semplice presenza di un campo inducente, bensì dalla sua variazione nel
tempo. Nel tentativo di spiegare l’effetto induttivo e di definire le leggi che lo regolassero, egli
giunse a ideare il concetto di “linea di forza magnetica”. Questa possibilità gli fu suggerita
dall’osservazione delle configurazioni secondo cui si dispongono i frammenti di limatura di ferro
posti su un foglio sovrapposto a una calamita:
egli definì le linee di forza magnetiche come quelle curve particolari “che potrebbero venir
tracciate dalla limatura di ferro, ossia quelle a cui risulterebbe tangente un ago magnetico
piccolissimo”. L’insieme delle linee era geometricamente raffigurabile come famiglie di curve che
attraversavano lo spazio tra conduttori e magneti;
Linee di forza di campi magnetici
La rappresentazione geometrica tramite linee di forza non è solo utile perché visualizza ciò che,
altrimenti, avremmo difficoltà a rappresentarci, ma perché suggerisce intuitivamente alcune
proprietà che le descrizioni matematiche faranno emergere.
Per prima cosa le linee di flusso non si intersecano mai.
Il punto A è un punto i cui tutte le linee di campo divergono (sono uscenti); il punto B è un punto in
cui tutte le linee di forza convergono (sono entranti): questi 2 punti hanno proprietà diverse da tutti
gli altri punti dello spazio, proprio perché in essi tutte le linee di forza convergono o divergono. È
possibile costruire un opportuno operatore matematico, che si chiama divergenza che, applicato ad
una campo vettoriale (come quello elettrico o magnetico), esprime, puntualmente, se si tratti di:
Un punto da cui passa una sola linea di forza che da una parte “entra” e dall’altra “esce”, in
questo caso la divergenza è zero (punto C della figura),
Un punto da cui passino infinite linee di forza “uscenti”, in tal caso la divergenza è positiva
(punto A della figura),
un punto da cui passino infinite linee di forza “entranti”, in tal caso la divergenza è
negativa (punto B).
(APPROFONDIMENTO)
L’ENERGIA DI UN’ONDA ELETTROMAGNETICA
Una caratteristica dell’onda meccanica è quella di poter trasportare energia associata alle vibrazioni
delle particelle del mezzo attraversato. Dato che la radiazione elettromagnetica è di carattere
ondulatorio, anch’essa trasporterà energia. Come facciamo a calcolarla?
Calcoliamo prima quella legata ad un campo elettrico nel caso semplice di un condensatore. La sua
capacità è espressa dalla seguente relazione
C=
se E =
se σ =
σ
ε
allora
ΔV =
σ
⋅d
ε
Q
ΔV
Qd
Q
allora ΔV =
quindi
Sε
S
dove ΔV = E ⋅ d
C = Q⋅
Sε S
= ⋅ε
Qd d
La quantità di energia immagazzinata in un condensatore è data dalla seguente formula:
1 Q2 1 Q2 d
= ⋅
⋅
Wc = ⋅
2 C
2 ε S
Dato che tra le armature di un condensatore carico vi è un campo elettrico, che si annulla con la
scarica, l’energia immagazzinata nel condensatore è spesa per creare questo campo.
Da questa osservazione possiamo determinare una nuova grandezza: la densità di energia del campo
elettrico. Essa rappresenta l’energia contenuta nell’unità di volume.
Vc = Sd
WE =
WE =
1 Q2 d 1
1 Q2
1
⋅
⋅ ⋅
=
⋅
=
2 ε
S Sd
2ε S 2
2ε
Wc
quindi
Sd
2
1
⎛Q ⎞
(σ
⋅⎜ ⎟ =
S
2
ε
⎝ ⎠
)2
=
1
⋅ε
2
⎛σ ⎞
⋅⎜ ⎟
⎝ε ⎠
2
La densità di energia del campo elettrico sarà quindi uguale a
1
⋅ ε 0 ⋅ E 2 (1)
2
Consideriamo la proporzionalità diretta tra il campo magnetico e quello elettrico nel vuoto
WE =
B = ε 0 μ0 ⋅ E
da questo ricaviamo che E =
B
ε 0 μ0
Sostituendo questo rapporto alla formula (1) otteniamo quella della densità di energia del campo
magnetico
1 B2
(2)
WB = ⋅
2 μ0
La densità di energia associata al campo elettromagnetico si “dovrebbe” ottenere dalla somma delle
formule (1) e (2)
W oem
*
=
1
⋅ε0 ⋅ E
2
2
+
1 B2
⋅
2 μ0
Bisogna considerare, però, che E e B hanno un andamento sinusoidale. Per questo motivo è
necessario calcolare la densità di energia media trasportata da un’onda.
*
Woem
1 ⎛1
1 B2 ⎞ 1
1 B2
⎟⎟ = ⋅ ε 0 ⋅ E 2 + ⋅
= ⋅ ⎜⎜ ⋅ ε 0 ⋅ E 2 + ⋅
Woem =
2
2 ⎝2
2 μ0 ⎠ 4
4 μ0
Sostituendo alla B del secondo addendo E ⋅ ε 0 μ 0 otteniamo
Woem =
1
1 E 2 ⋅ ε 0 ⋅ μ0
⎛1
⎞ 1
⋅ε0 ⋅ E2 + ⋅
= 2 ⋅⎜ ⋅ε0 ⋅ E2 ⎟ = ⋅ε0 ⋅ E2
μ0
4
4
⎝4
⎠ 2
.












