PDAR03

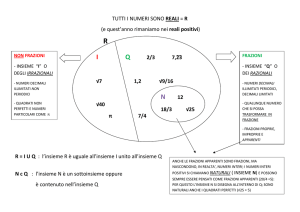
OPERAZIONI CON FRAZIONI
L'interesse degli studenti può essere sollecitato anche da problemi di carattere puramente numerico,
a condizione che questi si presentino in forma sufficientemente aperta da suscitare interrogativi e
da stimolare discussioni. Attraverso problemi di questo tipo si possono sviluppare abilità
computazionali; riteniamo che la pratica di calcolo finalizzata ad uno scopo ( manipolare dati
iniziali per mettere a fuoco i termini di un problema, fare congetture, verificare o dimostrare ipotesi)
produca più comprensione ed esperienza di un addestramento meccanico.
Non escludiamo, naturalmente, che sia altrettanto importante curare l'acquisizione del concetto di
frazione come operatore lavorando su problemi concreti.
È prerequisito agli esercizi seguenti una sufficiente dimestichezza nell'ordinamento e nelle
operazioni con frazioni; le attività possono essere svolte a piccoli gruppi, con supervisione finale
dell'insegnante.
E' interessante osservare il tipo di strategie che gli studenti mettono in atto per ricavare informazioni
sulle conoscenze e sulle abilità di ciascuno di essi.
SCHEDA DI LAVORO n. 1
Le frazioni egizie1
Gli antichi egiziani conoscevano le frazioni proprie con numeratore maggiore di 1, ma non erano
2
capaci di trattarle come numeri singoli; ad eccezione della frazione , avevano simboli solo per
3
le unità frazionarie (cioè per le frazioni con numeratore 1 ).
1 1
3 1 1 1
3
 
Essi scrivevano quindi  al posto di ,
al posto di .
4 4 7 28
7
2 4
Osserva che, per ciascuna frazione da scindere, ogni denominatore viene usato una sola volta.
 Pensi che tutte le frazioni proprie si possano scrivere così?
 Pensi che ci sia un unico modo per scindere una frazione propria in un numero finito di unità
3
frazionarie distinte? Se no, prova a scindere
in un modo diverso dal precedente.
7
5 3 4 5
; ; ; .
 Prova a scrivere in frazioni egizie
6 8 5 7
 Riesci ad individuare un metodo per scindere una frazione propria qualsiasi in un numero
finito di unità frazionarie distinte?
L'esercizio mette in gioco conoscenze ed abilità che riguardano l'equivalenza di frazioni e le
nozioni di MCD e mcm. Richiede un buon controllo di calcolo e la capacità di ipotizzare possibili
soluzioni e di fare previsioni sui risultati.
1
Vedere l'articolo di M. Gardner: Le frazioni egiziane e la teoria dei numeri, dal quaderno n. 45 di Le scienze,
dicembre 1988.
Cenni alle frazioni egizie si trovano anche sul libro di C. Boyer: Storia della Matematica, A. Mondadori , pag.15 e seg.
Il fatto che una stessa frazione possa essere scritta in due o più modi diversi (ad es.
3 1 1 1 1 1 1
1
  
  

) può far discutere su quale possa essere la "migliore"
7 4 7 28 6 7 14 21
scomposizione di una frazione: quella con il numero minore di addendi o quella con i denominatori
più piccoli? La domanda si collega a che cosa vuol dire “semplificare” in matematica e sul fatto
che la “semplificazione” è legata alla situazione- problema specifica.
Non è detto che gli studenti riescano a ricavare un metodo di scomposizione; si può proporre
l’algoritmo di Fibonacci:
a
Data la frazione propria
b
a
1) si cerca la più grande unità frazionaria contenuta in , cioè il più piccolo
b
intero maggiore di b:a
a
2) si sottrae tale unità da ottenendo un certo resto
b
3) si ripete il procedimento sul resto fino a ottenere una frazione generatrice con numeratore
unitario
a
4)
è uguale alla somma delle frazioni con numeratore unitario ottenute
b
Applichiamo ad esempio il metodo di Fibonacci a
4
:
5
4 1 1 1
 

5 5 1,... 2
4
4 1 3
2)  
5 2 10
3
1
1
1
3 1 2 1
3)
 

;
  
10 10 3,... 4
10 4 40 20
3
4 1 1 1
Quindi    .
5 2 4 20
E' bene precisare agli studenti che non si intende dimostrare la validità di tale metodo in generale
( anche se una dimostrazione esiste), precisando la differenza fra dimostrazione e verifica.
1)
SCHEDA DI LAVORO n. 2
Le frazioni di Farey2
Considera tutte le frazioni proprie che hanno come denominatore 4 o un numero minore di 4:
1 1 1 2 3
2
; ; ; ;
( che fine ha fatto la frazione ?)
2 3 4 3 4
4
Disponile in ordine crescente:
1 1 1 2 3
; ; ; ;
4 3 2 3 4
Questo insieme di frazioni, così ordinato, prende il nome di successione di Farey di ordine 4, dal
nome del geologo britannico che le studiò agli inizi del 1800.
 Scrivi le successioni di Farey di ordine 2, 3, 5, 6, 7.
 Considera la successione di ordine 7. Prendi una coppia qualsiasi di numeri di Farey consecutivi;
moltiplica il numeratore del secondo per il denominatore del primo ed il numeratore del primo
per il denominatore del secondo; fai la differenza dei risultati: che cosa ottieni?
Ripeti questo calcolo con un'altra coppia di numeri successivi.
Che cosa trovi?
Verifica se la tua scoperta è vera in generale.
 Sempre con riferimento alla serie di ordine 7, considera tre numeri consecutivi di Farey, e trova
se è possibile ottenere quello di mezzo dai due estremi.
Verifica se la regola ottenuta si può applicare a tutte le terne.
 Compila una tabella che metta in relazione il numero d'ordine delle diverse successioni che hai
costruito con il numero di frazioni che compone ogni successione. Esiste una regola generale ?
a c
e
di una successione di Farey, allora i prodotti "in
b d
croce" ad e bc sono interi consecutivi.
a c
Inoltre, presi tre numeri consecutivi, quello che sta fra gli estremi e
si può ricavare come
b d
ac
. E' bene richiamare all'attenzione degli studenti che questa operazione non dà la somma
bd
delle due frazioni estreme!
Il numero dei termini di una successione di ordine n+1 si può ricavare per ricorrenza da quello
della successione di ordine n, aggiungendo al numero di termini della successione di ordine n il
numero di frazioni proprie con denominatore n+1 (ma attenzione alle frazioni equivalenti!).
Se prendiamo due numeri consecutivi
2
Il riferimento è al testo di J. Conway: Il libro dei numeri, Hoepli ed. , pag 130 e seg.