STATISTICA ALGEBRICA

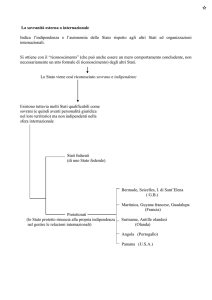
Università degli Studi di Torino
Dipartimento di Matematica G. Peano
UN POMERIGGIO DI
STATISTICA ALGEBRICA
Mercoledı̀ 10 Luglio 2013 – Palazzo Campana – Aula C
PROGRAMMA
14:45 Davide Alberelli
Introduzione al problema del grado di massima verosimiglianza
15:30 Paolo Lella
Risolvere equazioni polinomiali per continuazione omotopica
(break)
16:45 Fulvio Ricceri
Metodi algebrici per l’analisi dell’interazione tra variabili epidemiologiche
17:30 Valentina Triolo
Metodi algebrici per modelli di indipendenza: una implementazione in Maple
Sito web: www.personalweb.unito.it/paolo.lella/AlgStat/
Per informazioni: [email protected]
ABSTRACT
Davide Alberelli
Introduzione al problema del grado di massima verosimiglianza
Seminario introduttivo al problema di trovare il grado ML (maximum likelihood)
di un modello statistico algebrico. Nella prima parte del seminario verranno proposti alcuni teoremi generali ed esempi che nascono nell’ambito delle applicazioni
statistiche (curva di Hardy-Weinberg, criterio di indipendenza di variabili aleatorie).
Nella seconda parte del seminario ci si concentrerà sullo studio del grado ML dell’ipersuperficie di Fermat, presentando alcuni risultati ottenuti in collaborazione con
Daniele Agostini, Francesco Grande e Paolo Lella, alcuni problemi ancora aperti e
possibili approcci futuri per la soluzione di questi problemi.
Paolo Lella
Risolvere equazioni polinomiali per continuazione omotopica
Negli ultimi 25 anni, i metodi per risolvere numericamente sistemi di equazioni
polinomiali hanno avuto un grande sviluppo. Questo ambito di ricerca, chiamato
geometria algebrica numerica, è in continua evoluzione, anche per le sempre più
frequenti applicazioni di queste tecniche a problemi provenienti dal mondo dell’ingegneria e delle scienze applicate. Nel seminario, verrà discusso il concetto di continuazione omotopica e di come quest’idea viene utilizzata per il calcolo di soluzioni
numeriche di equazioni polinomiali.
Fulvio Ricceri
Metodi algebrici per l’analisi dell’interazione tra variabili epidemiologiche
L’obiettivo della presentazione è mostrare come metodi di algebra computazionale
(nello specifico: ideali torici, basi di Gröbner e l’algoritmo di Diaconis-Sturmfels)
possano essere utilizzati per lo studio dell’interazione tra variabili epidemiologiche
e, in particolare, nell’analisi dell’interazione gene-gene e gene-ambiente. Si descriverà la trattazione algebrica del modello di indipendenza di due variabili aleatore
e dei 5 modelli di indipendenza possibili per tre variabili aleatorie. Utilizzando poi
la teoria delle varietà toriche e delle basi di Gröbner si mostrerà come è possibile
sviluppare un test di indipendenza per l’opportuno modello, basato sull’algoritmo
di Diaconis-Sturmfels. Verrà poi mostrata un’applicazione ad un caso reale (interazione tra polimorfismi di geni metabolici e coinvolti nella riparazione del DNA e
tumori fumo-correlati) da cui si possono trarre conclusioni sull’efficacia del metodo.
Valentina Triolo
Metodi algebrici per modelli di indipendenza: una implementazione in Maple
Metodi di statistica algebrica sono stati di recente molto utilizzati per analisi in campo medico e biologico. In particolare, sfruttando la teoria delle basi di Gröbner, delle
basi di Markov e delle varietà toriche, è stato sviluppato un test d’ipotesi per modelli di indipendenza basato sull’algoritmo di Diaconis-Sturmfels, più efficiente di
altri metodi classici nel caso in cui non si abbia a disposizione un gran numero di
osservazioni.
In questo seminario presentiamo un pacchetto Maple che permette di applicare
questo metodo ad un modello di indipendenza tra un numero arbitrario di variabili
aleatorie che assumano un numero qualsiasi (ovviamente finito) di valori. Semplicemente a partire da un file Excel contenente i dati scritti in modo opportuno, i comandi a disposizione permettono di calcolare il p-value e ottenere altre informazioni
relative al modello di indipendenza, come ad esempio la matrice associata e il vettore delle frequenze delle osservazioni, senza bisogno che l’utente conosca la teoria su
cui questo metodo si basa.
Referenze consigliate:
• J. Huh, B. Sturmfels, Likelihood Geometry, arXiv:1305.7462 (2013).
• L. Patcher, B. Sturmfels, Algebraic Statistics for computational biology, Cambridge
University Press, 2005.
• M. Drton, B. Sturmfels, S. Sullivant, Lectures on Algebraic Statistics, Oberwolfach
Seminars, Vol 40, Birkhauser, Basel, 2009.
• F. Ricceri, C. Fassino, G. Matullo, M. Roggero, M.-L. Torrente, P. Vineis, L. Terracini, Algebraic Methods for Studying Interactions Between Epidemiological Variables, Mathematical Modelling of Natural Phenomena, 7 (03) , pp 227-252
(2012).