Densità spettrale dell’emissione
di corpo nero
1. Teoria
La teoria che interpreta lo spettro di emissione termica del corpo nero è sviluppata nei corsi di
Meccanica Quantistica e di Introduzione alla Fisica Moderna. Si può anche fare riferimento al testo
“Quantum Physics” di R. Eisberg e R. Resnick per approfondimenti. Qui si ricorda solo che la
densità spettrale è descritta dalla curva “planckiana”
Intensità (arb)
dc3 hexp(h/KT)-1) d
che origina dalla combinazione di due fattori:
1. la conta dei modi disponibili per la radiazione elettromagnetica confinata in una cavità
(primo fattore del prodotto), che dà luogo alla crescita di a bassa energia, prevista
anche classicamente;
2. il fattore statistico di Bose Einstein (secondo fattore del prodotto) che dà la probabilità che
ciascun modo sia popolato, e causa la riduzione di ad alta energia, rendendo finito
l’integrale sulle frequenze della e risolvendo così il paradosso classico.
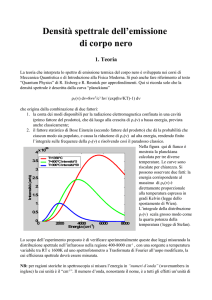
Nella figura qui di fianco è
26
x 10
mostrata la planckiana
4
calcolata per tre diverse
T=1350°C
temperature. Le curve sono
3.5
T=800°C Intensità*5
T=300°C Intensità*50
riscalate per chiarezza. Si
3
possono osservare due fatti: la
energia corrispondente al
2.5
massimo di è
direttamente proporzionale
2
alla temperatura espressa in
1.5
gradi Kelvin (legge dello
spostamento di Wien).
1
L’integrale della distribuzione
0.5
come la quarta potenza della
temperatura ( legge di Stefan).
0
0
2000
4000 -1
Energia (cm )
6000
8000
Lo scopo dell’esperimento proposto è di verificare sperimentalmente queste due leggi misurando la
distribuzione spettrale nell’infrarosso nella regione 400-8000 cm-1 , con una sorgente a temperatura
variabile tra RT e 1600K ed uno spettrofotometro a Trasformata di Fourier all’uopo modificato, la
cui efficienza spettrale dovrà essere misurata.
NB: per ragioni storiche in spettroscopia si misura l’energia in “numeri d’onda” (wavenumbers in
inglese) la cui unità è il “cm-1”. Il numero d’onda, nonostante il nome, è a tutti gli effetti un’unità di
misura dell’energia (8.066 cm-1= 1 meV). Dal numero d’onda si ricava agevolmente la lunghezza
d’onda che, espressa in cm, è l’inverso del numero d’onda.
Quindi (m)=0.01/wavenumeber(cm-1).
2. Lo spettrofotometro FT-IR
Principio di funzionamento (generale):
Per la misura si utilizza lo spettrofotometro a trasformata di Fourier Jasco FT-IR 420, il cui schema
essenziale è illustrato qui sotto.
Il principio di funzionamento è il seguente: la luce “bianca” proveniente dalla sorgente (light
source) viene inviata ad un interferometro di Michelson in cui uno dei due specchi è fisso mentre
l’altro è mobile, come illustrato nella figura. La luce ricombinata dal beam splitter, uscente sulla
destra viene poi misurata da un detector. La distribuzione spettrale della luce si ottiene dalla
Trasformata di Fourier dell’interferogramma, cioè dell’intensità della luce misurata dal detector in
funzione della posizione dello specchio mobile.
Ciò può essere intuito considerando prima il comportamento di una sola componente
monocromatica ( fissata) della luce emessa dalla sorgente: quando la distanza tra beam splitter e
specchio mobile è uguale a quella tra beam splitter e
specchio fisso, i due fasci si ricombinano in fase e
danno interferenza costruttiva. Lo stesso accade
quando la differenza di cammino ottico è pari ad un
multiplo di /2. Viceversa si ha interferenza distruttiva
quando la differenza di cammino ottico è Questo
risulta in un andamento oscillante dell’intensità in
funzione della posizione dello specchio mobile, come
illustrato qui di fianco a sinistra. Se ora consideriamo
cosa accade quando diverse lunghezze d’onda attraversano l’interferometro, troviamo la situazione
illustrata qui a destra.
Dovrebbe apparire
quindi plausibile che
l’interferogramma
registrato corrisponde
alla Trasformata di
Fourier della
composizione spettrale
della luce incidente
Spettrofotometri a doppio e singolo fascio:
In generale uno spettrofotometro misura la trasmittanza ad una certa lunghezza d’onda
confrontando l’intensità della radiazione trasmessa attraverso il campione con quella emessa dalla
sorgente. Negli strumenti a doppio fascio ciò avviene misurando simultaneamente i due fasci.
Viceversa negli strumenti a singolo fascio, come il Jasco 420, si misura prima lo spettro della
sorgente, e poi quello trasmesso attraverso il campione. Visto che a noi interessa solo lo spettro
emesso dalla sorgente, dobbiamo imbrogliare lo strumento ed ottenere direttamente lo spettro della
sorgente, selezionando il modo “singolo fascio”.
Assorbimento della radiazione IR:
La radiazione nel suo cammino dalla sorgente al detector viaggia in aria, in cui è presente vapore
d’acqua, ed è riflessa da specchi su cui sono presenti tracce di materiali organici contenti catene
alchiliche -(CH2)n . Entrambi questi gruppi molecolari assorbono la radiazione IR a ben determinate
lunghezze d’onda, causando dei “buchi” nella densità spettrale misurata. A noi questo fenomeno
interessa solo come artefatto, mentre l’utilizzo della misura accurata di questi “buchi” costituisce
proprio il nocciolo della misura di assorbimento FT-IR, che è oggetto del corso di Spettroscopia.
In ogni caso si può ridurre l’effetto dell’assorbimento da vapore d’acqua purgando lo
spettrofotometro con azoto.
Particolari importanti:
Per l’esecuzione dell’esperimento, gli elementi chiave su cui concentrare l’attenzione sono:
1. La sorgente, che è assimilabile ad un corpo nero
2. Beam splitter costituito da un sottile film di Ge depositato su substrato di KBr
3. Il detector DLATGS
Riguardo alla sorgente: è una spirale ceramica, la cui resistenza a temperatura ambiente vale circa
42. All’aumentare della temperatura la resistenza della sorgente aumenta linearmente fino alla
massima temperatura raggiungibile, che è T=1350oC se alimentata con Veff=80V AC.
Lo spettrofotometro è stato modificato in modo che la lampada è alimentata attraverso un
autotrasformatore VARIAC regolabile, che eroga al massimo 80Veff. Tramite un voltmetro ed un
amperometro inseriti in parallelo ed in serie nel circuito, è possibile misurare in tempo reale la
resistenza e quindi la T della sorgente. Attenzione ai cambiamenti bruschi di alimentazione, che
danno luogo a gradienti di temperatura!
Il BeamSplitter è la causa principale di non linearità della risposta dello strumento. E’ costituito da
un sottile film di Ge (indice di rifrazione n≈4 nel range IR di utilizzo) depositato su KBr (indice di
rifrazione n≈1.54 nel range IR di utilizzo) secondo lo schema riportato nella pagina successiva. E’
inoltre dotato di un secondo piatto di KBr per la compensazione dei cammini ottici. La non linearità
del BS origina dalle frange di interferenza dovute alle riflessioni tra le diverse interfacce,
principalmente tra Ge/aria e Ge/KBr.
Infine il detector è un sensore piroelettrico il Triglicin Solfato (TGS) che è deuterato per alzarne la
temperatura di Curie, ed è drogato con Alanina che ne assicura la polarizzazione permanente
(DLATGS, GEC-Marconi Infra-Red Ltd http://galileo.fis.unipr.it/~gigi/dida/Lab_Fis_Mod_I/detector_IR.pdf ).
La efficienza di questo detector è praticamente indipendente dalla lunghezza d’onda della
radiazione IR incidente, nel range di utilizzo.
Dettagli sul beam splitter
3. Esecuzione dell’esperimento
Per inizializzare correttamente l’interfaccia SCSI bisogna accendere prima lo strumento e poi il
computer. Attivare quindi il programma Jasco, e da questo attivare l’icona “spectra
measurement”, quindi, dal menù settings selezionare:
Source Standard
Detector TGS
Measurement range 7981-400 cm-1
Dal menù parameters STANDARD selezionare:
Numero di scan fisso (per es. 4)
Resolution 16 cm-1
Background SINGLE (modo a singolo fascio)
Sample SINGLE (modo a singolo fascio)
GAIN 1
Scan speed auto
Filter auto
Le misure si effettuano in modo singolo, e dopo ogni misura bisogna copiare a mano il file dalla
directory di lavoro del programma C:\jascosoft\id1\sample.jws ad una directory in cui si vuole
lavorare, per esempio C:\Lab Fis Mod I\xxx.jws Il programma fornito dalla Jasco offre limitate
possibilità di analisi per cui conviene poi salvare i files in formato testo ed analizzarli in Matlab.
E’ estremamente difficile calcolare a priori l’efficienza spettrale dello spettrofotometro, che è
dovuta a diversi fattori, principalmente alla dipendenza dalla lunghezza d’onda dell’efficienza degli
specchi e del beam splitter ed in misura minima al sensore DLATGS. Conviene invece ricavare
l’efficienza spettrale dal rapporto tra lo spettro d’emissione della lampada misurato ad una certa
temperatura (poniamo 1000K) e confrontarlo con la curva planckiana teorica calcolata per la
medesima temperatura. Questa curva di efficienza spettrale –essendo dovuta agli elementi ottici a
valle della sorgente- dovrà valere qualunque sia la temperatura della sorgente, quindi è utilizzabile
per riscalare le densità spettrali misurate ed ottenere così per ogni temperatura la densità spettrale
sperimentale corrette, da confrontarsi con quella teoricamente predetta per la medesima
temperatura. Di fianco è
130
riportato un tipico spettro
misurato con la sorgente
alla temperatura
T=1350°C.
100
SB
50
0
400
2000
4000
W a v e n u m b e r [ c m -1 ]
6000
8000