LA LEZIONE
Le relazioni di indeterminazione
Quando nel 1930 Werner Heisenberg pubblicò per la prima volta in lingua inglese “I
principi fisici della teoria dei quanti”, le relazioni di indeterminazione non erano ancora
conosciute come il principio di indeterminazione.
fig.1 Particolare della copertina del libro di Heisenberg,The physical principles of quantum theory, Dover,
1949. Riproduzione del lavoro pubblicato per la prima volta nel 1930 dalla University Chicago press.; fig.2
Istituto di fisica teorica di Copenaghen nel 1920
L’inconciliabilità tra il comportamento ondulatorio e quello corpuscolare dei processi
atomici era da tre anni propagandata da Niels Bohr. Secondo il fisico danese, entrambi
i punti di vista erano possibili, ma la scelta del dispositivo sperimentale definiva
l’ambito (ondulatorio o particellare) della trattazione del problema. Onde e particelle si
escludevano a vicenda come esemplificato in seguito nella maggioranza dei testi di
fisica dei quanti col famoso esperimento della doppia fenditura (si veda la lezione
L'interferenza).
Heisenberg non considerava però questo il nocciolo per la risoluzione della questione
fisica sollevata dal suo amico Wolfgang Pauli nel 1926 con la frase: “perché non si può
fissare il valore delle p insieme a quello delle q?” L’impossibilità, per la meccanica
quantistica di misurare contemporaneamente e con precisione arbitraria quantità di
moto e posizione di una particella era ora associata al concetto di elettrone come
“pacchetto di onde” avente estensione limitata nello spazio. Provare a ridurre tale
incertezza produceva un’indeterminazione nelle velocità tanto più grande quanto più
era piccola la regione di spazio associata al pacchetto di onde. Il prodotto delle due
incertezze, secondo il fisico tedesco, doveva essere almeno dell’ordine della costante di
Planck h. E poche pagine dopo, rifacendosi a un lungo articolo di Carle Hesse Kennard
del 1927, affermava: “che le relazioni di indeterminazione possono essere dedotte
senza l’uso esplicito delle onde, ma solo dallo schema matematico della teoria dei
quanti.”
La familiare e precisa espressione della disuguaglianza: Δp Δq ≥ h/4π, tra le incertezze
di due generiche variabili canoniche coniugate (p e q) si affermava con i lavori di
Howard Percy Robertson. In essi, come del resto in quello di Kennard, le incertezze
erano calcolate come deviazioni standard. L’unica relazione che non poteva essere
dimostrata in questo modo era quella della coppia di grandezze energia e tempo:
ΔE Δt ≥ h/4π. Ritornando ad Heisenberg, accanto alle dimostrazioni delle relazioni di
indeterminazione in cui erano impiegate le proprietà delle onde o il formalismo della
fisica quantistica, il teorico giustificava l’indeterminazione attraverso un esperimento
ideale conosciuto nella letteratura come il microscopio a raggi gamma (fig.3).
Immaginando di poter eseguire una misura della posizione di un
elettrone per mezzo di una radiazione di lunghezza d’onda λ
piccola rispetto alla luce visibile si riduceva l’incertezza Δx sulla
sua coordinata x. D’altra parte, l’elevata frequenza dei raggi
gamma amplificava lo scambio energetico (per effetto Compton)
tra radiazione ed elettrone, producendo una grande incertezza
Δpx nella quantità di moto. In termini matematici se l’errore Δx
è proporzionale al valore della lunghezza d’onda, l’errore sulla
componente x della quantità di moto corrispondente è
inversamente proporzionale a λ.
fig.3 Il microscopio ideale di Heisenberg-Bohr
Il prodotto delle due incertezza era, nei primi articoli di Heisenberg, approssimato alla
costante di Planck secondo la relazione: Δx Δpx ≈ h.
Il dibattito tra Bohr ed Einstein, sempre con esperimenti ideali, che seguì
l’interpretazione ortodossa della meccanica quantistica non è oggetto di questa lezione.
Vale però la pena soffermarsi su un ultimo “esperimento” proposto da von Neumann
oltre vent’anni dopo l’inizio del dibattito sulle relazioni di indeterminazione in meccanica
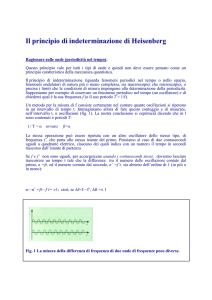
quantistica. Facendo riferimento alle figure che seguono, la velocità di un sistema
quantistico è analizzata attraverso la misura dell’effetto Doppler subito da un fotone
nell’interazione con la particella massiva: Δf/f=-2v/c. Se il fotone ha un’unica
frequenza f1, dopo la diffusione, la sua frequenza, per un sistema di riferimento
solidale con il laboratorio, diviene f2. La differenza tra le due frequenze è appunto Δf
che permette di ricavare la velocità v (c è la velocità della luce). Per non avere un
impulso (treno di onde) di durata infinita invece di un’unica frequenza il fotone può
essere pensato come un pacchetto di onde (si veda la lezione La propagazione delle
onde).
fig.4 Esperimento ideale di von Neumann per la misura della velocità di una particella a partire dall’effetto
Doppler; fig.5 (a destra) Il pacchetto di onde
Il pacchetto di onde di durata τ del fotone è diffuso dal corpuscolo determinando un
errore Δω dell’ordine di τ-1 che si può mettere in relazione con l’incertezza sulla
quantità di moto. D’altra parte la durata dell’interazione tra pacchetto di onde e
particella è indeterminata, a causa sempre del tempo τ e produce un’incertezza nella
rilevazione della coordinata del corpuscolo. Il prodotto delle due incertezze è tale che
Δx Δpx ≅ ħ/2. Nell’esempio precedente l’incertezza sul tempo associato al pacchetto di
onde si riflette nell’indeterminazione della posizione dell’oggetto quantistico, mentre
l’incertezza sull’energia (frequenza) è legata all’errore sulla misura della quantità di
moto del sistema quantistico. Il disturbo Δx sulla variabile coniugata alla quantità di
moto del sistema in esame deriva quindi dall’incertezza della variabile coniugata
utilizzata per la misura. Le relazioni di indeterminazione sulle osservabili incompatibili
sono allora originate dalla relazione di incertezza dell’apparato di misura: Δω τ ≅1.
Interpretazione statistica della meccanica ondulatoria e
indeterminazione minima
Nel periodo immediatamente precedente al V Congresso Solvay del 1927, furono
ampiamente analizzate le basi fisiche della teoria quantistica. Un ultimo tassello
rispetto alle considerazioni precedenti fu l’interpretazione statistica della meccanica
ondulatoria dovuta a Max Born. La funzione d’onda, introdotta da Schrödinger,
divenne, da allora, l’ampiezza di probabilità di trovare un sistema quantistico come
l’elettrone nell’intorno della posizione x al tempo t. In modo tale che il modulo del suo
quadrato moltiplicato per il volume ΔV rappresenta la probabilità di trovare la particella
nel volumetto in questione. L’unica conoscenza possibile, secondo l’interpretazione
statistica, è la probabilità di trovare l’elettrone (considerato come corpuscolo) in diversi
punti dello spazio. Di nuovo, la posizione in un dato istante non è un concetto ben
definito. Fissata la funzione di distribuzione delle probabilità è possibile, come in tutti i
problemi statistici, calcolare il valore medio di x (< x >) e anche i momenti superiori. Il
più importante dei quali è la deviazione quadratica media (in genere indicata come
Δx=[< (x - <x>)2 >]1/2= (<x2> - <x>2)1/2. Essa rappresenta l’incertezza della
misura della posizione o equivalentemente la fluttuazione della grandezza, poiché, per
una funzione simmetrica rispetto al valore medio, < x - <x> >= 0. La funzione d’onda
come funzione della posizione ha una rappresentazione analoga nello spazio delle
quantità di moto. Per particolari sistemi è possibile che le distribuzioni di probabilità
siano costanti nel tempo, si parla allora di stati stazionari. Si può allora cercare di
ridurre al minimo il prodotto delle incertezze su impulso e posizione secondo il valore
più piccolo della relazione di indeterminazione Δx Δpx=ħ/2. Ciò accade per funzioni
d’onda dell’impulso e della posizione che seguono una distribuzione gaussiana (di
nuovo teoria degli errori).
fig.6 Rappresentazione della funzione di distribuzione gaussiana al variare del valore medio di x e dello
scarto quadratico medio; fig.7 (a sinistra) Stati a incertezze minime e rappresentazione nello spazio delle
fasi
Nello spazio delle fasi (q, p) l’incertezza minima è così rappresentata da un’area
all’interno della quale si colloca una eventuale misura. Negli ultimi anni è stato possibile
modificare le proprietà dei sistemi quantistici in modo da
migliorare la precisione di una delle due misure a discapito
ovviamente dell’altra. Il procedimento, detto in inglese
squeezing (spremitura), trasforma gradualmente le figure,
approssimabili a ellissi di ugual area, riducendo
un’incertezza e amplificando la coniugata. Nella figura
seguente è descritto schematicamente il processo per
misure in un condensato di Bose-Einstein.
fig.8 Spazio delle fasi in un processo di squeezing. Le due osservabili
sono lo spin e una grandezza collegata alla fase nematica (intermedia tra liquido e solido)
Sviluppi recenti
Le relazioni di indeterminazione: Δpx Δx ≥ ħ/2, Δpy Δy ≥ ħ/2, Δpz Δz ≥ ħ/2, ΔE Δt ≥
ħ/2, ecc., non rappresentarono per molti anni certo una guida per gli sperimentatori.
La loro verifica fino al 1980 era sempre associata a considerazioni statistiche. Dopo
aver preparato un insieme di sistemi identici, l’ensemble per il 50% era sottoposto alla
misura di un’osservabile q e l’altra metà di sistemi identici serviva per la misura
dell’osservabile incompatibile p. Allora le varianze (Δq)2 e (Δp)2 soddisfacevano la
disuguaglianza: Δq Δp ≥ ħ/2. Le relazioni di indeterminazione ormai chiamate principio
di Heisenberg, secondo il quale in ogni processo di misura su un singolo sistema
quantistico non si possono misurare simultaneamente, con una precisione piccola a
piacere, le due osservabili non commutative p e q, non trovava allora un’attenzione a
causa diciamo delle possibilità tecnologiche. Eppure da anni gli apparati alla Stern e
Gerlach e i principi di Heisenberg e Bohr erano l’introduzione della meccanica
quantistica. Solo negli ultimi tre decenni gli esperimenti idealizzati dai padri fondatori
della meccanica quantistica hanno trovato possibilità di applicazioni pratiche nel campo
dell’ottica quantistica e nella fisica atomica, quando sono state realizzate tecniche
sperimentali rivoluzionarie che permettono oggi la misura e la manipolazione di singoli
sistemi quantistici.
Anche il principio di indeterminazione ( o di incertezza come dicono i madrelingua
tedeschi) ha avuto negli ultimi quindici anni diverse rivisitazioni. In particolare, l’idea di
Heisenberg di disturbo-errore nella misura è stata separata da quella statistica di
Kennard e Robertson. L’incertezza di una misura quantistica, secondo alcuni autori, di
cui il capostipite si può considerare Masanao Ozawa, è dovuta a due fattori: il primo, è
legato all’apparato di misurazione; il secondo, è un’incertezza intrinseca dei sistemi
quantistici. Secondo questa nuova interpretazione è possibile realizzare esperimenti in
cui il prodotto tra l’errore εA della grandezza A e il disturbo ηB della grandezza B sia
reso anche più piccolo del valore ħ/2, proprio considerando le fluttuazioni σ A e σB
intrinseche delle due osservabili quantistiche. La disuguaglianza di Heisenberg è allora
trasformata secondo un’espressione del tipo:
εA ηB +εA σB +σAηB≥ ħ/2.
L’incertezza quantistica dipende dalla somma di un fattore perturbativo dovuto alla
misura e da un secondo termine intrinseco alla natura quantistica del sistema. Prima di
accennare ai tentativi di verifica sperimentale della nuova disuguaglianza, bisogna però
parlare di un secondo sviluppo, non ancora condiviso dalla comunità scientifica, in cui il
singolo sistema quantistico è sottoposto a una successione di misure, distinguibili per la
loro intensità. Per presentare il concetto di misura debole, per la prima volta introdotto
da Yakir Aharonov nel 1998, si può utilizzare una variante degli esperimenti di Stern e
Gerlach.
fig.9 Misure forti e deboli nella meccanica quantistica
Un atomo di argento con lo spin “su”, lungo l’asse x, attraversa un magnete orientato
secondo z. Se il campo è sufficientemente intenso la distinzione tra atomi con spin “su”
e “giù” secondo l’asse z è chiara. Se invece si riduce l’intensità del campo, le deviazioni
dei due gruppi sono così piccole che non si capisce quali siano gli atomi con spin “su” e
“giù”, quindi si può pensare che una misura debole non influenzi il sistema. Eppure
combinando una misura debole con una forte (come rappresentato nella terza
immagine) si ottiene un risultato per certi versi inaspettato. Senza il magnete debole
tutti gli atomi sarebbero finiti verso sinistra (condizione che si avrebbe con il solo
magnete orientato secondo l’asse x), invece adesso pochi atomi si raggruppano in un
fascio a destra come se il primo magnete dividesse effettivamente gli atomi secondo
due caratteristiche. Su queste basi un gruppo di ricerca coordinato da A. Steinberg
dell’Università di Toronto, lavorando sulla polarizzazione di fotoni, ha realizzato il
classico esperimento della doppia fenditura ottenendo figure di interferenza delle
particelle insieme a traiettorie particellari medie, “violando” in qualche modo l’assunto
di Bohr di complementarità.
fig.10 Aspetti ondulatori e particellari medi misurati contemporaneamente dai ricercatori dell’Università di
Toronto
A partire dalla combinazione di apparati deboli e forti disposti in successione per la
misura di spin di neutroni, Y. Hasegawa e il suo team del Politecnico di Vienna pensano
di aver avvalorato la disuguaglianza di Ozawa.
fig.11 Schema misura debole dello spin di neutroni; fig.12 (a destra) Schema dell’apparato sperimentale
per la verifica della disuguaglianza di Ozawa
Forse è ancora presto per un radicale ripensamento del principio di indeterminazione di
Heisenberg, per la revisione del principio di complementarità di Bohr, per la messa in
discussione della teoria della misura quantistica di von Neumann o dell’interpretazione
statistica di Born. Certo è che gli esperimenti ideali dei padri fondatori della meccanica
quantistica non sono più oggetto di culto, ma sono “sporcati” da ricercatori che
possono lavorare su sistemi quantistici individuali e stanno cercando di rivedere
sperimentalmente e teoricamente il concetto di misura.