Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
DOMINIO E IMMAGINE DI UNA FUNZIONE REALE DI VARIABILE
REALE
La prima operazione che dobbiamo fare quando ci accingiamo a studiare una
funzione (per poterne poi determinare il grafico) è quella di individuare il
DOMINIO della funzione, ovvero di individuare l’insieme di valori reali che si
possono attribuire alla variabile indipendente x in modo da poter determinare il
corrispondente valore reale y.
Il DOMINIO si chiama anche INSIEME DI DEFINIZIONE oppure INSIEME DI
ESISTENZA della funzione.
Se da una parte il dominio è l’insieme di variabilità della x (variabile
indipendente), l’insieme di valori di variabilità per la variabile y (variabile
dipendente) si chiama IMMAGINE.
L’IMMAGINE è, in altre parole, l’insieme di valori reali che la funzione può
assumere.
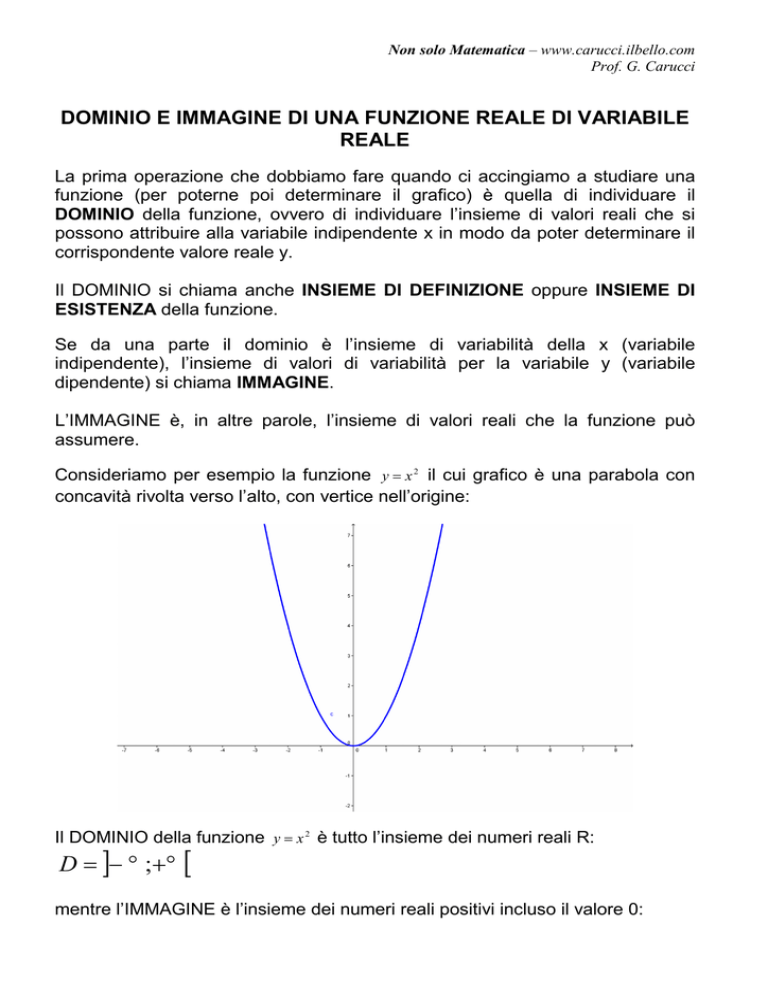
Consideriamo per esempio la funzione y = x 2 il cui grafico è una parabola con
concavità rivolta verso l’alto, con vertice nell’origine:
Il DOMINIO della funzione y = x 2 è tutto l’insieme dei numeri reali R:
D = ]− ∞;+∞[
mentre l’IMMAGINE è l’insieme dei numeri reali positivi incluso il valore 0:
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
C = [0;+∞[
ovvero, la parabola è disegnata nel semipiano positivo per tutte le x
appartenenti al dominio e non ha rami nel semipiano delle y negative.
Consideriamo la funzione y = x 2 − 9 il cui grafico è il seguente:
Il DOMINIO della funzione y = x 2 − 9 è l’insieme dei numeri reali minori di -3
(incluso il valore -3) e maggiori di +3 (incluso il valore +3), mentre l’IMMAGINE
è l’insieme dei numeri reali positivi incluso il valore 0:
D = ]− ∞;−3] U [+ 3;+∞[
C = [0;+∞[
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
Consideriamo la funzione y =
x−4
il cui grafico è il seguente:
x−3
Il DOMINIO della funzione y =
x−4
è l’insieme di tutti i numeri reali escluso il
x−3
valore +3, mentre l’IMMAGINE è l’insieme di tutti i numeri reali escluso il valore
+1:
D = ℜ − {+ 3}
D = ℜ − {+ 1}
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
DETERMINAZIONE DEL DOMINIO DI FUNZIONI REALI DI
VARIABILE REALE
Vediamo ora come si determina il dominio di una funzione reale di variabile
reale.
FUNZIONI RAZIONALI INTERE
Esempi di funzioni razionali intere sono:
y = x 3 + 3 x − 11
x4 − 3
y=
2
5
y = ( x − 3)
Per tutte le funzioni razionali intere il dominio è l’insieme R dei numeri reali.
FUNZIONI RAZIONALI FRATTE
Il dominio di una funzione razionale fratta si determina imponendo il
denominatore della frazione diverso da 0; se il denominatore fosse 0 non
sarebbe infatti possibile determinare il valore della funzione (la divisione per 0
non è ammissibile!).
Consideriamo la funzione razionale fratta:
x2 + 3
y=
x−4
Per calcolare il dominio occorre risolvere l’equazione di primo grado x − 4 = 0 ;
la soluzione di questa equazione deve essere esclusa dall’insieme dei numeri
reali in quanto fa diventare 0 il denominatore della funzione di cui sopra.
Il dominio, pertanto, è:
D = ℜ − {+ 4}
Consideriamo la funzione razionale fratta:
y=
3
x2 − 5
Per calcolare il dominio occorre risolvere l’equazione di secondo grado
x 2 − 5 = 0 ; poiché l’equazione ha due soluzioni distinte ( + 5 ;− 5 ), entrambe
devono essere escluse dall’insieme dei numeri reali in quanto fanno diventare 0
il denominatore della funzione assegnata.
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
Il dominio, pertanto, è:
{
D = ℜ − + 5 ;− 5
}
Consideriamo la funzione razionale fratta:
x3 − x
y=
1 + x2
Per calcolare il dominio occorre risolvere l’equazione di secondo grado
x 2 + 1 = 0 ; poiché l’equazione non ha soluzioni (il determinante è infatti minore
di 0), il denominatore della funzione assegnata è sempre diverso da 0. Pertanto
il dominio della funzione è tutto l’insieme dei numeri reali:
D=ℜ
FUNZIONI IRRAZIONALI
Il dominio di una funzione irrazionale si determina imponendo il radicando
maggiore o uguale 0; se il radicando fosse minore di 0 non sarebbe infatti
possibile determinare il valore della funzione (la radice di un numero negativo
non esiste!).
Consideriamo la funzione irrazionale:
y = 2x − 3
Per determinare il dominio occorre risolvere la disequazione di primo grado
2 x − 3 ≥ 0 ; i valori reali della variabile x che risolvono questa disequazione
costituiscono il dominio della funzione assegnata. Pertanto il dominio è:
3
D = + ;+∞
2
Consideriamo la funzione irrazionale:
y = − x2 + 9
Per determinare il dominio occorre risolvere la disequazione di secondo grado
− x 2 + 9 ≥ 0 ; i valori reali della variabile x che risolvono questa disequazione
costituiscono il dominio della funzione assegnata. Si trova che il dominio è:
D = [− 3;+3]
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
FUNZIONI ESPONENZIALI
Esempi di funzioni esponenziali, aventi cioè la variabile x all’esponente, sono:
y = 32 x −6
2
y=
3
y=5
x 2 −7
x
x+ 2
Poiché la funzione esponenziale elementare y = a è definita in tutto l’insieme
dei numeri reali, per determinare il dominio di una funzione esponenziale
occorre determinare il dominio della funzione esponente.
Pertanto, per le funzioni di sopra i domini sono, nell’ordine, i seguenti:
x
D=ℜ
D = ℜ − {0}
D = [− 2;+∞[
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
OSSERVAZIONE PER LA DETERMINAZIONE DEL DOMINIO DI
FUNZIONI REALI DI VARIABILE REALE
Se la funzione della quale si vuole determinare il dominio non è semplicemente
razionale fratta o irrazionale o esponenziale, ma è una funzione più complessa
nella quale si possono riconoscere funzioni razionali fratte, irrazionali ed
esponenziali, occorre procedere come negli esempi seguenti.
Consideriamo la funzione irrazionale fratta (la x è sia al denominatore che sotto
il segno di radice):
y=
3
+ x −1
x2 − 4
La prima parte della funzione
3
è definita per tutti i valori reali escluso
x2 − 4
quelli che annullano il denominatore:
(1)
D = ℜ − {− 2;+2}
La seconda parte della funzione
o uguali ad 1:
(2)
x − 1 è definita per tutti i valori reali maggiori
D = [+ 1;+∞[
La funzione assegnata è pertanto definita per tutti i valori reali appartenenti sia
al primo intervallo (1) che al secondo (2) , cioè per tutti i valori maggiori o uguali
ad 1, escluso il valore +2:
D = [+ 1;+∞[ − {+ 2}
Consideriamo la funzione irrazionale fratta:
y=
x −1
x2 − 4
La prima parte della funzione
uguali ad 1:
(1)
D = [+ 1;+∞[
x − 1 è definita per tutti i valori reali maggiori o
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
1
La seconda parte della funzione
x2 − 4
è definita per tutti i valori reali che
2
soddisfano la disequazione di secondo grado: x − 4 > 0 (solo maggiore di 0
poiché il denominatore non può essere 0!)
(2)
D = ]− ∞;−2[ U ]+ 2;+∞[
La funzione assegnata è pertanto definita per tutti i valori reali appartenenti sia
al primo intervallo (1) che al secondo (2) , cioè per tutti i valori maggiori di 2:
D = ]+ 2;+∞[
Consideriamo la funzione irrazionale fratta:
y=
x−3
− x +1
Per determinare il dominio occorre risolvere la disequazione fratta
x−3
≥ 0;
− x +1
i valori reali della variabile x che risolvono questa disequazione fratta
costituiscono il dominio della funzione assegnata.
Per risolvere la disequazione fratta occorre risolvere i seguenti sistemi:
(1)
x − 3 ≥ 0
− x + 1 > 0
x − 3 ≤ 0
(2) − x + 1 < 0
Nota: il radicando − x + 1 è solo maggiore o minore di 0; in una funzione
razionale fratta, infatti, il denominatore non può annullarsi.
La funzione assegnata è pertanto definita per tutti i valori reali appartenenti al
seguente intervallo:
D = ]+ 1;+3]
Il valore +3 è incluso poiché annulla la funzione (pertanto è un valore
ammissibile); mentre il valore +1 è escluso perché, annullando il denominatore,
non permette di assegnare un valore alla funzione.
Non solo Matematica – www.carucci.ilbello.com
Prof. G. Carucci
Consideriamo la funzione esponenziale fratta:
1 x
2
y = x
3
3
2
−1
1
+
x+2
La prima parte della funzione
1
2
3
x −1
2
è definita per tutti i valori reali ad
esclusione di -1 e +1:
(1)
D = ℜ − {− 1;+1}
1
La seconda parte della funzione x
3
è definita per tutti i valori reali (il
denominatore non si annulla mai):
(2)
D=ℜ
La terza parte della funzione
1
x+2
è definita per tutti i valori reali ad
esclusione del valore -2 che annulla il denominatore:
(3)
D = ℜ − {− 2}
La funzione assegnata è pertanto definita per tutti i valori reali ad esclusione di
-1, +1 e -2:
D = ℜ − {− 2;−1;+1}










