Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
TERMODINAMICA
La termodinamica ci permette di studiare gli scambi energetici e le possibilità di
trasformazione di una porzione di materia macroscopica. Ogni percettibile quantità di
materia su cui possa effettuarsi una osservazione macroscopica, viene detta sistema
termodinamico; tutto ciò che è esterno a tale porzione di materia viene detto ambiente. Il
sistema più l'ambiente costituiscono l'universo. Un sistema si dice aperto se può
scambiare con l’ambiente sia calore che materia, chiuso se può scambiare solamente
calore, isolato se non può scambiare né calore né materia.
Descrivere un sistema dal punto di vista termodinamico significa dare i valori del numero
minimo di parametri (come ad es. temperatura, volume, pressione, etc.) che definiscono
univocamente il sistema; la conoscenza dei valori di tali parametri, usualmente indicati
come variabili di stato, consente a chiunque di costruire una esatta replica del sistema
descritto.
La variazione del valore di ciascuna variabile di stato, causata dal passaggio di un sistema
da uno stato 1 a uno stato 2, non dipende dal cammino percorso durante la
trasformazione, ma soltanto dallo stato iniziale 1 e dallo stato finale 2. I valori delle
variabili di stato di un sistema (ad esempio P, T) devono essere riferite al sistema in
equilibrio; in tale condizione infatti, nella quale le proprietà fisiche e chimiche di ogni
porzione del sistema restano invariate nel tempo, i valori delle predette variabili di stato
sono costanti per ogni porzione del sistema. Il fatto di riferirsi soltanto a sistemi in
equilibrio è una caratteristica essenziale della termodinamica.
La termodinamica si articola essenzialmente su due principi; il primo esprime la
impossibilità di creare o distruggere energia; il secondo si occupa di capire quando una
determinata trasformazione possa avvenire ed esprime l'impossibilità di trasformare
integralmente il calore in lavoro. Dalla elaborazione di questi due principi derivano le basi
razionali che consentono di rendersi razionalmente conto dell'andamento dei fenomeni
chimici.
Cap8-1
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
Primo principio della termodinamica
Il primo principio della termodinamica postula che l'energia può essere convertita da una
forma in un'altra, ma che non può essere né creata né distrutta: ciò significa affermare che
il contenuto di energia dell'universo è costante.
Ogni sistema ha un suo contenuto di energia, energia interna (E), nella quale si sommano
tutte le forme di energia legate al suo stato (energia dovuta agli elettroni, ai legami chimici,
energia cinetica, energia nucleare, etc.). Il valore assoluto della E, per un determinato
sistema in un determinato stato, non è noto; ma l'ignoranza di un tale dato non
rappresenta una difficoltà per la termodinamica, perché essa non considera i valori
assoluti del contenuto di energia di un sistema ma solo le differenze fra i valori delle
energie interne del sistema stesso prima e dopo una trasformazione. In base al primo
principio, perché si abbia una variazione dell'energia interna di un sistema è necessario
che questo possa scambiare energia con l’esterno, cioè che non sia un sistema isolato.
Ogni scambio di energia fra un sistema e l'esterno avviene o con un intermedio
meccanico, ed allora si parla di lavoro, o per passaggio di calore, subordinatamente
all'esistenza di una differenza di temperatura fra il sistema e l'esterno; lavoro e calore non
sono entità materiali, ma modi di trasferimento, equivalenti, dell'energia; essi
rappresentano, per così dire, energia in transito.
Il calore è l'energia trasferità in virtù di una differenza di temperatura: la quantità di calore
che viene acquistata da un sistema è quindi proporzionale alla variazione di temperatura
del sistema stesso:
q ∝ ΔT
Tale proporzionalità dipende da una proprietà del sistema che viene detta capacità termica
C che è la quantità di calore necessaria ad aumentare di un grado la temperatura del
sistema e dipende dalle caratteristiche del sistema stesso (per riscaldare di 1°C un pezzo
di ferro a 25°C occorre meno calore che per riscaldare un pezzo di legno alla stessa
temperatura) e dalla sua temperatura (per riscaldare di 1°C un pezzo di ferro a 25°C
occorre più calore che per riscaldane un pezzo a 100°C).
Questa proprietà dipende però anche dalla massa del sistema (per riscaldare di 1°C, 1
grammo di ferro occorre meno calore che per riscaldarne 10 g): si preferisce quindi
descrivere tale proprietà come calore specifico che è la quantità di calore necessaria ad
aumentare di un grado la temperatura di un grammo di sostanza. Per cui detto c il calore
specifico avremo:
q = c x ΔT x m
Per gli scambi di energia occorre adottare una convenzione riguardante i segni da
attribuire ai valori del calore e del lavoro che un sistema scambia con l'esterno:
q = calore scambiato dal sistema con l'ambiente: viene considerata positiva la quantità di
calore acquistata dal sistema e negativa quella perduta dal sistema; così se un sistema
acquista dall'ambiente la quantità di calore q1 (ad es. 15 calorie) e cede successivamente
Cap8-2
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
all'esterno la quantità di calore q2 (ad es. 10 calorie), avremo q1 = 15 cal e q2 = -10 cal ed il
bilancio termico del sistema sarà dato dalla somma algebrica delle quantità di calore in
gioco: q = q1 + q2 = 15 - 10 = +5 cal; in totale il sistema avrà acquistato (segno +) 5
calorie;
w (work) = lavoro scambiato dal sistema con l'ambiente: viene considerato negativo il
lavoro che il sistema compie sull'ambiente (diminuzione dell’energia interna del sistema) e
negativo quello compiuto dall'ambiente sul sistema; così se un sistema compie un lavoro
w1 sull'ambiente (ad es. 10 joule), e successivamente l'ambiente compie sul sistema un
lavoro w2 (ad es. 15 joule), il bilancio energetico del sistema sarà w = w1 +w2 = - 10 + 15 =
+5 joule. In totale il sistema avrà acquistato (segno +) 5 joule.
Se un sistema la cui composizione resta costante è chiuso e passa da uno stato 1 (con
energia interna E1) ad uno stato 2 (con energia interna E2) deve scambiare energia con
l'ambiente; indicando con q ed w le quantità di calore e di lavoro scambiate e con ΔE la
differenza E2 -E1, avremo che per il primo principio della termodinamica, in base alle
convenzioni viste sopra:
ΔE = q + w
(1)
La (1) significa che la variazione dell'energia interna di un sistema è pari alla somma fra le
quantità di calore e di lavoro scambiate con l'ambiente (tenendo presente le convenzioni
circa i segni del lavoro e del calore).
Il passaggio del sistema dallo stato 1 allo stato 2 può realizzarsi in infiniti modi;
l'esperienza dimostra che il valore di ΔE = E2 -E1, è costante, indipendentemente dal
cammino percorso per passare da 1 a 2.
Da questo comportamento si deduce che E è una funzione di stato del sistema, ed il primo
principio della termodinamica può così anche enunciarsi affermando che l'energia interna
di un sistema è una funzione di stato.
A questo punto va fatta un'osservazione assai importante: nella (1) è il valore di ΔE che
non dipende dal cammino percorso, ma non i valori di q e di w presi singolarmente;
ciascuno di questi infatti varia generalmente a seconda del cammino percorso, ed è solo il
valore della loro differenza che resta costante; cioè soltanto E è una funzione di stato, ma
non q ed w separatamente.
Se consideriamo una trasformazione che avvenga a volume costante come il processo di
riscaldamento di un litro di ossigeno da 25° C a 30° C in un vaso chiuso, abbiamo che il
sistema non compie lavoro in quanto il volume è costante e quindi avremo che w = 0 e
quindi ΔE = q. Potremo quindi misurare la variazione di energia semplicemente
misurando il calore fornito al sistema.
V = cost
P = cost
Poiché però la maggior parte dei processi e delle reazioni chimiche avvengono all’aperto e
quindi a pressione costante, ripetiamo l’esperimento precedente in modo che la pressione
Cap8-3
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
si mantenga costante durante la trasformazione e cioè in un recipiente chiuso da un
pistone a cui si oppone solo la pressione esterna che sarà uguale alla pressione
atmosferica.
Il questo caso il riscaldamento provocherà anche l’espansione dell’ossigeno e il sistema
dovrà compiere anche un lavoro contro la pressione esterna che sarà
w = -PΔV. In questo caso la variazione di energia interna del sistema sarà ΔE = q – PΔV
e quindi in calore fornito al sistema dovrà essere maggiore e sarà q = ΔE + PΔV. Tale
calore acquistato o ceduto dal sistema a pressione costante è dato dalla somma di tutte
funzioni di stato (E, P, V) e sarà quindi anch’esso una funzione di stato del sistema che
viene definita entalpia (H).
ΔH = qp
dove, se cp è il calore specifico a pressione costante:
qp = cp x ΔT x m
L’entalpia e l’energia sono legate dalla relazione:
ΔH = ΔE + Δ(PV).
Poiché i gas sono capaci di espandere notevolmente il loro volume per riscaldamento
mentre i liquidi e i solidi in genere non lo fanno, per questi ultimi possiamo fare
l’approssimazione che ΔV ≈ 0 e quindi:
ΔH ≈ ΔE.
Per mezzo della variazione di entalpia possiamo quindi misurare il calore ceduto o
acquistato durante una reazione chimica, assumendo che il sistema sia rappresentato
dalla reazione chimica in esame e che tale reazione avvenga a pressione costante.
Se il sistema cede calore all'ambiente la sua entalpia diminuisce: quindi se una reazione
avviene con produzione di calore il ΔH relativo alla reazione sarà negativo e la reazione si
dirà esotermica.
Se il sistema acquista calore dall'ambiente la sua entalpia invece aumenta: quindi se una
reazione per avvenire ha bisogno di assorbire calore, il ΔH relativo alla reazione sarà
positivo e la reazione si dirà endotermica.
ΔH < 0
ΔH > 0
esotermica
endotermica
Poiché il valore dell'entalpia (che sia entalpia di formazione di un composto, o entalpia di
una qualsiasi reazione) dipende dalla temperatura e dalla pressione a cui si opera, sono
state stabilite, per rendere confrontabili i valori delle entalpie, delle condizioni sperimentali,
dette condizioni standard: le entalpie determinate in condizioni standard vengono indicate
col simbolo ΔH°. Perché un sistema chimico sia nel suo stato standard occorre che ogni
Cap8-4
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
specie chimica che lo costituisce sia nel suo stato standard, cioè alla temperatura di 25°C,
alla pressione di 1 atmosfera e nella forma molecolare e di aggregazione stabile in tali
condizioni.
In maniera analoga a quanto avviene per l’energia interna è impossibile calcolare l'entalpia
assoluta di un sistema: poiché però quello che studia la termodinamica sono solamente le
variazioni di entalpia legate ad una trasformazione, per superare tale problema è stato
sufficiente adottare una convenzione che assuma che l'entalpia di tutti gli elementi nel loro
stato standard sia uguale a 0. Per mezzo di questa convenzione e poiché l'entalpia è una
funzione di stato, l'entalpia standard di un qualsiasi composto risulta essere uguale alla
differenza di entalpia legata alla sua reazione di formazione dagli elementi.
C + O2 = CO2
ΔH°reazione = H°stato finale - H°stato iniziale = H°prodotti - H°reagenti =
= H°(CO2(gas)) - [H°(C(grafite) + H°(O2(gas))] = H°(CO2(gas)) - 0
da cui:
ΔH°reazione = H°(CO2)
In questo modo potendo conoscere l'entalpia di qualsiasi composto solamente misurando
la variazione di entalpia associata alla reazione di formazione del composto desiderato
dagli elementi, diventa molto semplice calcolare la variazione di entalpia associata ad una
qualsiasi reazione chimica:
ΔH°reazione = H°prodotti - H°reagenti
Quando una reazione chimica può essere scritta come somma di due o più reazioni,
l’entalpia della reazione globale è uguale alla somma delle entalpie associate alle
rispettive reazioni intermedie: questa affermazione viene detta Legge di Hess.
Grazie alla legge di Hess si possono determinare entalpie di reazione che non sono
misurabili direttamente.
Esempio:
Note le entalpie di reazione delle due reazioni seguenti si può calcolare per differenza
quella della terza, che sperimentalmente sarebbe difficile da determinare.
ΔH o (kJ mol-1)
− 393.5
1) C(s) + O2 (g) → CO2 (g)
2) CO (g) + ½ O2 (g) → CO2 (g)
− 283.0
3) C(s) + ½ O2 (g) → CO (g)
?
ΔH(3) = ΔH(1) - ΔH(2) = − 110.5
La situazione è riassunta nel seguente diagramma dei livelli di entalpia:
Le variazioni di entalpia possono essere riferite sia alle reazioni chimiche che a tutte le
trasformazioni e quindi potremo avere vari tipi di entalpia a seconda della trasformazione
che prendiamo in considerazione:
Cap8-5
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
Entalpia di COMBUSTIONE: è la variazione di entalpia associata ad una reazione di
combustione cioè alla reazione di un qualsiasi composto organico con l'ossigeno per
formare anidride carbonica ed acqua.
Entalpia di LEGAME: è la variazione di entalpia associata al processo di rottura di un
legame in una specie allo stato gassoso: ci dà una misura della forza del legame.
Entalpia di ATOMIZZAZIONE: è la variazione di entalpia associata alla demolizione di una
specie allo stato gassoso per formare gli atomi che la costituivano.
Entalpia di SUBLIMAZIONE: è la variazione di entalpia associata alla trasformazione di un
cristallo di metallo in atomi di metallo allo stato gassoso
Entalpia di SOLUZIONE: è la variazione di entalpia associata alla dissoluzione di un soluto
in un solvente.
Entalpia di FUSIONE: è la variazione di entalpia associata alla trasformazione di un solido
in un liquido.
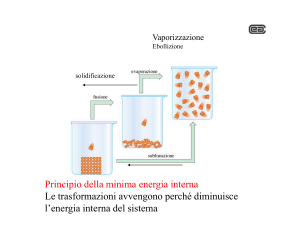
Secondo principio della termodinamica
La termodinamica si occupa anche di capire quando una determinata trasformazione
possa avvenire. La risposta a questo quesito ci viene data dalla seconda legge della
termodinamica che dice che durante una trasformazione spontanea il disordine
dell'universo aumenta.
Δ(Disord)universo > 0
Quindi per stabilire se una trasformazione possa o no avvenire spontaneamente dobbiamo
cercare di misurare il grado di disordine che essa porta all’intero universo e cioè sia al
sistema che all’ambiente. Questo sarà dato da:
Δ(Disord)universo = Δ(Disord)sistema + Δ(Disord)ambiente
Per definire il disordine del sistema è stata introdotta una funzione di stato che viene detta
entropia (S) che è proporzionale al numero di modi diversi in cui si possono disporre le
particelle del sistema (S = k lnW). Come tutte le funzioni di stato essa è una funzione
dello stato del sistema e non può essere quindi definita né per l'ambiente né per l'universo
dei quali non è definibile lo stato in quanto non sono descrivibili in maniera completa.
La descrizione del disordine dell’ambiente e la sua variazione è infatti molto più complicata
in quanto l’ambiente è qualcosa di infinito e quindi i cambiamenti che avvengono in esso
sono difficilmente misurabili. Poiché però la variazione di disordine che avviene
nell’ambiente come conseguenza di una trasformazione è dovuta alla trasformazione
stessa, che avviene nel sistema da noi considerato, possiamo cercare di mettere in
relazione la variazione del disordine dell’ambiente con la variazione delle funzioni di stato
del sistema in esame.
Il ruolo essenziale dell’ambiente, durante una trasformazione termodinamica, è quello di
fornire o sottrarre calore al sistema, fungendo da enorme “pozzo” di calore, così grande
che la sua temperatura rimane costante, anche se il suo disordine varia a causa della
cessione o dell’acquisto di calore. La variazione del disordine dell’ambiente è quindi
direttamente proporzionale alla quantità di calore trasferita dal o al sistema. Anche la
temperatura dell'ambiente prima del trasferimento di calore influenza il disordine
dell’ambiente. Consideriamo l'effetto di una reazione esotermica sull’ambiente che si trovi
Cap8-6
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
a una temperatura bassa o a una temperatura alta. A una temperatura bassa il
movimento casuale delle particelle nell'ambiente è molto ridotto, quindi l'ambiente è
relativamente ordinato. Perciò, il trasferimento di una certa quantità di calore all'ambiente
ha un grande effetto sul suo grado di ordine. A una temperatura più alta l'ambiente è già
relativamente disordinato, quindi il trasferimento della stessa quantità di calore ha un
effetto minore sul grado di ordine. In altre parole, la variazione di disordine dell'ambiente è
maggiore quando gli viene fornito calore a una temperatura più bassa. Perciò, riunendo
questi concetti, la variazione di disordine dell'ambiente è direttamente proporzionale al
calore ceduto dal sistema e inversamente proporzionale alla temperatura dell’ambiente.
Poiché l’ambiente è così grande che si può ammettere che durante tale trasformazione la
sua temperatura e la sua pressione rimangano costanti, possiamo descrivere la variazione
del disordine dell’ambiente in funzione della variazione di entalpia del sistema e della
temperatura.
Δ(Disord)ambiente = - ΔH/T
Potremo quindi descrivere la variazione totale del disordine dell'universo come la somma
della variazione di entropia del sistema più la variazione del disordine dell'ambiente e cioè:
Δ(Disord)universo = ΔS - ΔH/T
Questa relazione ci permette di calcolare la variazione totale del disordine dell’universo da
informazioni sul solo sistema.
Se modifichiamo questa equazione nel modo seguente:
-T x Δ(Disord)universo = ΔH - TΔS
possiamo introdurre una nuova funzione di stato, G detta energia libera di Gibbs, che non
è altro che l'espressione dell'ordine totale dell'universo, per cui:
-T x Δ(Disord)universo = Δ(Ord)universo = ΔG
e quindi:
ΔG = ΔH - T ΔS
Abbiamo visto che per la seconda legge le trasformazioni spontanee avvengono se
aumenta il disordine dell'universo il che equivale a dire, se diminuisce l'ordine dell'universo
stesso: poiché con G indichiamo l'ordine dell'universo, una trasformazione avverrà
spontaneamente se la G diminuisce e quindi se:
ΔG < 0
Questo succederà se il sistema aumenta il proprio disordine (ΔS > 0) o se si ha una
diminuzione dell'entapia del sistema (ΔH < 0) che comporta un aumento del disordine
dell'ambiente.
Esisterà quindi una semplice relazione fra il segno del ΔG associato ad una determinata
reazione e la spontaneità della stessa:
Se ΔG < 0 la reazione avviene spontaneamente da sinistra a destra
Se ΔG = 0 la reazione è all'equilibrio il che equivale a dire che la proporzione tra
reagenti e prodotti rimane invariata nel tempo.
Se ΔG > 0 la reazione non avviene spontaneamente da sinistra a destra ma da destra a
sinistra: perché avvenga la reazione da sinistra a destra dovremo compiere
un certo lavoro.
Cap8-7
Dispense CHIMICA GENERALE E ORGANICA (STAL)
2011/12
Prof. P. Carloni
Abbiamo visto come la funzione di stato energia libera sia la somma di altre due funzioni di
stato, l'entalpia e l'entropia: questi due termini rappresentano rispettivamente l'entropia
dell'ambiente (-ΔH/T) e l'entropia del sistema (ΔS). Andiamo ora ad analizzare come questi
due fattori influenzino la spontaneità dei processi.
Se entrambi questi fattori tendono ad aumentare l'entropia dell'universo (se ΔH < 0
ΔDisordambiente >0 e ΔS > 0) avremo un ΔG < 0 e quindi la trasformazione sarà spontanea.
Se entrambi questi fattori tendono a diminuire l'entropia dell'universo (se ΔH > 0
ΔDisordambiente <0 e ΔS < 0) avremo un ΔG > 0 e la reazione non sarà spontanea.
Quando i due fattori entropia del sistema (ΔS) ed entropia dell'ambiente (-ΔH/T) hanno
tendenze opposte la trasformazione avverrà solo in determinate condizioni e cioè quando
uno dei due fattori prevarrà sull'altro rendendo l'entropia totale dell'universo positiva. In
questi casi la temperatura avrà un ruolo importante nel favorire o sfavorire la spontaneità
della reazione. Nel caso in cui l'entropia del sistema è negativa (ΔS < 0) e l'entropia
dell'ambiente è positiva (ΔH < 0) la reazione avverrà spontaneamente solo quando |ΔH/T|
> |ΔS| e quindi a temperature basse. Nel caso opposto, entropia del sistema positiva (ΔS >
0) ed entropia dell'ambiente negativa (ΔH > 0), perché la reazione avvenga
spontaneamente dovremo fare in modo che sia |ΔH/T| < |ΔS| e quindi dovremo lavorare ad
alte temperature.
Ogni processo spontaneo può essere sfruttato per produrre lavoro: ad esempio l'acqua di
una cascata può servire a produrre energia elettrica, la combustione della benzina può
servire a far muovere un veicolo; ma il lavoro ricavabile dall'avvenire di una determinato
processo spontaneo dipende dal modo in cui tale processo viene fatto avvenire.
Ad esempio sappiamo che bruciando della benzina possiamo riuscire a far muovere un
veicolo: perché questo accada la combustione deve però avvenire all'interno di un
apposito macchinario perché se bruciassimo benzina in un recipiente aperto non si
produrrebbe nessun lavoro.
Nella pratica comunque noi non otteniamo mai la massima quantità di lavoro che si
potrebbe produrre da un qualsiasi processo spontaneo: la funzione energia libera di Gibbs
ci permette di calcolare il lavoro massimo ottenibile da un processo spontaneo: infatti a
temperatura e pressione costante il massimo lavoro ottenibile da un processo spontaneo è
uguale alla variazione di energia libera che si ha durante il processo.
Nel caso opposto, cioè nel caso di un processo non spontaneo, la funzione di Gibbs ci dà
la misura del minimo lavoro che dovremmo fare perché il processo possa avvenire: nella
realtà sarà però necessario investire una quantità di lavoro superiore a causa delle perdite
di efficienza del processo.
A questo punto è possibile dare una spiegazione realistica della funzione di Gibbs: essa
rappresenta la parte ordinata dell'energia interna di un sistema che può passare in uno
stato meno ordinato e quindi produrre lavoro.
Cap8-8