Esercizi di Fisica: lavoro ed energia – classe 3 BS
Esercizio 1 Un’automobile di massa 1500 kg parte da ferma e accelera per 5 s percorrendo 75 m. Calcola:
• la forza esercitata dal motore dell’auto; [9 · 103 N]
• il lavoro motore compiuto. [7 · 105 J]
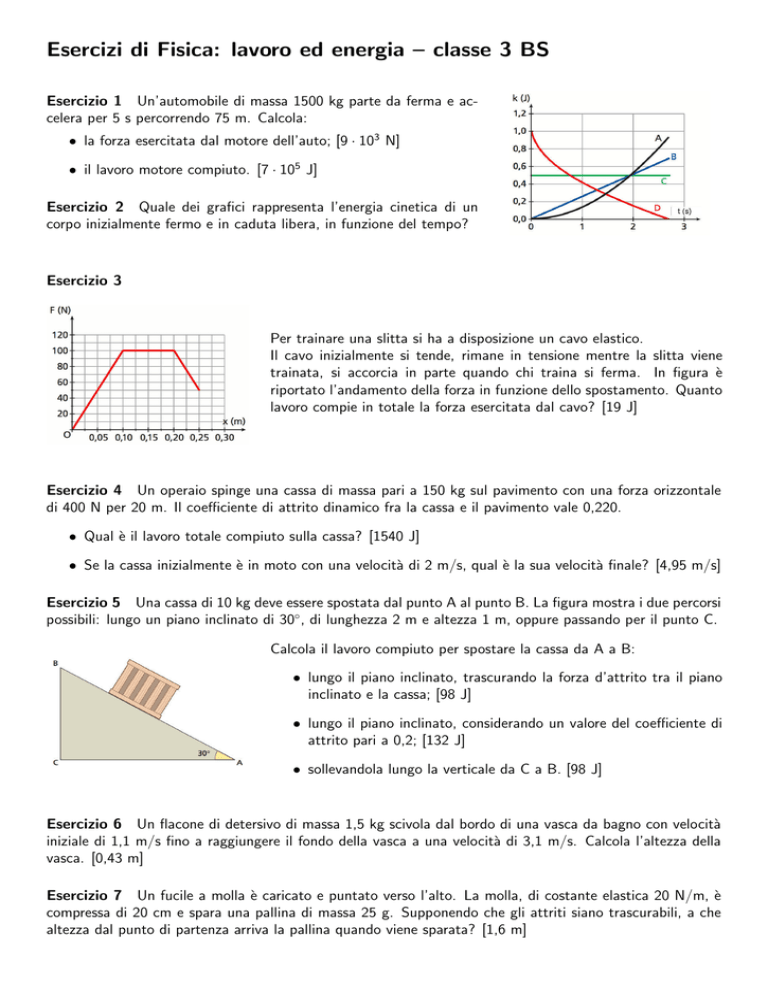
Esercizio 2 Quale dei grafici rappresenta l’energia cinetica di un
corpo inizialmente fermo e in caduta libera, in funzione del tempo?
Esercizio 3
Per trainare una slitta si ha a disposizione un cavo elastico.
Il cavo inizialmente si tende, rimane in tensione mentre la slitta viene
trainata, si accorcia in parte quando chi traina si ferma. In figura è
riportato l’andamento della forza in funzione dello spostamento. Quanto
lavoro compie in totale la forza esercitata dal cavo? [19 J]
Esercizio 4 Un operaio spinge una cassa di massa pari a 150 kg sul pavimento con una forza orizzontale
di 400 N per 20 m. Il coefficiente di attrito dinamico fra la cassa e il pavimento vale 0,220.
• Qual è il lavoro totale compiuto sulla cassa? [1540 J]
• Se la cassa inizialmente è in moto con una velocità di 2 m/s, qual è la sua velocità finale? [4,95 m/s]
Esercizio 5 Una cassa di 10 kg deve essere spostata dal punto A al punto B. La figura mostra i due percorsi
possibili: lungo un piano inclinato di 30◦ , di lunghezza 2 m e altezza 1 m, oppure passando per il punto C.
Calcola il lavoro compiuto per spostare la cassa da A a B:
• lungo il piano inclinato, trascurando la forza d’attrito tra il piano
inclinato e la cassa; [98 J]
• lungo il piano inclinato, considerando un valore del coefficiente di
attrito pari a 0,2; [132 J]
• sollevandola lungo la verticale da C a B. [98 J]
Esercizio 6 Un flacone di detersivo di massa 1,5 kg scivola dal bordo di una vasca da bagno con velocità
iniziale di 1,1 m/s fino a raggiungere il fondo della vasca a una velocità di 3,1 m/s. Calcola l’altezza della
vasca. [0,43 m]
Esercizio 7 Un fucile a molla è caricato e puntato verso l’alto. La molla, di costante elastica 20 N/m, è
compressa di 20 cm e spara una pallina di massa 25 g. Supponendo che gli attriti siano trascurabili, a che
altezza dal punto di partenza arriva la pallina quando viene sparata? [1,6 m]
Esercizio 8 Un ragazzo di massa 60 kg si lascia cadere in acqua da un trampolino alto 3 m. Calcola le
quantità mancanti nella tabella.
Esercizio 9 Un peso di massa 8 kg è appeso a un’altezza di 10 m dal suolo. Il filo che lo sostiene
all’improvviso si rompe e il peso cade, in assenza di forze esterne.
• Quanto vale la velocità acquistata quando si trova a 4 m dal suolo? [11 m/s]
• A che altezza si trova quando possiede una velocità di 6 m/s? [8,2 m]
Esercizio 10 Un pallone da pallacanestro, che ha massa 0,6 kg, viene lasciato cadere da fermo da un’altezza
di 1,30 m. Rimbalza al suolo e risale fino all’altezza di 0,8 m. Quanta energia meccanica si è dispersa (sotto
forma di calore) per attrito con l’aria e nel rimbalzo? [2,94 J]
Esercizio 11 Uno sciatore di 80 kg affronta un dosso alto 3,1 m alla velocita di 50 km/h. Durante la
salita, l’attrito con la neve e con l’aria trasforma 3300 J della sua energia meccanica in altre forme di energia.
Quanto vale la velocità dello sciatore quando raggiunge la sommità del dosso? [7 m/s]
Esercizio 12 Una biglia di massa 300 g viene attaccata ad una molla compressa di 10 cm e disposta
orizzontalmente. Lasciando il sistema libero, la biglia acquista una velocità di 4 m/s quando la molla ripassa
per la sua posizione di riposo. Qual è la costante elastica della molla? [480 N/m]
Esercizio 13 Un blocco di 4 kg si muove verso destra con una velocità di 3 m/s. Esso urta un blocco di
1 kg inizialmente fermo.
• Qual è la quantità di moto totale del sistema costituito dai due blocchi? [12 kg m/s]
• Calcola la velocità finale di ciascun blocco nel caso di urto elastico. [1,8 m/s, 4,8 m/s]
Esercizio 14 Un blocco di 4 kg si muove verso destra con una velocità di 3 m/s. Esso urta un blocco di
6 kg che si muove verso sinistra con una velocità di 2 m/s.
• Qual è la quantità di moto totale del sistema costituito dai due blocchi? [0 kg m/s]
• Calcola la velocità finale di ciascun blocco nel caso di urto elastico. [−3 m/s, 2 m/s]
Esercizi di Fisica: forza di gravità
Esercizio 1 Tre corpi allineati hanno massa rispettivamente mA = 90 kg, mB = 60 kg, mC = 30 kg. La
distanza AC misura 5 m.
a) Calcola modulo, direzione e verso della forza risultante sul corpo
B, se AB = 4 m.
b) Calcola quale posizione deve avere il corpo B se si vuole che la
forza risultante su di esso risulti nulla.
Suggerimento: chiama x la distanza AB, allora BC sarà 5 − x...
c) La distanza trovata al punto precedente dipende da mB , ovvero
cambierebbe se mB cambiasse?
[a) F = 9,76 · 10−8 N, verso destra; b) x = 52 (3 −
ovvero B esterno al segmento AC ; c) no...]
√
3) m ≃ 3,17 m oppure x = 52 (3 +
√
3) ≃ 11,83 m,
Esercizio 2 Ai vertici di un quadrato di lato 2 m sono posti quattro corpi di massa rispettivamente
mM = mP = mQ = 5 kg e mN = 10 kg.
a) Calcola modulo, direzione e verso della forza risultante sul corpo N.
Suggerimento: non è necessario scomporre le forze, poiché la forza di M su
N e la forza di P su N hanno lo stesso modulo e sono perpendicolari, quindi
la loro somma sarà diretta lungo la diagonale NQ...
b) Calcola modulo, direzione e verso della forza risultante al centro del quadrato,
se vi fosse posto un corpo O di massa mO = 1 kg.
Suggerimento: per simmetria la forza di M su O e la forza di P su O si
annullano...
[a) F = 1,60 · 10−9 N, diretta lungo NQ verso Q; b) F = 1,67 · 10−10 N, diretta lungo NQ verso N]
b misuri 120◦ . Le masse dei
Esercizio 3 Tre corpi sono disposti come in figura, in modo che l’angolo ABC
corpi sono rispettivamente mA = mC = 100 kg e mB = 10 kg; le distanze AB = BC misurano 5 m.
a) Calcola modulo, direzione e verso della forza risultante sul corpo
B.
b = 90◦ .
b) Ripeti l’esercizio nel caso in cui ABC
b la forza risultante
c) Secondo te, per quale ampiezza dell’angolo ABC
sul corpo B è massima?
[a) F = 2,67 · 10−9 N, diretta lungo l’asse di AC verso il basso; b) F = 3,77 · 10−9 N, diretta lungo l’asse
di AC verso il basso; c) ...]
Esercizio 4 Considera i dati relativi al periodo orbitale della Terra e alla sua distanza dal Sole. Il periodo
dell’orbita di Marte è di 686,98 d. Calcola la distanza media di Marte dal Sole. [2,29 · 1011 m]
Esercizio 5 Un satellite artificiale descrive un’orbita circolare con un raggio pari a quattro volte il raggio
terrestre. Calcola il suo periodo di rivoluzione. [4,06 · 104 s]
Esercizio 6 Un uomo ha una massa di 70 kg. Determina il suo peso a 20 000 m sul livello del mare.
Assumi come raggio della Terra 6400 km. [681,7 N]
Esercizio 7 A che distanza dalla superficie della Terra dovrebbe essere una persona, affinché il suo pesoi
dimezzi? [2651 km]
Esercizio 8 Se la Terra, mantenendo la stessa massa, avesse un raggio doppio di quello che ha in realtà,
come varierebbero la tua massa e il tuo peso? [...]
Esercizio 9 Sapendo che il periodo di rivoluzione della Luna attorno alla Terra è di 27,32 d e che il raggio
dell’orbita lunare è approssimativamente di 3,844 · 105 km, calcola la massa della Terra. [5,9 · 1024 kg]
Esercizio 10 Un satellite artificiale di massa pari a 24 kg viene portato su un’orbita di raggio pari a 50 · 106
m intorno alla Terra.
• Qual è la velocità con cui il satellite percorre la sua orbita? [[2,8 · 103 m/s]
• Quale sarebbe la velocità di un satellite di massa doppia? [...]
Esercizio 11 La distanza media Venere-Sole è di 1,1 · 108 km. Il periodo orbitale di Venere Il periodo
orbitale è di 224,70 d. Assumendo che l’orbita sia circolare, calcola:
• il modulo della velocità tangenziale di Venere; [3,6 · 104 m/s]
• il modulo della velocità angolare di Venere; [3,2 · 10−7 rad/s]
• la massa del Sole. [1, 99 · 1030 kg]
Esercizio 12 Due satelliti artificiali vengono messi in orbita. Il raggio dell’orbita del satellite più esterno è
4 volte quello dell’orbita del satellite più interno.
• Quale dei due satelliti compie un maggior numero di orbite in un dato intervallo di tempo? [...]
• Quante orbite completa il satellite più veloce nel tempo in cui il satellite più lento ne compie una? [8]
Esercizio 13 Un proiettile viene sparato dalla superficie terrestre verso l’alto con una velocità di 6 km/s.
Quale quota massima raggiunge? (utilizza per l’energia potenziale gravitazionale U = −GMT m/r e ricorda
che r non è la quota ma la distanza dal centro della Terra) [2570 km]
Esercizi di Fisica: moto parabolico
Esercizio 1 Un barista lancia sul bancone un boccale di birra ad un cliente che, momentaneamente distratto, non lo
vede arrivare. Sapendo che il bancone è alto 1,05 m e che il boccale di birra cade al suolo ad una distanza pari a 1,80
m dalla base del bancone, si determini:
a) il tempo di volo del boccale [0,46 s];
b) la velocità del boccale nell’istante in cui inizia a cadere dal bancone [3,89 m/s];
c) il modulo della velocità del boccale un attimo prima di giungere al suolo [5,98 m/s];
d) l’equazione cartesiana della traiettoria (dopo aver scelto un sistema di assi cartesiani) [y = 1,05 − 0,324x 2 ]
Esercizio 2 Luigi ha parcheggiato la sua auto lungo una discesa (θ = 10◦ ) posta sopra a una scogliera alta 12 m.
Purtroppo si è dimenticato di inserire la marcia e tirare il freno a
mano, quindi l’auto parte giù per la discesa. Sapendo che l’auto si
schianta a 10 m dalla base della scogliera (punto Z ), si determini:
a) il modulo della velocità con cui ha raggiunto la fine della
discesa (punto B) [7,03 m/s];
b) il tempo di volo [1,44 s].
Esercizio 3 Un ragazzo calcia un pallone con un angolo iniziale di 60◦ ; il grafico della traiettoria è il seguente:
Tenendo conto del fatto che la traiettoria passa
dal punto P(2; 3), determinare:
a) le componenti della velocità iniziale
[v0x = 6,5 m/s, v0y = 11,26 m/s];
b) il modulo della velocità dopo 2 s dal calcio
[10,57 m/s];
c) l’altezza massima raggiunta dal pallone
[6,47 m].
Esercizio 4 Una palla viene lanciata da un’altezza di 5 m con velocità iniziale di modulo v0 = 15 m/s ed avente un
angolo α = 60◦ rispetto all’orizzontale. Si determini:
a) il tempo di volo e il punto di impatto con il suolo [t = 2,99 s; x = 22,43 m];
b) l’altezza massima raggiunta [13,61 m];
c) il modulo della velocità un attimo prima di giungere al suolo [17,95 m/s].
Esercizio 5 Durante il servizio un tennista cerca di colpire la pallina orizzontalmente.
a) Qual è la velocità minima v0 che deve essere
impressa alla pallina (colpita a 2,5 m di altezza) per superare la rete alta 90 cm, posta
a 12 m di distanza dal tennista? [21 m/s]
b) Dove cadrà la palla, se sfiora la rete? [15 m]












