I MUSCOLI
I MUSCOLI
I MUSCOLI
La specializzazione delle cellule muscolari è quella di contrarsi: tutte le funzioni muscolari sono realizzate dalla contrazione
coordinata delle cellule muscolari. Il meccanismo della contrazione è basato sull’interazione dei filamenti proteici di actina e
miosina.
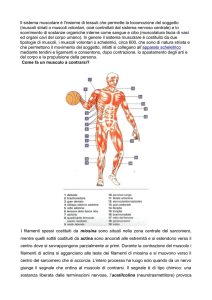
Ci sono due tipi principali di tessuto muscolare, il muscolo striato, che ha un aspetto a bande, ed il muscolo liscio (senza
striature)
Il tessuto muscolare liscio circonda le pareti degli organi interni, come gli organi dell’apparato digerente, l’utero, la vescica, i vasi
sanguigni etc. I muscoli che muovono lo scheletro sono muscoli striati e sono talvolta detti volontari.
Il muscolo cardiaco, che costituisce la parete del cuore, è un particolare tipo di muscolo striato.
Il tessuto muscolare liscio e quello cardiaco non sono, tranne in rari casi, sotto un diretto controllo volontario, e sono pertanto
classificati come involontari.
Circa il 40% del peso corporeo di un uomo (20% nella donna) è costituito da muscolo striato scheletrico. Un muscolo scheletrico è
tipicamente collegato a due o più ossa, sia direttamente sia, più spesso, indirettamente mediante tendini, costituiti da robuste
strisce di tessuto connettivo. Alcuni tendini, come quelli che collegano le ossa delle dita ai rispettivi muscoli dell’avambraccio,
possono essere molto lunghi.
Tipicamente, quando il muscolo si contrae, le ossa cui è collegato si muovono intorno a un’articolazione [...].
La maggior parte dei muscoli scheletrici che fanno capo ad un articolazione lavorano in coppie antagoniste, in cui un muscolo
flette e l’altro estende.
Inoltre, gruppi di coppie antagoniste possono contrarsi insieme per stabilizzare un’articolazione (es: mantenimento della postura
eretta). [...]
Anche le cellule del muscolo liscio contengono actina e miosina, ma le molecole non sono assembate in maniera regolare e non
hanno un aspetto striato. Le cellule del muscolo liscio sono fusiformi e mononucleate. Dal punto di vista funzionale il muscolo
liscio si contrae molto meno rapidamente di quello scheletrico e le sue contrazioni sono più prolungate, ed in genere non sono
sotto controlo volontario. In gran parte degli organi cavi, come l’intestino, le fibre del muscolo liscio sono sono organizzate in
strisce disposte su due strati, uno esterno longitudinale ed uno interno circolare, che possono contrarsi alternativamente (simile al
meccanismo che consente il moto del lombrico). Negli organi interni dei vertebrati le variazioini di diametro e di forma,
provocate dalla contrazione alternata delle due serie di muscoli, vengono utilizzate per per spingere i liquidi o i materiali
semisolidi (come il cibo) lungo questi organi. Nei vasi sanguigni i fasci di fibre muscolari lisce che circondano le pareti
contribuiscono al controllo del flusso sanguigno ed alla regolazione della pressione.
Helena Curtis – N.Sue Barnes, “Biologia”, Zanichelli, 3ed, 1994
I MUSCOLI
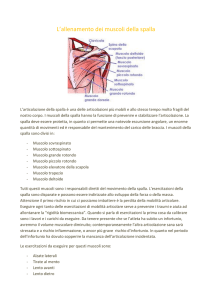
I muscoli scheletrici striati sono gli organi deputati alla generazione delle forze
impiegate per il movimento. Dal punto di vista meccanico sono dunque elementi
attivi, costituiscono gli “attuatori” dell’apparato muscolo-scheletrico.
I muscoli sono giuntati ai segmenti ossei dello scheletro per mezzo dei tendini, che
dal punto di vista meccanico sono elementi passivi, così come le ossa.
La parte centrale del muscolo è
denominata ventre muscolare e
rappresenta la parte carnosa,
costituita da fibre muscolari, vasi
sanguigni, tessuto connettivo. Le parti
terminali del muscolo vengono
generalmente definite origine e
inserzione.
• Origine è il punto di terminazione
del muscolo allo scheletro, che si trova
più vicino al tronco (o meno mobile).
• Inserzione rappresenta invece il
punto di fissazione allo scheletro più
distante dal tronco (o più mobile).
punti di origine
ventre muscolare
punto di inserzione
Esempio in figura: muscolo bicipite brachiale.
punti di origine: tubercolo sopraglenoideo (Capo lungo) e apice del processo coracoideo della scapola
punto di inserzione: tuberosità del radio
I MUSCOLI
La denominazione dei muscoli è molto varia e può
ad esempio riferirsi:
alla forma (muscoli lunghi, brevi, anulari e larghi,
oppure…muscolo deltoide, muscolo quadrato dei
lombi, muscolo romboide, muscolo trapezio ecc.);
all'azione che essi svolgono (muscoli flessori,
muscoli estensori, muscoli pronatori, muscoli
adduttori, muscoli abduttori ecc.);
alla forma e alla funzione (muscolo pronatore
rotondo, muscolo pronatore quadrato);
all'organo servito (muscoli laringei, muscoli
esofagei, muscoli gastrici);
alle ossa alle quali sono inseriti (muscoli tibiali,
muscoli peronieri);
al numero dei capi d'inserzione (bicipiti, tricipiti,
quadricipiti) o alla loro direzione (obliqui, retti,
trasversi).
I MUSCOLI
bicipite brachiale
•flessione del gomito
•supinazione della mano
brachiale
•flessione del gomito
I MUSCOLI - Classificazione in base ai punti di origine e di inserzione
Classificazione in base ai punti di origine
• muscoli monocipiti: sono quelli che hanno un solo punto di
origine
• muscoli bicipiti: sono quelli che hanno due punti di origine
• muscoli tricipiti: sono quelli che hanno tre punti di origine
• muscoli quadricipiti: sono quelli che hanno quattro punti
di origine
Classificazione in base ai punti di inserzione:
• muscoli monocaudati: sono quelli che hanno un solo punto
di inserzione.
• muscoli bicaudati: sono quelli che hanno due punti di
inserzione.
• muscoli tricaudati: sono quelli che hanno tre punti di
inserzione.
• muscoli pluricaudati: sono quelli che hanno più punti di
inserzione.
I MUSCOLI - Classificazione in base ai punti di origine e di inserzione
bicipite brachiale
tricipite brachiale
tricipite della sura
quadricipite femorale
I MUSCOLI - Classificazione in funzione della disposizione delle fibre
Muscoli a fasci paralleli
• Muscoli fusiformi: sono
quelli che hanno fasci muscolari
pressoché paralleli tra di loro e
che si fanno convergenti su un
tendine in corrispondenza di
una o di entrambe le estremità
•Muscoli nastriformi: sono
quelli che hanno fasci muscolari
organizzati parallelamente fra
di loro da una estremità all'altra
•Muscoli larghi: sono quelli che
fusiforme
unipennato
multipennato
bipennato
hanno fasci muscolari piatti che
si fondono con le aponeurosi
alle estremità
•Muscoli a ventaglio: sono quelli in cui i fasci muscolari divergono in corrispondenza di una
estremità e convergono su un tendine di inserzione all'altra estremità
Muscoli a fasci obliqui o pennati
• Muscoli pennati: sono quelli che hanno un tendine centrale sul quale vanno a confluire e a tendersi le fibre
muscolari
• Muscoli semipennati: sono quelli che hanno due lamine tendinee fra le quali sono tese le fibre muscolari
• Muscoli pluripennati: sono quelli che hanno molti tendini di origine sui quali vanno a confluire e a tendersi le
fibre muscolari
La disposizione delle fibre è associata alla funzione del muscolo: i muscoli veloci sono solitamente a fasci paralleli, quelli
forti pennati.
I MUSCOLI - STRUTTURA
I MUSCOLI – FIBRA MUSCOLARE (o miocita o miocellula)
MUSCOLO
(epimisio)
FASCICOLI
(perimisio)
FIBRE MUSCOLARI
(endomisio)
Le fibre muscolari sono cellule fusiformi (diametro ≈10 ÷ 100µm) polinucleate che si
estendono da un capo all’altro del muscolo o solo in parte di esso, e terminano in
tessuto tendineo o connettivo. Le fibre sono raggruppate in fasci e fascicoli per mezzo
di tessuti connettivi. La membrana che avvolge la singola cellula-fibra, il sarcolemma
(analogamente alla membrana assonica), consente la propagazione del potenziale
d’azione (il “segnale elettrico”) che attiva la contrazione. La massa delle fibre muscolari
è 75% acqua e 25% proteine (solubili 30% , miosina 38%, actina 12%).
Tra gli altri elementi, all’interno della cellula sono presenti le miofibrille (80% in
volume della cellula), che costituiscono la parte contrattile vera e propria della cellula.
Le miofibrille sono costituite da una sequenza organizzata di strutture di filamenti
proteici (sarcomeri) che si ripete periodicamente.
I MUSCOLI – SARCOMERO
La miofibrilla è una sequenza periodica di strutture
elementari dette sarcomeri.
Il sarcomero è l’unità anotomo-funzionale elementare del
muscolo scheletrico. È costituito da una matrice regolare di
filamenti proteici (principalmente actina e miosina) disposti
in parallelo.
All’esame della miofibrilla al polariscopio si identificano le
zone diversamente colorate: il sarcomero è la porzione tra
due bande Z consecutive.
Lunghezza sarcomero: 2-3µm nei mammiferi
La linea M e la linea Z sono costituite da tessuto connettivo
CONTRAZIONE: la banda I e la banda H si accorciano (le
due linee Z si avvicinano), la banda A rimane inalterata.
Lunghezza sarcomero: 2-3mm nei mammiferi
I MUSCOLI – Unità motoria
L'unità motoria è costituita da un motoneurone e da tutte le fibre
muscolari da esso innervate. Dal punto di vista fisiologico è l'unità
funzionale minima dell'apparato neuromuscolare, infatti le fibre
muscolari appartenenti a una medesima unità si contraggono in
maniera sincrona, secondo la legge del "tutto o nulla".
In dettaglio l'unità motoria è composta dal corpo cellulare del
motoneurone, situato nel midollo spinale, dal suo assone (che è unito
ad altri in fasci a formare nervi periferici), dalle fibre muscolari
innervate dal medesimo assone e dalla giunzione neuromuscolare, che
permette le contrazione muscolare a seguito dell'impulso nervoso.
Il tipo di fibre muscolari appartenenti a una medesima unità è sempre
lo stesso (I, IIA o IIX) mentre il numero può variare di alcuni ordini di
grandezza. In muscoli di ridottissime dimensioni ma in cui è
necessario un controllo fine del movimento, come i muscoli estrinseci
degli occhi, un'unità motoria comprende al massimo 10-20 fibre,
mentre nei muscoli degli arti inferiori, deputati a movimenti ampi che
richiedono molta forza, possono arrivare ad un paio di migliaia (nel
gastrocnemio, ad esempio).
Nella contrazione muscolare l'ordine di attivazione delle unità motorie
è fisso: per prime vengono attivate le fibre di tipo I ("rosse"), capaci di
forza contrattile minore, e solo se necessario le fibre più grosse di tipo
II.
I MUSCOLI – Unità motoria
Helena Curtis – N.Sue Barnes, “Biologia”, Zanichelli, 3ed, 1994
I MUSCOLI – Meccanismo della contrazione
Il potenziale d’azione dell’assone del motoneurone si trasmette alla impulso nervoso raggiunge
la giunzione neuromuscolare, causa il rilascio di un trasmettitore che eccita chimicamente la
fibra muscolare, producendo un potenziale d’azione che percorre il sarcolemma (1- 3m/s) .
Tale variazione del potenziale elettrico del sarcolemma attiva un complesso fenomeno chimico
all’interno della cellula, che ha l’effetto di alterazione dei legami (cross bridges) della teste di
miosina con i filamenti di actina. Le teste tendono a compiere dei movimenti rotatori alternati e
compiere nuovi legami in posizioni più “avanzate”.
L’azione dei ponti non può essere sincrona, mentre alcuni tirano, altri si stanno appena
attaccando, altri staccando per spostarsi verso un nuovo sito di attacco. La forza di picco in
ogni momento riflette il numero medio di ponti attivi al momento.
L’effetto globale è una riduzione della lunghezza del sarcomero, che si traduce in una forza di
contrazione riscontrabile ai capi della fibra.
I MUSCOLI – Meccanismo contrattile
Rilassamento:
il rilassamento muscolare è completamente passivo, consiste nella cessazione di
produzione di forza e può o meno essere associato all’allungamento del muscolo, le fibre
muscolari sono incapaci di allungarsi autonomamente.
Forza contrattile:
è condizionata dal tipo di stimolo, dalla lunghezza del muscolo al momento dello
stimolo e durante la contrazione, dalla velocità alla quale il muscolo si contrae.
I muscoli possono essere indotti a contrarsi con mezzi naturali o artificiali
Artificialmente, lo stimolo può essere applicato direttamente al muscolo, oppure
indirettamente al nervo. Quando l’impulso è applicato al motoneurone tutte le fibre
innervate si attivano (tutte o nessuna), aumentare l’ampiezza dello stimolo non aumenta
l’intensità della risposta delle fibre.
Quando un singolo impulso adeguato è applicato all’intero muscolo questo si contrae
velocemente in uno spasmo. L’entità dello spasmo varia con il numero di fibre che
hanno risposto allo stimolo, e con l’ampiezza dell’impulso.
Nello spasmo, dopo un breve periodo di latenza, la forza comincia ad aumentare in
maniera iperbolica fino ad un picco (periodo di contrazione), quindi decresce più
lentamente fino a zero (periodo di rilassamento).
La forza esterna misurata nello spasmo è inferiore all’intera capacità contrattile del
materiale, a causa delle componenti viscoelastiche del tessuto muscolare. Al fine di
generare una contrazione un singolo impulso deve avere una certa intensità minima per
generare una contrazione.
I MUSCOLI – Meccanismo contrattile
Artificialmente un muscolo può essere stimolato con impulsi elettrici o chimici e la
singola stimolazione produce un evento contrattivo (twitch) della durata variabile
tra pochi ms fino a circa 150ms. L’inizio della contrazione è ritardato rispetto alla
stimolazione esterna (sia naturale che artificiale). Tale ritardo è detto periodo di
latenza.
I MUSCOLI – Meccanismo contrattile
Sperimentalmente si osserva che l’ampiezza e il tipo di forza contrattile sviluppata
dipendono dalla frequenza della stimolazione. Una serie di stimolazioni ripetute, con
frequenza inferiore a 6 Hz, produce contrazioni separate e distinguibili, con uguale
forza massima.
Al crescere della frequenza nascono effetti additivi e i twitch tendono a fondersi
(meccanismo della sommazione).
Il valore della forza generata a regime tende ad un limite, legato alla frequenza di
stimolazione. Per frequenze superiori a 60 Hz si ha saturazione (regime tetanico).
La forza generata dalle fibre muscolari dipende dalla frequenza di stimolazione.
Al disopra di 100 Hz, un ulteriore aumento della
frequenza ha un effetto trascurabile sul valore
della forza generata. È interessante notare come
la frequenza di stimolazione corrispondente al
regime tetanico, sia molto vicina alla frequenza
elettrica di rete negli usi domestici.
I dati presentati nella figura, provenienti dagli
esperimenti di A.V. Hill, sono stati ottenuti in
condizioni isometriche, cioè con il muscolo
vincolato a lunghezza costante.
I MUSCOLI – Meccanismo contrattile
tetano completo
tetano incompleto
tetano incompleto
scossa muscolare semplice
I MUSCOLI – Valutazione del comportamento meccanico
Il ricercatore A.V. Hill (premio Nobel per la medicina e fisiologia nel 1922) dedicò parte della
sua attività scientifica alla comprensione del comportamento meccanico dei muscoli, ed i
risultati del suo lavoro sono alla base dei modelli meccanici usati ancora oggi.
I parametri rilevanti per la descrizione del comportamento meccanico sono forza,
lunghezza e spostamento. Nella realtà fisica sono presenti innumerevoli situazioni
con diversi valori di forza esterna, condizioni di vincolo, esigenze cinematiche. Nei
suoi esperimenti Hill definì alcune “trasformazioni” tipiche:
• Contrazione Isometrica . Si ottiene fissando le estremità del complesso muscolo
tendineo.
• Contrazione Isotonica.Uno dei capi del muscolo-tendine è fisso all’altro è applicata una forza
costante, ad esempio un peso.
• Contrazione libera. Uno degli estremi è fisso, l’altro è libero e privo di carichi. È un
particolare caso di contrazione isometrica.
• Rilascio rapido (quick release). Si tratta di una trasformazione ottenuta combinando
le prime due. Il muscolo è prima portato all’eccitazione tetanica in condizioni isometriche
con un’opportuna stimolazione, quindi è rilasciato uno degli estremi, al quale è applicato un
carico costante.
I MUSCOLI – contrazione ISOMETRICA ed ISOTONICA
I MUSCOLI – contrazione ISOMETRICA
I MUSCOLI – contrazione ISOTONICA
I MUSCOLI – CONTRAZIONE ISOMETRICA
Negli esperimenti di Hill, i risultati di una serie di contrazioni isometriche
mostrarono che la forza tetanica sviluppata dipendeva dalla lunghezza con una
legge approssimativamente parabolica. La figura rappresenta quest’andamento
riferito a un singolo sarcomero. La lunghezza sulle ascisse è riportata sia in termini
assoluti che relativi, mentre in ordinate abbiamo il rapporto tra la forza generata e
quella massima, in percentuale. Si può osservare che la lunghezza massima del
muscolo giunge a circa 1.8 il valore a riposo, quella minima a 0.6. Alla luce della
teoria dei filamenti scorrevoli si riesce a dare una giustificazione qualitativa della
forma della curva. Se assumiamo che la forza generata durante la contrazione sia
proporzionale al numero delle teste dei filamenti di actina e miosina che possono
interagire, è evidente che, in mancanza di sovrapposizione, la forza generata è nulla
(situazione D). Quando nasce una sovrapposizione dei filamenti per scorrimento
relativo, la forza generata aumenta. Questo incremento ha termine quando la
sovrapposizione è completa, per giungere a un massimo di forza, nella regione
comunemente chiamata plateau region. Se il muscolo continua a contrarsi, la forza
riprende a diminuire, per annullarsi completamente quando i due filamenti contigui
di actina cominciano a sovrapporsi. Il diagramma presentato si riferisce a condizioni
di eccitazione tetanica, riporta quindi per ogni valore della lunghezza del sarcomero
la forza massima che il muscolo può produrre.
I MUSCOLI – CONTRAZIONE ISOMETRICA (Relazione forza/lunghezza del sarcomero)
Tensione - % del valore massimo
Gli esperimenti di Hill hanno permesso di valutare la forza massima che può esprimere una
fibra muscolare in funzione della sua lunghezza. Condizioni sperimentali: contrazione
isometrica, stimolazione tetanica. Il grafico in figura riporta la forza normalizzata rispetto alla
forza massima misurata F/Fmax (sarcomero) .
L0 = lunghezza del muscolo a riposo, L = lunghezza del muscolo durante la singola prova
Se il muscolo viene stimolato alla sua lunghezza “naturale” esso sviluppa la forza maggiore. Se
le fibre sono troppo estese o troppo compattate non riescono ad esprimere tutta la forza
potenzialmente erogabile. Una possibile giustificazione lega la forza massima al numero di cross
bridges che riescono a formarsi all’interno dei sarcomeri: con il crescere dell’allungamento della
fibra si ha una riduzione del grado sovrapposizione dei filamenti di actina e miosina con
conseguente riduzione del numero teste di miosina in grado di creare i legami utili. Viceversa,
quando le fibre si accorciano troppo, l’interferenza tra i filamenti proteici ne ostacolerebbe lo
scorrimento.
100%
C
80%
B
60%
D
40%
20%
A
E
0.6
1
1.8
L/L0
1.2µm
2µm
3.6µm
L
Lunghezza del sarcomero (assoluta e relativa alla lunghezza di riposo)
I MUSCOLI – CONTRAZIONE ISOMETRICA (Effetto della rigidezza sulla forza totale)
Le prove per ottenere i punti sperimentali alla destra di L/L0 =1 sono condotte su muscoli con
lunghezza iniziale maggiore di quella di riposo: occorre sottoporre il muscolo ad una forza di
trazione per portarlo alla lunghezza voluta (forza passiva).
Durante gli esperimenti la forza realmente misurata è la forza totale. Per ottenere la forza
relativa alla sola forza imputabile al sarcomero occorre sottrarre la forza passiva.
La forza passiva ha un andamento tipicamente non lineare, a causa delle caratteristiche non
lineari del tessuto connettivo presente nel muscolo.
F = Fpassiva
F = Fpassiva + Fattiva
F=0
L = L0
L > L0
L > L0
I MUSCOLI – QUICK RELEASE (relazione forza / velocità di contrazione)
F=0
F = Mg
F = Fmax
Lf
Li
S: tensione sviluppata dal muscolo;
v: velocità di contrazione;
S0: tensione isometrica massima;
a, b: costanti con dimensioni rispettivamente di forza e velocità.
Se nell’equazione precedente si pone v = 0 si ottiene:
(S+a) ∗ b = (S0+a) ∗b S= S0. (4.5.2)
Se si pone S = 0 si ha invece:
a ∗ (v+b) = (S0+a) ∗b
∗ v=S0 ∗ b
a = v0. (4.5.3)
Poiché S0 e v0 sono determinabili sperimentalmente come la
massima tensione isometrica
a velocità nulla e la massima velocità di contrazione a forza
nulla, possiamo
ottenere il rapporto a/b dalla (4.5.3). Vedremo in seguito come
giungere al valore
delle due costanti.
Li
M
M
M
V = (Lf – Li)/Δt
I MUSCOLI – EQUAZIONE DI HILL
Hill sintetizzò i dati sperimentali raccolti nelle prove descritte in precedenza nella formula:
S: tensione sviluppata dal muscolo;
v: velocità di contrazione;
S0: tensione isometrica massima (dipende da L0);
a, b: costanti con dimensioni rispettivamente di forza e
velocità.
(S + a) ⋅ (v + b) = (S0 + a) ⋅ b
v=0
S=0
(S + a) = (S0 + a)
a ⋅ (v + b) = (S0 + a) ⋅ b
S = S0
v=
(S0 + a) ⋅ b
S ⋅b
−b= 0
a
a
v=
S0 ⋅ b
= v0
a
v0
Poiché S0 e v0 sono determinabili
sperimentalmente come la massima
tensione isometrica a velocità nulla
e la massima velocità di contrazione
a forza nulla, possiamo ottenere il
rapporto a/b.
S0
I MUSCOLI – EQUAZIONE DI HILL (forma adimensionale)
È conveniente scrivere l’equazione di Hill in forma adimensionale:
(S + a) ⋅ (v + b) = (S0 + a) ⋅ b
(S0 + a)
(S + a)
(S + a)
(S + a) − b ⋅ (S + a)
(S − S)
v= 0
−b= 0
= b⋅ 0
(S + a)
(S + a)
(S + a)
(v + b) = b ⋅
S
S
S0 ⋅ 1 −
S0 ⋅ 1 −
S0
S0
v = b⋅
= b⋅
S S
S
a ⋅ 0 + 1
a ⋅ 1 + c ⋅
S0
S0a
ponendo
c=
S0
a
S
1 −
S0
v
=
v0
S
1 + c ⋅
S0
v0 =
S0 ⋅ b
a
v
1 −
v0
S
=
S0
v
1 + c ⋅
v0
Nella forma adimensionale le costanti
da determinare sono S0,v0, e c.
Queste costanti dipendono da numerosi fattori, come
la lunghezza iniziale del muscolo e altri parametri
chimico-fisici.
S0 (massima tensione isometrica) è legata a L0
(lunghezza del muscolo a riposo) da una legge
approssimativamente parabolica (si ottiene dalle
prove di contrazione isometrica).
v0 (massima velocità di accorciamento ) è
indipendente da L0 (con ragionevole
approssimazione), quindi si può ritenere in via
approssimata che a sia proporzionale ad S0, secondo
la (4.5.6), mentre
b = v0/c.
I valori di c variano nel campo
c = 1.2 ÷ 1.4 (per il muscolo scheletrico)
Ricavato quindi S0 sulla base di L0 e v0 da dati
sperimentali o valutazioni su dati esistenti in
letteratura, sarà possibile ottenere le costanti che
appaiono nelle due forme dell’equazione di Hill.
I MUSCOLI – EQUAZIONE DI HILL
(S + a) ⋅ (v + b) = (S0 + a) ⋅ b
v
S
= 1 −
S0
v0
S
1 + c ⋅
S0
forma classica
da determinare: S0, a, b
forma
adimensionale
da determinare: S0, v0, c
S0
prove di
contrazione isometrica
S0= f(L0)
v0
quick release
a carico nullo
v0 ≠f(L0)
c
altre prove, letteratura
a
c=
b
v0 =
S0
a
S0 ⋅ b
a
c = 1.2 ÷ 1.4
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI (sarcomero)
L’equazione di Hill descrive solo le proprietà attive del muscolo scheletrico durante il tetano. È
necessario un modello più completo per descrivere il comportamento del muscolo non
stimolato, o durante il singolo spasmo, o il fenomeno delle sovrapposizione delle onde: il più
conosciuto è il modello funzionale di Hill a 3 elementi.
CE: elemento contrattile
(rappresenta lo scorrimento dei filamenti
di actina-miosina dove l’attacco e distacco
dei ponti in risposta all’attivazione
produce una tensione attiva).
SE: elemento elastico in serie
(elasticità dei filamenti, bande Z e tessuto
connettivo. Può derivare anche dalla non
uniformità della lunghezza del
sarcomero).
PE: elemento elastico in parallelo
(elasticità del tessuto connettivo, delle
membrane cellulari, dei mitocondri e degli
strati collaginei).
L - lunghezza del sarcomero (fattore di scala → lunghezza del muscolo)
M - lunghezza del filamento di Miosina
C - lunghezza del filamento di Actina
2C+M - lunghezza massima del sarcomero (nessuna sovrapposizione Lmax)
Δ - sovrapposizione tra i filamenti
Lc - lunghezza di CE = 2C+M-Δ = Lmax - Δ
η - elongazione di SE
S - tensione su SE e CE
P - tensione su PE
T - tensione totale (fattore di scala → tensione nel muscolo)
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI (sarcomero)
Congruenza delle lunghezze
(*)
L = L c + η = 2C + M - ∆ + η = L max - ∆
Equilibrio dei carichi
T =S+P
Tensione elemento elastico in serie
S = S(η)
Tensione elemento elastico in parallelo
(
)
P = P + βP ⋅ e
*
α P (L −L* )
- βP
P * , L* stati di riferimento
Se si assume che l’equazione di Hill valga solo
per l’elemento contrattile (cioè che la v non
dipenda da η), dalla prima relazione e
dall’equazione di Hill, si può scrivere:
S (L ) − S
v = -L& = ∆& = b 0 C
S+a
L - lunghezza del sarcomero (fattore di scala → lunghezza del muscolo)
M - lunghezza del filamento di Miosina
C - lunghezza del filamento di Actina
2C+M - lunghezza massima del sarcomero (nessuna sovrapposizione Lmax)
Δ - sovrapposizione tra i filamenti
Lc - lunghezza di CE = 2C+M-Δ = Lmax - Δ
η - elongazione di SE
S - tensione su SE e CE
P - tensione su PE
T - tensione totale (fattore di scala → tensione nel muscolo)
La formula di Hill vale in condizioni eccitazione tetanica.
Se si effettuano gli stessi esperimenti con eccitazione a
frequenza minore, si misurano forze inferiori: si può
tenere conto di questo fatto introducendo una funzione
di attivazione, compresa tra 0 (stimolazione nulla) ed 1
(stimolazione tetanica), che va a moltiplicare S0 .
(*) Lmax= 2C+M, lunghezza del sarcomero alla sua massima estensione
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI (sarcomero)
La formula di Hill vale in condizioni eccitazione tetanica.
Se si effettuano gli stessi esperimenti con eccitazione a
frequenza minore, si misurano forze inferiori: si può
tenere conto di questo fatto introducendo una funzione
di attivazione f(t), compresa tra 0 (stimolazione nulla) ed
1 (stimolazione tetanica), che va a moltiplicare S0 .
f(t) ⋅ S0 (L C ) − S
v = -L& = ∆& = b
; 0 ≤ f(t) ≤ 1
S+a
In forma adimensionale diventa:
S
f(t) −
S0 ( LC )
v = ∆& = v 0 ⋅
S
1 + c ⋅
S
(
L
)
0
C
v0 = b ⋅
c=
S0 (L C )
a
massima velocità di accorciamento tetanica
S0 (LC )
a
Ricordando che L = Lc + η e considerando che η è qualche percento di L , si può assumere L ≈ Lc
Inoltre, se 2 ≤ L ≤ 2.2µm , la dipendenza da L risulta così piccola che si può scrivere:
S
f(t) −
S0
∆& = v 0 ⋅
S
1 + c ⋅
S0
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI (sarcomero)
Abbiamo 6 incognite (L, Δ, η, S, P, T) e 5 equazioni.
1
L = L c + η = 2C + M - ∆ + η
S = S(η)
)
P = P * + β P ⋅ e αP (L−L ) - β P
5
S
∆& = v 0 ⋅ f(t) −
S0
2 T =S+P
3
(
4
*
S
1 + c ⋅
S0
Per risolvere il problema indeterminato si puo procedere in due modi:
1. Definire la relazione tra S e P, ovvero la relazione che definisce come i due rami (CE+SE e
PE) si ripartiscono il carico.
2. Assumere L o T noti in ingresso al sistema
L
muscolo
L costante:
prova isometrica
T
T
muscolo
L
T costante:
prova isotonica
prova di quick release: prova isometrica + prova isotonica.
I due schemi funzionali permettono di caratterizzare i blocchi funzionali del
modello a tre elementi sulla base delle prove di quick release.
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI
Accenniamo il caso semplificato in cui
η = L - L max + ∆
1
L = L c + η = 2C + M - ∆ + η
1
2
T =S+P
3 S = S(η)
4 P = (P * + β P )⋅ e α
*
P (L − L )
- βP
L ≅ L0 ⇒ P ≅ 0
5 ∆& = v 0 ⋅ f(t) − S
S0
S
1 + c ⋅
S0
Rimangono 3 equazioni (n° 1, 3 e 5) e 4 variabili (L, Δ, η, S)
(Condizione di ingresso: Δ(0) = Δ0
Il sistema è determinato se si assume L in ingresso.
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI
Rimangono 3 equazioni (n° 1, 3 e 5) e 4 variabili (L, Δ, η, S)
(Condizione di ingresso: Δ(0) = Δ0
Il sistema è determinato se si assume L in ingresso.
L
muscolo
T
L costante:
prova isometrica
Eq.1
η = L - L max + ∆
Eq.3
S = S(η)
S
∆& = v 0 ⋅ f(t) −
S0
Eq.5
S
1 + c ⋅
S0
1. Si entra in eq.1 con L e Δ0 e si calcola η
2. Si entra con η in eq.3 e si trova S(η)
dell’istante iniziale
3. Con S(η) e f(t) – è ipotizzato un certo
grado di attivazione – si ricava v
(=dΔ/dt)
4. Si integra v (le condizioni iniziali sono
note) per trovare il nuovo valore di Δ
con il quale si ricolacola η con l’eq.1
(ritorno al punto 1)
Eseguendo il ciclo si ottiene il valore di S (=
T) in funzione del tempo
I MUSCOLI – MODELLO FUNZIONALE A TRE ELEMENTI
Rimangono 3 equazioni (n° 1, 3 e 5) e 4 variabili (L, Δ, η, S)
(Condizione di ingresso: Δ(0) = Δ0
Il sistema è determinato se si assume T in ingresso.
T
muscolo
L
T costante:
prova isotonica
Eq.1
η = L - L max + ∆
Eq.3
S = S(η)
S
∆& = v 0 ⋅ f(t) −
S0
Eq.5
S
1 + c ⋅
S0
1. Si assume un valore di S (= T)
2. Dalla relazione di eq.3, noto S, si
ricava η
3. Dalla relazione di eq.5, noto S ed il
grado di attivazione f(t) si ricava v
(=dΔ/dt).
4. Si integra v (le condizioni iniziali
sono note) per trovare il nuovo valore
di Δ.
5. con i valori di Δ del punto4 e di η del
punto2 si calcola L con l’eq.1 (ritorno
al punto 1)
Eseguendo il ciclo si ottiene il valore di L
in funzione del tempo