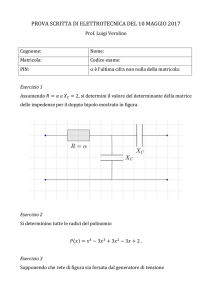
elettrotecnica_i - Aspiranti Ingegneri

Elettrotecnica I
Angelo Castiglione
15 giugno 2015
Indice
1
Cenni di elettromagnetismo
1.1
1.2
Operatori dierenziali
1.4
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Divergenza di un campo vettoriale
. . . . . . . . . . . . . . . . . .
13
1.1.2
Rotore di un campo vettoriale . . . . . . . . . . . . . . . . . . . . .
13
1.1.3
Teorema della divergenza
14
1.1.4
Teorema del rotore o di Stokes
. . . . . . . . . . . . . . . . . . . .
15
1.1.5
Teorema di Helmoltz . . . . . . . . . . . . . . . . . . . . . . . . . .
16
1.1.6
Gradiente di una funzione scalare . . . . . . . . . . . . . . . . . . .
16
Equazioni di Maxwell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.2.1
Forma locale delle leggi del campo elettromagnetico
. . . . . . . .
17
1.2.2
Forma globale delle leggi del campo elettromagnetico . . . . . . . .
21
. . . . . . . . . . . . . . . . . . . . . . .
~
per il vettore campo induzione dielettrica d
~
per il vettore campo induzione magnetica b
1.2.2.1
Legge di Gauss
1.2.2.2
Legge di Gauss
1.2.2.3
Legge di Faraday . . . . . . . . . . . . . . . . . . . . . . .
22
1.2.2.4
21
21
Legge di Ampere . . . . . . . . . . . . . . . . . . . . . . .
22
Condizioni di interfaccia . . . . . . . . . . . . . . . . . . . . . . . .
23
Proprietà dei materiali . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
1.3.1
Materiali lineari isotropi e lineari anisotropi . . . . . . . . . . . . .
25
1.3.2
Materiali non lineari
25
1.3.3
Dispersività dei materiali
1.3.4
Materiali chirali . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
1.3.5
Isteresi nei materiali
27
. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
Scomposizione del problema elettromagnetico
26
. . . . . . . . . . . . . . . .
28
1.4.1
Problema di campo di corrente statico . . . . . . . . . . . . . . . .
28
1.4.2
Problema di campo elettrostatico . . . . . . . . . . . . . . . . . . .
28
1.4.3
Problema di campo magnetostatico . . . . . . . . . . . . . . . . . .
29
1.4.4
Problema di campo quasi statico
29
. . . . . . . . . . . . . . . . . . .
Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.1
13
1.1.1
1.2.3
1.3
13
Problema di campo di corrente statico
30
. . . . . . . . . . . . . . . . . . . .
30
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
2.1.1
Introduzione
2.1.2
Riformulazione del problema di campo di corrente statico
2.1.3
Funzione armonica . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
2.1.4
Le condizioni al contorno
34
2.1.5
. . . . .
. . . . . . . . . . . . . . . . . . . . . . .
31
Dal problema di campo di corrente statico ai concetti di conduttanza e resistenza . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
36
Indice
2.1.6
Potenza dissipata dal resistore . . . . . . . . . . . . . . . . . . . . .
37
2.1.7
Applicazione: deduzione della seconda legge di Ohm
39
2.1.8
Generaltà sui resistori
. . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
Resistore lineare tempo-invariante
. . . . . . . . . . . . .
43
2.1.8.2
Resistore lineare tempo-variante
2.1.8.3
. . . . . . . . . . . . . .
44
Resistore non lineare tempo-invariante . . . . . . . . . . .
45
2.1.8.4
Resistore non lineare tempo-variante . . . . . . . . . . . .
45
2.1.8.5
Resistore controllato in corrente e resistore controllato in
tensione . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.8.6
2.1.8.7
Generatore ideale di tensione e generatore reale di tensione 47
Legge di Kirchoo delle tensioni (L.K.T.) . . . .
49
2.1.8.6.2
Resistori in serie e legge del partitore di tensione
50
2.1.8.6.3
Potenza istantanea assorbita e potenza istanta. . . . . . . . . . . . . . . . . . . .
Legge di Kirchoo delle correnti (L.K.I.) . . . . .
2.1.8.7.2
Resistori in parallelo e legge del partitore di cor-
2.1.8.7.3
Potenza istantanea assorbita e potenza istanta-
. . . . . . . . . . . . . . . . . . . . . . . .
nea generata
. . . . . . . . . . . . . . . . . . . .
Lato alla Thevenin e lato alla Norton
54
54
55
. . . . . . . . . . .
56
Problema di campo elettrostatico . . . . . . . . . . . . . . . . . . . . . . .
57
2.2.1
Introduzione
2.2.2
Riformulazione del problema di campo elettrostatico
2.2.3
Le condizioni al contorno
2.2.4
Metodo integrale per la risoluzione del problema di campo elettro-
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
. . . . . . . .
58
. . . . . . . . . . . . . . . . . . . . . . .
60
statico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
2.2.5
Dal problema di campo elettrostatico al concetto di capacità
. . .
63
2.2.6
Circuito del primo ordine RC: carica e scarica di un capacitore
. .
71
Generalità sui capacitori . . . . . . . . . . . . . . . . . . . . . . . .
73
2.2.7.1
73
2.2.7
Capacitore lineare tempo-invariante
2.2.7.1.1
. . . . . . . . . . . .
Energia immagazzinata da un capacitore lineare
tempo-invariante . . . . . . . . . . . . . . . . . .
2.2.7.2
Capacitore lineare tempo-variante
2.2.7.2.1
2.2.7.3
. . . . . . . . . . . . .
74
75
Energia immagazzinata da un capacitore lineare
tempo-variante . . . . . . . . . . . . . . . . . . .
76
Capacitore non lineare tempo-invariante . . . . . . . . . .
76
2.2.7.3.1
Energia immagazzinata da un capacitore non lin. . . . . . . . . . . . . . .
76
Capacitore non lineare tempo-variante . . . . . . . . . . .
eare tempo-invariante
77
Problema di campo magnetostatico . . . . . . . . . . . . . . . . . . . . . .
77
2.3.1
Introduzione
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
2.3.2
Riformulazione del problema di campo magnetostatico . . . . . . .
80
2.2.7.4
2.3
51
Generatore ideale di corrente e generatore reale di corrente 52
2.1.8.7.1
rente
2.1.8.8
46
2.1.8.6.1
nea generata
2.2
42
2.1.8.1
3
Indice
2.3.3
Metodo integrale per la risoluzione del problema di campo magnetostatico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
82
2.3.4
Legge dell'azione elementare . . . . . . . . . . . . . . . . . . . . . .
86
2.3.5
Strutture ferromagnetiche . . . . . . . . . . . . . . . . . . . . . . .
86
2.3.6
Coppia di induttori mutuamente accoppiati
97
2.3.7
Dispositivi a n bipoli e dispositivi n-polari . . . . . . . . . . . . . . 101
2.3.8
Induttore isolato
2.3.9
Circuito del primo ordine RL: carica e scarica di un induttore . . . 104
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
2.3.10 Generalità sugli induttori
2.3.10.1
. . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . 107
Induttore lineare tempo-invariante . . . . . . . . . . . . . 107
2.3.10.1.1
Energia immagazzinata da un induttore lineare
tempo-invariante . . . . . . . . . . . . . . . . . . 108
2.3.10.2
Induttore lineare tempo-variante . . . . . . . . . . . . . . 109
2.3.10.2.1
Energia immagazzinata da un induttore lineare
tempo-variante . . . . . . . . . . . . . . . . . . . 109
2.3.10.3
Induttore non lineare tempo-invariante
2.3.10.3.1
eare tempo-invariante
2.3.10.4
. . . . . . . . . . 110
Energia immagazzinata da un capacitore non lin. . . . . . . . . . . . . . . 110
Induttore non lineare tempo-variante . . . . . . . . . . . . 110
2.3.11 Generalità sulla coppia di induttori mutuamente accoppiati
2.3.11.0.1
. . . . 111
Energia immagazzinata dalla coppia di induttori
mutuamente accoppiati
. . . . . . . . . . . . . . 111
2.3.12 Trasformatore ideale . . . . . . . . . . . . . . . . . . . . . . . . . . 113
2.3.12.1
3
Proprietà del trasformatore ideale
Generatori pilotati e forme d'onda
3.1
3.2
Generatori pilotati
. . . . . . . . . . . . . 115
120
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
3.1.1
Generatore di corrente pilotato in corrente . . . . . . . . . . . . . . 120
3.1.2
Generatore di corrente pilotato in tensione . . . . . . . . . . . . . . 120
3.1.3
Generatore di tensione pilotato in corrente . . . . . . . . . . . . . . 121
3.1.4
Generatore di tensione pilotato in tensione . . . . . . . . . . . . . . 121
Forme d'onda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
3.2.1
Funzione costante . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
3.2.2
Sinusoide o cosinusoide . . . . . . . . . . . . . . . . . . . . . . . . . 122
3.2.3
Gradino unitario
3.2.3.1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
gradino unitario traslato . . . . . . . . . . . . . . . . . . . 123
3.2.4
Impulso di durata nita
3.2.5
Impulso di Diràc
. . . . . . . . . . . . . . . . . . . . . . . . 123
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
3.2.5.1
Impulso di Diràc traslato
. . . . . . . . . . . . . . . . . . 124
3.2.5.2
Proprietà del campionamento . . . . . . . . . . . . . . . . 124
3.2.5.3
Proprietà della delta di Diràc . . . . . . . . . . . . . . . . 125
3.2.6
Rampa unitaria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
3.2.7
Rampa parabolica
3.2.8
Doppietto . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
. . . . . . . . . . . . . . . . . . . . . . . . . . . 126
4
Indice
3.3
4
Proprietà dei segnali elettrici
. . . . . . . . . . . . . . . . . . . . . . . . . 127
3.3.1
Valore medio o componente continua . . . . . . . . . . . . . . . . . 128
3.3.2
Potenza media normalizzata . . . . . . . . . . . . . . . . . . . . . . 128
3.3.3
Energia media normalizzata . . . . . . . . . . . . . . . . . . . . . . 129
3.3.4
Valore ecace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
3.3.5
Segnali di potenza e segnali di energia
. . . . . . . . . . . . . . . . 130
Reti elettriche
131
4.1
Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
4.2
Scrittura delle L.K. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
4.3
Regime costante
4.3.1
Equazione dierenziale di ordine minimo per una variabile di rete . 136
4.3.1.1
4.3.2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
Ordine minimo dell'equazione dierenziale . . . . . . . . . 137
Risoluzione equazioni dierenziali . . . . . . . . . . . . . . . . . . . 139
4.3.2.1
Ricerca dell'integrale generale dell'omogenea associata . . 140
4.3.2.1.1
4.3.2.2
Rete elettrica priva di generatori . . . . . . . . . 142
Ricerca dell'integrale particolare dell'equazione dierenziale di ordine minimo . . . . . . . . . . . . . . . . . . . . 144
4.3.3
Esempio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
4.3.3.1
Ricerca dell'integrale generale dell'omogenea associata . . 146
4.3.3.2
Ricerca dell'integrale particolare
4.3.3.2.1
4.3.3.3
. . . . . . . . . . . . . . 146
Il signicato sico dell'integrale particolare
Determinazione delle costanti
. . . 146
k e ϕ mediante le condizioni
iniziali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
4.3.4
I controlli sulla correttezza dell'equazione dierenziale di ordine
minimo
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
4.4
Risposta transitoria e risposta permanente . . . . . . . . . . . . . . . . . . 151
4.5
Risposta con stato zero e con ingresso zero . . . . . . . . . . . . . . . . . . 152
4.6
Metodi integrali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
4.6.1
Integrale di convoluzione e risposta all'impulso
Signicato sico dell'integrale di convoluzione . . . . . . . 156
4.6.1.2
Dimostrazione dell'integrale di convoluzione . . . . . . . . 156
4.6.1.3
4.6.2
. . . . . . . . . . . 155
4.6.1.1
Metodo del bilanciamento delle funzioni singolari . . . . . 159
4.6.1.3.1
Le risposte all'impulso per un circuito elettrico . 163
4.6.1.3.2
Analisi energetica della rete . . . . . . . . . . . . 165
Integrale di Duhamel e risposta al gradino . . . . . . . . . . . . . . 166
4.6.2.1
Risposta al gradino
4.6.2.2
Integrale di Duhamel
. . . . . . . . . . . . . . . . . . . . . 166
4.6.2.3
Integrale di Duhamel nel caso di sollecitazione
. . . . . . . . . . . . . . . . . . . . 170
x (t)
dis-
continua in t=0 s . . . . . . . . . . . . . . . . . . . . . . . 171
4.6.2.4
4.7
Signicato sico dell'integrale di Duhamel . . . . . . . . . 172
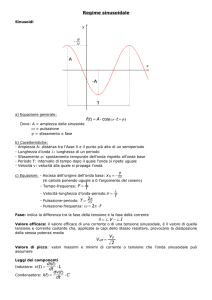
Regime sinusoidale
4.7.1
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
Ricerca dell'integrale particolare dell'equazione dierenziale di ordine minimo (metodo dei fasori)
5
. . . . . . . . . . . . . . . . . . . 174
Indice
4.7.2
Esempio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
4.7.2.1
4.7.3
4.7.4
4.7.5
Ricerca dell'integrale particolare
4.7.3.1
L.K.T. nel dominio dei fasori . . . . . . . . . . . . . . . . 180
4.7.3.2
L.K.I. nel dominio dei fasori
4.7.4.1
Resistore lineare tempo-invariante
4.7.4.2
Capacitore lineare tempo-invariante
4.7.4.3
Induttore lineare tempo-invariante . . . . . . . . . . . . . 182
4.7.4.4
Impedenza del bipolo elementare . . . . . . . . . . . . . . 182
4.7.4.5
Coppia di induttori mutuamente accoppiati . . . . . . . . 183
4.7.4.6
Trasformatore ideale . . . . . . . . . . . . . . . . . . . . . 183
4.7.4.7
Generatore ideale di tensione . . . . . . . . . . . . . . . . 183
4.7.4.8
Generatore ideale di corrente . . . . . . . . . . . . . . . . 184
Impedenza del bipolo composito
4.7.5.2
. . . . . . . . . . . . 181
. . . . . . . . . . . . . . . . . . . 184
Legge del partitore di tensione
. . . . . . . . . . 188
Impedenze in parallelo . . . . . . . . . . . . . . . . . . . . 189
4.7.5.2.1
Legge del partitore di corrente
. . . . . . . . . . 190
4.7.6
Rete elettrica nel dominio dei fasori
4.7.7
Potenza in regime sinusoidale . . . . . . . . . . . . . . . . . . . . . 193
. . . . . . . . . . . . . . . . . 190
4.7.7.1
La potenza media o attiva o reale P
4.7.7.2
La potenza reattiva Q . . . . . . . . . . . . . . . . . . . . 198
4.7.7.3
La potenza complesa
4.7.7.3.1
4.7.7.4
Ȧ
. . . . . . . . . . . . 193
. . . . . . . . . . . . . . . . . . . 198
La potenza apparente A.
Rifasamento
. . . . . . . . . . . . . 199
. . . . . . . . . . . . . . . . . . . . . . . . . 199
Circuiti del secondo ordine RLC a regime costante
5.1
Esempio 1. Circuito RLC serie
5.2
Esempio 2. Circuito RLC parallelo
204
. . . . . . . . . . . . . . . . . . . . . . . . 204
. . . . . . . . . . . . . . . . . . . . . . 207
Circuiti del secondo ordine RLC a regime sinusoidale
6.1
7
. . . . . . . . . . . . . 181
Impedenze in serie . . . . . . . . . . . . . . . . . . . . . . 188
4.7.5.1.1
6
. . . . . . . . . . . . . . . . 181
L.L. nel dominio dei fasori . . . . . . . . . . . . . . . . . . . . . . . 181
4.7.5.1
5
. . . . . . . . . . . . . . 179
L.K. nel dominio dei fasori . . . . . . . . . . . . . . . . . . . . . . . 180
Esempio. Circuito RLC serie
210
. . . . . . . . . . . . . . . . . . . . . . . . . 210
Metodi di analisi delle reti elettriche
7.1
Metodo dei potenziali ai nodi
7.1.1
. . . . . . . . . . . . . . . . . . . . . . . . . 214
Il concetto di grafo . . . . . . . . . . . . . . . . . . . . . . . . . . . 214
7.1.1.1
La matrice di incidenza totale nodi-lati
7.1.1.1.1
7.1.2
213
. . . . . . . . . . 215
matrice di incidenza nodi-lati . . . . . . . . . . . 216
Descrizione del metodo . . . . . . . . . . . . . . . . . . . . . . . . . 217
7.1.2.1
Trasformazione Thevenin-Norton . . . . . . . . . . . . . . 219
7.1.2.2
Regole di ispezione visiva
. . . . . . . . . . . . . . . . . . 221
[GN ] . .
[igN ]
7.1.2.2.1
Matrice delle conduttanze di nodi
7.1.2.2.2
Vettore colonna dei generatori di nodi
6
. . . 221
. . . 221
Indice
7.1.2.2.3
Esempio1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 222
7.1.2.4
Teorema di Millman . . . . . . . . . . . . . . . . . . . . . 224
7.1.2.5
Metodo dei potenziali ai nodi modicato
Esempio2 . . . . . . . . . . . . . . . . . . . . . . . . . . . 226
Modo poco furbo . . . . . . . . . . . . . . . . . 227
7.1.2.6.2
Modo furbo . . . . . . . . . . . . . . . . . . . . 227
La matrice di incidenza totale anelli-lati . . . . . . . . . . 231
7.2.1.1.1
Matrice di incidenza anelli-lati
. . . . . . . . . . 232
Descrizione del metodo . . . . . . . . . . . . . . . . . . . . . . . . . 233
7.2.2.1
7.2.3
. . . . . . . . . . . . . . . . . . . . . . . . 227
Elementi di teoria dei gra: il concetto di anello . . . . . . . . . . . 227
7.2.1.1
7.2.2
. . . . . . . . . 224
7.1.2.6.1
Metodo delle correnti di anello
7.2.1
. . . . . . . . . . . . . . . . . . . . . . 222
7.1.2.3
7.1.2.6
7.2
Consiglio
Regole di ispezione visiva
. . . . . . . . . . . . . . . . . . 237
[RA ]
7.2.2.1.1
Matrice delle resistenze di anello
. . . . . . 237
7.2.2.1.2
Vettore colonna dei generatori di anello
[vgA ]
. . 237
7.2.2.2
Esempio1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 238
7.2.2.3
Metodo delle correnti di anello modicato . . . . . . . . . 239
7.2.2.3.1
Modo poco furbo . . . . . . . . . . . . . . . . . 240
7.2.2.3.2
Modo furbo . . . . . . . . . . . . . . . . . . . . 240
Rete elettrica con coppia di induttori mutuamente accoppiati
. . . 241
7.3
Criterio per la scelta del metodo
7.4
Metodo degli insiemi di taglio . . . . . . . . . . . . . . . . . . . . . . . . . 243
7.4.1
. . . . . . . . . . . . . . . . . . . . . . . 242
Elementi di teoria dei gra: il concetto di albero e di insieme di
taglio fondamentale . . . . . . . . . . . . . . . . . . . . . . . . . . . 243
7.4.1.1
7.5
7.5.1
Elementi di teoria dei gra: il concetto di maglia
7.5.1.1
7.6
. . . . . . . 245
. . . . . . . . . . 249
La matrice di incidenza maglie fondamentali-lati
. . . . . 249
Esempi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 251
7.6.1
Esempio 1. Metodo delle correnti di maglia
7.6.2
Esempio 2. Metodo delle correnti di anello . . . . . . . . . . . . . . 254
7.6.3
Esempio 3. Metodo dei potenziali ai nodi
7.6.4
Esempio 4. Metodo delle correnti di maglia
7.6.5
Esempio 5. Metodo dei potenziali ai nodi
7.6.6
Esempio 6. Metodo delle correnti di maglia
. . . . . . . . . . . . . 251
. . . . . . . . . . . . . . 255
. . . . . . . . . . . . . 256
. . . . . . . . . . . . . . 257
. . . . . . . . . . . . . 259
7.7
Metodo delle equazioni di stato . . . . . . . . . . . . . . . . . . . . . . . . 260
7.8
Tecniche di integrazione numerica . . . . . . . . . . . . . . . . . . . . . . . 263
7.8.1
Metodo delle dierenze all'indietro
7.8.1.1
8
La matrice di incidenza insiemi di taglio-lati
Metodo delle correnti di maglia . . . . . . . . . . . . . . . . . . . . . . . . 249
. . . . . . . . . . . . . . . . . . 265
Esempio (rete elettrica a regime costante) . . . . . . . . . 266
7.8.2
Metodo delle dierenze all'avanti . . . . . . . . . . . . . . . . . . . 269
7.8.3
Metodo di Crank-Nicholson
. . . . . . . . . . . . . . . . . . . . . . 269
Reti elettriche in regime periodico non sinusoidale
8.1
270
Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
7
Indice
8.2
Analisi armonica: serie di Fourier . . . . . . . . . . . . . . . . . . . . . . . 271
8.2.1
Funzioni ortogonali e funzioni ortonormali . . . . . . . . . . . . . . 271
8.2.2
Insieme completo di funzioni
8.2.3
Teorema della rappresentazione dei segnali su base ortogonale . . . 273
8.2.4
Serie di Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274
8.2.4.1
8.3
9
. . . . . . . . . . . . . . . . . . . . . 272
Forma trigonometrica o cartesiana della seirie di Fourier . 275
8.2.5
Rappresentazione spettrale dei segnali periodici non sinusoidali
8.2.6
Energia media normalizzata di un segnale periodico non sinusoidale 278
8.2.7
Valore ecace di un segnale periodico non sinusoidale
Risposta a regime periodico non sinusoidale
. . 277
. . . . . . . 280
. . . . . . . . . . . . . . . . . 282
Teoremi sulle reti elettriche
289
9.1
Teorema di sostituzione
9.2
Sovrapposizione degli eetti . . . . . . . . . . . . . . . . . . . . . . . . . . 290
9.3
Teorema di Tellegen
9.2.1
9.4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 289
Esempio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 294
9.3.1
Teorema della conservazione della potenza istantanea . . . . . . . . 297
9.3.2
Tesi del teorema di Tellegen nel dominio dei fasori
9.3.3
Teorema di Boucherot o della conservazione della potenza
9.3.4
Tesi del teorema di Tellegen nel dominio di Laplace . . . . . . . . . 299
Teorema di Thevenin/Norton
. . . . . . . . . 298
. . . . . 298
. . . . . . . . . . . . . . . . . . . . . . . . . 300
9.4.1
Esempio 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309
9.4.2
Esempio 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314
9.5
Teorema di reciprocità . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315
9.6
Teorema del massimo trasferimento di potenza
9.5.1
Esempio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 322
. . . . . . . . . . . . . . . 325
10 Reti elettriche nel dominio di Laplace
10.1 Sommabilità di una funzione in
329
. . . . . . . . . . . . . . . . . . . . . . 329
R.
10.2 Trasformata di Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335
10.2.1 Denizioni . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335
10.2.2 Proprietà della trasformata di Laplace
. . . . . . . . . . . . . . . . 338
10.2.3 Trasformata di Laplace di alcune forme d'onda
10.2.3.1
. . . . . . . . . . . 341
Trasformata di Laplace del gradino . . . . . . . . . . . . . 341
10.2.3.1.1
Trasformata di Laplace del gradino traslato.
. . 342
10.2.3.2
Trasformata di Laplace della funzione sinusoidale . . . . . 342
10.2.3.3
Trasformata di Laplace della funzione cosinusoidale
10.2.3.4
Tabella delle trasformate di Laplace di alcune funzioni . . 343
10.2.4 L.K nel dominio di Laplace
. . . 343
. . . . . . . . . . . . . . . . . . . . . . 344
10.2.4.1
L.K.T. nel dominio di Laplace
10.2.4.2
L.K.I. nel dominio di Laplace . . . . . . . . . . . . . . . . 344
10.2.5 L.L. nel dominio di Laplace
. . . . . . . . . . . . . . . 344
. . . . . . . . . . . . . . . . . . . . . . 344
10.2.5.1
Resistore lineare tempo-invariante
10.2.5.2
Capacitore lineare tempo-invariante
8
. . . . . . . . . . . . . 344
. . . . . . . . . . . . 345
Indice
10.2.5.3
Induttore lineare tempo-invariante . . . . . . . . . . . . . 346
10.2.5.4
Impedenza del bipolo elementare . . . . . . . . . . . . . . 346
10.2.5.5
Coppia di induttori mutuamente accoppiati . . . . . . . . 347
10.2.5.6
Trasformatore ideale . . . . . . . . . . . . . . . . . . . . . 348
10.2.5.7
Generatore ideale di tensione . . . . . . . . . . . . . . . . 348
10.2.5.8
Generatore ideale di corrente . . . . . . . . . . . . . . . . 349
10.3 Antitrasformata di Laplace
. . . . . . . . . . . . . . . . . . . . . . . . . . 349
10.3.1 Il problema dell'antitrasformabilità . . . . . . . . . . . . . . . . . . 349
10.3.2 Proprietà dell'antitrasformata di Laplace . . . . . . . . . . . . . . . 351
10.3.3 Antitrasformata di Laplace delle funzioni razionali fratte . . . . . . 351
10.4 Risoluzione reti elettriche mediante trasformata di Laplace . . . . . . . . . 355
11 La teoria dei doppi bipoli
360
11.1 Il doppio bipolo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 360
11.1.1 Rappresentazione del doppio bipolo mediante la matrice delle impedenze e la matrice delle ammettenze . . . . . . . . . . . . . . . . 363
11.1.1.1
Matrice delle impedenze . . . . . . . . . . . . . . . . . . . 363
11.1.1.1.1
11.1.1.2
Esempio.
Matrice delle ammettenze . . . . . . . . . . . . . . . . . . 368
11.1.1.2.1
Esempio.
h i . h. . i. . . . . . . . . . . . . . . . . . . 371
11.1.2 Relazioni tra le matrice
11.1.2.1
Ż
Ẏ
e
. . . . . . . . . . . . . . . . . . 373
Passaggio dalla matrice delle impedenze
delle ammettenze
11.1.2.2
. . . . . . . . . . . . . . . . . . . . . . 365
h i
Ẏ
h i
Ż alla matrice
. . . . . . . . . . . . . . . . . . . . 373
Passaggio dalla matrice delle ammettenze
trice delle impedenze
h i
Ż
h i
Ẏ
alla ma-
. . . . . . . . . . . . . . . . . . 374
11.1.3 Rappresentazione del doppio bipolo mediante la matrice ibrida e
la matrice ibrida inversa . . . . . . . . . . . . . . . . . . . . . . . . 374
11.1.3.1
matrice ibrida
11.1.3.1.1
11.1.3.2
Proposizione. . . . . . . . . . . . . . . . . . . . . 377
matrice ibrida inversa
11.1.3.2.1
Ḣ
e
Ḣ
0
. . . . . . . . . . . . . . . . . 383
Passaggio dalla matrice ibrida
inversa
11.1.4.2
. . . . . . . . . . . . . . . . . . . . 378
Proposizione.
h i h . .i . . . . . . . . . . . . . . . . . . 380
11.1.4 Relazioni tra le matrice
11.1.4.1
. . . . . . . . . . . . . . . . . . . . . . . . 374
h
Ḣ
i
0
h i
Ḣ
alla matrice ibrida
. . . . . . . . . . . . . . . . . . . . . . . . . 383
Passaggio dalla matrice ibrida inversa
ibrida
h i
Ḣ
h
Ḣ
0
i
alla matrice
. . . . . . . . . . . . . . . . . . . . . . . . . . 383
9
Indice
11.1.5 Relazioni tra le matrici
11.1.5.1
h i
Ḣ
. . . . . . . . . . . . . . . 384
h i
Ż alla matrice
. . . . . . . . . . . . . . . . . . . . . . . . . . 384
h i
Ḣ
h i
Ż
alla ma-
h i
Ḣ
alla matrice delle im-
. . . . . . . . . . . . . . . . . . . . . . . . . 385
Passaggio dalla matrice ibrida
mettenze
h i
Ẏ
. . . . . . . . . . . . . . . . . . . . . . . 385
Passaggio dalla matrice ibrida
pedenze
11.1.5.4
h i
Ẏ
Passaggio dalla matrice delle ammettenze
trice ibrida
11.1.5.3
e
Passaggio dalla matrice delle impedenze
ibrida
11.1.5.2
h i h i
Ḣ , Ż
h i
Ẏ .
h i
Ḣ alla matrice delle am-
. . . . . . . . . . . . . . . . . . . . . . . . 386
11.1.6 Rappresentazione del doppio bipolo mediante la matrice di trasmissione e la matrice di trasmissione inversa . . . . . . . . . . . . . . . 387
11.1.6.1
matrice di trasmissione diretta
11.1.6.1.1
11.1.6.2
matrice di trasmissione inversa . . . . . . . . . . . . . . . 392
11.1.6.2.1
Proposizione.
h i h . i. . . . . . . . . . . . . . . . . . . 395
11.1.7 Relazioni tra le matrice
11.1.7.1
Ṫ
e
Ṫ
0
. . . . . . . . . . . . . . . . . . 395
Passaggio dalla matrice di trasmissione diretta
matrice di trasmissione inversa
11.1.7.2
11.1.8
. . . . . . . . . . . . . . . 387
Proposizione. . . . . . . . . . . . . . . . . . . . . 391
h
h i
Ṫ
11.1.8.3
11.1.8.4
h i
Ż alla matrice
. . . . . . . . . . . . . . . . . 396
h i
Ṫ
h i
Ż
h i
Ẏ
11.1.9 Simmetria di un doppio bipolo
h i
Ẏ
alla ma-
. . . . . . . . . . . . . . 397
h i
Ṫ
alla
. . . . . . . . . . . . . . . . 398
Passaggio dalla matrice di trasmissione diretta
matrice delle ammettenze
alla
. . . . . . . . . . . . . . . 396
Passaggio dalla matrice di trasmissione diretta
matrice delle impedenze
h 0i
Ṫ
. . . . . . . . . . . . . . . 396
Passaggio dalla matrice delle ammettenze
trice di trasmissione diretta
alla
. . . . . . . . . . . . 395
Passaggio dalla matrice delle impedenze
di trasmissione diretta
11.1.8.2
i
Passaggio dalla matrice di trasmissione inversa
h i
matrice diretta Ṫ
. . . . . .
h i h i h i
Relazioni tra le matrici Ṫ , Ż e Ẏ
11.1.8.1
Ṫ
0
h i
Ṫ
h i
Ṫ
alla
. . . . . . . . . . . . . . . 399
. . . . . . . . . . . . . . . . . . . . 400
11.1.9.1
Matrice delle impedenze . . . . . . . . . . . . . . . . . . . 400
11.1.9.2
Matrice delle ammettenze . . . . . . . . . . . . . . . . . . 400
10
Indice
11.1.9.3
11.1.9.4
Matrice ibrida
. . . . . . . . . . . . . . . . . . . . . . . . 401
Rappresentazione mediante la matrice di trasmissione diretta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 402
11.2 Impedenza in un doppio bipolo
. . . . . . . . . . . . . . . . . . . . . . . . 404
11.2.1 Impedenza a vuoto . . . . . . . . . . . . . . . . . . . . . . . . . . . 404
11.2.2 Impedenza iterativa
. . . . . . . . . . . . . . . . . . . . . . . . . . 405
11.2.3 Impedenza di cortocircuito
. . . . . . . . . . . . . . . . . . . . . . 405
11.2.4 Impedenza immagine . . . . . . . . . . . . . . . . . . . . . . . . . . 406
11.2.5 Impedenza caratteristica . . . . . . . . . . . . . . . . . . . . . . . . 406
11.2.6 Espressioni analitiche delle impedenze del doppio bipolo
. . . . . . 406
11.3 Il quadripo composito e il doppio bipolo composito . . . . . . . . . . . . . 410
11.3.1 Interconnessione serie-serie
. . . . . . . . . . . . . . . . . . . . . . 410
11.3.2 interconnessione parallelo-parallelo
. . . . . . . . . . . . . . . . . . 411
11.3.3 Interconnessione serie-parallelo
. . . . . . . . . . . . . . . . . . . . 411
11.3.4 Interconnessione parallelo-serie
. . . . . . . . . . . . . . . . . . . . 412
11.3.5 Interconnessione cascata . . . . . . . . . . . . . . . . . . . . . . . . 412
11.3.6 Il doppio bipolo composito . . . . . . . . . . . . . . . . . . . . . . . 412
11.3.7 Trasformazione stella-triangolo
. . . . . . . . . . . . . . . . . . . . 414
12 Linee di trasmissione
422
12.1 Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 422
12.2 Linea di trasmissione biconduttore
. . . . . . . . . . . . . . . . . . . . . . 422
12.3 Linea di trasmissione in regime transitorio . . . . . . . . . . . . . . . . . . 424
12.3.1 Equazioni dei telegrasti . . . . . . . . . . . . . . . . . . . . . . . . 424
12.3.2 Linea di trasmissione non distorcente . . . . . . . . . . . . . . . . . 429
12.3.2.1
Esercizio
. . . . . . . . . . . . . . . . . . . . . . . . . . . 438
12.3.3 Bilancio energetico per una linea di trasmissione
. . . . . . . . . . 439
12.4 Linea di trasmissione in regime sinusoidale . . . . . . . . . . . . . . . . . . 443
12.4.1 Rappresentazione fasoriale . . . . . . . . . . . . . . . . . . . . . . . 443
12.4.2 Equazioni dei telegrasti nel dominio dei fasori e parametri secondari della linea di trasmissione
. . . . . . . . . . . . . . . . . . . . 444
12.4.3 I parametri secondari nel caso di linea di trasmissione non distorcente452
12.4.4 Impedenza di linea e coecienti di riessione
12.4.5 Linea di trasmissione adattata
. . . . . . . . . . . . 453
. . . . . . . . . . . . . . . . . . . . 455
12.4.6 Rappresentazione della linea mediante la sintassi dei doppi bipoli . 456
12.4.6.1
Rappresentazione attraverso la matrice di trasmissione
diretta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 456
12.4.6.2
Rappresentazione attraverso la matrice di trasmissione
inversa
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 458
12.4.6.3
Rappresentazione attraverso la matrice delle impedenze
12.4.6.4
Rappresentazione attraverso la matrice delle ammettenze
12.4.6.5
Circuito equivalente a
12.4.6.6
Circuito equivalente a
12.4.6.7
Linea di trasmissione corta
11
T
Π
. 460
460
. . . . . . . . . . . . . . . . . . . 461
. . . . . . . . . . . . . . . . . . . 462
. . . . . . . . . . . . . . . . . 463
Indice
12.4.6.8
Impedenza di ingresso di una linea di trasmissione
. . . . 464
12.4.7 Linea di trasmisssione ideale . . . . . . . . . . . . . . . . . . . . . . 465
12.4.8 Potenze in regime sinusoidale
. . . . . . . . . . . . . . . . . . . . . 469
12.4.8.1
Linea di trasmissione non distorcente
. . . . . . . . . . . 471
12.4.8.2
Linea di trasmissione adattata
12.4.8.3
Linea di trasmissione ideale . . . . . . . . . . . . . . . . . 472
. . . . . . . . . . . . . . . 472
12.5 Linee di trasmissione in regime transitorio . . . . . . . . . . . . . . . . . . 472
12.6 Linee di trasmissione multiconduttori . . . . . . . . . . . . . . . . . . . . . 472
12.7 Applicazioni . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 472
13 Problema di campo quasi stazionario
473
14 Circuiti trifase
474
15 Cenni sulle macchine elettriche
475
16 Appendice A: Teoria delle distribuzioni
476
17 Appendice B: Trasformata di Fourier nel senso delle distribuzioni
477
18 Appendice C: Trasformata di Laplace nel senso delle distribuzioni
478
12
1 Cenni di elettromagnetismo
1.1 Operatori dierenziali
1.1.1 Divergenza di un campo vettoriale
Sia
f~ = f~ (x, y, z)
un campo vettoriale, si chiama
divergenza del campo vettoriale f~,
la somma delle derivate parziali delle componenti del campo rispetto alle coordinate
spaziali:
∂
∂
∂
div f~ =
fx +
fy +
fz
∂x
∂y
∂z
(1.1.1)
La divergenza di un campo vettoriale è uno scalare e si può anche scrivere mediante la
notazione:
div f~ = ∇ · f~
dove
∇
(1.1.2)
(nabla) è un operatore vettoriale simbolico denito come segue:
∇ = x̂
∂
∂
∂
+ ŷ
+ ẑ
∂x
∂y
∂z
(1.1.3)
1.1.2 Rotore di un campo vettoriale
Il rotore di un campo vettoriale
f~ si
denisce come segue:

x̂
ŷ
ẑ

rot f~ = ∇ × f~ = det 
∂
∂x
∂
∂y
∂
∂z

fx
fy
fz
Il rotore di un campo vettoriale
f~
(1.1.4)
è un vettore le cui componenti si individuano
trovando il determinante della matrice in
(1.4).
La componente lungo l'asse
~x
di
rot f~ è
dunque:
x̂
∂
∂
fz −
fy
∂y
∂z
Le altre componenti, cioè quelle lungo l'asse
per
permutazioni cicliche
~y
e l'asse
~z
di
degli indici: si tratta di trasformare
Pertanto la componente lungo l'asse
~y
è:
13
rot f~
x
in
si possono ottenere
y, y
in
z
e
z
in
x.
1 Cenni di elettromagnetismo
ŷ
∂
∂
fx −
fz
∂z
∂x
~z
mentre la componente lungo l'asse
In denitiva
rot f~ espresso
rot f~ = ∇ × f~ = x̂
è:
∂
∂
fy −
fx
∂x
∂y
ẑ
mediante le sue componenti è:
∂
∂
fz −
fy
∂y
∂z
+ ŷ
∂
∂
fx −
fz
∂z
∂x
+ ẑ
∂
∂
fy − − fx
∂x
∂y
(1.1.5)
1.1.3 Teorema della divergenza
Teorema 1.1. (della divergenza)
Sia f~ una funzione vettoriale denita in Ω ⊆ R3 , f~ : Ω ⊆ R3 → R3 , sia inoltre
0
f~ ∈ C (Ω); dunque f~ è un campo vettoriale. Indicando con ∂Ω la supercie chiusa di Ω
e con n̂ il versore normale uscente da ∂Ω si ha (Figura 1.1):
ˆ
˛
∇ · fˆ dΩ =
f~ · n̂ d∂Ω
Ω
Possiamo dare un signicato sico alla divergenza di un campo vettoriale
P (x, y, z)
(1.1.6)
∂Ω
f~ in un punto
dello spazio.
Si consideri un punto
esso e chiamiamo
∂Ω
P (x, y, z)
dello spazio e si consideri un volumetto
la sua supercie.
usso del campo vettoriale
f~ attraverso
˛
Se
f~
Ω
attorno ad
è un campo vettoriale si può calcolare il
la supercie
∂Ω
:
f~ · n̂ d∂Ω
∂Ω
Alla quantità:
¸
lim
Ω→0
si dà il nome di
ˆ · n̂ d∂Ω
∂Ω f
Ω
= div f~ (P )
divergenza del campo vettoriale f~ nel punto P (x, y, z).
Figura 1.1.1: dominio di analisi
14
(1.1.7)
1 Cenni di elettromagnetismo
1.1.4 Teorema del rotore o di Stokes
Teorema 1.2. (del rotore o di Stokes )
Sia f~ un campo vettoriale e sia S una supercie bilatera (è una supercie con due
faccie e un orlo, Figura 1.2). Supponiamo di orientare una delle due faccie della supercie bilatera S mediante un versore normale n̂. Sia Γ l'orlo della superce bilatera S,
orientatom concordemente al versore n̂ secondo la regola della mano destra.
~ il tratto elementare orientato dell'orlo Γ si ha:
Se indichiamo con dΓ
˛
ˆ
∇ × f~ dS =
~
f~ · dΓ
(1.1.8)
Γ
S
Figura 1.1.2: Supercie bilatera
Possiamo dare un signicato sico pure al rotore di un campo vettoriale
P (x, y, z)
dello spazio.
Si consideri un punto
il punto
P
P
dello spazio e si consideri una supercie
S
avente come centro
(si noti che una circonferenza nello spazio si può orientare in inniti modi).
n̂
A questo punto si ssa un versore normale
della mano destra con la normale
lungo
f~ in un punto
n̂
e si orienta l'orlo
Γ
di
S
secondo la regola
in modo che si possa calcolare la circuitazione di
f~
Γ:
˛
~
f~ · dΓ
Γ
A questo punto come fatto con la divergenza si potrebbe pensare al rotore di un campo
vettoriale
f~ in
un punto
P (x, y, z)
dello spazio come:
¸
lim
~ · dΓ
~
Γf
(1.1.9)
S
S→0
Però quest'ultimo limite restituisce un numero che dipende dal come è stata orientata
la supercie
S
nello spazio.
Per eetto di questa dipendenza, il modulo di
∇ × f~
si
denisce come segue:
(¸
~ ~
Γ f · dΓ
S
)
mentre direzione e verso si prendono tramite la normale
n̂
∇ × f~ = lim max
S→0
orientazione della supercie per cui la
(1.9)
(1.1.10)
risulta massima.
15
relativa a quella particolare
1 Cenni di elettromagnetismo
1.1.5 Teorema di Helmoltz
Teorema 1.3. (di Helmoltz)
Sia f~ un campo vettoriale tale che
∇ × f~ = x̂Fx (x, y, z) + ŷFy (x, y, z) + ẑFz (x, y, z)
(1.1.11)
∇ · f~ = G (x, y, z)
(1.1.12)
e
essendo Fx , Fy , Fz , e G funzioni note. Allora esiste ed è unico il campo vettoriale f~ che
soddisfa contemporaneamente le condizioni (1.11) e (1.12).
So osservi che sono inniti i campi vettoriali
f~
che soddisfano singolarmente le con-
dizioni (1.11) e (1.12).
1.1.6 Gradiente di una funzione scalare
Sia
f = f (x, y, z)
una funzione scalare; si chiama
componenti sono le derivate parziali della funzione
∇f = x̂
f
gradiente di f
quel vettore le cui
rispetto alle coordinate spaziali:
∂
∂
∂
f + ŷ f + ẑ f
∂x
∂y
∂z
(1.1.13)
f = f (x, y, z) si può rappresentare nello spazio con le cosiddette superci
di livello, ovvero superci nelle quali il valore di f = f (x, y, z) rimane costante.ù
Consideriamo un punto P nello spazio di una qualunque supercie di livello e valutiamo
il gradiente della funzione f = f (x, y, z). Quello che si trova è un vettore in direzione
ortogonale alla supercie di livellorivolto verso il massimo aumento della funzione f =
f (x, y, z) a parità di passo (vedi Figura 1.3)
Il modulo del gradiente della funzione f dà la derivata della funzione f lungo quella
direzione in cui si ha il massimo aumento della funzione f :
Una funzione
∂
f (x, y, z)
∂n
scalare f = f (x, y, z)
|∇f | =
Conoscere il gradiente di una funzione
(1.1.14)
torna molto utile quando
si vuole conoscere la derivata direzionale della stessa funzione:
∂
f (x, y, z) = ∇f · t̂ = |∇f | cos α
∂t
16
(1.1.15)
1 Cenni di elettromagnetismo
Figura 1.1.3: superci di livello
1.2 Equazioni di Maxwell
1.2.1 Forma locale delle leggi del campo elettromagnetico
l'elettromagnetismo classico macroscopico trovano spiegazione
equazioni di Maxwell, le quali, nella loro forma vettoriale moderna, scritte nel
I fenomeni che riguardano
nelle
sistema di misura SI, rispetto ad un sistema di riferimento inerziale, si scrivono, in
funzione del raggio vettore
~r
e del tempo
t,
nella forma:
~ × ~e(~r, t) = − ∂ ~b(~r, t)
∇
∂t
(1.2.1)
~ r, t) + ~j(~r, t)
~ × ~h (~r, t) = ∂ d(~
∇
∂t
(1.2.2)
~ r, t) = ρ(~r, t)
~ · d(~
∇
(1.2.3)
~ · ~b(~r, t) = 0
∇
(1.2.4)
Esse sono delle equazioni dierenziali lineari alle derivate parziali nelle quali
~e (~r, t)
è
intensità di campo elettrico misurato in V /m, ~h (~r, t) è il vettore intensità di
campo magnetico misurato in A/m , d~ (~r, t) è il vettore induzione elettrica misurato in
C/m2 , ~b(~r, t) è il vettore induzione magnetica misurato in W b/m2 , ~j (~r, t) è il vettore
il vettore
17
1 Cenni di elettromagnetismo
corrente areica misurato in A/m2 , ed inne ρ(~r, t) è la carica elettrica volumica misurata
in
A/m3 .
equazione di continuità
Dalle equazioni (1.2.2) e (1.2.3) si deduce l'
che esprime il
principio di conservazione della carica elettrica:
~ · ~j (~r, t) = − ∂ ρ(~r, t)
∇
∂t
(1.2.5)
Quando si arontano i problemi di elettromagnetismo, per tener conto della connessione tra i fenomeni elettromagnetici e quelli meccanici, si fa uso di un'ulteriore equazione
detta
equazione della forza di Lorentz:
f~ (~r, t) = ρ~e (~r, t) + ~j (r̂, t) × ~b (~r, t)
(1.2.6)
f~(~r, t) è la forza elettromagnetica volumica nel vuoto misurata in N/m3 .
I vettori ~
e, ~h, d~, ~b deniscono il campo elettromagnetico ; tali vettori si suppongono
generalmente continui assieme alle loro derivate nel dominio di analisi Ω considerato.
dove
E' importante osservare che
Le equazioni di Maxwell assieme all'equazione di continuità non risultano essere tutte indipendenti tra di loro.
Le uniche equazioni indipen-
denti sono le equazioni di Maxwell ai rotori.
Infatti, non è dicile provare quanto detto:
ˆ
le equazioni di Maxwell
(1.2.3) , (1.2.4)
si determinano a partire dalle equazioni ai
rotori, con l'ausilio dell' equazione di continuità.
Prendendo la divergenza di entrambi i membri dell'equazione
(1.2.1)
si ha:
−
~ ·∇
~ ×→
~ · ∂ ~b
∇
e = −∇
∂t
Quest'ultima equazione, per una nota identità vettoriale e per il fatto che risulta
possibile scambiare gli operatori dierenziali
~ (.),
∇
∂
∂t
(.)
per il teorema di Schwarz, si
scrive:
∂ ~ ~
∇·b=0
∂t
da cui segue che
~ · ~b (~r, t)
∇
è costante nel tempo:
~ · ~b (~r, t) = Cb (~r)
∇
(1.2.7)
Postulando che il campo sia stato eccitato ad un certo istante e che prima di quell'istante fosse nullo, ne segue che la costante
segue
Cb
risulta zero. Pertanto dalla relazione
(1.2.7)
(1.2.4) .
Analogamente, prendendo la divergenza di entrambi i membri dell'equazione
18
(1.2.2)
1 Cenni di elettromagnetismo
−
~ ·∇
~ ×→
~ · ∂ d~ + ∇
~ · ~j
∇
h =∇
∂t
si ha:
0=
quindi
~ · d~ (~r, t)
−ρ + ∇
∂ ~ · d~
−ρ + ∇
∂t
è costante nel tempo:
~ · d~ (~r, t) = Cd (~r)
ρ−∇
(1.2.8)
Ancora una volta, postulando che il campo sia stato eccitato ad un certo istante e che
prima di quell'istante fosse nullo, ne segue che la costante
relazione
ˆ
(1.2.8)
segue
Cd
risulta zero. Pertanto dalla
(1.2.3).
L'equazione di continuità si ricava a partire dall'equazione
dell'equazione
(1.2.2)
e facendo uso
(1.2.3).
Prenendo la divergenza di entrambi i membri dell'equazione
(1.2.2)
−
~ r, t) + ∇
~ ·→
~ ·∇
~ × ~h = ∇
~ · ∂ d(~
j (~r, t)
∇
∂t
e utilizzando una nota identità vettoriale, si ha:
Inne invertendo
fornisce l'equazione
~ r, t) + ∇
~ · ∂ d(~
~ · ~j(~r, t)
0=∇
∂t
l'ordine di derivazione e utilizzando (1.2.3) ,
di continuità (1.2.5).
quest'ultima relazione
Le equazioni di Maxwell indipendenti costituiscono un sistema di equazioni dierenziali
alle derivate parziali, in cui il numero di incognite supera il numero di equazioni.
E' chiaro allora che per arontare il problema elettromagnetico non bastano le sole
equazioni di Maxwell. Quando si aronta un problema elettromagnetico bisogna stabilire:
ˆ
il dominio di analisi
ˆ
i mezzi materiali presenti in
ˆ
l'intervallo di tempo
Ω
in cui si svolgono i vettori campo;
(ti , tf )
Stabilire il dominio di analisi
Ω;
in cui viene osservato il fenomeno elettromagnetico.
Ω signica conoscere la geometria della regione di spazio in
cui sono deniti i vettori del campo; le proprietà dei mezzi materiali che compongono il
Ω vengono descritte attraverso i parametri costitutivi ε ( permettività dielettrica
µ (permettività magnetica H/m), σ ( conducibilità elettrica S/m ), che legano i
dominio
F/m
),
vettori del campo secondo le cosiddette
lineari, isotropi e non dispersivi
equazioni costitutive,
le quali nel caso di mezzi
si scrivono:
d~ (~r, t) = ε~e (~r, t)
19
(1.2.9)
1 Cenni di elettromagnetismo
Nell'equazione
(1.2.11)
~b (~r, t) = µ~h (~r, t)
(1.2.10)
~j (~r, t) = σ~e (~r, t) + j~s
(1.2.11)
gura la densità di corrente impressa
~js = σ~es
che rappresenta
una sorgente per il campo elettromagnetico. L'altra sorgente del campo elettromagnetico
è rappresentata dalla carica volumica
ρs .
In questi mezzi i parametri costitutivi assumono la forma:
ε = ε (~r) = ε0 εr (~r)
(dove
nome di
ε0 ' 8.85 · 10−12 F/m
(1.2.12)
è la permettività dielettrica del vuoto, nota pure con il
costante dielettrica del vuoto e εr (~r) è la funzione dielettrica relativa ),
µ = µ (~r) = µ0 µr (~r)
(essendo
nome di
µ0 = 4π · 10−7 H/m
(1.2.13)
la permettività magnetica del vuoto, nota pure con il
permeabilità magnetica del vuoto e µr (~r)
la
permettività magnetica relativa
),
ed inne:
σ = σ (~r)
(1.2.14)
Cioè i parametri costitutivi dipendono soltanto dal punto
P
individuato dal vettore
~r.
Le quazioni di Maxwell indipendenti, assieme alle equazioni costitutive, realizzano un
sistema dierenziale alle derivate parziali determinato (5 equazioni vettoriali in 5 incognite vettoriali) che ammette una soluzione unica (il campo elettromagnetico) se ad esso
vengono abbinate le condizioni iniziali che specicano i valori dei campi all'istante
ti
in
cui inizia l'analisi elettromagnetica e le condizioni al contorno che danno informazioni
∂Ω del dominio Ω. Pertanto in denitiva il problema elettromagnetico consiste nel risolvere il seguente sistema dierenziale alle derivate parziali con
sui campi sulla frontiera
annesse condizioni iniziali e condizioni al contorno:

~ × ~e = − ∂ ~b

∇

∂t



~ × ~h = ∂ d~ + ~j

∇

∂t


d~ = ε~e


~b = µ~h



~j = σ~e + j~s




condizioni iniziali t0




condizioni al contorno su ∂Ω
20
(1.2.15.1)
(1.2.15.2)
(1.2.15.3)
(1.2.15.4)
(1.2.15.5)
(1.2.15.6)
(1.2.15.7)
(1.2.15)
1 Cenni di elettromagnetismo
1.2.2 Forma globale delle leggi del campo elettromagnetico
Le equazioni di Maxwell sono delle relazioni
portamento dei campi all'istante generico
Ω;
dierenziali
o
locali
che descrivono il com-
t in un punto ~r ordinario del dominio di analisi
le relazioni più generali che riguardano l'elettromagnetismo sono le leggi di Maxwell
in forma integrale o globale.
Tali relazioni si ricavano da quelle dierenziali applican-
do semplicemente i teoremi della divergenza e del rotore. La formulazione globale delle
equazioni di Maxwell consente, per esempio, lo studio di problemi elettromagnetici in cui
la sorgente è rappresentata da cariche elettriche discrete; consente di determinare pure il
comportamento dei campi in corrispondenza di cariche o correnti distribuite su superci
o in linee ove si manifestano discontinuità delle proprietà costitutive del mezzo materiale.
1.2.2.1 Legge di Gauss per il vettore campo induzione dielettrica
Integrando l'equazione
(1.2.3)
in un dominio
Ω
ˆ
d~
(Figura 1.1.1),
ˆ
~ · d~ dΩ =
∇
ρ dΩ
Ω
(1.2.16)
Ω
ed applicando il teorema della divergenza si ha:
˛
ˆ
d~ · n̂ d∂Ω =
∂Ω
(1.2.17) prende
Secondo (1.2.17)
chiusa ∂Ω,
˛
La relazione integrale
po induzione elettrica.
attraverso la supercie
ρ dΩ = q
(1.2.17)
Ω
legge di Gauss per il vettore cam-
il nome di
il usso del vettore campo induzione elettrica
d~ · n̂ d∂Ω
∂Ω
eguaglia la carica elettrica totale interna alla supercie
∂Ω.
Questa relazione si interpreta
dicendo che le uniche sorgenti per il campo elettrico sono le cariche elettriche.
1.2.2.2 Legge di Gauss per il vettore campo induzione magnetica
Integrando l'equazione
(1.2.4)
su un dominio
Ω
~b
(Figura 1.1.1),
ˆ
~ · ~b dΩ = 0
∇
(1.2.18)
Ω
ed applicando il teorema della divergenza si ha la
induzione magnetica
~b:
legge di Gauss
per il vettore campo
˛
~b · n̂ d∂Ω = 0
(1.2.19)
∂Ω
Secondo
(1.2.19)
il usso del vettore campo induzione magnetica attraverso una su-
percie chiusa risulta nullo.
Questa relazione implica la non esistenza delle cariche
mqgnetiche.
21
1 Cenni di elettromagnetismo
1.2.2.3 Legge di Faraday
(1.2.1)
ˆ
Integrando l'equazione
su una supercie bilatera
ˆ
~ × ~e · n̂ dS = −
∇
S
S
ed applicando il teorema di Stokes si ha la
~e · t̂ dΓ = −
S
Γ
(Figura 1.1.2),
∂~
b · n̂ dS
∂t
(1.2.20)
legge di Faraday :
ˆ
˛
S
∂~
b · n̂ dS
∂t
(1.2.21)
Supposta ssa la supercie S nel tempo si può portare l'operatore
∂
∂t
(.) fuori dal segno
di integrale.
Esiste una importante forma alternativa alla forma integrale
(3.2.6)
che utilizza inte-
grali di volume e supercie anziché integrali di linea e supercie. Integrando l'equazione
(1.2.1)
in un dominio
Ω
(Figura 1.1.1),
ˆ
ˆ
~ × ~e dΩ = −
∇
Ω
Ω
∂~
b dΩ
∂t
(1.2.22)
ed applicando la formula del rotore si ha :
˛
ˆ
n̂ × ~e d∂Ω = −
∂Ω
Ω
∂~
b dΩ
∂t
(1.2.23)
1.2.2.4 Legge di Ampere
(1.2.2)
Integrando l'equazione
su una supercie bilatera
ˆ
ˆ
~ × ~h · n̂ dS =
∇
S
S
∂ ~
d · n̂ dS +
∂t
ed applicando il teorema di Stokes si ha la
ˆ
˛
~h · t̂ dΓ =
Γ
S
S
ˆ
(Figura 1.1.2),
~j · n̂ dS
(1.2.24)
S
legge di Ampere :
∂ ~
d · n̂ dS +
∂t
ˆ
S
~j · n
b dS
(1.2.25)
Come nel caso precedente, supposta ssa la supercie S nel tempo si può portare
l'operatore
∂
∂t
(.)
fuori dal segno di integrale.
Anche in questo caso esiste una importante forma alternativa alla forma integrale
(1.2.25)
che utilizza integrali di volume e supercie anziché integrali di linea e supercie.
Integrando l'equazione
(1.2.2) in un dominio Ω (Figura 1.1.1),
ˆ
ˆ
ˆ
∂ ~
~
~
∇ × h dΩ =
d dΩ + ~j dΩ
Ω
Ω ∂t
Ω
(1.2.26)
ed applicando la formula del rotore si ha:
˛
ˆ
n̂ × ~h d∂Ω =
∂Ω
Ω
22
∂ ~
d dΩ +
∂t
ˆ
~j dΩ
Ω
(1.2.27)
1 Cenni di elettromagnetismo
1.2.3 Condizioni di interfaccia
Come detto in precedenza, nei punti ordinari dello spazio in cui i parametri costitutivi
dei mezzi e le sorgenti variano in modo continuo, i vettori campo si assumono continui.
Questo non vale per i punti appartenenti a superci che segnano bruschi cambiamenti dei
parametri costitutivi o che sono sede di cariche o correnti superciali. Su tali superci, i
vettori campo presentano in generale delle discontinuità.
Il comportamento dei vettori campo in corrispondenza di dette superci si determina
applicando opportunamente le equazioni di Maxwell in forma globale.
Consideriamo due mezzi materiali: il mezzo 1 di parametri costitutivi
mezzo 2 di parametri costitutivi
ε2 , µ2 , σ2 .
ε1 , µ1 , σ1
e il
Inichiamo con S la supercie o interfaccia di
separazione dei due mezzi e orientiamo un versore normale
n̂
come mostrato in Figura
1.2.1.
Consideriamo inne un cilindro di volume
Ω che
attraversa l'interfaccia S con le
basi disposte parallelemente ad S.
La legge di Gauss per il campo
d~ nel ca-
so specico del volume cilindrico di Figura
1.2.1 si scrive:
ˆ
ˆ
~
n̂·d2 dS+
S2
interfaccia
ˆ ˆ
ˆ ˆ Figura 1.2.1:
ˆ
~
(−n̂)·d~1 dS+
n̂S ·ddhdC
=
ρdhdS+ ρs dS
S1
C
h
S
h
S
S
dove l'integrale
ˆ
ρs dS
S
compare solo se vi è una carica superciale
h→0
Passando al limite per
S1 , S2
le basi
ρs sulla supercie di separazione.
e S vanno a coincidere, gli integrali
doppi
tendono a zero e la legge di Gauss diventa:
ˆ
ˆ
n̂ · d~2 dS +
S
ˆ
(−n̂) · d~1 dS =
S
ρs dS
S
da cui segue la relazione:
n̂ · d~2 − d~1 = ρs
(1.2.28)
d~ attraverso
superciale ρs .
che esprime la discontinuità della componente normale del vettore
supercie su cui è distribuita una carica areica con densità
una
Analogamente scrivendo la legge di Gauss per il vettore campo induzione magnetica
~b
nel caso specico del volume cilindrico di Figura 1.2.1 si trova la relazione:
n̂ · ~b2 − ~b1 = 0
23
(1.2.29)
1 Cenni di elettromagnetismo
che esprime la continuità della componente normale del vettore
~b
attraverso una
supercie che separa due mezzi con proprietà costitutive dierenti.
La legge di Faraday
(3.2.8)
nel caso specico del dominio cilindrico di Figura 1.2.1 si
scrive:
C
S1
Passando al limite per
h→0
le basi
−
n̂S × ~e dhdC =
(−n̂) × ~e1 dS +
n̂ × ~e dS +
S2
ˆ ˆ
ˆ ˆ
ˆ
ˆ
S1 , S2
S
h
e
S
h
∂~
b dhdS
∂t
vanno a coincidere, gli integrali doppi
tendono a zero e la legge di Faraday diventa:
ˆ
ˆ
(−n̂) × ~e1 dS = 0
n̂ × ~e2 dS +
S
S
da cui segue la relazione:
n̂ × (~e2 − ~e1 ) = 0
(1.2.30)
che esprime la continuità della componente tangente del vettore
~e
alla supercie di
separazione S.
Analogamente la legge di Ampere
(3.2.12)
nel caso specico del volume cilindrico di
Figura 1.2.1, si scrive:
ˆ
ˆ
n̂×~h2 dS+
S2
ˆ ˆ
ˆ ˆ
ˆ ˆ
ˆ
∂ ~
~j dhdS+ ~js dS
(−n̂)×~h1 dS+
n̂S ×~h dhdC =
d dhdS+
S1
C h
S h ∂t
S h
S
dove l'integrale
ˆ
~js dS
S
compare solo se vi è una corrente lineica
Passando al limite per
h→0
~js
sulla supercie di separazione.
si ricava inne:
n̂ × ~h2 − ~h1 = ~js
che esprime la discontinuità della componente tangente del vettore
supercie su cui scorre una corrente elettrica avente
(1.2.31)
~h
attraverso una
densità ~
js .
(1.2.31) segue:
n̂ × ~h2 − ~h1 = 0
In assenza di densità di corrente allora da
(1.2.32)
1.3 Proprietà dei materiali
I materiali all'interno del dominio di analisi
Ω
denti tra loro.
24
godono di alcune proprietà tutte indipen-
1 Cenni di elettromagnetismo
1.3.1 Materiali lineari isotropi e lineari anisotropi
Un materiale è detto lineare isotropo se le equazioni costitutive che legano i vettori campo
assumono le forme (1.2.9), (1.2.10), (1.2.11). Per questi mezzi i parametri costitutivi sono
delle semplici funzioni del punto.
Nel caso dei materiali anisotropi i parametri costitutivi vengono espressi mediante delle
matrici 3x3 dette
tensori
e le equazioni costitutive si scrivono:

εxx εxy
d~ (~r, t) =  εyx εyy
εzx εzy

µxx µxy
~b (~r, t) =  µyx µyy
µzx µzy

σxx σxy
~j (~r, t) =  σyx σyy
σzx σzy

εxz
εyz  ~e (~r, t)
εzz

µxz
µyz  ~h (~r, t)
µzz

σxz
σyz  ~e + j~s
σzz
(1.3.1)
(1.3.2)
(1.3.3)
L'uso dei tensori spiega il fatto che in presenza dei materiali lineari anisotropi, il
comportamento dei vettori campo dipende dalla direzione oltre che dal punto considerato.
1.3.2 Materiali non lineari
I materiali non lineari isotropi sono caratterizzati dalle equazioni costitutive:
d~ (~r, t) = ε (~e) ~e (~r, t)
(1.3.4)
~b (~r, t) = µ ~h ~h (~r, t)
(1.3.5)
~j (~r, t) = σ (~e) ~e (~r, t) + j~s
(1.3.6)
mentre quelli non lineari anisotropi sono caratterizzati dalle equazioni costitutive:

εxx (~e)
d~ (~r, t) =  εyx (~e)
εzx (~e)

µxx ~h

~b (~r, t) = 
 µyx ~h

µzx ~h

σxx (~e)
~j (~r, t) =  σyx (~e)
σzx (~e)

εxz (~e)
εyz (~e)  ~e (~r, t)
εzz (~e)

µxz ~h


µyz ~h  ~h (~r, t)

µzz ~h

σxy (~e) σxz (~e)
σyy (~e) σyz (~e)  ~e + j~s
σzy (~e) σzz (~e)
εxy (~e)
εyy (~e)
εzy (~e)
µxy ~h
µyy ~h
µzy ~h
25
(1.3.7)
(1.3.8)
(1.3.9)
1 Cenni di elettromagnetismo
1.3.3 Dispersività dei materiali
I materiali possono essere dispersivi spazialmente o temporalmente.
I materiali
dispersivi spazialmente
sono caratterizzati dalle equazioni costitutive:
ε
4πr2
d~ (~r, t) =
ˆ
~e (~r, t) dΩ
(1.3.10)
Ω
ˆ
µ
~h (~r, t) dΩ
4πr2 Ω
ˆ
~j (~r, t) = σ
~e (~r, t) dΩ + j~s
4πr2 Ω
~b (~r, t) =
Secondo (1.3.10), il valore del vettore campo
vettore campo
del punto
~e
nel punto
~r
d~ in
un punto
(1.3.11)
(1.3.12)
~r
non dipende soltanto dal
ma anche dal valore del vettore campo
~e
in un intorno
Ω
~r.
In maniera analoga si ragiona con le altre equazioni.
I materiali
dispersivi temporalmente
sono caratterizzati dalle equazioni costitutive:
ε
d~ (~r, t̄) =
4
ˆ
t̄
~e (~r, t) dt
(1.3.13)
4
ˆ
~h (~r, t) dt
~b (~r, t̄) = µ
4 Ω
ˆ
~j (~r, t̄) = σ
~e (~r, t) dt + j~s
4 4
(1.3.14)
(1.3.15)
d~ in un istante di tempo t̄ non dipende
soltanto dal vettore campo ~
e all'istante di tempo t̄ ma anche dal valore del vettore campo
~e in un intervallo di tempo passato 4.
Secondo (1.3.13), il valore del vettore campo
In maniera analoga si ragiona con le altre equazioni.
1.3.4 Materiali chirali
I materiali chirali sono molto usati nelle telecomunicazioni. Per i materiali chirali
dipende solo da
~e
ma pure
d~ = ε~e + η~h
Analogamente
~b
d~ non
da ~
h:
non dipende solo da
~h,
ma pure da
~b = µ~h + ξ~e
26
(1.3.16)
~e:
(1.3.17)
1 Cenni di elettromagnetismo
1.3.5 Isteresi nei materiali
Imateriali soggetti a isteresi sono i ferromagneti. Per questa classe di materiali la relazione
tra i campi
~b
e
~h
non è più lineare ma nemmeno univoca.
L'andamento dei valori
dipende anche dalla storia passata dagli stessi campi nel materiale; tale fenomeno si
chiama
isteresi.
Ad ogni modo essi sono di grande utilità tecnologica; vale quindi la pena
soermarsi nel loro studio seppure qualitativamente.
Curva di isteresi
Per comprendere al meglio qualitativamente le proprietà magnetiche di un ferromagnete
si studia la curva che mostra la dipendenza di
~b
da
~h;
tale curva si dice di isteresi.
Esaminiamo i punti salienti di tale curva:
1. si parte dallo stato vergine del materiale: tutti i campi all'interno di esso sono nulli.
~h e corrispondentemente si osserva un andamento del campo
~b decisamente non lineare; la pendenza della curva è molto elevata nei confronti dei
2. Si aumenta il campo
materiali lineari.
3. Oltre un certo valore del campo ~
h , detto di saturazione
più, attestandosi al valore
Bs
Hs , l'induzione ~b non cresce
o almeno cresce molto lentamente. In tali condizioni
essa cresce essa cresce ulteriormente solo per eetto della corrente di conduzione
che genera il campo
~h,
siccome il contributo del materiale è saturo.
4. A questo punto si comincia a decrescere il campo
~h:
l'induzione magnetica
~b
segue
una nuova curva al di sopra della precedente, e in particolare si nota che, una volta
azzerato il campo ~
h: rimane una induzione non nulla chiamata
residua.
induzione magnetica
5. Per annullare l'induzione magnetica residua, bisogna quindi diminuire ulteriormente il campo ~
h e quindi invertirlo rispetto alla direzione originaria: si raggiungerà
così tale valore detto
coercitivo Hc .
6. Diminuendo ulteriormente il valore del campo
~h
si presenta la stessa condizione
di saturazione incontrata precedentemente ma stavolta con induzione opposta; il
fenomeno è quindi completamente speculare.
7. A tal punto si aumenta di nuovo il campo
~h e l'induzione segue ancora una curva al
di sotto della precedente con una nuova induzione residua opposta alla precedente
e un nuovo campo coercitivo per poi ritornare alla saturazione in direzione positiva:
la curva diventa chiusa realizzando così il ciclo di isteresi.
27
1 Cenni di elettromagnetismo
Figura 1.3.1: ciclo di isteresi
1.4 Scomposizione del problema elettromagnetico
Dal problema elettromagnetico dato in (2.1.15) si ricavano i cosidetti problemi di campo statico.
Prima di scrivere le equazioni che descrivono i problemi di campo statico
osserviamo che l'equazione di continuità in condizioni statiche si scrive:
~ · ~j (~r, t) = 0
∇
(1.4.1)
1.4.1 Problema di campo di corrente statico
Il problema di campo di corrente statico è dato dal seguente sistema:

~ · ~j = 0

∇



∇
~ × ~e = ~0
~j = σ~e



condizioni al contorno su ∂Ω
e permette di denire il concetto di
(1.4.2)
resistenza.
1.4.2 Problema di campo elettrostatico
Il problema di campo elettrostatico è dato dal seguente sistema:

~ · d~ = ρ

∇



∇
~ × ~e = ~0

d~ = ε~e



condizioni al contorno su ∂Ω
e permette di denire il concetto di
capacità.
28
(1.4.3)
1 Cenni di elettromagnetismo
1.4.3 Problema di campo magnetostatico
Il problema di campo magnetostatico è dato dal seguente sistema:

~ · ~b = 0

∇



∇
~ × ~h = ~j
~b = µ~h




condizioni al contorno su ∂Ω
e permette di denire i concetti di
induttanza
e
(1.4.4)
mutua induttanza.
1.4.4 Problema di campo quasi statico
Trascurando la corrente di spostamento
si ricava il
∂ ~
∂t d dal problema elettromagnetico dato in (1.2.15)
problema di campo quasi statico:

~ × ~e = − ∂ ~b

∇

∂t



~
~
~
∇ × h = j




d~ = ε~e

~b = µ~h



~j = σ~e + j~s





condizioni iniziali t0




condizioni al contorno su ∂Ω
(1.4.5)
Nei prossimi capitoli verranno trattati i problemi di campo statico e soltanto alla ne
del corso verrà trattato il problema di campo quasi statico
29
2 Dall'elettromagnetismo
all'elettrotecnica: i dispositivi elettrici
2.1 Problema di campo di corrente statico
2.1.1 Introduzione
Attraverso il problema di campo di corrente statico

~ · ~j = 0

∇



∇
~ × ~e = ~0
~j = σ~e




condizioni al contorno su ∂Ω
si vuole determinare l'andamento della densità di corrente
(2.1.1)
~j
in un corpo massiccio.
Illustriamo un tipico problema di campo di corrente statico.
Esempio.
Si consideri un pezzo di materiale conduttore massiccio. Supposto che esso
sia fatto di rame allora sarà caratterizzato da una conducibilità elettrica data da
σ =
56 · 106 s/m.
Collegando il pezzo di rame massiccio ad una pila ideale
V0 attraverso dei li conduttori
p.e.c (perfect electrical cundoctor), cioè a conducibilità innita, si osserva un passaggio
di corrente costante
I
nei li conduttori e nel pezzo di rame massiccio. Dalla Figura 2.1.1
è possibile osservare che i il pezzo di materiale massiccio è connesso ai li mediante delle
placchette di materiale p.e.c.
Figura 2.1.1: conduttore massiccio
30
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Il problema di campo di corrente statico consiste nel determinare la corrente I che
attraversa il pezzo di rame massiccio.
Dato che la corrente elettrica è una grandezza
sica macroscopica data da:
ˆ
ˆ
~ =
~j · ds
I=
S
si capisce che bisogna determinare
~j · n̂ ds
(2.1.2)
S
~j
in ogni punto del pezzo di rame massiccio per
risolvere il problema di campo di corrente statico.
Qualitativamente le linee di campo del vettore
~j
tendono ad occupare tutta la sezione
S del pezzo di rame massiccio come mostrato in Figura 2.1.2
Figura 2.1.2: conduttore massiccio
Volendo fare un paragone idrauilico, possiamo immaginare che
V0
sia una pompa e che
il pezzo di rame massiccio sia una vasca piena o parzialmente piena d'acqua. In questo
caso si vuole determinare la portata d'acqua I e il vettore velocità ~
j in ogni punto interno
alla vasca. La corrente I si può determinare in due modi:
ˆ
si realizza il prototipo del pezzo di rame massiccio e attraverso un amperometro
opportunamente collegato si determina il valore della corrente I;
ˆ
si risolvono le equazioni del problema di campo di corrente statico , si trova la
densità di corrente
~j
e attaverso la (2.1.2) si trova la corrente I.
2.1.2 Riformulazione del problema di campo di corrente statico
Esiste un modo che permette di semplicare notevolmente il problema di campo di corrente statico. Esso consiste nell'introdurre una nuova variabile detta
elettrico v = v (x, y, z), attraverso la nota formula:
potenziale scalare
~
~e = −∇v
Utilizzando quest'ultima equazione, il problema di campo di corrente statico (2.1.1)
diventa:
31
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici

~ · ~j = 0

∇




~
~

∇ × ~e = 0
~
~e = −∇v



~j = σ~e




condizioni al contorno su ∂Ω
(2.1.3.1)
(2.1.3.2)
(2.1.3.3)
(2.1.3.4)
(2.1.3.5)
(2.1.3)
Utilizzando la (2.1.3.3), la (2.1.3.2) viene automaticamente soddisfatta in quanto il
rotore del gradiente di una funzione scalare è sempre nullo, qualunque sia la funzione
scalare v considerata.
Sostituendo (2.1.3.3) in (2.1.3.4) si ricava:
~
~j = −σ ∇v
(2.1.4)
Sostiuendo inoltre (2.1.4) in (2.1.3.1) si ottiene:
~ · −σ ∇v
~
∇
=0
Pertanto il problema di campo di corrente statico risulta equivalente al seguente:
(
~ · −σ ∇v
~
∇
=0
(2.1.5.1)
(2.1.5)
condizioni al contorno su ∂Ω (2.1.5.2)
L'equazione in (2.1.5.1) prende il nome di
equazione di Laplace.
Se il materiale conduttore è uniforme, come nel caso del rame, si ha che
σ = cost.
e
l'equazione di Laplace si scrive:
~ · ∇v
~ =0
∇
Deniendo l'operatore dierenziale
(2.1.6)
laplaciano
2
2
2
~ ·∇
~ = ∂ + ∂ + ∂
∇2 = ∇
∂x2 ∂y 2 ∂z 2
(2.1.7)
∇2 v = 0
(2.1.8)
(
∇2 v = 0
(2.1.9.1)
condizioni al contorno su ∂Ω (2.1.9.2)
(2.1.9)
la (2.16) si scrive:
e il problema in (2.1.5) diventa:
La (2.1.8) è chiamata ancora una volta equazione di Laplace.
L'equazione di Laplace è un'equazione dierenziale alle derivate parziali omogenea che
deve essere ovviamente integrata nel
to.
volume ⊗
del pezzo di rame massiccio considera-
Tale equazione ammette innite soluzioni e si dimostra che abbinando ad essa le
condizioni al contorno ammette una unica soluzione.
32
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.1.3 Funzione armonica
Una funzione
v = v (x, y, z)
che soddisfa l'equazione di Laplace si dice
armonica.
Nel caso monodimensionale l'equazione di Laplace si scrive:
d2
v (x) = 0
dx2
(2.1.10)
Attraverso semplici passaggi si trova che le funzioni che soddisfano la (2.1.10) sono le
rette del piano x-v:
d
dx
ˆ
d
d
v (x) = 0 ⇒
v (x) = k1 ⇒ v (x) = k1 dx = k1 x + k2
dx
dx
v (x) = k1 x + k2
(2.1.11)
Analogamente nel caso bidimensionale si trova che le soluzioni dell'equazione di Laplace
∂2
∂2
v
(x,
y)
+
v (x, y) = 0
∂x2
∂y 2
(2.1.12)
v (x, y) = ax + by + c
(2.1.13)
sono le funzioni:
Proprietà del minimo e del massimo delle funzioni armoniche
Si dimostra che una funzione armonica avrà massimi e minimi assoluti solo nei punti di
frontiera e non nei punti interni al dominio.
Proprietà del valore medio delle funzioni armoniche
Per funzioni armoniche di due variabili si ha:
1
v (x0 , y0 ) =
πR2
ˆ
1
v (x, y) dxdy =
2πR
cerchio
˛
v (l) dl
(2.1.14)
circonf erenza
Per funzioni armoniche di tre variabili si ha:
1
v (x0 , y0 , z0 ) = 4 3
3 πR
ˆ
1
v (x, y, z) dxdydz =
4πR2
sf era
33
˛
v (l) dl
superf icie sf era
(2.1.15)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.1.4 Le condizioni al contorno
Consideriamo nuovamente il problema di campo di corrente statico (2.1.9) e concentriamo
l'attenzione sulle condizioni al contorno
Neuman.
∂Ω che possono essere di tipo
Dirichelet
Una condizione si dice di tipo Dirichelet se il potenziale scalare elettrico
in una parte
analisi
Ω
∂Ω1
della frontiera
∂Ω
v
o di
tipo
risulta noto
(supercie del conduttore massiccio) del dominio di
(volume del conduttore massiccio):
∀P ∈ ∂Ω1
v = f (P )
(2.1.16)
Una condizione si dice di tipo Neuman se la derivata normale del potenziale scalare elettrico
v risulta nota nella rimanente parte ∂Ω2 della frontiera ∂Ω (supercie del conduttore
Ω (volume del conduttore massiccio):
massiccio) del dominio di analisi
∂
v = g (P )
∂n
∀P ∈ ∂Ω2
(2.1.17)

2

∀P ∈ Ω
∇ v = 0
v = f (P )
∀P ∈ ∂Ω1

∂
∂n v = g(P ) ∀P ∈ ∂Ω2
(2.1.18)
Si dimostra che la soluzione al problema
esiste ed è unica.
∂Ω+
∂Ω collegata alla placchetta riferita al
∂Ω− la parte di supercie di ∂Ω collegata alla placchetta
riferita al morsetto negativo, visto che la d.d.p tra le due placchette è V0 , possiamo ssare
Se indichiamo con
la parte di supercie di
morsetto positivo della pila e con
due condizioni di tipo Dirichelet nel seguente modo:
v = V0 ∀P ∈ ∂Ω+
v = 0 ∀P ∈ ∂Ω−
essendo
∂Ω+ U ∂Ω− = ∂Ω1 .
Per la parte rimanente della frontiera
∂Ω,
ovvero
(2.1.19)
¯ 1,
∂Ω2 = ∂Ω
bisogna ssare una
condizione di tipo Neuman.
Innanzitutto chiariamo il signicato di derivata normale di
v:
∂
∂
v = lim
v
P →P0 ∂n0
∂n
Il pezzo di rame massiccio (Ω) è una materializzazione di un tubo di usso per gli
elettroni e pertanto le linee di campo della densità di corrente
~j
sono in ogni punto
tangente alla supercie del pezzo di rame
massiccio; in altri termini ciò vuol dire
Figura 2.1.3: derivata normale
34
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
che la componente normale della densità
di corrente
~j
è nulla:
jn = 0
(2.1.20)
Se fosse il contrario si avrebbe che la corrente esce fuori dalla supercie del conduttore
e ciò è assurdo perchè fuori dal pezzo di rame massiccio c'è aria e la conducibilità dell'aria
è nulla.
Manipolando la (2.1.20):
~ · n̂ = 0 ⇒ ∇v
~ · n̂ = 0
jn = 0 ⇒ ~j · n̂ = 0 ⇒ σ~e · n̂ = 0 ⇒ −σ ∇v
si trova la condizione di tipo Neuman:
∂
∂n v
= 0 ∀P ∈ ∂Ω2
La (2.1.21) equivale a dire che nei punti di
elettrico
v
Ω
(2.1.21)
ortogonali a
∂Ω2
il potenziale scalare
rimane costante; tali punti costituiscono le cosiddette superci di livello per il
potenziale scalare elettrico
v.
Una supercie di livello è dunque un insieme di punti di
ortogonale a
∂Ω2
Ω
posti su di un piano
dove il potenziale risulta costante e pari ad un valore:
Figura 2.1.4: superci di livello
Le traiettorie del vettore campo
~j
(e quindi del vettore campo
~e)
sono ortogonali alle
superci di livello.
Si possono usare le superci di livello per dare una misura qualitativa del modulo
del vettore campo elettrico
~e
oppure del modulo del vettore densità di corrente
esempio tracciando le superci di livello con passo costante
4v
5
=
e=
d
d
essendo
d
V
m
4v = 5V
~j .
Per
si avrebbe:
(2.1.22)
la distanza ortogonale tra due superci di livello consecutive:
Dalla (2.1.22) si capisce che laddove le superci di livello si inttiscono il modulo del
campo elettrico aumenta a parità di passo.
35
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.5: superci di livello a passo costante
2.1.5 Dal problema di campo di corrente statico ai concetti di
conduttanza e resistenza
Esplicitando le condizioni al contorno come in (2.1.19) e (2.1.21) si ha che il problema di
campo di corrente statico in (2.1.18) si scrive:


∇2 v = 0



v = V
0

v
=
0



∂ v=0
∂n
essendo
∂Ω+ U ∂Ω− = ∂Ω1
e
∀P
∀P
∀P
∀P
∈Ω
∈ ∂Ω+
∈ ∂Ω−
∈ ∂Ω2
(2.1.23)
¯1
∂Ω2 = ∂Ω
Risolvendo tale problema si trova l'espressione analitica del potenziale scalare elettrico
v , noto il potenziale scalare elettrico v , attraverso la (2.1.3.3) si trova il campo
~e, noto il campo elettrico ~e, tramite la (2.1.3.4) si trova il vettore densità di
~j ed inne notoil vettore densità di corrente ~j , attraverso la (2.1.2) si trova la
elettrico
corrente
corrente
elettrica I:
ˆ
ˆ
~ =
~j · ds
I=
S
ˆ
ˆ
~j · n̂ ds =
S
~ · n̂ ds
σ ∇v
σ~e · n̂ ds = −
S
(2.1.24)
S
Osserviamo che tutte le equazioni del campo di corrente statico sono omogenee tranne
l'equazione
v = V0 ∀P ∈ ∂Ω+
Vista la linearità del problema si ha che se raddoppia
che
V0
ed I sono proporzionali.
Il fattore di proporzionalità tra I e
V0
si chiama
V0
raddoppia pure I; si ha cioè
conduttanza G
del
resistore
essendo
quest'ultimo il nome dato al pezzo di rame massiccio considerato:
ˆ
~ = G V0 =⇒ G = 1
I = ~j · ds
V0
S
36
ˆ
~ · n̂ ds
−σ ∇v
S
(2.1.25)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
L'unità di misura della conduttanza è il
siemens s, dato dal rapporto ampere su volt:
(2.1.26)
resistenza R
L'inverso della conduttanza G si chiama
R=
L'unità di misura della resistenza è
A
s=
V
del resistore:
1
G
(2.1.27)
l'ohm Ω, dato dal rapporto ampere volt su ampere:
V
s=
A
(2.1.28)
Il parametro G (oppure R) riassume tutte le proprietà costitutive e geometriche del
pezzo di rame massiccio da cui siamo partiti. In Figura 2.1.6 viene mostrato i simboli
utilizzati per indicare un resistore nei circuiti elettrici
Figura 2.1.6: simboli per indicare il resistore
2.1.6 Potenza dissipata dal resistore
Il passaggio di corrente nel resistore di conduttanza G (o resistenza R) produce calore
per eetto joule sul resistore stesso: si trova che la temperatura del resistore percorso
da corrente è maggiore della temperatura ambiente; si ha una dissipazione di energia
elettrica in calore.
In altri termini il resistore è un dispositivo che pompa energia dal circuito all'ambiente
esterno.
Se consideriamo un elemento innitesimo del pezzo di rame massiccio di volume
Ω
possiamo valutare quanto calore si genera in esso.
La potenza dissipata dal cubetto elementare
dΩ = dxdydz
del conduttore massiccio
Ω
è data da:
dP = ~e · ~j dΩ
Integrando su tutto il volume
dissipata
Ω
del pezzo di rame massiccio si ricava la
dal resistore:
37
potenza totale
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
ˆ
~e · ~j dΩ
P =
Ω
Osservando che il campo elettrico e la densità di corrente sono due vettori paralleli tra
di loro, quest'ultima espressione si può manipolare come:
~e · ~j dΩ =
P =
Ω
Ω
2
σ |~e| dΩ =
e σ e dΩ =
e j dΩ =
ˆ
ˆ
ˆ
ˆ
ˆ
Ω
Ω
Ω
2
~ σ ∇v
dΩ
(2.1.29)
Questa potenza si può conoscere una volta risolto il problema di campo di corrente
statico con cui si trova il potenziale scalare elettrico
v.
D'altra parte la potenza dissipata dal resistore si può pure ricavare mediante la relazione:
P = V0 I = V0 G Vo = G V02
(2.1.30)
Confrontando (2.1.29) e (2.1.30) si ricava una nuova espressione per la conduttanza G:
1
G= 2
V0
ˆ
σ |V0 |2 dΩ
(2.1.31)
Ω
Quindi in generale se indichiamo con V la d.d.p tra i morsetti di un resistore e con I
la corrente che lo attraversa, allora la relazione che ne regola il funzionamento è:
V = RI
(2.1.32)
I = GV
(2.1.33)
oppure:
tale relazione è nota con il nome di
prima legge di Ohm.
Si osservi che la prima legge di Ohm resta valida purchè la corrente attraversi il resistore passando dal suo nodo a potenziale più alto al suo nodo a potenziale più basso
(convenzione dell'utilizzatore):
Figura 2.1.7: convenzione dell'utilizzatore
Se la tensione ai capi del resistore è lentamente variabile nel tempo,
approssimazione continua a valere la prima legge di Ohom che si scrive:
38
v (t),
con buona
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
v (t) = R i (t)
(2.1.34)
i (t) = G v (t)
(2.1.35)
oppure:
Figura 2.1.8: caso lentamente variabile
Nel caso lentamente variabile nel tempo la potenza dissipata dal resistore prende il
nome di
potenza istantanea
dissipata dal resistore ed assume una delle seguenti forme
equivalenti:
p (t) = v (t) i (t)
(2.1.36)
p (t) = R i (t)2
(2.1.37)
p (t) =
v (t)2
R
p (t) = G iv (t)
p (t) =
i (t)2
G
(2.1.38)
(2.1.39)
(2.1.40)
2.1.7 Applicazione: deduzione della seconda legge di Ohm
Consideriamo un tratto di lo conduttore massiccio di forma cilindrica retta avente
sezione S e lunghezza d come in Figura 2.1.9.
Supponimo che le basi
∂Ω+
e
∂Ω−
siano collegate a due placchette di materiale p.e.c
grandi quanto le basi e che queste siano collegate ad una pila di tensione costante
V0
mediante due li conduttori p.e.c.
Per la struttura mostrata in Figura 2.1.9, che si suppone posta in aria, si può scrivere
il seguente problema di campo di corrente statico:
39
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.9: tratto di lo conduttore cilindrico


∇2 v = 0



v = V
0

v=0



 ∂ v=0
∂n2
essendo
Ω
e
∂Ω = ∂Ω+ U ∂Ω− U ∂ΩL
∀P
∀P
∀P
∀P
∈Ω
∈ ∂Ω+
∈ ∂Ω−
∈ ∂ΩL
(2.1.41)
, rispettivamente, il volume e la supercie del lo
conduttore massiccio.
Visto che il potenziale varia solo lungo l'asse
~z
e viste le condizioni al contorno allora
esso sarà la retta nel piano z-v passante per i punti di coordinate
P0 = (0, V0 )
e
Pd =
(d, 0):
v − V0 =
0 − V0
(z − 0)
d−0
ovvero:
v = v (z) = −
V0
z + V0
d
(2.1.42)
Proviamo che (2.1.42) è la soluzione per il problema in (2.1.41)
ˆ
visto che
d
d
v (z) =
dz
dz
V0
− z + V0
d
V0
d
=−
=⇒ ∇2 v (z) =
d
dz
d
v (z)
dz
d
=
dz
resta provato che la (2.1.42) soddisfa la prima equazione in (2.1.41)
ˆ
visto che
v (z) |z=0 = −
V0
0 + V0 = V0
d
40
v (z) |z=d = −
V0
d + V0 = 0
d
V0
−
=0
d
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
resta provato che la (2.1.42) soddisfa la seconda e la terza equazione in (2.1.41)
ˆ
Inne visto che
∂
~ (z) · n̂2 = ẑ d v (z) · n̂2 = −ẑ V0 · (x̂ cos α + ŷ sin α) = 0
v (z) = ∇v
∂n2
dz
d
resta provato che la (2.1.42) soddisfa la quarta equazione in (2.1.41).
Noto il potenziale scalare elettrico
densità di
v (z)
possiamo determinare il campo elettrico
~e
la
corrente ~
j
~ (z) = −
~e = −∇v
d
dz
−
V0
V0
z + V0 ẑ =
ẑ
d
d
(2.1.43)
~j = σ~e (z) = σ V0 ẑ
d
(2.1.44)
I:
ˆ
ˆ
ˆ
V0
S
V0
~ =
σ ẑ · n̂1 dS = σ
dS = σ V0
I = ~j · dS
d
d
d
S
S
S
e quindi la corrente elettrica
S
I = σ V0
d
(2.1.45)
Dalla relazione in (2.1.45) risulta evidente che si è supposto di utilizzare un materiale
conduttore omogeneo; inoltre si vede subito che la conduttanza del resistore vale:
G=σ
S
d
(2.1.46)
R=ρ
d
S
(2.1.47)
mentre la resistenza vale:
essendo:
ρ=
la
resistività
1
σ
(2.1.48)
del conduttore.
Sottoponendo la (2.1.47) si trova subito che la resistività si misura in
Ω m.
La (2.1.47) riassume tutte le proprietà costitutive e geometriche del resistore e prende
il nome di
seconda legge di Ohm.
41
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.1.8 Generaltà sui resistori
L'unico resistore no ad ora studiato è quello che soddisfa alla prima legge di Ohm,
secondo cui la tensione ai capi del resistore risulta proporzionale alla corrente che uisce
in esso.
Se la corrente attraversa il resistore dal morsetto a potenziale maggiore al morsetto a
potenziale minore, come mostrato in Figura 2..1.10 , si parla di
zatore
convenzione dell'utiliz-
e la prima legge di Ohm si scrive
v (t) = R i (t)
(2.1.49)
Figura 2.1.10: convenzione dell'utilizzatore
Viceversa se la corrente attraversa il resistore dal morsetto a potenziale minore al
morsetto a potenziale maggiore , come mostrato in Figura 2..1.11 , si parla di
del generatore
convenzione
e la prima legge di Ohm si scrive
v (t) = −R i (t)
(2.1.50)
Figura 2.1.11: convenzione del generatore
Vedremo adesso che esistono altri tipi di resistori.
Il resistore è un dispositivo bipolare (ovvero avente due terminali) che mette in relazione
tensione e corrente tramite una legge di tipo algebrico.
In altri termini un elemento a due terminali (o morsetti) viene chiamato resistore se
v (t)
i − v.
in qualsiasi istante di tempo t, la sua tensione
una relazione denita da una curva nel piano
Questa curva è chiamata la
e la sua corrente
caratteristica del resistore
di tutti i possibili valori che la coppia
soddisfano ad
all'istante t e specica l'insieme
(i, v) può assumere all'istante t.
42
i (t)
Ogni resistore può
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
essere classicato in quattro modi possibili, a secoda che sia lineare o non lineare, tempo
invariante o tempo variante.
Un resistore è detto
lineare
se la sua caratteristica in ogni istante di tempo è una retta
passante per l'origine del piano
Un resistore è detto
i − v,
i − v.
non lineare
se la sua caratteristica è una curva generica del piano
oppure una retta non passante per l'origine.
Un resistore è detto
invariante
tempo variante
se la sua caratteristica varia col tempo,
tempo
se la sua caratteristica non varia col tempo.
2.1.8.1 Resistore lineare tempo-invariante
Un resistore lineare tempo-invariante ha una caratteristica che non varia con il tempo e
i − v:
rappresenta una retta passante per l'origine del piano
Figura 2.1.12: caratteristica del resistore lineare tempo-invariante
Quindi la relazione tra la sua tensione e la sua corrente è espressa dalla prima legge di
OHm:v
(t) = R i (t)
oppure
i (t) = G v (t)
essendo
1
G costante.
R=
Due tipi speciali di resistore lineare tempo-invariante sono il
circuito
Un elemento a due morsetti è detto
circuito aperto
circuito aperto
e il
corto-
se ha una corrente identica a zero
per qualsiasi tensione ai suoi capi:
i (t) = 0 A
∀v (t)
(2.1.51)
Come mostrato in Figura 2.1.13 la caratteristica del circuito aperto (asse delle tensioni)
è a pendenza innita:
R=∞
o equivalentemente
Un elemento a due morsetti è detto
G=0
cortocircuito se ha una tensione ai suoi capi identica
a zero per qualsiasi corrente che lo attravera:
v (t) = 0 V
∀i (t)
(2.1.52)
Come mostrato in Figura 2.1.14 la caratteristica del cortocircuito (asse delle correnti)
è a pendenza nulla:
R=0
o equivalentemente
43
G=∞
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.13: caratteristica del circuito aperto
Figura 2.1.14: caratteristica del cortocircuito
In Figura 2.1.15 sono riportati i simboli utilizzati per il circuito aperto e per il cortocircuito:
Figura 2.1.15: simboli circuitali per circuito aperto e cortocircuito
2.1.8.2 Resistore lineare tempo-variante
La caratteristica di un resistore lineare tempo-variante è descritta dalla seguente equazione:
v (t) = R (t) i (t) ⇔ i (t) = G (t) v (t)
44
(2.1.53)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Come mostrato in Figura 2.1.16 la caratteristica è un fascio proprio di rette con centro
nell'origine del piano
i − v.
Figura 2.1.16: caratteristica del resistore lineare tempo-variante
2.1.8.3 Resistore non lineare tempo-invariante
Il resistore non lineare tempo-invariante è descritto da una equazione algebrica del tipo:
f (v (t) , i (t)) = 0
(2.1.54)
Essa non dipende dal tempo e può essere una retta non passante per l'origine del piano
i − v,
oppure una qualunque curva del medesimo piano come mostrato in Figura 2.1.17
Figura 2.1.17: caratteristica del resistore non lineare tempo-invariante
2.1.8.4 Resistore non lineare tempo-variante
Il resistore non lineare tempo-variante è descritto da una equazione algebrica del tipo:
f (v (t) , i (t) , t) = 0
45
(2.1.55)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
i−v
Come mostrato in Figura 2.1.17 nel piano
si distinguono diverse curve al variare
del tempo
Figura 2.1.18: caratteristica del resistore non lineare tempo-variante
2.1.8.5 Resistore controllato in corrente e resistore controllato in tensione
Consideriamo l'equazione del resistore non lineare tempo-invariante:
f (v (t) , i (t)) = 0
Essa rappresenta una funzione implicita nelle variabili
v (t)
e
i (t).
Ci chiediamo adesso se è possibile esplicitare in ogni caso una variabile rispetto all'altra.
Se il resistore ha una caratteristica del tipo mostrata in Figura 2.1.19 è ovvio che non è
possibile esplicitare
i (t) in funzione di v (t),
ovvero non è possibile scrivere una relazione
del tipo:
i (t) = g (v (t))
E' possibile tuttavia esplicitare
v (t)
in funzione di
i (t):
v (t) = h (i (t))
perchè ad un sol valore della correntte corrisponde un sol valore della tensione.
Un resistore per cui è possibile esplicitare la tensione rispetto alla corrente si dice
resistore controllato in corrente:
v (t) = h (i (t))
(2.1.56)
Un resistore per cui è possibile esplicitare la corrente rispetto alla tensione si dice
resistore controllato in tensione:
i (t) = h (v (t))
46
(2.1.57)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.19: caratteristica del resistore controllato in corrente
2.1.8.6 Generatore ideale di tensione e generatore reale di tensione
Un
generatore ideale di tensione
una data tensione
v0
è un elemento a due morsetti che presenta ai suoi capi
qualunque sia la correntei (t) che lo attraversi:
v (t) = v0 (t)
Se
v0 (t) = V0 = cost.
tensione costante.
∀i (t)
il generatore ideale di tensione si dirà
(2.1.58)
generatore ideale di
Per esso la caratteristica è una retta parallela all'asse delle correnti:
Figura 2.1.20: caratteristica del generatore ideale di tensione costante
In Figura 2.1.20 viene mostrato il simbolo circuitale del generatore ideale di tensione.
Figura 2.1.21: simbolo circuita del generatore ideale di tensione
47
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Si osservi che per tale elemento circuitale vale la convenzione del generatore visto che
la corrente che lo attraversa si sposta dal morsetto a potenziale più basso al morsetto a
potenziale più alto.
Si osservi pure che qualunque sia il carico connesso al generatore ideale di tensione, ai
capi di quest'ultimo ci sarà sempre la tensione
v0
Figura 2.1.22: generatore ideale di tensione connesso ad un carico
Nella pratica è impossibile realizzare un generatore ideale di tensione poichè ci sarà
sempre una caduta di tensione all'interno di esso. Si parla in questo caso di generatore
reale di tensione.
Un
generatore reale di tensione
eratore ideale di tensione
v0 (t)
è un dispositivo a due morsetti costituito da un gen-
e un resistore lineare tempo-invariante di resistenza
R0
aventi un morsetto a comune. Si osservi che il generatore ideale di tensione e il resistore
lineare tempo invariante così disposti sono attraversati dalla stessa corrente
tale ragione si dicono in
serie.
i (t)
e per
In Figura 2.1.23 viene mostrato un generatore reale di tensione connesso ad un carico
resistivo di resistenza
R.
Figura 2.1.23: generatore reale di tensione connesso ad un carico
48
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La tensione ai capi del generatore reale di tensione,
del generatore ideale di tensione,
v0 (t),
v (t),
è pari alla tensione ai capi
meno la caduta di tensione
vR0 (t)
su
R0 .
v (t) = v0 (t) − vR0 (t)
(2.1.59)
2.1.8.6.1 Legge di Kirchoo delle tensioni (L.K.T.)
scrivendo per il circuito mostrato in Figura 2.1.23 la
Asserzione
. (legge di kirchoo delle tensioni ).
2.1
La (2.1.59) si ricava subito
legge di Kirchoo delle tensioni.
La somma algebrica delle cadute di
tensione in un circuito elettrico è identicamente nulla:
X
vk (t) = 0
k
Per stabilire il segno da attribuire alle cadute di tensione nel circuito occorre:
ˆ
utilizzare per i generatori la convenzione del generatore e per i resistori la convenzione dell'utilizzatore
ˆ
associare al circuito una linea chiusa dotata di verso di percorrenza arbitrario
chiamata
ˆ
anello.
stabilire per ciascuna caduta di tensione, il segno che si incontra percorrendo
l'anello.
Con riferimento al circuito mostrato in Figura 2.1.23 si ha:
− v0 (t) + v (t) + vR0 (t) = 0
(2.1.60)
E' immediato vericare che la (2.1.60) porta alla (2.1.59).
Tenedo conto che per il resistore di resistenza
R0 è
stata utilizzata la convenzione
dell'utilizzatore, la prima legge di Ohm si scrive:
vR0 (t) = R0 i (t)
Sostituendo (2.1.61) in (2.1.59) si ricava la
caratteristica
(2.1.61)
del generatore reale di ten-
sione:
v (t) = v0 (t) − R0 i (t)
Riportando su uno stesso piano
i−v
(2.1.62)
la caratteristica del generatore reale di tensione
e la caratteristica
v (t) = R i (t)
del carico R, si ricava il
(2.1.63)
punto di lavoro Q del carico R che esprime corrente e tensione
per il carico R durante il suo funzionamento:
49
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.24: punto di lavoro del carico R
2.1.8.6.2 Resistori in serie e legge del partitore di tensione
Risolvendo il sistema
costituito dalle relazioni in (2.1.62) e (2.1.63) si determinano le espressioni di corrente e
tensione del punto di lavoro Q del carico R:
v0 (t)
R0 + R
(2.1.64)
R
v0 (t)
R0 + R
(2.1.65)
iQ (t) =
vQ (t) =
Attraverso (2.1.64) si deduce che due resistori in serie sono equivalenti ad un resistore
avente come resistenza la somma delle resistenze dei due resistori.
Rs = R0 + R
(2.1.66)
La (2.1.66) si estende facilmente al caso di n resistori connessi in serie:
Rs = R1 + R2 + ... + Ri + ... + Rn
(2.1.67)
Attraverso (2.1.65) si deduce che in una serie, la caduta di tensione su un carico è una
frazione della tensione del generatore ideale di tensione.
La (2.1.65) è nota con il nome di
legge del partitore di tensione
e si può estendere
facilmente al caso di n resistori connessi in serie:
vi (t) =
Ri
v0 (t)
R1 + R2 + ... + Ri + ... + Rn
50
(2.1.68)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La Figura 2.1.25 chiarisce quanto detto
Figura 2.1.25: Resistori in serie
2.1.8.6.3 Potenza istantanea assorbita e potenza istantanea generata
Consideriamo
la caratteristica del resistore lineare tempo-.invariante e del generatore ideale di tensione
mostrate in Figura 2.1.26
Figura 2.1.26: resistore lineare tempo invariante Vs generatore ideale di tensione
La caratteristica del resistore lineare tempo-invariante giace nei quadranti I e III e ciò
implica che la potenza istantanea risulta essere sempre non negativa:
p (t) = v (t) i (t) ≥ 0
Visto che (2.1.69) risulta essere concorde con la convenzione dell'utilizzatore
istantanea è assorbita
dal resistore:
p (t) = pass. (t)
(2.1.69)
la potenza
.
La caratteristica del generatore ideale di tensione giace nei quadranti I e II se risulta
v0 (t) > 0.
Questo fatto implica che
p (t) =
v (t) i (t) ≥ 0 se i (t) ≥ 0 (2.1.70.1)
v (t) i (t) < 0 se i (t) < 0 (2.1.70.2)
51
(2.1.70)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La potenza in (2.1.70.1) risulta essere concorde con la convenzione del generatore e per-
i (t) ≥ 0 la potenza istantanea è generata dal generatore ideale di tensione:p (t) =
pgen. (t) ≥ 0; viceversa la potenza in (2.1.70.2) risulta essere discorde con la convenzione
del generatore e pertanto per i (t) < 0 la potenza istantanea è assorbita dal generatore
ideale di tensione:p (t) = pgen. (t) < 0. In questo caso si dice che il generatore ideale di
tanto per
tensione è in
fase di carica.
2.1.8.7 Generatore ideale di corrente e generatore reale di corrente
Un
generatore ideale di corrente
una data corrente
i0 (t)
è un elemento a due morsetti che viene attraversato da
qualunque sia la tensione
i (t) = i0 (t)
Se i0
v (t)
ai suoi capi:
∀v (t)
(2.1.71)
(t) = i0 = cost. il generatore ideale di corrente si dirà generatore ideale di corrente
costante.
Per esso la caratteristica è una retta parallela all'asse delle tensioni:
Figura 2.1.27: caratteristica del generatore ideale di corrente costante
In Figura 2.1.20 viene mostrato il simbolo circuitale del generatore ideale di tensione.
Figura 2.1.28: simbolo circuita del generatore ideale di corrente
Si osservi che per tale elemento circuitale vale la convenzione del generatore visto che
la corrente che lo attraversa si sposta dal morsetto a potenziale più basso al morsetto a
potenziale più alto.
Si osservi pure che qualunque sia il carico connesso al generatore ideale di corrente, la
corrente che lo attraversa sarà sempre
i0 (t):
52
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.29: generatore ideale di corrente connesso ad un carico
Nella pratica è impossibile realizzare un generatore ideale di corrente poichè ci sarà
sempre una perdita di corrente all'interno di esso. Si parla in questo caso di generatore
reale di corrente.
Un
generatore reale di corrente
eratore ideale di corrente
i0 (t)
è un dispositivo a due morsetti costituito da un gen-
e un resistore lineare tempo-invariante di resistenza
R0
aventi i morsetti a due a due a comune. Si osservi che il generatore ideale di corrente e il
resistore lineare tempo invariante così disposti presentano ai loro capi la stessa tensione
v (t)
e per tale ragione si dicono in
parallelo.
In Figura 2.1.23 viene mostrato un generatore reale di corrente connesso ad un carico
resistivo di resistenza
R.
Figura 2.1.30: generatore reale di corrente connesso ad un carico
La corrente che attraversa il generatore reale di corrente,
atttraversa il generatore ideale di corrente,
i0 (t),
i (t),
è pari alla corrente che
meno la corrente
iR0 (t)
che scorre su
R0 .
i (t) = i0 (t) − iR0 (t)
53
(2.1.72)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.1.8.7.1 Legge di Kirchoo delle correnti (L.K.I.)
La (2.1.72) si ricava subito scriven-
legge di Kirchoo delle correnti.
Asserzione 2.2. (legge di kirchoo delle correnti ). La somma algebrica delle correnti in
do per il circuito mostrato in Figura 2.1.30 la
un nodo di circuito elettrico è identicamente nulla:
X
ik (t) = 0
k
Per stabilire il segno da attribuire alle correnti di un nodo del circuito occorre:
ˆ
utilizzare per i generatori la convenzione del generatore e per i resistori la convenzione dell'utilizzatore,
ˆ
associare il segno - alla corrente che converge verso il nodo,
ˆ
associare il segno + alla corrente che lascia il nodo.
Con riferimento al circuito mostrato in Figura 2.1.23 si ha:
− i0 (t) + i (t) + iR0 (t) = 0
(2.1.73)
E' immediato vericare che la (2.1.73) porta alla (2.1.72).
R0 è
stata utilizzata la convenzione
vR0 (t)
v (t)
=
R0
R0
(2.1.74)
Tenedo conto che per il resistore di resistenza
dell'utilizzatore, la prima legge di Ohm si scrive:
iR0 (t) =
Sostituendo (2.1.74) in (2.1.72) si ricava la
caratteristica
del generatore reale di cor-
rente:
i (t) = i0 (t) −
Riportando su uno stesso piano
i−v
v (t)
R0
(2.1.75)
la caratteristica del generatore reale di corrente
e la caratteristica
v (t) = R i (t)
del carico R, si ricava il
(2.1.76)
punto di lavoro Q del carico R che esprime corrente e tensione
per il carico R durante il suo funzionamento:
2.1.8.7.2 Resistori in parallelo e legge del partitore di corrente
Risolvendo il sistema
costituito dalle relazioni in (2.1.62) e (2.1.63) si determinano le espressioni di corrente e
tensione del punto di lavoro Q del carico R:
iQ (t) =
R0
i0 (t)
R0 + R
54
(2.1.77)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.31: punto di lavoro del carico R
vQ (t) =
R R0
i0 (t) =
R0 + R
1
R
1
1
1 i0 (t) = G + G i0 (t)
+ R0
0
(2.1.78)
Attraverso (2.1.78) si deduce che due resistori in parallelo sono equivalenti ad un
resistore avente come resistenza l'inverso della somma delle conduttanze dei due resistori.
Rp =
1
G + G0
(2.1.79)
La (2.1.79) si estende facilmente al caso di n resistori connessi in parallelo:
Rp =
1
G1 + G2 + ... + Gi + ... + Gn
(2.1.80)
Attraverso (2.1.77) si deduce che in un parallelo, la corrente cha attraversa un carico
è una frazione della corrente del generatore ideale di corrente.
La (2.1.77) è nota con il nome di
legge del partitore di corrente.
2.1.8.7.3 Potenza istantanea assorbita e potenza istantanea generata
Consideriamo
la caratteristica del resistore lineare tempo-.invariante e del generatore ideale di corrente
mostrate in Figura 2.1.26
Figura 2.1.32: resistore lineare tempo invariante Vs generatore ideale di tensione
55
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La caratteristica del resistore lineare tempo-invariante giace nei quadranti I e III e ciò
implica che la potenza istantanea risulta essere sempre non negativa:
p (t) = v (t) i (t) ≥ 0
(2.1.81)
Visto che (2.1.81) risulta essere concorde con la convenzione dell'utilizzatore
istantanea è assorbita
dal resistore:
p (t) = pass. (t)
la potenza
.
La caratteristica del generatore ideale di tensione giace nei quadranti I e IV se risulta
i0 (t) > 0.
Questo fatto implica che
p (t) =
v (t) i (t) ≥ 0 se v (t) ≥ 0 (2.1.82.1)
v (t) i (t) < 0 se v (t) < 0 (2.1.82.2)
(2.1.82)
La potenza in (2.1.82.1) risulta essere concorde con la convenzione del generatore
v (t) ≥ 0 la potenza istantanea è generata dal generatore ideale di
tensione:p (t) = pgen. (t) ≥ 0; viceversa la potenza in (2.1.82.2) risulta essere discorde con
la convenzione del generatore e pertanto per v (t) < 0 la potenza istantanea è assorbita
dal generatore ideale di tensione:p (t) = pgen. (t) < 0.
e pertanto per
2.1.8.8 Lato alla Thevenin e lato alla Norton
Consideriamo la caratteristica del generatore reale di tensione e del generatore reale di
corrente mostrate in Figura 2.1.33:
Figura 2.1.33: generatore reale di tensione Vs generatore reale di corrente
Dal confronto tra le due gure è evidente che il generatore reale di tensione e il
generatore reale di corrente sono equivalenti se si pone:
v0 (t) = R0 i0 ⇔ i0 =
v0 (t)
R0
(2.1.83)
La formula in (2.1.83) è nota con il nome di formula di conversione Thevenin/Norton
lato alla Thevein
lato alla Norton o
e permette di trasformare un generatore reale di tensione, chiamato
bipolo alla Thevenin, in un generatore
bipolo alla Norton, e viceversa.
o
reale di corrente chiamato,
56
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.1.34: Thevenin/Norton
2.2 Problema di campo elettrostatico
2.2.1 Introduzione
Supponiamo che tutto lo spazio
S3
sia costituito da aria (costante dielettrica
ε0 ) e che al
suo interno ci sia una nuvola d'aria in cui è distribuita una carica con densità volumica
ρ cm/m3 .
Supponiamo che nelle vicinanze della nuvola carica ci sia un pezzo di vetro
su cui è distribuita una carica con densità volumica
ρ1
(costante dielettrica del vetro
ε1 ).
Supponiamo ancora che nelle vicinanze della nuvola carica e del pezzo di vetro carico vi
sia un conduttore carico avente una certa carica Q ottenuta attraverso un processo di
carica a causa di una tensione
V0 .
Supponiamo inne che ci sia pure un conduttore scarico
(ciò signica che la carica al suo interno è nulla). Se chiamiamo
la frontiera di tutto lo spazio
S3
Γ∞
(piano improrpio)
è possibile schematizzare quanto detto come mostrato
in Figura 2.2.1.
Si vuole determinare il campo elettrico
~e
in tutto lo spazio
S3.
In condizioni statiche (nel sistema appena descritto non ci sono cariche in movimento)
si ha che la carica nei conduttori si distribuisce nelle loro superci in modo tale che il
campo elettrico al loro interno risulti nullo.
Quindi in condizioni statiche la carica nei conduttori si distribuisce con densità superciale
σ C/m2 .
Il problema di campo elettrostatico consiste quindi nel determinare il campo elettrico
in tutto lo spazio
S3
meno lo spazio occupato dai conduttori dove il campo elettrico è
nullo.
57
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.1: problema di campo elettrostatico
Il processo attraverso cui si distribuisce la carica sul conduttore,
˛
Q=
σ ds
(2.2.1)
Γc
(essendo
di tensione
Γc la supercie del conduttore carico), avviene attraverso un generatore ideale
V0 ; questo processo avviene in un tempo nullo.
Consideriamo adesso il conduttore scarico. Anche se ha una carica nulla, poichè esso
si trova in condizioni statiche, si ha che gli elettroni al suo interno si distribuiscono sulla
supercie per eetto dell'induzione elettrostatica dovuta alle cariche circostanti in modo
che il campo elettrico al suo interno sia nullo.
In Figura 2.2.1 viene mostrato il processo di carica del conduttore e il fatto che in
entrambi i conduttori il campo elettrico è nullo.
Supponiamo per semplicità che all'interno dello spazio
S3
non ci siano conduttori
scarichi. Se così è il problema di campo elettrostatico si risolve attraverso il sistema di
equazioni:

~ · d~ = ρ

∇


∇
~ × ~e = ~0

d~ = ε~e



condizioni al contorno
(2.2.2)
2.2.2 Riformulazione del problema di campo elettrostatico
Come nel caso del problema di campo di corrente statico esiste un modo che permette di
semplicare notevolmente il problema di campo elettrostatico. Si introduce il
58
potenziale
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
scalare elettrico v = v (x, y, z), attraverso la nota formula:
~
~e = −∇v
e si riscrive il problema di campo elettrostatico (2.2.2) come segue:

~ · d~ = ρ

∇




~ × ~e = ~0
∇

~
~e = −∇v



d~ = ε~e




condizioni al contorno
(2.2.3.1)
(2.2.3.2)
(2.2.3.3)
(2.2.3.4)
(2.2.3.5)
(2.2.3)
Utilizzando la (2.2.3.3), la (2.2.3.2) viene automaticamente soddisfatta in quanto il
rotore del gradiente di una funzione scalare è sempre nullo, qualunque sia la funzione
scalare v considerata.
Sostituendo (2.2.3.3) in (2.2.3.4) si ricava:
~
d~ = −ε∇v
(2.2.4)
Sostiuendo inoltre (2.2.4) in (2.2.3.1) si ottiene:
~ · −ε∇v
~
∇
=ρ
Pertanto il problema di campo di corrente statico risulta equivalente al seguente:
(
~ · −ε∇v
~
∇
=ρ
(2.2.5.1)
(2.2.5)
condizioni al contorno (2.2.5.2)
L'equazione in (2.2.5.1) prende il nome di
Visto che nel dominio di analisi dato,
equazione di Poisson.
ρ 6= 0 solo nella nuvola carica e nel pezzo di vetro
carico, si ha che la soluzione del problema di campo elettrostatico è ovunque arminica
tranne che nella nuvola carica e nel pezzo di vetro carico.
Se
ε
è uniforme l'equazione di Poisson si scrive:
∇2 v = −
ρ
ε
(2.2.6)
e il problema di campo elettrostatico si semplica come segue:
(
∇2 v = − ρε
(2.2.7.1)
condizioni al contorno (2.2.7.2)
59
(2.2.7)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.2.3 Le condizioni al contorno
Bisogna specicare a questo punto le condizioni al contorno. Poichè il potenziale scalare
elettrico v è denito a meno di una costante possiamo porre:
v = 0V
in Γ∞
(2.2.8)
Inoltre dato che il campo elettrico all'interno del conduttore è nullo si ha che il
potenziale scalare elettrico v nel conduttore è costante e pari a
v = V0 V
V0
in Γc
(2.2.9)
Note le relazioni (2.2.8) e (2.2.9) (condizioni al contorno di tipo Dirichlet), il problema
di campo elettrostatico in (2.2.7) si scrive:

ρ
2

∇ v = − ε
v = 0 V in Γ∞


v = V0 V in Γc
(2.2.10.1)
(2.2.10.2)
(2.2.10.3)
(2.2.10)
Si dimostra che esiste ed è unica la soluzione al problema (2.2.10). Una volta trovato
~e,
~e, attraverso la (2.2.3.4) si determina il vettore induzione elettrica
d~. Inine nota l'induzione elettrica d~ nel conduttore a potenziale V0 , si conosce pure la
densità di carica suprciale σ del conduttore dato che
σ = d~ = d
(2.2.11)
il potenziale scalare elettrico v, utilizzando la (2.2.3.3) si determina il campo elettrico
noto il campo elettrico
e quindi la carica Q che si distribuisce sul conduttore facendo uso della relazione (2.2.1).
2.2.4 Metodo integrale per la risoluzione del problema di campo
elettrostatico
Il più semplice problema di campo elettrostatico è quello che prevede tutto lo spazio
omogeneo
S3
3
. In Figura (2.2.2) è illustrata una situazione in cui tutto lo spazio S è aria
(costante dielettrica
ρ1
e
ε0 )
con all'interno due nuvole con densità di carica rispettivamente
ρ2 .
La soluzione v del problema di campo elettrostatico può essere espressa mediante un
integrale; il potenziale scalare elettrico
v
in un punto
P
dello spazio
S3
ˆ
1
ρ (P0 )
v (P ) = v (x, y, z) =
dP0 =
ε0 S 3 4π rP P0
ˆ
1
ρ (x0 , y0 , z0 )
=
h
i1/2
ε0 S 3
4π (x − x0 )2 + (y − y0 )2 + (z − z0 )2
La (2.2.12) viene fuori dalla formula del potenziale scalare elettrico
carica puntiforme Q nel punto
P0 :
60
risulta dato da:
(2.2.12)
v
prodotto da una
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.2: spazio
S3
v (P ) = v (x, y, z) =
Denendo la
Q
4π ε0 rP P0
(2.2.13)
funzione di Green :
G (P, P0 ) =
si capisce che la (2.212) è un
ρ (P0 )
l'eccitazione,
1
4π rP P0
(2.2.14)
integrale di convoluzione :
1
v (P ) =
ε0
essendo
omogeneo
v (P )
ˆ
ρ (P0 ) G (P, P0 ) dP0
(2.2.15)
S3
la risposta e
G (P, P0 )
la funzione peso che dà una
misura dell'eccitazione.
Più grande è
G (P, P0 )
maggiore sarà il potenziale dovuto a
ρ
nel punto
P.
Si osservi
che la (2.2.15) è una relazione lineare infatti se si fa riferimento al sistema mostrato in
Figura 2.2.2 si osservano due distribuzioni di carica e quindi una densità volumica di
ρ1 + ρ2 . Se indichiamo con v1
ρ1 e con v2 quello dovuto
v (P ) = v1 (P ) + v2 (P )
carica pari a
il potenziale scalare elettrico nel punto
dovuto alla densità
a
che
ρ2 ,
P0
vista la linearità della soluzione si ha
Inserendo nel sistema mostrato in Figura 2.2.2 un pezzo di vetro (costante dielettrica
ε1 )
il problema elettrostatico da studiare risulta essere
non omogeneo.
Per un problema
del genere non risulta possibile utilizzare la (2.2.15) visto che si dovrebbe utilizzare una
funzione di Green diversa da quella in (2.2.14) di cui non si conosce l'espressione.
Nel caso del problema di campo elettrostatico non omogeneo bisogna quindi agire per
forza risolvendo l'equazione di Poisson con le opportune condizioni al contorno.
Se i materiali all'interno dello spazio
S3
realizzano una struttura omogenea a tratti
come mostrato in Figura 2.2.3 si riesce a trovare la funzione di Green sottoforma di
uno svilppo in serie e in questo caso risulta possibile utilizzare il metodo che fa uso
dell'integrale.
61
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.3: spazio
S 3 riempito
Supponiamo che tutto lo spazio
S3
con materiale omogeneo a tratti
sia riempito di materiale omogeneo (per esempio
aria) e supponiamo inoltre che vi sia una nuvoletta carica con densità di carica
ρ
come
mostrato in Figura 2.2.4
Figura 2.2.4: spazio
S3
riempito con materiale omogeneo
Si vuole determinare il potenziale scalare elettrico
Se indichiamo con
punto
P0
Λ
v
in un punto
P0
dello spazio
S3.
il volume della nuvoletta carica, il potenziale scalare elettrico nel
risulta dato da:
1
v (P ) =
ε0
ˆ
ρ (P0 ) G (P, P0 ) dP0
(2.2.16)
Λ
Decomponendo la nuvoletta di carica in n cubetti elementari di spigolo d e baricentro
Pi (xi , yi , zi )
è possibile approssimare la (2.2.16) per serie come segue:
n
d3 X
v (P ) '
h
4πε0
i=1
ρ (xi , yi , zi )
(x0 − xi )2 + (y0 − yi )2 + (z0 − zi )2
62
i1/2
(2.2.17)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Esistone dei problemi in cui tutto lo spazio
S3
risulta riempito con materiale omogeneo
ma che non si possono risolvere utilizzando metodi integrali:
uno di questi è quello
illustrato in Figura 2.2.5
Figura 2.2.5: Spazio
S3
riempito con materiale omogeneo
La gura induce ad utilizzare una formula per determinare il potenziale scalare elettrico
v
del tipo:
1
v (P0 ) =
ε0
ˆ
˛
ρ (P ) G (P, P0 ) dP +
Λ
σ (P ) G (P, P0 ) dP
(2.2.18)
Γc
Tutto però risulta vano perchè del conduttore si conosce soltanto il potenziale scalare
elettrico pari a
V0
e non la carica Q su di esso distribuita, ne tanto meno la sua densità
di carica superciale
σ(P0 ).
2.2.5 Dal problema di campo elettrostatico al concetto di capacità
Fino ad ora abbiamo visto diversi problemi di campo elettrostatico senza però addentrarci
notevolmente nella trattazione vista la complessità dei problemi stessi. Viene trattato
adesso un caso particolare di problema di campo elettrostatico con l'intento di denire il
concetto di
capacità.
Supponiamo che lo spazio
S3
sia aria (costante dielettrica
ε0 )
e che in esso vi sia
un dispositivo costituito da due dischi conduttori aventi spessore s raggio R, ortogonali
all'asse di simmetria passante per i loro centri, separati da un materiale dielettrico di
costante dielettrica
ε1 :
Il dispositivo così realizzato si chiama
allele.
capacitore
o
condensatore a faccie piane e par-
I due dischi del capacitore si chiamano armature del capacitore e come adesso
vedremo, hanno il compito di accumulare la carica elettrica. Il capacitore mostrato in
Figura 2.2.6 si dice che è
isolato
perchè si trova lontano da una qualsiasi sorgente di
campo elettromagnetico, inoltre si dice che è
scarico
perchè sulle armature non vi è
depositata alcuna carica.
Non appena cerchiamo di perturbare in qualche modo lo stato di equilibrio del capacitore scarico ed isolato inizia il problema di campo elettrostatico.
63
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.6: condensatore a faccie piane e parallele isolato
In Figura 2.2.7 viene mostrato il circuito attraverso cui si porta il capacitore dallo stato
di dispositivo isolato e scarico allo stato di dispositivo carico.
Come mostrato in gura, le armature del capacitore sono connesse ad un generatore
ideale di tensione costante
un resistore di resistenza
V0
Rf
mediante un lo conduttore reale modellizzato attraverso
ed un interruttore T in modo che sia possibile aprire e
chiudere il circuito così formato.
Figura 2.2.7: capacitore connesso al circuito di carica
Alla chiusura del tasto T, il capacitore si carica; tale fatto si può spiegare in modo
qualitativo.
Alla chiusura del tasto T, il generatore ideale di tensione costante
una pompa che preleva elettroni dall'armatura collegata al morsetto
l'armatura connessa al morsetto
morsetto
1
0
1.
V 0 funziona come
1 e li deposita sul-
Trascorso un certo tempo t, l'armatura connessa al
si trova una carica complessiva positiva e l'armatura connessa al morsetto
1
0
si trova una carica complessiva negativa.
Il processo di separazione della carica innescato dalla chiusura del tasto T si arresta
quando tra le due armature si crea un campo elettrico
64
~e
tale da opporsi ad una ulteriore
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
separazione della carica. Tale campo elettrico risulta essere ortogonale alle armature del
capacitore e risulta orientato dal disco carico positivamente al disco carico negativamente.
1
Considerando un qualunque percorso interno al dielettrico che va dal morsetto
morsetto
0
1,
si determina facilmente la tensione
vc (t)
al
tra le armature del capacitore:
ˆ
vc (t) =
_
110
~
~e · dl
(2.2.19)
La tensione in (2.2.19) risulta essere chiaramente in contrapposizione con la tensione
V0
del generatore ideale.
All'istatnte t=0, quando si chiude l'interruttore, la corrente ic
risulta massima e pari al valore
Mano a mano che trascorre il
mantre la tensione
vc (t)
tende
(t) circolante nel circuito
0
v c (t) ai morsetti 1 1 risulta nulla.
tempo t, la corrente ic (t) tende asintoticamente a zero
asintoticamente alla tensione V0 .
V0
Rf , mentre la tensione
In Figura 2.2.8 vengono mostrate le curve, seppur qualitative, di corrente e tensione
per il capacitore (tali curve saranno ricavate analiticamente nella prossima sezione):
Figura 2.2.8: carica del condensatore: corrente e tensione
Una volta che il capacitore acquista ai suoi capi la tensione
V0 ,
possiamo aprire l'in-
teruttore T: si ottiene un dispositivo ai cui capi si ha una tensione
V0 :
nel processo di
carica del capacitore l'energia elettrica fornita dal generatore ideale di tensione è stata
trasformata in energia potenziale (Figura 2.2.9)
Per scaricare il capacitore basta collegare i morsetti 1 e 1' attraverso un lo conduttore
reale. In questo modo si verica che l'energia potenziale precedentemente accumulata si
trasforma in energia cinetica (Figura 2.2.10)
Dopo aver capito, qualitativamente, come si carica e si scarica il capacitore, concentriamo l'attenzione sul capacitore completamente carico. La situazione statica che si vuole
studiare è ben descritta in Figura 2.2.9: si vuole determinare il campo elettrico
~e
inun
3
qualunque punto dello spazio S .
Il problema elettrostatico che si vuole caratterizzare è a simmetria assiale e per tale
ragione ssiamo un sistema di riferimento in modo tale che l'asse del capacitore coincida
con l'asse
~z.
Inoltre facciano in modo che il baricentro del capacitore coincida con l'orig-
ine del sistema di riferimento. Una rappresentazione per sezione di quanto detto viene
mostrato in Figura 2.2.11:
65
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.9: Capacitore carico ed isolato
Dato che la d.d.p tra le armature del capacitore è
connessa al morsetto 1 sia a potenziale
potenziale
V0 /2
V0 ,
supponiamo che l'armatura
e che quella connessa al morsetto 1' sia a
−V0 /2.
Vista la simmetria del problema si ha che:
v (r, z) = v (−r, z)
(2.2.20)
quindi possiamo arontare il problema di campo elettrostatico solo per
che per
r<0
r > 0,
visto
la situazione è del tutto analoga.
Osserviamo pure che:
v (r, −z) = −v (r, z)
Secondo (2.2.21) il potenziale scalare elettrico
(r, −z)
dierisce soltanto per un segno
campo elettrostatico solo per
Le condizioni
−
v
tra due punti di coordinate
S3
(r, z)
e
, quindi possiamo arontare il problema di
z > 0.
(
r > 0 (2.2.22.1)
z > 0 (2.2.22.2)
deniscono pertanto il dominio di analisi elettrostatica
dello spazio
(2.2.21)
(2.2.22)
D
che risulta essere un quarto
meno lo spazio occupato dalla quarta parte dell'armatura connessa al
morsetto 1 del capacitore visto che in esso il campo elettrico risulta nullo.
In Figura 2.2.12 viene mostrata una sezione del dominio di analisi
D
La frontiera di detta sezione risulta essere costituita dall'asse r positivo, dall'asse z
positivo meno la spessore s dell'armatura, dalla retta impropria
Γ∞ ,
dal contorno
Γc
della sezione della quarta parte dell'armatura del capacitore.
A questo punto appare evidente perchè si è scelto di porre a potenziale
matura e a potenziale
−V0 /2
l'altra armatura:
66
V0 /2
un'ar-
in questo modo il potenziale scalare
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.10: capacitore scarico ed isolato
elettrico risulta essere nullo sull'asse r e per continuità uguale al potenziale scelto per la
retta impropria
Γ∞ .
Su
Γc
il potenziale scalare elettrico è
V0 /2
; in questo modo stiamo
specicando due condizioni di tipo Dirichlet:
v=0
su asse r e Γ∞
v = V0 /2
su Γc
(2.2.23)
Sulla rimanente parte della frontiera della sezione di D non è possibile specicare una
condizione di tipo Dirichlet.
Cerchiamo di capire perchè sull'asse z positivo meno la spessore s non è possibile
scrivere una condizione al contorno di tipo Dirichlet.
Sappiamo con buona approssimazione che, sull'asse z, partendo dall'origine e dirigendosi verso l'armatura del capacitore, attraversando il dielettrico
linearmente.
ε1 ,
il potenziale cresce
Nella parte dell'asse che sta al di fuori del capacitore il potenziale deve
diminuire e tendere a zero all'innito.
Siccome in questa parte di asse z si trova la disomogeneità
ca l'andamento del potenziale scalare elettrico
v
ε0 ,
nulla si può dire cir-
e quindi non è possibile scrivere una
condizione al contorno di tipo Dirichlet.
Osserviamo che il problema di campo elettrostatico non presenta alcun accumulo di
carica sottoforma di densità volumica di carica
che si distribuisce con densità
σ
ρ in quanto l'unica carica presente è quella
sulla supercie dell'armatura del capacitore; ciò implica
che la soluzione del problema elettrostatico in D e quindi pure in
S3
è armonica.
Appare chiaro che la formulazione matematica del problema elettrostatico trattato
è del tutto simile a quella del problema di campo di corrente statico: occorre quindi
specicare una condizione al contorno di tipo Neuman per determinare la soluzione del
problema.
Per far questo consideriamo due punti, A e B, aventi la stessa ordinata z e ascissa
e opposta come mostrato in Figura 2.2.12.
67
Il potenziale scalare elettrico
v
può avere
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.11: condesatore carico ed isolato in sezione
uno qualunque degli andamenti mostrati in Figura 2.2.12; ad ogni modo anche se non
sappiamo esattamente quali sono le linee del potenziale scalare elettrico si ha che:
∂
v |r=0 = 0
∂r
(2.2.24)
cioè in r=0 tutte le tangenti alle linee del potenziale sono orizzontali. A questo punto
come si può ben vedere da Figura 2.2.12, l'asse r e la normale
n̂,
sono opposti e quindi
la (2.2.24) equivale a:
∂
v |r=0 = 0 cioè
∂n
∂
v = 0 su asse z positivo meno spessore s
∂n
(2.2.25)
Quindi si tratta di risolvere il problema di campo elettrostatico:
 ~ ε∇v
~

∇
=0




v=0

v = V20



∂
∂n v = 0
in D
su asse r positivo e Γ∞
su Γc
su asse z positivo meno spessore s
(2.2.26)
magari mediante un opportuno codice di calcolo numerico.
Da un punto di vista molto qualitativo possiamo dire che le superci di livello per il
potenziale elettrostatico
v
sono quelle mostrate in Figura 2.2.13:
Noto il potenziale scalare elettrico v, attraverso la 2.2.3.3 si trova il campo elettrico
noto il campo elettrica
~e,attraverso
la 2.2.3.4 si trova l'induzione elettrica
carica Q che si distribuisce con densità
σ
d~ e
~e,
quindi la
sull'armatura del capacitore:
˛
Q=
σ ds
Γc
68
(2.2.27)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.12: sezione del dominio di analisi D
Figura 2.2.13: superci di livello
Le equazioni in (2.2.26) sono tutte omogenee tranne la terza:
v=
V0
2
Siccome tutte le equazioni sono lineari si verica che se raddoppia
carica Q sull'armatura del capacitore.
V0
raddoppia la
Il fattore di proporzionalià tra la carica Q dis-
tribuita sulla supercie del capacitore e la tensione applicata
V0
, si chiama
capacità C
del capacitore:
˛
Q=
σ ds = C V0
Γc
69
(2.2.28)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Se consideriamo le superci di livello a passo p=5 V e indichiamo con d la distanza
tra due superci di livello successive si può determinare il modulo del campo elettrico
~e
attraverso la relazione:
e=
Il campo elettrico
5V
p
=
d
d
(2.2.29)
~e risulta essere sempre in direzione ortogonale alla supercie di livello
con verso opposto al verso di crescita del potenziale scalare elettrico v.
Noto il modulo del campo elettrico
elettrica
~e
si conosce pure il modulo del vettore induzione
d~:
5V
d=ε
=
d
Se è
ε1 = 10ε0
(
ε0
ε1
5V
d
5V
d
(2.2.30)
si ha che il campo è prevalentemente all'interno del capacitore.
Se indichiamo con L la distanza tra le armature del capacitore si trova un'espressione
molto qualitativa della carica Q:
Q = σπR2 = ε1
V0
πR2
L
(2.2.31)
La relazione (2.2.28) vale anche nel caso in cui la tensione ai capi del capacitore è
lentamente variabile nel tempo,
v0 (t);
in tal caso si ha:
q (t) = C v0 (t)
(2.2.32)
Derivando rispetto al tempo quest'ultima espressione si ricava la corrente che attraversa
il capacitore:
i0 (t) =
dQ (t)
d
= C v0 (t)
dt
dt
Figura 2.2.14: capacitore connesso ad una pila
70
(2.2.33)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.15: carica e scarica del capacitore
2.2.6 Circuito del primo ordine RC: carica e scarica di un capacitore
Consideriamo il circuito elettrico mostrato in Figura 2.2.15.
− l'interruttore T sia aperto; in questo modo la tensione
Supponiamo che all'istante t=0
ai capi del capacitore è zero:
v0 0− = 0 V
(2.2.34)
Per t>0 (chiusura dell'interruttore T) si può scrivere la LKT:
v0 (t) − V0 + Rf i0 (t) = 0
(2.2.35)
Utilizzando la (2.2.33) la (2.2.35) si scrive:
v0 (t) − V0 + Rf C
Posto
τ = Rf C
d
v0 (t) = 0
dt
(2.2.36)
e riordinando i termini, la (2.2.36) si scrive:
d
1
1
v0 (t) + v0 (t) = V0
dt
τ
τ
(2.2.37)
Le equazioni (2.2.34), (2.2.37) costituiscono il problema di Cauchy che permette di
determinare la tensione ai capi del capacitore per t>0:
(
d
dt v0 (t)
+ τ1 v0 (t) = τ1 V0
v0 (0) = 0
Risoluzione del problema di Cauchy
(2.2.38)
Determiniamo l'integrale generale della (2.2.37)
L'integrale generale della (2.2.37) è la somma tra l'integrale generale dell'omogenea
associata alla (2.2.37) e l'integrale particolare della (2.2.37):
71
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
v0 (t) = v0omog. (t) + v0part. (t)
(2.2.39)
Omogenea associata
d
1
v0 (t) + v0 (t) = 0
dt
τ
Equazione caratteristica
λ+
1
=0
τ
λ=−
1
τ
Integrale generale omogenea associata
t
v0omog. (t) = k e− τ
Ricerca dell'integrale particolare
V0 ,
(2.2.40)
Visto che il termine noto della (2.2.37) è la costante
l'integrale particolare va ricercato tra le costanti.
Posto
v0 (t) = v0part. (t) = cost.
, la (2.2.37) si scrive:
1
1
0 + v0part. (t) = V0
τ
τ
da cui si ricava:
v0part. (t) = V0
(2.2.41)
Sostituendo (2.2.40) e (2.2.41) in (3.3.39) si ricava l'integrale generale della (2.2.37):
t
v0 (t) = k e− τ + V0
(2.2.42)
Per determinare la costante k si utilizza la condizione iniziale data in (2.2.34)
0
v0 (0) = k e− τ + V0 = 0
k = −V0
(2.2.43)
Sostituendo (2.2.43) in (2.2.42) si ricava l'espressione analitica della tensione ai capi
del capacitore:
t
v0 (t) = V0 1 − e− τ
La (2.2.44) è l'espressione analitica della tensione
Visto che
72
vc (t)
(2.2.44)
mostrata in Figura 2.2.8.
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
lim v0 (t) = 0
t→0+
e che
v 0− = 0
ne segue che la tensione ai capi del capacitore è una funzione continua del tempo.
Per determinare la corrente che attraversa il capacitore basta sostituire (2.2.44) in
(2.2.33)
i0 (t) = C
d
V0 − t
v0 (t) =
e τ
dt
Rf
La (2.2.45) è l'espressione analitica della corrente
ic (t)
(2.2.45)
mostrata in Figura 2.2.8.
2.2.7 Generalità sui capacitori
I capacitori sono elementi a due morsetti capaci di immagazzinare cariche elettriche. In
ogni istante di tempo t, la carica immagazzinata dal capacitore e la tensione ai suoi capi
soddisfano ad una relazione denita nel piano V-q, chiamata
caratteristica del capacitore.
Quello studiato no ad ora è il capacitore lineare tempo invariante. Come nel caso dei
resistori, anche per i capacitori possono esserci quattro possibilità.
2.2.7.1 Capacitore lineare tempo-invariante
Il capacitore
lineare tempo-invariante
è caratterizzato dall'equazione caratteristica:
q (t) = C v0 (t)
La capacità C per un capacitore lineare tempo invariante non dipene nè da
t;
(2.2.46)
v0
nè da
dunque nel piano V-q la caratteristica del capacitore lineare tempo-invariante è una
retta passante per l'origine di pendenza C:
Figura 2.2.16: caratteristica del capacitore lineare tempo-invariante
73
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Derivando rispetto al tempo la (2.2.46) si ottiene l'espressione della corrente che
attraversa il capacitore:
i (t) =
dispositivo a memoria.
Si dice che il capacitore è un
infatti la corrente
i (t),
dq (t)
d
= C v (t)
dt
dt
(2.2.47)
Ciò si capisce subito dalla (2.2.47),
ad un certo istante di tempo t non dipende solo dalla tensione
all'istante t ma anche dagliistanti di tempo immediatamente precedenti. Per convincerci
di ciò basta scrivere la (2.2.47) tenendo conto della denizione di derivata:
i (t) =
La corrente all'istante
tensione all'istante
t0
t
dq (t)
d
v (t) − v (t0 )
= C v (t) = C lim
t→t
dt
dt
t − t0
0
non dipende solo dalla tensione all'istante
t0
essendo
un'istante di tempo precedente a
(2.2.48)
t,
ma anche dalla
t.
Osservando la (2.2.48) potrebbe sembrare che il valore della corrente all'istante di
tempo
t dipenda da un passato estremamente precedente;
in realtà invertendo la (2.2.47)
appare in modo chiaro che il capacitore è un dispositivo che tiene conto di tutto il passato.
Possiamo invertire la (2.2.47) integrando nell'intervallo di tempo
ˆ
ˆ
t
t
i (τ ) dτ = C
t0
t0
ˆ
ˆ
d
v (τ ) dτ = C
dτ
v(t)
v(t0 )
[t0 , t]:
dv (τ ) = C [v (τ )]vv(t)
t
0
t
i (τ ) dτ = C [v (t) − v (t0 )]
t0
v (t) = v (t0 ) +
ˆ
1
C
t
i (τ ) dτ
(2.2.49)
t0
Secondo (2.2.49) la tensione ai capi del capacitore lineare tempo-invariante all'istante
di tempo
t,
dipende dalla tensione all'istante di tempo
della corrente
i (t),
t0 e da
[t0 , t].
tutta la storia passata
cioè dalla corrente in tutto l'intervallo
Quindi per un capacitore lineare tempo-invariante tutto il passato conta per la formazione del presente.
Passando al limite per
t → t0 ,
la (2.2.49) fornisce:
1
lim v (t) = v (t0 ) +
lim
t→t0
C t→t0
ˆ
t
i (τ ) dτ = v (t0 )
(2.2.50)
t0
Secondo (2.2.50) è evidente che la tensione ai capi del capacitore è una funzione
continua in
t0 .
2.2.7.1.1 Energia immagazzinata da un capacitore lineare tempo-invariante
sideriamo il capacitore mostrato in Figura 2.2.17:
Si osservi che per esso vale la convenzione dell'utilizzatore come per il resistore.
Supponiamo che all'istante di tempo
t = 0−
74
esso sia scarico:
Con-
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.17: convenzione dell'utilizzatore
v 0− = 0 V
(2.2.51)
Alimentando il capacitore, per esempio come mostrato in Figura 2.2.15, si ha che al
tempo
t,
avrà tensione
dall'istante
t=
v t
0− all'istante
ˆ
e corrente
t=t
(t̄) =
ˆ
t
p (t) dt =
0−
L'energia immagazzinata dal capacitore
vale:
ˆ
t
i (t̄).
0−
ˆ
=C
t
v (i) i (t) dt =
v (t) C
0−
d
v (t) dt =
dt
t
2
1
v (t) dv = Cv t
2
0−
(2.2.52)
La (2.2.52) fa capire che la grandezza importante è la tensione e non la corrente.
Utilizzando la (2.2.46) ponendo
t = t
è chiaro che la (2.2.52) si può scrivere nelle
seguenti forme equivalenti:
2 1
1q t 2
1
(t̄) = Cv t = q t v t =
2
2
2 C
(2.2.53)
2.2.7.2 Capacitore lineare tempo-variante
Se il capacitore è lineare tempo-variante, la sua caratteristica è una rette passante per
l'origine del piano V-q la cui pendenza dipende dal valore assunto dalla capacità che è
una funzione del tempo
t:
q (t) = C (t) v (t)
(2.2.54)
Derivando rispetto al tempo la (2.2.54) si determina l'espressione della corrente che
attraversa il capacitore lineare tempo-variante:
i (t) =
d
d
d
q (t) = C (t) v (t) + v (t) C (t)
dt
dt
dt
75
(2.2.55)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.18: caratteristica capacitore lineare tempo-variante
2.2.7.2.1 Energia immagazzinata da un capacitore lineare tempo-variante
Consid-
eriamo un condensatore lineare tempo-variante e supponiamo che all'istante di tempo
t = 0−
esso sia scarico:
v 0− = 0 V
(2.2.56)
Alimentando il capacitore, per esempio come mostrato in Figura 2.2.15, si ha che al
tempo
t,
avrà tensione
dall'istante
t=
v t
0− all'istante
e corrente
t=t
ˆ
i (t̄).
vale:
ˆ
t
(t̄) =
t
v (t)
=
t
p (t) dt =
0−
ˆ
L'energia immagazzinata dal capacitore
0−
v (i) i (t) dt =
0−
d
d
C (t) v (t) + v (t) C (t) dt
dt
dt
(2.2.57)
2.2.7.3 Capacitore non lineare tempo-invariante
Il capacitore non lineare tempo-invariante è denito tramite una relazione del tipo:
f (q, v) = 0
(2.2.58)
La caratteristica pertanto può essere una retta non passante per l'origine o una curva
di tipo quadratico come mostrato in Figura 2.2.19:
2.2.7.3.1 Energia immagazzinata da un capacitore non lineare tempo-invariante
−
L'energia immagazzinata dal capacitore dall'istante t = 0 all'istante t = t vale:
ˆ
ˆ
t
(t̄) =
t
p (t) dt =
0−
v (i) i (t) dt =
0−
76
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.2.19: caratteristica del capacitore lineare tempo-invariante
ˆ
t
=
v (i)
0−
d
q (t) dt =
dt
ˆ q(t)
v (q) dq
(2.2.59)
q(0− )
Si tenga presente che per il capacitore non lineare tempo-invariante NON vale la
relazione
d
i (t) = C dt
v (t)
2.2.7.4 Capacitore non lineare tempo-variante
Il capacitore non lineare tempo-variante è denito tramite una relazione del tipo:
f (q, v, t) = 0
Figura 2.2.20: caratteristica del capacitore non lineare tempo-variante
2.3 Problema di campo magnetostatico
2.3.1 Introduzione
Il problema di campo magnetostatico è dato dal seguente sistema:
77
(2.2.60)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici

~ · ~b = 0

∇



∇
~ × ~h = ~j
~b = µ~h




condizioni al contorno
(2.3.1.1)
(2.3.1.2)
(2.3.1.3)
(2.3.1.4)
Esso permette di determinare in tutti i punti dello spazio
l'induzione magnetica
~b,
nota la densità di corrente
S3,
(2.3.1)
il campo magnetico
~h
e
~j .
Dato che nei problemi di campo magnetostatico l'unica sorgente è la densità di corrente
~j ,
dall'equazione di continuità:
~ · ~j + d ρ = 0
∇
dt
si deduce che deve essere:
~ · ~j = 0
∇
(2.3.2)
Illustriamo alcuni tipici problema di campo magnetostatico.
Consideriamo un lo di rame di sezione S molto piccola, percorso da una corrente I
e supponiamo che lo spazio circostante il lo sia aria.
Dal punto di vista magnetico
tutto lo spazio presenta materiali omogenei visto che la permeabilità magnetica è
µ0 =
4π10−7 H/m.
Visto che si è stabilito di scegliere la sezione S del lo di rame molto piccola si ha che
la densità di corrente
di
~j
è ortogonale alla sezione S del lo, in direzione della corrente I e
modulo ~
j = I/S .
Figura 2.3.1: problema di campo magnetostatico omogeneo
Nota la densità di corrente
~j
nel lo di rame, attraverso il problema di campo magne-
tostatico si determinano in ogni punto dello spazio i campi
~h e ~b.
Supponiamo che ci sia un altro lo di rame che sia sorgente del campo magnetico.
Immaginiamo che tale lo di rame sia massiccio.
Dato che il lo di rame è massiccio per determinare la densità di corrente ~
j è opportuno
prima risolvere un problema di campo di corrente statico.
Supponiamo di aver trovato la densità di corrente
Quindi adesso il problema è trovare i campi
~h
nota la densità di corrente nei due li di rame.
78
e ~
b
~j
pure nel lo di rame massiccio.
in qualunque punto dello spazio
S3
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Come nel caso precedente lo spazio è a mezzi omogenei dal punto di vista magnetico
visto che ovunque la permeabilità magnetica è
µ0 .
Figura 2.3.2: problema di campo magnetostatico omogeneo
Non è così se in prossimità dei due li di rame si va ad inserire un pezzo di ferro;
in questo caso il problema di campo magnetostatico diviene non omogeneo in quanto è
stato introdotto un materiale a dierente comportamento magnetico.
Figura 2.3.3: problema di campo magnetostatico non omogeneo
La permeabilità magnetica dei materiali viene descritta nel piano B-H. Se il materiale
è lineare vale la relazione
~b = µ~h
e la permeabilità magnetica risulta essere la pendenza
di una retta del piano B-H:
Viceversa se il materiale è non lineare ed isteretico, come ad esempio il ferro, il legame
costitutivo è dato dal ciclo di isteresi.
Il problema di campo magnetostatico descritto in Figura 2..3.3 si semplica notevolmente se si cerca di appossimare il comportamento magnetico del ferro mediante una
relazione lineare del tipo:
~b = µ~h.
Se le correnti elettriche in gioco, in questo caso le correnti che circolano nei due li
di rame, sono di intensità tali da non far saturare il ferro, possiamo approssimare la
caratteristica del ferro, come nel caso dei materiali lineari, ad una retta passante per
l'origine, la cui pendenza è
µ,diecimila
volte più grande della pendenza
rame.
79
µ0
dell'aria e del
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.4: materiale magnetico lineare
In questo modo il problema rimane sempre non omogeneo, in quanto ci sono punti
dello spazio in cui la permeabilità magnetica è
µ0
e punti in cui è
µ,
ma risulta meno
complicato in quanto lineare.
2.3.2 Riformulazione del problema di campo magnetostatico
Ci proponiamo di risolvere il problema di trovare i campi ~
h e ~b in tutto lo spazio costituito
dai due li di rame percorsi da correnti tali da non fare saturare il pezzo di ferro situato
in prossimità di essi; il materiale che separa i li di rame dal pezzo di ferro è aria.
Esistono diversi modi per risolvere un problema del genere; qui ci adiamo al metodo
che fa uso del
potenziale vettore magnetico ~a.
L'equazione (2.3.1.1) suggerisce di introdurre una nuova variabile, per l'appunto il
potenziale vettore magnetico
magnetica
~a,
in modo che il rotore di
~a
coincida con l'induzione
~b:
~b = ∇
~ × ~a
(2.3.3)
Introducendo la (2.3.3), la (2.3.1.1) è automaticamente soddisfatta essendo nulla la
divergenza del rotore di un vettore.
D'altra parte sappiamo che sono inniti i campi vettoriali
~a
tali da soddisfare la
condizione data in (2.3.3), infatti si ha che:
~b = ∇
~ × ~a + ∇ψ
~
essendo
ψ
una funzione scalare.
Per rendere unico il potenziale vettore magnetico
dizione sulla divergenza del vettore magnetico
~a
~a
occorre specicare pure una con-
in accordo con il teorema di Helmoltz.
Vedremo tra breve che il problema di campo magnetostatico suggerisce di prendere tale
condizione come segue:
~ · ~a = 0
∇
80
(2.3.4)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Quindi il potenziale vettore magnetico
~a
viene denito mediante le relazioni (2.2.3),
(2.2.4).
Sostituendo (2.2.3) in (2.3.1.3) si ricava:
~h = 1 ∇
~ × ~a
µ
(2.3.5)
Sostituendo (2.3.5) in (2.3.1.2) si ricava:
~ ×
∇
1~
∇ × ~a = ~j
µ
(2.3.6)
Se la permeabilità è costante nell'aria nei due li e nel ferro, la (2.3.6) diventa:
~ × ∇ × ~a = µ~j
∇
(2.3.7)
~ ×∇
~ × ~a = ∇
~ ∇
~ · ~a − ∇2~a
∇
(2.3.8)
~ ∇
~ · ~a − ∇2~a = µ~j
∇
(2.3.9)
Utilizzando l'identità vettoriale:
la (2.3.7) diventa:
A questo punto è chiaro che la scelta fatta in (2.3.4) è la migliore possibile visto che
grazie ad essa la (2.3.9) si semplica come segue:
∇2~a = −µ~j
La (2.3.10) prende il nome di
(2.3.10)
equazione vettoriale di Poisson
e in forma scalare si
scrive:

2

∇ ax = −µjx
∇2 ay = −µjy

 2
∇ az = −µjz
(2.3.1.1)
(2.3.1.2)
(2.3.1.3)
(2.3.11)
Nota l'equazione di Poisson, il problema di campo magnetostatico si scrive:
(
∇2~a = −µ~j
(2.3.12.1)
condiizioni al contorno (2.3.12.2)
(2.3.12)
Il problema di campo magnetostatico (2.3.12) si può risolvere con i metodi numerici
usando un codice di calcolo.
Ricavato il potenziale vettore magnetico
(2.3.3) si ricave il vettore induzione magnetica
~b,
mediante la relazione (2.3.1.3) si ricava il campo magnetico
81
~a,
mediante la
noto il vettore induzione magnetica
~h.
~b
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.3.3 Metodo integrale per la risoluzione del problema di campo
magnetostatico
Supponiamo di voler determinare i campi
~b
ed
~h
nel caso omogeneo mostrato in Figura
2.3.5.
Figura 2.3.5: problema di campo magnetostatico
Il problema di campo magnetostatico nel caso omogeneo risulta matamaticamente
analogo, al problema di campo elettrostatico.
In Figura 2.3.6 sono messi a confronto il problema di campo elettrostatico e il problema
di campo magnetostatico: nel primo caso la sorgente del campo è la densità volumica di
carica
ρ
di una nuvoletta d'aria, nel secondo caso è il vettore densità di corrente
lo di rame massiccio.
Figura 2.3.6: analogia tra problemi di campo
Assumendo nullo il potenziale scalare elettrico
v = 0V
v
all'innito:
in Γ∞
l'equazione di Poisson che deriva dal problema di campo elettrostatico
82
~j
in un
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
∇2 v = −
ρ
ε0
ammette un'unica soluzione data da
v (P ) =
1
ε0
ˆ
Ω
ρ (P0 )
dP0
4πr
(2.3.13)
Per analogia matematica, assumendo nullo il potenziale vettore magnetico ~
a all'innito:


ax = 0 in Γ∞
ay = 0 in Γ∞


az = 0 in Γ∞
(2.3.14)
l'equazione vettoriale di Poisson che deriva dal problema di campo magnetostatico

2

∇ ax = −µjx
∇2 ay = −µjy

 2
∇ az = −µjz
ammette un'unica soluzione data da

´

ax (P ) = µ0 ´Ω
ay (P ) = µ0 Ω

´

az (P ) = µ0 Ω
jx (P0 )
4πr dP0
jy (P0 )
4πr dP0
jz (P0 )
4πr dP0
(2.3.15)
La (2.3.15) in forma compatta si scrive:
ˆ ~
j (P0 )
~a (P ) = µ0
dP0
Ω 4πr
La (2.3.16) esprime il potenziale vettore magnetico
massiccio di volume
Ω
(2.3.16)
~a
nel caso di un lo di rame
caratterizzato da una densità di corrente
Noto il potenziale vettore magnetico
minare pure l'induzione magnetica
~b (P ) = ∇
~ × ~a (P ) = ∇
~ ×
~b,
~a
~j .
in un punto P dello spazio è possibile deter-
nel medesimo punto P, utilizzando la (2.3.3):
!
ˆ
ˆ ~
j (P0 )
µ0
~ ×
µ0
dP0 =
∇
4π Ω
Ω 4πr
~j (P0 )
r
Utilizzando le coordinate cartesiane si ha:
~ ×
∇
~j (P0 )
r
!
=
x̂
ŷ
ẑ
∂
∂x
jx (P0 )
r
∂
∂y
jy (P0 )
r
∂
∂z
jz (P0 )
r
83
=
!
dP0
(2.3.17)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
= x̂
∂ jx (P0 )
∂ jy (P0 )
∂ jz (P0 )
∂ jy (P0 )
∂ jz (P0 )
∂ jx (P0 )
+ŷ
+ẑ
−
−
−
∂y r
∂z r
∂z r
∂x r
∂x r
∂y r
(2.3.18)
Tenendo conto che
∂ jz (P0 )
1
∂
= jz (P0 )
n
o1/2 =
∂x r
∂x
(x − x0 )2 + (y − y0 )2 + (z − z0 )2
(x − x0 )
(x − x0 )
− jz (P0 ) n
o3/2 = −jz (P0 )
r3
(x − x0 )2 + (y − y0 )2 + (z − z0 )2
(2.3.19)
∂ jx (P0 )
1
∂
= jx (P0 )
o1/2 =
∂y r
∂y n
2
2
2
(x − x0 ) + (y − y0 ) + (z − z0 )
(y − y0 )
(y − y0 )
− jx (P0 ) n
o3/2 = −jz (P0 )
r3
(x − x0 )2 + (y − y0 )2 + (z − z0 )2
(2.3.20)
∂ jy (P0 )
∂
1
= jy (P0 )
n
o1/2 =
∂z r
∂z
2
2
2
(x − x0 ) + (y − y0 ) + (z − z0 )
(z − z0 )
(z − z0 )
− jy (P0 ) n
o3/2 = −jy (P0 )
r3
(x − x0 )2 + (y − y0 )2 + (z − z0 )2
(2.3.21)
la (2.3.18) diventa:
~ ×
∇
~j (P0 )
r
!
=−
~j × r̂
1~
j × ~r = − 2
3
r
r
(2.3.22)
sostituendo inne (2.3.22) in (2.3.18) si ricava:
~b (P ) = − µ0
4π
ˆ ~
j × r̂
dP0
2
Ω r
(2.3.23)
La (2.3.16) si può particolarizzare al caso di lo di rame non massiccio.
Osserviamo innanzitutto che si può scrivere
~
~jdP0 = ~j dl dS = j dS dl
essendo dS l'elemento di sezione del lo massiccio e
come ~
j
84
~
dl
un tratto elementare diretto
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.7: problema di campo magnetostatico
Fatta questa osservazione l'integrale in (2.3.16) si può sviluppare come segue:
ˆ ˛
~a (P ) = µ0
S
C
j ~
dldS = µ0
4πr
˛ ˆ
j ~
dS
dl = µ0
4πr
S
C
˛
C
Sj ~
dl = µ0
4πr
˛
C
I ~
dl
4πr
ottendo così l'espressione
˛
I ~
dl
4πr
~a (P ) = µ0
C
(2.3.24)
essendo C la lunghezza del lo di rame non massiccio
La (2.3.24) resta valida purchè si assuma che la sezione S del lo di rame sia molto
piccola.
Il potenziale vettore magnetico
~a in
un punto P dello spazio dovuto a N li conduttori
non massicci percorsi da corrente è dato da:
~a (P ) = µ0
N
X
˛
Ik
Ck
k=1
Dividendo il k-esimo lo conduttore in
una
formula approssimata
M
1 ~
dl
4πr
trattini di lunghezza
(2.3.25)
4l
possiamo scrivere
della (2.3.18):
~a (P ) = µ0
N
X
Ik
k=1
M
X
1 ~
4lj
4πrj
j=1
In modo analogo si determina l'espressione del vettore induzione magnetica
(2.3.26)
~b
in un
punto P dovuto a N li conduttori non massicci percorsi da corrente:
~b (P ) = − µ0
4π
N
X
k=1
85
˛
Ik
Ck
~ × r̂
dl
r2
(2.3.27)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.3.4 Legge dell'azione elementare
Il contributo elementare di potenziale vettore magnetico
densità di
corrente ~
j
che attraversa il cubetto elementare
d~a
dP0
nel punto P dovuto alla
si ricava facilmente dalla
(2.3.16):
d~a (P ) = µ0
Questo risultato è noto con il nome di
~j (P0 )
dP0
4πr
(2.3.28)
legge dell'azione elementare
ed esprime il fatto
che in un qualunque punto P dello spazio il contributo elementare del potenziale vettore
magnetico
d~a
risulta essere parallelo alla densità di corrente
~j
che attraversa il cubetto
elemetare del lo conduttore massiccio.
Figura 2.3.8: legge dell'azione elementare
2.3.5 Strutture ferromagnetiche
Ci sone delle situazioni particolari che ci consentono di condurre l'analisi elettromagnetica
(cioè trovare i campi) senza risolvere nè equazioni dierenziali, nè equazioni integrali.
Ovviamente per far questo bisogna ipotizzare delle situazioni geometriche e siche
assai semplici e incominciare a fare delle approssimazioni piuttosto pesanti, e ciò vuol
dire che i risultati trovati saranno delle approssimazioni, per esempio del 10-15% della
realtà sica.
Si possono fare esercizi di campo magnetico, senza bisogno di avere un programma di calcolo di campi magnetici, ma semplicemente risolvendo un circuito elettrico
analogo. Vediamo di cosa si tratta.
Introduciamo una
netica lineare :
struttura ferromag-
si tratta di un dispositi-
vo che lavora nella zona lineare del ciclo
di isteresi, dove vale la relazione
~b = µ~h.
Le correnti che interessano la struttura devono essere tali da farla lavorare lontano
dalla regione di saturazione.
Figura 2.3.9: ciclo di isterisi: curva di prima
magnetizzazione
Supponiamo che tale struttura ferromagnetica lineare sia
snella.
Una strut-
tura ferromagnetica lineare snella è una struttura realizzata rispettando opportune ipote-
86
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
si geometriche: deve essere tale che il raggio medio della sezione dei pezzi costituenti la
struttura ferromagnetica sia molto piccolo rispetto alla lunghezza dei pezzi stessi. Tale
struttura può essere realizzata intammente in ferro, oppure con più sostanze ferromag-
omogenea, nel secondo
caso è disomogenea. In entrambi i casi la struttura può presentare un traferro : si tratta
netiche, per esempio acciaio e ferro; nel primo caso la struttura è
di una breve interruzione della struttura stessa.
Una
struttura
ferromagnetica
lineare
snella deve rispettare le seguenti ipotesi:
l, m >> R
1.
essendo R il raggio della
sezione S della struttura;
δ
2. traferro
La
molto piccolo;
3.
µF e >> µ0 = 4π107 H/m;
4.
~b 6= ~0
5.
~b
solo nel ferro e nel traferro;
uniforme nella sezione S.
struttura
ferromagnetica
snella
è
l tubo di usso
una materializzazione de
Figura 2.3.10: struttura ferromagnetica lineare snella
(Figura 2.3.11).
Ricordiamo cosa si intende per tubo di
usso. Sia P un punto dello spazio;per tale
punto passa una ed una sola linea di campo
~b.
Poichè deve valere la solenoidalità
del campo
~b, ∇
~ · ~b = 0,
la linea di campo
passante per il punto P è una linea chiusa.
Se P è un punto di una certa supercie
bilatera S, si avrà che per ogni punto di detta supercie passerà una ed una sola linea di
campo chiusa. L'insieme delle linee di campo passanti per i punti della supercie bilatera
costituiscono il tubo di usso.
Poichè le lineedi forza del campo
~b
nel-
la struttura ferromagnetica snella mostrata in Figura 2.3.10 sono tutte incanalate e
non sono al suo esterno, si ha che essa è un
tubo di usso. Il tubo di usso gode della
seguente proprietà:
ˆ
ΦS ~b = ~b · n̂ dS 6= 0
Figura 2.3.11: tubo di usso
(2.3.29)
S
essendo S una supercie bilatera orientata mediante il versore
Figura 2.3.11.
Si noti che
ΦS ~b = 0
se e solo S è una supercie chiusa.
87
n̂
come mostrato in
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La struttura di Figura 2.3.10 rimane ancora una struttura ideale in quanto il campo
~b
non può esistere se non in corrispondenza di una data sorgente. Possiamo accendere il
campo
~b
all'interno della struttura snella attraverso la corrente elettrica come mostrato
in Figura 2.3.12, applicando opportune bobine.
L'obiettivo è dunque trovare i campi
ed
si
~h
~b
in tutti i punti dello spazio. In aria
ha ~
b = ~h = 0;
dobbiamo vedere dunque
cosa succede nella struttura snella. Se S è
una generica supercie bilatera ortogonale
a ciascun tratto della struttura snella si ha
che il usso (2.3.29) si scrive:
ˆ
ˆ
dS = b S
b dS = b
ΦS ~b =
S
S
ovvero:
ΦS ~b = b S
essendo ~
b ed
(2.3.30)
n̂ paralleli e ~b uniforme nel-
la sezione S. A questo punto noto il usso
Figura 2.3.12: struttura
lineare
snella
con
bobine
del campo attraverso S e nota la geometria della struttura snella, ovvero la sezione S, è
possibile stabilire l'intensità del campo
~b:
ΦS ~b
b=
(2.3.31)
S
Figura 2.3.13: approssimazione delle linee di campo nel traferro
Inne nota l'intensità del campo
pure l'intensità del
~b,
attraverso l'equazione costitutiva
campo ~
h:
88
~b = µ~h
si ricava
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
ΦS ~b
h=
(2.3.32)
µS
~ ~
In questo modo
abbiamo spostato il problema dalla ricerca dei campi b ed h alla ricerca
del usso
ΦS ~b
. Nella trattazione che segue si scegli di approssimare le linee di campo
in prossimità del traferro come mostrato in Figura 2.3.13.
Γ come indicato
˛
ΦΓ ~b = ~b · n̂ dS = 0
Se consideriamo una supercie chiusa
in Figura 2.3.14 si ha:
(2.3.33)
Γ
Se il usso
ϕ3 ,
ΦS ~b
ϕ1 , ϕ2 ,
lo si può pensare come la somma di tre contributi di usso:
la (2.3.33) si può scrivere come segue:
˛
Γ
S3
S2
S1
~b · n̂ dS =
~b · n̂ dS +
~b · n̂ dS +
~b · n̂ dS +
ˆ
ˆ
ˆ
ˆ
~b · n̂ dS =
Γ−S1 −S2 −S3
= −ϕ1 + ϕ2 + ϕ3 = 0
(2.3.34)
ˆ
essendo
~b · n̂ dS = 0
Γ−S1 −S2 −S3
dato che
Γ − S1 − S2 − S3
è quella parte della supercie di
Figura 2.3.14:
89
Γ
in cui c'è aria (~
b
= ~0).
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Consideriamo a questo punto l'altra equazione integrale, ovvero la legge di Ampere nel
caso statico:
˛
~h · dl
~ = IΓ
(2.3.35)
Γ
Secondo tale relazione la ciruitazione del campo ~
b lungo
IΓ
concatenata con la linea chiusa
Γ
Γ eguaglia la corrente elettrica
(Figura 2.3.15)
Figura 2.3.15:
Applichiamo la (2.3.35) alla situazione illustrata in Figura 2.3.16.
Figura 2.3.16: circuito ferromagnetico
Chiamiamo
Γ
la linea chiusa cosituita dai tratti
Γ1 , Γ2 ;
tale linea passa per i centri
delle sezioni dei tratti della struttura snella (in questo modo siamo sicuri che la linea
chiusa
Γ
è una linea di campo).
90
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Γ
Osserviamo che la linea di campo
siccome
Γ è percorsa in senso orario ,
n̂
e la normale
n̂,
la normale
sono concordemente orientate:
ortogonale al foglio di questa pagina,
risulta entrante nel foglio.
Poichè il campo magnetico
di campo
Γ
~h
(o equivalentemente il campo
~b)
e il tratto
~
dl
della linea
sono tra di loro paralli, il primo mebro della (2.3.35) si scrive:
˛
ˆ
ˆ
~h · dl
~ =
ˆ
h dl =
Γ
h dl +
Γ
h dl
Γ1
Γ2
Tenendo conto della relazione (2.3.32), quest'ultima espressione si scrive:
˛
ˆ
~h · dl
~ = ϕ1
Γ
Γ1
1
dl + ϕ2
µS
ˆ
Γ2
1
dl
µS
(2.3.36)
Le quantità:
ˆ
R1 =
ˆ
Γ1
R2 =
Γ2
1
1
dl =
µS
µ1 S
1
1
dl =
µS
µ1 S
=
si chiamano
ˆ
1
(2l + m)
µ1 S
ˆ
1
dl +
dl =
µ0 S δ
dl =
ˆ
Γ1
Γ2 −δ
(2.3.37)
1
1
(m − δ) +
δ
µ1 S
µ0 S
(2.3.38)
riluttanze e dipendono solo dalle caratteristiche geometriche della struttura
ferromagnatica.
La riluttanza
R2
conta di 2 contributi perchè ntantochè ci troviamo nel ferro, la
permeabilità magnetica è
La riluttanza si misura
µ1 , mentre nel traferro è µ0 .
−1 . L'inverso della riluttanza
in H
si chiama
permeanza P :
R−1 = P
e si misura in
(2.3.39)
H.
Utilizzando (2.3.37) e (2.3.38) la (2.3.36) si scrive:
˛
~h · dl
~ = ϕ1 R1 + ϕ2 R2
(2.3.40)
Γ
Vediamo chi è il secondo mebro della (2.3.35), ossia la corrente concatenata con la
linea chiusa
Γ.
La corrente
interessano la linea
Γ).
IΓ
conta di due contributi (tanti quante sono le bobine che
Come mostrato in Figura 2.3.16, chiamiamo
ha per orlo la linea chiusa
Γ.
La normale alla supercie
pagina, è orientata rispetto alla direzione di
La corrente
corrente
I1
I1
risulta entrante in
Σ, N1
Γ
N1
la supercie che
Σ, n̂, entrante nel foglio di questa
rispettando la regola della mano destra.
volte, così come la normale
è concordemente orientata con la normale
alla bobina di
Σ
spire è positivo:
+N1 I1
91
n̂,
~n.
Siccome la
il contributo di corrente dovuto
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La corrente
I2
risulta invece uscente da
mente orientata con la normale
0
Σ, N2
volte. Siccome la corrente
I2
è discorde0
n̂, il contributo di corrente dovuto alla bobina di N2
spire
è negativo:
0
−N2 I2
Quindi la corrente concatenata con la linea chiusa vale:
0
IΓ = N1 I1 − N2 I2
Le quantità
0
N1 I1 , N2 I2
si chiamano
(2.3.41)
forze magnetomotrici.
Inne utilizzando (2.3.40) e (2.3.41) la (2.3.35) si scrive:
0
ϕ1 R1 + ϕ2 R2 = N1 I1 − N2 I2
(2.3.42)
A questo punto utilizzando nuovamente la (2.3.35) possiamo scrivere una terza equazione
nelle incognite
ϕ1 , ϕ2
e
ϕ3
Γ
se per linea chiusa
utilizziamo quella mostrata in Figura
2.3.17
La linea chiusa
Γ2
Γ3
e
Γ
è costituita dai tratti
ed orientata con la normale alla
n̂
supercie
in accordo con la regola della
mano destra.
In questo caso il primo membro della
(2.3.35) si scrive:
˛
~h · dl
~ = −ϕ2 R2 + ϕ2 R2
(2.3.43)
Γ
essendo
ˆ
R3 =
Γ
1
1
dl =
(2l + m − n) +
µS
µ1 S
+
1
c
µ2 S
(2.3.44)
Figura 2.3.17: circuito ferromagnetico
La corrente concatenata con la linea chiusa
0
Γ
in questo caso è:
00
IΓ = N2 I2 + N2 I2
(2.3.45)
Sostituendo (2.3.43) e (2.3.45) in (2.3.35) si ricava inne:
0
00
− ϕ2 R2 + ϕ3 R3 = N2 I2 + N2 I2
Risolvendo il sistema costituito dalle equazioni (2.3.34) (2.3.42) (2.3.46):
92
(2.3.46)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici


−ϕ1 + ϕ2 + ϕ3 = 0
0
ϕ1 R1 + ϕ2 R2 = N1 I1 − N2 I2

0
00

−ϕ2 R2 + ϕ2 R3 = N2 I2 + N2 I2
si determinano i ussi
ϕ1 , ϕ2
e
(2.3.47.1)
(2.3.47.2)
(2.3.47.3)
(2.3.47)
ϕ3 .
Nel passaggio dal ferro all'aria il campo
~b
non cambia in termini di intensità
poichè altromenti non sarebbe soddisfatta
~ ~
¸l'equazione ∇ · b = 0 (o equivalentemente
~ ~
Γ b · dS = 0). Essenzialmente il usso entrante nella supercie chiusa Γ deve essere
uguale al usso uscente:
ΦS ~b
Fe
= ΦS ~b
0
ovvero:
bF e SF e = b0 S0
(2.3.48)
Figura 2.3.18: traferro
A questo punto poichè
SF e = S0 ,
dalla (2.3.48) segue che:
bF e = b0
(2.3.49)
Ovvero l'intensità del campo ~
b, non varia dal passaggio dal ferro all'aria. Questo fatto
si esprime pure dicendo che la componente normale del campo ~
b non cambia nel passaggio
di una supercie:
bn2 = bn2
(2.3.50)
Lo stesso discorso non si ripete per il
campo
~h,
infatti:
hF e =
bF e
b0
1
=
=
b0
µF e
µ0 µr
µr
cioè:
hF e =
1
b0
µr
(2.3.51)
Figura 2.3.19:
Stiamo trovando che l'intensità del campo magnetico
all'aria. Poichè la permeabilità magnetica relativa
magnetico ~
h
3
nel ferro è 10
÷
µr
~h
cambia nel passaggio dal ferro
vale
103 ÷ 104 ,
104 meno intenso che nell'aria.
93
si ha che il campo
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Questo fatto si esprime pure dicendo che la componente normale del campo
~h,
è dis-
continua attraversando una supercie che delimita due mezzi a permeabilità magnetica
dierente.
Ragioniamo in termini di riluttanza. La riluttanza del tratto
Γ2
(2.3.38) si può scrivere
come segue:
R2 =
avendo posto
m − n = lF e
e
1
1
1
lF e +
δ=
µ0 µ r S
µ0 S
µ0 S
lF e
+δ
µr
µ1 = µ0 µ r .
Attraverso (2.3.52) è evidente che si il traferro ha una lunghezza di
e
µr = 103
(2.3.52)
1 mm = 10−3 m
, anchè la riluttanza del ferro coincida con quella dell'aria, occore che la
lunghezza del ferro sia pari a
1 m,
cioè
lF e = 1 m
Concludendo allora si ha che 1 m di ferro ha la stessa riluttanza di 1 mm di aria se
µr = 103 .
Il circuito ferromagnetico n qui studiato è equivalente a un circuito elettrico puramente resistivo: ciascuna riluttanza gioca il ruolo di una resistenza e ciascuna bobina
gioca il ruolo di una forza elettromotrice.
Quando si vuole scrivere il circuito elettrico equivalente di un circuito ferromagnetico,
bisogna innanzitutto calcolare le riluttanze, che come abbiamo visto dipendono esclusivamente dalla geometria della struttura ferromagnetica; fatto ciò si scrive la topologia
del circuito elettrico equivalente.
Il circuito ferromagnetico n qui studiato è equivalente ad un circuito elettrico formato da due nodi e tre lati; su ciascun lato troviamo una riluttanza ed una forza
magnetomotrice.
Si ssano in modo arbitrario i ussi e si determinano le polarità delle forze magnetomotrici utilizzando la regola della mano destra.
Inne si ssano arbitrari versi di
percorrenza di anello e si scrivono le L.K.
Figura 2.3.20: circuito magnetico e circuito elettrico equivalente
94
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
LKI
− ϕ1 + ϕ2 + ϕ3 = 0
LKT
(2.3.53)
0
ϕ1 R1 + ϕ2 R2 − N1 I1 + N2 I2 = 0
00
− ϕ2 R2 + ϕ3 R3 − N I2 − N2 I2 = 0
(2.3.54)
(2.3.55)
Come mostrato in Figura 2.3.20, i versi dei ussi sono stati presi in modo arbitrario;
nel proseguio della trattazione i ussi saranno orientati nella stessa direzione dei versi di
spinta delle forze magnetomotrici.
Esempio 2.1.
Consideriamo il circuito ferromagnetico mostrato in Figura 2.3.21
I dati del problema sono:
a = 30 cm N1 = 100
0
b = 40 cm N2 = 50
00
δ = 1 mm N2 = 150
S = 2 cm2 µr = 103
Il circuito ferromagnetico è equivalente
a un circuito elettrico formato da tre lati
e due nodi. Le riluttanze di lato valgono:
R1 =
(2a + b)
2 30 10−2 + 40 10−2
1 8 −1
=
=
10 H
−7
3
−4
µ0 µr S
4π 10 10 2 10
8π
(2.3.56)
R3 = R1
R2 =
(2.3.57)
b−δ
δ
b
δ
+
'
+
=
µ 0 µr S µ 0 S
µ 0 µr S µ0 S
=
Figura 2.3.21: Circuito ferromagnetico
1 8 1, 4 8
0, 4 8
10 +
10 =
10
8π
8π
8π
(2.3.58)
Dalla (2.3.58) si vede che
RF e =
0, 4 8 −1
10 H
8π
R0 =
1 8 −1
10 H
8π
ovvero la riluttanza di 1 mm di aria è maggiore della riluttanza di 40 cm di ferro.
95
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Così come la
resistenza
è ciò che si op-
pone al passaggio di corrente innescata da
una
forza elettromotrice, la riluttanza è ciò
che si oppone al usso di campo magnetico
prodotto da una
forza magnetomotrice.
Dopo aver trattato le riluttanze si trattano le bobine.
A ciascuna bobina del
circuito ferromagnetico corrisponde una
forza magnetomotrice data dal prodotto
tra la corrente che interessa la bobina e
il numero di spire della bobina stessa.
A ciascuna bobina bisogna associare una
polarità che si determina con la regola della mano destra.
Figura 2.3.22: circuito elettrico equivalente
Si tratta di orientare le
dita del palmo della mano destra lungo la direzione della corrente che interessa la bobina
e scegliere come polo positivo quello indicato dalla direzione del pollice.
Quindi il circuito elettrico equivalente del circuito ferromagnetico è quello indicato
in Figura 2.3.22.
I generatori
presente che i ussi
ϕ1 , ϕ2
e
ϕ3
0
00
N1 I1 , N2 I2 , N2 I2
spingono tutti verso l'alto.
Si tenga
si possono orientare in modo arbitrario; in genere però è
conveniente orientarli concordemente alle forze magnetomotrici come indicato in Figura
2.3.22, infatti in questo modo si è sicuri che per i generatori vale la convenzione dei
generatori e per le riluttanze la convenzione dell'utilizzatore.
Da una semplice ispezione visiva del circuito elettrico di Figura 2.3.22 si ricava il
seguente sistema risolvente ottenuto scrivendo le L.K:

0

R1 ϕ1 − R2 ϕ2 = N1 I1 − N2 I2
0
00
R2 ϕ2 − R3 ϕ3 = N2 I2 − N2 I2


ϕ1 + ϕ2 + ϕ3 = 0
(2.3.59)
Risolvendo rispetto ai ussi si trova che essi sono delle combinazioni lineari delle
correnti che scorrono nelle bobine:




ϕ1 =
ϕ2 =


ϕ =
3
0
00
N2 +1,4N2
2,4N1
I2
3,8R I1 −
3,8R
0
00
2N2 −N2
N1
− 3,8R
I1 + 3,8R
I2
00
00
2,4N2 −N2
1
− 1,4N
I2
3,8R I1 +
3,8R
(2.3.60)
essendo:
R = R1 = R3
R2 = 1, 4R
Sostituendo i valori numerici si ricava inne:
96
(2.3.61)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici

−5
−5

ϕ1 = 1, 58 10 I1 − 1.71 10 I2
ϕ2 = −6, 61 10−6 I1 − 3, 30 10−6 I2


ϕ3 = −9, 25 10−6 I1 + 2, 05 10−5 I2
(2.3.62)
2.3.6 Coppia di induttori mutuamente accoppiati
Consideriamo nuovamente il circuito ferromagnetico mostrato in Figura 2.3.21 e chiudiamo i morsetti
0
2.
e
1
e
0
1
mediante un lo di rame; allo stesso modo chiudiamo i morsetti
Così facendo si ottiene il circuito ferromagnetico mostrato in Figura 2.3.23.
Chiudendo i morsetti
N1
della bobina avente
0
1 e 1 l'avvolgimento
spire rappresenta
una linea chiusa ossia un orlo
Γ1
qualunque linea chiusa,
una certa supercie bilatera
amo l'orlo
I1
2
Γ1
n̂
Come
SΓ1 .
Orienti-
come il verso della corrente
e la supercie
normale
Γ1 .
sarà l'orlo di
SΓ1
attraverso un versore
concorde alla corrente
I1
per la
regola della mano destra.
Il
usso
del
~b
campo
supercie bilatera
SΓ1
attraverso
si chiama
la
usso
concatenato con la bobina avente N1 spire:
Φ1 := ΦSΓ1
Figura 2.3.23: circuito ferromagnetico
ˆ
~b =
~b · n̂ dS
(2.3.63)
SΓ1
Analogamente per l'altra bobina possiamo scrivere:
Φ2 := ΦSΓ2
essendo
SΓ1
la supercie bilatera dell'orlo
Vediamo a cosa corrisponde il usso
Consideriamo l'orlo
Γ1
senso di avvolgimento delle
1
0
0
1.
~b · n̂ dS
(2.3.64)
SΓ2
Γ1 .
Φ1 .
e supponiamo di poterlo allungare a nostro piacimento no a
formare un cerchio su di un piano.
al morsetto
ˆ
~b =
N1 spire
Facendo riferimento a Figura 2.3.23 si vede che il
è antiorario attraversando la bobina dal morsetto
Ora visto che la corrente
I1
entra dal morsetto
1
1
ed esce dal morsetto
e che l'orlo è orientato come la corrente si ha che quest'ultimo è orientato in senso
antiorario. Si noti che la supercie a forma di cerchio continua ad essere
SΓ1 .
Se indichiamo con S la sezione della struttura ferromagnetica lineare snella, individueremo nella supercie
ovvero
SΓ1
tante areole di supercie S quante sono le spire della bobina,
N1 .
97
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Le areole di supercie S non sono altro
che le intersezioni tra
SΓ1
e la struttura
ferromagnetica lineare snella.
E' chiaro che
SΓ1 − S
è una supercie
d'aria dove i campi sono ovviamente nulli.
Quindi il usso
Φ1
ˆ
~b·n̂ dS =
Φ1 =
vale:
N1 ˆ
X
SΓ1
b1 dS = +N1 ϕ1
S
i=1
Figura 2.3.24: bobina appiattita a forma di
(2.3.65)
cerchio
Φ1 > 0 poichè si
è scelto di denire il versore n̂ concorde
al campo ~
b (in Figura 2.3.24, n̂ e ~b sono
Si osservi che risulta
ortogonali uscenti dal foglio di questa pagina).
Si osservi che con il simbolo
superci S delle
N1
b1
~b
ortogonale alle
Γ2
su di un piano
viene indicato il modulo del campo
spire della bobina.
Allo stesso modo allunghiamo a nostro piacimento la linea chiusa
no a formare un cerchio (Figura 2.3.25); il usso del
campo ~
b
attraverso la supercie
SΓ2 vale:
ˆ
Φ2 := ΦSΓ2 ~b =
~b · n̂ dS =
SΓ2
N2 ˆ
X
0
=
Φ2 ,
00
b2 dS +
S
i=1
I contributi al usso
N2 ˆ
X
i=1
0
00
b3 dS = N2 ϕ2 + N2 ϕ3
(2.3.66)
S
sono entrambi
positivi poichè ancora una volta si è scelto
di denire il versore
~b
(in Figura 2.3.25,
n̂ concorde al campo
n̂ e ~b sono ortogonali
uscenti dal foglio di questa pagina)
Sostituendo
(2.3.60)
in
(2.3.65)
e
(2.3.66) si trova facilmente che anche i
ussi conatenati con le bobine sono delle
combinazioni lineari delle correnti che le
Figura 2.3.25: bobina apppiattita a forma di
cerchio
alimentano:
0

00

Φ1 = 2,4N12 I1 − N1 N2 +1,4N2 I2
3,8R
3,8R
0 2
00 2
0 00
0
00

2 N2 +2,4 N2 −N2 N2
N
N
+1,4N
1
2
2
Φ = −
I
+
I2
2
1
3,8R
3,8R
98
(2.3.67)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Ponendo
2, 4N12
3, 8R
00 2
0 2
0
00
2 N2 + 2, 4 N2 − N2 N2
L1 =
L2 =
M12 = M21 = −
(2.3.68)
(2.3.69)
3, 8R
0
00
N1 N2 + 1, 4N2
(2.3.70)
3, 8R
la (2.3.67) si scrive:
(
Φ1 = L1 I1 + M12 I2
Φ2 = M21 I1 + L2 I2
Le quantità
L1
ed
L2
si chiamano
(2.3.71)
coecienti auto-induttanza
bobina 1 e della bobina 2.
Le quantità
M12
ed
M21
si chiamano invece coecienti di
rispettivamente della
muta-induttanza.
Il risultato (2.3.70) è la verica del teorema di reciprocità nel caso della muta-induttanza
(il teorema di reciprocità verrà trattato nel capitolo 7).
M12 = M21 = M
(2.3.72)
Il signicato sico delle auto-induttanze e delle mutue-induttanze si intuisce dall'osservazione delle relazioni in (2.3.71).
L'auto-induttanza
L1
è il usso concatenato con la
bobina 1 quando quest'ultima viene alimentata con una corrente di 1 A e la bobina 2
non viene alimentata. Analogamente L'auto-induttanza
L2
è il usso concatenato con
la bobina 2 quando quest'ultima viene alimentata con una corrente di 1 A e la bobina 1
non viene alimentata.
La mutua-induttanza
M12
è il usso concatenato con la bobina 1 quando quest'ultima
è spenta e sulla bobina 2 scorre una corrente di 1 A. Allo stesso modo
M21
è il usso
concatenato con la bobina 2 quando quest'ultima è spenta e sulla bobina 2 scorre una
corrente di 1 A
In altri termini possiamo dire che la muta-induttanza
M = M12 = M21
dà una misura
di come una bobina accesa inuenza una bobina spenta.
Guardando la prima delle equazioni in (2.3.67) è chiaro che la bobina 2 fa diminuire il
usso concatenato con la bobina 1.
Valgono le seguenti proprietà:
1. I coecienti di auto-induttanza sono sempre positivi;
2. I coecienti di mutua-induttanza possono essere entrambi positivi o entrambi
negativi.
99
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
La dimostrazione della prima proprietà è banale:
L1 > 0
dato che
N12
ed
R
sono quantità positive;
L2 > 0
se risulta:
0 2
00 2
0
00
2 N1 + 2, 4 N2 2N2 N2 > 0
.
0
Quest'ultima è una disequazione di secondo grado nella variabile
x=
N2
00 :
N2
x2 − x + 1, 2 > 0
che risulta vericata
∀x∈ R
dato che ha discriminante negativo:
4 = 1 − 4 (1) (1, 2) =
−3, 8.
Il circuito ferromagnetico di Figura 2.3.23 n qui studiato è un dispositivo molto utilizzato nelle reti elettriche; esso si chiama
coppia di induttore mutuamente accoppiati
e
si denota con il simbolo mostrato in Figura 2.3.26.
D'ora in avanti considereremo i coecienti di mutua-induttanza sempre positivi.
Il segno dei coecienti di mutua induttanza dipende da diversi fattori quali la
geometria, il senso di avvolgimento delle
bobine e il verso delle correnti nelle bobine.
Per far sapere al circuitista con quali
correnti si hanno mutue positive, il progettista fa uso del
trassegni.
meccanismo dei con-
Per esempio per due induttori
mutuamente accoppiati si ha la situazione
mostrata in Figura 2.3.26.
ni
•
I contrasseg-
indicano al circuitista che se le cor-
renti sono entranti dai morsetti
1
il coeciente di mutua induttanza
e
M
2
Figura 2.3.26: Coppia di induttori mutuamente accoppiati
0
è
positivo.
Consideriamo adesso le tre bobine a due a due mutuamente accoppiate mostrate in
Figura 2.3.27.
Con le correnti aventi i versi mostrati in gura le espressioni dei ussi concatenati con
le bobine sono:


Φ1 = L1 I1 + M12 I2 + M13 I3
Φ2 = M12 I1 + L2 I2 − M23 I3


Φ3 = M13 I1 − M23 I2 + L3 I3
Il coeciente di mutua-induttanza
I1
e
I2
M12
(2.3.73)
è preceduto dal segno + poichè le correnti
hanno il medesimo comportamento rispetto al contrassegno
il contrassegno).
100
• (I1
e
I2
lasciano
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.27: bobine a due a due mutuamente accoppiate
Il coeciente di mutua-induttanza
I1
e
I3
M13
è preceduto dal segno + poichè le correnti
hanno il medesimo comportamento rispetto al contrassegno
◦ (I1
e
I3
entrano
dal contrassegno).
Il coeciente di mutua-induttanza
I3 hanno comportamento discorde
e I3 entra dal contrassegno).
M23 è preceduto dal segno - poichè le correnti I2 e
I (I2 lascia il contrassegno
rispetto al contrassegno
2.3.7 Dispositivi a n bipoli e dispositivi n-polari
poli accoppiati
Un dispositivo a n-bipoli è un componente elettrico dotato di 2n morsetti, (
a due a due ).
La corrente che entra in uno dei poli di una coppia è uguale alla corrente
uscente dall'altro polo della stessa coppia.
Figura 2.3.28: dispositivo a n-bipoli
Ciascuna coppia del dispositivo a n-bipoli si chiama
porta
del dispositivo.
Un dispositivo n-polare è anch'esso un componente elettrico dotato di 2n morsetti; per
questo dispositivo però non esiste nessun tipo di accoppiamento tra i suoi morsetti.
Il più semplice dispositivo n-polare è il tripolo mostrato in Figura 2.3.28.
101
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.29: tripolo
Le variabili per il tripolo sono
I1 , I2 , V12 , V23
mentre
I3
e
V13
sono combinazioni lineari
delle variabili del tripolo:
I3 = I1 + I2
V13 = V12 + V23
2.3.8 Induttore isolato
La coppia di induttori mutuamente accoppiati è stata descritta nel caso statico mediante
le equazioni in (2.3.71); tali equazini continuano a valere anche nel caso lentamente
variabile del tempo:
(
Φ1 (t) = L1 i1 (t) + M12 i2 (t)
Φ2 (t) = M21 i (t)1 + L2 i2 (t)
(2.3.74)
Se tra gli induttori non c'è accoppiamento (M=0), questi si diranno isolati e saranno
descritti mediante le equazioni:
(
Φ1 (t) = L1 i1 (t)
Φ2 (t) = L2 i2 (t)
(2.3.75)
Quindi un induttore isolato di induttanza L è un bipolo per cui vale la relazione:
Φ (t) = Li (t)
(2.3.76)
La (2.3.76) si trova banalmente studiando il problama magnetostatico mostrato in
Figura 2.3.31 e approssimando al caso lentamente variabile nel tempo.
102
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.30: induttore isolato
In Figura 2.3.31 viene mostrato il circuito elettrico equivalente del problema magnetostatico da cui si ricava:
Φ = Nϕ = N
N2
N2
NI
=
I = 4a I = LI
R
R
µS
(2.3.77)
Quest'ultima nel caso lentamente variabile è la (2.3.76).
Figura 2.3.31: circuito ferromagnetico; circuito elettrico equivalente
Derivando rispetto al tempo la (2.3.76) si ricava:
d
d
Φ (t) = L i (t)
dt
dt
(2.3.78)
Per capire cosa rappresenta in primo membro della (2.3.78) consideriamo il circuito
elettrico mostrato in Figura 2.3.32.
Se indichiamo con
Γ
la linea chiusa for-
mata dalla bobina di N spire, la resistenza
R e il generatore ideale di tensione
v0 (t)
possiamo scrivere la legge di Faraday:
˛
~ + d Φ (t) = 0
~e · dl
dt
Γ
(2.3.79)
Guardando il circuito possiamo pure
scrivere la L.K.T:
Figura 2.3.32: circuito elettrico
103
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
− v0 (t) + vR (t) + vL (t) =
(2.3.80)
Adesso visto che
˛
~ = −v0 (t) + vR (t)
~e · dl
(2.3.81)
Γ
dal confronto tra (2.3.79) e (2.3.80) segue che:
d
Φ (t) = vL (t)
dt
(2.3.82)
Sostituendo (2.3.82) in (2.3.78) si ricava inne:
vL (t) = L
d
i (t)
dt
Quest'ultima espressione è nota con il nome di
legge di lato dell'induttore.
(2.3.83)
Essa ovvi-
amente vale se per l'induttore adottiamo la convenzione dell'utilizzatore come mostrato
in Figura 2.3.33.
Dalla (2.3.83) si può condurre l'analisi dimensionale che permette di denire
l'unità di misura dell'induttanza L:
H = [L] =

 [V[I]][t] =
[V ][t]

[Q]
[t]
=
V s
A
V s
C
s
= Ωs
=
V s2
C
2.3.9 Circuito del primo ordine
RL: carica e scarica di un induttore
Consideriamo il circuito elettrico mostrato
in Figura 2.3.34.
Supponiamo che all'istante t=0
Figura 2.3.33: convenzione dell'utilizzatore
− l'inter-
ruttore T sia aperto; in questo modo la
corrente che attraversa l'induttore è zero:
i L 0− = 0 V
(2.3.84)
Per t>0 (chiusura dell'interruttore T) si può scrivere la LKT:
vL (t) − V0 + Rf iL (t) = 0
(2.3.85)
Utilizzando la (2.3.83) la (2.3.85) si scrive:
L
Posto
τ=
d
iL (t) − V0 + Rf iL (t) = 0
dt
L
Rf e riordinando i termini, la (2.3.86) si scrive:
104
(2.3.86)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.34: carica e scarica dell'induttore
d
1
1
iL (t) + iL (t) = V0
dt
τ
L
(2.3.87)
Le equazioni (2.3.84), (2.3.87) costituiscono il problema di Cauchy che permette di
determinare la corrente che attraversa l'induttore per t>0:
(
d
1
dt iL (t) + τ iL (t)
iL (0− ) = 0
Risoluzione del problema di Cauchy
=
1
L V0
(2.3.88)
Determiniamo l'integrale generale della (2.3.87)
L'integrale generale della (2.3.87) è la somma tra l'integrale generale dell'omogenea
associata alla (2.3.87) e l'integrale particolare della (2.3.87):
iL (t) = iLomog. (t) + iLpart. (t)
(2.3.89)
Omogenea associata
d
1
iL (t) + iL (t) = 0
dt
τ
Equazione caratteristica
λ+
1
=0
τ
λ=−
1
τ
Integrale generale omogenea associata
t
iLomog. (t) = k e− τ
105
(2.3.90)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Ricerca dell'integrale particolare
V0 ,
Visto che il termine noto della (2.2.37) è la costante
l'integrale particolare va ricercato tra le costanti.
Posto
iL (t) = iLpart. (t) = cost.
, la (2.2.37) si scrive:
1
1
0 + ILpart. (t) = V0
τ
L
da cui si ricava:
iLpart. (t) =
V0
Rf
(2.3.91)
Sostituendo (2.3.90) e (2.3.91) in (2.3.89) si ricava l'integrale generale della (2.3.87):
t
iL (t) = k e− τ +
V0
Rf
(2.3.92)
Per determinare la costante k si utilizza la condizione iniziale data in (2.2.34)
0
iL (0) = k e− τ +
k=−
V0
=0
Rf
V0
Rf
(2.3.93)
Sostituendo (2.2.43) in (2.2.42) si ricava l'espressione analitica della tensione ai capi
del capacitore:
iL (t) =
t
V0 1 − e− τ
Rf
(2.3.94)
Visto che
lim iL (t) = 0
t→0+
e che
i L 0− = 0
ne segue che la corrente che attraversa l'induttore è una funzione continua del tempo.
Per determinare la tensione ai capi dellìinduttore basta sostituire (2.3.94) in (2.3.833)
vL (t) = L
t
d
iL (t) = V0 e− τ
dt
106
(2.3.95)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.3.10 Generalità sugli induttori
Gli induttori sono elementi a due morsetti capaci di immagazzinare usso del campo magnetico. In ogni istante di tempo t, il usso immagazzinato dall'induttore e la corrente che
lo attraversa soddisfano ad una relazione denita nel piano I-Φ, chiamata
dell'induttore.
caratteristica
Quello studiato no ad ora è l'induttore lineare tempo-invariante. Come nel caso dei
resistori e dei capacitori, anche per gli induttori possono esserci quattro possibilità.
2.3.10.1 Induttore lineare tempo-invariante
induttore lineare tempo-invariante
L'
è caratterizzato dall'equazione caratteristica:
Φ (t) = L i (t)
(2.3.96)
L'induttanza L per un induttore lineare tempo-nvariante non dipene nè da
i
nè da
t;
dunque nel piano I-Φ la caratteristica dell'induttore lineare tempo-invariante è una retta
passante per l'origine di pendenza L:
Figura 2.3.35: caratteristica dell induttore lineare tempo-invariante
Derivando rispetto al tempo la (2.3.96) si ottiene l'espressione della tensione ai capi
dell'induttore:
v (t) =
dΦ (t)
d
= L i (t)
dt
dt
Anche l'induttore, come il capacitore, è un
dalla (2.3.97), infatti la tensione
v (t),
(2.3.97)
dispositivo a memoria.
Ciò si capisce subito
ad un certo istante di tempo t non dipende solo
dalla corrente all'istante t ma anche dagli istanti di tempo immediatamente precedenti.
Per convincerci di ciò basta scrivere la (2.3.97) tenendo conto della denizione di derivata:
v (t) =
La tensione all'istante
corrente all'istante
t0
t
dΦ (t)
d
i (t) − i (t0 )
= L i (t) = L lim
t→t
dt
dt
t − t0
0
non dipende solo dalla corrente all'istante
essendo
t0
un'istante di tempo precedente a
107
t.
(2.3.98)
t,
ma anche dalla
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Osservando la (2.3.98) potrebbe sembrare che il valore della tensione all'istante di
tempo
t dipenda da un passato estremamente precedente;
in realtà invertendo la (2.3.97)
appare in modo chiaro che l'induttore è un dispositivo che tiene conto di tutto il passato.
Possiamo invertire la (2.3.97) integrando nell'intervallo di tempo
ˆ
ˆ
t
t
v (τ ) dτ = L
t0
ˆ
ˆ
d
i (τ ) dτ = L
dτ
t0
[t0 , t]:
i(t)
i(t0 )
i(t)
di (τ ) = L [i (τ )]it
0
t
v (τ ) dτ = L [i (t) − i (t0 )]
t0
1
i (t) = i (t0 ) +
L
ˆ
t
v (τ ) dτ
(2.3.99)
t0
Secondo (2.3.99) la corrente che attraversa l'induttore lineare tempo-invariante all'istante di tempo t, dipende dalla corrente all'istante di tempo t0 e da tutta la storia passata
della tensione
v (t),
cioè dalla tensione in tutto l'intervallo
[t0 , t].
Quindi per un induttore lineare tempo-invariante tutto il passato conta per la formazione del presente.
Passando al limite per
t → t0 ,
la (2.3.99) fornisce:
lim i (t) = i (t0 ) +
t→t0
1
lim
L t→t0
ˆ
t
vτ dτ = i (t0 )
(2.3.100)
t0
Secondo (2.3.100) è evidente che la corrente che attraversa l'induttore è una funzione
continua in
t0 .
2.3.10.1.1 Energia immagazzinata da un induttore lineare tempo-invariante
Con-
sideriamo il circuito mostrato in Figura 2.3.34 e supponiamo che all'istante di tempo
t = 0−
l'induttore sia scarico:
i L 0− = 0 A
(2.3.101)
L'energia immagazzinata dall'induttore dall'istante
ˆ
ˆ
t
(t̄) =
0−
0−
ˆ
=L
ˆ
t
p (t) dt =
t = 0−
vL (i) iL (t) dt =
all'istante
t
0−
L iL (t)
t=t
vale:
d
iL (t) dt =
dt
iL (t)
2
1
iL (t) diL = LiL t
2
iL (0− )
(2.3.102)
La (2.3.102) fa capire che la grandezza importante è la corrente e non la tensione.
Utilizzando la (2.3.76) ponendo
t = t
è chiaro che la (2.3.102) si può scrivere nelle
seguenti forme equivalenti:
2 1
1Φ t 2
1
(t̄) = LiL t = Φ t iL t =
2
2
2 L
108
(2.3.103)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.3.10.2 Induttore lineare tempo-variante
Se l'induttore è lineare tempo-variante, la sua caratteristica è una rette passante per
l'origine del piano I-Φ la cui pendenza dipende dal valore assunto dall'induttanza che è
una funzione del tempo
t:
Φ (t) = L (t) i (t)
(2.3.104)
Figura 2.3.36: caratteristica capacitore lineare tempo-variante
Derivando rispetto al tempo la (2.3.104) si determina l'espressione della tensione ai
capi dell'induttore lineare tempo-variante:
v (t) =
d
d
d
Φ (t) = L (t) i (t) + i (t) L (t)
dt
dt
dt
2.3.10.2.1 Energia immagazzinata da un induttore lineare tempo-variante
(2.3.105)
Conside-
riamo un induttore lineare tempo-variante e supponiamo che all'istante di tempo
t = 0−
esso sia scarico:
i 0− = 0 A
(2.3.106)
Alimentando l'induttore, per esempio come mostrato in Figura 2.3.34, si ha che al
tempo
t,
avrà tensione
dall'istante
t = 0−
v t
all'istante
e corrente
t=t
ˆ
i (t̄).
ˆ
t
(t̄) =
t
i (t)
=
0−
t
p (t) dt =
0−
ˆ
L'energia immagazzinata dal capacitore
vale:
v (i) i (t) dt =
0−
d
d
L (t) i (t) + i (t) L (t)
dt
dt
109
dt
(2.3.107)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
2.3.10.3 Induttore non lineare tempo-invariante
L'induttore non lineare tempo-invariante è denito tramite una relazione del tipo:
f (Φ, i) = 0
(2.3.108)
La caratteristica pertanto può essere una retta non passante per l'origine o una curva
di tipo quadratico come mostrato in Figura 2.2.19:
Figura 2.3.37: caratteristica dell'induttore non lineare tempo-invariante
2.3.10.3.1 Energia immagazzinata da un capacitore non lineare tempo-invariante
−
L'energia immagazzinata dal capacitore dall'istante t = 0 all'istante t = t vale:
ˆ
ˆ
t
(t̄) =
0−
ˆ
t
=
i (t)
0−
t
p (t) dt =
i (t) v (t) dt =
0−
d
Φ (t) dt =
dt
ˆ
Φ(t)
i (Φ) dΦ
(2.3.109)
Φ(0− )
Si tenga presente che per l'induttore non lineare tempo-invariante NON vale la relazione
d
v (t) = L dt
i (t)
2.3.10.4 Induttore non lineare tempo-variante
Il capacitore non lineare tempo-variante è denito tramite una relazione del tipo:
f (Φ, i, t) = 0
110
(2.3.110)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.38: caratteristica dell'induttore non lineare tempo-variante
2.3.11 Generalità sulla coppia di induttori mutuamente accoppiati
Consideriamo la coppia di induttori mutuamente accoppiati mostrata in Figura 2.3.39.
Le equazioni che caratterizzano il dispositivo sono
(
Φ1 (t) = L1 i1 (t) + M i2 (t)
Φ2 (t) = M i1 (t) + L2 i2 (t)
(2.3.111)
Derivando rispetto al tempo le equazioni in (2.3.111) si ottiene:
(
v1 (t) =
v2 (t) =
d
dt Φ1 (t)
d
dt Φ2 (t)
d
= L1 dt
i1 (t) + M
d
= M dt i1 (t) + L2
d
dt i2 (t)
d
dt i2 (t)
(2.3.112)
Si osservi che valgono le relazioni in (2.3.112) purchè per le porte del dipositivo valga
la convenzione dell'utilizzatore (Figura 2.3.39).
Si
M
si
osservi
che
misura
in
la
mutua-induttanza
henry,
H,
così
come
l'auto-induttanza L.
2.3.11.0.1 Energia immagazzinata dalla
coppia di induttori mutuamente accoppiati
Supponiamo che all'istante t=0 ssi
abbia:
i1 (0) = 0 A
i2 (0) = 0 A
(2.3.113)
Figura 2.3.39: coppia
In questo caso non si avrà campo magnetico
e
di
conseguenza
il
t̄
induttori
mutua-
dispositivo
non avrà accumulato alcuna energia.
all'istante
di
mente accopppiati
Se
sarà
i1 (t̄) 6= 0 A
i2 (t̄) 6= 0 A
allora il dispositivo avrà accumulato dal tempo
111
t=0
al tempo
(2.3.114)
t = t̄,
l'energia:
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
ˆ
ˆ
t̄
{v1 (t) i1 (t) + v2 (t) i2 (t)} dt =
0
ˆ t̄ L1 i1 (t)
=
0
ˆ t̄ =
0
0
d
d
d
d
i1 (t) + M i1 (t) i2 (t) + M i2 (t) i1 (t) + L2 i2 (t) i2 (t) =
dt
dt
dt
dt
d
L1 i1 (t) i1 (t) + M
dt
ˆ
t̄
= L1
0
d
dt
t̄
{p1 (t) + p2 (t)} dt =
ε (t̄) =
d
d
d
i1 (t) i2 (t) + i2 (t) i1 (t) + L2 i2 (t) i2 (t) =
dt
dt
dt
ˆ t̄ ˆ t̄ 1 2
d
d 1 2
i1 (t) dt + M
i1 (t) i2 (t) dt + L2
i2 (t) dt =
2
dt
2
0
0 dt
1
1
= L1 i21 (t̄) + M i1 (t̄) i2 (t̄) + L2 i22 (t̄)
2
2
Ovvero:
1
1
ε (t̄) = L1 i21 (t̄) + M i1 (t̄) i2 (t̄) + L2 i22 (t̄)
2
2
(2.3.115)
Secondo (2.3.115), l'energia immagazzinata da una coppia di induttori mutuamente
accoppiati non è la semplice sovrapposizione delle energie accumulate da due induttori
M i1 (t̄) i2 (t̄).
(ε (t̄) ≥ 0) e per essere tale la mutua-induttanza
tra di loro isolati poichè compare il termine
L'energia è una quantità non negativa
deve sottostare alla condizione:
0≤M ≤
p
L1 L2
(2.3.116)
La dimostrazione della (2.3.116) è banale.
Visto che
i2 (t̄) > 0
la (2.3.115) si può scrivere come segue:
ε (t̄)
1
= L1
i2 (t̄)
2
Adesso anchè sia
ε (t̄) ≥ 0
i1 (t̄)
i2 (t̄)
2
dt + M
occorre che sia
ε(t̄)
i2 (t̄)
i1 (t̄)
i2 (t̄)
≥0
1
+ L2
2
(2.3.117)
e cio accade se:
4 = M 2 − L1 L2 ≤ 0
(2.3.118)
da cui si ricava la (2.3.116).
A seconda dei valori assunti dalla mutua-induttanza M si possono avere due casi
particolari:
ˆ
Se è
M =0
allora gli induttori sono
mutuamente accoppiati ;
isolati dall'altro
112
o equivalentemente
non sono
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
In tal caso l'energia immagazzinata risulta:
1
1
ε (t̄) = L1 i21 (t̄) + L2 i22 (t̄)
2
2
ˆ
Se è
M=
√
L1 L2
allora gli induttori sono
(2.3.119)
perfettamente accoppiati ;
In tal caso l'energia immagazzinata risulta:
p
1
1
ε (t̄) = L1 i21 (t̄) + L1 L2 i1 (t̄) i2 (t̄) + L2 i22 (t̄)
2
2
(2.3.120)
Di norma per una coppia di induttori mutuamente accoppiati si utilizza il
di accoppiament k, così denito:
k=√
coeciente
M
L1 L2
(2.3.121)
Tale parametro deve rispettare la condizione:
0≤k≤1
(2.3.122)
in accordo con la (2.3.116).
Ovviamente:
ˆ
se
k=1
gli induttori non sono accoppiati;
ˆ
se
k=1
gli induttori sono perfettamente accoppiati.
2.3.12 Trasformatore ideale
Un trasformatore ideale è una coppia di induttori mutuamente accoppiati con bobine
avvolte in una struttura ferromagnetica lineare snella a permeabilità magnetica innita.
In Figura 2.3.40 viene mostrata una coppia di induttori mutuamente accoppiati con
accoppiamento perfetto e il corrispondente circuito elettrico equivalente
Dalla LKT:
N1 I1 + N2 I2 = Rϕ
(2.3.123)
si determina facilmente il usso del campo magnetico attraverso la sezione S della
struttura:
ϕ=
N1 I1 + N2 I2
R
(2.3.124)
Figura 2.3.40: coppia di induttori con accop-
essendo:
piamento
R=
4a
µS
113
perfetto;
circuito
elettrico equivalente
(2.3.125)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Nota la (2.3.124), è ovvio che i ussi concatenati con le bobine valgono:
(
Φ1 = N1 ϕ =
Φ2 = N2 ϕ =
N12
N1 N2
R I1 + R I2
N22
N1 N2
R I1 + R I2
(2.3.126)
Dalle equazioni in (2.3.126) risulta occiamente che:
L1 =
N12
R
L2 =
M=
N22
R
(2.3.127)
N1 N2
R
(2.3.128)
Si vede subito che le espressioni in (2.3.127) e (2.3.128) soddisfano la condizione di
accoppiamento perfetto
Nell'ipotesi
µ = ∞,
M=
√
L1 L2 .
ovviamente da (2.3.125) segue che
R=0
e da (2.3.123) segue che:
N1 I1 + N2 I2 = 0
(2.3.129)
Nel caso lentamente variabile del tempo quest'ultima relazione si scrive:
N1 i1 (t) + N2 i2 (t) = 0
Da cui si ricava la
prima equazione
(2.3.130)
del trasformatore ideale:
i1 (t)
1
=−
i2 (t)
t
(2.3.131)
dove:
t=
è il
N1
N2
(2.3.132)
rapporto di trasformazione.
Nel caso lentamente variabile del tempo le equazioni in (2.3.126) si scrivono:
(
Φ1 (t) = N1 ϕ (t)
Φ2 (t) = N2 ϕ (t)
(2.3.133)
Derivando rispetto al tempo le equazioni in (2.3.133) si ricavano le espressioni delle
tensioni ai capi delle bobine:
(
v1 (t) =
v2 (t) =
d
dt Φ1 (t)
d
dt Φ2 (t)
d
= N1 dt
ϕ (t)
d
= N2 dt ϕ (t)
Dividendo membro a membro le equazioni in (2.3.134) si ricava la
(2.3.134)
seconda equazione
del trasformatore:
v1 (t)
=t
v2 (t)
114
(2.3.135)
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
In Figura viene mostrato il simbolo elettrico del trasformatore ideale il cui funzionamento è regolato dalle equazioni in (2.3.132) e (2.3.135).
Figura 2.3.41: trasformatore ideale
Si osservi che alle porte la tensione e la corrente sono in accordo con la convenzione
dell'utilizzatore.
2.3.12.1 Proprietà del trasformatore ideale
ˆ
Il dispositivo descritto è ideale perchè può funzionare anche con correnti e tensioni
costanti nel tempo.
ˆ
Il trasformatore ideale assorbe potenza istantanea nulla:
p (t) = v1 (t) i1 (t) + v2 (t) i1 (t) =
= v1 (t) i1 (t) +
v1 (t)
(−ti1 (t)) = 0
t
(2.3.136)
Il trasformatore ideale in ogni istante di tempo non è capace nè di assorbire nè erogare potenza; esso è come una lastra trasparente all'energia transitata, in grado solo di
modicare tensione e corrente lasciando inalterata la potenza.
Figura 2.3.42: Trasformatore ideale:potenza transitata
ˆ
Il trasformatore ideale ha la caratteristica di riportare alla porta 1, un resistore che
sta alla porta 2 come mostrato in Figura 2.3.43.
115
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.43: Resistenza equivalente vista dalla porta 1
La resistenza equivalente
resistore di resistenza
Req.
vista dalla porta 1 quando la porta 2 viene chiusa con un
R si ricava banalmente combinando le equazioni (2.3.132) (2.3.135).
Dalla (2.3.135) si ricava:
v1 (t) = tv2 (t)
(2.3.137)
i2 (t) = −ti1 (t)
(2.3.138)
Dalla (2.3.132) si ricava:
Osservando Figura 2.3.43 si vede che per il resistore
R
vale la convenzione del genera-
tore e pertanto:
v2 (t) = −Ri2 (t)
(2.3.139)
Sostituendo (2.3.138) in (2.3.139) e (2.3.139) in (2.3.137) si ricava:
v1 (t) = t2 Ri1 (t)
(2.3.140)
da cui segue:
Req. =
ˆ
v1 (t)
= t2 R
i1 (t)
(2.3.141)
I trasformatori vengono utilizzati per trasportare energia a grandi distanze.
Per
evidenziare questo fatto si capisce nella rappresentazione di Figura 2.3.42 occorre
che la potenza vada da siistra verso destra e ciò è possibile sostituendo alla corrente
i2 (t),
la corrente
−i2 (t)
come mostrato in Figura 2.3.44.
Per un trasformatore ideale in cui le correnti uiscono da sinistra verso destra, diremo
che la potenza entrante
p1 (t) nel trasformatore, risulta uguale alla potenza uscente p2 (t):
p1 (t) = v1 (t) i1 (t) = v2 (t) i2 (t) = p2 (t)
ˆ
Il trasformatore ideale può essere utilizzato come
innalzatore di tensione.
116
(2.3.142)
abbassatore di tensione
o come
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Figura 2.3.44: trasformatore ideale
Nel primo caso si avrà:
(
v2 (t) < v1 (t)
i2 (t) > i1 (t)
(2.3.143)
(
v2 (t) > v1 (t)
i2 (t) < i1 (t)
(2.3.144)
nel secondo caso si avrà:
purchè venga sempre rispettata la (2.3.142).
Figura 2.3.45: alimentazione scorretta di un carico U
Immaginiamo di avere un generatore di energia elettrica G ed un certo utente U posto
a grande distanza da G. Non è possibile trasportare energia dal generatore G all'utente
U come mostrato in Figura 2.3.45 fondamentalmente per due motivi:
1. Il generatore di energia elettrica G eroga una elevata potenza a media tensione,
dell'ordine dei 10 kV. Ciò vuol dire che nella linea di trasmissione che collega
direttamente G ad U scorrerà una elevata corrente elettrica. Per far scorrere una
elevata corrente elettrica occorrerebberodei li conduttori molto grossi; ovviamente
in questo modo si avrà un consumo notevole di rame;
2. nella linea in ogni caso si avranno perdite di potenza del tipo:
Rlinea i2linea
sottofor-
ma di calore. Quindi nel caso di elevate correnti sulla linea si avranno forti perdite
di energia.
117
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Per ovviare a questi problemi basta collegare in prossimità del generatore G un innalzatore di tensione che porti la media tensione (M.T.) in alta tensione (A.T) e in prossimità
dell'utente U un abbassatore di tensione riporti l'A.T. in M.T. (Figura 2.3.46).
In questo modo il tratto di linea compreso tra i due trasformatori si potrà realizzare con
li conduttori più sottili in quanto la corrente in gioco risulterà notevolmente abbassata.
Figura 2.3.46: alimentazione corretta di un carico U
Un tipico utente che utilizza la M.T. potrebbe essere un'industria chimica, un'industria
meccanica, eccetera.
Le comuni abitazioni domestiche utilizzano la bassa tensione (b.t). Per ottenere la b.t.
basta utilizzare un trasformatore abbassatore che porti la M.T. in b.t. come mostrato in
Figura 2.3.47.
Figura 2.3.47: A.T, M.T., b,t.
I trasformatori utilizzati nello schema di Figura 2.3.47 li abbiamo supposti ideali. Per
essi abbiamo detto che vale la (2.3.142).
Nella realtà però succede che per ognuno di essi si avrà:
p2 (t) < p1 (t)
in quanto per un
trasformatore reale,
(2.3.145)
l'accoppiamento non sarà mai perfetto e non
potrà mai essere realizzato con materiali a permeabilità magnetica innita in quanto non
esistono. Ad ogni modo nel trasformatore reale si avranno perdite di energia; tali perdite
si classicanoin
perdite nel rame e perdite nel ferro.
Le perdite nel rame possono essere:
ˆ
alla porta 1:
R1 i21
W;
ˆ
alla porta 1:
R1 i21
W.
118
2 Dall'elettromagnetismo all'elettrotecnica: i dispositivi elettrici
Le perdite nel ferro sono dovute:
ˆ
all'isteresi:
f Aisteresi Vf erro
l'area del ciclo di isteresi e
ˆ
alle correnti parassite:
W, essendo
Vf erro
f
la frequenza di lavoro del ferro,
Aisteresi
il volume;
σf erro e2 Vf erro
W.
Si possono ridurre le perdite per isteresi inserendo piccole quantità di silicio nel ferro; in
questo modo si riduce l'area del ciclo di isteresi.
Se il campo magnetico all'interno del ferro è variabile nel tempo, cioè
l'equazione di Maxwell
~ × ~e =
∇
∂~
− ∂t
b, si avrà un campo elettrico
~e
tiipo
6= 0,
per
ortogonale alla linea
σf erro ,vi sarà
~j = σf erro~e che produce perdite di potenze del
di campo magnetico e per il fatto che il ferro ha conducibilità elettrica
una corrente elettrica parassita di densità
∂~
∂t b
σf erro e2 Vf erro .
119
3 Generatori pilotati e forme d'onda
3.1 Generatori pilotati
Un generatore pilotato è un dispositivo con due porte, dove la porta 2 è un generatore
di tensione o di corrente e la porta 1 è un cortocircuito o un circuito aperto.
La forma d'onda del generatore alla porta 2 è una funzione della tensione ai capi del
circuito aperto o una funzione della corrente che attraversa il cortocircuito.
Si hanno
quattro possibilita e a ogni modo i generatori pilotati vengono rappresentati con un
rombo.
3.1.1 Generatore di corrente pilotato in corrente
Figura 3.1.1: generatore di corrente pilotato in corrente
La corrente alla porta 2 è una funzione della corrente alla porta 1:
i2 (t) = h i1 (t)
essendo
h=
(3.1.1)
i1 (t)
12 (t) una quantità adimensionale.
3.1.2 Generatore di corrente pilotato in tensione
La corrente alla porta 2 è una funzione della tensione alla porta 1:
i2 (t) = g v1 (t)
essendo
g=
i2 (t)
v1 (t) una quantità avente la dimensione di una conduttanza.
120
(3.1.2)
3 Generatori pilotati e forme d'onda
Figura 3.1.2: generatore di corrente pilotato in tensione
Figura 3.1.3: generatore di tensione pilotato in corrente
3.1.3 Generatore di tensione pilotato in corrente
La tensione alla porta 2 è una funzione della corrente alla porta 1:
v2 (t) = r i1 (t)
essendo
r=
(3.1.3)
v2 (t)
i1 (t) una quantità avente la dimensione di una resistenza.
3.1.4 Generatore di tensione pilotato in tensione
Figura 3.1.4: generatore di tensione pilotato in tensione
La tensione alla porta 2 è una funzione della tensione alla porta 1:
v2 (t) = k v1 (t)
essendo
k=
v2 (t)
v1 (t) una quantità adimensionale.
121
(3.1.4)
3 Generatori pilotati e forme d'onda
3.2 Forme d'onda
Sia i generatori ideali di tensione che di corrente che tutti i generatori pilotati possono
avere una qualunque delle seguenti forme d'onda
3.2.1 Funzione costante
Figura 3.2.1: funzione costante
∀t
f (t) = k
(3.2.1)
3.2.2 Sinusoide o cosinusoide
Figura 3.2.2: cosinusoide
f (t) = A cos (ωt + ϕ)
La costante
frequenza
A
si chiama
e la costante
ϕ
ampiezza della
fase.
sinusoide mentre la costante
(3.2.2)
ω
si chiama
si chiama
3.2.3 Gradino unitario
(
1 se t ≥ 0
u (t) =
0 se t < 0
122
(3.2.3)
3 Generatori pilotati e forme d'onda
Figura 3.2.3: gradino unitario
Figura 3.2.4: gradino unitario traslato
3.2.3.1 gradino unitario traslato
(
1
u (t − t0 ) =
0
se t ≥ t0
se t < t0
(3.2.4)
3.2.4 Impulso di durata nita
Figura 3.2.5: impulso di durata nita
p∆ (t) =


0
1
∆

0
Si osservi che l'area sottesa da
p∆ (t) =
se t < 0
se 0 ≤ t ≤ ∆
se t > 0
per qualunque
123
∆.
(3.2.5)
3 Generatori pilotati e forme d'onda
3.2.5 Impulso di Diràc
Figura 3.2.6: impulso di Diràc
L'impulso di Diràc è una distribuzione e solo in questo ambito la intenderemo come
una funzione denita ponendo:
(
0
t 6= 0
δ (t) = lim p∆ (t) =
+
∆→0
+∞ t = 0
(3.2.6)
Il simbolo 1 accanto al graco della delta di Diràc indica che l'area sottesa da
quest'ultima è pari a uno, esattamente come nel caso dell'impulso di durata nita:
ˆ
+∞
δ (t) dt = 1
(3.2.7)
−∞
Questo risultato si dimostra nella teoria delle distribuzioni; ovviamente nell'ambito
dell'integrale di Lebesgue si avrebbe un'area sottesa nulla per la delta di Diràc.
3.2.5.1 Impulso di Diràc traslato
Figura 3.2.7: impulso di Diràc traslato
(
0
se t 6= t0
δ (t − t0 ) =
+∞ se t = t0
3.2.5.2 Proprietà del campionamento
ˆ
ˆ
+∞
+∞
f (t) δ (t − t0 ) dt =
−∞
f (t0 ) δ (t) dt =
−∞
124
(3.2.8)
3 Generatori pilotati e forme d'onda
ˆ
+∞
= f (t0 )
δ (t) dt = f (t0 )
(3.2.9)
−∞
Figura 3.2.8: campionamento della funzione
f (t)
in
t0
3.2.5.3 Proprietà della delta di Diràc
δ (t) =
d
u (t)
dt
(3.2.10)
Per dimostrare la (3.2.10) basta osserva la Figura 3.2.9.
Figura 3.2.9: composizione di gradini per formare un impulso di durata nita
Si vede che si può scrivere:
1
1
u (t) − u (t − ∆)
u (t) − u (t − ∆) =
∆
∆
∆
+
∆ → 0 la (3.2.11) fornisce la (3.2.10):
p∆ (t) =
Passando al limite per
δ = lim p∆ (t) = lim
∆→0+
∆→0+
u (t) − u (t − ∆)
d
= u (t)
∆
dt
(3.2.11)
(3.2.12)
Ovviamente invertendo (3.2.10) si ottiene:
ˆ
(
0
u (t) =
δ (τ ) dτ =
1
−∞
t
125
se t < 0
se t ≥ 0
(3.2.13)
3 Generatori pilotati e forme d'onda
Figura 3.2.10: rampa unitaria
3.2.6 Rampa unitaria
(
t
r (t) =
0
se t ≥ 0
se t < 0
(3.2.14)
Si osservi che la rampa unitaria si ricava integrando il gradino unitario:
ˆ
(
0
r (t) =
u (τ ) dτ =
t
−∞
t
se t < 0
se t ≥ 0
(3.2.15)
3.2.7 Rampa parabolica
Figura 3.2.11: rampa parabolica
(
p (t) =
t2
2
se t ≥ 0
se t < 0
0
(3.2.16)
Si osservi che la rampa parabolica si ricava integrando la rampa unitaria:
ˆ
t
p (t) =
r (τ ) dτ =
−∞
(
0
t2
2
se t < 0
se t ≥ 0
3.2.8 Doppietto
Si chiama doppietto la derivata prima della delta di Diràc:
126
(3.2.17)
3 Generatori pilotati e forme d'onda
Figura 3.2.12: funzione doppietto
d
δ (t)
dt
(3.2.18)
Il suo graco viene mostrato in Figura 3.2.12.
3.3 Proprietà dei segnali elettrici
Le forme d'onda in esame possono essere la tensione in funzione del tempo
rente in funzione del tempo
i (t).
v (t)
o la cor-
Spesso è possibile usare le stesse tecniche matematiche
per ciascuno dei due tipi di forma d'onda e di conseguenza per dare generalità al discorso
conviene indicare la forma d'onda semplicemente con
w (t)
quando l'analisi si applica ad
entrambi i casi.
Si denisce
operatore media temporale, l'espressione:
1
< . >= lim
T →∞ T
ˆ
T
2
[.] dt
− T2
(3.3.1)
L'operatore media temporale è lineare,infatti si ha che
< a w1 (t) + b w (t) >= a < w1 (t) > +b < w2 (t) >
Un segnale
w (t)
si dice
periodico di periodo T0
se risulta
w (t + T0 ) = w (t)
essendo
T0
(3.3.2)
∀t
(3.3.3)
il più piccolo numero positivo che soddisfa tale relazione.
Per un segnale periodico l'operatore media temporale si scrive:
1
< . >=
T0
ˆ
T0
+a
2
−
T0
+a
2
127
[.] dt
a∈R
(3.3.4)
3 Generatori pilotati e forme d'onda
3.3.1 Valore medio o componente continua
Il
valore medio
o
componente continua
di un segnale
w (t)
è dato dalla sua media
temporale:
WDC
Se
w (t)
ˆ
1
< w (t) >= lim
T →∞ T
è periodico di periodo
WDC
T0 ,
T
2
w (t) dt
− T2
(3.3.5)
il suo valore medio è:
1
< w (t) >=
T0
ˆ
T0
2
−
T0
2
w (t) dt
(3.3.6)
3.3.2 Potenza media normalizzata
La potenza istantanea
p (t)
è per denizione il lavoro per unità di tempo:
p (t) =
L
t
(3.3.7)
Per determinare l'espressione generale della potenza di un elemento a due morsetti
basta ricordare la denizione di tensione elettrica e di corrente elettrica.
La tensione elettrica ai capi di un elemento circuitale a due morsetti è il lavoro per
unità di carica:
v (t) =
L
q
(3.3.8)
mentre la corrente che attraversa lo stesso dispoditivo è la carica per unità di tempo:
i (t) =
q
t
(3.3.9)
A questo punto moltiplicando e dividendo il secondo membro di (3.3.7) per la carica
q
e usando (3.3.8) e (3.3.9) si ottiene:
p (t) =
Lq
Lq
=
= v (t) i (t)
tq
q t
ovvero:
p (t) = v (t) i (t)
(3.3.10)
Applicando l'operatore media temporale a (3.3.10) si ricava la potenza media del bipolo:
P =< p (t) >=< v (t) i (t) >
(3.3.11)
Se il bipolo è puramente resistivo allora la tensione ai suoi capi e la correntte che lo
attraversa sono legati tra di loro mediante la legge di Ohm:
v (t) = R i (t)
128
(3.3.12)
3 Generatori pilotati e forme d'onda
Combinando (3.3.10) con (3.3.12) si ricavano altre formule equivalenti per la potenza
istantanea:
p (t) = v (t) i (t) = R i2 (t) =
v 2 (t)
R
(3.3.13)
Nota la (3.3.13) è ovvio che la potenza media dissipata dal resistore sipuò scrivere nelle
seguenti forme equivalenti:
< v 2 (t) >
R
P =< p (t) >= R < i2 (t) >=
Se la resistenza R del bipolo vale 1
zata:
Ω,
dalla (3.3.14) segue la
(3.3.14)
potenza media normaliz-
P =< p (t) >=< i2 (t) >=< v 2 (t) >
Dalla (3.3.15) segue che la potenza media normalizzata di un segnale
(3.3.15)
w (t)
è il valore
medio del segnale al quadrato:
1
P =< w (t) >= lim
T →∞ T
ˆ
T
2
2
w2 (t) dt
− T2
(3.3.16)
Nel caso di segnale periodico la potenza media normalizzata risulta:
ˆ
1
P =< w (t) >=
T0
2
Si chiama
potenza di picco
T0
2
−
T0
2
w2 (t) dt
(3.3.17)
il massimo della potenza istantanea:
Ppicco = max {v (t) i (t)}
(3.3.18)
3.3.3 Energia media normalizzata
Si chiama
energia media normalizzata
l'espressione:
ˆ
E =< w2 (t) >= lim
T
2
T →∞ − T
2
Per un segnale periodico di periodo
T0
w2 (t) dt
(3.3.19)
si ha:
ˆ
2
E =< w (t) >=
129
T0
2
T
− 20
w2 (t) dt
(3.3.20)
3 Generatori pilotati e forme d'onda
3.3.4 Valore ecace
Si chiama
valore ecace del segnale w (t)
la radice quadrata della potenza media nor-
malizzata:
√
Wef f. =
v
u
ˆ
u
p
P = < w2 (t) > = t lim
T
2
T →∞ − T
2
w2 (t) dt
(3.3.21)
3.3.5 Segnali di potenza e segnali di energia
Grazie alle denizioni date, i segnali si possono classicare in
di energia.
Un segnale
w (t)
si dice di
potenza
segnali di potenza e segnali
se è caratterizzato da una potenza media normal-
izzata P nita e non nulla:
0 < P < +∞
Un segnale
w (t) si dice di energia
(3.3.22)
se è caratterizzato da una energia media normalizzata
E nita e non nulla:
0 < E < +∞
(3.3.23)
Proprietà
Se un segnale è di potenza allora non è di energia e viceversa.
Per vericare quanto detto basta esprimere la potenza media normalizzata in funzione
dell'energia media normalizzata e viceversa.
Combinando le relazioni in (3.3.16) e (3.3.19) si ricavano le relazioni
1
P = E lim
T →+∞ T
E=P
1
lim
T →+∞ T
Dalla prima di queste ultime due relazioni si deduce che
potenza media normalizzata nulla.
Dalla seconda si deduce invece che
normalizzata innita.
−1
un segnale di energia w (t) ha
un segnale di potenza w (t) ha energia media
130
4 Reti elettriche
4.1 Introduzione
Dopo aver introdotto i dispositivi elettrici possiamo occuparci delle
reti elettriche
sono per l'appunto interconnessioni di dispositivi elettrici.
I dispositivi elettrici costituenti le reti
elettriche sono connessi tra di loro attraverso dei li a conducibilità innita
(p.e.c).
Un tratto di lo a conducibilità innita che separa 2 nodi si chiama cortocircuito; se in una rete elettrica un cortocircuito separa i nodi 1 e 2, allora questo si
può rappresentare attraverso un unico noFigura 4.1.1: cortocircuito e nodi
do; viceversa un nodo può essere sempre
pensato come un cortocircuito che separa
due nodi (Figura 4.1.1)
4.2 Scrittura delle L.K.
Consideriamo la rete elettrica mostrata in Figura 4.2.1.
Essa risulta costituita da un generatore
ideale di tensione, da un generatore ideale di corrente, da due resistori lineari
tempo-invariante, da un capacitore lineare
tempo-invariante e da un induttore lineare
tempo invariante.
Osservando la rete si
vede che i nodi 4 e 5 sono connessi tra di
loro attraverso un cortocircuito: non cambia nulla nello studio della rete se pensiamo di fondere i nodi 4 e 5.
Potrem-
mo ridisegnare la rete elettrica fondendo
assieme i nodi 4 e 5 ma ciò non cambia
nulla nel prosegui dello studio della rete
elettrica.
Si denisce
nodo
Figura 4.2.1: rete elettrica
quel punto della rete
elettrica in cui convergono due o più
lati
131
che
4 Reti elettriche
elementari.
Per lato elementare si intende un tratto di circuito contenente un solo
dispositivo elementare.
In realtà esiste un certo grado di arbitrarietà quando si denisce un nodo. Per esempio
se conveniamo di denire i
lati compositi (un lato composito è un bipolo in cui i dispositivi
elementari possono essere interconnessi tra di loro in serie e/o in parallelo), possiamo
pensare la serie costituita dal generatore ideale di tensione
vg (t)
e il resistore
R1
come
un lato e quindi non denire il nodo 1. In Figura 4.2.1 si può vedere che è stata adottata
la convenzione secondo cui un nodo è l'interconnessione elementare di due o più lati
elementari.
Immaginando di fondere il nodo 4 con il nodo 5, allora la rete elettrica mostrata in
Figura 4.2.1 risulta essere costituita da N=4 nosi ed L=6 lati.
Le incognite per una rete elettrica sono le correnti di lato e le tensioni di lato. Per una
rete elettrica costituita da L lati si avranno allora 2L incognite:
vk , ik
k = 1, 2, ...., L
(4.2.1)
Per risolvere un problema di 2L incognite occorrono 2L equazioni.
Si dimostra che basta scrivere L leggi di Kirccho (LK) ed L leggi di lato (LL) per
risolvere il problema di una rete elettrica formata da L lati.
Mentre le LK sono equazioni topologiche, ossia equazioni che danno informazioni sul
come sono connessi i lati in un circuito, le LL sono equazioni che danno informazioni sul
come sono fatti i lati della rete elettrica stessa.
Ovviamente le 2L equazioni che servono per risolvere la rete elettrica devono essere tra
di loro linearmente indipendenti.
Anchè le equazioni possano essere linearmente indipendenti tra di loro basta scrivere:
N −1
leggi di Kirccho delle tensioni (LKT),
L−N +1
leggi di Kirccho delle correnti (LKI), ed
L
leggi di lato (LL).
Facendo riferimento alla rete elettrica mostrata in Figura 4.2.1 occorre scrivere:
ˆ
N-1=4-1=3 LKT;
ˆ
L-N+1=6-4+1=3 LKI;
ˆ
L=6 LL.
132
4 Reti elettriche
Quindi per risolvere la rete elettrica occorre scrivere:
LKT + LKI + LL = 12
equazioni.
Per scrivere queste 12 equazioni occorre scrivere per ciascun lato la tensione e la corrente.
Se ciascun lato è un resistore o un capacitore o un induttore la tensione e la
corrente si scriveranno adottando la convenzione dell'utilizzatore. Viceversa per i generatori ideali e per i generatori pilotati, si scriveranno tensione e corrente adottando la
convenzione del generatore.
La Figura 4.2.2 mostra per ogni elemento circuitale la tensione e la corrente di lato;
per i resistori , il capacitore e l'induttore viene adottata la convenzione dell'utilizzatore
mentre per i generatori viene adottata la convenzione del generatore.
Figura 4.2.2: rete elettrica
In base a ciò che è stato detto prima, per la rete mostrata si devono scrivere N-1=3
leggi di Kircchoof delle correnti, quindi occorre scartare un nodo visto che la rete ne
presenta 4. Normalmete si scarta il nodo verso cui converge il numero maggiore di lati;
nell'esempio considerato viene scartato il nodo 4.
Le LKI ai nodi 1,2 e 3 sono:


LKI1
−iA (t) + i1 (t) = 0
−i1 (t) + ic (t) + iL (t) = 0 LKI2


−iL (t) − ig (t) + i2 (t) = 0 LKI3
(4.2.2)
Seguendo l'orientazione degli anelli I, II e III si scrivono le LKT:


−vA (t) + v1 (t) + vc (t) = 0 LKT 1
−vc (t) + vL (t) + vB (t) = 0 LKT 2


−vB (t) + v2 (t) = 0
LKT 3
Inne attraverso una semplice ispezione visiva si scrivono le LL:
133
(4.2.3)
4 Reti elettriche


vA (t) = vg (t)





iB (t) = ig (t)



v (t) = R i (t)
1
1 1

v2 (t) = R2 i2 (t)




d

vc (t)
ic (t) = C dt



v (t) = L d i (t)
L
dt L


LL1
vA (t) = vg (t)





LL2
iB (t) = ig (t)




LL3
v1 (t) − R1 i1 (t) = 0
=⇒

LL4
v2 (t) − R2 i2 (t) = 0




d

LL5
vc (t) = 0
ic (t) − C dt




d
LL6
vL (t) − L dt iL (t) = 0
LL1
LL2
LL3
LL4
LL5
LL6
(4.2.4)
Si osservi che tutte le equazioni scritte sono omogenee tranne la LL1 e la LL2.
Le equazioni in (4.2.2) (4.2.3) (4.2.4) costituiscono un sistema algebrico dierenziale
lineare di 12 equazioni in 12 incognite.
Visto che il sistema è in parte dierenziale occorre specicare pure le condizioni sullo
stato energetico dei dispositivi a memoria all'istante t=0s; nel caso specico possiamo
ssare le condizioni iniziali come segue:
(
vc (0) = V0
iL (0) = I0
c.i.1
c.i.2
(4.2.5)
Siccome il sistema è algebrico dierenziale lineare possiamo adottare una strategia di
risoluzione che prevede di separare le equazioni algebriche da quelle dierenziali.
In
questo modo otteniamo da un lato un sistema algebrico lineare di 10 equazioni in 12
incognite e dall'altro un sistema dierenziale lineare di 2 equazioni in 4 incognite:


vA (t) = vg (t)





iB (t) = ig (t)





v1 (t) − R1 i1 (t) = 0





v2 (t) − R2 i2 (t) = 0



−i (t) + i (t) = 0
1
A
−i1 (t) + ic (t) = −iL (t)




−ig (t) + i2 (t) = iL (t)





−vA (t) + v1 (t) = −vc (t)





vL (t) + vB (t) = vc (t)



−v (t) + v (t) = 0
2
B
LL1
LL2
LL3
LL4
LKI1
(4.2.6.1)
LKI2
LKI3
LKT 1
LKT 2
LKT 3
(
d
vc (t) LL5
ic (t) = C dt
(4.2.6.2)
d
vL (t) = L dt iL (t) LL6
equazioni di stato
Vedremo alla ne che questa strategia conduce alle
elettrico.
(4.2.6)
del circuito
Si tratta di equazioni dierenziali lineari del primo ordine in cui le uniche
incognite sono le variabili energetiche presenti nel circuito.
Concentriamo l'attenzione sul sistema
(4.2.6.1).
Quello che si fa è portare a secondo membro la
vc (t)e
riguardano il contenuto energetico della rete elettrica.
la
iL (t),
cioè le grandezze che
In altri termini si assumono le
variabili energetiche come funzioni note; in questo modo si ha che il sistema (4.2.6.1) è
come se fosse di 10 equazioni in 10 incognite:
134
4 Reti elettriche


vA (t) = vg (t)





iB (t) = ig (t)





v1 (t) − R1 i1 (t) = 0





v2 (t) − R2 i2 (t) = 0



−i (t) + i (t) = 0
1
A

−i1 (t) + ic (t) = −iL (t)




−ig (t) + i2 (t) = iL (t)




−vA (t) + v1 (t) = −vc (t)





vL (t) + vB (t) = vc (t)



−v (t) + v (t) = 0
2
B
LL1
LL2
LL3
LL4
LKI1
LKI2
LKI3
LKT 1
LKT 2
LKT 3
(4.2.7)
Fatto ciò possiamo immaginare allora la rete elettrica data, come un circuito resistivo
in cui le sorgenti sono i generatori ideali
iL (t)
vg (t)
e
ig (t)
e i
generatori assimilati vc (t) e
(Figura 4.2.3).
Siccome il sistema (4.2.7) è lineare, quello che si troverà è che qualunque variabile di rete è una combinazione lineare
di
vg (t) , ig (t) , vc (t) , iL (t).
Per
esempio
per
la
i1 (t)
corrente
troveremo:
i1 (t) = k1 vg (t)+k2 ig (t)+k3 vc (t)+k4 iL (t)
La
di
strategia
determinare
analoghe
di
risoluzione
dal
grandezze
sistema
alle
prevede
(4.2.7)
variabili
le
ener-
getiche , ovvero la corrente che attraversa
ic (t), e la tensione
dell'induttore, vL (t) in modo da
in capacitore,
ai capi
Figura 4.2.3: rete elettrica resistiva
poterle
utilizzare successivamente per risolvere il sistema dierenziale (4.2.6.2).
Attraverso semplici operazioni algebriche dal sistema (4.2.7) si ricavano le seguenti
relazioni:
(
ic (t) = −iL (t) − R11 vc (t) + R11 vg (t) (4.2.8.1)
vL (t) = vc (t) − R2 ig (t) − R2 iL (t)
(4.2.8.2)
(4.2.8)
Le equazioni in (4.2.8) si possono ricavare in maniera veloce dalla rete resistiva mostrata
in Figura 4.2.3 senza passare dalla risoluzione del sistema (4.2.7). La (4.2.8.1) si deduce
facilmente scrivendo la LKI al nodo 2:
−i1 (t) + ic (t) + iL (t) = 0 ⇒ ic (t) = i1 (t) − iL (t) =⇒
135
4 Reti elettriche
=⇒ ic (t) =
vg (t) − vc (t)
− iL (t)
R1
La (4.2.8.2) si deduce facilmente scrivendo la LKT all'anello II:
−vc (t) + vL (t) + v2 (t) = 0 ⇒ vL (t) = vc (t) − v2 (t) =⇒
=⇒ vL (t) = vc (t) − R2 i2 (t) =⇒ vL (t) = vc (t) − R2 (iL (t) + ig (t))
Note le equazioni in (4.2.8), il sistema dierenziale dato in (4.2.6.2) si scrive:
(
d
dt vc (t)
d
dt iL (t)
= − R11C vc (t) − C1 iL (t) + R11C vg (t)
= L1 vc (t) − RL2 iL (t) − RL2 ig (t)
Le equazioni in (4.2.9) sono le
energetiche
vc (t)
e
iL (t)
(4.2.9)
equazioni di stato del circuito elettrico mentre le variabili
variabili di stato.
vengono dette
Quando si risolve una rete elettrica di solito si incorre nel problema di determinare
la condizione iniziale sulla derivata prima della variabile di interesse. La ricerca di tale
condizione è ardua e può portare alla scrittura di LK alla rinfusa senza mai arrivare alla
conclusione.
Pertanto la strategia migliore per la risoluzione di una rete elettrica è quella che conduce
alle equazioni di stato che per t=0 s forniscono direttamente la condizione iniziale sulla
derivata prima delle variabili di stato:
(
d
dt vc (t) |t=0
d
dt iL (t) |t=0
= − R11C vc (0) − C1 iL (0) + R11C vg (0) (4.2.10.1)
= L1 vc (0) − RL2 iL (0) − RL2 ig (0)
(4.2.10.2)
(4.2.10)
4.3 Regime costante
4.3.1 Equazione dierenziale di ordine minimo per una variabile di rete
Abbinando alle equazioni di stato date in (4.2.9) le condizioni iniziali date in (4.2.5) si
ottiene il seguente problema dierenziale:

d
1
1
1


dt vc (t) = − R1 C vc (t) − C iL (t) + R1 C vg (t)


 d i (t) = 1 v (t) − R2 i (t) − R2 i (t)
dt L
L c
L L
L g

vc (0) = V0



i (0) = I
0
L
Possiamo risolvere tale sistema in modo scalare.
(4.3.1.1)
(4.3.1.2)
(4.3.1.3)
(4.3.1.4)
(4.3.1)
Basta ricavare da una equazione
un'incognita e sostituirla nell'altra equazione; così facendo da due equazioni dierenziali del primo ordine si ricava un'unica equazione dierenziale del secondo ordine nella
variabile
vc (t) o iL (t).
iL (t) dalla
Ricavando
(4.3.1.1) e sostituendo nella (4.3.1.2) si ricava:
136
4 Reti elettriche
d2
vc (t) +
dt2
=
1
R2
+
R1 C
L
vc (t).
d
1
vc (t) +
dt
LC
R2
1+
R1
vc (t) =
1 d
R2
R2
vg (t) +
vg (t) +
ig (t)
R1 C dt
R1 LC
LC
La (4.3.2) prende il nome di
di stato
equazione dierenziale di ordine minimo
(4.3.2)
nella variabile
Per integrare tale equazione occorre conoscere le condizioni iniziali:
vc (0) = V0
(4.3.3)
d
V0
I0 vg (0)
vc (t) t=0 = −
−
+
dt
R1 C
C
R1 C
(4.3.4)
La condizione (4.3.4) è stata dedotta a partire dall'equazione di stato del capacitore.
Se riuscissimo a dedurre la (4.3.2) senza passare dalle equazioni di stato è possibile
ricavare la condizione in (4.3.4)?
La risposta è SI. Basta studiare il circuito all'istante
t = 0
s che viene mostrato in
Figura 4.3.1.
L'equazione costitutiva del capacitore
all'istante
t=0
s
si
scrive:
ic (0)
=
d
vc (t) |t=0 da cui si ricava:
C dt
d
1
vc (t) t=0 = ic (0)
dt
C
(4.3.5)
Scrivendo la LKI al nodo 2:
−i1 (0) + ic (0) + iL (0) = 0
si ricava:
ic (0) = i1 (0) − iL (0) =
vg (0) − V0
− I0
R1
(4.3.6)
Figura 4.3.1: rete elettrica all'istante t=0 s.
Sostituendo (4.3.6) in (4.3.5) si ricava la (4.3.4).
Ovviamente per circuiti più complicati è sconsigliata questa strategia.
4.3.1.1 Ordine minimo dell'equazione dierenziale
Facendo altre sostituzioni, avremmo potuto ottenere dal sistema algebrico dierenziale
lineare, un'altra equazione dierenziale di ordine minimo in qualunque altra variabile di
rete. Quindi tutte le variabili di rete soddisfano ad una equazione dierenziale di ordine
minimo che in generale potrebbe essere diversa da variabile a variabile; quello che si
trova è che pere qualunque variabile di rete, l'equazione dierenziale ha sempre lo stesso
ordine
n.
Per il circuito mostrato in Figura 4.2.1, l'equazione dierenziale per qualunque
variabile di rete, è di ordine
n = 2.
137
4 Reti elettriche
L'ordine minimo dell'equazione differenziale, ossia del circuito elettrico, corrisponde al numero di condizioni iniziali
che bisogna specicare per caratterizzare
tutto il contenuto energetico della rete
elettrica.
Nella rete elettrica mostrata in Figura
4.2.1 bisogna specicare quindi la tensione
ai capi del capacitore e la corrente che at-
Figura 4.3.2: insieme di taglio di lati tutti
induttivi
traversa l'induttore alll'istante di tempo
t=0 s.
Applicare la regola per stabilire l'ordine minimo dell'equazione dierenziale non è
sempre semplice.
Se una rete elettrica presenta un insieme di taglio fatto tutto da lati induttivi, allora una
condizione iniziale sul patrimonio energetico di un induttore è combinazione lineare delle
altre condizioni iniziali relative ai patrimoni energetici degli altri induttori dell'insieme
di taglio.
Per esempio se la rete elettrica presenta tre lati induttivi che ipoteticamente possono
essere tagliato da una supercie gaussiana, come mostrato in Figura 4.3.2, possiamo
scrivere una LKI all'insieme di taglio:
i1 (t) + i2 (t) + i3 (t) = 0
(4.3.7)
In questo caso per caratterizzare tutto il
contenuto energetico dovuto a tali induttori , bastano solo 2 condizioni iniziali sulle
correnti ( per esempio le condizioni iniziali
i1 (0),i2 (0)),
perchè la terza è una combi-
nazione lineare delle precedenti (i3
(0) =
−i1 (0) − i2 (0)).
Quindi per un insieme di taglio fatto
tutto
da
induttori,
si
esclude
una
condizione iniziale perchè combinazione
lineare delle altre.
Un ragionamento analogo vale per gli
Figura 4.3.3: anello di capacitori
anelli fatti solo da capacitori.
Se la rete elettrica presenta un'anello (o maglia) fatta tutta da lati capacitivi, allora una
condizione iniziale sul patrimonio energetico di un capacitore è combinazione lineare delle
altre condizioni iniziali relative ai patrimoni energetici degli altri capacitori dell'anello.
Per esempio se la rete elettrica presenta un anello formato da 4 capacitori come
mostrato in Figura 4.3.3, si può scrivere la LKT:
v1 (t) + v2 (t) + v3 (t) + v4 (t) = 0
138
(4.3.8)
4 Reti elettriche
In questo caso per caratterizzare tutto il contenuto energetico dovuto a tali capacitori, bastano solo 3 condizioni iniziali sulle tensioni ( per esempio le condizioni in-
v1 (0),v2 (0) , v3 (0)) perchè la
(0) = −v1 (0) − v2 (0) − v3 (0)).
iziali
(v4
quarta è una combinazione lineare delle precedenti
Quindi per un anello fatto tutto da capacitori, si esclude una condizione iniziale perchè
combinazione lineare delle altre.
n di una rete elettrica si ottiene tramite la seguente
In denitiva l'ordine di derivazione
formula:
n = Nc + NL − Mc − TL
essendo
Nc
(4.3.9)
il numero di caapacitori presenti nella rete elettrica,
induttori presenti nella rete elettrica,
rete elettrica ed inne
TL
Mc
NL
il numero di
il numero di anelli di capacitori presenti nella
il numero di insiemi di taglio di induttori presente nella rete
elettrica.
4.3.2 Risoluzione equazioni dierenziali
Se indichiamo con
y(t)
una qualunque variabile della rete elettrica e con
xk (t)
il k-
esimo ingresso che sollecita la rete, possiamo scrivere la forma generale dell'equazione
dierenziuale di ordine minimo:
n
X
i=0
E' chiaro che i coecienti
G M
k
XX
d i
d j
ai i y (t) =
bk,j j xk (t)
dt
dt
(4.3.10)
k=1 j=0
ai
relativi all'equazione dierenziale di ordine minimo data
in (4.3.2) sono:
a2 = 1; a1 =
1
R2
+
R1 C
L
1
; a0 =
LC
R2
1+
R1
Si può osservare che essi dipendono solo dai resistori e dai dispositivi a memoria nonchè
dal come essi sono connessi tra di loro e pertanto risultano essere quantità sempre positive.
I coecienti
ai
non dipendono dai generatori della rete che inuenzano soltanto il
secondo membro dell'equazione dierenziale di ordine minimo.
Siccome il secondo membro della (4.3.10) contiene solo termini noti, esso si può scrivere
in forma compatta mediante una funzione
n
X
i=0
ai
f (t):
d i
y (t) = f (t)
dti
Per integrare la (4.3.11) occorre specicare n-1 condizioni iniziali:
139
(4.3.11)
4 Reti elettriche


y (t) |t=0




d


dt y (t) |t=0


.

.





.



 dn−1 y (t) |
t=0
dtn−1
(4.3.12)
La (4.3.11) è un'equazione dierenziale di ordine n a coecienti costanti non omogenea.
Si dimostra che l'integrale generale della (4.3.11) è:
y (t) = yomog. (t) + ypart. (t)
dove
yomog. (t)
è l'integrale generale dell'omogenea associata:
n
X
ai
i=0
e
ypart. (t)
(4.3.13)
d i
y (t) = 0
dti
(4.3.14)
è l'integrale particolare della (4.3.11).
4.3.2.1 Ricerca dell'integrale generale dell'omogenea associata
Consideriamo l'equazione omogena indicata in (4.3.14). Si scrive l'equazione caratteristica ad essa associata:
(P
n
i
i=0 ai λ
=0
(4.3.15)
λ∈C
Siccome l'equazione caratteistica è inquadrata nell'ambito dei numeri complessi, avrà
n-radici che possono essere reali o complesse con le relative molteplicità.
Visto che i coecienti
ai
sono numeri reali,le radici della (4.3.15) sono a coppia
complesse coniugate, cioè se
λ = δ + jω
(4.3.16)
è una radice dell'equazione caratteristica, lo è pure:
λ̄ = δ − jω
Se la radice
ν
λ ha molteplicità ν
pure la coniugata
(4.3.17)
λ̄ avrà molteplicità ν (la molteplicità
ν -volte λ, e ν -volte λ̄).
indica che l'equazione caratteristica ammette come soluzione,
Il numero reale
Re {λ} = δ
si chiama parte reale del numero complesso
140
λ,
mentre il numero reale
(4.3.18)
4 Reti elettriche
Im {λ} = ω
si chiama parte immaginaria del numero complesso
(4.3.19)
λ.
δ = 0, l'equazione caratteristica ammette come soluzioni le radici complesse coniuλ = jω , λ̄ = −jω dette radici immaginarie coniugate.
Se ω = 0, l'equazione caratteristica ammette come soluzione la radice reale λ = δ .
Se
gate
Riassumendo l'equazione caratteristica data in (4.3.15) può ammettre radici complesse
e coniugate, radici immaginarie e conigute, radici reali.
A ciascuna delle radici dell'equazione caratteristica possiamo associare dei termini
dell'integrale generale dell'omogenea associata; di seguito viene proposto un elenco di
queste possibilità:
ˆ
Se l'equazione caratteristica ammette come soluzione una radice
reale λ = δ con
molteplicità ν allora l'integrale generale dell'omogenea associata conterrà il seguente
pacchetto di
ν
termini:
k1 eδt + k2 t eδt + ...... + kν tν−1 eδt
dove
ˆ
k1 , k2 , ......, kν
sono
ν -costanti
(4.3.20)
da determinare.
nulla λ = 0 con
molteplicità ν allora l'integrale generale dell'omogenea associata conterrà il seguente
Se l'equazione caratteristica ammette come soluzione una radice
pacchetto di
ν
termini:
n1 + n2 t + ...... + nν tν−1
dove
ˆ
n1 , n2 , ......, nν
sono
ν -costanti
(4.3.21)
da determinare.
Se l'equazione caratteristica ammette come soluzione una coppia di radici immaginari e coniugate
λ = jω
e
λ̄ = −jω
con molteplicità
ν
allora l'integrale generale
dell'omogenea associata conterrà il seguente pacchetto di
ν
termini:
h1 cos (ωt + ϕ1 ) + h2 t cos (ωt + ϕ2 ) + ...... + hν tν−1 cos (ωt + ϕν )
dove
ˆ
h1 , h2 , ......, hν , ϕ1 , ϕ2 , ......, ϕν
(4.3.22)
sono 2ν -costanti da determinare.
Se l'equazione caratteristica ammette come soluzione una coppia di radici complesse
e coniugate
λ = δ + jω
e
λ̄ = δ − jω
con molteplicità
ν
allora l'integrale generale
dell'omogenea associata conterrà il seguente pacchetto di
ν
termini:
p1 eδt cos (ωt + ψ1 ) + p2 t eδt cos (ωt + ψ2 ) + ...... + pν tν−1 eδt cos (ωt + ψν )
dove
p1 , p2 , ......, pν , ψ1 , ψ2 , ......, ψν
(4.3.23)
sono 2ν -costanti da determinare.
E' facile vericare che la somma delle varie molteplicità coincide con l'ordine
n
dell'e-
quazione dierenziale di ordine minimo:
n=
X
k
141
νk
(4.3.24)
4 Reti elettriche
4.3.2.1.1 Rete elettrica priva di generatori
Precedentemente è stato detto che
il primo membro dell'equazione dierenziale di ordine minimo dipende solo dalla
rete elettrica, mentre il secondo membro
dipende dal come la rete viene eccitata: è
ovvio allora che azzerando i generatori (il
che vuol dire considerare l'equazione omogenea associata) riusciamo a capire chi è
realmente la rete elettrica.
Un generatore di tensione si annulla
sostituendolo con un cortocircuito, men-
Figura 4.3.4: rete
elettrica
priva
di
generatori
tre un generatore di corrente si azzera
sostituendolo con un circuito aperto.
Quindi la rete elettrica di Figura 4.2.1 priva di eccitazioni è quella mostrata in Figura
4.3.4.
A
B
Figura 4.3.5: A modo corretto; B modo scorretto
Analogamente per eccitare una rete elettrica tramite un generatore di tensione basta
considerare un lato della rete, tagliarlo in due punti, e inserirvi il generatore di tensione.
Per eccitare la rete attraverso un generatore di corrente basta interporre il generatore
tra due nodi del circuito.
Per esempio un modo corretto di eccitare la rete elettrica di Figura 4.3.4 è quello
mostrato in Figura 4.3.5.A, un modo scorretto di eccitare la rete è quello mostrato in
Figura 4.3.5.B.
Da queste considerazioni si deduce che le reti mostrate in Figura 4.2.1 e Figura 4.3.5.A
prive di eccitazioni coincidono con la rete mostrata in Figura 4.3.4; il che vuol dire che se
consideriamo per esempio l'equazione dierenziale di ordine minimo relativa alla tensione
v1 (t), troveremo per entrambe le reti, un'equazione dierenziale con gli stessi coecienti
ai ; tali equazioni dieriranno solamente per il secondo membro in quanto le reti sono
dierentemente eccitate. Si capisce inoltre che la topologia della rete elettrica mostrata
142
4 Reti elettriche
in Figura 4.3.5.B non è più quella indicata in Figura 4.3.4, e per essa troveremmo altri
coecienti
ai
nell'equazione dierenziale di ordine minimo nella variabile di rete
v1 (t).
E' bene inteso che qual'ora la rete presentasse generatori pilotati, questi NON si possono azzerare in quanto rappresentano elementi di accoppiamento tra due lati della rete
elettrica.
Supponiamo che la rete elettrica che si vuole studiare sia priva di generatori pilotati.
Una volta azzerati tutti i generatori ideali, qualunque variabile di rete
y (t)
sarà
governata da un'equazione dierenziale omogenea a coecienti costanti tipo quella in
(4.3.14).
Il suo integrale generale sarà composto da termini additivi tipo quelli indicati in
(4.3.20÷23).
Siccome ora nella rete elettrica non ci sononè generatori ideali nè generatori pilotati, le
uniche fonti di energia sono quelle dovute alle condizioni iniziali sui dispositivi a memoria.
Visto che nella rete elettrica sono presenti pure resistori, i quali tensono a sottrarre energia
dalla rete trasformandola in calore, il contenuto energetico della rete tenderà ad esaurirsi
col tempo t tendente all'innito.
Questo in altri termini vuol dire che in assenza di fonti di energia, quali i generatori
ideali e i geneatori pilotati, così come per il contenuto energetico della rete, anche per
tutte le grandezze di rete avremo un decadimento per t che tende all'innito.
Adesso siccome una qualunque grandezza di rete, analiticamente corrisponde all'integrale generale di un'equazione dierenziale omogenea a coecienti costanti, essa potrà
contenere solo alxxcuni termini delle relazioni in (4.3.20÷23).
Per esempio guardando la (4.3.21), si capisce che se l'equazione caratteristica ammette
una radice reale nulla, questa sarà obbligatoriamente con molteplicità 1.
Una radice
nulla con molteplicità maggiore di 1 darebbe luogo nell'integrale generale dell'omogenea
associata ad addendi del tipo:
n2 t, n3 t2 , ......, nν tν−1
tutti divergenti per t che tende all'innito e ciò vorrebbe dire che da qualche parte
della rete esiste una qualche fonte di energia contrariamente a quanto detto.
Guardando la (4.3.22) si capisce che lo stesso discorso si ripete per le radici immaginarie
e coniugate; cioè se queste ci sono, obbligatoriamente dovranno essere con molteplicità 1,
se no viceversa darebbere luogo a termini additivi nell'integrale generale divergenti per t
che tende all'innito.
Radici immaginarie complesse sono indice di cattiva modellazione della rete in quanto producono grandezze oscillanti che fanno riscaldare i dispositivi presenti nella rete
elettrica.
Guardando le relazioni in (4.3.20) e (4.3.23) è chiaro che radici reali e radici complesse
e coniugate possono essere ammesse con qualunque molteplicità purchè risultino sempre
con parte reale strettamente negativa:
Re {λ} = δ < 0
143
(4.3.25)
4 Reti elettriche
Nella Figura 4.3.6 riassumiamo le possibili radici con le corrispondenti molteplicità,
che possono dare luogo all'integrale generale dell'omogenea associata qual'ora la rete
elettrica risultasse priva di generatori pilotati e con i generatori ideali azzerati; in queste
condizioni l'integrale generale si chiama
evoluzione libera.
Figura 4.3.6: radici ammesse per comporre l'integrale generale dell'omogenea
4.3.2.2 Ricerca dell'integrale particolare dell'equazione dierenziale di ordine
minimo
Vogliamo determinare l'integrale particolare dell'equazione dierenziale di ordine minimo
nel caso generale quando le eccitazioni per la rete sono dei generatori costanti.
In questo caso il secondo membro dell'equazione dierenziale di ordine minimo
n
X
ai
i=0
d i
y (t) = f (t)
dti
(4.3.26)
f (t) = K
(4.3.27)
è una costante:
Si dimostra che se la forzante
f (t)
è una costante allora anche l'integrale particolare
dell'equazione dierenziale di ordine minimo è una costante:
ypart. (t) = C.
Ponendo nella (4.3.25)
y(t) = ypart. (t),
(4.3.28)
e sostituendo (4.3.26) e (4.3.27) si determina
il valore della costante C:
a0 C = K =⇒ C =
144
K
a0
(4.3.29)
4 Reti elettriche
Sostituendo (4.3.28) in (4.3.27) si ricava l'espressione dell'integrale particolare dell'equazione dierenziale di ordine minimo nel caso in cui la rete viene eccitata con generatori
di tensione e di corrente costanti:
ypart. (t) =
K
a0
(4.3.30)
4.3.3 Esempio
Consideriamo nuovamente la rete elettica di Figura 4.2.1 che per comodità riportiamo
sul foglio di questa pagina:
Figura 4.3.7: rete elettrica
Per determinare la tensione ai capi del capacitore occorre dunque risolvere il problema
di Cauchy che si ottiene mettendo a sistema (4.3.2) (4.3.3) e (4.3.4):
 2
R2
1
1
d
d

v
(t)
+
+
v
(t)
+

R1 C
L
dt c
LC 1 +
dt2 c



R2
d
2
= R11C dt
vg (t) + RR
vg (t) + LC
ig (t)
1 LC

vc (0) = V0



d
vg (o)
V0
I0
dt vc (t) |t=0 − R1 C − C + R1 C
R2
R1
vc (t) =
(4.3.31.1)
(4.3.31.2)
(4.3.31)
(4.3.31.3)
Posto:
R1 = R2 = 1Ω, L = 1H, C = 1F
il problema di Cauchy si scrive:
 2
d
d

v (t) + 2 dt
vc (t) + 2vc (t) =

dt2 c


= d v (t) + v (t) + i (t)
(4.3.32.1)
g
g
dt g
vc (0) = V0
(4.3.32.2)



 d v (t) |
t=0 = −V0 − I0 + vg (0) (4.3.32.3)
dt c
145
(4.3.32)
4 Reti elettriche
Determiniamo l'integrale generale della (4.3.32.1)
L'integrale generale della (4.3.32.1) è la somma tra l'integrale generale dell'omogenea
associata alla (4.3.32.1) e l'integrale particolare della (4.3.32.1):
vc (t) = vcomog. (t) + vcpart. (t)
(4.3.33)
4.3.3.1 Ricerca dell'integrale generale dell'omogenea associata
Omogenea associata
d
d2
vc (t) + 2 vc (t) + 2vc (t) = 0
2
dt
dt
Equazione caratteristica
λ2 + 2λ + 2 = 0
λ=
−1 ±
(
p
λ1 = −1 − j
1 − (1)(2)
=
1
λ2 = −1 + j
Integrale generale omogenea associata
vcomog. (t) = k e−t cos (t + ϕ)
(4.3.34)
4.3.3.2 Ricerca dell'integrale particolare
Supponiamo che la rete si trovi a regime costante e che i generatori ideali abbiano valore:
vg (t) = Vg = 9V,
ig (t) = Ig = 1A
Visto che il termine noto della (4.3.32.1) è la costante
Vg + Ig = 10,
l'integrale
particolare va ricercato tra le costanti.
Posto
vc (t) = vcpart. (t) = cost.
, la (4.3.32.1) si scrive:
2vcpart. (t) = 10
da cui si ricava:
vcpart. (t) = 5
4.3.3.2.1 Il signicato sico dell'integrale particolare
(4.3.35)
Siccome la rete elettrica di
Figura 4.3.7 è abbastanza semplice, è possibile dedurre l'integrale particolare dato in
(4.3.35) per altra via.
Quando il tempo t tende all'innito, cioè a regime, l'evoluzione libera tende a zero
e l'integrale generale dell'equazione dierenziale di ordine minimo va a coincidere con
l'integrale particolare che in questo caso è costante:
146
4 Reti elettriche
vc (t) = vcpart. (t) = Vc = cost.
Esaurita l'evoluzione libera tutte le grandezze della rete sono costanti cos' come i
generatori.
d
C dt
Vc = 0,
Se così è allora dall'equazione costitutiva del capacitore si vede che
Ic =
e ciò vuol dire che per t che tende all'innito a regime costante il capacitore
si comporta come un
circuito aperto.
Analogamente dall'equazione costitutiva dell'induttore si vede che
0,
d
VL = L dt
IL =
il che vuol dire che per t che tende al-
l'innito, l'induttore si comporta come un
cortocircuito.
Pertanto
a
regime
la
rete
elettrica
mostrata in Figura 4.3.7 diventa come indicato in Figura 4.3.8 nell'ipotesi in cui
le sorgenti siano generatori ideali costanti.
A regime costante la rete elettrica diventa
puramente resistiva.
vcpart. (t) = Vc
resistore R2 . Tale
E' ovvio che la tensione
è la tensione ai capi del
Figura 4.3.8: rete elettrica a regime costante
tensione si può pensare come la somma di
due contributi:
0
00
vcpart. (t) = Vc = Vc + Vc
A
(4.3.36)
B
Figura 4.3.9: A:agisce solo
Il contributo
0
Vc
Vg ,
B: agisce solo
Vg
si ha quando agisce solo il generatore
Ig
(il generatore di corrente è un
circuito aperto) e per determinarlo basta semplicemente applicare la legge del partitore
di tensione (Figura 4.3.9.A):
0
Vc =
Il contributo
00
Vc
R2
9
Vg = V
R1 + R2
2
si ha quando agisce solo il generatore
cortocircuito). Esso vale (Figura 4.3.9.B):
147
Ig
(4.3.37)
(il generatore di tensione è un
4 Reti elettriche
00
Vc = R2 I2 = R2
1
R1
Ig = V
R1 + R2
2
(4.3.38)
Sostituendo (4.3.37) e (4.3.38) in (4.3.36) si ritrova (4.3.35)
4.3.3.3 Determinazione delle costanti
e
k
ϕ
mediante le condizioni iniziali
Sostituendo (4.3.34) e (4.3.35) in (4.3.33) si ricava l'integrale generale della (4.3.32.1):
vc (t) = k e−t cos (t + ϕ) + 5
(4.3.39)
Derivando rispetto al tempo quest'ultima espressione si ricava:
Per determinare
d
vc (t) = −k e−t cos (ωt + ϕ) − k e−t sin (ωt + ϕ)
dt
le costanti k e ϕ si utilizza le condizioni iniziale date
(4.3.40)
in (4.3.32.2) e
(4.3.32.3); supponendo che sia:
vc (0) = V0 = 1V,
iL (0) = I0 = 1A
tali condizioni si scrivono:
vc (0) = 1V
(4.3.41)
d V
vc t=0 = −1 − 1 + 9 = 7
dt
s
(4.3.42)
Utilizzando (4.3.41) la (4.3.39) si scrive:
k cos ϕ + 5 = 1
(4.3.43)
Utilizzando (4.3.42) la (4.3.40) si scrive:
− k cos ϕ − k sin ϕ = 7
Risolvendo il sistema costituito dalle equazioni in (4.3.40) e (4.3.41):
(
k cos ϕ + k sin ϕ = −7
k cos ϕ + 5 = 1
k e ϕ:
(
(
k cos ϕ + k sin ϕ = −7
k cos ϕ = −4
=⇒
=⇒
k cos ϕ = −4
−4 + k sin ϕ = −7
(
(
k cos ϕ = −4
k 2 = 16 + 9 = 25
=⇒
=⇒
=⇒
k sin ϕ = −3
tan ϕ = 34
si determinano le costanti
148
(4.3.44)
4 Reti elettriche
(
√
k = 25 = 5
=⇒
ϕ = π + arctan 34 = 3, 78509
Sostituendo inne i valori di
k
e
ϕ
(4.3.45)
in (4.3.36) si ottiene l'espressione analitica della
tensione ai capi del capacitore:
vc (t) = 5 e−t cos (t + 3, 78509) + 5 V
(4.3.46)
vc (t)
Figura 4.3.10: tensione
4.3.4 I controlli sulla correttezza dell'equazione dierenziale di ordine
minimo
E' possibile eettuare dei
controlli
sulla correttezza della dell'equazione dierenziale di
ordine minimo:
ˆ
analisi dimensionale.
una prima verica che è possibile eettuare è l'
Con riferimento alla (4.3.31.1), siccome
d2
v (t) si misura in sV2 , tutti i termini della
dt2 c
(4.3.2) dovrebbero avere la medesima unità di misura.
Osservando che:
[R1 C] = s;
R2
1
= ; [LC] = s2
L
s
si vede subito la correttezza dal punto di vista dell'analisi dimensionale della (4.3.2).
149
4 Reti elettriche
ˆ
Se la rete elettrica è priva di generatori pilotati, i coecienti
ai
devono essere
tutti positivi e tutti presenti, cioè devono esserci per tutti gli ordini di derivazione
nell'equazione dierenziale di ordine minimo.
Quanto detto si può facilmente dimostrare.
Consideriamo l'equazione caratteristica
n
X
ai λ i = 0
i=0
Se la rete è priva di generatori pilotati è stato detto che l'equazione caratteristica
può ammettere una radice nulla con molteplicità 1, radici immaginarie e coniugate con
molteplicità 1, radici reali con qualunque molteplicità purchè strettamente negative e
radici complesse e coniugate con qualunque molteplicità purchè abbiano parte reale strettamente negativa. Detto ciò è ovvio che l'equazione caratteristica si può scrivere nella
seguente forma fattorizzata:
an · λ · (λ − δ1 ) ·ν1 ... · (λ − λp )νp · (λ − jω1 ) · (λ + jω1 ) · ... (λ − jωq ) · (λ + jωq ) ·
· [λ − (δ1 − jω1 )]µ1 · [λ − (δ1 + jω1 )] ·µ1 ... · [λ − (δs − jωs )] ·µs [λ − (δs + jωs )]µs =
= an · λ · (λ − δ1 ) ·ν1 ... · (λ − λp )νp · λ2 + ω12 · ... · λ + ωq2 ·
· [λ − δ1 + jω1 ] ·µ1 [λ − δ1 − jω1 ] ·µ1 ... · [λ − δs + jωs ] ·µs [λ − δs − jωs ]µs =
= an · λ · (λ − δ1 ) ·ν1 ... · (λ − λp )νp · λ2 + ω12 · ... · λ + ωq2 ·
h
iµ1
h
iµs
· (λ − δ1 )2 + ω12
· ... · (λ − δs )2 + ωs2
=
= an · λ · (λ + |δ1 |) ·ν1 ... · (λ + |λp |)νp · λ2 + ω12 · ... · λ + ωq2 ·
h
iµ1
h
iµs
· (λ + |δ1 |)2 + ω12
· ... · (λ + |δs |)2 + ωs2
=0
ovvero:
an · λ · (λ + |δ1 |) ·ν1 ... · (λ + |λp |)νp · λ2 + ω12 · ... · λ + ωq2 ·
h
iµ1
h
iµs
· (λ + |δ1 |)2 + ω12
· ... · (λ + |δs |)2 + ωs2
=0
150
(4.3.47)
4 Reti elettriche
I fattori presenti in (4.3.47) sono tutti polinomi positivi, inoltre la somma dei loro gradi
(le molteplicità) è pari a
n;
da questi fatti segue che sviluppando i prodotti in (4.3.47)
ne viene fuori un polinomio di grado
n
completo avente coecienti positivi.
Normalmente l'equazione caratteristica presenta al primo membro un polinomio il
cui grado minimo è zero; al più il grado minimo può essere uno e ciò avviene quando
l'equazione caratteristica ammentte la radice nulla (cattiva modellazione della rete).
Se la potenza minima risulta pari a due, vuol dire che ci sono stati errori nella
ricavazione dell'equazione dierenziale di ordine minimo.
4.4 Risposta transitoria e risposta permanente
Sappiamo che qualunque variabile di rete
y (t)
per un circuito lineare tempo-invariante
si può scrivere sottoforma di somma di due termini: l'integrale generale dell'omogenea
associata
yomog. (t)
e l'integrale particolare dell'equazione dierenziale di ordine minimo
ypart. (t):
y (t) = yomog. (t) + ypart. (t)
(4.4.1)
L'integrale generale dell'omogenea associata è una funzione del tempo che dipende dai
dispositivi costituenti la rete e dal come sono connessi tra di loro (topologia del circuito),
mentre l'integrale particolare è una funzione del tempo che è inuenzata dai generatori
che eccitano la rete. Esso va ricercato tra le costanti se i generatori presenti nella rete
sono costanti; vedremo in seguito che se i generatori sono sinusoidali allora l'integrale
particolare sarà una combinazione lineare di funzioni sinusoidali che si ricaverà con il
metodo dei fasori.
La (4.4.1) è una prima classicazione della variabile di rete
y (t)
detta pure
risposta.
In realtà esistono altri modi per classicare la variabile di rete. Per esempio la risposta
y (t)
si può scrivere pure come somma di due termini chiamati rispettivamente
transitoria ytras. (t) e risposta permanente yperm. (t):
y (t) = ytrans. (t) + yperm. (t)
risposta
(4.4.2)
La risposta transitoria risulta nulla per tche tende all'innito:
lim ytrans. (t) = 0
(4.4.3)
t→+∞
mentre la risposta permanente non si annulla per t che tende all'innito: essa contiene
dei termini additivi che possono essere divergenti per t che tende all'innito, costanti
oppure sinusoidali; in genere tali termini sono indotti dai generatori ideali.
Nel caso particolare in cui l'equazione caratteristica ha tutte le radici con
strettamente negativa
(nessuna radice sull'asse immaginario):
δ<0
allora possiamo dire che tutta la
yomog. (t)
è sicuramente
151
transitoria :
parte reale
4 Reti elettriche
yomog. (t) = ytrans. (t)
Se i generatori sono
costanti
o
sinusoidali, la ypart. (t) è sicuramente permanente :
ypart. (t) = yperm. (t)
In generale però se non risulta
δ < 0 potrebbe capitare che termini additivi di yomog. (t),
sono permanenti, così come se i generatori non sono costanti o sinusoidali, potrebbe
capitare che termini additivi di
ypart. (t)
sono transitori.
4.5 Risposta con stato zero e con ingresso zero
La risposta
y (t) si può scrivere pure come somma di un termine dovuto solo ai generatori,
e uno dovuto
solo allo stato energetico iniziale
della rete elettrica.
Per calcolare la risposta dovuta solo ai generatori si devono considerare nullo il patrimonio energetico iniziale della rete elettrica, mentre per calcolare la risposta dovuta allo
stato energetico iniziale della rete si devono azzerare tutti i generatori idealipresenti nella
rete.
La risposta dovuta solo ai generatori, cioè quella calcolata con lo stato energetico
iniziale nullo si chiama
risposta con stato zero:
yS.Z. (t)
La risposta dovuta solo allo stato energetico iniziale della rete, cioè quella calcolata
con i generatori ideali azzerati, si chiama
risposta con ingresso zero:
yI.Z. (t)
Sommando questi due contributi si ristabilisce la risposta
y (t):
y (t) = yS.Z. (t) + yI.Z. (t)
(4.5.1)
A sua volta la risposta con stato zero si può intendere come la somma di un numero di
risposte pari al numero di generatori presenti nella rete elettrica e la risposta con ingresso
zero come la somma di un numero di risposte pari al numero di condizioni iniziali sullo
stato energetico della rete.
Se consideriamo nuovamente la rete elettrica mostrata in Figura 4.3.7 poichè sono
presenti 2 generatori, la risposta con stato zero si può intendere come somma di due
contributi: quello dovuto al generatore
vg (t)
e quello dovuto al generatore ig
(t).
Inoltre
poichè sono presenti due dispositivi a memoria, la risposta con ingresso zero si può
intendere come somma tra il contributo dovuto alla condizione iniziale sul capacitore e la
condizione iniziale sull'induttore. Pertanto per la rete su suddetta la risposta
y (t) risulta
essere:
y (t) = yS.Z.1 (t) + yS.Z.2 (t) + yI.Z.1 (t) + yI.Z.2
152
(4.5.2)
4 Reti elettriche
Le classicazioni fatte in (4.4.1), (4.4.2), (4.5.1), (4.5.2) ovviamente sono tutte possibili
purchè il circuito elettrico sia
lineare.
In realtà la distinzione tra ingressi e stato può essere superata in quanto è possibile
trasformare le condizioni iniziali sui dispositivia memoria in
generatori equivalenti
(ve-
dremo che questo fatto equivale a soddisfare il teorema di sostituzione). Se teniamo conto
dell'equazione costitutiva del capacitore in forma integrale:
1
vc (t) = vc (0) +
C
ˆ
t
0
1
ic (τ ) dτ = V0 +
C
ˆ
t
ic (τ ) dτ
(4.5.3)
0
possiamo immaginare il capacitore come la serie costituita da un generatore ideale di
tensione costante
V0
e da un capacitore scarico.
Figura 4.5.1: generatore di tensione equivalente
Analogamente se teniamo conto dell'equazione costitutiva dell'induttore in forma integrale:
1
iL (t) = iL (0) +
L
ˆ
t
0
1
vL (τ ) dτ = I0 +
L
ˆ
t
ic (τ ) dτ
(4.5.4)
0
possiamo immaginare l'induttore come il parallelo costituito da un generatore ideale di
corrente costante
I0
e da un induttore scarico.
Figura 4.5.2: generatore di corrente equivalente
Fatte queste osservazioni, il circuito elettrico mostrato in Figura 4.3.7 risulta equivalente alla rete mostrata in Figura 4.5.3.
153
4 Reti elettriche
Figura 4.5.3: rete elettrica equivalente
4.6 Metodi integrali
Fino ad ora abbiamo capito che trovare una variabile direte ( tensione o corrente di
lato) equivale a risolvere un problema di Cauchy. Il fatto che le equazioni di Maxwell
si presentano sia in forma dierenziale che in forma integrale ci suggerisce che pure per
le reti elettriche esiste questa dualità; ossia se una variabile di rete si può determinare
mediante la risoluzione di un'equazione dierenziale, si può determinare pure attraverso
una relazione integrale.
Figura 4.6.1: rete lineare tempo invariante (L.T.I.)
Si vuole determinare la generica variabile di
y (t)
di una rete lineare tempo-invariante
attraverso metodi integrali.
La rete elettrica può essere vista come un sistema costituito da dispositivi lineari
tempo-invariante come ad esempio resistori, capacitori, induttori, induttori mutuamente
accoppiati, trasformatori ideali e generatori pilotati, eccitato mediante generatori variabili nel tempo
vg (t), ig (t)
e da generatori costanti
V0 , I0
equivalenti alle condizioni
iniziali sullo stato energetico della rete elettrica (Figura 4.6.1).
Tanto per chiarire le
vg (t), la risposta in uscita sarà y1 (t),
se sollecitiamo la rete elettrica con la corrente ig (t), la risposta in uscita sarà y2 (t) e così
idee, se sollecitiamo la rete elettrica con la tensione
via.
154
4 Reti elettriche
Naturalmente se la rete elettrica fosse eccitata da N sorgenti, la risposta
y (t)
risul-
terebbe la sovrapposizione di N risposte.
Facendo agire uno alla volta i generatori presenti nella rete elettrica signicherebbe studiare il circuito N-volte e ciò ovviamente è un disastro dal punto di vista computazionale
(perchè per risolvere una rete elettrica occorre fare molti calcoli?). Pertanto quando si
studia una rete elettrica si cerca di evitare l'uso della sovrapposizione salvo casi molto
semplici. Si osservi inoltre che non è detto che sia possibile applicare sempre la sovrapposizione; essa si può applicare soltanto se la rete elettrica trattata è lineare; basta avere
in una rete elettrica un dispositivo non lineare (per esempio un diodo) e non si può più
applicare la sovrapposizione. In una rete come quella mostrata in Figura 4.6.1, se agissero soltanto i generatori ideali la risposta in uscita sarebbe quella a stato zero; viceersa
se agissero soltanto i generatori equivalenti agli stati energetici dei dispositivi a memoria,
la risposta in uscita sarebbe quella con ingresso zero.
4.6.1 Integrale di convoluzione e risposta all'impulso
Si vuole determinare la risposta con stato zero (tutti i dispositivi a memoria presenti nella
rete elettrica scarichi) di una particolare rete elettrica sollecitata da un unico ingresso
x (t)
come indicato in Figura 4.
Figura 4.6.2: rete lineare tempo invariante (L.T.I.) con stato zero (S.Z)
Dalla conoscenza della rete elettrica L.T.I. con S.Z. e dalla conoscenza della sollecitazione
x (t) è possibile determinare la risposta con stato zero y (t) = yS.Z. (t) (ovvero
l'integrale generale dell'omogenea associata se tutte le radici dell'equazione caratteristica
sono con parte reale strettamente negativa) a partire da una relazione integrale detta
integrale di convoluzione.
lecitazione è
x (t),
Per determinare la risposta con stato zero, quando la sol-
quello che si fa, innanzitutto è sollecitare la rete elettrica, anzichè
x (t), con una forma d'onda canonica come per esempio la delta di Diràc δ (t): la
risposta h (t) in corrispondenza della sollecitazione δ (t) si chiama risposta all'impulso e
con
rappresenta una
evoluzione libera, cioè un segnale che è nullo per t<0 e che tende a zero
per t tendente all'innito se la rete elettrica conserva la proprietà di essere L.T.I. con
S.Z. (Figura 4.6.3)
Nota la risposta all'impulso
h (t),
mediante l'integrale di convoluzione, si trova la
risposta con stato zero:
155
4 Reti elettriche
Figura 4.6.3: rete lineare tempo invariante (L.T.I.) con stato zero (S.Z)
ˆ
t
x (τ ) h (t − τ ) dτ
y (t) = yS.Z. (t) =
(4.6.1)
0
4.6.1.1 Signicato sico dell'integrale di convoluzione
Per conscere la risposta
y (t) = yS.Z. (t)
conoscere
tutto il passato signicativo τ
al tempo
t − τ,
all'istante di tempo t,cioè nel
della sollecitazione
x (t)
presente,
occorre
e la risposta all'impulso
cioè a quell'istante di tempo che si ottiene sottraendo al presente tutto
il passato
Figura 4.6.4: sollecitazione
x (τ )
e risposta all'impulso
h (t)
4.6.1.2 Dimostrazione dell'integrale di convoluzione
Per dare una dimostrazione dell'integrale di convoluzione si parte dall'idea che se eccitiamo la rete elettrica L.T.I con S.Z
Figura 4.6.5: risposta all'impulso di durata nita
156
4 Reti elettriche
con l'impulso di durata nita
τ → +∞
p∆ (τ ),
h∆ (τ ) nulla per τ → 0
p∆ (τ ) → δ (t) si avrà che
si avrà una risposta
e di conseguenza passando al limite per
e
h∆ (τ ) → h (τ )
Osserviamo na da subito che se l'ingresso è una combinazione lineare di impulsi di
durata nita tra di loro traslati, si avrà che la risposta è una combinazione lineare di
risposte egualmente tralate con gli stessi coecienti:
Figura 4.6.6: risposta all'impulso di durata nita
Tale proprietà risulta valida purchè la rete elettrica si L.T.I.
Grazie alla proprietà su citata si cerca di scrivere l'ingresso
x (t)
in una combinazione
lineare di implulsi di durata nita.
Se si vuole conoscere la risposta
τ =t
y (τ ) = yS.Z. (τ )
si deve scomporre l'intervallo di osservazione
all'ingresso
[0, t]
x (τ )
all'istante di tempo
in N intervalli tutti uguali tra di
loro cioè di ampiezza
∆=
t
N
Ovviamente più grande è il numero di intervalli N, tanto migliore sarà l'approssimazione dell'ingresso
x (τ )
mediante gli impulsi di durata nita.
Figura 4.6.7: ingresso
x (τ )scomposto
157
in impulsi di durata nita
4 Reti elettriche
Facendo riferimento alla rappresentazione mostrata in Figura 4.6.7 possiamo scrive:
x (τ ) = x (0) p4 (τ ) ∆+x (∆) p∆ (τ − ∆) ∆+......+x ((N − 1) ∆) p4 (τ − (N − 1) ∆) ∆ =
=
N
−1
X
x (k∆) p∆ (τ − k∆) ∆
(4.6.2)
k=0
Per la proprietà vista prima si avrà che la risposta
y (τ )
è la seguente combinazione
lineare:
y (τ ) =
N
−1
X
x (k∆) h∆ (τ − k∆) ∆
k=0
Quest'ultima al tempo
τ =t
vale:
y (t) =
N
−1
X
x (k∆) h∆ (t − k∆) ∆
k=0
Per
N → +∞ si avrà che ∆ → dτ ,
Pn−1
k=0
.∆ →
ˆ
´ +∞
0
(4.6.3)
. dτ, k4 → τ
e la (4.6.3) si scrive:
+∞
x (τ ) h (t − τ ) dτ
y (t) = yS.Z. (t) =
(4.6.4)
0
Inne poichè nell'intervallo
funzione
x (τ )
non
risulta
]0, +∞[
denita,
la
da
(4.6.4) segue l'integrale di convoluzione
dato in (4.6.1).
Secondo (4.6.1) si ha che per conoscere
la risposta con S.Z all'ingresso
x (t) och (t)
corre conoscere la risposta all'impulso
al tempo
t − τ;
cioè la risposta all'impulso
caratterizza la rete elettrica cos' come i coecienti
ai e bj
Figura 4.6.8: algoritmi di passaggio
dell'equazione dierenziale
di ordine minimo.
Quindi i coecienti
all'impulso
h (t)
ai
e
bj
dell'equazione dierenziale di ordine minimo e la risposta
sono informazioni semanticamente equivalenti, nel senso che entrambe
permettono di ricavare l'espressione analitica di una qualunque variabile di rete, anche
se sintatticamente dierenti.
Siccome entrambe le informazioni permettono di scrivere l'espressione di una qualunque
variabile di rete è evidente allora che esistono degli
di ricavare dai coecienti
all'impulso
h (t),
ai
i coecienti
bj la risposta
ai e bj :
e
158
algoritmi di passaggio che permettono
all'impulso
h (t)
e viceversa dalla risposta
4 Reti elettriche
Nella prossima sezione si vedrà come sia possibile ricavare dall'equazione dierenziale
di ordine minimo, in una qualunque variabile di rete, la risposta all'impulso mediante il
metodo del
bilanciamento delle funzioni singolari
(B.F.S.).
E' possibile ricavare la risposta all'impulso a partire dall'equazione dierenziale di
anti-trasformata di Laplace, mentre il passaggio inverso
trasformata di Laplace; in Figura 4.6.9 viene schematizzato quanto
ordine minimo anche mediante l'
è possibile mediante la
detto.
Figura 4.6.9: algoritmi di passaggio
4.6.1.3 Metodo del bilanciamento delle funzioni singolari
Facciamo vedere come ricavare la risposta all'impulso a partire dall'equazione dierenziale
di ordine minimo mediante il metodo del bilanciamento delle funzioni singolari.
Consideriamo la rete elettrica mostrata in Figura 4.6.10:
Figura 4.6.10: rete elettrica a singolo ingresso
Si osservi che tale rete è quella mostrata in Figura 4.1.2, priva del generatore ideale di
corrente
ig (t) .
159
4 Reti elettriche
Si tratta di una particolare rete avente una sola eccitazione; siccome si vuole calcolare
la risposta all'impulso, tale rete deve essere a S.Z. cioè con contenuto energetico iniziale
nullo.
Si deve considerare una qualunque variabile di rete e scrivere per essa l'equazione
dierenziale di ordine minimo. Se come variabile di rete si prende in esame la tensione
ai capi del capacitore,
vc (t),
il problema si può schematizzare come mostrato in Figura
4.6.11:
Figura 4.6.11: rete elettrica a singolo ingresso
Nell'ipotesi che tutti i componenti del circuito siano unitari (come mostrato in Figura
4.6.9) l'equazione dierenziale di ordine minimo nella variabile di rete
(4.3.32.1) avendo posto
vc (t) è l'espressione
ig (t) = 0A:
d2
d
d
vc (t) + 2 vc (t) + 2vc (t) = vg (t) + vg (t)
dt2
dt
dt
(4.6.5)
Se la rete elettrica viene eccitata mediante l'impulso di Diràc:
vg (t) = δ (t)
la tensione ai capi del capacitore
vc (t)
(4.6.6)
sarà una delle risposte all'impulso della rete
elettrica:
vc (t) = h (t)
(4.6.7)
La delta di Diràc interviene sulla rete elettrica all'istante t=0 s fornendo una quantità
nita di energia; si ha la seguente situazione.
t = 0− s la delta di Diràc trova la rete elettrica allo stato zero,
all'istante di tempo t = 0 s interviene fornendo al circuito una certa quantità di energia
+
che a partire dall'istante t = 0 s si va scemando facendo ritornare la rete allo stato zero
All'istante di tempo
per evoluzione libera.
Per il fatto che la delta di Diràc è capace di fornire alla rete elettrica una energia nita
in un tempo nullo (ciò vuol dire che la potenza fornita dalla delta di Diràc al circuito è
innita) si ha che la tensione ai capi del capacitore e la corrente che attraversa l'induttore
sono funzioni del tempo discontinue in t=0 s.
Se il circuito è eccitato mediante la deltà di Diràc, l'equazione dierenziale di ordine
minimo data in (4.6.5) si scrive:
160
4 Reti elettriche
d
d
d2
h (t) + 2 h (t) + 2h (t) = δ (t) + δ (t)
2
dt
dt
dt
(4.6.8)
Come prima spiegato, la risposta all'impulso è un'evoluzione libera che inizia all'istante
di tempo nullo, ossia all'istante in cui interviene la delta di Diràc. Siccome la risposta
integrale generale dell'omogenea
all'impulso è un'evoluzione libera per t>0, essa sarà l'
associata :
h (t) = ke−t cos (t + ϕ) · u (t)
(N.B. la presenza di
u (t)
(4.6.9)
marca il fatto che la risposta all'impulso è valida per t>0).
A questo punto chi ci assicura che all'istante di tempo t=0 s, la risposta all'impulso
possa contenere delle delta di Diràc o addirittura delle sue derivate? Nessuno!! Bisogna
quindi ipotizzare che nella risposta all'impulso ci siano pure la delta di Diràc e le sue
derivate successive.
Per semplicità supponiamo che nella risposta all'impulso compaiono solo la delta di
Diràc e la sua derivata prima:
0
h (t) = ke−t cos (t + ϕ) · u (t) + C0 δ (t) + C1 δ (t)
(4.6.10)
Derivando rispetto al tempo la (4.6.10) si ottiene:
0
0
00
h (t) = −ke−t [cos (t + ϕ) + sin (t + ϕ)] · u (t) + ke−t cos (t + ϕ) δ (t) + C0 δ (t) + C1 δ (t)
Applicando la proprietà del campionamento quest'ultima espressione si scrive:
0
0
00
h (t) = −ke−t [cos (t + ϕ) + sin (t + ϕ)] · u (t) + k cos ϕδ (t) + C0 δ (t) + C1 δ (t)
(4.6.11)
Derivando rispetto al tempo la (4.6.11) si ottiene:
00
h (t) = 2ke−t sin (t + ϕ) · u (t) − ke−t [cos (t + ϕ) + sin (t + ϕ)] δ (t) +
0
00
000
+k cos ϕδ (t) + C0 δ (t) + C1 δ (t)
Applicando la proprietà del campionamento quest'ultima espressione si scrive:
00
h (t) = 2ke−t sin (t + ϕ) · u (t) − k (cos ϕ + sin ϕ) δ (t) +
0
00
000
+ k cos ϕδ (t) + C0 δ (t) + C1 δ (t)
Sostituendo (4.6.10) (4.6.11) e (4.6.12) in (4.6.8) si ottiene:
161
(4.6.12)
4 Reti elettriche
0
00
000
(k cos ϕ − k sin ϕ + 2C0 ) δ (t)+(k cos ϕ + 2C0 + 2C1 ) δ (t)+(c0 + 2C1 ) δ (t)+(C1 ) δ (t) =
0
= δ (t) + δ (t)
Applicando il principio di identità dei polinomi a quest'ultima uguaglianza si ricava il
sistema risolvente:


k cos ϕ − k sin ϕ + 2C0 = 1



k cos ϕ + 2C + 2C = 1
0
1
C0 + 2C1 = 0



C = 0
1
che permette di determinare le costanti
k , ϕ, C0
e
C1 :


k=1



ϕ = 0

C0 = 0



C = 0
1
(4.6.13)
Sostituendo (4.6.13) in (4.6.10) si ottiene l'espressione analitica della risposta all'impulso:
h (t) = e−t cos t · u (t)
Figura 4.6.12: risposta all'impulso
(4.6.14)
hvc (t)
In Figura 4.6.12 viene mostrato il graco della risposta all'impulso data in (4.6.14).
Si può osservare che per t=0 s la tensione ai capi del capacitore è discontinua:
162
4 Reti elettriche
vc 0− = 0 vc (0+) = vc (0) = 1 V
Ciò vuol dire che all'istante t=0 s, il capacitore ha accumulato l'energia:
1
ε (0) = Cvc2 (0) = 1 J
2
(4.6.15)
Si può osservare inoltre che per t che tende all'innito la tensione ai capi del capacitore
è in evoluzione libera.
Vale la seguente REGOLA:
Se l'ordine di derivazione
n
del pri-
mo membro dell'equazione dierenziale di
ordine minimo è maggiore dell'ordine di
derivazione
m
del secondo membro, allo-
ra la risposta all'impulso non conterrà nè
delte di Diràc nè derivate della delta di
Diràc.
Se l'ordine di derivazione
mo
membro
dell'equazione
n
del pri-
dierenziale
di ordine minimo è uguale alll'ordine di
derivazione
m
del secondo membro, allo-
ra la risposta all'impulso conterrà la delta
di Diràc centrata in t=0 s.
Se l'ordine di derivazione
n
del pri-
mo membro dell'equazione dierenziale di
ordine
minimo
derivazione
m
è
minore
dell'ordine
Figura 4.6.13: rete elettrica eccitata mediante impulso di Diràc
di
del secondo membro, allo-
ra la risposta all'impulso conterrà un numero di derivate della delta di Diràc pari a
m − n.
E' stata così ricavata la risposta all'impulso partendo dall'equazione dierenziale di
ordine minimo utilizzando il metodo del bilanciamento delle funzioni singolari; in realtà
è possibile arrivare alla risposta all'impulso per altre vie. Per esempio dato che
δ (t) = lim p∆ (t)
∆→0
p4 (t) ottenendo
∆ → 0 si ricava la
possiamo eccitare la rete elettrica mediante l'impulso di durata nita
così la risposta
h∆ (t).
Nota quest'ultima passando al limite per
risposta all'impulso:
h (t) = lim h∆ (t)
∆→0
4.6.1.3.1 Le risposte all'impulso per un circuito elettrico
Una rete elettrica contiene
tante risposte all'impulso quante sono le variabili di rete: per una rete formata da L lati
allora ci saranno 2L risposte all'impulso.
163
4 Reti elettriche
L'espressione (4.6.14) è una delle risposte all'impulso del circuito mostratoin Figura
(4.6.10); essa rappresenta la tensione ai capi del capacitore.
Siccome potremmo pure
ricavare le risposte all'impulso per le altre variabili di rete è conveniente sostituire nella
(4.6.14) ,al simbolo
h (t),
il simbolo
hvc (t):
hvc (t) = e−t cos t · u (t)
Si vuole adesso determinare la risposta
hiL (t)
(4.6.16)
in quanto l'induttore è un altro dispos-
itivo in grado di accumulare energia.
osserviamo innanzirurro che sfruttando l'equazione costitutiva del capacitore possiamo
ricavare la corrente che lo attraversa:
hic (t) = C
d
hv (t) = −e−t [(cos t + sin t) u (t) − δ (t)]
dt c
(4.6.17)
Considerando il circuito mostrato in Figura 4.6.13 si vede che:
hi1 (t) =
δ (t) − hvc (t)
= δ (t) − hvc (t)
R1
(4.6.18)
Sostituendo (4.6.16) in (4.6.18) si ottiene:
hi1 (t) = δ (t) − e−t cos t · u (t)
(4.6.19)
Inne scrivendo la LKI al nodo 2 e utilizzando le espressioni trovate in (4.6.17) e (4.6.19)
si ottiene l'espressione della risposta
hiL (t):
hiL (t) = hi1 (t) − hic (t) = δ (t) − e−t cos t · u (t) + e−t cos t · u (t) + e−t sin t · u (t) − e−t δ (t)
= δ (t) + e−t sin t · u (t) − e−t δ (t) =
= e−t sin t · u (t)
In Figura 4.6.14 è riportata la rappresentazione graca della risposta
(4.6.20)
hiL (t):
Si osservi che per t=0 s la corrente che attraversa l'induttore è continua:
iL 0− = iL 0+ = iL (0) = 0 A
Va detto che in generale ciò non accade se la sollecitazio per il circuito è la delta di
Diràc.
Ciò vuol dire che all'istante t=0 s, l'induttore non ha accumulato energia:
1
ε (0) = Li2L (0) = 0 J
2
(4.6.21)
Dai risultati in (4.6.15), (4.6.21) è evidente che all'istante t=0 s l'energia viene tutta
accumulata istantaneamente dal capacitore, mentre l'energia accumulata dall'induttore
è nulla.
164
4 Reti elettriche
Figura 4.6.14: risposta all'impulso
Osservando (4.6.17) si vede che la risposta
hiL (t)
hiL (t) contiene una delta di Diràc e ciò vuol
dire che essa viene fuori da una equazione dierenziale di ordine minimo il cui secondo
membro ha lo stesso ordine di derivazione del primo membro, ossia
4.6.1.3.2 Analisi energetica della rete
n = m = 2.
Per descrivere lo stato energetico della rete
elettrica basta predisporre sugli assi di un sistema cartesiano le variabili energetiche
hvc (t)
e
hiL (t);
il graco che ne viene fuori si chiama
traiettoria di stato
del sistema.
Per t=0 le relazioni in (4.6.16) e (4.6.20)
forniscono:
hvC (0) = 1 V
Per
t =
hIL (0) = 0 A
π
2 le relazioni in (4.6.16) e
(4.6.20) forniscono:
hvC (0) = 0 V
Per
t = +∞
hIL (0) = 0208 A
le relazioni in (4.6.16) e
(4.6.20) forniscono:
hvC (0) = 1 V
hIL (0) = 0 A
Figura 4.6.15: traiettoria di stato
Ne segue che la traiettoria di stato del circuito elettrico analizzato è quella mostrata
in Figura 4.6.15.
165
4 Reti elettriche
4.6.2 Integrale di Duhamel e risposta al gradino
4.6.2.1 Risposta al gradino
Eccitando la rete elettrica attraverso un gradino unitario
si chiama
risposta al gradino g (t):
u (t),
la risposta con stato zero
Figura 4.6.16: risposta al gradino
h (t) si può scrivere in termini della risposta
Facciamo vedere che la risposta all'impulso
al gradino
g (t).
Supponiamo di eccitare la rete elettrica attraverso l'impulso di durata nita
p∆ (t), che
come sappiamo si può scrivere come combinazione lineare di gradini unitari:
p∆ (t) =
Se l'eccitazione
p∆ (t)
1
1
u (t) − u (t − ∆)
∆
∆
è una combinazione lineare di gradini, la risposta
(4.6.22)
h∆ (t)
sarà
una combinazione lineare di risposte al gradino:
h∆ (t) =
Passando al limite per
h (t)
∆→0
1
1
g (t) − g (t − ∆)
∆
∆
(4.6.23)
quest'ultima espressione fornisce la risposta all'impulso
in termini della risposta al gradino
g (t):
g (t) − g (t − ∆)
d
= g (t)
∆→0
∆
dt
h (t) = lim h∆ (t) = lim
∆→0
ovvero:
d
g (t)
dt
h (t) =
(4.6.24)
Secondo (4.6.24) la risposta all'impulso è la derivata prima rispetto al tempo della
risposta al gradino.
Invertendo (4.6.24) si ottiene la risposta al gradino in termini della risposta all'impulso:
ˆ
t
g (t) =
h (τ ) dτ
0−
166
(4.6.25)
4 Reti elettriche
Le formule in (4.6.24) e (4.6.25) rappresentano rispettivamente gli algoritmi di passaggio dalla risposta al gradino alla risposta all'impulso e dalla risposta all'impulso alla
risposta al gradino.
In Figura 4.6.17 viene mostrato lo schema logico che mostra gli algoritmi di passaggio
dalla risposta al gradino alla risposta all'impulso e viceversa, nonchè gli algoritmi di
passaggio dalla risposta al gradino ai coecienti
ai , bj
dell'equazione dierensiale di
ordine minimo, e viceversa.
Figura 4.6.17: algoritmi di passaggio
Eccitando la rete elettrica mostrata in Figura 4.6.10 con il gradino unitario,
u (t),
l'equazione dierenziale di ordine minimo relativa alla tensione
vc (t)
vg (t) =
si scrive:
d2
d
d
g (t) + g (t) + 2g (t) = u (t) + u (t)
2
dt
dt
dt
Quest'ultima per la (3.2.10) si scrive:
d2
d
g (t) + g (t) + 2g (t) = δ (t) + u (t)
2
dt
dt
(4.6.26)
Si trova facilmente che l'integrale generale dell'omogenea associata è:
gomog. (t) = ke−t cos (t + ϕ) u (t)
(4.6.27)
Per t>0 è possibile determinare l'integrale particolare della (4.6.26) poichè per t>0 il
gradino non è nulllo (si noti che per t>0 la
δ (t)
è nulla).
Visto che il gradino unitario è una costante l'integrale particolare di (4.6.26) va ricercato tra le costanti; si trova banalmente che
1
gpart. (t) = u (t)
2
167
(4.6.28)
4 Reti elettriche
Sommando i contributi in (4.6.27) e (4.6.28) si ricava l'integrale generale della (4.6.26):
1
g (t) = ke−t cos (t + ϕ) u (t) + u (t)
2
(4.6.29)
Come per la risposta all'impulso, anche per la risposta al gradino, si applica il metodo
delle funzioni singolari. Pertanto supponiamo, per semplicità, che la risposta al gradino
(4.6.29) contenga una delta di Diràc:
1
g (t) = ke−t cos (t + ϕ) u (t) + u (t) + C0 δ (t)
2
(4.6.30)
Derivando rispetto al tempo la (4.6.30) si ricava:
0
−t
g (t) = −ke
1
0
δ (t) + C0 δ (t)
[cos (t + ϕ) sin (t + ϕ)] u (t) + k cos ϕ +
2
(4.6.31)
Derivando rispetto al tempo la (4.6.31) si ricava:
00
g (t) = 2ke
−t
1 0
00
sin (t + ϕ) u (t) − k (cos ϕ + sin ϕ) δ (t) + k cos ϕ +
δ (t) + C0 δ (t)
2
(4.6.32)
Sostituendo (4.6.30) (4.6.31) e (4.6.32) in (4.6.26) si ottiene:
1 0
00
δ (t)+C0 δ (t) = u (t)+δ (t)
u (t)+(k cos ϕ − k sin ϕ + 2C0 + 1) δ (t)+ k cos ϕ + 2C0 +
2
Applicando il principio di identità dei
polinomi
a
quest'ultima
uguaglianza
si
ricava il sistema risolvente:


k cos ϕ − k sin ϕ + 2C0 + 1 = 1
k cos ϕ + 2C0 + 21 = 0


C0 = 0
che permette di determinare le costanti
k , ϕ e C0 :

1

k cos ϕ = − 2
k sin ϕ = − 12


C0 = 0
Figura 4.6.18: circonfenza goniometrica
√

2

k
=

2
⇒ tan ϕ = 1


C0 = 0
(4.6.33)
Per determinare
riportati i valori di
ϕ dall'equazione tan ϕ = 1, basta
k cos ϕ e k sin ϕ. Si capisce che:
168
osservare Figura 4.6.18 dove sono
4 Reti elettriche
ϕ=π+
π
5
= π
4
4
(4.6.34)
Tenendo conto dei valori dei coecienti trovati la (4.6.30) si scrive:
"√
g (t) =
#
2 −t
5
1
u (t)
e cos t + π +
2
4
2
(4.6.35)
Figura 4.6.19: risposta al gradino
E' possibile vericare la correttezza della (4.6.35), infatti sostituendola in (4.6.24) ,si
dovrebbe ottenere la (4.6.14).
Verica della correttezza della (4.6.35)
Sostituendo (4.6.35) in (4.6.24) si ha:
( √
)
2 −t
5
5
−
u (t) +
e
cos t + π + sin t + π
2
4
4
1 √ −t
5
+
2e cos t +
+ 1 δ (t)
2
4
d
h (t) = g (t) =
dt
Per la proprietà del campionamento quest'ultima espressione si scrive:
d
h (t) = g (t) =
dt
( √
(√
)
)
5
5
5
1
2 −t
2
−
e
cos t + π + sin t + π
cos
+
u (t)+
δ (t) =
2
4
4
2
4
2
169
4 Reti elettriche
)
√ !
1
2
−
+
δ (t) =
2
2
( √
=
(√
)
5
2 −t
5
2
cos t + π + sin t + π
−
e
u (t) +
2
4
4
2
"√
(
√
#)
2
5
2
5
cos t + π +
sin t + π
u (t)
2
4
2
4
−t
−e
=
Posto:
√
2
π
π
= cos = sin
2
4
4
quest'ultima espressione si scrive:
h (t) =
−t
−e
π
5
π
5
cos cos t + π + sin sin t + π
u (t)
4
4
4
4
Per la formula di sottrazione del coseno, quest'ultima espressione si scrive:
h (t) =
−t
−e
cos
5
π
−t− π
4
4
u (t) = −e−t cos (−t − π) u (t) =
= −e−t cos (t + π) u (t) = −e−t [− cos t] u (t) =
= e−t cos t u (t)
e con ciò è stata ritrovata la (4.6.14)
4.6.2.2 Integrale di Duhamel
Come detto in precedenza, conoscendo la risposta all'impulso
la risposta
y (t)
a qualunque altro ingresso
x (t)
h (t),
è possibile conoscere
integrale di convoluzione,
utilizzando l'
che può essere scritto in una forma più generale rispetto a quella introdotta in (4.6.1):
ˆ
t+
x (τ ) h (t − τ ) dτ
y (t) = yS.Z (t) =
(4.6.36)
0−
t = 0−
In questa forma, l'estremo di integrazione
sta ad indicare che nella risposta
all'impulso, all'istante t=0 può intervenire una delta di Diràc; analogamente l'estremo
di integrazione
t = t+
sta ad indicare che nella risposta all'impulso, all'istante t può
intervenire una delta di Diràc.
Conoscendo la risposta al gradino
altro ingresso
x (t)
g (t), è possibile conoscere la risposta y (t) a qualunque
integrale di Duhamel :
utilizzando l'
ˆ
y (t) = yS.Z (t) =
t+
0−
d
x (τ ) g (t − τ ) dτ
dτ
170
(4.6.37)
4 Reti elettriche
Sviluppando per parti l'integrale in (4.6.37) è facile vericare che le relazioni in (4.6.36)
e (4.6.37) sono equivalenti:
ˆ
y (t) = yS.Z (t) =
t+
0−
ˆ t+
+
d
d
x (τ ) g (t − τ ) dτ =
x (τ ) g (t − τ ) dτ = [x (τ ) g (t − τ )]t0− −
dτ
dτ
−
0
ˆ
+
=x t
+
g t−t
−x 0
−
t+
x (τ ) h (t − τ ) (−1) dτ =
g (t) −
0−
ˆ
=x t
+
t+
0 − 0 g (t) +
x (τ ) h (t − τ ) dτ =
0−
ˆ
t+
x (τ ) h (t − τ ) dτ
=
0−
4.6.2.3 Integrale di Duhamel nel caso di sollecitazione
Supponiamo che l'ingresso
x (t)
x (t)
discontinua in t=0 s
sia discontinuo in t=0 s e che abbia un andamento del
tipo mostrato in Figura 4.6.20:
Figura 4.6.20: sollecitazione discontinua in t=0 s
Visto che la sollecitazione
x (t)
presenta una discontinuità, il modo migliore per calco-
larne la derivata prima è inquadrarla nelll'ambito delle
distribuzioni.
La derivata prima x (t) nell'ambito delle distribuzioni risulta uguale alla derivata ordinaria della stessa, ossia quella nel senso delle funzioni più la delta di Diràc concentrata
0
nel punto di discontinuità moltiplicata per il salto della funzione che in questo caso è
x (0+ ):
d
0
x (t) = x 0+ δ (t) + x (t) u (t)
dt
(4.6.38)
Nel caso di sollecitazioni discontinue l'integrale di Duhamel si scrive:
ˆ
y (t) = yS.Z (t) =
t+
0
x (τ ) g (t − τ ) dτ
0−
171
(4.6.39)
4 Reti elettriche
Utilizzando (4.6.38) la (4.6.39) si scrive:
ˆ
t+
d
+
x 0 δ (τ ) +
y (t) = yS.Z (t) =
x (τ ) u (τ ) g (t − τ ) dτ =
dτ
0−
ˆ t+ d
+
x 0 δ (τ ) +
=
x (τ ) u (τ ) g (t − τ ) dτ =
dτ
0−
ˆ
ˆ
t+
+
=
x 0
t+
g (t − τ ) δ (τ ) dτ +
0−
0−
d
x (τ ) u (τ ) g (t − τ ) dτ
dτ
Applicando il teorema del campionamento a quest'ultima espressione si ricava la formula generale dell'integrale di Duhamel:
ˆ
y (t) = yS.Z. (t) =
ˆ
ˆ
t+
0−
0−
ˆ
t+
t+
x 0+ g (t) δ (τ ) dτ +
=
0−
0−
ˆ
=x 0
+
t+
x 0+ g (t) δ (τ ) dτ +
ˆ
t+
g (t)
t+
δ (τ ) dτ +
0−
ˆ
0−
t+
= x 0+ g (t) +
0−
d
x (τ ) u (τ ) g (t − τ ) dτ =
dτ
d
x (τ ) u (τ ) g (t − τ ) dτ =
dτ
d
x (τ ) u (τ ) g (t − τ ) dτ =
dτ
d
x (τ ) g (t − τ ) dτ
dτ
ovvero:
ˆ
+
y (t) = yS.Z. (t) = x 0
t+
g (t) +
0−
d
x (τ ) g (t − τ ) dτ
dτ
(4.6.40)
4.6.2.4 Signicato sico dell'integrale di Duhamel
Supponiamo che la rete elettrica sia eccitata mediante un ingresso
x (t)
discontinuo in
y (t) a partire dalla risposta al
g (t).
+
Il segnale x (t) si può pensare come la somma tra un gradino di ampiezza nita x (0 ):
t=0 s e che si voglia calcolare una qualunque risposta
gradino
x 0+ u (t)
che descrive la discontinuità pert=0 s e un insieme di gradini di ampiezza innitesima
dx (τ )
del tipo:
dx (τ ) u (t − τ )
x (t) da 0 a t (Figura 4.6.21)
Quindi la risposta y (t) al tempo t è la sovrapposizione
+
La risposta al gradino x (0 ) u (t) è ovviamente:
che discretizzano
172
di due termini.
4 Reti elettriche
Figura 4.6.21: discretizzazione di
x (t)
y1 (t) = x 0+ g (t)
La risposta al gradino elementare
dx (τ ) u (t − τ )
(4.6.41)
vale invece:
dy2 (τ ) = dx (τ ) g (t − τ )
Tenendo conto che il dierenziale della funzione
x
nel punto
(4.6.42)
τ
vale:
0
dx (τ ) = x (τ ) dτ
la (4.6.42) si scrive:
0
dy2 (τ ) = x (τ ) g (t − τ ) dτ
ovvero:
d
x (τ ) g (t − τ ) dτ
dτ
tipo (4.6.43) per ogni τ ∈ ]0, t]
dy2 (τ ) =
Sommando tutti i contributi del
ˆ
ˆ
y2 (t+ )
0−
dy2 (τ ) =
0
t
(4.6.43)
si ottiene:
d
x (τ ) g (t − τ ) dτ
dτ
ovvero:
ˆ
y2 (t) =
t+
0−
d
x (τ ) g (t − τ ) dτ
dτ
(4.6.44)
Sommando i contributi in (4.6.40) e (4.6.44) si ricompone l'integrale di Duhamel.
173
4 Reti elettriche
4.7 Regime sinusoidale
4.7.1 Ricerca dell'integrale particolare dell'equazione dierenziale di
ordine minimo (metodo dei fasori)
n nella variabile di rete generica
x (t):
Consideriamo l'equazione dierenziale di ordine minimo
y (t)
nel caso di rete eccitata con un singolo ingresso
n
X
i=0
m
X dj
di
ai i y (t) =
bj j x (t) = f (t)
dt
dt
e supponiamo che l'ingresso
(4.7.1)
j=0
x (t)
sia sinusoidale:
x (t) = X cos (ωt + ϕ)
(4.7.2)
x (t) è un segnale sinusoidale di pulsazione ω anche f (t) è un segnale
pulsazione ω :
Si dimostra che se
sinusoidale di
f (t) =
m
X
bj
j=0
dj
x (t) = F cos (ωt + ψ)
dtj
(4.7.3)
Per dimostrare la (4.7.3) basta vericare le due seguenti proprietà:
Proprietà 1
Le derivate successive di un segnale sinusoidale avente pulsazione
ω
soidali aventi la medesima pulsazione.
Si ha facilmente:
x (t) = X cos (ωt + ϕ)
d
π
x (t) = −ωX sin (ωt + ϕ) = ωX cos ωt + ϕ +
dt
2
d2
π π
2
x
(t)
=
ω
X
cos
ωt
+
ϕ
+
+
dt2
2
2
.
.
.
.
.
dm
π
m
x
(t)
=
ω
X
cos
ωt
+
ϕ
+
m
dtm
2
174
sono segnali sinu-
4 Reti elettriche
Proprietà 2
La combinazione lineare di segnali sinusoidali aventi pulsazione
ω è un segnale sinusoidale
avente la medesima pulsazione.
Dimostrazione. Consideriamo i segnali sinusoidali
a (t) = A cos (ωt + ϕ) e b (t) = B cos (ωt + ψ)
in combinazione lineare:
k1 a (t) + k2 b (t)
(4.7.4)
Applicando la formula di addizione del coseno la (4.7.4) si scrive:
k1 a (t) + k2 b (t) = k1 A cos (ωt + ϕ) + k2 B cos (ωt + ψ) =
= k1 A cos ωt cos ϕ − k1 A sin ωt sin ϕ + k2 B cos ωt cos ψ − k2 B sin ωt sin ψ =
= (k1 A cos ϕ + k2 B cos ψ) cos ωt − (k1 A sin ϕ + k2 B sin ψ) sin ωt
(4.7.5)
Le quantità
m = k1 A cos ϕ + k2 B cos ψ
n = − (k1 A sin ϕ + k2 B sin ψ)
sono delle costanti rispetto al tempo e permettono di scrivere la (4.7.5) come segue:
k1 a (t) + k2 b (t) = m cos ωt + n sin ωt
Quest'ultima espressione suggerisce la formula di sottrazione del coseno, infatti ponendo:
m = C cos γ
n = C sin γ
si ha:
k1 a (t) + k2 b (t) = C cos γ cos ωt + C sin γ sin ωt = C cos (ωt − γ)
e ciò dimostra la proprietà.
Consideriamo nuovamente l'equazione dierenziale di ordine minimo
n
X
i=0
ai
di
y (t) = f (t)
dti
175
n:
(4.7.6)
4 Reti elettriche
Nell'ipotesi in cui la sollecitazione
x (t)
è un segnale sinusoidale di pulsazione
ω,
il
termine noto
f (t) =
m
X
bj
j=0
dj
x (t)
dtj
(4.7.7)
ω.
f (t) è un segnale sinusoidale di pulsazione ω , lo sarà pure l'integrale
è dunque un segnale sinusoidale di pulsazione
Se il termine noto
ypart. (t)
particolare
Denizione.
Sia
x (t)
che si determina mediante il
metodo dei fasori.
(Fasore)
un segnale sinusoidale di pulsazione
ω
del tipo:
x (t) = X cos (ωt + ϕ)
Si chiama fasore associato al segnale sinusoidale
x (t),
il numero complesso:
X
Ẋ = √ ejϕ
2
(4.7.8)
Ẋ = Xejϕ
(4.7.9)
Oppure il numero complesso:
La notazione in (4.7.8) viene adoperta in Europa, mentre quella in (4.7.9) viene
adoperata in USA.
In questo testo adopereremo la notazione indicata in (4.7.8).
Con riferimento alla (4.7.8), il fasore
Ẋ ,
si può scrivere anche nelle seguenti forme
equivalenti:
X
X
X
Ẋ = √ ∠ϕ = √ ejϕ = √ {cos ϕ + j sin ϕ} =
2
2
2
n o
n o
X
X
= √ cos ϕ + j √ sin ϕ = Re Ẋ + j Im Ẋ
2
2
(4.7.10)
Ẋ
x (t) .
In Figura viene mostrata la rappresentazione nel piano complesso del fasore
La quantità
Xef f. =
X
√
si chiama
2
valore ecace
del segnale sinusoidale
Dato il fasore (4.7.10) è possibile risalire al corrispondente segnale sinusoidale
x (t)
(4.7.2) mediante la relazione:
x (t) = Re
n√
2Ẋejωt
o
(4.7.11)
Infatti sostituendo (4.7.10) in (4.7.11) si ritrova (4.7.2):
x (t) = Re
n√
2Ẋe
jωt
o
√ X jϕ jωt
= Re
2√ e e
2
n
o
= Re Xej(ωt+ϕ) =
= Re {X cos (ωt + ϕ) + j sin (ωt + ϕ)} = X cos (ωt + ϕ)
176
4 Reti elettriche
Figura 4.7.1: rappresentazione graca del fasore
Il fasore della derivate successive di
x (t)
Qui di seguito sono riportate il segnale
x (t)
e le sue derivate successive no all'ordine
m
con i corrispondenti fasori
X
x (t) = X cos (ωt + ϕ) ⇐⇒ Ẋ = √ ejϕ
2
d
π
X π
x (t) = ωX cos ωt + ϕ +
⇐⇒ ω √ ej 2 ejϕ = jω Ẋ
dt
2
2
d2
π π
X π π
2
x
(t)
=
ω
X
cos
ωt
+
ϕ
+
+
⇐⇒ ω 2 √ ej 2 ej 2 ejϕ = (jω)2 Ẋ
2
dt
2
2
2
.
.
.
.
.
π m
dm
π
m
m X
√
ej 2
x
(t)
=
ω
X
cos
ωt
+
ϕ
+
m
⇐⇒
ω
ejϕ = (jω)m Ẋ
dtm
2
2
Dai calcoli risulta evidente che un ordine di derivazione sulla funzione
un fattore
(jω)
(4.7.12)
x (t) fa comparire
nel fasore.
Utilizzando la (4.7.12) è possibile scrivere l'equazione dierenziale di ordine minimo
n
X
i=0
n:
m
X dk
di
ai i y (t) =
bk k x (t)
dt
dt
k=0
nel dominio dei fasori:
n
X
i=0
ai (jω)i Ẏ =
m
X
k=0
177
bk (jω)k Ẋ
(4.7.13)
4 Reti elettriche
Da quest'ultima espressione si ricava il fasore
Ẏ :
Pm
bk (jω)k
Ẋ
Ẏ = Pk=0
n
i
a
(jω)
i
i=0
(4.7.14)
a cui corrisponde l'integrale particolare dell'omogenea associata:
ypart. (t) = Re
n√
2Ẏ ejωt
o
(4.7.15)
L'espressione in (4.7.13) è un'uguaglianza tra numeri complessi e per essere valida
occorre fare vedere che essi sono uguali in parte reali e in parte immaginarie.
Per far vedere ciò consideriamo la (4.7.13) e applichiamo ai fasori presenti la (4.7.11):
n
X
n√
ai Re
i
2 (jω) Ẏ e
jωt
o
=
m
X
i=0
Re
2 (jω)k Ẋejωt
!
i
ai (jω)
√
)
2Ẏ e
m
X
(
jωt
= Re
!
bk Re (jω)
√
k
)
2Ẋe
mentre per
t
n
X
!
i
ai (jω)
√
)
2Ẏ
m
X
(
= Re
i=0
π
, si ha:
= 2ω
(
Re
jωt
∀t
(4.7.17)
k=0
Visto che la (4.7.17) deve essere valida per ogni t; pertanto per
Re
(4.7.16)
parte reale Re {.} è lineare la (4.7.16) si può scrivere come segue:
i=0
(
o
∀t.
Tale relazione deve essere valida
n
X
n√
k=0
Visto che l'operatore
(
bk Re
j
n
X
!
k
bk Re (jω)
√
t=0
)
si ha:
2Ẋ
(4.7.18)
k=0
!
ai (jω)i
√
)
2Ẏ
(
= Re j
i=0
m
X
!
bk Re (jω)k
√
2Ẋ
)
k=0
ovvero:
(
Im
n
X
!
i
ai (jω)
√
)
2Ẏ
(
= Im
i=0
m
X
!
bk Re (jω)
k
√
)
2Ẋ
(4.7.19)
k=0
Secondo (4.7.17) e (4.7.18), i numeri complessi:
n
X
m
X
√
ai (jω) 2Ẏ ,
i
i=0
bk Re (jω)k
√
2Ẋ
k=0
coincidono nella parte reale e nella parte immaginaria e ciò vuol dire che sono uguali:
n
X
i=0
ai (jω)
i
√
2Ẏ =
m
X
bk Re (jω)k
k=0
Da quest'ultima equazione si deduce la (4.7.13).
178
√
2Ẋ
4 Reti elettriche
4.7.2 Esempio
Consideriamo nuovamente la rete elettica di Figura 4.2.1 che per comodità riportiamo
sul foglio di questa pagina:
Figura 4.7.2: rete elettrica
Sappiamo già che l'equazione dierenziale di ordine minimo nella variabile di rete
vc (t)
è:
d2
d
d
vc (t) + 2 vc (t) + 2vc (t) = vg (t) + vg (t) + ig (t)
2
dt
dt
dt
(4.7.20)
4.7.2.1 Ricerca dell'integrale particolare
Supponiamo che la rete si trovi a regime sinusoidale e che i generatori valgano:
√
π
vg (t) = 5 2 cos 3t + 3
V
2
√
π
A
ig (t) = 2 2 cos 3t + 5
2
Per determinare l'integrale particolare si applica il metodo dei fasori.
I fasori della tensione e della corrente di eccitazione per la rete sono rispettivamente:
π 3
π
V̇g = 5ej3 2 = 5 ej 2
= 5 (j)3 = −j5 V
(4.7.21)
π 5
π
I˙g = 2ej5 2 = 2 ej 2
= 2 (j)5 = j2 V
(4.7.22)
La (4.7.20) nel dominio dei fasori si scrive:
(jω)2 V̇c + 2 (jω) V̇c + 2V̇c = (jω) V̇g + V̇g + I˙g
Da quest'ultima espressione si ricava il fasore
179
V̇c :
(4.7.23)
4 Reti elettriche
V̇c =
1
1 + jω
V̇g +
I˙g
2
2
(2 − ω ) + j2ω
(2 − ω ) + j2ω
Tenendo conto che i generatori oscillano con pulsazione
ω = 3 rad/s,
(4.7.24)
la (4.7.25) si
scrive:
V̇c =
1 + j3
1
V̇g +
I˙g
−7 + j6
−7 + j6
(4.7.25)
Sostituendo (4.7.22) e (4.7.23) in (4.7.26) si ottiene:
1 + j3
1
(−j5) +
j2 =
−7 + j6
−7 + j6
123
69
−
= 1, 66ej(−2,63) V
+j −
85
85
V̇c =
(4.7.26)
Nota la (4.7.26) si determina l'integrale particolare:
vcpart. (t) = Re
n√
o
2V̇c eiωt = 2, 35 cos (3t − 2, 63) V
(4.7.27)
E' evidente che se una rete elettrica presenta più generatori sinusoidale oscillanti con
pulsazione
ω,
ω , tutte le grandezze di rete saranno sinusoidale oscillanti alla stessa pulsazione
una volta esaurito il transitorio.
4.7.3 L.K. nel dominio dei fasori
4.7.3.1 L.K.T. nel dominio dei fasori
La LKT nel dominio del tempo
X
vk (t) = 0
(4.7.28)
k
nel dominio dei fasori si scrive:
X
V̇k = 0
(4.7.29)
k
Dimostrazione. Basta applicare la (4.7.11) alla (4.7.28):
X
vk (t) = 0
k
X
Re
n√
o
2V̇k eiωt = 0 ∀t
k
√
2Re
(
X
)
V̇k eiωt
k
180
= 0 ∀t
(4.7.30)
4 Reti elettriche
Per
t=0
la (4.7.30) si scrive:
Re
X
V̇k = 0
(4.7.31)
k
Per
t=
π
2ω la (4.7.30) si scrive:
(
)
Re j
X
V̇k
=0
k
ovvero:
Im
(
X
)
V̇k
=0
(4.7.32)
k
Visto che valgono le relazioni in (4.7.31) e (4.7.32) segue la tesi (4.7.29).
4.7.3.2 L.K.I. nel dominio dei fasori
La LKI nel dominio del tempo
X
ik (t) = 0
(4.7.33)
k
nel dominio dei fasori si scrive:
X
I˙k = 0
(4.7.34)
k
4.7.4 L.L. nel dominio dei fasori
4.7.4.1 Resistore lineare tempo-invariante
Figura 4.7.3: resistore nel dominio dei fasori
v (t) = R i (t) ⇐⇒ V̇ = R I˙
(4.7.35)
4.7.4.2 Capacitore lineare tempo-invariante
i (t) = C
d
v (t) ⇐⇒ I˙ = jωC V̇
dt
181
(4.7.36)
4 Reti elettriche
Figura 4.7.4: capacitore nel dominio dei fasori
4.7.4.3 Induttore lineare tempo-invariante
Figura 4.7.5: induttore nel dominio dei fasori
v (t) = L
d
i (t) ⇐⇒ V̇ = jωL I˙
dt
(4.7.37)
4.7.4.4 Impedenza del bipolo elementare
Le relazioni fasoriali presenti in (4.7.35), (4.7.36) e (4.7.37) si possono compattare nella
relazione fasoriale:
V̇ = Ż I˙
(4.7.38)
dove la quantità:
Ż =
si chiama


R
1
 jωC
1
−j ωC
=

jωL = XL
= Xc
(resistenza)
(reattanza capacitiva)
(4.7.39)
(reattanza induttiva)
impedenza del bipolo elementare.
Figura 4.7.6: impedenza
Si possono pure compattare nella seguente relazione fasoriale:
I˙ = Ẏ V̇
182
(4.7.40)
4 Reti elettriche
dove la quantità:
1

R = G
1
= jωC = BC
Ẏ =

Ż
 1
1
jωL = − ωL = BL
si chiama
conduttanza
sucettanza capacitiva
suscettanza induttiva
(4.7.41)
ammettenza.
4.7.4.5 Coppia di induttori mutuamente accoppiati
(
d
d
v1 (t) = L1 dt
i1 (t) ± M dt
i2 (t)
d
d
v2 (t) = ±M dt i1 (t) + L2 dt i2 (t)
(
V̇1 = jωL1 I˙1 ± jωM I˙2
⇐⇒
V̇2 = ±jωM I˙1 + jωL2 I˙2
(4.7.42)
Figura 4.7.7: coppia di induttori mutuamente accoppiati
4.7.4.6 Trasformatore ideale
(
v1 (t) = t v2 (t)
i1 (t) = − 1t i2 (t)
(
V̇1 = t V̇2
⇐⇒
I˙1 = − 1t I˙2
(4.7.43)
Figura 4.7.8: trasformatore ideale
4.7.4.7 Generatore ideale di tensione
v (t) = vg (t) ⇐⇒ V̇ = V̇g
183
(4.7.44)
4 Reti elettriche
4.7.4.8 Generatore ideale di corrente
i (t) = ig (t) ⇐⇒ I˙ = I˙g
(4.7.45)
4.7.5 Impedenza del bipolo composito
Estendiamo in questa sezione il concetto di impedenza al caso di un
bipolo composito.
Per bipolo composito si intende un dispositivo a due morsetti a più componenti elementari. Per esso si può denire l'impedenza solo se risulta
passivo.
Un bipolo composito si dice passivo se risulta costituito da resistori, capacitori, induttori,induttori mutuamente accoppiati e generatori pilotati (Figura 4.7.9).
Ovviamente se il bipolo composito contiene elementi di accoppiamento quali generatori pilotati e induttori mutuamente
accoppiati, questi non devono essere accoppiati con grandezze esterne al bipolo
in quanto la relazione tensione-corrente ai
morsetti 1 e 1' andrebbe a dipendere da
grandezze che stanno fuori dal bipolo.
Quindi per un bipolo composito passivo,
di
l'impedenza
proporzionalità
Ż
che
è
quel
lega
fattore
tensione
Figura 4.7.9: bipolo composito passivo
e
corrente:
V̇ = Ż I˙
(4.7.46)
L'impedenza di un bipolo composito passivo è un numero complesso avente sia la parte
reale che quella immaginaria diversa da zero:
n o
n o
Ż = Re Ż + j Im Ż
La parte reale dell'impedenza
Ż
si chiama
(4.7.47)
resistenza R, mentre la parte immaginaria
si chiama reattanza X:
Ż = R + j X
(4.7.48)
Facciamo attenzione n da adesso che la resistenza R e la reattanza X del bipolo
composito passivo sono numeri reali che dipendono dalla pulsazione
ω
(che è uguale in
tutti i generatori che sollecitano il bipolo) e da tutti i dispositivi elementari costituenti
il bipolo composito stesso.
A chiarimento di quanto detto consideriamo il bipolo composito costituito da un resistore di resistenza R e da un capacitore di capacità C posti in parallelo tra di loro come
mostrato in Figura 4.7.10.
L'impedenza del bipolo vale:
184
4 Reti elettriche
Ż =
=
1
R jωC
R+
1
jωC
=
R
jωC
1+jωRC
jωC
=
R
=
1 + jωRC
1 − jωRC
−ωR2 C
R
R
+
j
=
1 + jωRC 1 − jωRC
1 + (ωRC)2
1 + (ωRC)2
(4.7.49)
Quindi la resistenza del bipolo composito vale:
n o
Re Ż =
R
1 + ω 2 R2 C 2
(4.7.50)
n o
Im Ż =
−ωR2 C
1 + ω 2 R2 C 2
(4.7.51)
mantre la reattanza vale:
Attraverso (4.7.50) e (4.7.51) è evidente che sia la resistenza che la reattanza del bipolo
composito dipendono dalla pulsazione
ω.
E' evidente pure che NON è vero che la
resistenza di un bipolo composito è fatta
solo da resistenze e la reattanza è formata
solo da capacitori e/o induttori.
Questa circostanza si verica per i bipoli
compositi banali come quello mostrato in
Figura 4.7.11 per cui si ha:
Figura 4.7.10: impedenza RC
Ż = R + jω (L1 + L2 )
(4.7.52)
Figura 4.7.11: impedenza LRL
185
4 Reti elettriche
Forma polare dell'impedenza
Essendo
Ż
un numero complesso, questo può anche scriversi in forma polare:
Ż = R + j X = Z∠ϕz = Z ejϕz
(4.7.53)
p
Z = Ż = R2 + X 2
(4.7.54)
Dove
è il modulo del fasore
Ż ,
mentre
ϕz =
è la fase del fasore
Ż


arctan X

R


π
2

− π2



arctan X + π
R
se R > 0
se R = 0, X > 0
se R = 0, X < 0
se R < 0
(4.7.55)
come mostrato in Figura 4.7.12
Figura 4.7.12: rappresentazione polare
Valgono le seguenti proprietà
Proprietà 1
Se il circuito è RC, allora la parte immaginaria dell'impedenza è negativa, se il circuito
è RL, la parte immaginaria è positiva. Se il circuito è RLC non si può stabilire a priori
il segno della parte immaginaria del bipolo composito.
Proprietà 2
Se nel bipolo composito passivo mancano i generatori pilotati risulta sempre:
n o
Re Ż > 0
186
4 Reti elettriche
L'inverso dell'impedenza di un bipolo composito, come nel caso del bipolo elementare,
si chiama
ammettenza Ẏ .
Così come l'impedenza anche l'ammettenza per un bipolo
composito passivo avrà una parte reale e una parte immaginaria diversa da zero:
n o
n o
Ẏ = Re Ẏ + j Im Ẏ
La parte reale dell'ammettenza
naria si chiama
suscettanza B :
Ẏ
si chiama
conduttanza
(4.7.56)
G, mentre la parte immagi-
Ẏ = G + j B
Ω, G e B si misurano in siemens.
Ẏ = 1/Ż NON implica che G = 1/R e X = 1/X ;
(4.7.57)
Mentre R e X si misurano in
Si osservi che il fatto
ciò si prova
facilmente:
Ẏ =
1
1
R − jX
1
=
=
=
R + jX
R + jX R − jX
Ż
=
R2
−X
R
+j 2
2
+X
R + X2
(4.7.58)
Dalla (4.7.58) si vede immediatamente che:
G=
R2
B=−
Allo stesso modo sviluppando
Ż = 1/Ẏ
Ż =
R
+ X2
R2
X
+ X2
(4.7.59)
(4.7.60)
si trova:
G
−B
+j 2
G2 + B 2
G + B2
(4.7.61)
essendo:
R=
G2
X=−
G
+ B2
G2
B
+ B2
(4.7.62)
(4.7.63)
In Figura 4.7.13 vengono mostrati l'impedenza data in (4.7.48) e l'ammettenza in
(4.7.57) nell'iposi in cui R ed X sono positivi; ovviamente per impedenza e ammettenza si
devono utilizzare due scale dierenti se vengono riportate su uno stesso piano complesso.
187
4 Reti elettriche
Figura 4.7.13: impedenza e ammettenza in rappresentazione polare
4.7.5.1 Impedenze in serie
Due o più bipoli si dicono in serie se attraversati dalla stessa corrente:
V̇ = V̇1 + V̇2 + ...... + V̇N =
= Ż1 I˙ + Ż2 I˙ + ...... + ŻN I˙ = I˙
N
X
Żk = Żeq. I˙
k=1
V̇ = Żeq. I˙
Figura 4.7.14: bipoli in serie
4.7.5.1.1 Legge del partitore di tensione
Żk
V̇k = Żk I˙ =
V̇
Żeq.
ovvero:
V̇k =
Żk
V̇
Ż1 + Ż2 + ...... + ŻN
188
4 Reti elettriche
4.7.5.2 Impedenze in parallelo
Due o più bipoli si dicono in parallelo se ai loro capi hanno la stessa tensione:
I˙ = I˙1 + I˙2 + ...... + I˙N =
= Ẏ1 V̇ + Ẏ2 I˙ + ...... + ẎN V̇ = V̇
N
X
Ẏk = Ẏeq. I˙
k=1
I˙ = Ẏeq. V̇
Żeq. =
1
1
=
=
Ẏeq.
Ẏ1 + Ẏ2 + ...... + ẎN
=
1
Ż1
+
1
Ż2
1
+ ...... +
1
ŻN
=
1
Ż2 ·Ż3 ·...ŻN +Ż1 ·Ż3 ·...·ŻN +......+Ż1 ·Ż2 ·...·ŻN −1
Ż1 ·Ż2 ·......·ŻN
ovvero:
Żeq. =
Ż1 · Ż2 · ...... · ŻN
Ż2 · Ż3 · ... · ŻN + Ż1 · Ż3 · ... · ŻN + ...... + Ż1 · Ż2 · ...ŻN
Figura 4.7.15: bipoli in parallelo
189
(4.7.64)
4 Reti elettriche
4.7.5.2.1 Legge del partitore di corrente
Ẏk
V̇
I˙k = Ẏk V̇ =
Ẏeq.
ovvero:
V̇k =
Ẏk
V̇
Ẏ1 + Ẏ2 + ...... + ẎN
4.7.6 Rete elettrica nel dominio dei fasori
Quando si studia una rete elettrica si può convenire di scriverla nel dominio dei fasori
indipendentemente dal regime in cui si trova e scrivere per essa l'espressione fasoriale
della variabile di rete di interesse.
Nota quest'ultima espressione non solo siamo in grado di ricavare l'integrale particolare nel caso in cui la rete si trovi a regime sinusoidale, ma siamo in grado anche di
ricavare l'espressione dell'equazione dierenziale di ordine minimo nella variabile di rete
di interesse.
Il vantaggio di procedere seguendo questo approccio risiede nel fatto che nella determinazione dell'espressione di una qualunque variabile di rete non si scrivono equazioni
dierenziali ma semplicemente equazioni algebriche come nel caso delle reti puramente
resistive.
Per determinare l'espressione di una qualunque variabile di rete si può procedere, come
nel caso dell'analisi della rete nel dominio del tempo, scrivendo le L.k. al ne di scrivere
un sistema risolvente nelle variabili di stato.
N.B. Si deve sempre ricondurre lo studio di una rete elettrica ad un sistema risolvente
nelle variabili di rete per non incorrere successivamente nel problemna di determinare le
condizioni iniziali sulle derivate della variabile di interesse.
Non far ciò signicherebbe scrivere LK in maniera scriteriata (perdendo solo tempo)
al ne di determinare tali condizioni iniziali.
Vediamo quanto detto attraverso lo studio della solita rete introdotta in Figura 4.1.2.
Tale rete viene riproposta nel dominio dei fasori in Figura 4.7.3
Si vuole determinare come al solito l'espressione analitica della tensione
vc (t)
ai capi
del capacitore.
Per far ciò si procede dapprima determinando il sistema risolvente nelle variabili di
stato
V̇c
e
I˙L .
Avendo denito N=4 nodi la rete risulta avere L=6 lati e pertanto occorre scrivere
N-1=3 LKI ed L-N+1=4 LKT:
190
4 Reti elettriche
Figura 4.7.16: rete elettrica nel dominio dei fasori


−I˙A + I˙1 = 0




−I˙1 + I˙c + I˙L = 0



−I˙ − I˙ + I˙ = 0
g
2
L

−
V̇
+
V̇
+
V̇
g
1
c =0





−V̇c + V̇L + V̇B = 0



−V̇ + V̇ = 0
2
B
LKI1
LKI2
LKI3
LKT 1
LKT 2
LKT 3
(4.7.65)
Inoltre occorre scrivere L=6 LL:


V̇A = V̇g





V̇1 = R1 I˙1



I˙ = jωC V̇
c
c
˙

V̇L = jωL IL





I˙B = I˙g


V̇ = R I˙
2
2 2
LL1
LL2
LL3
LL4
LL5
LL6
Le equazioni in (4.7.65) e (4.7.66) si sistemano come si seguito indicato:
191
(4.7.66)
4 Reti elettriche


−I˙A + I˙1 = 0





−I˙1 + I˙c + I˙L = 0




−I˙L − I˙g + I˙2 = 0





−V̇g + V̇1 + V̇c = 0



−V̇ + V̇ + V̇ = 0
c
L
B

−V̇B + V̇2 = 0





V̇A = V̇g





V̇1 = R1 I˙1





I˙B = I˙g



V̇ = R I˙
2
2 2
LKI1
LKI2
LKI3
LKT 1
LKT 2
(4.7.67.1)
LKT 3
LL1
LL2
LL5
LL6
(
I˙c = jωC V̇c
V̇L = jωL I˙L
LL3
(4.7.67.2)
LL4
(4.7.67)
Dal sistema (4.7.67.1) si ricavano le grandeze analoghe alle variabili di stato, ossia
e
I˙c
V̇L :
(
I˙c = −I˙L − R11 V̇c + R11 V̇g
V̇L = V̇c − R2 I˙g − R2 I˙L
(4.7.68.1)
(4.7.68.2)
(4.7.68)
Sostituendo (4.7.68) in (4.7.67.2) si ricavano le equazioni di stato nel dominio dei fasori:
(
1
1
jω V̇c = − CR
V̇c − C1 I˙L + CR
V̇g
1
1
R
R
1
jω I˙L = V̇c − 2 I˙L − 2 I˙g
L
L
L
(4.7.69.1)
(4.7.69.2)
Sostituendo i valori numeri si ottiene:
(
jω V̇c = −V̇c − I˙L + V̇g
jω I˙L = V̇c − I˙L − I˙g
(4.7.69.1)
(4.7.69.2)
(4.7.69)
Pertanto trasportando le equazioni in (4.7.69) nel dominio del tempo si ricavano le
equazioni di stato che per t=0 forniscono le condizioni iniziali sulle derivate delle variabili
di stato.
Ricavando
fasore
I˙L
dalla (4.7.69.1) e sostituendo in (4.7.69.2) si ricava un'equazione nel
V̇c :
(jω)2 V̇c + 2 (jω) V̇c + 2V̇c = jω V̇g + V̇g + I˙g
(4.7.70)
e con ciò stiamo ritrovando la (4.7.23) che nel caso di rete a regime sinusoidale conduce
all'integrale particolare. Si osservi che trasportando la (4.7.70) nel dominio del tempo si
ricava l'equazione dierenziale di ordine minimo. Nota quest'ultima è possibile ricavare
l'integrale generale dell'omogenea associata nonchè l'integrale particolare nel caso di rete
a regime costante.
192
4 Reti elettriche
4.7.7 Potenza in regime sinusoidale
4.7.7.1 La potenza media o attiva o reale P
Consideriamo un bipolo, cioè una parte di una rete più complicata, contenente resistori, capacitori, induttori, induttori mutuamente accoppiati, generatori pilotati e pure
generatori ideali come mostrato in Figura 4.7.17.
Si noti che per detto bipolo continua
a valere la convenzione dell'utilizzatore
anche se contiene generatori ideali.
Se indichiamo con
v (t) = V cos (ωt + ϕV )
(4.7.71)
e
Figura 4.7.17: bipolo composito contenente
generatori ideali
i (t) = I cos (ωt + ϕI )
(4.7.72)
la tensione e la corrente del bipolo nell'ipotesi di regime sinusoidale, si ha che la potenza
istantanea vale:
p (t) = v (t) i (t) = V I cos (ωt + ϕV ) cos (ωt + ϕI ) =
=V I
=
1
1
cos (ϕV − ϕI ) + cos (2ωt + ϕV + ϕI ) =
2
2
VI
VI
cos (ϕV − ϕI ) +
cos (2ωt + ϕV + ϕI ) =
2
2
= P + p0 (t)
(4.7.73)
Secondo (4.7.73) la potenza istantanea assorbita dal bipolo composito è la somma tra
un contributo costante:
P =
VI
cos (ϕV − ϕI )
2
(4.7.74)
e un contributo uttuante di pulsazione doppia rispetto a quella della tensione e della
corrente:
p0 (t) =
VI
cos (2ωt + ϕV + ϕI )
2
(4.7.75)
In Figura 4.7.18 vengono mostrati i graci di tensione, corrente, potenza istantanea,
potenza costante e potenza uttuante del bipolo composito assumendo i valori:
V = 10 V, I = 5 A,
ω = 5 rad/s, ϕV = 0 rad, ϕI =
193
π
rad
3
4 Reti elettriche
Figura 4.7.18: rappresentazione graca
Si osservi che per alcuni valori di t, la potenza istantanea è negativa e ciò vuol dire che
il bipolo composito sta restituendo potenza alla rimanente parte della rete complessiva.
Per determinare l'
tempo
t1
e
energia, bisogna integrare la potenza istantanea p (t) tra 2 istanti di
t2 :
ˆ
t2
ε (t2 − t1 ) =
p (t) dt
(4.7.76)
t1
Se teniamo conto che la tensione di rete è a 50 Hz si avrà che il periodo T della
tensione è 0,02 s e ciò vuol dire che il periodo della potenza istantanea è T/2= 0.01 s;
quindi si capisce che la potenza tra due generici istanti di tempo t1 e t2 , quando il tempo
è dell'ordine di T/2 non ha sigmicato. Si dà signicato invece alla potenza istantanea
in un intervallo di tempo pari a nT con n intero:
ˆ
t1 +nT
ε (nT ) =
p (t) dt
t1
Sostituendo (4.7.73) in (4.7.77) si ricava:
ˆ
ˆ
t1 +nT
t1 +nT
{p0 (t) + P } dt =
p (t) dt =
ε (nT ) =
t1
t1
ˆ
ˆ
t1 +nT
=
t1 +nT
p0 (t) dt +
t1
P dt =
t1
ˆ
t1 +nT
=0+P
dt = n T P
t1
194
(4.7.77)
4 Reti elettriche
ovvero:
ε (nT ) = n T
VI
cos (ϕV − ϕI )
2
(4.7.78)
Signicato sico della potenza costante P
Dalla teoria dei segnali si sa che il
valore medio
di un segnale
p (t)
periodico di periodo
T è per denizione:
1
hp (t)i =
T
ˆ
T /2
p (t) dt
(4.7.79)
−T /2
Sostituendo (4.7.73) in (4.7.79) si determina il valore medio della potenza istantanea
del bipolo composito:
hp (t)i =
1
T
ˆ
T /2
{p0 (t) + P } dt =
−T /2
1
P
T
ˆ
T /2
dt =
−T /2
1
PT =P
T
(4.7.80)
La (4.7.80) conduce al signicato sico di P: il contributo di potenza costante P è il
valore medio della potenza istantanea
p (t).
Il valore medio P della potenza istanta-
potenza media
potenza reale o potenza attiva.
nea
p (t)
si chiama pure
o
Non è dicile provare che la potenza media si può esprimere anche come
prodotto scalare tra fasori:
P = V̇ · I˙
(4.7.81)
essendo
Figura 4.7.19: fasori della tensione e della
corrente del bipolo composito
V
V̇ = √ ejϕV
2
(4.7.82)
I
I˙ = √ ejϕI
2
(4.7.83)
Sostituendo (4.7.82) e (4.7.83) in (4.7.81) si ricompone la (4.7.74):
P =
V
√ ejϕV
2
I jϕI
V I
VI
· √ e
= √ √ cos (ϕV − ϕI ) =
cos (ϕV − ϕI )
2
2
2 2
Si noti che tutte le formule trovate valgono in generale perchè si riferiscono a un bipolo
composito che può contenere pure generatori ideali.
195
4 Reti elettriche
Se il bipolo composito è passivo come indicato in Figura 4.7.20 è possibile denire il
concetto di impedenza e quindi scrivere la relazione:
Figura 4.7.20: bipolo composito passivo
V̇ = Ż I˙
(4.7.84)
Ż = Z ejϕZ
(4.7.85)
essendo
Sostituendo (4.7.82), (4.7.83) e (4.7.85) in (4.7.85) si ottiene:
V
I
√ ejϕV = Z ejϕZ √ ejϕI
2
2
Vef f. ejϕV = Z Ief f. ej(ϕZ +ϕI )
Uguagliando i moduli e le fasi, l'equazione complessa in (4.7.86) equivale alle seguenti
equazioni reali:
(
Vef f. = Z Ief f.
ϕV = ϕZ + ϕI =⇒ ϕV − ϕI = ϕZ
(4.7.86.1)
(4.7.86)
Sostituendo (4.7.87) in (4.7.74) si ottiene:
P = Vef f. Ief f. cos ϕZ
(4.7.87)
Ovviamente combinando (4.7.86.1) e (4.7.87) si ricavano le seguenti altre forme per la
potenza media:
2
2
P = Vef f. Ief f. cos ϕZ = ZIef
f. cos ϕZ = R Ief f
(4.7.88)
L'ultima uguaglianza in (4.7.88) si capisce osservando Figura 4.7.21.
Si possono avere altre forme equivalenti se si decide di combinare (4.7.87) con
Vef f.
Z :
196
Ief f. =
4 Reti elettriche
Figura 4.7.21: rappresentazione nel piano complesso
P = Vef f. Ief f. cos ϕZ =
=
2
Vef
f. Z
Z Z
cos ϕZ =
2
Vef
f.
Z2
R=
2
Vef
f.
R2
Z
cos ϕZ =
R
2
V 2 = GVef
f.
+ X 2 ef f.
(4.7.89)
Figura 4.7.22: rappresentazione nel piano complesso
ϕY = −ϕZ ,
ammettenza Ẏ :
Come mostrato in Figura 4.7.22 si ha che
può esprimere pure in termini di
pertanto la potenza media si
P = Vef f. Ief f. cos ϕY
Tenedo conto che
Ief f. = Y Vef f
(4.7.90)
è chiaro che da (4.7.90) seguono le relazioni:
2
2
P = Vef
f. Y cos ϕY = Vef f. G
(4.7.91)
L'ultima uguaglianza in (4.7.91) si capisce osservando Figura 4.7.22.
Si possono avere altre forme equivalenti se si decide di combinare (4.7.91) con
Ief f.
Y :
197
Vef f. =
4 Reti elettriche
P = Vef f. Ief f. cos ϕY =
=
2
Ief
f. Y
Y
Y
cos ϕY =
2
Ief
f.
Y
2
G=
2
Ief
f.
Y
G2
cos ϕY =
G
2
I 2 = R Ief
f.
+ B 2 ef f.
(4.7.92)
4.7.7.2 La potenza reattiva Q
Per analogia matematica si va a denire la
Q=
potenza reattiva Q :
VI
sin (ϕV − ϕI )
2
La potenza reattiva, così come la potenza attiva, si misura in watt.
(4.7.93)
In realtà però,
nell'uso tecnico la potenza reattiva si misura in VAR (Volt-Ampère-Reattivo), proprio
per evidenziare il fatto che la potenza reattiva Q è una potenza ttizia.
La (4.7.93) si può esprimere pure utilizzando i valori ecaci ed è di carattere generale:
Q = Vef f Ief f sin (ϕV − ϕI )
(4.7.94)
Essa rimane valida anche per i bipoli compositi contenenti i generatori ideali.
Per i bipoli compositi passivi la potenze reattiva si scrive in una delle formi equivalenti:
2
Q = Vef f. Ief f. sin ϕZ = Z Ief f Ief f. sin ϕZ = X Ief
f. =
=−
B2
B
I2
+ G2 ef f.
Q = Vef f. Ief f. sin ϕZ = Vef f.
=
4.7.7.3 La potenza complesa
R2
2
Vef
Vef f.
Z
f.
sin ϕZ
=X
=
Z
Z
Z2
X
2
V 2 = −B Vef
f.
+ X 2 ef f.
(4.7.96)
Ȧ
Avendo denito la potenza attiva P e la potenza reattiva Q, sipuò denire la
complessa Ȧ:
Ȧ = P + jQ
La potenza complessa si misura in VA (Volt-Ampere).
Sostituendo (4.7.74) e (4.7.93) in (4.7.97) si ottiene:
Ȧ = P + jQ =
(4.7.95)
VI
VI
cos (ϕV − ϕI ) + j
sin (ϕV − ϕI ) =
2
2
198
potenza
(4.7.97)
4 Reti elettriche
=
VI
V I j(ϕV −ϕI )
{cos (ϕV − ϕI ) + j sin (ϕV − ϕI )} =
e
=
2
2
V
I
√ ejϕV √ ej(−ϕI ) = V̇ I˙∗
2
2
ovvero:
Ȧ = V̇ I˙∗
(4.7.98)
Ovviamente le relazioni in (4.7.97) e (4.7.98) valgono nel caso generale di bipolo
composito contenente generatori ideali.
4.7.7.3.1 La potenza apparente A.
Il modulo della potenza complessa si chiama
potenza apparente A:
A=
p
P 2 + Q2 = V I
(4.7.99)
La potenza apparente si misura come quella complessa, ovvero in VA.
4.7.7.4 Rifasamento
In Figura 4.7.23 viene mostrato un problema di utenza domenstica.
L'Enel fornisce
all'utente la tensione
√
vg (t) = 220 2 cos (100πt)
Il fasore della tensione di rete è ovviamete:
V̇g = 220∠0
Figura 4.7.23: problema di utenza domestica
Il dispositivo che dà una misura dell'energia fornita dall'Enel all'utente domestico è il
contatore ; tale dispositivo non fa altro che integrare la potenza media.
A monte di un contatore, in un impianto domestico, vi è sempre un interruttore
bipolare, il cui compito è di aprire e chiudere contemporaneamente il neutro e la fase.
Supponiamo di accendere una stufa elettrica (impedenza puramente resistiva).
R0 = 220π Ω
è l'impedenza della stufa elettrica, la corrente da essa assorbita sarà:
199
Se
4 Reti elettriche
Vg
V̇g
1
=
∠0 = ' 0, 32∠0 A
I˙0 =
R0
R0
π
Tale corrente è in fase con la tensione di alimentazione
V̇g ,
come si può osservare in
Figura 4.7.24:
Figura 4.7.24: rappresentazione graca
Pertanto la potenza media assorbita è:
P0 = Vg I0 cos 0 = 70, 03 W
Accendendo pure una lavatrice,di impedenza
Ż1 = R1 + jωL1 = 100π + j100π Ω,
su
di essa passerà la corrente:
V̇g
Vg ∠0
Vg
I˙1 =
=
∠ − ϕZ1 =
=
Z1
Z1 ∠ϕZ1
Z1
√
100π
2
π
π
220
∠ − arctan
=
∠ − ' 0, 45∠ − A
=q
100π
π
4
4
(100π)2 + (100π)2
Secondo quest'ultima relazione è evidente che la corrente
tensione di rete
V̇g
I˙1 è
in ritardo rispetto alla
di un angolo di 45° come mostrato in Figura 4.7.25:
La corrente totale assorbita dai dispositivi accesi dall'utente è:
√
1
2
π
0
˙
I = I0 + I1 = ∠0 +
∠− =
π
π
4
√ n
π
π o
1
2
= {cos 0 + j sin 0} +
cos −
+ j sin −
=
π
π
4
4
√ (√
√ )
1
2
2
2
1
1
1
−j
= + −j =
= +
π
π
2
2
π π
π
200
4 Reti elettriche
Figura 4.7.25:
√
2
5
1
1
= +j −
=
' 0, 71∠ − 0, 46 A
∠ − arctan
π
π
π
2
Secondo quest'ultima relazione è evidente che la corrente
tensione di rete
V̇g
0
I˙1 è
in ritardo rispetto alla
di un angolo di circa 26°,56 come mostrato in Figura 4.7.25.
La potenza media assorbita dai due utilizzatori accesi è dunque:
√
0
0
P = Vg I cos 0 − ϕI 0 = 220
5
cos (arctan (1/2)) =
5
√
√
5
5
440
220
2
=
' 140, 06 W
5
π
π
Si immagini inne che sia stata accesa una lampadina di impedenza
j100π Ω.
Ż2 = jωL2 =
Su di essa passerà la corrente:
V̇g
Vg ∠0
Vg
I˙2 =
=
=
∠ − ϕZ2 =
Z2
Z2 ∠ϕZ2
Z2
220
100π
11 1
π
π
=
∠ − ' 0, 70∠ − A
=q
∠ − arctan
0
5 π
2
2
(0)2 + (100π)2
La corrente totale assorbita dai dispositivi accesi dall'utente è:
0
I˙ = I˙0 + I˙1 + I˙2 = I˙ + I˙2 =
√
5
1
11 1
π
=
∠ − arctan
+
∠− =
π
2
5 π
2
√
=
π
π o
5
11 n
{cos (− arctan (1/2)) + j sin (− arctan (1/2))} +
cos −
+ j sin −
=
π
5π
2
2
201
4 Reti elettriche
√ ( √
√ )
11
5 2 5
5
+
=
−j
{0 − j} =
π
5
5
5π
1
11
2
16
2
= +j −
=
= −j −j
π
π
5π
π
5π
√
2 89
∠ arctan (5/8) − π/2 ' 1, 20∠ − 1, 01 A
5π
La potenza media assorbita dai tre utilizzatori accesi è dunque:
√
2 89
cos (arctan (5/8) − π/2) =
P = Vg I cos (0 − ϕI ) = 220
5π
√
√
2 89 5 89
440
= 220
=
' 140, 06 W
5π
89
π
Figura 4.7.26:
Stiamo trovando che a fronte di una maggiore corrente utilizzata, la potenza media
assorbita dagli utilizzatori è sempre la stessa.
L'aumento di corrente è a discapito della linea dell'Enel. La lampadina ad escandescenza non produce un aumento della potenza media, infatti confrontanto
delle correnti rispetto a
V̇g ,
rimane sempre la stessa,
0
I1 cos −ϕI 0
I˙
e
0
I˙
le proiezioni
.
In altri termini accendendo o spegnendo la lampadina, la potenza media assorbita è
sempre la stessa; la lampadina accesa però produce un aumento della potenza reattiva
che èdannosa per la rete elettrica dell' Enel.
Mentre l'utente introduce utilizatori di tipo induttivo, l' Enel gradirebbe che utilizzasse
dispositivi resistivi di modo che la corrente assorbita risulti in fase con la tensione
V̇g .
E' possibile far diminuire la potenza reattiva inserendo un capacitore; il fenomeno
descritto si chiama rifasamento.
202
4 Reti elettriche
Ai grandi utenti (industrie), l'Enel ore contratti diversi rispetto agli utenti domestici.
Le industrie utilizzano elevate correnti per far funzionare le loro macchine, facendo aumentare la potenza reattiva. In questi casi, l'Enel, oltre a fare pagare la potenza attiva
P, si fa pagare anche la potenza reattiva Q; di contro il grande utente per far fronte
a questo problema, di tasca sua, costruisce un impianto di rifasamento cosi da pagare
bollette meno salate.
203
5 Circuiti del secondo ordine RLC a
regime costante
Esistono circuiti elettrici molto semplici che si possono risolvere in modo veloce utilizzando semplicemente le L.K.
Di seguito vengono proposti 2 esempi.
5.1 Esempio 1. Circuito RLC serie
Dato il circuito elettrico mostrato in Figura 5.1.1 si vogliono determinare le espressioni
analitiche della corrente che attraversa l'induttore e della tensione ai capi del capacitore
assumendo:
R = 1Ω L = 1H C = 1F
vg (t) = Vg = 1V
vc (0− ) = 0V
iL (0− ) = 0A
Figura 5.1.1: Circuito RLC serie
Per t>0 l'interruttore T è chiuso e si può scrivere la LKT per l'anello I mostrato in
Figura 5.1.1:
− vg (t) + Ric (t) + vL (t) + vc (t) = 0
(5.1.1)
Tenendo conto che:
ic (t) = C
d
vc (t) = iL (t)
dt
204
(5.1.2)
5 Circuiti del secondo ordine RLC a regime costante
vL (t) = L
d
iL (t)
dt
(5.1.3)
la (5.1.1) si scrive:
−vg (t) + RC
d
d
vc (t) + L iL (t) + vc (t) = 0
dt
dt
ovvero:
−vg (t) + RC
d
d2
vc (t) + LC 2 vc (t) + vc (t) = 0
dt
dt
Riordinando i termini quest'ultima espressione si scrive:
LC
d2
d
vc (t) + RC vc (t) + vc (t) = vg (t)
dt2
dt
Per integrare la (5.1.4) occorrono le condizioni iniziali:
vc (0+ )
(5.1.4)
e
d
dt vc (t) |t=0+ .
La prima si ricava dai dati del problema visto che la tensione ai capi del capacitore è
una funzione continua del tempo:
vc 0+ = vc 0− = 0V
(5.1.5)
Per ricavare la seconda basta porre t=0 in (5.1.2) e sfruttare il fatto che la corrente
che attraversa l'induttore è una funzione continua del tempo:
d
1
1
vc (t) |t=0+ = iL 0+ = iL 0− = 0
d
C
C
(5.1.6)
Si tratta dunque di risolvere il seguente problema di Cauchy:

d
d2

LC dt2 vc (t) + RC dt vc (t) + vc (t) = vg (t)
vc (0+ ) = 0

d
dt vc (t) |t=0+ = 0
(5.1.7)
che sostituendo i valori numerici diventa:
 2
d
d

 dt2 vc (t) + dt vc (t) + vc (t) = Vg
vc (0+ ) = 0

d
dt vc (t) |t=0+ = 0
Risoluzione del problema di Cauchy
(5.1.8.1)
(5.1.8.2)
(5.1.8.3)
(5.1.8)
Determiniamo l'integrale generale della (5.1.8.1)
L'integrale generale della (5.1.8.1) è la somma tra l'integrale generale dell'omogenea
associata alla (5.1.8.1) e l'integrale particolare della (5.1.8.1):
vc (t) = vcomog. (t) + vcpart. (t)
205
(5.1.9)
5 Circuiti del secondo ordine RLC a regime costante
Omogenea associata
d 2
d
vc (t) + vc (t) + vc (t) = 0
2
dt
dt
Equazione caratteristica
λ2 + λ + 1 = 0
λ=
−1 ±
p
1 − 4 (1) (1)
=
2
(
√
− 12 + i 23
− 12 − i
√
(5.1.10)
3
2
Integrale generale omogenea associata
√
vcomog. (t) = k e
Ricerca dell'integrale particolare
Vg ,
− 2t
cos
3
t+ϕ
2
!
(5.1.11)
Visto che il termine noto della (5.1.8.1) è la costante
l'integrale particolare va ricercato tra le costanti.
Posto
vc (t) = vcpart. (t) = cost.
, la (5.1.8.1) si scrive:
0 + +0 + vcpart. (t) = Vg
da cui si ricava:
vcpart. (t) = Vg = 1V
(5.1.12)
Sostituendo (5.1.11) e (5.1.12) in (5.1.9) si ricava l'integrale generale della (5.1.8.1):
√
vc (t) = k e
− 2t
cos
!
3
t+ϕ +1
2
(5.1.13)
Derivando rispetto al tempo la (5.1.13) si ricava:
√
!
√
3
3 −t
t+ϕ −k
e 2 sin
2
2
t
d
k
vc (t) = − e− 2 cos
dt
2
Per determinare le costante
k
e
ϕ
√
3
t+ϕ
2
!
(5.1.14)
si utilizzano la condizione iniziale data in (5.1.8.2)
e (5.1.8.3); utilizzando (5.1.8.2) la (5.1.13) fornisce
k cos ϕ + 1 = 0
(5.1.15)
Utilizzando (5.1.8.3) la (5.1.14) fornisce:
ovvero:
√ k
k
cos ϕ + 3 sin ϕ = 0
2
2
√
k cos ϕ + 3k sin ϕ = 0
206
(5.1.16)
5 Circuiti del secondo ordine RLC a regime costante
Risolvendo il sistema costituito dalle equazioni (5.1.15) e (5.1.16)
(
k cos ϕ − 1 = 0
√
k cos ϕ + 3k sin ϕ = 0
si determinano le costanti
k
e
(5.1.17)
ϕ:
(
(
k cos ϕ = 1
k cos ϕ = 1
√
√
=⇒
=⇒
k cos ϕ + 3k sin ϕ = 0
k sin ϕ = − 33


√ √
ϕ = arctan − 3 = − π
tan ϕ = − 3
3
6
3 √ 2 =⇒
q
=⇒
√
k = 4 = √2 = 2 3
k 2 = 1 + − 3
3
3
3
3
(5.1.18)
Sostituendo i valori (5.1.18) in (5.1.13) si determina l'espressione analitica della tensione ai capi del capacitore:
2√ − t
vc (t) =
3 e 2 cos
3
√
3
π
t−
2
6
!
+1
(5.1.19)
Sostituendo inne (5.1.19) in (5.1.2) si determina pure l'espressione analitica della
corrente che attraversa l'induttore:
√
d
3 −t
e 2 cos
iL (t) = C vc (t) = −
dt
3
√
π
3
t−
2
6
√
!
−e
− 2t
sin
π
3
t−
2
6
!
(5.1.20)
5.2 Esempio 2. Circuito RLC parallelo
Dato il circuito elettrico mostrato in Figura 5.1.1 si vogliono determinare le espressioni
analitiche della corrente che attraversa l'induttore e della tensione ai capi del capacitore
assumendo:
R = 1Ω L = 1H C = 1F
vg (t) = Vg = 1V
vc (0− ) = 0V
iL (0− ) = 0A
Per t>0 l'interruttore T è chiuso e si può scrivere la LKT per l'anello I:
vg (t) − vL (t) − Rig (t) = 0
(5.2.1)
ig (t) = iC (t) + iL (t)
(5.2.2)
e la LKI al nodo A:
Sostituendo (5.2.2) in (5.2.1) si ottiene:
vg (t) − vL (t) − RiC (t) − RiL (t) = 0
207
(5.2.3)
5 Circuiti del secondo ordine RLC a regime costante
Figura 5.2.1: Circuito RLC parallelo
Tenendo conto che:
ic (t) = C
d
d
vC (t) = C vL (t)
dt
dt
(5.2.4)
la (5.2.4) si scrive:
vg (t) − vL (t) − RC
d
vL (t) − RiL (t) = 0
dt
(5.2.5)
Inne tenedo conto che:
vL (t) = L
d
iL (t)
dt
(5.2.6)
si ottiene l'equazione dierenziale di ordine minimo nella variabile di stato
d2
1 d
1
1
iL (t) +
iL (t) +
iL (t) =
vg (t)
dt2
RC dt
LC
RLC
iL (t):
(5.2.7)
Le condizioni iniziali sono:
iL 0+ = iL 0− = 0A
1
1
d
iL (t) t=0+ = vL 0+ = vC 0+ = 0
dt
L
L
Si tratta di risolvere quindi il seguente Problema di Cauchy:
 2
d
d

 dt2 iL (t) + dt iL (t) + iL (t) = Vg
iL (0+ ) = 0

d
dt iL (t) |t=0+ = 0
208
(5.2.8.1)
(5.2.8.2)
(5.2.8.3)
(5.2.8)
5 Circuiti del secondo ordine RLC a regime costante
dove la (5.2.8.1) è stata ricavata dalla (5.2.7) sostituendo i valori numerici.
La soluzione del problema di Cauchy (5.2.8) è
√
2√ − t
iL (t) =
3 e 2 cos
3
π
3
t−
2
6
!
+1
(5.2.9)
Sostituendo inne (5.2.9) in (5.2.6) si ricava l'espressione analitica della tensione ai
capi dell'induttore nonchè la tensione ai capi del capacitore:
√
d
3 −t
vc (t) = vL (t) = L iL (t) = −
e 2 cos
dt
3
√
209
3
π
t−
2
6
√
!
−e
− 2t
sin
3
π
t−
2
6
!
(5.2.10)
6 Circuiti del secondo ordine RLC a
regime sinusoidale
Viene analizzate nel seguito la prima rete vista nel capitolo precedente supponendo che
il generatore di tensione sia sinusoidale.
6.1 Esempio. Circuito RLC serie
Dato il circuito elettrico mostrato in Figura 6.1.1 si vogliono determinare le espressioni
analitiche della corrente che attraversa l'induttore e della tensione ai capi del capacitore
assumendo:
R = 1Ω L = 1H C = 1F
vg (t) = Vg = 1V
vc (0− ) = 0V
iL (0− ) = 0A
nell'ipotesi di regime sinusoidale:
π
vg (t) = 3 cos 5t +
4
Figura 6.1.1: Circuito RLC serie
Sappiamo già che la tensione ai capi del capacitore si determina risolvendo il seguente
problema di Cauchy:
 2
d
d

 dt2 vc (t) + dt vc (t) + vc (t) = Vg
vc (0+ ) = 0

d
dt vc (t) |t=0+ = 0
210
(6.1.1.1)
(6.1.1.2)
(6.1.1.3)
(6.1.1)
6 Circuiti del secondo ordine RLC a regime sinusoidale
Sappiamo pure che l'
integrale generale dell'omogenea associata
√
vcomog. (t) = k e
− 2t
cos
3
t+ϕ
2
è:
!
(6.1.2)
Ora visto che la sorgente per il circuito è un generatore sinusoidale, per determinare
l'integrale particolare occorre fare uso del metodo dei fasori.
Ricerca dell'integrale particolare (metodo dei fasori)
Il fasore della tensione
3 π
V̇g = √ ej 4
2
La pulsazione della tensione
vg (t)
vg (t)
è:
(6.1.3)
è:
ω = 5 rad/s
(6.1.4)
La (6.1.1.1) nel dominio dei fasori si scrive:
(jω)2 V̇c + (jω) V̇c + V̇c = V̇g
da cui si ricava il fasore della tensione ai capi del capacitore:
V̇c =
V̇g
2
(jω) + (jω) + 1
(6.1.5)
Sostituendo (6.1.3) e (6.1.4) in (6.1.5) si ricava:
√
1
2
2 jπ
1
2
1+j
√ e 4 =
√ (1 + j)
V̇c =
=
= 0, 05768 e−j2,1508
2
−24 + j5 2
2
−24 + j5
(j5) + (j5) + 1 2
(6.1.6)
La (6.1.6) nel dominio del tempo restituisce l'integrale particolare:
vcpart. (t) = Re
n√
o
o
n
2 · 0.05768 e−j2,1508 ej5t = Re 0, 0816 ej(5t−2,1508) =
= 0, 0816 Re {cos (5t − 2, 1508) + j sin (5t − 2, 1508)} = 0, 0816 cos (5t − 2, 1508)
(6.1.7)
Sommando (6.1.2) e (6.1.7) si ricava l'integrale generale della (6.1.1.1):
√
vc (t) = k e
− 2t
cos
!
3
t + ϕ + 0, 0816 cos (5t − 2, 1508)
2
Derivando rispetto al tempo la (5.1.13) si ricava:
211
(6.1.8)
6 Circuiti del secondo ordine RLC a regime sinusoidale
t
d
k
vc (t) = − e− 2 cos
dt
2
√
!
√
3
3 −t
t + ϕ −k
e 2 sin
2
2
√
!
3
t + ϕ − 0.4079 sin (5t − 3, 1508)
2
(6.1.9)
Per determinare le costante
k
e
ϕ
si utilizzano la condizione iniziale data in (6.1.1.2)
e (6.1.1.3); utilizzando (6.1.1.2) la (6.1.8) fornisce:
k cos ϕ + 0, 0447 = 0
(6.1.10)
Utilizzando (6.1.1.3) la (6.1.9) fornisce:
−
√ k
k
cos ϕ − 3 sin ϕ − 0, 0038 = 0
2
2
ovvero:
k cos ϕ +
√
3k sin ϕ + 0, 0076 = 0
(6.1.11)
Risolvendo il sistema costituito dalle equazioni (6.1.10) e (6.1.11)
(
k cos ϕ + 0, 0447 = 0
√
k cos ϕ + 3k sin ϕ + 0, 0076 = 0
si determinano le costanti
k
e
ϕ:
(
k cos ϕ = −0, 0447
√
k cos ϕ + 3k sin ϕ = −0, 0076
=⇒

tan ϕ = −0, 4792
k 2 = (−0, 0447)2 +
(6.1.12)
0,0371
√
3
2
(
k cos ϕ = −0, 0447
=⇒
√
k sin ϕ = 0,0371
3
=⇒
(
ϕ = arctan (−0, 4792) = −0, 45
=⇒
√
k = 0, 002457 = 0, 05
(6.1.13)
Sostituendo i valori (6.1.13) in (6.1.8) si determina l'espressione analitica della tensione
ai capi del capacitore:
√
vc (t) = 0, 05 e
− 2t
cos
!
3
t − 0, 45 + 0, 0816 cos (5t − 2, 1508)
2
212
(6.1.14)
7 Metodi di analisi delle reti elettriche
Scrivere le LK non è l'unico modo che consente di ottenere il sistema risolvente nelle
variabili di stato per un circuito elettrico.
Risolvere una rete elettrica mediante la stesura delle LK è il modo più lento che possa
esistere.
L'obiettivo principale del circuitista è quello di scrivere nella maniera più rapida possibile il sistema risolvente nelle variabili di stato e per far ciò si avvale dei
delle reti elettriche.
metodi di analisi
I metodi di analisi delle reti elettriche sono:
ˆ
il metodo dei potenziali ai nodi
ˆ
il metodo degli insiemi di taglio
ˆ
il metodo delle correnti di anello
ˆ
il metodo delle correnti di maglia
ˆ
il metodo delle equazioni di stato
Il metodo degli insiemi di taglio è una generalizzazione del metodo dei potenziali ai nodi,
mentre il metodo delle correnti di maglia è una generalizzazione del metodo delle correnti
di anello.
Tutti i metodi di analisi si basano sulla riscrittura delle LK attraverso delle incognite
ausiliarie, in modo da rendere automaticamente soddisfatte le LKT oppure le LKC.
In conseguenza di ciò si riesce a scrivere un sistema risolvente nella sole incognite
ausiliarie. Note queste ultime si deducono poi tutte le altreincognite di rete.
Se si fa attenzione, il discorso è del tutto simile a quello impostato per risolvere il
prblema di campo di corrente statico. In quel caso si introduceva come variabile ausiliaria,
~ in modo ra rendere
~e = −∇v
~
automaticamente soddisfatta l'equazione ∇ × ~
e = 0. In conseguenza di ciò si riusciva
a scrivere una sola equazione nella variabile v . Ricavata da quest'ultima equazione, il
potenziale scalare elettricov , si riuscivano a determinare poi i campi ~
e e ~j risolvendo così
il potenziale scalare elettrico
v,
mediante la nota formula
completamente il problema.
Vedremo con degli esempi che applicare il metodo di analisi vuol dire non preoccuparsi
più di andare a scrivere per ciascun la tensione e la corrente.
213
7 Metodi di analisi delle reti elettriche
7.1 Metodo dei potenziali ai nodi
7.1.1 Il concetto di grafo
Bisogna innanzitutto introdurre il concetto di
grafo.
Da un punto di vista matematico, il grafo è una terna costituita da un insieme di nodi
N,
un insieme di lati
L,
e da una legge
ordinata di nodi dell'insieme
N
f
che fa corrispondere a ciascun lato una coppia
in cui il primo nodo è quello di partenza e il secondo
nodo è quello di arrivo (in conseguenza di ciò i lati si dicono orientati):
G = {N , L, f : L → N × N }
(7.1.1)
Un grafo può essere rappresentato in tre diversi modi: disegno, tabella, matrice.
Se indichiamo con N la cardinalità dei nodi dell'insieme
dell'insieme
L,
N
e con L la cardinalità
quello rappresentato in Figura 7.1.1 è un grafo formato da N=3 nodi e
L=5 lati.
Figura 7.1.1: grafo rappresentato mediante un disegno
La legge
f : L → N ×N
per esempio permette di dire che al lato 1 corrisponde la
coppia ordinata di nodi (2,1) essendo 2 il nodo di partenza e 1 il nodo di arrivo; al lato
3 corrisponde la coppia ordinata (3,1) e così via.
Figura 7.1.2: grafo rappresentato mediante una tabella
214
7 Metodi di analisi delle reti elettriche
Il grafo di Figura 4.7.1 può essere rappresentato anche attraverso una tabella come
indicato in Figura 7.1.2.
7.1.1.1 La matrice di incidenza totale nodi-lati
Un altro modo per rappresentare il grafo è la

a11
 a21



[Atot. ] = 




matrice di incidenza totale [Atot. ]:
a12
a22
aN 1 aN 2
... ... a1L
... ... a2L
.
.
.
.
... ... aN L










(7.1.2)
La matrice di incidenza totale ha un numero di righe pari al numero di nodi e un
N × L.
numero di colonne pari al numero di lati; quindi si tratta di una matrice
indichiamo con
i-esimo e
j
aij
il generico elemento della matrice di incidenza totale,
i
Se
sarà il nodo
sarà il lato j-esimo.
Il generico elemento
aij
della matrice di incidenza è costruito mediante la regola
mostrata in Figura 7.1.3:
Figura 7.1.3: regola per la costruzione della matrice
Atot.
Quindi la matrice di incidenza totale del grafo mostrato in Figura 7.1.1 è:


−1 1 −1 0
0
0
0
1
1 
[Atot. ] =  1
0 −1 1 −1 −1
Osserviamo che la matrice di incidenza totale è per costruzione tale che ciascuna
colonna presenta un 1, un -1 e tutti gli altri elementi 0.
In questo moto risulta che la somma degli elementi per ciascuna colonna è 0. Ciò vuol
dire che le righe della matrice di incidenza totale sono linearmente dipendenti.
215
7 Metodi di analisi delle reti elettriche
La matrice di incidenza totale può essere utilizzata per scrivere le LKC, infatti si ha
che:
[Atot. ]
[i]
[0]
=
N ×L L×1
(7.1.3)
N ×1
Per il caso specico del grafo mostrato in Figura 7.1.1 si ha:




−1 1 −1 0
0


 1

0
0
1
1


0 −1 1 −1 −1
i1
i2
i3
i4
i5

 

0

=  0 ⇒


0
3×1
3×5
5×1


LKC1
−i1 + i2 − i3 = 0
⇒ i1 + i4 + i5 = 0
LKC2


−i2 + i3 − i4 − i5 = 0 LKC3
Le LKC trovate valgono per il grafo
mostrato in Figura 7.1.1 se si decide di
orientare le correnti di lato come sono
orientati i lati del grafo (Figura 7.1.4).
7.1.1.1.1 matrice di incidenza nodi-lati
Con
il
sistema
in
(7.1.3)
si
ottengono
N LKC. Come sappiamo nella risoluzioni
delle reti elettriche mediante le LK si
scrivono N-1 leggi di Kirchoo delle cor-
Figura 7.1.4: grafo
renti. Quindi dal sistema in (7.1.3) occorre
scartare un'equazione.
D'altro canto questo fatto viene sugger-
ito dalla matrice di incidenza totale che presenta N righe linearmente dipendenti. Si noti
che eliminando una riga dalla matrice di incidenza totale, non si ha perdita di informazione, infatti la riga eliminata si può sempre ottenere come combinazione lineare delle
altre righe.
Eliminando la terza riga dalla matrice di incidenza totale relativa al grafo mostrato in
Figura 7.1.1 si ottiene la cosiddetta
nodi-lati:
[A] =
matrice di incidenza ridotta [A] o matrice di incidenza
−1 1 −1 0
0
0 −1 1 −1 −1
216
7 Metodi di analisi delle reti elettriche
Come detto prima, non c'è perdita di informazione, infatti la riga eliminata si può
ripristinare se teniasmo conto che per ciascuna colonna della matrice di incidenza totale
la somma degli elementi deve fare 0. Nell'esempio la riga eliminata è evidentemente:
0 −1 1 −1 −1
Uguagliando a zero il prodotto tra la matrice di incidenza nodi-lati e il vettore colonna
delle correnti di lato si ricavano N-1 LKC linearmente indipendenti:
[A. ]
[i]
[0]
=
(N − 1) × L L × 1
(7.1.4)
(N − 1) × 1
7.1.2 Descrizione del metodo
Sulla matrice di incidenza nodi-lati si basa il
metodo dei potenziali ai nodi.
Supponiamo di avere una rete elettrica formata da N nodi ed L lati; si avranno allora
2L incognite: le tensioni e le correnti di lato:
vk , ik
k = 1, 2, ...., L
A questo punto si deniscono altre incognite, ossia i
e fanno tutti riferimento al
nodo di riferimento
eh
(7.1.5)
potenziali di nodo.
Essi sono N-1
posto al potenziale nullo (0 V):
h = 1, 2, ...., N − 1
(7.1.6)
A livello circuitale, il nodo di riferimento (0 V), si realizza portando a massa il nodo
che fa riferimento alla riga eliminata dalla matrice di incidenza totale.
Visto che per il la matrice di incidenza totale del grafo di Figura 7.1.1 è stata eliminata
la terza riga, va posto a massa il nodo 3 come indicato in Figura 7.1.4.
Figura 7.1.5: grafo con nodo 3 posto a 0 V
Il problema così posta risulta costituito da 2L+N-1 incognite e per tanto servono
2L+N-1 equazioni. N-1 equazioni sono le LKC date in (7.1.4). Serve pertanto scrivere
altre 2L equazioni; di queste 2L equazioni, L sono le cosiddette
delle tensioni (
LKT ∗
)
pseudo leggi di Kirchho
che esprimono le tensioni di lato in termini dei potenziali ai nodi.
Facendo riferminto a Figura 7.1.5 si ha:
217
7 Metodi di analisi delle reti elettriche


v1





v2
v3



v4




v5
Le
LKT ∗
= e2 − e1
= e1 − 0
= 0 − e1
= e2 − 0
= e2 − 0
LKT ∗ 1
LKT ∗ 2
LKT ∗ 3
LKT ∗ 4
LKT ∗ 5
si possono pure esprimere in termini della matrice di incidenza nodi-lati,
cioè vale la relazione:
[A. ]T
[e]
[v]
=
L × (N − 1) (N − 1) × 1
Ovviamente le
(7.1.7)
L×1
LKT ∗ sono semanticamente delle LKT ma non lo sono sintatticamente.
Attraverso di esse le LKT sono automaticamente soddisfatte e questo fatto lo si può
provare immediatamente: dal grafo di Figura 7.1.5 si consideri per esempio la seguente
LKT:
v1 + v2 − v4 = 0
Tale equazione è automaticamente soddisfatta dalle
LKT ∗ ,
infatti si ha:
e2 − e1 + e1 − 0 − (e2 − 0) = 0
Le altre L equazioni che si possono scrivere per risolvere il problema avente 2L+N-1
incognite sono le leggi di lato (LL) alla Norton.
Proposizione. Quando si applica il metodo dei potenziali ai nodi bisogna ipotizzare che
ciascun lato sia alla Norton.
Come mostrato in Figura 7.1.6 ciascun lato di una rete elettrica può presentarsi alla
Thevenin o alla Norton. Si ossrvi che per i lati mostrati in Figura 7.1.6 è stata utilizzata
la convenzione dell'utilizzatore.
Per il lato Thevenin vale la relazione:
vk (t) = vgk (t) + Rk igk (t)
(7.1.8)
Per il lato Norton vale la relazione:
ik (t) = −igk (t) + Gk vk (t)
218
(7.1.9)
7 Metodi di analisi delle reti elettriche
Figura 7.1.6: lato Thevenin; lato Norton
7.1.2.1 Trasformazione Thevenin-Norton
Esistono delle formule di passaggio che permettono di ottenere un lato Thevenin da
un lato Norton e viceversa. Anchè si possono ricavare tali formule è occorre imporre
l'equivalenza tra (7.1.8) e (7.1.9).
Pertanto dall (7.1.9) si ricava
vk (t):
vk (t) = Rk igk (t) + Rk igk (t)
(7.1.10)
e quindi uguagliando (7.1.8) e (7.1.10):
vgk (t) + Rk igk (t) = Rk igk (t) + Rk igk (t)
si ottiene la formula di passaggio
N orton → T hevenin:
vgk (t) = Rk igk (t)
e la formula di passaggio
(7.1.11)
T hevenin → N orton:
igk (t) =
1
vg (t)
Rk k
(7.1.12)
Si osservi che le formule di passaggio hanno senso solo se:
Rk 6= 0
Per una rete elettrica aventi L lati di tipo Norton valgono le relazioni:
219
(7.1.13)
7 Metodi di analisi delle reti elettriche


i1 = G1 v1 − ig1





i2 = G2 v2 − ig2
.



.




iL = GL vl − igL
che si possono compattare in forma matriciale come segue:
[i] = [G] [v] − [ig ]
L×1L×LL×1L×1
(7.1.14)
dove




[G] = 



è la
G1 0 . . . . 0
0 G2 0 . . . 0
.
0 . . . .
.
.
. . . . .
.
.
. . . . . 0
0
0 . . . 0 GL
matrice delle conduttanze di lato








(7.1.15)
(nel caso più generale matrice delle ammettenze
di lato).
L'insieme delle equazioni date in (7.1.4), (7.1.7) e (7.1.14) costituisce il sistema risolvente di 2L+N-1 equazioni in 2L+N-1 incognite:


(7.1.16.1)
[A] [i] = [0]
T
[v] = [A] [e]
(7.1.16.2)


[i] = [G] [v] − [ig ] (7.1.16.3)
N − 1 LKC
L LKT ∗
L LL
(7.1.16)
Moltiplicando a sinistra tutti i termini della (7.1.16.3) si ottiene:
[A] [i] = [A] [G] [v] − [A] [ig ]
(7.1.17)
Per la (7.1.16.1), la (7.1.17) si scrive:
[A] [G] [v] − [A] [ig ] = [0]
(7.1.18)
Per la (7.1.16.2) la (7.1.18) si scrive:
[A] [G] [A]T [e] − [A] [ig ] = [0]
ovvero:
[A] [G] [A]T [e] = [A] [ig ]
Visto che
[A], [G]
e
[ig ]
(7.1.19)
sono quantità note, è evidente che (7.1.19) è un sistema
risolvente nelle sole N-1 incognite
eh .
220
7 Metodi di analisi delle reti elettriche
Denendo la
matrice delle conduttanze di nodi :
[GN ] = [A] [G] [A]T
e il
(7.1.20)
vettore colonna dei generatori di nodi :
[igN ] = [A] [ig ]
(7.1.21)
la (7.1.19) si può scrivere ancora in forma più compatta, come segue:
[GN ] [e] = [igN ]
(7.1.22)
eh , noti i potenziali ai nodi, attraverso
∗
leLKT si trovano le tensioni di lato vk , note le tensioni di lato, attraverso le LL si trovano
Risolvendo (7.1.22) si trovano i potenziali ai nodi
le cprrenti di lato
ik .
Proposizione. Se nella rete elettrica non ci sono generatori pilotati, allora la matrice
delle conduttanze di nodi è simmetrica.
Il metodo proposto sembrerebbe pazzesco, ma in realtà è molto semplice dato che la
matrice delle conduttanze di nodi e il vettore colonna dei generatori di nodi, si possono
scrivere di getto guardando semplicemente il circuito, se nella rete elettrica non ci sono
generatori pilotati.
7.1.2.2 Regole di ispezione visiva
7.1.2.2.1 Matrice delle conduttanze di nodi
[GN ]
I termini che si trovanno sulla
diagonale principale valgono
gii =
X
Li ⊆ L
Gk
(7.1.23)
k∈Li
essendo
Li
l'insieme dei lati che auiscono al nodo
i
indipendentemente dal verso
associato al lato l, mentre i termini che stanno fuori dalla diagonale principale, valgono:
gij = gji = −
X
Li ∩ L j ⊆ L
Gk
(7.1.24)
k∈Li ∩Lj
essendo
Li ∩ Lj
l'insieme di tutti i lati che collegano direttamente il nodo
7.1.2.2.2 Vettore colonna dei generatori di nodi
[igN ]
i
al nodo
j.
I termini che si trovanno sulla
diagonale principale valgono
igNi =
X
±igk
Li ⊆ L
(7.1.25)
k∈Li
Vale il segno + se la corrente del generatore
la corrente del generatore
i gk
esce dal nodo
igk entra
nel nodo
i,
vale il segno - se
i.
Il metodo dei potenziali ai nodi vale nel dominio del tempo, nel dominio dei fasori, nel
dominio di Laplace e anche nel dominio di Fourier.
221
7 Metodi di analisi delle reti elettriche
7.1.2.2.3 Consiglio
Se la rete elettrica presenta induttori mutuamente accoppiati è
SCONSIGLIATO il metodo dei potenziali ai nodi (vedremo che conviene utilizzare il
metodo delle correnti di anello o di maglia).
7.1.2.3 Esempio1
Consideriamo la rete elettrica nel dominio dei fasori mostrata in Figura 7.1.7:
Figura 7.1.7: rete elettrica nel dominio dei fasori
Quando si applica il metodo dei potenziali ai nodi occorre che tutti i lati della rete siano
alla Norton. Con riferimento al circuito mostrato in Figura 7.1.7 si immagina soltanto di
trasformare il lato Thevenin costituito da
V̇g
ed
R1
in lato alla Norton. In questo modo
risulta evidente che i nodi veri del circuito sono tre.
Per applicare il metodo si pone a massa il nodo verso coi auiscono in maggior numero
i lati della rete e si indicano i potenziali di nodo degli altri nodi.
Visto che la rete è inquadrata nel dominio dei fasori è ovvio che i potenziali di nodo
sono dei fasori e la matrice di conduttanze di nodi è in realta la matrice delle ammettenze
dei nodi.
In Figura 7.1.8 viene mostrata la rete avendo denito come nodo di riferimento il nodo
3, e i potenziali di nodo
Ė1
ed
Ė2 .
Applicando le regole di ispezione visiva si ha immediatamente il sistema risolvente:
"
1
R1
+ iωC +
1
− jωL
1
jωL
1
− jωL
1
1
R2 + jωL
#
Ė1
Ė2
""
=
V̇g
R1
##
I˙g
Possiamo immediatamente provare la correttezza del metodo visto che lo abbiamo
applicato alla solita rete che no ad ora abbiamo studiato.
Scrivendo una semplice
LKT ∗
possiamo trovare l'espressione del fasore della tensione
ai capi del capacitore:
V̇c = Ė1 − 0̇ = Ė1
Per determinare il fasore
V̇c
occorre dunque ricavare
temente trovato:
222
Ė1
dal sistema risolvente preceen-
7 Metodi di analisi delle reti elettriche
Figura 7.1.8: rete elettrica nel dominio dei fasori


1
1
1
R1 + jωC+ jωL Ė1− jωL Ė2
− 1 Ė1 + 1 + 1 Ė2 = I˙g
jωL
R2
jωL
=
V̇g
R1

 1 + jω + 1 Ė1 − 1 Ė2 = V̇g
jω
jω
=⇒
1
1
˙
− Ė1 + 1 +
jω
jω Ė2 = Ig
(moltiplicando entrambe le equazioni per
jω )
(
=⇒
1 + jω + (jω)2 Ė1 − Ė2 = jω V̇g
−Ė1 + (1 + jω) Ė2 = jω I˙g
(moltiplicando la prima equazione per
=⇒
(1 + jω))
i
(h
1 + jω + (jω)2 (1 + jω) Ė1 − (1 + jω) Ė2 = jω (1 + jω) V̇g
=⇒
−Ė1 + (1 + jω) Ė2 = jω I˙g
Sommando membro a membro le due equazioni si ottiene:
i
o
h
i
nh
1 + jω + (jω)2 (1 + jω) − 1 Ė1 = jω (1 + jω) V̇g + I˙g =⇒
n
o
h
i
=⇒ (1 + jω)2 + (jω)2 (1 + jω) − 1 Ė1 = jω (1 + jω) V̇g + I˙g =⇒
n
o
h
i
=⇒ 1 + 2 (jω) + (jω)2 + (jω)2 + (jω)3 − 1 Ė1 = jω (1 + jω) V̇g + I˙g =⇒
n
o
h
i
=⇒ 2 (jω) + 2 (jω)2 + (jω)3 Ė1 = jω (1 + jω) V̇g + I˙g =⇒
n
o
=⇒ 2 + 2 (jω) + (jω)2 Ė1 = (1 + jω) V̇g + I˙g
223
=⇒
7 Metodi di analisi delle reti elettriche
Tenendo conto che
V̇c = Ė1
è ovvio che con quest'ultima equazione stiamo ritrovando
(4.7.23) vericando così la correttezza del metodo dei potenziali ai nodi.
7.1.2.4 Teorema di Millman
Il metodo dei potenziali ai nodi per una rete avente solo due nodi è noto con il nome
di Teorema di Millman e conduce alla scrittura di una equazione in una sola incognita,
ossia il potenziale di nodo.
Possiamo vedere un'applicazione molto semplice. Consideriamo la rete elettrica precedente privandola del generatore di corrente
I˙g :
Figura 7.1.9: rete elettrica a due nodi
Si ha immediatamente la formula:
1
1
+ jωC +
R1
R2 + jωL
Ė1 =
V˙g
R1
Sostituendo i valori numerici e riordinando i termini si trova:
h
i
(jω)2 + 2 (jω) + 2 Ė = (1 + jω) V˙g
7.1.2.5 Metodo dei potenziali ai nodi modicato
Cosa succede se la rete presenta un lato contenente solo un generatore ideale di tensione?
E' possibile applicare ugualmente il metodo dei potenziali ai nodi?
LA RISPOSTA è SI!!
Quando ci si trova un circuito in cui un
generatore ideale di tensione sitrova tra
due punti distinti del circuito dovremmo
essere contenti perchè in realtà abbiamo
un'incognita in meno.
224
Figura 7.1.10:
7 Metodi di analisi delle reti elettriche
Quando ci si trova in una situazione del
genere bisogna avere l'umiltà di scrivere
il sistema risolvente in forma scalare (e
quindi non di getto se non si è esperti!!).
Consideriamo la stessa rete elettrica che
per comodità riportiamo in Figura ; nessuno ci obblioga a pensare che la serie costituita dal generatore ideale di tensione
e il resistore
R1
V̇g
è un unico lato. possiamo pensare che essi costituiscano due lati distinti.
Così facendo il generatore
V̇g
collega due distinti punti del circuito (Figura 7.1.10).
Applichiamo il metodo del potenziale ai nodi. Colleghiamo il nodo 4 a massa e chiamiamo
Ė1
il potenziale al nodo 1,
Ė2
il potenziale al nodo 2. Il potenziale al nodo 3 non
è incognito, ma è un valore noto, ovvero
seguente
V̇g .
Quest'ultimo fatto viene fuori scrivendo la
LKT ∗ :
V̇g = Ė3 − 0̇ = Ė3
Si osservi in Figura 7.1.11 che per ciascun nodo è stato costruito un insieme di taglio
supponendo per ciascuno di essi, tutte le correnti uscenti.
Figura 7.1.11:
All'insieme di taglio 1 si ha la LKC:
Ė1 − 0̇
1
jωC
+
Ė1 − Ė2 Ė1 − V̇g
+
=0
jωL
R1
(7.1.26)
All'insieme di taglio 2 si ha la LKC:
Ė2 − Ė1 Ė2 − 0̇
+
− I˙g = 0
jωL
R2
225
(7.1.27)
7 Metodi di analisi delle reti elettriche
Inne all'insieme di taglio 3 si ha la LKC:
V̇g − Ė1
− I˙ = 0
R1
(7.1.28)
Osserviamo che in quest'ultima equazione e soltanto in quest'ultima, compare una
nuova incognita, ossia
I˙.
Quello che si fa è dunque risolvere il sistema costituito dalle equazioni in (7.1.26) e
(7.1.27) determinando così i potenziali ai nodi
la corrente
I˙,
Ė1 ,
e
Ė2 .
Se poi si vuole conoscere pure
si utilizza la (7.1.28).
7.1.2.6 Esempio2
Consideriamo la rete elettrica mostrata in Figura 7.1.12.
Figura 7.1.12:
Ė1 , il potenziale al nodo 1.
∗
Per determinare il potenziale al nodo 2 si scrive la LKT relativa al lato costituito dal
E' stato posto a massa il nodo 3 ed è stato chiamato
generatore ideale di tensione:
V̇g = Ė2 − Ė1
Da quest'ultima relazione si vede immediatamente che il potenziale al nodo 2 è:
Ė2 = V̇g + Ė1
Quindi il potenziale incognito è solo quello presente al nodo 1 perchè quello al nodo 2
si ottiene sommando
V̇g
a
Ė1 .
226
7 Metodi di analisi delle reti elettriche
E' possibile scrivere il sistema risolvente relativo al circuito di Figura 7.1.12 in 2 modi,
indicati nel seguito.
7.1.2.6.1 Modo poco furbo
Si possono scrivere le LKC agli insiemi di taglio 1 e 2 indicati in Figura 7.1.13.
Facendo
così
occorre
introdurre
nuova incognita, ossia la corrente
una
I˙,
che
attraversa il generatore ideale di tensione
V̇g .
Si tratta dunque di risolvere il sistema
nelle incognite


Ė1
R1 +jωL
Ė1 , I˙:
+
Ė1
1
jωC
+ I˙ = 0
=⇒
 Ė1 +V̇g − I˙ − I˙ = 0
g
R2
⇒
Ė1 + V̇g
Ė1
Ė1
+
+
+−I˙ = 0
R1 + jωL 1/jωC
R2
(7.1.29)
Figura 7.1.13:
7.1.2.6.2 Modo furbo
Basta
scrivere
la
LKC
all'insiemi
di
taglio indicato in Figura 7.1.14.
L'insieme di taglio non taglia la corrente
I˙,
quindi si ha facilmente che:
Ė1 + V̇g
Ė1 − 0̇
Ė1
+
+
− I˙ = 0
R1 + jωL 1/jωC
R2
(7.1.30)
esattamente come in (7.1.29).
7.2 Metodo delle correnti di anello
7.2.1 Elementi di teoria dei gra: il concetto di anello
Il metodo delle correnti di anello si applica solo a
reti planari.
Una rete elettrica si dice planare quando può essere disegnata su un foglio di carta
evitando che ci siano sovrapposizioni in punti che non sono nodi.
circuito si dice
non planare.
227
In caso contrario il
7 Metodi di analisi delle reti elettriche
Figura 7.1.14:
In sostanza il circuito planare è un circuito 2D, mentre il circuito non planare è un
circuito 3D: quindi un circuito planare è piùsemplice.
Per un circuito planare possiamo denire il concetto di
anello.
L'anello è un percosrso chiuso all'interno del circuito in modo tale che non ci siano
altri lati del circuito al proprio interno.
Figura 7.2.1: denizione di anello
Proposizione. Se la rete elettrica è planare il numero di anelli è dato da
Na = L − N + 1
(7.2.1)
essendo L il numerodi lati ed N il numero di nodi della rete.
Dimostrazione.
La (7.2.1) si dimostra per induzione.
Consideriamo un circuito formato da un solo
anello come mostrato in Figura 7.2.2; per esso il numero di lati L coincide con il numero
228
7 Metodi di analisi delle reti elettriche
di nodi N. Come chiarisce la Figura 7.2.2, se N=5 è il numero di nodi allora L=5 è il
numero di lati (si noti che in gura i nodi sono stati indicati con i numeri romani).
Il numero di lati coincide con il numero
di nodi per un circuito formato da un solo
anello:
L=N
(7.2.2)
Infatti sostituendo (7.2.2) in (7.2.1), si
ottiene
N1 = 1.
Visto che la dimostrazione viene fatta per induzione occorre supporre che nel
Figura 7.2.2: circuito
caso di una rete elettrica planare complicata risulti:
formato
da
un
solo
anello
Na = L − N + 1
(7.2.3)
e che tale relazione continui a valere anche aggiungendo un anello.
Conosderiamo allora la rete elettrica planare mostrata in Figura 7.2.3 avente
lati ed
N =6
L = 10
nodi:
Figura 7.2.3: rete elettrica planare
Aggiungendo ad essa
0
L =4
lati ed
0
N =3
nodi si ottiene la rete elettrica precedente
con un anello in più:
Figura 7.2.4: rete con un anello in più
La relazione tra i nuovi nodi e i nuovi lati introdotti è:
229
7 Metodi di analisi delle reti elettriche
0
0
L =N +1
(7.2.4)
Il numero di anelli della rete mostrata in Figura 7.2.4 è ovviamente:
0
0
Na+1 = Na + 1 = L + L − N + N + 1
da cui si ricava:
0
0
Na = L + L − N + N
(7.2.5)
Andando a sostituire (7.2.4) in (7.2.5) si ottiene l'ipotesi in (7.2.3).
Proposizione. Il numero di anelli
denizione di nodo.
Na
in una rete elettrica planare non dipende dalla
Figura 7.2.5: arbitrarietà nella denizione di nodo
Come sappiamo c'è una certa arbitrarietà nella denizione di nodo. Se intendiamo per
lato un tratto di circuito contenente un solo dispositivo elementare, per la rete mostrata
in Figura 7.2.5.A si avrà
N =3
ed
L = 5.
In questo caso il numero di anelli vale:
Na = L − N + 1 = 3
Denendo invece pure i lati compositi come mostrato in Figura 7.2.5.B si avrà
ed
L = 6,
ma ancora una volta
anello esterno
Denendo l'
N =4
Na = 3.
come il persorso chiuso all'esterno della rete,
la formula che esprime il numero di anelli di un circuito si scrive:
Na = L − N + 2
(7.2.6)
Come sappiamo il grafo è una rappresentazione topologica orientata della rete elettrica:
ciascun lato del grafo è orientato come la corrente che scorre nel lato della rete. A questo
punto si possono orientare pure gli anelli del grafo, per esempio tutti in senso orario come
mostrato in Figura 7.2.7:
oppure dato che l'orientazione degli anelli è del tutto arbitraria si può pensare di
orientare tutti gli anelli interni in senso orario e l'anello esterno in senso antiorario come
mostrato in Figura 7.2.8:
230
7 Metodi di analisi delle reti elettriche
Figura 7.2.6: anello esterno
Figura 7.2.7: anelli orientati in senso orario
7.2.1.1 La matrice di incidenza totale anelli-lati
Con gli anelli (compreso quello esterno) è possibile costruire la
anelli-lati.
Na = L − N + 2
(L − N + 2) × L.
Poichè il numero di anelli è
matrice è di ordine

m11
m21




[Mtot. ] = 




e il numero di lati è
m12
m22
m(N −L+2)1 m(N −L+2)2
Il generico elemento
mij
matrice di incidenza totale
L,
... ...
m1L
... ...
m2L
.
.
.
.
... ... m(N −L+2)L
si ha che tale










(7.2.7)
della matrice di incidenza totale anelli-lati è costruito mediante
la regola mostrata in Figura 7.2.9:
Consideriamo il grafo mostrato in Figura 7.2.10.
Visto che si ha
N =3
ed
L=5
si ha che
Na = 4
in accordo con (7.2.6). Seguendo
la regola mostrata in Figura 7.2.9 si ha che la matrice di incidenza totale anelli-lati di
ordine
4 × 5,
vale:
231
7 Metodi di analisi delle reti elettriche
Figura 7.2.8: anello esterno orientato in senso antiorario
Figura 7.2.9: regola per la costruzione della matrice
Mtot.


1
1
0 −1 0
 0 −1 1
0
0 

[Mtot. ] = 
 0
0
0
1 −1 
−1 0 −1 0
1
Si osservi che tale matrice ha le righe linearmente dipendenti, infatti la somma degli
elementi di ciascuna colonna è nulla esattamente come avveniva con la matrice
7.2.1.1.1 Matrice di incidenza anelli-lati
[Atot. ] .
Quello che si fa è eliminare la riga che fa
riferimento all'anello esterno, pochè combinazione lineare delle altre righe. Così facendo
ovviamente non si ha perdita di informazione perchè in qualsiasi momento risulta possibile ripristinare la riga eliminata dato che deve essere composta da elementi tali che se
sommati per colonna devono restituire zero come prima osservato.
Eliminando quindi la riga riferita all'anello esterno dalla matrice
matrice di incidenza anelli-lati:
[M ]
di ordine
(L − N + 1) × L.
232
[Mtot. ]
si ricava la
7 Metodi di analisi delle reti elettriche
Figura 7.2.10: grafo
Uguagliando a zero il prodotto tra la matrice di incidenza anelli-lati e il vettore colonna
delle tensioni di lato si ricavano
L−N +1
[M ]
LKT:
[v]
[0]
=
(L − N + 1) × L L × 1
(7.2.8)
(L − N + 1) × 1
Per Il grafo di Figura 7.2.11, il sistema di equazioni in (7.2.28) si scrive:




1 1 0 −1 0

 0 −1 1 0
0  


0 0 0 1 −1
v1
v2
v3
v4
v5






 = 




0
0
0
0
0



⇒




 v1 + v2 − v4 = 0 LKT 1
⇒
−v2 + v3 = 0
LKT 2


v4 − v5 ==
LKT 3
In Figura 7.2.11 viene riportato il grafo precedente avendo specicato le tensioni e le
correnti di lato
Si può osservare che le equazioni precedentemente trovate sono corrette.
7.2.2 Descrizione del metodo
Sulla matrice di incidenza anelli-lati si basa il
metodo de lle correnti di anello .
Supponiamo di avere una rete elettrica formata da N nodi ed L lati; si avranno allora
2L incognite: le tensioni e le correnti di lato:
vk , ik
k = 1, 2, ...., L
A questo punto si deniscono altre incognite, ossia
L-N+1, ossia tante quanti sono gli anelli della rete:
233
le correnti di anello.
(7.2.9)
Esse sono
7 Metodi di analisi delle reti elettriche
Figura 7.2.11: grafo
jh
h = 1, 2, ...., L − N + 1
(7.2.10)
Le correnti di anello sono semplicemente correnti matematiche , quindi di nessun
signicato sico.
Ciascuna corrente di anello può coincidere con una corrente di lato o al limite può
essere la sovrapposizione di due correnti di lato.
Il problema così posto risulta costituito da 2L-N+1 incognite e per tanto servono 3LN+1 equazioni. L-N+1 equazioni sono le LKT date in (7.2.28). Serve pertanto scrivere
altre 2L equazioni; di queste 2L equazioni, L sono le cosiddette
delle correnti (LKC ∗ )
pseudo leggi di Kirchho
che legano le correnti di lato alle correnti di anello.
Facendo
riferminto a Figura 7.21 si ha:


i1




i2
i3



i4




i5
Le
LKT ∗
= j1
= j1 − j2
= j2
= −j1 + j3
= −j3
LKC ∗ 1
LKC ∗ 2
LKC ∗ 3
LKC ∗ 4
LKC ∗ 5
si possono pure esprimere in termini della matrice di incidenza anelli-lati,
cioè vale la relazione:
[M. ]T
[j]
[i]
=
L × (L − N + 1) (L − N + 1) × 1
Ovviamente le
(7.2.11)
L×1
LKC ∗ sono semanticamente delle LKC ma non lo sono sintatticamente.
Attraverso di esse le LKC sono automaticamente soddisfatte e questo fatto lo si può
provare immediatamente: dal grafo di Figura 7.2.11 si consideri per esempio la seguente
LKC:
234
7 Metodi di analisi delle reti elettriche
−i1 + i2 + i3 = 0
Tale equazione è automaticamente soddisfatta dalle
LKC ∗ ,
infatti si ha:
−j1 + j1 − j2 + j2 = 0
Le altre L equazioni che si possono scrivere per risolvere il problema avente 3L+N-1
incognite sono le leggi di lato (LL) alla Thevenin.
Figura 7.2.12: lato Thevenin
Proposizione. Quando si applica il metodo delle correnti di anello ipotizzare che ciascun
lato sia alla Thevenin.
In Figura 7.2.12 viene mostrato il lato alla Thevenin. Si osservi che per il lato mostrato
in gura è stata utilizzata la convenzione dell'utilizzatore.
Per il lato Thevenin vale la relazione:
vk (t) = vgk (t) + Rk igk (t)
(7.2.12)
Per una rete formata da L lati si possomo scrivere L equazioni del tipo (7.2.12) che si
possono compattare nella seguente forma matriciale:
[v] = [R] [i] + [vg ]
L×1L×LL×1
(7.2.13)
dove




[R] = 



R1 . . . . . 0
0 R2 0 . . . 0
.
0 . . .
.
.
. . . .
.
.
. . . .
0
0
0 . . . 0 RL
235








(7.2.14)
7 Metodi di analisi delle reti elettriche
è la
matrice delle resistenze di lato (nel caso generale matrice delle impedenze di lato).
L'insieme delle equazioni date in (7.2.8), (7.2.11) e (7.2.13) costituisce il sistema
risolvente di 2L+N-1 equazioni in 2L+N-1 incognite:


(7.2.15.1)
[M ] [V ] = [0]
T
[i] = [M ] [j]
(7.2.15.2)


[v] = [R] [i] + [vg ] (7.2.15.3)
N − 1 LKT
L LKC ∗
L LL
Moltiplicando a sinistra tutti i termini della (7.2.15.3) per
[M ]
(7.2.15)
si ottiene:
[M ] [v] = [M ] [R] [i] + [M ] [vg ]
(7.2.16)
Per la (7.2.15.1), la (7.2.16) si scrive:
[M ] [R] [i] + [M ] [vg ] = [0]
(7.2.17)
Per la (7.2.15.2) la (7.2.17) si scrive:
[M ] [R] [M ]T [j] + [M ] [vg ] = [0]
ovvero:
[M ] [R] [M ]T [j] = − [M ] [vg ]
Visto che
[A], [G]
e
[ig ]
sono quantità note, è evidente che (7.1.19) è un sistema
risolvente nelle sole N-1 incognite
Denendo la
eh .
matrice delle resistenze di anell o:
[RA ] = [M ] [R] [M ]T
e il
(7.2.18)
(7.2.19)
vettore colonna dei generatori di anell o:
[vgA ] = − [M ] [vg ]
(7.2.20)
la (7.2.18) si può scrivere ancora in forma più compatta, come segue:
[RA ] [j] = [vgA ]
Risolvendo (7.2.21) si trovano le correnti di anello
traverso leLKC
∗ si trovano le correnti di lato
LL si trovano le tensioni di lato
ik ,
(7.2.21)
jh ,
note le correnti di anello, at-
note le correnti di lato, attraverso le
vk .
Proposizione. Se nella rete elettrica non ci sono generatori pilotati, allora la matrice
delle conduttanze di nodi è simmetrica.
La matrice delle resistenze di anello e il vettore colonna dei generatori di anello, si
possono scrivere di getto guardando semplicemente il circuito, se nella rete elettrica non
ci sono generatori pilotati e induttori mutuamente accoppiati.
236
7 Metodi di analisi delle reti elettriche
7.2.2.1 Regole di ispezione visiva
7.2.2.1.1 Matrice delle resistenze di anello
[RA ]
I termini che si trovanno sulla diagonale principale valgono
rii =
X
Rk
(7.2.22)
k∈i
essendo i l'anello i-esimo, mentre i termini che stanno fuori dalla diagonale principale,
valgono:
rij = rji = ±
X
Rk
(7.2.23)
k∈i ∩j
essendo i l'anello i-esimo e essendo j l 'anello j-esimo.
Il segno + va messo quando le correnti nell'anello i e nell'anello j sono concordi
all'intersezione:
Figura 7.2.13: correnti concordi
Il segno - va messo quando le correnti nell'anello i e nell'anello j sono discordi
all'intersezione:
Figura 7.2.14: correnti discordi
7.2.2.1.2 Vettore colonna dei generatori di anello
[vgA ]
Il vettore colonna presenta gli elementi:
vgAi =
X
±vgk
k∈i
Vale il segno + se il generatore
vale il segno - se il generatore
vgk
vgk
ji :
ji :
agevola la corrente di anello
ostacola la corrente di anello
237
7 Metodi di analisi delle reti elettriche
Figura 7.2.15: correnti discordi
Figura 7.2.16: coorenti discordi
Il metodo delle correnti di anello vale nel dominio del tempo, nel dominio dei fasori,
nel dominio di Laplace e anche nel dominio di Fourier esattamente come il metodo dei
potenziali ai nodi.
7.2.2.2 Esempio1
Consideriamo la rete elettrica nel dominio dei fasori mostrata in Figura 7.2.17:
Figura 7.2.17: rete elettrica nel dominio dei fasori
Quando si applica il metodo dei potenziali ai nodi occorre che tutti i lati della rete
siano alla Thevenin. Con riferimento al circuito mostrato in Figura 7.2.17 si immagina
238
7 Metodi di analisi delle reti elettriche
soltanto di trasformare il lato Norton costituito da
I˙g
ed
R2
in lato alla Thevenin (Figura
7.2.18).
Figura 7.2.18: rete elettrica nel dominio dei fasori
In questo modo risulta evidente che gli anelli veri del circuito sono due e non tre.
Visto che la rete è inquadrata nel dominio dei fasori è ovvio che le correnti di anello
sono dei fasori e la matrice delle resistenze di anello è in realta la matrice delle impedenze
di anello.
Applicando le regole di ispezione visiva si ha immediatamente il sistema risolvente:
"
1
R1 + jωC
1
− jωC
1
− jCL
1
R2 + jωC
+ jωL
#
J˙1
J˙2
=
V̇g
−R2 I˙g
7.2.2.3 Metodo delle correnti di anello modicato
Cosa succede se la rete presenta un lato contenente solo un generatore ideale di corrente?
E' possibile applicare ugualmente il metodo delle correnti di anello?
LA RISPOSTA è SI!!
Si può operare come descritto di seguito
239
7 Metodi di analisi delle reti elettriche
7.2.2.3.1 Modo poco furbo
Si individuano gli anelli I,II e III come indicato in Figura 7.2.19.
Il sistema risolvente che si ottiene:
1
R1 + jωC
 − 1
jωC
0

risulta
4

1
− jCL
0
1
0 
jωC + jωL
0
R2
costituito
incognite.
Per
da
3
rendere

 
V̇g
J˙1
J˙2  =  −V̇ 
V̇
J˙3
equazioni
in
determinato
il sistema occorre introdurre una nuova
equazioni per la presenza dell'incognita
V̇
(tensione ai capi del generatore ideale di
corrente).
Questa equazione è la
V̇ .
LKC ∗ contenente
Figura 7.2.19:
Dal circuito mostrato in Figura 7.2.19
si vede che tale equazione è:
V̇ = J˙3 − J˙2 R2
Questo modo di operare è il peggiore che possa esistere (anche se corretto) perchè per
risolvere un circuito del secondo ordine richiede la risoluzione di un sistema
2×2
4 × 4 anzichè
.
7.2.2.3.2 Modo furbo
Visto che il resistore di resistenza
R2
e il generatore ideale di corrente
I˙g
sono in
parallelo tra di loro, li possiamo invertire di posizione come mostrato in Figura 7.2.20:
Figura 7.2.20:
Scriviamo il sistema risolvente in forma scalare.
La LKT all'anello I è
240
7 Metodi di analisi delle reti elettriche
−V̇g + R1 J˙1 +
1 ˙
J1 − J˙2 = 0
jωC
La LKT all'anello II è
1 ˙
˙
˙
˙
˙
J2 − J1 + jωLJ2 + R2 J2 + Ig = 0
jωC
La LKT all'anello III è
−V̇ + R2 J˙2 + I˙g = 0
Si osservi che l'incognita
V̇ ,
questa volta, gura soltanto nella terza equazione. PEr-
tanto il circuito si risolve facendo sistema tra le prime due equazioni.
-Quanto vale la potenza media assorbita da
R2 ?
Si ha ovviamente che
2
P2 = R2 I˙2 Resta da capire allora chi è la corrente
Figura 7.2.19 viene da dire
conto della corrente
I˙g .
I˙2 = J˙3 .
I˙2 .
Dovremmo scrivere una
LKC ∗ .
Guardando
In realtà non è così perchè non stiamo tenendo
Guardando il circuito mostrato in Figura 7.2.20 è chiaro che
deve essere:
I˙2 = I˙g + J˙2
Per essere sicuri di non sbagliare a scrivere una pseudo leggo di Kirchho delle correnti
è evidente che occorre andare a scrivere la matrice di incidenza anelli-lati e risolvere il
sistema dato in (7.2.11) in caso di dubbio.
7.2.3 Rete elettrica con coppia di induttori mutuamente accoppiati
Figura 7.2.21:
241
7 Metodi di analisi delle reti elettriche
In Figura 7.2.21 viene riportata una rete elettrica nel dominio dei fasori avente una
coppia di induttori mutuaente accoppiati. PEr la presenza degli induttori mutuamente
accoppiati non si scrive di getto il sistema risolvente.
Le LKT agli anelli I e II sono:
−V̇g + R1 J˙1 + jωL1 J˙1 − J˙2 + jωM J˙2 = 0 LKT I
jωL2 J˙2 − jωM J˙2 − J˙1 + R2 J2 +˙ ˙Ig + jωL1 J˙2 − J˙1 − jωM J˙2 = 0 LKT 2
Cerchiamo di capire i segni che precedono i termini in LKTI.
Percorrendo il senso dell'anello I si incontra il segno -generatore, quindi nella LKT1
va messo
−V̇g .
Assumendo positiva la corrente
J˙1 − J˙2
, allora l'auto-reattanza
jωL1
deve essere preceduta dal segno +.
Per decidere ilsegno della
mutua-reattanza
to delle correnti
J˙1 − J˙2
J˙1 − J˙2
e
J˙2
jωM ,
occorre vedere il comportamen-
rispetto ai contrassegni.
, essa avrà lo stesso senso di percorrenza di
J˙1 ,
Assunta positiva la corrente
pertanto visto che
J˙1
e
J˙2
han-
no lo stesso comportamento rispetto ai contrassegni (entrambe entranti dai contrassegni),
la mutua-reattanza
jωM
deve avere segno +.
7.3 Criterio per la scelta del metodo
Quando si analizza una rete elettrica bisogna scegliere il metodo di analisi da utilizzare.
Ovviamente il metodo migliore è sempre quello che permette di scrivere il minor numero
di equazioni per il sistema risolvente.
Nel caso del metodo dei potenziali ai nodi il sistema risolvente è costituito da N-1
equazioni:
[GN ] [e] = [igN ]
(7.3.1)
Nel caso del metodo delle correnti di anello il sistema risolvente è invece costituito da
L-N+1 equazioni:
[RA ] [j] = [vgA ]
(7.3.2)
Pertanto una volta denito il numero di nodi N e quindi di lati L, si vanno a valutare
i numeri N-1 ed L-N+1 e quello più piccolo decide il metodo da utilizzare.
Se risulta N-1 minore di L-N+1 si utilizza il metodo dei potenziali ai nodi. In caso
contrario si utilizza il metodo delle correnti di anello.
242
7 Metodi di analisi delle reti elettriche
7.4 Metodo degli insiemi di taglio
7.4.1 Elementi di teoria dei gra: il concetto di albero e di insieme di
taglio fondamentale
Dato un grafo:
G = {N , L, f : L → N × N }
si chiama
(7.4.1)
albero un sottografo formato da N nosi ed L = N − 1 lati tali da non formare
0
percorsi chiusi:
n
o
0
0
A = N, L , g : L → N × N ⊆ G
I lati che non appartengono all'albero si chiamano
corde.
lati di coalbero
(7.4.2)
o semplicemente
Quindi se N-1 sono i lati d'albero, allora L-N+1 sono le corde; è ovvio allora che a
ciascun grafo corrispondono più alberi.
Per esempio al grafo di Figura 7.4.1
Figura 7.4.1: grafo con N=5 nodi ed L=9 lati
corrispondono gli alberi mostrati in Figura 7.4.2
Consideriamo l'albero B di Figura 7.4.2, evidenziando pure i lati di coalbero come
mostrato in Figura 7.4.3. Si può osservare che i lati del grafo sono stati numerati indicando prima i lati di coalbero e poi quelli di albero anche se questa scelta è in realtà del
tutto arbitraria.
Si chiama
insieme di taglio fondamentale
quella supercie gaussiana che taglia asclu-
sivamente un solo lato d'albero.
Siccome ilati d'albero sono N-1, saranno N-1 gli insiemi di taglio fondamentali.
L'albero mostrat in Figura 7.4.3 è formato da 4 lati e pertanto avrà 4 insiemi di taglio
fondamentali come mostrato in Figura 7.4.4
Si osservi che non è detto che un insieme di taglio fondamentale coincide sempre con un
insieme di taglio al nodo (l'insieme di taglio fondamentale 4 NON coincide con l'insieme
di taglio al nodo 4).
243
7 Metodi di analisi delle reti elettriche
Figura 7.4.2: albero: N=5 nodi, N-1=4 lati
Figura 7.4.3: albero: N=5 nodi, N-1=4 lati; coalbero: N=5 nodi; L-N+1=5
A questo punto possiamo denire la matrice
di incidenza insiemi di taglio-lati.
Visto chegli insiemi di taglio fondamentale sono N-1 ed i lati sono L, la matrice di
incidenza insiemi di taglio-lati è dimensionalmente





[A] = 




a11
a21
a12
a22
a(N −1)1 a(N −1)2
Il generico elemento
aij
(N − 1) × L:
... ...
a1L
... ...
a2L
.
.
.
.
... ... a(N −1)L










(7.4.3)
della matrice di incidenza insiemi di taglio-lati è costruito
mediante la regola mostrata in Figura 7.4.5:
Asserzione.
Di volata in volta conviene scegliere il versore normale all'insieme di taglio
concordemente al verso del lato d'albero interessato dall'insieme di taglio stesso.
244
7 Metodi di analisi delle reti elettriche
Figura 7.4.4: albero: N=5 nodi, N-1=4 lati; coalbero: N=5 nodi; L-N+1=5
Figura 7.4.5: regola per la costruzione della matrice
A
7.4.1.1 La matrice di incidenza insiemi di taglio-lati
Attraverso la matrice di incidenza insiemi di taglio-lati, si possono scrivere N-1
LKC
linearmente indipendenti:
[A. ] [i] = [0]
(7.4.4)
Questo fatto si può provare subito utilizzando il grafo mostrato in Figua 7.4.4.
matrice di incidenza insiemi di taglio-lati è:

−1
 1
[A] = 
 0
1
0 0 −1 0 0 0
1 0
0 −1 1 0
1 1
0
0 0 1
0 −1 1
0 0 0
Sostituendo quest'ultima espressione in (7.4.4) si ottiene:
245
0
0
0
1

1
0 

0 
0
La
7 Metodi di analisi delle reti elettriche


−1
 1

 0
1
0 0 −1 0 0 0
1 0
0 −1 1 0
1 1
0
0 0 1
0 −1 1
0 0 0
0
0
0
1
1
0
0
0













i1
i2
i3
i4
i5
i6
i7
i8
i9


 
 
 
 
 
 
=
 
 
 
 
 
 
0
0
0
0
0
0
0
0
0
















−i1 − i4 + i9 = 0



i + i − i + i = 0
1
2
5
6

i
+
i
+
i
=
0
2
3
7



i − i + i + i = 0
1
3
4
8
Queste ultime relazioni sono le LKC agli insiemi di taglio fondamentali indicati in
Figura 7.4.6
Figura 7.4.6: albero: N=5 nodi, N-1=4 lati; coalbero: N=5 nodi; L-N+1=5
Denendo le tensioni dei lati d'albero:
eh
h = 1, 2, ...., N − 1
(7.4.5)
attraverso la matrice di incidenza insiemi di taglio-lati, si possono ricavare le relazioni
che legano le tensioni di lato della rete alle tensioni dei lati d'albero, cioè le
[A. ]T
[e] = [v]
LKT ∗ :
(7.4.6)
Con riferimento al grafo mostrato in Figura 7.4.7, le tensioni dei lati d'albero sono:
246
7 Metodi di analisi delle reti elettriche
e1
e2
e3
e4
= v9
= v6
= v7
= v8
Pertanto la (7.4.6) si scrive:



v1
−1 1 0 1
 v2 
 0
1 1 0 




 v3 

 0


0 1 −1 



e
1


 −1 0 0 1 
  e2   v4 

 =  v5  ⇒
 0 −1 0 0  

  e3  

 v6 
 0
1 0 0 


 e4

 v7 
 0
0 1 0 




 v8 
 0
0 0 1 
v9
1
0 0 0


−e + e2 + e4 = v1

 1



e2 + e3 = v2




e3 − e4 = v3






−e1 + e4 = v4
=⇒ −e2 = v5




e2 = v6






e3 = v7 


 → tensioni dei lati d0 albero



e4 = v8 





e1 = v9

Attraverso le
LKT + ,
le
LKT
risultano automaticamente soddisfatte. Questo fatto si
prova subito, considerando per esempio la segunte LKT:
v1 − v4 − v6 = 0
e andando a sostituire le
LKT ∗ precedentemente
trovate:
(e1 + e2 + e4 ) − (e1 + e4 ) − (e2 ) = 0
Avendo introdotto come incognite ausiliarie le N-1 tensioni dei lati d'albero, si hanno
2L+N-1 incognite considerando le tensioni e le correnti di lato.
Servono quindi 2l+N-1 equazioni per risolvere la rete elettrica.
Attraverso (7.4.4) e
(7.4.6) si hanno L+N-1 equazioni; le altre equazioni sono le leggi di lato, nell'ipotesi che
tutti i lati della rete siano alla Norton. Quindi le L equazioni mancanti sono:
[i] = [G] [v] − [ig ]
247
(7.4.7)
7 Metodi di analisi delle reti elettriche
L'insieme delle equazioni date in (7.4.4), (7.4.6) e (7.4.7) costituisce il sistema risolvente
di 2L+N-1 equazioni in 2L+N-1 incognite:


(7.4.8.1)
[A] [i] = [0]
T
[v] = [A] [e]
(7.4.8.2)


[i] = [G] [v] − [ig ] (7.4.8.3)
N − 1 LKC
L LKT ∗
L LL
(7.4.8)
Moltiplicando a sinistra tutti i termini della (7.4.8.3) si ottiene:
[A] [i] = [A] [G] [v] − [A] [ig ]
(7.4.9)
Per la (7.4.8.1), la (7.4.9) si scrive:
[A] [G] [v] − [A] [ig ] = [0]
(7.4.10)
Per la (7.4.8.2) la (7.4.10) si scrive:
[A] [G] [A]T [e] − [A] [ig ] = [0]
ovvero:
[A] [G] [A]T [e] = [A] [ig ]
Visto che
[A], [G]
e
[ig ]
sono quantità note, è evidente che (7.4.11) è un sistema
risolvente nelle sole N-1 incognite
Denendo la
(7.4.11)
eh .
matrice delle conduttanze di
taglio:
[GT ] = [A] [G] [A]T
e il
(7.4.12)
vettore colonna dei generatori degli insiemi di taglio :
[igT ] = [A] [ig ]
(7.4.13)
la (7.4.11) si può scrivere ancora in forma più compatta, come segue:
[GT ] [e] = [igT ]
Risolvendo (7.2.14) si trovano le tensioni dei lati d'albero
traverso leLKT
∗ si trovano le tensioni di lato
LL si trovano le correnti di lato
ik .
vk ,
(7.4.14)
eh ,
noti queste ultime, at-
note le tensioni di lato, attraverso le
Si osservi che il metodo degli insiemi di taglio non introduce alcuna novità rispetto al
metodo dei potenziali ai nodi pertanto questo metodo viene accantonato preferendogli il
metodo dei potenziali ai nodi che tra l'altro risulta molto più semplice da applicare.
248
7 Metodi di analisi delle reti elettriche
7.5 Metodo delle correnti di maglia
7.5.1 Elementi di teoria dei gra: il concetto di maglia
Noto il grafo di una rete elettrica, possiamo considerare un suo qualsiasi albero. In Figura
7.5.1 viene mostrato un grafo avente N=4 nodi ed L=6 lati. Viene mostrato pure uno dei
suoi possibili alberi. Si osservi che i lati del grafo sono stati numerati indicando prima
quellli di coalbero e poi quelli di albero.
Figura 7.5.1: albero: N=4 nodi, N-1=3 lati; coalbero: N=4 nodi; L-N+1=3
Si denisce
maglia fondamentale
quel percorso chiuso che si ottiene aggiungendo al-
l'albero un lato di coalbero.
Visto che i lati sono L-N+1, ci saranno L-N+1 maglie fondamentali. Nel caso specico
del grafo mostrato in Figura 7.5.1, si hanno L-N+1=6-4+1=3 maglie fondamentali come
indicato in Figura 7.5.2.
A ciascuna maglia si può associare una corrente di maglia che si può orientare in modo
del tutto arbitrario, oppure è possibile preferire di orientarla in modo tale che risulti
concorde con la corrente del lato di coalbero corrispondente ( Figura 7.5.2)
7.5.1.1 La matrice di incidenza maglie fondamentali-lati
Per una rete elettrica formata da N nodi ed L lati si denisce matrice di incidenza maglie
fondamentali-lati, la matrice
(L − N + 1) × L:

m11
m21




[M ] = 




m12
m22
m(N −1)1 m(N −1)2
dove il generico elemeto
mij
... ...
m1L
... ...
m2L
.
.
.
.
... ... m(N −1)L










(7.5.1)
è costruito mediante la regola descritta in Figura 7.5.3:
Seguendo la regola, si ha che la matrice di incidenza maglie fondamentali-lati vale:
249
7 Metodi di analisi delle reti elettriche
Figura 7.5.2: albero: N=4 nodi, N-1=3 lati; coalbero: N=4 nodi; L-N+1=3
Figura 7.5.3: regola per determinare il generico elemento di
[M ]


1 0 0 1 −1 −1
1
1 
[M ] =  0 1 0 0
0 0 1 −1 −1 0
Si osservi che la scelta fatta relativamente all'orientazione delle correnti di maglia ha
prodotto in
[M ]
la sottomatrice identità:


1 0 0
 0 1 0 
0 0 1
Attraverso
[M ]
si ricavano le
LKT
e le
LKT ∗ ,
250
esattamente come nel caso del metodo
7 Metodi di analisi delle reti elettriche
delle correnti di maglia:
LKT
LKT +
[M ] [v] = [0]
(7.5.2)
[i] = [M ]T [j]
(7.5.3)
Così come con il metodo delle correnti di anello, anche con il metodo delle correnti di
maglia, i lati del circuito devono essere alla Thevenin; quindi le L leggi di lato sono:
[v] = [R] [i] + [vg ]
LL
(7.5.4)
Combinando opportunamente le equazioni matriciali in () () () si ttiene il sistema
risolvente di 3L-N+1 equazioni in altrettante incognite:
[RM ] [j] = [vgM ]
(7.5.5)
[RM ] = [M ] [R] [M ]T
(7.5.6)
dove
è la
matrice delle resistenze di maglia
(di impedenze di maglia nel caso generale) e
[vgM ] = − [M ] [vg ]
è il vettore colonna dei generatori di
maglia.
Le regole di ispezione visiva per determinare
ricavare
[RA ]
(7.5.7)
[RM ]
sono analoghe a quelle viste per
col metodo delle correnti di anello.
7.6 Esempi
7.6.1 Esempio 1. Metodo delle correnti di maglia
Si consideri la rete elettrica mostrata in Figura 7.6.1
Cominciamo a denire i nodi della rete elettrica. Come si sa, quando si vanno a denire
i nodi c'è sempre un certo grado di arbitrarietà. Se indichiamo i nodi come indicato in
Figura 7.6.1, si tratta di studiare una rete elettrica formata da N=5 nodi ed L= 7 lati.
Applichiamo il metodo delle correnti di maglia.
La rete è formata da N-1=4 lati
d'albero ed L-N+1=3 lati di coalbero.
Quando la rete elettrica presenta, come nel caso mostrato in Figura 7.6.1, lati alla
Norton che non si possono trasformare alla Theven e induttori mutuamente accoppiati,
è molto utile seguire le seguenti regole:
Regola 1
Qualora la rete elettrica presentasse induttori mutuamente accoppiati si deve fare in modo
che su ciascun induttore circoli una sola corrente di maglia; ciò vuol dire considerare
l'induttore come lato di coalbero.
251
7 Metodi di analisi delle reti elettriche
Figura 7.6.1: rete elettrica nel dominio dei fasori
Regola 2
Qualora la rete presentasse lati Norton che non si possono trasformare in lati Thevenin,
si deve fare in modo che su ciascun lato Norton circoli una sola corrente di maglia;
ciò vuol dire considerare i lati alla Norton non ytasformabili alla Thevenin come lati di
coalbero.
Utilizzando queste due regole possiamo ridisegnare il circuito come mostrato in Figura
7.6.2: viene evidenziato in rosso i lati di albero (R1 ,
R2 , R3 , C ).
Figura 7.6.2: rete elettrica nel dominio dei fasori
La rete elettrica presenta 3 lati di coalbero e quindi 3 maglie fondamentali:
Individuate le maglie fondamentali, si scrive il sistema risolvente. Ovviamente la presenza degli induttori mutuamente accoppiati suggerisce di scrivere il sistema risolvente
252
7 Metodi di analisi delle reti elettriche
Figura 7.6.3: rete elettrica nel dominio dei fasori
in forma scalare:
 ˙1 − J˙2 − I˙g + 1 J˙1 − J˙2 − I˙g + jωL1 − jωM J˙2 = 0

R
J
1


jωC


R J˙ + R J˙ + I˙ + 1 J˙ + I˙ − J˙ + R J˙ + I˙ − J˙ +
2
g
1
2 2
3
2
g
1
2
g
1
jωC

˙
˙
+jωL2 J2 −jωM J1 = V̇g




R I˙ + R I˙ + J˙ − J˙ + 1 I˙ + J˙ − J˙ + R I˙ + J˙ = V̇
0 g
1
g
2
Si osservi che l'incognita
1
V̇
jωC
g
2
1
3
g
LKT I
LKT II
LKT III
2
gura soltanto nella LKT III e pertanto il sistema risolvente
risulta composto dalla LKT I e dalla LKT II.
Tale sistema viene di seguito scritto in forma matriciale:
"
1
R1 + jωC
+ jωL1
1
−R1 − jωC − jωM
1
jωC
−R1 −
− jωM
1
R1 + R2 + R3 + jωC
+ jωL2
#
J˙1
J˙2

=
R1 +
− R1 +
1
jωC
Si osservi che nel sistema risolvente non gura da nessuna parte il resistore
trova in serie al generatore ideale di corrente
I˙g .

I˙g

+ R3 I˙g + V̇g
1
jωC
R0
che si
Con ciò stiamo trovando la seguente
regola:
Regola 3
La serie costituita da un generatore ideale di corrente I˙g ed una impedenza Ż equivale al
solo generatore ideale di corrente I˙g :
Dualmente si ha la seguente regola:
253
7 Metodi di analisi delle reti elettriche
Figura 7.6.4: generatore ideale di corrente in serie con una impedenza
Regola 4
Il parallelo costituita da un generatore ideale di tensione V̇g ed una impedenza Ż equivale
al solo generatore ideale di tensione V̇g :
Figura 7.6.5: generatore ideale di tensione in parallelo con una impedenza
7.6.2 Esempio 2. Metodo delle correnti di anello
Risolviamo l'esercizio visto nella sezione precedente, applicando il metodo delle correnti
di anello.
Come in precedenza sono stati deniti N=5 nodi e L=7 lati, pertanto la rete elettrica
presenta un numero di anelli pari a
Na = L − N + 1 = 3.
Tali anelli sono rappresentati
in Figura 7.6.6.
La presenza degli induttori mutuamente accoppiati suggerisce di scrivere il sistema
risolvente in forma scalare:

1 ˙
˙
˙
˙
˙

R
J
+
J
+
jωL
J
+
J

1 1
1
1
2 − jωM J3 = 0
jωC 1


R3 J˙2 + R0 J˙2 − J˙3 + jωL1 J˙2 + J˙1 − jωM J˙3 = V̇



R2 J˙3 + R0 J˙3 − J˙2 + jωL2 + J˙3 − jωM J˙1 + J˙3 = V̇g − V̇
LKT I
LKT II
LKT III
Così facendo è stato scritto un sistema di 3 equazioni in 4 incognie e pertanto serve
na quarta equazione che non sia combinazione lineare delle precedenti. Tale equazione
va ricercata tra le
LKC ∗ ;osservando
il circuito si trova facilmente la seguente
254
LKC ∗ :
7 Metodi di analisi delle reti elettriche
Figura 7.6.6: rete elettrica nel dominio dei fasori
I˙g = J˙2 − J˙3 LKC ∗
Si tratta dunque di risolvere un sistema molto più complicato rispetto a quella che è
in realtà la comlplessità del circuito. La rete proposta essendo un circuito del secondo
ordine va risolto con un sistema
2×2
e non
4 × 4.
Quindi anche se il metodo delle correnti di anello conduce alla soluzione, in questo caso
si ricorre al metodo delle correnti di maglia essendo quello che conduce alla soluzione in
modo più veloce.
7.6.3 Esempio 3. Metodo dei potenziali ai nodi
Si consideri la rete elettrica mostrata in Figura 7.6.7
Figura 7.6.7: rete elettrica nel dominio dei fasori
255
7 Metodi di analisi delle reti elettriche
Cominciamo a denire i nodi della rete elettrica. Se indichiamo i nodi come indicato
in Figura 7.6.7, si tratta di studiare una rete elettrica formata da N=3 nodi ed L= 5 lati.
Applichiamo il metodo dei potenziali ai nodi.
Come mostrato in Figura 7.6.7 si è
preferito di portare a massa il nodo 3 ed di iindicare con
Ė2
Ė1
il potenziale al nodo 1 e con
il potenziale al nodo 2.
In presenza di generatori pilotati non conviene scrivere di getto il sistema risolvente,
pertanto come indicato in gura si considerano gli insimi di taglio ai nodi e si scrivono
le LKC:

 Ė1 −V̇g +
R1
Ė1
1
jωC
+
 Ė2 −Ė1 − g V̇ +
c
jωL
Ė1 −Ė2
jωL
Ė2
R2
= 0 LKC1
=0
LKC2
La corrente del generatore pilotato dipende dalla tensione ai capi del capacitore, bisogno pertanto esprimerla in termini dei potenziali ai nodi e per far ciò si deve scrivere la
seguente
LKT ∗ :
V̇c = Ė1 − 0̇ = Ė1 LKT ∗
Quindi il sistema risolvente si scrive:

 Ė1 −V̇g +
R1
Ė1
1
jωC
+
 Ė2 −Ė1 − g Ė +
1
jωL
Ė1 −Ė2
jωL
Ė2
R2
= 0 LKC1
=0
LKC2
Riordinando i termini e scrivendo in forma matriciale si ottiene inne:
"
1
R1
1
+ jωC + jωL
1
−g
− jωL
1
− jωL
1
1
jωL + R2
#
Ė1
Ė2
=
1
R1 V̇g
0
Si osservi che in presenza di generatori pilotati si perde la simmetria nella matrice delle
impedenze di anello.
7.6.4 Esempio 4. Metodo delle correnti di maglia
Risolviamo l'esercizio visto nella sezione precedente, applicando il metodo delle correnti
di maglia.
Come in precedenza sono stati deniti N=3 nodi ed L=5 lati, pertanto la rete elettrica presenta
N −1 = 2
lati d'albero e L-N+1=3 lati di coalbero e quindi 3 maglie
fondamentali.
In presenza di generatori pilotati è conveniente fare uso della seguente regola:
Regola 5
In presenza di generatori pilotati si fa in modo che essi siano interessati da una sola
corrente di maglia; in altri termini ciò vuol dire considerarli come lati di coalbero.
In Figura 7.6.8 sono state indicate le maglie seguendo la regola appena data.
256
7 Metodi di analisi delle reti elettriche
Figura 7.6.8: rete elettrica nel dominio dei fasori
La presenza del generatore pilotato suggerisce di scrivere il sistema risolvente in forma
scalare:

1
˙
˙
˙

R
J
+
J
−
J
LKT 1

1 1
2 − V̇g = 0
jωC 1

 1
J˙2 − J˙1 + jωLJ˙2 = 0 LKT 2
R2 J˙2 + g V̇c + jωC



R2 g V̇c + J˙2 − V̇ = 0
LKT 3
La LKT3 si può subito scartare perchè l'incognita
Nella LKT2 gura la variabile di pilotaggio
seguente
LKC ∗
V̇c
V̇
gura in essa soltanto.
che si può esprimere attraverso la
(vedi Figura 7.6.8):
jωC V̇c = J˙1 − J˙2
Pertanto il sistema risolvente si scrive:

R1 J˙1 +
J˙1 − J˙2 − V̇g = 0
R2 J˙2 + R2 g 1 J˙1 − J˙2 + 1 J˙2 − J˙1 + jωLJ˙2 = V̇
jωC
jωC
1
jωC
LKT 1
LKT 2
Riordinando i termini e scrivendo in forma matriciale si ottiene inne:
"
1
R1 + jωC
R2 g
1
jωC − jωC
1
− jωC
R2 g
1
R2 − jωC
+ jωC
+ jωL
#
J˙1
J˙2
=
V̇g
0
7.6.5 Esempio 5. Metodo dei potenziali ai nodi
In precedenza è stato detto che per una rete elettrica avente induttori mutuamente accoppiati si preferisce utilizzare il metodo delle correnti di anello o di maglia, tuttavia in
questa sezione si fa vedere come operare su una rete elettrica avente induttori mutuamente
accoppiati con il metodo dei potenziali ai nodi.
Consideriamo la rete elettrica mostrata in Figura 7.6.9.
N=3 nodi e quindi L=5 lati.
257
Per essa sono stati deniti
7 Metodi di analisi delle reti elettriche
Figura 7.6.9: rete elettrica con induttori mutuamente accoppiati
Si osservi che si è scelto di porre a massa il nodo 3 e di indicare con
al nodo 1 e con
Ė2
Ė1
il potenziale
il potenziale al nodo 2.
Scrivendo le LKT agli insiemi di taglio si ricava il sistema risolvente:
(
Ė1 −V̇g
R1
+ I˙2 + I˙1 = 0 LKT 1
Ė2
−I˙1 − I˙g + R
=0
LKT 2
2
In (7.6.1) compaiono le correnti
I˙1
e
I˙2 ,
(7.6.1)
che attraversano gli induttori.
Si capisce che occorre esprimere tali correnti in termini dei potenziali ai nodi.
Per
far ciò basta scrivere le equzioni che caratterizzano una coppia di induttori mutuamente
accoppiati. Facendo riferimento a Figura 7.6.9 si ha che
(
V̇1 = jωL1 I˙1 − jωM I˙2
V̇2 = −jωM I˙1 + jωL2
Utilizzando le seguenti
(7.6.2)
LKT ∗
V̇1 = Ė1 − Ė2
V̇2 = Ė1 − 0̇ = Ė1
le equazioni in (7.6.2) si scrivono:
(
Ė1 − Ė2 = jωL1 I˙1 − jωM I˙2
Ė1 = −jωM I˙1 + jωL2
Quest'ultimo in forma matriciale si scrive:
Ė1 − Ė2
Ė1
=
jωL1
−jωM
−jωM
jωL2
Se tra gli induttori non c'è accoppiamento perfetto:
258
I˙1
I˙2
(7.6.3)
7 Metodi di analisi delle reti elettriche
L1 L2 − M 2 6= 0
il sistema in
(7.6.3)
si può invertire,permettendo cosi di ricavare le espressioni delle
correnti che attraversano gli induttori in funzione dei porenziali ai nodi:
I˙1
I˙2
I˙1
I˙2
1
=
2
(jω) (L1 L2 − M 2 )
jωL2 jωM
jωM jωL1
Ė1 − Ė2
Ė1
ovvero:
1
=
(jω) (L1 L2 − M 2 )
L2 M
M L1
Ė1 − Ė2
Ė1
(7.6.4)
Il sistema in (7.6.4), in forma scalare si scrive:
(
I˙1 =
I˙2 =
L2 +M
Ė
jω(L1 L2 −M 2 ) 1
L1 +M
Ė
jω(L1 L2 −M 2 ) 1
+
+
−L2
Ė
jω(L1 L2 −M 2 )2 2
−M
Ė
jω(L1 L2 −M 2 ) 2
(7.6.5)
Sostituendo (7.6.5) in (7.6.1) si ottiene il sistema risolvente in termini dei potenziali ai
nodi:
h

i
L1 +L2 +2M
jω(L1 L2 −M 2 )
− L2 +M 2 Ė1 +
jω(L1 L2 −M )
1
R1
+
V̇
g
Ė1 − jω(LL12L+M
2 Ė2 = R
1
2 −M ) i
h
L2
1
Ė
=
I˙g
+
2
R2
jω(L1 L2 −M 2 )
Si osservi che in assenza di generatori pilotati la matrice delle ammetenze sta risultando
simmetrica.
7.6.6 Esempio 6. Metodo delle correnti di maglia
Si consideri la rete elettrica mostrata in Figura 7.6.10.
Figura 7.6.10: rete elettrica nel dominio dei fasori
Siccome
R1 è
in parallelo ad un generatore ideale di tensione ed
R0
è in serie ad un
generatore ideale di corrente, la rete data è equivalente a quella mostrata in Figura 7.6.11.
Nella gura vengono evidenziate le maglie fondamentali.
Per esse si scrivono le seguenti LKT:
259
7 Metodi di analisi delle reti elettriche
Figura 7.6.11: rete elettrica nel dominio dei fasori

R2 J˙ + jωL1 J˙ − jωM J˙ + αI˙1 + jωL2 J˙ + αI˙1 − jωM J˙ = V̇g
jωL2 αI˙1 + J˙ − jωM J˙1 − V̇ = 0
Visto che l'incognita
V̇
LKT 1
LKT 2
gura solo in LKT2, si può escludere quest'ultima equazione.
Per quanto riguarda la prima resta da esprimere la variabile di pilotaggio in termini delle
correnti di maglia mediante una
LKT ∗ .Dal
circuito si vede subito che
I˙1 = J˙;
quindi la
LKT1 si scrive:
[R2 + jω (L1 + (1 + α) L2 − (2 + α) M )] J˙ = V̇g
7.7 Metodo delle equazioni di stato
Il metodo delle equazioni di stato si basa sul concetto di
albero proprio.
Si chiama albero proprio, l'albero di un grafo che contiene tutti i capacitori e nessun
induttore.
Consideriamo la rete elettrica mostrata in Figura 7.7.1. Denendo i nodi come indicato
in gura, si tratta di studiare una rete elettrica avente N=3 nodi ed L=5 lati.
Questo metodo esige che per ciascun lato si esplicano tensioni e correnti con le opportune convenzioni dell'utilizzatore e del generatore.
Pertanto il grafo relatvo alla rete elettrica data è quello mostrato in Figura 7.7.2
Un qualunque albero associato al grafo di Figura 7.7.2 avrà N=3 nodi ed L=N-1. Tra
tutti gli alberi del grafo possiamo determinare l'albero proprio che in questo caso deve
contenere il capacitore di capacità C e non deve contenere l'induttore di induttanza L
(Figura 7.7.3).
Una volta noto l'albero proprio associato alla rete elettrica, si vanno a costruire gli
insiemi di taglio associati ai lati d'albero capacitivi e le maglie fondamentali
associate ai
lati di coalbero induttivi.
Relativamente all'albero propiro indicato nella gura precedente è possibile individuare
un insieme di taglio e una maglia come mostrato in Figura 7.7.4
260
7 Metodi di analisi delle reti elettriche
Figura 7.7.1: rete elettrica nel dominio del tempo
Figura 7.7.2: grafo della rete elettrica: N=3, L=5
Individuati nella rete elettrica gli insiemi di taglio associati ai lati capacitivi e le maglie
associate ai lati induttivi si vanno a scrivere le corrispondenti LK.
In Figura 7.7.5 viene riproposta la rete elettrica di partenza avendone evidenziato
l'insieme di taglio associato al capacitore di capacità C e la maglia fondamentale associata
all'induttore di induttanza L.
Le LK all'insieme di taglio e alla maglia fondamentale sono:
(
−i1 (t) + iL (t) + ic (t) = 0 LKC
−vc (t) + vL (t) + v2 (t) = 0 LKT
Utilizzando le equazioni costitutive dei dispositivi a memoria
d
ic (t) = C dt
vc (t)
d
vL (t) = L dt
iL (t) e
riordinando i termini, le LK precedenti si scrivono:
(
d
dt vc (t)
d
dt iL (t)
=
=
1
C i1 (t) −
1
L vc (t) −
261
1
C iL (t)
1
L v2 (t)
LKC
LKT
(7.7.1)
7 Metodi di analisi delle reti elettriche
Figura 7.7.3: albero proprio
Figura 7.7.4: insieme di taglio e maglia fondamentale
In quest'ultimo sistema igurano le variabili
stato nè ingressi; esse vengono dette
i1 (t)
e
variabili intruse.
v2 (t)
che non sono nè variabili di
Tali variabili sono sempre esprimibili come combinazione lineare degli ingressi e delle
variabili energetiche della rete.
vc (t) e iL (t) sono note in ogni istante di tempo, allora possiamo
vc (t), e all'inideale di corrente etichettato con iL (t) come indicato in Figura
Se le variabili di stato
sostituire al capacitore un generatore ideale di tensione etichettato con
duttore un generatore
7.7.6.
Studiando la rete mostrata in Figura 7.7.6 (mediante uno dei metodi di analisi precedenti) si determinano le variabili intruse. In casi molto semplici come quello di Figura
7.7.6 è eccessivo scomodare uno dei metodo di analisi studiati in precedenza visto che:
(
v (t)−v (t)
i1 (t) = g R1 c = R11 vg (t) − R11 vc (t)
v2 (t) = R2 i2 (t) = R2 (iL (t) + ig (t)) = R2 iL (t) + R2 ig (t)
(7.7.2)
Sostituendo inne, (7.7.2) in (7.7.1) si determinano le espressioni delle equazioni di
stato:
(
d
dt vc (t)
d
dt iL (t)
= − R11C vc (t) − C1 iL (t) + R11C vg (t)
= L1 vc (t) − RL2 iL (t) − RL2 ig (t)
262
(7.7.3)
7 Metodi di analisi delle reti elettriche
Figura 7.7.5: rete elettrica
Figura 7.7.6: rete elettrica
Esattamente come in (4.2.9).
7.8 Tecniche di integrazione numerica
Sappiamo che una rete elettrica si riduce alla risoluzione di un sistema di equazioni
dierenziali nelle variabili di stato, con le opportune condizioni iniziali. E' stato visto
come risolvere un problema del genere con ingressi costanti e sinusoidali.
Quando gli ingressi per il sistema sono complicati, il problema si può risolvere per via
numerica attraverso formule ricorsive.
Bisogna innanzitutto suddividere l'intervallo di osservazione
ampiezza
263
[0, t]
in N intervallini di
7 Metodi di analisi delle reti elettriche
∆=
t
N
e per i tempi
t0 = 0; t1 = ∆; t2 = 2∆; ...; tk = k∆; tk+1 = (k + 1) ∆; ...; tN = N ∆
, detti istanti di campionamento, andare a valutare gli ingressi del sistema.
I valori degli ingressi in corrispondenza degli istanti di campionamento si chiamano
campioni degli ingressi.
Determineremo adesso delle formule ricorsive che ci permettono
di determinare i valori assunti dalle variabili di stato in corrispondenza degli istanti di
campionamento.
Consideriamo il seguente problema dierenziale

d

 dt [x (t)] = [A] [x (t)] + [B] [u (t)] (7.8.1.1)


[x (0)] = [X0 ]
dove
[x (t)]
(7.8.1)
(7.8.1.2)
[B] è il vettore degli ingressi.
[0, t] si ottiene:
ˆ t
ˆ t
ˆ t
d
[u (τ )] dτ
[x (τ )] dτ + [B]
[x (τ )] dτ = [A]
0
0
0 dτ
#
"ˆ
ˆ t
ˆ t
x(t)
x (τ ) dτ + [B]
u (τ ) dτ
dx (τ ) dτ = [A]
è il vettore delle variabili di stato e
Integrando (7.8.1.1) nell'intervallo
0
x(0)
0
ovvero:
ˆ
t
[x (t)] − [X0 ] = [A]
ˆ t
x (τ ) dτ + [B]
u (τ ) dτ
0
Si osservi che
τ
(7.8.2)
0
è semplicemente una variabile di appoggio che viene utilizzata solo per
non fare confusione con la variabile di integrazione
t.
Valutiamo la (7.8.2) in due istanti di tempo successivi,
ˆ
k∆
[x (tk )] − [X0 ] = [A]
tk =
ˆ
u (τ ) dτ
(7.8.3)
0
#
(k+1)∆
[x (tk+1 )] − [X0 ] = [A]
tk+1 :
k∆
x (τ ) dτ + [B]
0
"ˆ
e
"ˆ
x (τ ) dτ + [B]
0
#
(k+1)∆
u (τ ) dτ
0
Sottraendo a (7.8.4) la (7.8.3) si ottiene:
"ˆ
ˆ
(k+1)∆
[x (tk+1 )] − [x (tk )] = [A]
x (τ ) dτ −
0
#
x (τ dτ ) +
0
264
k∆
(7.8.4)
7 Metodi di analisi delle reti elettriche
"ˆ
ˆ
(k+1)∆
u (τ ) dτ −
+ [B]
u (τ ) dτ =
0
"ˆ
0
ˆ
k∆
= [A]
x (τ ) dτ +
k∆
0
ˆ
ˆ
(k+1)∆
#
k∆
u (τ ) dτ −
u (τ ) dτ +
x (τ dτ )
0
k∆
0
#
k∆
x (τ ) dτ −
k∆
+ [B]
ˆ
(k+1)∆
x (τ ) dτ +
0
"ˆ
#
k∆
Ovvero:
"ˆ
[x (tk+1 )] − [x (tk )] = [A]
"ˆ
#
(k+1)∆
x (τ ) dτ + [B]
k∆
#
(k+1)∆
x (τ ) dτ
(7.8.5)
k∆
In base a come si approssimano gli integrali in (7.5.8) si hanno dierenti tecniche di
discretizzazione del problema dierenziale.
7.8.1 Metodo delle dierenze all'indietro
Approssimando gli integrali in (7.8.5) con dei rettangoli di base
∆ e altezza x ((k + 1) ∆) =
x (tk+1 ), u ((k + 1) ∆) = u (tk+1 ),
´ (k+1)∆
k∆
´ (k+1)∆
x (τ ) dτ = ∆x (tk+1 )
k∆
u (τ ) dτ = ∆u (tk+1 )
la (7.8.5) fornisce la relazione:
[x (tk+1 )] − [x (tk )] = ∆ [A] [x (tk+1 )] + ∆ [B] [u (tk+1 )]
che può essere posta anche come segue:
1
1
[I] − [A] [x (tk+1 )] = [x (tk )] + [B] [u (tk+1 )]
∆
∆
La (7.8.6) è una formula ricorsiva che permette di conoscere il vettore di stato
l'istante di tempo
tk+1
[u (t)]
all'istante di tempo
trasformazione di Eulero all'indietro
o
metodo delle dierenze all'indietro.
Per k=0, la (7.8.6) fornisce il vettore dei campioni di stato
[x (t1 )]:
1
1
[I] − [A] [x (t1 )] = [X0 ] + [B] [u (t1 )]
∆
∆
Per k=1, la (7.8.6) fornisce:
1
1
[I] − [A] [x (t2 )] = [x (t1 )] + [B] [u (t2 )]
∆
∆
265
[x]
al-
[x (t)] all'istante precedente tk
tk+1 . Essa è nota con il nome di
conoscendo il vettore degli stati
e il vettore degli ingressi
(7.8.6)
7 Metodi di analisi delle reti elettriche
e così via per calcolare gli altri campioni del vettore di stato.
Ovviamente maggiore è N, più la soluzione approssimata si avvicna alla soluzione
esatta.
7.8.1.1 Esempio (rete elettrica a regime costante)
Consideriamo la rete elettrica mostrata in Figura 7.8.1
Figura 7.8.1: rete elettrica nel dominio dei fasori
Sappiamo che ad essa corrisponde il seguente sistema dierenziale nelle variabili di
stato
vc (t)
e
iL (t):

d


dt vc (t) = −vc (t) − iL (t) + vg (t)


 d i (t) = v (t) − i (t) − i (t)
c
g
L
dt L

vc (0) = 1



i (0) = 1
L
che in forma matriciale si scrive:
# "
#"
# "
#"
#
 "

vc (t)
−1 −1
vc (t)
1 0
vg (t)

d

=
+
(7.8.7.1)


1 −1
iL (t)
0 −1
ig (t)
 dt iL (t)

# " #
"



1
v
(0)

c


=

iL(0)
1
(7.8.7)
(7.8.7.2)
Confrontando (7.8.7) con (7.8.1) si vede subito che:
−1 −1
1 −1
vc (t)
[x (t)] =
iL (t)
[A] =
266
1 0
0 −1
vg (t)
[u (t)] =
ig (t)
[B] =
(7.8.8)
(7.8.9)
7 Metodi di analisi delle reti elettriche
Note le matrici in (7.8.8) e i vettori in (7.8.9), la formula ricorsiva in (7.8.6) si scrive:

1
∆
+1

1
∆
−1

1
vc (tk+1 )

+1
iL (tk+1 )


= 1 
∆
vc (tk )


1

0
+

0 −1
iL (tk )
vg (tk+1 )


ig (tk+1 )
(7.8.10)
Supponendo che sia
∆=
10−3 s,
vg (tk+1 ) = 9 V, ig (tk+1 ) = 1 A ∀k
(ingressi costanti),
il sistema in (7.810) diventa:

1001

1

vc (tk+1 )
1001

vc (tk )
 = 103 

−1

iL (tk+1 )


9
+

(7.8.11)

−1
iL (tk )
Premoltiplicando entrambi i membri di (7.8.11) per la matrice

1001
−1
1


−1

=
1001
1001
1002002
1
− 1002002
1
1002002
1001
1002002


Il sistema in (7.8.11) si scrive:

vc (tk+1 )


 = 103 

iL (tk+1 )
1001
1002002
1
− 1002002
1
1002002
1001
1002002

vc (tk )
 
+

iL (tk )
1001
1002002
1
1002002
1
1002002
1001
1002002

9


−1
ovvero

vc (tk+1 )


0, 999
−0, 000998
=

iL (tk+1 )

vc (tk )
0, 999

0, 008992
+

0, 000998

iL (tk )


−0, 00099
Quest'ultimo in forma scalare si scrive


 vc (tk+1 ) = 0, 999vc (tk ) − 0, 000998iL (tk ) + 0, 008992


(7.8.12)
iL (tk+1 ) = 0, 000998vc (tk ) + 0, 999iL (tk ) − 0, 00099
Qui di seguito viene proposto il codice MATLAB che implementa il sistema di equazioni
in (7.8.12)
267

7 Metodi di analisi delle reti elettriche
Codice MATLAB
a=0.999;
b=0.000998;
c=0.008992;
d=-0.00099;
t=[0:0.001:10];
l=length(t);
v=zeros(1,l);
i=zeros(1,l);
v(1)=1;
i(1)=1;
for k=1:(l-1)
v(k+1)=a*v(k)-b*i(k)+c;
i(k+1)=b*v(k)+a*i(k)+d;
end
plot(t,v)
Una volta lanciato il programma in ambiente MATLAB comparirà il graco della
tensione
vc (t)
che viene mostrato in Figura 7.8.2
Figura 7.8.2: tensione
vc (t)
Si osservi che stiamo ritrovando lo stesso graco incontrato in Figura 4.3.10 a verica
della correttezza del metodo di integrazione numerica.
268
7 Metodi di analisi delle reti elettriche
7.8.2 Metodo delle dierenze all'avanti
Approssimando gli integrali in (7.8.5) con dei rettangoli di base
∆
e altezza
x (k∆) =
x (tk ), u (k∆) = u (tk ),
´ (k+1)∆
k∆
´ (k+1)∆
x (τ ) dτ = ∆x (tk )
k∆
u (τ ) dτ = ∆u (tk )
la (7.8.5) fornisce la relazione:
[x (tk+1 )] − [x (tk )] = ∆ [A] [x (tk )] + ∆ [B] [u (tk )]
che può essere posta anche come segue:
1
[x (tk+1 )] =
∆
1
[I] + [A] [x (tk )] + [B] [u (tk+1 )]
∆
(7.8.13)
La (7.8.6) è una formula ricorsiva che permette di conoscere il vettore di stato
l'istante di tempo
tk+1
[x]
al-
[x (t)] all'istante precedente tk
tk+1 .Essa è nota con il nome di
conoscendo il vettore degli stati
e il vettore degli ingressi
[u (t)]
all'istante di tempo
trasformazione di Eulero all'avanti
o
metodo delle dierenze all'avanti.
7.8.3 Metodo di Crank-Nicholson
Approssimando gli integrali in (7.8.5) come segue:
´ (k+1)∆
k∆
x (τ ) dτ = ∆
x(tk )+x(tk+1 )
2
´ (k+1)∆
k∆
u (τ ) dτ = ∆
u (tk ) + u (tk+1 )
2
la (7.8.5) fornisce la relazione:
u (tk ) + u (tk+1 )
x (tk ) + x (tk+1 )
+ ∆ [B]
[x (tk+1 )] − [x (tk )] = ∆ [A]
2
2
che può essere posta anche come segue:
2
2
I − [A] [x (tk+1 )] =
[I] + [A] [x (tk )] + [B] [u (tk ) + u (tk+1 )]
∆
∆
(7.8.14)
La (7.8.14) è una formula ricorsiva per determinare il vettore delle variabili di stato ed
è nota con il nome di
Trasformazione di Tustin o metodo di Crank-Nicholson.
269
8 Reti elettriche in regime periodico non
sinusoidale
8.1 Introduzione
In questo capitolo viene arontato lo studio delle reti elettriche aventi generatori caratterizzati da forme d'onda periodica ma non sinusoidale.
analisi armonica.
Per studiare queste reti occorre preliminarmente condurre l'
Si tratta
di un procedimento basato sulla serie di Fourier che consente di approssimare il generatore
periodico non sinusoidale alla somma tra un generatore costante e una combinazione
lineare di N generatori sinusoidali oscillanti a frequenze multiplo di una certa frequenza
f0
detta
frequenza della forma d'onda fondamentale :


f1 = k1 f0





f2 = k2 f0




.



.

fi = ki f0





.





.



f = k f
N
N 0
(8.1.1)
ki ∈ N
Ovviamente l'approssimazione è tanto migliore quanto più grande è N.
Se risulta possibile scrivere ciascuna frequenza
rete elettrica è in
fi
regime periodico non sinusoidale.
come multiplo di
f0 ,
si dirà che la
Se indichiamo con
T0 =
il periodo della
1
f0
forma d'onda fondamentale, da (7.9.1) segue che
270
(8.1.2)
8 Reti elettriche in regime periodico non sinusoidale


T1 = Tk10





T2 = Tk20





.



.

Ti = Tk0i





.




.



T = T0
N
kN
(8.1.3)
ki ∈ N
sono i periodi delle forme d'onda dei generatori sinusoidali presenti nella rete elettrica.
Ovviamente si ha che tali periodi sono tutti più piccoli del periodo
T0
della forma
d'onda fondamentale.
Una volta condotta l'analisi armonica viene semplice calcolare l'integrale particolare
dell'equazione dierenziale di ordine minimo, infatti basta applicare il principio di sovrapposizione degli eetti facendo agire uno alla volta gli N+1 generatori che approssimano
il generatore periodico non sinusoidale.
Ovviamente in presenza di più generatori periodici non sinusoidali, si conduce l'analisi
armonica per ogni generatore e poi quando si applica la sovrapposizione degli eetti, si
fanno agire per volta i generatori che oscillano alla stessa frequenza.
8.2 Analisi armonica: serie di Fourier
8.2.1 Funzioni ortogonali e funzioni ortonormali
Sia
{ϕn (t)}
con
n = 1, 2, ..., ∞
un insieme di funzioni denite nell'intervallo
I = [a, b].
Tali funzioni sono in generale complesse di variabile reale.
Si dice che le funzioni
ˆ
b
ϕn (t)
costituiscono un insieme
ϕn (t) ϕ∗m (t) dt
a
(
0
=
kn
ortogonale
in I se succede che
se n 6= m
= kn δnm
se n = m
(8.2.1)
essendo
δnm
(
0 se n 6= m
=
1 se n = m
δnm si chiamano delta di Kronecker. Se le costanti kn sono
1, le funzioni {ϕn (t)} si dicono ortonormali.
∗
Con il simbolo ϕm è stata indicata la coniugata della funzione ϕm .
Le funzioni
271
(8.2.2)
tutte uguali a
8 Reti elettriche in regime periodico non sinusoidale
Esempio
Consideriamo le
funzioni esponenziali complesse :
n
o
j2πn Tt
0
{ϕn (t)} = e
I = [0, T0 ] .
denite nell'intervallo
I, infatti per
n 6= m
Tali funzioni costituiscono un insieme ortogonale in
si ha:
ˆ
T0
j2πn Tt
e
0
e
−j2πm Tt
0
ˆ
T0
j2π(n−m) Tt
dt =
0
=
(8.2.3)
e
0
dt =
0
h
n
o
i
1
1
j2π(n−m) Tt T0
0
e
=
ej2π(n−m) − 1 = 0
j2π (n − m)
j2π (n − m)
0
mentre per
n=m
si ha:
ˆ
T0
j2πn Tt
e
0
e
−j2πm Tt
0
ˆ
dt = T0
0
0
Consideriamo le
funzioni esponenziali complesse :
{ϕn (t)} =
denite nell'intervallo
ortonormali in I, infatti
ˆ
T0
dt =
I = [0, T0 ].
per n 6= m si
1 j2πn Tt
0
√ e
T0
(8.2.4)
Tali funzioni costituiscono un insieme di funzioni
ha:
ˆ T0
1
1 j2πn Tt 1 −j2πm Tt
j2π(n−m) Tt
0
0
0 dt =
√ e
√ e
dt =
e
T0 0
T0
T0
0
i
h
n
o
1
1
1
1
j2π(n−m) Tt T0
0
=
e
=
ej2π(n−m) − 1 = 0
T0 j2π (n − m)
T0 j2π (n − m)
0
mentre per
T0
n=m
si ha:
ˆ
T0
0
1 j2πn Tt 1 −j2πm Tt
0 √
0 dt =
√ e
e
T0
T0
ˆ
T0
0
1
dt = 1
T0
8.2.2 Insieme completo di funzioni
Una successione di funzioni
Cauchy
{ϕn (t)}
con
n = 1, 2, ..., ∞
denite in
I = [a, b]
si dice di
se
∀ε > 0∃ν ∈ N : ∀k, h > ν ⇒ kϕk (t) − ϕh (t)k < ε
Le funzioni
ϕn (t)
con
n = 1, 2, ..., ∞
denite in
I = [a, b],
si dice che costituiscono un
insieme completo in I se ogni successione di Cauchy risulta convergente.
Si dimostra che le funzioni
272
8 Reti elettriche in regime periodico non sinusoidale
ˆ
esponenziali complesse
ˆ
armoniche sinusoidali
ˆ
di Bessel
ˆ
di Legendre
sono funzioni di insiemi completi.
8.2.3 Teorema della rappresentazione dei segnali su base ortogonale
Sia
f (t)
un segnale elettrico denito nell'intervallo
I
funzioni denite nell'intervallo
I = [a, b]
e sia
{ϕn (t)}
un insieme di
ortogonale e completo in I. Allora si ha che
+∞
X
f (t) =
an ϕn (t)
(8.2.5)
f (t) ϕ∗n dt
(8.2.6)
n=−∞
essendo
ˆ
1
an =
kn
b
a
Dimostrazione.
Anchè sia valida la (8.2.5) basta trovare i coecienti
´b
an
.
Applicando l'operatore
∗
a [.] ϕm (t) dt alla (8.2.5) si ricava:
ˆ
ˆ
b
f
(t) ϕ∗m (t) dt
a
an ϕn (t) ϕ∗m (t) dt =
a n=−∞
=
ˆ
∞
X
b
an
ϕn (t) ϕ∗m (t) dt
a
n=−∞
Visto che
∞
X
b
=
{ϕn (t)} è un insieme di funzioni ortogonale in I,
´b
a
ϕn (t) ϕ∗m (t) dt = kn δnm ,
quest'ultima espressione si scrive:
ˆ
b
a
Inne poichè
∞
X
f (t) ϕ∗m (t) dt =
an kn δnm
n=−∞
{ϕn (t)} è anche un insieme di funzioni completo in I, la serie deve essere
convergente:
ˆ
b
f
(t) ϕ∗m (t) dt
∞
X
=
a
an kn δnm = am km
n=−∞
Da quest'ultima espressione si ricava la tesi:
am =
1
km
ˆ
b
f (t) ϕ∗m (t) dt
a
273
8 Reti elettriche in regime periodico non sinusoidale
8.2.4 Serie di Fourier
Utilizzando l'insieme delle funzioni complesse
n
o
j2πn Tt
0
{ϕn (t)} = e
denite nell'intervallo
I
I = [a, a + T0 ],
un segnale
f (t)
(8.2.7)
denito nel medesimo intervallo
si può rappresentare su base ortogonale in virtù del teorema precedente:
+∞
X
f (t) =
cn e
j2πn Tt
(8.2.8)
0
n=−∞
essendo
1
cn =
T0
ˆ
a+T0
f (t) e
−j2πn Tt
0
dt
(8.2.9)
a
f (t) non è un segnale periodico di periodo T0 , la (8.2.8) vale solo per ogni istante
t dell'intervallo I = [a, a + T0 ].
Se f (t) è un segnale periodico di periodo T0 , la (8.2.8) vale per ogni istante di tempo
t e la costante reale a può essere qualunque: per esempio si può porre uguale a 0 oppure
T
uguale a − 0 . In questo caso si suole dire che sul segnale f (t) viene compiuta un'analisi
2
Se
di tempo
armonica.
La frequenza
f0 =
è detta
1
T0
(8.2.10)
armonica fondamentale, mentre la frequenza
fn = nf0 = n
è detta
armonica n-esima.
C 0 è il valore medio
Il coeciente
del segnale
ˆ
1
C0 =
T0
1
T0
f (t):
a+T0
f (t) dt
a
Proprietà
ˆ
Se
f (t)
è reale (cioè
f (t) = f (t)∗ )
allora
c−n = c∗n
Dimostrazione.
ˆ a+T0
1
j2πn Tt
0 dt =
c−n
f (t) e
dt =
f (t)∗ e
T0 a
a
ˆ a+T0
∗
ˆ a+T0 n
o
1
1
−j2πn Tt ∗
−j2πn Tt
0
0 dt
=
f (t) e
dt =
f (t) e
= c∗n
T0 a
T0 a
1
=
T0
ˆ
a+T0
(8.2.11)
j2πn Tt
0
274
(8.2.12)
8 Reti elettriche in regime periodico non sinusoidale
{c−n }∗ = cn
ˆ
Se
f (t)
è reale allora
ˆ
Se
f (t)
è reale e pari allora
ˆ
Se
f (t)
è reale e dispari allora
ˆ
teorema di Parseval:
ˆ
1
T0
cn
è reale
cn
a+T0
è immaginario puro
+∞
X
2
cn |f (t)|2 dt =
a
(8.2.13)
n=−∞
Dimostrazione
Si deve tener conto che
f (t)
è una funzione complessa di variabile reale e quindi
|f (t)|2 = f (t) f (t)∗
1
T0
(si scrivono
ˆ
a+T0
a
f (t) ed f (t)∗
1
|f (t)| dt =
T0
ˆ
a+T0
2
f (t) f (t)∗ dt =
a
in serie di Fourier; per non confondere i due sviluppi in serie
si usano due indici dierenti)
1
=
T0
ˆ
+∞
X
a+T0
a
+∞
X
j2πn Tt
cn e
0
n=−∞
−j2πm Tt
c∗m e
0
dt =
m=−∞
ˆ a+T0
+∞
+∞
+∞
+∞
1 X X
1 X X
j2π(n−m) Tt
∗
0
=
dt =
cn cm
e
cn c∗m T0 δnm =
T0 n=−∞ m=−∞
T0 n=−∞ m=−∞
a
(per
n=m
si ha che la delta di
=
Kronecker
+∞
X
+∞
X
vale uno,δnm
cn c∗n =
+∞
X
= 1)
|cn |2
n=−∞
n=−∞ n=−∞
8.2.4.1 Forma trigonometrica o cartesiana della seirie di Fourier
La forma trigonometrica o cartesiana della serie di Fourier si determina manipolando la
(8.2.8):
f (t) =
+∞
X
j2πn Tt
cn e
0
=
n=−∞
+∞ n
+∞ n
o
o
X
X
j2πn Tt
j2πn Tt
−j2πn Tt
2πn Tt
0
0
0 + cn e
0
= C0 +
c−n e
+ cn e
= C0 +
c∗n e
=
n=1
n=1
+∞ nh
i
o
X
j2πn Tt ∗
2πn t
0
= C0 +
cn e
+ cn e T0 =
n=1
275
8 Reti elettriche in regime periodico non sinusoidale
Tenendo conto che la somma tra 2 numeri complessi e coniugati è uguale a due volte
+ jb) + (a − jb) = 2a),
la parte reale ((a
f (t) = C0 +
+∞ nh
X
j2πn Tt
cn e
i∗
quest'ultima espressione si scrive:
j2πn Tt
+ cn e
0
o
0
= c0 + 2
n=1
= C0 + 2
+∞
X
n=1
+∞
X
o
n
j2πn Tt
0
=
Re cn e
n=1
t
t
+ j sin 2πn
=
Re {Re {cn } + j Im {cn }} cos 2πn
T0
T0
+∞
X
t
t
Re {cn } cos 2πn
− Im {cn } sin 2πn
+
T0
T0
n=1
t
t
+ Im {cn } cos 2πn
=
+j Re {cn } sin 2πn
T0
T0
= C0 + 2
= C0 + 2
Re
+∞ X
n=1
t
t
Re {cn } cos 2πn
− Im {cn } sin 2πn
T0
T0
Ovvero:
f (t) = C0 +
+∞
X
n=1
X
+∞
t
t
2Re {cn } cos 2πn
+
−2Im {cn } sin 2πn
T0
T0
Resta da capire chi sono
1
cn =
T0
ˆ
a+T0
f (t) e
1
=
T0
Re {cn }
ˆ
a
a+T0
Im {cn }.
e
1
0 dt =
T0
−j2πn Tt
a
(8.2.14)
n=1
ˆ
t
f (t) cos 2πn
T0
a+T0
a
Esplicitando (8.2.9) si ha:
t
t
f (t) cos 2πn
− j sin 2πn
=
T0
T0
1
dt − j
T0
ˆ
a+T0
a
t
f (t) sin 2πn
T0
dt
Da quest'ultima espressione si vede subito che:
ˆ
a+T0
t
f (t) cos 2πn
dt = an
T0
a
ˆ a+T0
t
2
− 2Im {cn } =
f (t) sin 2πn
dt = bn
T0 a
T0
2
2Re {cn } =
T0
(8.2.15)
(8.2.16)
sostituendo (8.2.15) e (8.2.16) in (8.2.14) si ottiene:
f (t) = C0 +
+∞
X
n=1
X
+∞
t
t
an cos 2πn
+
bn sin 2πn
T0
T0
n=1
276
(8.2.17)
8 Reti elettriche in regime periodico non sinusoidale
Posto
an = Cn cos ϕn
e
bn = Cn sin ϕn
la (8.2.17) si può scrivere come segue:
+∞ X
t
t
+ Cn sin ϕn sin 2πn
=
f (t) = C0 +
Cn cos ϕn cos 2πn
T0
T0
n=1
= C0 +
+∞
X
n=1
t
Cn cos 2πn − ϕn
T0
Secondo (8.2.18) è evidente che un segnale
la somma tra una costante
frequenze
C0
f (t)
(8.2.18)
periodico di periodo
T0
risulta essere
e una combinazione lineare di segnali sinusoidali aventi
fn = nf0 = n T10 .
In Figura 8.2.1 viene riportata una circonferenza goniometrica di raggio
possono ricavare le relazioni esistenti tra i coecienti
an , bn
e
Figura 8.2.1: circonferenza goniometrica di raggio
Cn2 = a2n + b2n
ϕn = arctan
bn
an
Cn
da cui si
Cn :
Ck
(8.2.19)
(8.2.20)
8.2.5 Rappresentazione spettrale dei segnali periodici non sinusoidali
f (t) un segnale periodico
F (f (t)) (f ) è a righe:
Sia
di periodo
F (f (t)) (t) =
T0 ,
+∞
X
n=1
essendo:
277
allora si ha che il suo spettro bilatero
cn δ (f − nf0 )
(8.2.21)
8 Reti elettriche in regime periodico non sinusoidale
1
cn =
T0
ˆ
a+T0
f (t) e
−j2πn Tt
0
dt
(8.2.22)
a
f0 =
1
T0
(8.2.23)
Dimostrazione.
Visto che
f (t) è un segnale periodico di periodo T0 , si può sviluppare in serie di Fourier:
+∞
X
f (t) =
cn e
j2πn Tt
0
n=−∞
essendo
1
cn =
T0
ˆ
a+T0
f (t) e
−j2πn Tt
0
dt
a
Applicando la trasformata di Fourier si ottiene la tesi
ˆ
+∞
X
+∞
F (f (t)) (f ) =
j2πn Tt
cn e
0
dt =
−∞ n=−∞
F (f (t)) =
ˆ
+∞
X
+∞
cn
e
j2πn Tt
0
dt =
−∞
n=−∞
+∞
X
cn δ (f − nf0 )
−∞
Teorema
Sia
f (t)
un segnale periodico di periodo
f (t) =
+∞
X
T0
rappresentato da
allora i coecienti
cn ej2πnf0 t
n=−∞
n=1
con
+∞
X
h (t − nT0 ) =
(
f (t) per |t| < T0 /2
h (t) =
0
altrove
cn
sono dati da:
cn = f0 F (h (t)) (nf0 )
8.2.6 Energia media normalizzata di un segnale periodico non sinusoidale
Secondo (3.3.20) l'energia media normalizzata di un segnale
ˆ
2
E =< f (t) >=
278
T0
2
T
− 20
f 2 (t) dt
f (t)
è data da:
8 Reti elettriche in regime periodico non sinusoidale
Tenendo conto del teorema di Parseval dato in (8.2.13) nel caso in cui si scegli la
costante reale
a
pari a
− T20 ,
è ovvio che l'energia media normalizzata si può scrivere
come segue:
ˆ
T0
2
2
E =< f (t) >=
T
− 20
f (t) dt = T0
|cn |2 =
n=−∞
(
C02 + 2
= T0
+∞
X
2
+∞
X
)
|cn |2
(8.2.24)
n=1
La (8.2.21) si può ulteriormente manipolare; basta scrivere
cn
in forma cartesiana e
utilizzare i risultati in (8.2.15) e (8.2.16):
1
1
cn = Re {cn } + j Im {cn } = an − j bn
2
2
Da quest'ultima espressione si ricava facilmente il modulo al quadrato di
1
1
|cn |2 = a2n + b2n
4
4
cn :
(8.2.25)
Sostituendo (8.2.22) in (8.2.21) si ottiene:
+∞
(
1X 2
an + b2n
+
2
C02
E = T0
)
(8.2.26)
n=1
Utilizzando (8.2.20) si ottiene:
+∞
(
C02
E = T0
1X 2
Cn
+
2
)
(8.2.27)
n=1
Denendo i coecienti
Cn
Cnef f. = √
2
(8.2.28)
La (8.2.37) si scrive:
(
E = T0
C02 +
+∞
X
)
Cn2ef f.
(8.2.29)
n=1
Il risultato in (8.2.29) è noto con il nome di Teorema di Pitagora. Dividendo l'energiamedia normalizzata per il periodo
T0
si ottiene il quadrato del valore ecace del segnale
f (t):
2
Fef
f.
1
=
T0
ˆ
T0
2
−
T0
2
2
f (t) dt =
C02
+
+∞
X
n=1
279
Cn2ef f.
(8.2.30)
8 Reti elettriche in regime periodico non sinusoidale
8.2.7 Valore ecace di un segnale periodico non sinusoidale
Dopo aver introdotto l'analisi armonica, in questa sezione viene approfondito il concetto
di valore ecace.
Si consideri un resistore di resistenza R attraversato da una corrente
i (t):
Figura 8.2.2: resistore lineare tempo invariante
Se
i (t)
è una corrente costante
nell'intervallo di tempo
[0, T0 ]
I0 ,
l'energia dissipata dal resistore per eeto jolule
è data da:
εT = R I02 T0
(8.2.31)
Se lo stesso resistore è attraversato da una corrente
i (t)
periodica di periodo
T0 ,
l'energia dissipata per eetto joule nello stesso intervallo di tempo è:
ˆ
T0
εT = R
i2 (t) dt
(8.2.32)
0
Uguagliando le relazioni in (2.2.31) e (2.2.32) si trova una formula per caratterizzare
il
valore ecace
della corrente
i (t)
periodicadi periodo
ˆ
R I02 T0
T0
=R
T0 :
i2 (t) dt ⇒
0
s
Ief f. = I0 =
Ief f.
I0 che
Il valore ecace
corrente costante
di una corrente
1
T0
i (t)
ˆ
T0
i2 (t) dt
periodica di periodo
uendo sulla stesso resistore di resistenza
stesso eetto joule nello stesso intrervallo di tempo
T0 .
Esempio 1
Consideriamo la corrente elettrica sinusoidale
t
i (t) = I cos 2π + ϕ
T0
periodica di periodo
T0 .
Utilizzano (8.2.33) si trova il suo valore ecace:
280
(8.2.33)
0
T0 è quel valore
R0 , produrrebbe
di
lo
8 Reti elettriche in regime periodico non sinusoidale
s
Ief f. = I0 =
1
T0
ˆ
T0
0
s
ˆ T0
t
t
I
2
2
2
cos 2π + ϕ dt
I cos 2π + ϕ dt = √
T0
T0
T0
0
(8.2.34)
Si tratta di risolvere il seguente integrale denito:
ˆ
0
T0
t
cos 2π + ϕ dt
T0
2
Integrando per parti si ha:
ˆ
ˆ
t
T0
t
2π T0
t
t
2
cos 2π + ϕ dt =
sin 2π + ϕ cos 2π + ϕ +
sin 2π + ϕ dt =
T0
2π
T0
T0
T0 2π
T0
2
ˆ T0
t
t
t
2
=
1 − cos 2π + ϕ
dt =
sin 2π + ϕ cos 2π + ϕ +
2π
T0
T0
T0
ˆ
ˆ
T0
t
t
t
2
=
sin 2π + ϕ cos 2π + ϕ + 1 dt − cos 2π + ϕ dt
2π
T0
T0
T0
ˆ
Ovvero:
ˆ
t
t
t
T0
t
2
sin 2π + ϕ cos 2π + ϕ + t − cos 2π + ϕ dt
dt =
cos 2π
T0
2π
T0
T0
T0
2
Trasportando al primo membro l'integrare presente al secondo membro e dividendo
tutti i termini dell'equazione per 2 si ottiene l'integrale indenito:
ˆ
t
t
t
t
T0
cos 2π
sin 2π + ϕ cos 2π + ϕ +
dt =
T0
4π
T0
T0
2
2
Inne applicando la formula di Laibnitz si ottiene il valore dell'integrale denito
ˆ
T0
cos
2
0
=
t
2π
T0
T0 T0
T0
t
t
t
dt =
sin 2π + ϕ cos 2π + ϕ
+
=
4π
T0
T0
2
0
0
T0
T0
T0
sin (2π + ϕ) cos (2π + ϕ) −
sin ϕ cos ϕ +
−0=
4π
4π
2
=
T0
T0
T0
T0
sin ϕ cos ϕ −
sin ϕ cos ϕ +
=
4π
4π
2
2
(8.2.35)
Sostituendo (8.2.35) in (8.2.34) si ottiene inne:
Ief f.
I
= I0 = √
T0
r
T0
I
=√
2
2
(8.2.36)
e con ciò resta provato che il valore ecace di una grandezza sinusoidale risulta uguale
al suo valore massimo diviso la radice quadrata di due.
281
8 Reti elettriche in regime periodico non sinusoidale
Esempio 2
Si consideri il segnale di tensione
v (t)
mostrato in Figura 8.2.3
Figura 8.2.3: onda quadra di periodo
T
T . Il suo valore ecace risulta:
v
v
r
r
u ˆ T
u ˆ A
u1
u1
2
2
1 2
A
t
t
2
2
= V0 =
V A=V
v (t) dt =
V dt =
T −T
T −A
T
T
Si tratta si un'onda quadra di periodo
Vef f.
2
Si osservi che se è
A=
2
T
2 allora
V
Vef f. = V0 = √
2
se è
A=
T
3 allora
V
Vef f. = V0 = √
3
8.3 Risposta a regime periodico non sinusoidale
Consideriamo la rete elettrica a regime periodico non sinusoidaale mostrata in Figura
8.3.1.
Figura 8.3.1: rete elettrica a regime periodico non sinusoidale
Si vuole determinare la tensione a regime ai capi di
282
R2 .
8 Reti elettriche in regime periodico non sinusoidale
La presenza del generatore periodico non sinusoidale imponone di condurre l'analisi
armonica. Visto che il segnale
vg (t)
è periodico di periodo
T,
esso in serie di Fourier si
scrive:
vg (t) = V0 +
+∞
X
n=1
X
+∞
t
t
an cos 2πn
bn sin 2πn
+
T
T
(8.3.1)
n=1
dove:
1
V0 =
T
ˆ
1
= V
T
2
an =
T
=
ˆ
− T4
T
2
− T2
1
vg (t) dt =
T
T
V
V
dt = [t]−4 T =
T
T
4
ˆ
T
4
V dt =
− T4
T
T
+
4
4
=
V
2
(8.3.2)
ˆ T
4
t
2
t
vg (t) cos 2πn
dt =
V cos 2πn
dt =
T
T −T
T
T
2
− T2
2
T
V
T 2πn
T
4
ˆ
4
ˆ
T
4
− T4
T
4
2πn
t
V
t
cos 2πn
=
dt =
sin 2πn
T
T
πn
T
−T
4
π i
V h π =
sin
n − sin − n =
πn
2
2
π V
sin
n
=2
πn
2
2
bn =
T
ˆ
T
2
− T2
(8.3.3)
ˆ T
4
2
t
t
dt =
dt =
vg (t) sin 2πn
V sin 2πn
T
T −T
T
4
=−
V
t
cos 2πn
nπ
T
T
4
− T4
= 0 ∀n ∈ N
(8.3.4)
Sostituendo (8.3.2), (8.3.3) e (8.3.4) in (8.3.1) si ottiene:
+∞
π X
V
t
vg (t) = V0 +
2
sin
n cos 2πn
πn
2
T
n=1
Esplicitando alcuni termini la serie in (8.3.5) si scrive:
V
2V
t
2V
t
vg (t) =
+
cos 2π
+0−
cos 6π
+ 0+
2
π
T
3π
T
2V
2V
t
t
+
cos 10π
+0−
cos 14π
+ .....
5π
T
7π
T
283
(8.3.5)
8 Reti elettriche in regime periodico non sinusoidale
Inne per rendere tutti i termini positivi, laddove occore si applica la proprietà degli
cos α = − cos (α + π):
V
2V
2V
t
t
vg (t) =
+0+
+
cos 2π
cos 6π + π + 0+
2
π
T
3π
T
2V
t
t
2V
+0+
cos 10π
cos 14π + π + .....
+
5π
T
7π
T
(8.3.6) il generatore ideale di tensione vg (t) risulta equivalente a un
archi associati
Secondo
(8.3.6)
generatore
costante di tensione e un insieme innito numerabile di generatori sinusoidali connessi in
serie.
Quindi il circuito dato risulta equivalente a quello mostrato in Figura 8.3.2.
Figura 8.3.2: rete elettrica a regime periodico non sinusoidale
essendo
V0 =
V
2,
vg5 (t) =
vg1 (t) =
2V
5π
2V
π
cos 2π Tt
cos 10π Tt
,
vg2 (t) = 0, vg3 (t) =
2V
3π
cos 6π Tt + π
,
vg4 (t) = 0,
e così via.
Da quest'ultima successione di funzioni segue che il generico generatore
vgn (t)
con
n
pari risulta nullo:
vgn (t) = 0
mentre per n dispari vale:
2V
t
vgn (t) =
cos 2πn + ϕn
nπ
T
essendo
(
0
ϕn =
π
se n = 1, 5, 9, ....
se n = 3, 7, 11, ..
(8.3.7)
(8.3.8)
Facendo agire per volta i generatori e applicando la sovrapposizione degli eetti si
determina facilmente l'integrale particolare dell'equazione dierenziale di ordine minimo,
ovvero la tensione ai capi del resistore di resistenza
284
R2
a regime.
8 Reti elettriche in regime periodico non sinusoidale
Se agisce il generatore di tensione costante
V0 ,
si ha che a regime il capacitore è
equivalente ad un circuito aperto mentre l'induttore è equivalente ad un cortocircuito
come mostrato in Figura 8.3.3:
Figura 8.3.3: rete elettrica
Si ha facilmente
R2
R2 V
V0 =
R1 + R2
R1 + R2 2
Se agisce il generico generatore sinusoidale vgn (t) con n dispari, si studia la
dominio dei fasori. Il fasore corrispondente al generatore vgn (t) è chiaramente:
(0)
v2 =
2V jϕn
e
V̇gn = √
2nπ
(8.3.9)
rete ne
(8.3.10)
In Figura 8.3.4 viene mostrata la rete elettrica nel dominio dei fasori
Figura 8.3.4: rete elettrica nel dominio dei fasori
Guardando il circuito si ha che:

V̇c(n) =
V̇ (n) =
2
Żp
V̇
Ż1 +Żp gn
(n)
Ż2
V̇
ŻL +Ż2 c
(n)
⇒ V̇2
285
=
Żp
Ż2
V̇gn
ŻL + Ż2 Ż1 + Żp
(8.3.11)
8 Reti elettriche in regime periodico non sinusoidale
Essendo
Ż1 = R1 , Ż2 = R2 , ŻL = jωL, Żc =
Żp =
1
jωC
1
jωC
(R2 + jωL)
+ R2 + jωL
=
1
jωC
(8.3.12)
R2 + jωL
1 + jωR2 C + (jω)2 LC
(8.3.13)
Sostituendo (8.3.12) e (8.3.13) in (8.3.11) si ottiene:
(n)
V̇2
=
R2
V̇gn
R1 LC (jω) + (L + R1 R2 C) jω + R1 + R2
(8.3.14)
2
Inne sostituendo (8.3.10) in (8.3.14) si ottiene:
(n)
V̇2
=
R2
2V jϕn
√
e
R1 LC (jω) + (L + R1 R2 C) jω + R1 + R2 2nπ
(8.3.15)
2
Assumendo che sia
R1 = R2 = 1Ω, L = 1H, C = 1F, V = 5V
la (8.3.15) si scrive:
(n)
V̇2
=
1
10 jϕn
√
e
(jω) + 2jω + 2 2nπ
(8.3.16)
2
Dalla (8.3.7) si vede facilmente che la pulsazione
ω=
ω
è:
2π
n
T
(8.3.17)
e pertanto la (8.3.16) si scrive:
(n)
V̇2
=
= r
10 jϕn
√
=
e
2nπ
+ 2j 2π
n
+
2
T
1
=
j 2π
T n
2−
2
1
4π 2 2
n
T2
+j
4π
T n
10 jϕn
e
=
√
2nπ
1
2T 2 −4π 2 n2
T2
2
+
4π
T n
2 j arctan
e
4πn
2T 2 −4π 2 n2
T
10 j
√
=p
e
4
4
4
2
2
2
4T + 16π n + 16π n (1 − T ) 2nπ
Scrivendo la (8.3.18) nel dominio del tempo si ha:
286
n
10 jϕn
√
e
=
2nπ
ϕn −arctan
4πn
2T 2 −4π 2 n2
o
(8.3.18)
8 Reti elettriche in regime periodico non sinusoidale
(n)
v2 (t)
=
10T
nπ
p
cos
4T 4 + 16π 4 n4 + 16π 2 n2 (1 − T 2 )
2πn
t + ϕn − arctan
T
4πn
2
2T − 4π 2 n2
(8.3.19)
Sovrapponendo tutti gli eetti si determina l'espressione della tensione ai capi del
resistore
R2 :
v2 (t) =
(0)
v2
+
+∞
X
(n)
v2 (t)
con n = 1, 3, 5, ..
(8.3.20)
n=1
che risulta essere un segnale periodico non sinusoidale di periodo
T.
Proposizione.
Per una rete a regime periodico non sinusoidale vale il principio di sovrapposizione
delle potenze
Si dimostra che per una rete a regime periodico non sinusoidale vale il principio di
sovrapposizione delle potenze poichè le sue armoniche godono della proprietà dell'ortogonalità.
La potenza attiva dissipata dal resistore
R2
per eetto joule è data da:
2
P2 = R2 Ief
f.
(8.3.21)
v2 (t), si può scrivere la corrente i2 (t) in serie di Fourier.
2
corrente ecace, Ief f. , si ottiene sommando al quadrato della
Così come fatto con la tensione
Pertanto il quadrato della
componente continua del segnale, i quadrati dei valori ecaci dei contributi di corrente
dovute alle armoniche di
i2 (t)
per il principio di sovrapposizione delle potenze. Cioè se
per esempio è
i2 (t) = I0 +
+∞
X
n=1
t
In cos 2πn − ϕn
T0
(8.3.22)
allora
+∞
X
I
√n
I02 +
2
n=1
(
P2 = R2
Nota.
)
(8.3.23)
Il principio di sovrapposizione delle potenze non vale in generale.
Per dimostrare quanto detto si consideri una rete elettrica avente due generatori
sinusoidale come indicato in Figura 8.3.5.
La potenza istantanea dissipata dal resistore
R2
è:
p2 (t) = R2 i22 (t)
La corrente
i2 (t)
per il principio di sovrapposizione vale:
287
(8.3.24)
8 Reti elettriche in regime periodico non sinusoidale
Figura 8.3.5: rete elettrica
0
00
i2 (t) = i2 (t) + i2 (t)
(8.3.25)
Quindi sostituendo (8.3.25) in (8.3.24) si ottiene:
0
2
00
p2 (t) = R2 i2 (t) + i2 (t) =
0
2
00 2
0
00
= R2 i2 (t) + R2 i2 (t) + 2R2 i2 (t) i2 (t)
In (8.3.26) compare il termine di potenza spurio
validità del principio di sovrapposizione delle potenze.
288
0
00
2R2 i2 (t) i2 (t)
(8.3.26)
che dimostra la non
9 Teoremi sulle reti elettriche
In questo capitolo vengono proposti i teoremi delle reti elettriche. Diciamo n da subito
che essi non semplicano la complessità di una rete elettrica.
Ciò vuol dire che se si
applica uno dei teoremi delle reti elettriche ad un circuito del secondo ordine rimarrà
sempre un circuito del secondo ordine con la sua complessità.
Tuttavia in casi molto
semplici, i teoremi sulle reti elettriche possono semplicare la rete dal punto di vista
computazionale. La loro utilità è prevalentemente teorica.
Di seguito si discuterà dei seguenti teoremi:
ˆ
teorema di sostituzione
ˆ
teorema di sovrapposizione degli eetti
ˆ
teorema di Tellegen
ˆ
teorema di Thevenin/Norton
ˆ
teorema di reciprocità
ˆ
teorema del massimo trasferimento di potenza
9.1 Teorema di sostituzione
Supponiamo di avere una rete elettrica che può essere lineare, non lineare con soluzione
unica
{vk (t) , ik (t)}
come mostrato in Figura 9.1.1.
Figura 9.1.1: rete elettrica
Supponiamo di sostituire al lato k-esimo della rete, un generatore di tensione
come mostrato in Figura 9.1.2.
Supponiamo inne che quest'ultima rete detta
unica.
289
vk (t),
rete modicata continui ad avere soluzione
9 Teoremi sulle reti elettriche
Figura 9.1.2: rete elettrica
Sotto queste ipotesi si ha che la parte rimanente della rete elettrica non si accorge del
cambiamento. Cioè il lato h-esimo ha la stessa tensione e la stessa corrente anche doppo
che è stato eettuato il cambiamento.
E' evidente che anchè ciò sia possibile, sul lato k-esimo deve scorrere sempre la
corrente
ik (t).
La dimostrazione di tale teorema è banale, infatti basta scrivere tutte le LK della rete
di partenza e della rete modicata e far vedere che non cambiano.
Si osservi che questo teorema in realtà è stato già applicato durante questo corso. Si
pensi per esempio a tutte quelle situazioni in cui il contenuto energetico iniziale di un
dispositivo a memoria veniva modellato con un generatore ideale equivalente.
9.2 Sovrapposizione degli eetti
Supponiamo di avere una rete elettrica lineare con stato zero che può essere tempo
variante o tempo invariante e supponiamo che abbia almeno due sollecitazioni (Figura
9.2.1).
Figura 9.2.1: rete elettrica
Si osservi che in Figura 9.2.1 sono stati evidenziati la tensione
rete e la corrente
icc (t)
v0 (t) tra due nodi della
che attraversa un qualunque cortocircuito della rete.
290
9 Teoremi sulle reti elettriche
Supponiamo di fare agire per volta le eccitazioni come mostrato in Figura 9.2.2.
Figura 9.2.2: rete elettrica
Allora si ha che:
0
00
v0 (t) = v0 (t) + v0 (t)
0
00
icc (t) = icc (t) + icc (t)
(9.2.1)
(9.2.2)
Se i generatori che eccitano la rete elettrica lineare con stato zero hanno la stessa
frequenza di oscillazione, allora la sovrapposizione degli eetti si può applicare sia nel
dominio del tempo che nel dominio dei fasori; viceversa se i generatori oscillano a frequenze dierenti, la sovrapposizione degli eetti non si può applicare direttamente nel
dominio dei fasori.
In questo caso quello che si fa è passare dal dominio dei fasori al
dominio del tempo e poi applicare la sovrapposizione degli eetti. Il teorema di sovrapposizione degli eetti si può applicare anche nel dominio di Laplace e nel dominio di
Fourier.
Figura 9.2.3: rete elettrica in presenza di generatori pulsanti a dierente frequenza
9.2.1 Esempio
Data la rete elettrica mostrata in Figura 9.2.3, si vuole determinare la risposta a regime
vcpart. (t).
291
9 Teoremi sulle reti elettriche
L'integrale particolare va ricercato applicando il metodo dei fasori e il teorema di
sovrapposizione degli eetti visto che la rete elettrica è in presenza di generatori pulsanti
a dierente frequenza.
Possiamo studiare la rete a partire dalla conoscenza dell'equazione dierenziale di
ordine minimo, tuttavia con il seguente esempio si vuole fare vedere anche come si
può scrivere la risposta a regime utilizzando alcune semplici regole, come il partitore
di tensione.
La rete elettrica nel dominio dei fasori quando agisce soltanto il generatore di tensione
ideale
vg (t)
viene mostrata in Figura 9.2.4.
Figura 9.2.4: rete elettrica sollecitata esclusivamente dal generatore di tensione
Utilizzando la regola del partitore di tensione si ha:
0
V̇c =
Żp
V̇g
Żp + Ż1
(9.2.3)
Tenendo conto che
Ż1 = 1 Ω
Żc ŻL + Ż2
Żp =
Żc + ŻL + Ż2
=
1
jω (jω + 1)
1
jω + jω + 1
=
1 + jω
Ω
1 + jω + (jω)2
l'espressione in (9.2.3) si scrive:
0
V̇c =
inoltre visto che
1+jω
1+jω+(jω)2
1+jω
+
1+jω+(jω)2
ω = 2 rad/s
1
V̇g =
1 + jω
V̇g
2 + 2jω + (jω)2
si ha:
√
1 + j2
5∠ arctan 2
V̇c =
V̇g = √
V̇g
2 (−1 + j2)
2 5∠π − arctan 2
0
Esplicitando il fasore
V̇g
si ha:
292
9 Teoremi sulle reti elettriche
√
5
5∠ arctan 2 10
√ ∠0 = √ ∠ − π + 2 arctan 2
V̇c = √
2 5∠π − arctan 2 2
2
0
(9.2.4)
Inne trasportando nel dominio del tempo la (9.2.4) si ottiene:
0
vcpart. (t) = 5 cos (2t + π − 2 arctan 2)
(9.2.5)
La rete elettrica nel dominio dei fasori quando agisce soltanto il generatore di corrente
ideale
ig (t)
viene mostrata in Figura 9.2.5.
Figura 9.2.5: rete elettrica sollecitata esclusivamente dal generatore di tensione
Il fasore della tensione ai capi del capacitore quando agisce il generatore di corrente è:
1 ˙
00
V̇c = Żc I˙c =
Ic
jω
(9.2.6)
Occorre quindi determinare il fasore della corrente che interessa il capacitore; quest'ultima si ricava applicando due volte la legge del partitore di corrente:
I˙c =
Ż2
Ż1
I˙g
Ż2 + ŻL + Żp1 Ż1 + Żc
Tenendo conto che
Ż1 = 1 Ω, Ż2 = 1 Ω, Żc =
1
jω
Ω, ŻL = jΩ Ω
1
Żp1 =
Ż1 Żc
1
jω
=
1 = 1 + jω
1 + jω
Ż1 + Żc
la (9.2.7) si scrive:
Sostituendo (9.2.8) in (9.2.6) si ottiene:
V̇c =
1
1
jω 1 + jω +
1
1+jω
293
1 ˙
1 Ig =
1 + jω
(9.2.7)
9 Teoremi sulle reti elettriche
=
1
1 + jω +
1
1+jω
1
I˙g =
1 + jω
1
I˙g
(1 + jω)2 + 1
=
Ovvero:
00
V̇c =
Inoltre visto che
ω = 1 rad/s
si ha:
00
V̇c =
Esplicitando il fasore
00
I˙g
1
I˙g
(jω) + 2jω + 2
2
1 ˙
1∠0
Ig = √
I˙g
1 + j2
5∠ arctan 2
si ha:
V̇c = √
1∠0
20 π
20
π
√ ∠ = √ √ ∠ − arctan 2
5∠ arctan 2 2 2
2 5 2
(9.2.8)
Inne trasportando nel dominio del tempo la (9.2.8) si ottiene:
π
20
00
vcpart. (t) = √ cos t − + arctan 2
2
5
(9.2.9)
Sovrapponendo i contributi in (9.2.5) e (9.2.9) si ricava la risposta a regime:
20
π
vcpart. (t) = 5 cos (2t + π − 2 arctan 2) + √ cos t − + arctan 2
2
5
(9.2.10)
Si osservi che la sovrapposizione è stata fatta nel dominio del tempo e non nel dominio
dei fasori.
9.3 Teorema di Tellegen
Supponiamo di avere due reti elettriche
ΠA
e
ΠB
aventi lo stesso grafo
G.
Supponiamo
che per ciascun lato del grafo si adotti la convenzione dell'utilizzatore (Figura 9.3.1).
Allora si ha che:
L
X
(A)
(t1 ) ik
(t2 ) = 0
(9.3.1)
(B)
(t1 ) ik (t2 ) = 0
(9.3.2)
vk
(B)
k=1
L
X
vk
(A)
k=1
Ovviamente gli apici (A) e (B) servono soltanto per distingure la rete
ΠB .
294
ΠA
dalla rete
9 Teoremi sulle reti elettriche
Figura 9.3.1: rete elettriche aventi lo stesso grafo
G
Dimostrazione 1.
Visto che le reti hanno lo stesso grafo
G,
ossia le stesse LK, si deve fare vedere che il
vettore delle tensioni di una delle due reti, per esempio
delle correnti dell'altra rete,
(A)
v (t1 ) , è ortogonale al vettore
(B)
i (t2 ) :
h
iT h
i
v (A) (t1 )
i(B) (t2 ) = 0
G e denendo i potenziali
t1 :
h
i h
i
[A]T e(A) (t1 ) = v (A) (t1 )
Ponendo a massa uno dei nodi del grafo
scrivere le
e le
LKC
LKT ∗
per la rete
per la rete
ΠB
ΠA
(9.3.3)
ai nodi si possono
al tempo
t2 :
h
i
[A] i(B) (t2 ) = [0]
(9.3.4)
all'istante
(9.3.5)
Si osservi che nelle espressini in (9.3.4) e (9.3.5) è stata utilizzata la stessa matrice di
incidenza nodi lati
[A],
G.
(A)
T (B)
v (t1 )
i (t2 )
visto che le reti hanno lo stesso grafo
Utilizzando le relazioni in (9.3.4) e (9.3.5) il prodotto
si scrive:
h
iT h
i n
h
ioT h
i
v (A) (t1 )
i(B) (t2 ) = [A]T e(A) (t1 )
i(B) (t2 ) =
h
iT
h
i h
iT
= e(A) (t1 ) [A] i(B) (t2 ) = e(A) (t1 ) [0] = 0
e ciò dimostra la tesi del teorema.
Si osservi che è stata utilizzata la proprietà delle matrici secondo cui il trasposto del
prodotto tra due matrici risulta uguale al prodotto delle matrici trasposte scambiate di
posto.
295
9 Teoremi sulle reti elettriche
Dimostrazione 2.
Per una rete elettica avente L lati le LKT e LKC sono dei sottospazi di un iperspazio
a L dimensioni.
Figura 9.3.2: iperspazio a L dimensioni
Il teorema si dimostra facendo vedere che i sottospazi LKT ed LKC sono ortogonali
tra di loro.
Ciò vuol dire che occorre far vedere che il prodotto scalare tra due basi
dei suddetti sottospazi risulta nulla. Una base di tensioni è una L-upla di tensioni che
soddisfa un sistema di L-N+1 leggi di Kirchho delle tensioni, mentre una base di correnti
è una L-upla di correnti che soddisfa un sistema di N-1 leggi di Kirchho delle correnti.
Supponiamo per semplicità che sia L=3 e consideriamo il grafo
G
mostrato in Figura
9.3.3. Si hanno allora L-N+1=2 LKT da cui è possibile ricavare una qualunque basi di
tensioni ed N-1=1 LKC da cui è possibile ricavare una qualunque base di correnti.
Figura 9.3.3: iperspazio a L dimensioni
Una qualunque base di tensioni che soddisfa le LKT
(
v1 (t) + v2 (t) = 0
v1 (t) + v3 (t) = 0
è per esempio:
(v1 (t) , v2 (t) , v3 (t)) = (10, −10, −10)
296
9 Teoremi sulle reti elettriche
mentre una qualunque base di correnti che soddisfa la LKC:
−i1 (t) + i2 (t) + i3 (t) = 0
è per esempio:
(i1 (t) , i2 (t) , i3 (t)) = (5, 2, 3)
Visto che il prodotto scalare tra la base delle tensioni e la base delle correnti sopra scritte
risulta:
(v1 (t) , v2 (t) , v3 (t)) · (i1 (t) , i2 (t) , i3 (t)) = 10 · 5 − 10 · 2, −10 · 3 = 0
resta provata nuovamente la tesi del teorema di Tellegen.
9.3.1 Teorema della conservazione della potenza istantanea
Per qualunque rete elettrica la somma algebrica tra tutte le potenze istantanee di lato
risulta identicamente nulla:
L
X
k=1
pk (t) =
L
X
vk (t) ik (t) = 0
(9.3.6)
k=1
La (9.3.6) è una diretta conseguenza del teorema di Tellegen; essa si ottiene da (9.3.1)
facendo coincidere le due reti,
Se per il grafo
G
ΠA = ΠB = Π,
e gli istanti di tempo,
t1 = t2 = t.
della rete elettrica si decide di distinguere il lati utilizzando sia la
convenzione del generatore che la convenzione dell'utilizzatore, la (9.3.6) si scrive:
0
L
X
(assorbite)
pk
(t)
=
(generate)
pk
(9.3.7)
k=L0 +1
k=1
In quest'ultima espressione,
L
X
0
L
rappresenta il numero di lati per i quali vale la conven-
zione dell'utilizzatore.
Esempio.
Consideriamo una qualunque rete elettrica il cui grafo
G
è quello mostrato in Figura ,
è immediato vericare la (9.3.6), infatti si ha:
6
X
pk (t) = 20 · 10 − 10 · 8 + 10 · 5 − 2 · 15 − 8 · 15 + 10 (−2) = 0
k=1
297
9 Teoremi sulle reti elettriche
Figura 9.3.4: grafo
G
9.3.2 Tesi del teorema di Tellegen nel dominio dei fasori
Se la rete elettrica si trova a regime sinusoidale, la tesi del teorema di Tellegen si può
scrivere nel dominio dei fasori in una delle seguenti forme equivalenti:
L
X
(A) ˙(B)
Ik
V̇k
=0
(9.3.8)
k=1
L
X
n
o
(B) ∗
I˙k
=0
(9.3.9)
L n
o
X
(A) ∗ ˙(B)
V̇k
Ik = 0
(9.3.10)
(A)
V̇k
k=1
k=1
L n
o n
o
X
(A) ∗
(B) ∗
V̇k
I˙k
=0
(9.3.11)
k=1
9.3.3 Teorema di Boucherot o della conservazione della potenza
I teoremi di Boucherot esprimono la conservazione della potenza nel dominio dei fasori
e si ricavano dalle espressioni in (9.3.8), (9.3.9), (9.3.10) e (9.3.11) facendo coincidere le
due reti,
ΠA = ΠB = Π.
ΠA coincide
Se la rete
con la rete
ΠB
L
X
la (9.3.9) si scrive:
V̇k
n o∗
I˙k = 0
k=1
298
(9.3.12)
9 Teoremi sulle reti elettriche
Osservando che
elettrica,
Ȧk ,
n o∗
V̇k I˙k
è la potenza complessa corrispondente al lato k-esimo della rete
la (9.3.12) si scrive:
L
X
Ȧk = 0
(9.3.13)
k=1
Tenendo conto inne del fatto che la potenza complessa corrispondente al lato k-esimo
si scrive
Ȧk = Pk + jQk ,
la (9.3.13) diventa:
L
X
(Pk + jQk ) = 0
(9.3.14)
k=1
da cui si ricavano i teoremi di Boucherot:
L
X
Pk = 0
(9.3.15)
Qk = 0
(9.3.16)
k=1
L
X
k=1
La somma algebrica tra tutte le potenze attive risulta identicamente nulla così come
la somma algebrica tra tutte le potenze reattive.
9.3.4 Tesi del teorema di Tellegen nel dominio di Laplace
Se la rete elettrica si trova a regime sinusoidale, la tesi del teorema di Tellegen si può
scrivere anche nel dominio di Laplace in una delle seguenti forme equivalenti:
L
X
(A)
(s) Ik
(B)
(s) Ik
Vk
(B)
(s) = 0
(9.3.17)
(A)
(s) = 0
(9.3.18)
k=1
L
X
Vk
k=1
ˆ
essendo
T
Vk (s) = L (vk (t)) (s) = lim
T →∞ 0
vk (t) e−st dt
(9.3.19)
la trasforma di Laplace della tensione del lato k-esimo e
ˆ
Ik (s) = L (ik (t)) (s) = lim
T →∞ 0
T
ik (t) e−st dt
(9.3.20)
la trasforma di Laplace della corrente del lato k-esimo in accordo con (3.3.34).
Ovviamente gli apici (A) e (B) servono soltanto per distingure la rete
ΠB .
299
ΠA
dalla rete
9 Teoremi sulle reti elettriche
Volendo si possono riscrivere i teoremi sulla conservazione della potenza come fatto nel
dominio dei fasori.
9.4 Teorema di Thevenin/Norton
Consideriamo una rete elettrica costituita da due bipoli compositi
Π e Π1
come mostrato
in Figura 9.4.1.
Figura 9.4.1: rete elettrica
Supponiamo che il bipolo composito
Π
sia una rete lineare tempo invariante oppura
anche tempo variante, contenete generatori ideali, generatori pilotati, resistori, capacitori, induttori, induttori mutuamente accoppiati e trasformatori ideali. Ovviamente le
grandezze di pilotaggio dei generatori pilotati devono essere grandezze relative al bipolo
Π stesso così come gli accoppiamenti negli induttori mutuamente accoppiati e nei trasformatori ideali devono avvenire tra grandezze relative al bipolo Π stesso altrimenti Π non
sarebbe più un bipolo. Si osservi che per il bipolo Π, tensione e corrente sono orientate
secondo la convenzione dell'utilizzatore.
Indichiamo con
i (t)
la corrente che attraversa il bipolo
Π1 ,
che può essere una rete
lineare o non lineare, tempo invariante o tempo variante e con
morsetti A e B del bipolo
Π.
300
v (t)
la tensione tra i
9 Teoremi sulle reti elettriche
Tesi di Thevenin
E' possibile sostituire al bipolo
Π,
un bipolo costituito dalla serie tra il
zato Π0 , ottenuto dal bipolo Π annullandovi i generatori ideali, e
bipolo passiviz-
il generatore ideale di
v0 (t), essendo v0 (t) la tensione a vuoto tra i morsetti A e B del bipolo Π, senza
bipolo Π1 senta il cambiamento (Figura 9.4.2).
tensione
che il
Figura 9.4.2: tesi di Thevenin
Il bipolo costituito dalla serie tra il bipolo passivizzato
v0 (t)
si chiama
bipolo Thevenin.
Π0
e il generatore di tensione
Tesi di Norton
E' possibile sostituire al bipolo Π, un bipolo costituito dal paralleo tra il bipolo passivizzato
Π0 , ottenuto dal bipolo Π annullandovi i generatori ideali, e il genera ideale di corrente
icc (t), essendo icc (t) la corrente che attraversa il cortocircuito tra i morsetti A e B del
bipolo Π, senza che il bipolo Π1 senta il cambiamento (Figura 9.4.3).
Il bipolo costituito dal parallelo tra il bipolo passivizzato Π0 e il generatore ideale di
corrente v0 (t) si chiama bipolo Norton.
301
9 Teoremi sulle reti elettriche
Figura 9.4.3: tesi di Norton
Dimostrazione nel dominio del tempo
Il teorema di thevenin/Norton vale nel dominio del tempo, nel dominio dei fasori, nel
dominio di Laplace, nel dominio di Fourier.
Dimostriamo la tesi di Thevenin nel dominio del tempo. In modoanalogo si dimostra
latesi di Norton.
La dimostrazione si basa sul teorema di sostituzione e sul teorema di sovrapposizione
degli eetti.
Si consideri la rete di Figura 9.4.1.
Siccome il bipolo
Π
è lineare allora
ammette un'unica soluzione e quindi per il teorema di sostituzione è possibile sostituire
il bipolo
Π1
con un generatore di corrente
i (t) ,come
mostrato in Figura 9.4.4:
Figura 9.4.4: rete elettrica equivalente
La tensione tra i morsetti A e B si ottiene applicando il teorema di sovrapposizione
degli eetti:
302
9 Teoremi sulle reti elettriche
0
00
v (t) = v (t) + v (t)
(9.4.1)
Quando agiscono soltanto i generatori ideali presenti all'interno del bipolo
Π,
la rete
da studiare è quella mostrata in Figura 9.4.5:
Figura 9.4.5: rete elettrica
Chiaramente la tensione tra i morsetti A e B e la tensione a vuoto:
0
v (t) = v0 (t)
(9.4.2)
Quando agisce soltanto il generatore ideale di corrente
i (t), la rete da studiare è quella
mostrata in Figura 9.4.6:
Figura 9.4.6: rete elettrica
Chiaramente la tensione tra i morsetti A e B,
passivizzato
Π0 .
00
v (t)
è la tensione ai capi del bipolo
Quindi è chiaro che sostituendo (9.4.2) in (9.4.1) si ottiene la relazione:
00
v (t) = v0 (t) + v (t)
da cui segue la tesi di Thevenin (Figura 9.4.7).
303
(9.4.3)
9 Teoremi sulle reti elettriche
Figura 9.4.7: rete elettrica
Il teorema di thevenin/Norton è molto importante dal punto di vista teorico ma di
scarsa utilità pratica. Per convincersi di questo fatto basta pensare che la rete elettrica
di partenza e quelle che si ottengono applicando la tesi di Thevenin o la tesi di Norton
hanno tutte la stessa
complessità,
infatti il numero di elementi a memoria in ogni caso
rimane lo stesso.
Non si pensi assolutamente al fatto che la complessità di un circuito elettrico dipenda dal numero di generatori presenti nella rete La complessità del circuito dipende dal
numero di condizioni iniziali.
Dimostrazione nel dominio dei fasori
Qui di seguito viene riproposta la rete di Figura 9.4.1 nel dominio dei fasori.
Figura 9.4.8: rete elettrica
Per i bipoli costituenti la rete elettrica di Figura 9.4.8 si possono scrivere le corrispondenti caratteristiche:
(
ȦV̇ + Ḃ I˙ + Ċ = 0̇
(9.4.4.1)
˙
Ȧ1 V̇ + Ḃ1 I1 + Ċ1 = 0̇ (9.4.4.2)
304
(9.4.4)
9 Teoremi sulle reti elettriche
con
Ȧ, Ḃ , Ċ , Ȧ1 , Ḃ1 , Ċ1
costanti
complesse.
moltiplicative
La coppia tensione corrente
V̇ , I˙
deve essere tale da soddisfare contemporaneamente
Π è per ipotesi lineare la sua carattteristica è lineare.
caratteristica del bipolo Π1 in quanto per quest'ultimo
le relazioni in (9.4.4). Siccome la rete
Lo stesso discorso non vale per la
è un bipolo qualunque.
Se è
Ȧ 6= 0̇,
la (9.4.4.1) si scrive:
V̇ = −
E' ovvio che il fattore moltiplicativo
tensione.
Dalla (9.4.5), per
I˙ = 0
− Ḃ
Ȧ
Ḃ ˙ Ċ
I−
Ȧ
Ȧ
è un'impedenza mentre il termine
− Ċ
Ȧ
è una
si ha che
V̇ = V̇0 = −
è la
(9.4.5)
tensione a vuoto tra i morsetti A e B
Ċ
Ȧ
del bipolo
(9.4.6)
Π
(Figura 9.4.9):
Figura 9.4.9: rete elettrica
Dalla (9.4.5), per
Ċ = 0
si ha che
Żeq. =
è l'impedenza del bipolo
Π
V̇
Ḃ
=−
˙
I
Ȧ
(9.4.7)
se e solo sè il bipolo è passivo (sezione 4.7.5), ovvero privo
di generatori ideali (Figura 9.4.10):
305
9 Teoremi sulle reti elettriche
Figura 9.4.10: rete elettrica
Sostituendo (9.4.6) e (9.4.7) in (9.4.5) si ha che
˙ I˙ + V̇0
V̇ = Zeq.
(9.4.8)
ovvero la tesi di Thevenin (Figura 9.4.11).
Figura 9.4.11: rete elettrica
Se è
Ḃ 6= 0̇,
la (9.4.4.1) si scrive:
Ȧ
Ċ
I˙ = − V̇ −
Ḃ
Ḃ
E' ovvio che il fattore moltiplicativo
corrente.
Dalla (9.4.9), per
V̇ = 0
Ȧ
− Ḃ
è un'ammettenza mentre il termine
(9.4.9)
Ċ
− Ḃ
è una
si ha che
Ċ
I˙ = I˙cc = −
Ḃ
306
(9.4.10)
9 Teoremi sulle reti elettriche
è la
corrente che attraversa il cortocircuito che collega i morsetti A e B
del bipolo
Π
(Figura 9.4.12):
Figura 9.4.12: rete elettrica
Dalla (9.4.9), per
Ċ = 0
si ha che
Ẏeq. =
è l'ammettenza del bipolo
I˙
Ȧ
=−
V̇
Ḃ
(9.4.11)
Π se e solo sè il bipolo è passivo (sezione 4.7.5), ovvero privo
di generatori ideali (Figura 9.4.13):
Figura 9.4.13: rete elettrica
Sostituendo (9.4.10) e (9.4.11) in (9.4.9) si ha che
I˙ = Ẏeq. V̇ + I˙cc
ovvero la tesi di Norton (Figura 9.4.14).
307
(9.4.12)
9 Teoremi sulle reti elettriche
Figura 9.4.14: rete elettrica
Se risulta
Ȧ 6= 0̇, Ḃ 6= 0̇,
esistono contemporaneamente il bipolo Thevenin e il bipolo
Norton. Per determinare le formule di passaggio dal lato Thevenin al lato Norton basta
rendere equivalenti le relazioni in (9.4.8) e (9.4.12). Moltiplicando tutti i termini della
(9.4.12) per
Żeq. ,
e isolando
V̇ ,
si ottiene:
V̇ = Żeq. I˙ − Żeq. I˙cc
(9.4.13)
Confrontando (9.4.8) con (9.4.13) si ha che deve essere:
V̇0 = −Żeq. I˙cc
(9.4.14)
1
I˙cc = −
V̇0
Żeq.
(9.4.15)
o equivalentemente:
La (9.4.14) è la formula di pasaggio che consente di trasformare il lato Norton mostrato
in Figura 9.4.14 nel lato Thevenin mostrato in Figura 9.4.11, mentre la (9.4.15) consente
di trasformare il lato Thevenin mostrato in Figura 9.4.11 nel lato Norton mostrato in
Figura 9.4.11.
Denendo la
e la
tensione di Thevenin:
V̇T h. = V̇0
(9.4.16)
I˙N. = −I˙cc
(9.4.17)
corrente di Norton
è chiaro che le relazioni in (9.4.14) e (9.4.15) si scrivono:
V̇T h. = Żeq. I˙N.
(9.4.18)
1
I˙N. =
V̇T h.
Żeq.
(9.4.19)
308
9 Teoremi sulle reti elettriche
Queste due relazioni sono le formule di trasformazione Thevenin/Norton quando il lato
Thevenin e il lato Norton sono come indicato in Figura 9.4.15.
Figura 9.4.15: trasformazione Thevenin/Norton
9.4.1 Esempio 1
Consideriamo la rete elettrica mostrata in Figura 9.4.16.
Figura 9.4.16: rete elettrica
Sappiamo già che il fasore della tensione ai capi del capacitore è (vedi relazione in
(4.7.24)):
V̇c =
1 + jω
1
V̇g +
I˙g
(2 − ω 2 ) + j2ω
(2 − ω 2 ) + j2ω
(9.4.20)
Si vuole determinare tale relazione applicando il Teorema di Thevenin/Norton tra i
nodi 2 e 4.
Utilizzando la tesi di Thevenin il circuito dato risulta equivalente al circuito mostrato
in Figura 9.4.17.
309
9 Teoremi sulle reti elettriche
Figura 9.4.17: rete elettrica
Il fasore
V̇c
, in quest'ultimo circuito si ricava applicando la legge del partitore di
tensione:
V̇c =
Tenendo conto che
Żc =
1
jωC
=
1
jω
Ω,
quest'ultima relazione si scrive:
V̇c =
L'impedenza equivalente
Żeq.
Żc
V̇T h.
Żc + Żeq.
1
V̇T h.
1 + jω Żeq.
(9.4.21)
si determina dal circuito mostrato in Figura 9.4.18
Figura 9.4.18: rete elettrica
Si trova immediatamente che essa risulta essere il parallelo tra
da
ŻL
e
Ż2 :
310
Ż1
e la serie costituita
9 Teoremi sulle reti elettriche
Ż1 ŻL + Ż2
Żeq. =
Tenendo conto cheŻ1
Ż1 + Ż2 + ŻL
= R1 = 1 Ω ,Ż2 = R2 = 1 Ω
,
ŻL = jωL = jω Ω,
quest'ultima
relazione si scrive:
Żeq. =
La tensione di Thevenin,
V̇T h. ,
1 + jω
2 + jω
(9.4.22)
si determina dal circuito mostrato in Figura 9.4.19
applicando il teorema di sovrapposizione degli eetti.
Figura 9.4.19: rete elettrica
Quando agisce soltanto
V̇g (I˙g
è un circuito aperto) si ha:
0
V̇T h. =
Ż2 + ŻL
V̇g
Ż1 + Ż2 + ŻL
ovvero:
0
V̇T h. =
Quando agisce soltanto
I˙g (V̇g
1 + jω
V̇g
2 + jω
(9.4.23)
è un cortocircuito) si ha:
00
V̇T h. = Ż1 I˙ = Ż1
Ż2
I˙g
Ż1 + Ż2 + ŻL
ovvero:
00
V̇T h. =
1
I˙g
2 + jω
Sommando i contributi in (9.4.23) 3 (9.4.24) si ottiene la tensione di Thevenin
311
(9.4.24)
V̇T h. :
9 Teoremi sulle reti elettriche
0
V̇T h. =
1
1 + jω
V̇g +
I˙g
2 + jω
2 + jω
(9.4.25)
Sostituendo (9.4.22) e (9.4.25) in (9.4.21) si ottiene:
2 + jω
V̇c =
2
(jω) + 2jω + 2
1 + jω
1
V̇g +
I˙g
2 + jω
2 + jω
cioè la (9.4.20).
Utilizzando la tesi di Norton il circuito dato in Figura 9.4.16 risulta equivalente al
circuito mostrato in Figura 9.4.20.
Figura 9.4.20: rete elettrica
Il fasore
V̇c
, in quest'ultimo circuito si ricava applicando la legge di Ohm:
V̇c =
Tenendo conto che
Żc =
1
jωC
=
1
jω
Ω,
quest'ultima relazione si scrive:
V̇c =
La corrente diNorton,
I˙N. ,
Żc Żeq. ˙
IN
Żc + Żeq.
Żeq.
I˙N.
1 + jω Żeq.
(9.4.26)
si determina dal circuito mostrato in Figura 9.4.21 appli-
cando il teorema di sovrapposizione degli eetti.
Quando agisce soltanto
V̇g (I˙g
è un circuito aperto) si ha:
V̇g
0
I˙N. =
Ż1
ovvero:
0
I˙N. = V̇g
312
(9.4.27)
9 Teoremi sulle reti elettriche
Figura 9.4.21: rete elettrica
Quando agisce soltanto
I˙g (V̇g
è un cortocircuito) si ha:
00
I˙N. =
Ż2
I˙g
Ż2 + ŻL
ovvero:
00
I˙N. =
1
I˙g
1 + jω
Sommando i contributi in (9.4.27) 3 (9.4.28) si ottiene la corrente di Norton
0
I˙N. = V̇g +
(9.4.28)
I˙N. :
1
I˙g
1 + jω
Sostituendo inne (9.4.22) e (9.4.29) in (9.3.26) si ottiene nuovamente (9.4.20).
313
(9.4.29)
9 Teoremi sulle reti elettriche
9.4.2 Esempio 2
Questo esempio vuole dimostrare che il teorema di Thevenin/Norton non è molto utile
dal punto di vista applicativo. Si consideri la rete elettrica mostrata in Figura 9.4.22.
Figura 9.4.22: rete elettrica
Si vuole determinare il fasore corrente
I˙,
applicando il teorema di Thevenin/Norton
tra i nodi A e B.
Si osservi innanzitutto che la serie costituita tra il generatore ideale di corrente
e l'impedenza
Ż
I˙g
risulta equivalente al solo
generatore. Si osservi pure che denendo
N=6 nodi si hanno L=9 lati e quindi risulta N-1=5 ed L-N+1=4; pertanto il metodo di analisi migliore per studiare tale rete
è quello delle correnti di maglia, tuttavia
cerchiamo di risolvere la rete applicando il
teorema di ùthevenin/Norton tra i nodi A
e B.
La tensione di Thevenin,
V̇T h. ,si
de-
termina a partire dal circuito mostratin
Figura 9.4.23
L'impedenza equivalente vista dai morsetti A e B, quando tutti i generatori ideali
Figura 9.4.23:
sono spenti si calcola a partire dal circuito
mostrato in Figura 9.4.24.
Come si può
ben vedere risulta impossibile trovare l'impedenza equivalente cercando di individuare
impedenze in serie o in parallelo. Per determinare l'impedenza equivalente, occorre in
314
9 Teoremi sulle reti elettriche
questo caso sapere le formule di trasformazione stella-triangolo che ancora non sono state
introdotte.
Figura 9.4.24: rete elettrica
Quindi stiamo trovando che applicare il teorema di Thevenin/Norton implica introdurre ulteriori complicazioni alla risoluzione della rete. Volendo è possibile inserire tra
i nodi A e B un generatore di tensione di prova
tensione del generatore di prova
V̇p ,
V̇p e trovare Żeq. come
I˙p che lo attraversa.
e la corrente
rapporto tra la
Facendo così si
è di fronte a un circuito che si deve studiare obbligatoriamente con uno dei noti metodi
di analisi. Tanto vale applicare il metodo di analisi direttamente senza perdere tempo
cercando di applicare il teorema di Thevenin/Norton con la speranza di semplicare la
risoluzione del problema.
9.5 Teorema di reciprocità
Si consideri una rete elettrica lineare tempo-invariante fatta solo da resistori, capacitori,
induttori, induttori mutuamente accoppiati ed eventualmente trasformatori ideali (Figura
9.5.1).
Figura 9.5.1: rete elettrica
315
9 Teoremi sulle reti elettriche
Dalla rete elettrica di Figura 9.5.1 si isoli da una parte un cortocircuito di uno qualunque
dei lati della rete e da un'altra parte due distinti nodi della rete stessa (Figura 9.5.2).
Figura 9.5.2: rete elettrica
In questo modo sono state evidenziate due porte per la rete elettrica. La porta 1 si può
eccitare solamente in tensione, mentre la porta 2 si può eccitare solamente in corrente.
Eccitando la porta 1 del circuito mostrato in Figura 9.5.2 attraverso un generatore ideale
di tensione
V̇g
si ha il circuito mostrato in Figura 9.5.3.
Figura 9.5.3: rete elettrica
Dallo schema di calcolo di Figura 9.5.3 si può denire il
Ġv (jω) =
guadagno di tensione a vuoto:
V̇2
V̇g
(9.5.1)
Eccitando la porta 2 del circuito mostrato in Figura 9.5.2 attraverso un generatore ideale
di corrente
I˙g
si ha il circuito mostrato in Figura 9.5.4.
Figura 9.5.4: rete elettrica
Dallo schema di calcolo di Figura 9.5.4 si può denire il
cortocircuito:
316
guadagno di corrente di
9 Teoremi sulle reti elettriche
I˙1
I˙g
(9.5.2)
I˙1
V̇2
=
= ĠI (jω)
V̇g
I˙g
(9.5.3)
ĠI (jω) =
Per il teorema di reciprocità si ha che:
Ġv (jω) =
La (9.5.3) è la
prima tesi del teorema di reciprocità.
Dalla rete elettrica di Figura 9.5.1 si isolino due distinti cortocircuiti:
Figura 9.5.5: rete elettrica
Restano così denite due porte che si possono eccitare solamente in tensione. Eccitando
la porta 1 del circuito mostrato in Figura 9.5.5 attraverso un generatore ideale di tensione
v̇g1
si ha:
Figura 9.5.6: rete elettrica
Dallo schema di calcolo di Figura 9.5.6 si può denire la
Ẏ21 (jω) =
trans-ammettenza:
I˙2
V̇g1
(9.5.4)
Con il termine trasammettenza si suole indicare un'ammettenza che fa riferimento a
grandezze relative a due porte distinte; di contro con il termine
autoammettenza
si suole
indicare un'ammettenza che fa riferimento a grandezze relative ad una stessa porta.
Eccitando la porta 2 del circuito mostrato in Figura 9.5.5 attraverso un generatore ideale
di tensione
V̇g2
si ha:
Dallo schema di calcolo di Figura 9.5.7 si può denire la
317
trans-ammettenza:
9 Teoremi sulle reti elettriche
Figura 9.5.7: rete elettrica
I˙1
V̇g2
(9.5.5)
I˙1
I˙2
=
= Ẏ12 (jω)
V̇g1
V̇g2
(9.5.6)
Ẏ12 (jω) =
Per il teorema di reciprocità si ha che:
Ẏ21 (jω) =
La (9.5.6) è la
seconda tesi del teorema di reciprocità.
Dalla rete elettrica di Figura 9.5.1 si isolino due distinte coppie di nodi:
Figura 9.5.8: rete elettrica
Restano così denite due porte che si possono eccitare solamente in corrente. Eccitando
la porta 1 del circuito mostrato in Figura 9.5.8 attraverso un generatore ideale di corrente
I˙g1
si ha il circuito mostrato in Figura 9.5.9.
Figura 9.5.9: rete elettrica
Dallo schema di calcolo di Figura 9.5.9 si può denire la
318
trans-impedenza:
9 Teoremi sulle reti elettriche
Ż21 (jω) =
V̇2
I˙g1
(9.5.7)
Eccitando la porta 2 del circuito mostrato in Figura 9.5.8 attraverso un generatore ideale
di corrente
I˙g2
si ha il circuito mostrato in Figura 9.5.10.
Figura 9.5.10: rete elettrica
Dallo schema di calcolo di Figura 9.5.10 si può denire la
trans-impedenza:
V̇1
I˙g2
(9.5.8)
V̇2
V̇1
=
= Ż12 (jω)
I˙g1
I˙g2
(9.5.9)
Ż12 (jω) =
Per il teorema di reciprocità si ha che:
Ż21 (jω) =
La (9.5.9) è la
terza tesi del teorema di reciprocità.
Dimostrazione della prima tesi del teorema di reciprocità
Si consideri la rete elettrica mostrata in Figura 9.5.2 e si supponga che per ciascun lato
di tale rete valga la convenzione dell'utilizzatore (C.U.).
(A)
l'impedenza Ż1 , e al circuito aperto, l'impedenza
Sostituendo al cortocircuito,
(A)
Ż2 si ottiene il circuito mostrato in
Figura 9.5.11.
Figura 9.5.11: rete elettrica
Analogamente sostituendo al cortocircuito, l'impedenza
(B)
Ż1 ,
(B)
l'impedenza Ż2
si ottiene il circuito mostrato in Figura 9.5.12.
319
e al circuito aperto
9 Teoremi sulle reti elettriche
Figura 9.5.12: rete elettrica
Sono stati ottenuti così due circuiti aventi lo stesso grafo, per i quali è possibile scrivere
il teorema di Tellegen. Tenendo conto che per i dispositivi all'interno della rete vale la
convenzione dell'utilizzatore e per quelli che chiudono le porte vale la convenzione del
generatore, il teorema di Tellegen si scrive in una delle seguenti forme:
(A) ˙(B)
I1
V̇1
(A) ˙(B)
I2
+ V̇2
=
L
X
(A) ˙(B)
Ik
(9.5.10)
V̇k
(B) ˙(A)
Ik
(9.5.11)
(B) ˙(A)
Ik
(9.5.12)
V̇k
k=1
(B) (A)
V̇1 I˙1
+
(B) (A)
V̇2 I˙2
=
L
X
k=1
Visto che
L
X
(A) (B)
V̇k I˙k
=
k=1
L
X
V̇k
k=1
dalle equazioni in (9.5.10) e (9.5.11) segue l'uguaglianza:
(A) ˙(B)
I1
V̇1
valida
(A)
(A)
(B)
(A) ˙(B)
I2
+ V̇2
(B) ˙(A)
I1
= V̇1
(B) ˙(A)
I2
+ V̇2
(9.5.13)
(B)
∀ Ż1 , Ż2 , Ż1 , Ż2 .
Facendo coincidere la rete di Figura 9.5.11 con la rete di Figura 9.5.3 e la rete di Figura
9.5.4 con la rete di Figura 9.5.12, la (9.5.13) si scrive:
V̇g −I˙1 + V̇2 I˙g = 0 · I˙1 + V̇2 · 0
da cui si ricava la prima tesi del teorema di reciprocità:
Ġv (jω) =
V̇2
I˙1
=
= ĠI (jω)
V̇g
I˙g
Per completare la dimostrazione occorre vericare l'uguaglianza in (9.5.12).
Se il lato k-esimo è un resistore di resistenza
Rk ,
(B)
(A) (B)
V̇k I˙k
si ha:
(B) (A)
(A) V̇k
= V̇k I˙k
= Rk I˙k
Rk
320
(9.5.14)
9 Teoremi sulle reti elettriche
e ciò verica la (9.5.12).
Se il lato k-esimo è un capacitore di capacità
(A) ˙(B)
Ik
V̇k
=
Ck ,
si ha:
1 ˙(A)
(B)
(B) (A)
Ik jωC V̇k = V̇k I˙k
jωC
e ciò verica la (9.5.12).
Se il lato k-esimo è induttore di induttanza
(A) ˙(B)
Ik
V̇k
Lk ,
si ha:
(B) (A)
(A) 1
V̇ (B) = V̇k I˙k
= jωL I˙k
jωL
e ciò verica la (9.5.12).
Se la rete L.T.I contiene una coppia di induttori mutuamente accoppiati di autoinduttanze
(A) ˙(B)
Ik
V̇k
Lk
ed
Lh
(A) ˙(B)
Ih
+ V̇h
e mutua-induttanzaM , si ha:
(A)
(A) ˙(B)
(A)
(A) ˙(B)
= jωLk I˙k + jωM I˙h
Ik + jωLh I˙h + jωM I˙k
Ih =
(A) (B)
(A) (B)
(A) (B)
(A) (B)
= jωLk I˙k I˙k + jωM I˙h I˙k + jωLh I˙h I˙h + jωM I˙k I˙h =
(B)
(B) ˙(A)
(B) (A)
(B) (A)
(B)
(B) ˙(A)
Ih = V̇k I˙k + V̇h I˙h
Ik + jωLh I˙h + jωM I˙k
= jωLk I˙k + jωM I˙h
e ciò verica la (9.5.12).
Se la rete L.T.I contiene un trasformatore ideale si ha:
(A) (B)
V̇1 I˙1
+
(A) (B)
V̇2 I˙2
=
(B)
I˙2
−
n
(A)
n V̇2
!
(A) ˙(B)
I2
+ V̇2
=0
e ciò verica la (9.5.12).
Nota.
Le tesi del teorema di reciprocità sono soltanto 3 ; verichiamo quanto detto.
Supponiamo di eccitare le porte della rete L.T.I in modo errato come mostrato in
Figura 9.5.13.
A
B
Figura 9.5.13: modo errato di eccitare le porte di una rete L.T.I
Denendo i guadagni
0
Ġv (jω) =
V̇2
,
V̇g1
00
Ġv (jω) =
quarta tesi del teorema di reciprocità:
321
V̇1
, NON E' VERO che vale una
V̇g2
9 Teoremi sulle reti elettriche
0
00
Ġv (jω) = Ġv (jω)
Per convincerci di questo fatto basta osservare che le reti elettriche mostrate in Figura
9.5.13 prive di eccitazioni sono diverse tra di loro; il chè è assurdo dato che per ipotesi
la rete elettrica è sempre la stessa.
Figura 9.5.14:
Π1
è la rete di Figura 9.5.14.A priva di eccitazioni;
Π2
è la rete di Figura
9.5.14.B priva di eccitazioni
Il teorema di reciprocità vale ntantochè la rete L.T.I non contiene generatori pilotati.
Potrebbe pure succedere però che la rete L.T.I. contiene generatori pilotati e continua
a valere il teorema di reciprocità.
Ciò vuol dire che il teorema di reciprocità è una
condizione suciente ma non necessaria.
9.5.1 Esempio
Data la rete elettrica mostrata in Figura 9.5.15 si vuole vericare la prima tesi del teorema
di reciprocità.
Figura 9.5.15: rete elettrica
Azzerando i generatori ideali la rete elettrica data diventa come mostrato in Figura
9.5.16. Si ricordi che azzerare un generatore idealedi tensione vuol dire sostituirlo con un
cortocircuito, mentre azzerare un generatore ideale di corrente vuol dire sostituirlo con
un circuito aperto.
322
9 Teoremi sulle reti elettriche
Figura 9.5.16: rete elettrica
Eccitando la porta 1 della rete con il generatore di tensione
V̇g
si ottiene la rete elettrica
mostrata in Figura 9.5.17.
Figura 9.5.17: rete elettrica
Si deve esprimere
V̇2
in funzione di
V̇g .
V̇2 =
Si ha:
Ż2
V̇c
Ż2 + Z˙L
Żp
V̇g
Żp + Ż1
Żc Ż2 + ŻL
V̇c =
Żp =
Ż2 + ŻL + Żc
Combinando le relazioni in (9.5.15) (9.5.16) e (9.5.17) si ottiene:
323
(9.5.15)
(9.5.16)
(9.5.17)
9 Teoremi sulle reti elettriche
Ż
Ż
+
Ż
c
2
L
V̇2
Ż2
Ġv =
=
V̇g
Ż2 + ŻL Żc Ż2 + ŻL + Ż1 Ż2 + ŻL + Żc
Sostituendo i valori numerici si ha:
Ġv =
1
V̇2
=
2
V̇g
(jω) + 2jω + 2
Eccitando la porta 2 della rete con il generatore di corrente
(9.5.18)
I˙g
si ottiene la rete elettrica
mostrata in Figura 9.5.18.
Figura 9.5.18: rete elettrica
Si deve esprimere
I˙1
in funzione di
I˙g .
Si ha:
I˙1 =
Żc
I˙L
Żc + Z˙1
(9.5.19)
I˙L =
Ż2
V̇g
Ż2 + Ż
(9.5.20)
Ż = ŻL +
Ż1 Żc
Ż1 + Żc
(9.5.21)
Combinando le relazioni in (9.5.19), (9.5.20), (9.5.21) e sostituendo i valori numerici si
ottiene:
ĠI =
1
I˙1
=
2
˙
Ig
(jω) + 2jω + 2
(9.5.22)
Quindi in denitiva resta vericata la prima tesi del teorema di reciprocità:
Ġv = ĠI =
1
(jω) + 2jω + 2
2
324
(9.5.23)
9 Teoremi sulle reti elettriche
9.6 Teorema del massimo trasferimento di potenza
Il teorema del massimo trasferimento di potenza è un'applicazione del teorema di Thevenin/Norton.
Esso si enuncia per le reti lineari tempo-invariente a regime sinusoidale.
Si consideri un bipolo
Π lineare, cioè costituito da generatori ideali, generatori pilotati,
resistori, capacitori, induttori, induttori mutuamente accoppiati e trasformatori ideali.
Supponiamo di chiudere il bipolo
Π
attraverso un'impedenza variabile
Ż = R + jX
con
R > 0e −∞ < X < +∞
(9.6.1)
(Figura 9.6.1).
Figura 9.6.1: rete elettrica
Si avrà una corrente
I˙
che attraversa l'impedenza
Ż
V̇ . Si
Π all'impedenza
a fronte di una tensione
vuole determinare il massimo trasferimento di potenza dal bipolo lineare
Ż = R + jX .
Per quali valori di R ed X è possibile rendere massima la potenza reale che assorbe
l'impedenza
Ż
dal bipolo lineare
Π
?
L'espressione della potenza reale assorbita da una impedenza
Ż
è data da:
P = R I2
essendo
I
il modulo del fasore
(9.6.2)
I˙.
Per determinare l'espressione della potenza reale P bisogna applicare innanzitutto il
teorema di Thevenin/Norton alla rete elettrica di Figura 9.6.1: si tratta di sostituire al
bipolo
Π,
il bipolo di Thevenin (Figura 9.6.2)
Poichè il fasore
I˙
è dato da:
I˙ =
V̇T h.
˙
Ż + Zeq.
la potenza reale data in (9.6.2) si scrive:
2
V̇
VT2h.
T h. P = R
=R
˙ Ż + Zeq.
(R + Req. )2 + (X + Xeq. )2
325
9 Teoremi sulle reti elettriche
Figura 9.6.2: rete elettrica
Stiamo trovando che la potenza reale è una funzione reale delle variabili reali R ed X:
P = P (R, X) = R
VT2h.
(9.6.3)
(R + Req. )2 + (X + Xeq. )2
Si tratta di denire il massimo della funzione
P (R, X)
denita in:
D = {(R, X) ∈ R : R ≥ 0, −∞ ≤ X ≤ +∞}
(9.6.4)
D è un dominio chiuso e limitato , i punti di massimo vanno ricercati tra i punti
della frontiera di D e tra i punti interni a D .
Per ogni punto che sta sulla retta R = 0 si ha ovviamente che:
Poichè
P = P (0, X) = 0
∀X ∈ R
Quindi i punti che stanno sulla retta
R=0
non sono candidati punti di massi-
mo. Non lo sono anche i punti che stanno
sulla retta impropria, infatti anche per essi si ha (un punto sulla retta impropria è
un punto per cui sia R che X divergono a
+∞):
P =
=R
lim
R,X→+∞
P (R, X) =
VT2h.
2
2
(R + Req. ) + (X + Xeq. )
=0
Figura 9.6.3: Dominio di denizione per la
potenza reale
Quindi i punti di massimo vanno ricercati tra i punti interni a
gradiente della funzione
P = P (R, X)
D
in cui si annulla il
poichè trattasi di una funzione di due variabili.
Si possono evitare calcoli complicati se si osserva che per
X = −Xeq.
326
(9.6.5)
9 Teoremi sulle reti elettriche
la (9.6.3) tende a diventare massimale. Fissando
una funzione reale della sola variabile reale
X
come in (9.6.5), la (9.6.3) diventa
R:
P = P (R) = R
VT2h.
(9.6.6)
(R + Req. )2
Quindi anzichè andare a trovare i punti per cui si annulla il gradiente della (9.6.3) si
vanno a trovare i punti per cui si annulla la derivata prima rispetto a
R
della (9.6.6):
V 2 (−R + Req. )
d
P (R) = T h.
=0
dR
(R + Req. )2
Da quest'ultima espressione si ricava:
R = Req.
essendo
(9.6.7)
VT2h. 6= 0.
Sostituendo (9.6.5) e (9.6.7) in (9.6.1) si trova l'impedenza per cui si ha il massimo
trasferimento di potenza reale dal bipolo
Π
all'utilizzatore
Ż :
∗
Ż = Req. − jXeq. = Zeq.
(9.6.8)
Attraverso (9.6.8) è evidente che si ha il massimo trasferimento di potenza dal bipolo
Π
all'utilizzatore quando quest'ultimo ha un'impedenza pari all'impedenza equivalente
coniugata del bipolo
Π
stesso; si suole dire che occorre adattare l'utilizzatore al bipolo
Π
su base coniugata.
Sostituendo (9.6.5) e (9.6.7) in (9.6.3) si ottiene la potenza reale massima assorbita
dall'utilizzatore:
PM AX =
VT2h.
4 Req.
(9.6.9)
L'espressione trovata in (9.6.9) non è soltanto la potenza reale massima assorbita dal-
∗ , ma è anche la potenza reale massima assorbita dall'impedenza
Ż = Zeq.
equivalente Zeq. In altri termini la potenza reale massima prodotta dal generatore ideale
gen.
∗
di tensione V̇T h. ,PM AX , va al 50% su Żeq. e al 50% su Żeq. , quindi quest'ultima è il
∗
doppio della potenza assorbita dall'utilizzatore Ż = Zeq. :
l'impedenza
(gen.)
PM AX = 2PM AX =
VT2h.
2 Req.
(9.6.10)
Del teorema appena dato, esiste una versione reale. Si tratta di chiudere il bipolo
Π,
attraverso un resistore di resistenza variabile
potenza reale trasferita dal bipolo
Π
R
e determinare
al resistore di resistenza
R
R
in modo tale che la
sia massima. In questo
caso l'espressione della potenza reale assorbita dal resistore risulta:
Stiamo trovando che la potenza reale è una funzione reale delle variabili reali R ed X:
327
9 Teoremi sulle reti elettriche
P = P (R) = R I 2 = R
VT2h.
2
(R + Req. )2 + Xeq.
(9.6.11)
Si tratta di trovare il punto di massimo per la funzione in (9.6.11), annullandone la
derivata prima rispetto a
R:
n
o
2
2
2 − 2R (R + R )
V
(R
+
R
)
+
X
eq.
eq.
eq.
T h.
d
=0
P (R) =
h
i2
dR
2
(R + Req. )2 + Xeq.
Da quest'ultima espressione si ricava l'equazione:
2
(R + Req. )2 + Xeq.
− 2R (R + Req. ) = 0 VT2h. 6= 0
Dalla (9.6.12) si ricava il valore di
(9.6.12)
R:
2
2
R = Req.
+ Xeq.
= Żeq. (9.6.13)
Sostituendo (9.6.13) in (9.6.11) si ottiene l'espressione della potenza reale massima
trasferita dal bipolo
Π
all'utilizzatore
PM AX
R:
2 + X2
Req.
eq.
=
VT2h. =
2
2
2
2
Req. + Xeq. + Req. + Xeq.
=
2
Req.
1
VT2h.
2
+ 1 + Xeq.
(9.6.14)
Inne tenendo conto che:
(
P (0) = lim
R→0
R
)
VT2h.
2
(R + Req. )2 + Xeq.
=0
(9.6.15)
(
P (+∞) = lim
R→+∞
R
)
VT2h.
2
(R + Req. )2 + Xeq.
=0
(9.6.16)
è chiaro che la potenza reale trasferita dal bipolo
Π
Figura 9.6.4: potenza trasferita dal bipolo
all'utilizzatore è carat-
all'utilizzatore R
terizzata dal graco mostrato in Figura
9.6.4.
328
Π
10 Reti elettriche nel dominio di Laplace
Fino ad ora, per studiare una rete elettrica si scelto di operare nel dominio del tempo o
nel dominio dei fasori. Tuttavia quando si risolvono le reti elettriche si può scegliere di
svolgere l'analisi nel dominio di Laplace. Prima di arontare lo studio di una rete elettrica
nel dominio di Laplace è opportuno introdurre alcuni concetti necessari per denire la
trasformata di Laplace e l'anti trasformata di Laplace.
10.1 Sommabilità di una funzione in R.
Si consideri una funzione
w :R → C
Si dice che tale funzione è
continua in
R.
sommabile in R se:
ˆ
+∞
w (t) dt
(10.1.1)
−∞
risulta nito. Per sommabilità in
R
di una funzione si può intendere la sommabilità nel
senso di Lebesgue, la sommablità in senso improprio oppure la sommabilità in valore
principale.
Funzione sommabile in
sommabile in
R
R
nel senso di Lebesgue.
Una funzione
w :R → C
si dice
nel senso di Lebesgue se:
ˆ
+∞
|w (t)| dt < +∞
(10.1.2)
−∞
L'insieme delle funzioni sommabili in
R
nel senso di Lebesgue si indica con il simbolo
L1 (]−∞, +∞[).
In tal caso,
ˆ
+∞
w (t) dt
−∞
è l'integrale di Lebesgue della funzione
Funzione sommabile in
bile in
R
R
w (t)
in
in senso improprio.
]−∞, +∞[.
Una funzione
w :R → C
si dice somma-
in senso improprio se i due limiti presenti nella seguente espressione esistono
niti:
∗
ˆ
ˆ
+∞
w (t) dt = lim
−∞
a→−∞ a
ˆ
0
w (t) dt + lim
329
b→+∞ 0
b
w (t) dt
(10.1.3)
10 Reti elettriche nel dominio di Laplace
In tal caso,
∗
ˆ
+∞
w (t) dt
−∞
w (t)
è l'integrale in senso improprio della funzione
Funzione sommabile in
bile in
R
R
in valore principale.
in
]−∞, +∞[.
Una funzione
w:R → C si dice somma-
in valore principale se il limite presente nella seguente espressione esiste nito:
ˆ
ˆ
+∞
R
w (t) dt = lim
V.P.
R→∞ −R
−∞
w (t) dt
(10.1.4)
In tal caso,
ˆ
+∞
V.P.
w (t) dt
−∞
è l'integrale in valore principale della funzione
w (t)
in
]−∞, +∞[.
Proposizione 1
Valgono le seguenti implicazione nessuna delle quali invertibile
Sommabilità
Sommabilità
Sommabilita
nel senso di =⇒
in senso
=⇒
in
Lebesgue
improrpio
valore principale
In altri termini se una funzione è sommabile secondo Lebesgue, allora l'integrale di
Lebesgue, l'integrale in senso improprio e l'integrale in valore principale coincidono:
ˆ
+∞
∗
ˆ
ˆ
+∞
w (t) dt =
+∞
w (t) dt = V.P.
−∞
−∞
w (t) dt
(10.1.5)
−∞
Alternativamente se una funzione è sommabile in senso improprio, allora l'integrale
improprio e quello in valore principale coincidono:
∗
ˆ
ˆ
+∞
+∞
w (t) dt = V.P.
−∞
w (t) dt
−∞
Quanto detto lo si può vericare subito tramite degli esempi.
Esempio 1.
Si consideri la funzione:
(
w (t) =
Poichè
sin t
t
1
per t > 0
per t = 0
sin t
=1
t→0 t
lim
330
(10.1.6)
10 Reti elettriche nel dominio di Laplace
si ha che
ˆ
w (t)
è continua in
Proviamo che
w (t)
[0, +∞[.
non è sommabile nel senso di Lebesgue in
[0, +∞[.
[0, +∞[ deve succedere che
|w (t)| dt = +∞ la funzione non
Anchè la funzione sia sommabile nel senso di Lebesgue in
´ +∞
0
|w (t)| dt < +∞,
viceversa se succede che
´ +∞
0
[0, +∞[.
risulta sommabile nel senso di Lebesgue in
Se riuscissimo a fare vedere che che esiste una successione numerica
+∞
{Tn }
divergente a
tale che:
ˆ
Tn
|sin t|
dt = +∞
t
lim
n→+∞ 0
allora per un noto teorema sui limiti che lega la successioni alle funzioni, si avrebbe pure
che:
ˆ
+∞
0
e ciò equivale a dire che la funzione
[0, +∞[.
|sin t|
dt = +∞
t
w (t)
non è sommabile nel senso di Lebesgue in
Si tratta dunque di trovare la successione numerica
{Tn }
divergente a
+∞.
Tale successione non è molto complicata se si osserva che:
|sin t| = sin t
|sin t| = − sin t
|sin t| = sin t
.
.
|sin t| = − sin t
se 0 < t < π
se π < t < 2π
se 2π < t < 3π
se (2n − 1) π < t < 2nπ
ovvero:
Figura 10.1.1: rappresentazione graca
A questo punto si capisce che la la successione numerica
denita ponendo
Tn = 2πn,
lim
2πn
n→+∞ 0
w (t)
divergente a
+∞
è
pertanto si tratta di provare che:
ˆ
per poter dire che
{Tn }
|sin t|
dt = +∞
t
non è sommabile secondo Lebesgue in
Decomponendo l'intervallo
[0, 2πn]
[0, +∞[.
come mostrato in Figura 10.1.1 e applicando la
proprietà dell'additività dell'integrale si può scrivere:
331
10 Reti elettriche nel dominio di Laplace
ˆ
2πn
0
|sin t|
dt =
t
ˆ
π
0
sin t
dt +
t
ˆ
2π
π
sin t
−
dt + ...... +
t
ˆ
2nπ
−
(2n−1)π
sin t
dt
t
Così facendo è stata trovata la ridotta di una serie. A questo punto basta minorare la
ridotta trovata con una ridotta di una serie divergente a
+∞.
Questa si trova subito,
infatti:
ˆ
π
0
1
≥
π
ˆ
π
0
sin t
dt +
t
ˆ
2π
π
1
sin t dt +
2π
ˆ
sin t
−
dt + ...... +
t
2π
π
=
ˆ
2nπ
−
(2n−1)π
1
− sin t dt + ...... +
2πn
ˆ
sin t
dt ≥
t
2nπ
− sin t dt =
(2n−1)π
1
1
1
+
+ ...... +
π 2π
2πn
In questo modo è stata trovata come minorante la ridotta della serie armonica divergente, pertanto
ˆ
w (t)
Proviamo che
non è è sommabile secondo Lebesgue in
w (t)
è sommabile in senso improprio in
[0, +∞[.
[0, +∞[.
Deve succedere che:
ˆ
T
lim
T →+∞ 0
sin t
dt
t
esiste nito.
Per T>1 possiamo srivere:
ˆ
T
0
sin t
dt =
t
ˆ
1
0
sin t
dt +
t
ˆ
T
1
sin t
dt
t
L'integrale:
ˆ
0
1
sin t
dt
t
risulta essere un numero in quanto si tratta di un integrale di una funzione continua in
un intervallo chiuso e limitato. Si tratta dunque di fare vedere che:
ˆ
T
lim
T →+∞ 1
sin t
dt
t
esiste nito.
Integrando per parti si ha:
ˆ
1
T
cos T
sin t
dt = −
+ cos 1 −
t
T
332
ˆ
1
T
cos t
dt
t2
10 Reti elettriche nel dominio di Laplace
A questo punto poichè
− cosT T
è il prodotto tra due funzioni di cui una è limitata e l'altr<
è innitesima si ha che:
lim −
T →+∞
Si tratta allora di fare vedere che:
cos T
=0
T
ˆ
T
cos t
dt
t2
lim
T →+∞ 1
esiste nito. Poichè vale la maggiorazione:
ˆ
T
1
ˆ
|cos t|
dt ≤
t2
T
1
1
dt = 1 −
2
t
T
1
e si ha che
1
1−
=1
T →+∞
T
lim
per il teorema del confronto si ha che
ˆ
T
lim
T →+∞ 1
|cos t|
dt
t2
esite nito e ciò implica che
ˆ
T
cos t
dt
t2
lim
T →+∞ 1
esiste nito. Ciò prova che
Esempio 2.
w (t)
è sommabile in senso improprio in
Si consideri la funzione:
con t ∈ R
w (t) = t
ˆ
Se
Proviamo che
w (t)fosse
[0, +∞[.
w (t)
non è sommabile in senso improprio in
sommabile in senso improprio in
∗
ˆ
]−∞, +∞[:
ˆ
+∞
w (t) dt = lim
a→−∞ a
−∞
]−∞, +∞[.
ˆ
0
t dt + lim
b→+∞ 0
b
t dt
in quest'ultima espressione, i due limiti dovrebbero esistere niti. Poichè
ˆ
0
t2
a2
= lim − = −∞
a→−∞ a
a→−∞ 2
a→−∞
2
a
2 b
ˆ b
t
b2
lim
t dt = lim
= lim
= +∞
b→+∞ 2
b→+∞ 0
b→+∞ 2 0
lim
si ha ovviamente che
w (t)
0
t dt = lim
non è sommabile in senso improprio in
333
]−∞, +∞[.
10 Reti elettriche nel dominio di Laplace
ˆ
Sia
Proviamo che
R > 0,
w (t)
è sommabile in valore principale in
]−∞, +∞[.
dobbiamo fare vedere che
ˆ
ˆ
+∞
V.P.
R
w (t) dt = lim
R→+∞ −R
−∞
t dt
esiste nito.
Si ha facilmente che:
ˆ
ˆ
+∞
R
w (t) dt = lim
V.P.
R→+∞ −R
−∞
e ciò dimostra che
w (t)
t dt = lim
R→+∞
t2
2
R
= lim
−R
è sommabile in valore principale in
Funzione localmente sommabile in
R.
R→+∞
R2 R2
−
2
2
=0
]−∞, +∞[.
w (t) una funzione sommabile in R nel senso
Sia
di Lebesgue , cioè tale che
ˆ
+∞
|w (t)| dt < +∞
(10.1.7)
−∞
Se
∀ [a, b] ⊆R
si ha che
ˆ
b
|w (t)| dt < +∞
(10.1.8)
a
allora
w (t)
si dice localmente sommabile in
R.
L'insieme delle funzioni localmente sommabili in
R si indica con il simbolo L1loc (]−∞, +∞[).
Vale la seguente proposizine.
Proposizione 2
w (t)∈ L1 (Ω) allora w (t)∈ L1loc (Ω).
1
detto che w (t)∈ L (Ω).
Se
è
Non vale il viceversa. Cioè se
w (t)∈ L1loc (Ω)
non
Per convincerci di quanto detto si consideri il seguente esempio.
Esempio 3.
w (t) = t.
Si consideri la funzione
Visto che:
ˆ
ˆ
1
1
w (t) dt =
0
si ha ovviamente che
sommabile in
R
t dt =
0
1
2
w (t) è localmente sommabile in R.
Tale funzione non è ovviamente
nel senso di Lebesgue visto che:
ˆ
+∞
t dt = +∞
0
Siamo ora in grado di denire le funzioni trasformabili secondo Laplace, nonchè la
trasformata di Laplace.
334
10 Reti elettriche nel dominio di Laplace
10.2 Trasformata di Laplace
10.2.1 Denizioni
L-trasformabile in s0 . Sia w (t) una funzione denita in R e a valori in C,
]−∞, 0[. Sia inoltre w (t) ∈ L1loc ([0, +∞[) ed s0 ∈ C. Si dice che
trasformabile secondo Laplace in s0 (o L-trasformabile in s0 ) se
Funzione
identicamente nulla in
w (t)
è
ˆ
T
w (t) e−s0 t dt
lim
T →∞ 0
(10.2.1)
esiste nito.
Proposizione 3
La funzione
w (t) e−s0 t
risulta sommabile in
[0, T ],
cioè
w (t) e−s0 t ∈ L1 ([0, T ]).
´T −s0 t dt < +∞.
0 w (t) e
[0, T ], si ha che:
Dimostrazione. Si tratta di provare che
Poichè la funzione
e−s0 t
è continua in
−s t e 0 < max e−s0 t [0.T ]
e quindi vale la maggiorazione:
w (t) e−s0 t < |w (t)| max e−s0 t [0.T ]
Con ciò stiamo trovando che il modulo della funzione
della funzione
w (t)
w (t) e−s0 t si maggiora con il modulo
moltipliato per la costante:
max e−s0 t [0.T ]
Poichè per ipotesi
w (t) ∈ L1loc ([0, +∞[),
e ciò equivale a dire che
in ogni intervallo chiuso e limitato contenuto in
ˆ
T
[0, +∞[,
w (t) risulta sommabile
si ha che:
|w (t)| max e−s0 t dt < +∞
[0,T ]
0
e quindi per il criterio del confronto si ha pure che.
ˆ
T
w (t) e−s0 t dt < +∞
0
Trasformata di Laplace di
w (t)
in
s.
Se
w (t)
risulta
ˆ
W (s) = L (w (t)) (s) = lim
T →∞ 0
rappresenta la trasformata di Laplace di
w (t)
335
in
s.
T
L-trasformabile
w (t) e−st dt
in
s ∈ C,allora
(10.2.2)
10 Reti elettriche nel dominio di Laplace
Osservazione
La trasformata di Laplace non richiede che la funzione sia denita in
]−∞, 0[ ;
tut-
tavia, in vista dell'estenzione della denizione di trasformata di Laplace nel senso delle
distribuzioni, è opportuno pensare la funzione denita in tutto
In altro modo si dice che la funzione
funzione
w (t) e−s0 t
risulta
∗
w (t)
ˆ
+∞
ˆ
w (t) e−st dt = lim
T
T →∞ 0
Potrebbe pure succedere che la funzione
[0, +∞[;
L-trasformabile
in
s0 ∈ C,
se la
sommabile in senso improprio in [0, +∞[, cioè se esiste nito:
0
in
risulta
R e nulla per t ∈ ]−∞, 0[.
w (t) e−s0 t
w (t) e−st dt
risulti
(10.2.3)
sommabile secondo Lebesgue
se ciò avviene si può dare la seguente denizione.
L-trasformabile in s0 . Sia w (t) una funzione denita in R e
1
a valori in C, identicamente nulla in ]−∞, 0[. Sia inoltre w (t) ∈ Lloc ([0, +∞[) ed s0 ∈ C.
Si dice che w (t) è assolutamente trasformabile secondo Laplace in s0 (o assolutamente
L-trasformabile in s0 ) se
ˆ +∞
w (t) e−s0 t dt < +∞
(10.2.4)
Funzione assolutamente
0
L-trasformabile in s0 è anche L-trasformabile
w (t) e−s0 t è sommabile secondo Lebesgue in [0, +∞[,
allora risulta sommabile in [0, +∞[ anche in senso improprio. Logicamente non vale
il viceversa, cioè se una funzione risulta L-trasformabile in s0 non è detto che sia
assolutamente L-trasformabile in s0 .
Naturalmente se una funzione è assolutamente
in
s0 ;
in altri termini se la funzione
Si dimostra il seguente lemma.
Lemma 1
Se w(t) è
L-trasformabile
in
s0 ∈ C,
allora è
L-trasformabile ∀s ∈ C
tale che
Re {s} >
Re {s0 }
Ascissa di convergenza.
camente nulla in
]−∞, 0[.
Sia
w (t)
una funzione denita in
Sia inoltre
w (t) ∈ L1loc ([0, +∞[).
R
e a valori in
C,
identi-
Consideriamo il seguente
insieme numerico
I = {s ∈ R : w (t) è L − trasf ormabile in s}
(10.2.5)
e poniamo:
(
inf I
%=
+∞
336
se I =
6 0
se I = 0
(10.2.6)
10 Reti elettriche nel dominio di Laplace
dove
%
prende il nome di
ascissa di convergenza.
Tenendonto del lemma 1 e della denizione di estremo inferiore, vale il seguente
teorema.
Teorema 1
w (t) una funzione denita in R e a valori in C, identicamente nulla in ]−∞, 0[. Sia
w (t) ∈ L1loc ([0, +∞[). Allora w (t) è L-trasformabile nel semipiano Re {s} > % e
non è L-trasformabile nel semipiano Re {s} < %; inne nulla si può dire se Re {s} = %.
Sia
inoltre
Dimostrazione.
Re {s} > % allora per la proprietà dell'estremo inferiore esiste un
∗
∗
tale che ϕ < s < Re {s} . Poichè in s la funzione è L-trasformabile,
∗
allora w (t) è L-trasformabile in s ∈ C tale che Re {s} > s
Se
Figura 10.2.1: semipiano di
numero
s∗ ∈ I
per il lemma 1
L-trasformabilità
Si prova un lemma molto simile al lemma 1, che riguarda le funzioni assolutamente
L-trasformabili
secondo Laplace.
Lemma 2
L-trasformabile in s0 ∈ C, allora è assolutamente L-trasformabile
Re {s} ≥ Re {s0 } .
Se w(t) è assolutamente
∀s ∈ C
tale che
Ascissa di assoluta convergenza.
C,
Sia
w (t)
una funzione denita in
R
e a valori in
w (t) ∈ L1loc ([0, +∞[).
Consideriamo il
I ∗ = {s ∈ R : w (t) è assolutamente L − trasf ormabile in s}
(10.2.7)
identicamente nulla in
]−∞, 0[.
Sia inoltre
seguente insieme numerico
e poniamo:
(
inf I ∗
%∗ =
+∞
337
se I =
6 0
se I = 0
(10.2.8)
10 Reti elettriche nel dominio di Laplace
dove
%∗
prende il nome di
ascissa di assoluta convergenza.
Tenendonto del lemma 2 e della denizione di ascissa di assoluta convergenza, vale il
seguente teorema.
Teorema 2
w (t) una funzione denita in R e a valori in C, identicamente nulla in ]−∞, 0[. Sia
w (t) ∈ L1loc ([0, +∞[). Allora w (t) è assolutamente L-trasformabile nel semipiano
Re {s} > %∗ e non è assolutamente L-trasformabile nel semipiano Re {s} < %∗ ; inne
∗
nulla si può dire se Re {s} = % .
Sia
inoltre
A dierenza del teorema 1, per il teorema 2 va detto che se si trova un punto che
Re {s} = %∗ in cui la funzione è assolutamente L-trasformabile, allora
risulta pure assolutamente L-trasformabile per ogni punto della medesima retta e ancora
∗
se si trova un punto della retta Re {s} = % in cui la funzione non è assolutamente
L-trasformabile, allora non lo è per ogni punto della medesima retta.
sta sulla retta
Si osservi inoltre che dal fatto che l'assoluta trasformabilità implica la trasformabilità
e non il viceversa si ha che
I∗ ⊆ I
e quindi:
% ≤ %∗
Figura 10.2.2: semipiano di
L-trasformabilità;
(10.2.9)
semipiano di assoluta
L-trasformabilità
Proposizione 4
Le funzioni a segno denitivamente costante sono funzioni in cui l'ascissa di convergenza
coincide con l'ascissa di assoluta convergenza.
10.2.2 Proprietà della trasformata di Laplace
Proprietà 1 (linearità della trasformata di Laplace) Siano date le funzioni w1 (t)
1
,w2 (t)∈ Lloc ([0, +∞[) identicamente nulle in ]−∞, 0[ L-trasformabili per Re {s} > %1 ,
Re {s} > %2 rispettivamente e siano λ1 , λ2 ∈ C. Si ha per Re {s} > max (%1 , %2 ) che:
338
10 Reti elettriche nel dominio di Laplace
L (λ1 w1 (t) + λ2 w2 (t)) (s) = λ1 L (w1 (t)) (s) + λ2 L (w2 (t)) (s)
(10.2.10)
Dimostrazione.
∗
ˆ
+∞
L (λ1 w1 (t) + λ2 w2 (t)) (s) =
(λ1 w1 (t) + λ2 w2 (t)) e−st dt =
0
∗
ˆ
+∞
∗
w1 (t) e
= λ1
−st
ˆ
+∞
dt + λ2
w2 (t) e−st dt =
0
0
= λ1 L (w1 (t)) (s) + λ2 L (w2 (t)) (s)
Proprietà 2 (formula del cambiamento di scala)
]−∞, 0[ ,L-trasformabile
identicamente nulla in
w (t)∈ L1loc ([0, +∞[)
a > 0. Allora si ha
Sia data la funzione
per
Re {s} > %,
e sia
che:
L (w (a · t)) (s) =
s
1
L (w (t))
a
a
Dimostrazione. Basta eettuare il cambiamento di variabile
∗
ˆ
+∞
L (w (a · t)) (s) =
ˆ
∗
−st
w (a · t) e
+∞
dt =
0
0
Proprietà 3 (formula di traslazione rispetto ad s)
]−∞, 0[ ,L-trasformabile
identicamente nulla in
(10.2.11)
a · t = y:
s
s 1
1
w (y) e− a y dy = L (w (t))
a
a
a
Sia data la funzione
per
Re {s} > %.
Allora si ha che:
L eαt w (t) (s) = L (w (t)) (s − α)
se
Re {s} > % + Re {α}
essendo
w (t)∈ L1loc ([0, +∞[)
(10.2.12)
α ∈ C.
Dimostrazione.
∗
ˆ
+∞
L eαt w (t) (s) =
∗
ˆ
eαt w (t) e−st dt =
0
w (t) e−(s−α)t dt = L (w (t)) (s − α)
0
Proprietà 4 (formula di traslazione rispetto a t)
identicamente nulla in
+∞
]−∞, 0[ ,L-trasformabile
Sia data la funzione
per
Re {s} > %.
Allora si ha che:
L (w (t − a) u (t − a)) (s) = e−as L (w (t)) (s)
se
Re {s} > % ea > 0.
339
w (t)∈ L1loc ([0, +∞[)
(10.2.13)
10 Reti elettriche nel dominio di Laplace
Proprietà 5 (trasformata di Laplace di una funzione periodica di periodo T )
w (t)
una funzione periodica di periodo T>0 localmente sommabile in
ha che
w (t)
è
L-trasformabile
per
Re {s} > 0
(0, T ).
Sia
Allora si
e vale la relazione_
1
L (w (t) u (t)) (s) =
1 − e−sT
ˆ
T
e−sτ w (τ ) dτ
(10.2.14)
0
Proprietà 6 (derivata n-esima della trasformata di Laplace) Sia data la funzione
w (t)∈ L1loc ([0, +∞[) identicamente nulla in ]−∞, 0[ ,L-trasformabile per Re {s} > %.
Allora si ha che
w (t)
è una funzione derivabile innite volte e vale la formula:
Dn (L (w (t)) (s)) = (−1)n L (tn w (t)) (s)
(10.2.15)
Proprietà 7 (trasformata di Laplace della funzione integrale) Sia data la funzione
w (t)∈ L1loc ([0, +∞[) identicamente nulla in ]−∞, 0[ ,L-trasformabile per Re {s} > %.
Allora si ha che
ˆ
L
t
w (τ ) dτ
0
per
1
(s) = L (w (t)) (s)
s
(10.2.16)
Re {s} > max (0, %).
Proprietà 7 (trasformata di Laplace della derivata prima)
0 L w (t) (s) = sL (w (t)) (s) − w 0+
(10.2.17)
Proprietà 8 (trasformata di Laplace della derivata seconda)
00 0
L w (t) (s) = s2 L (w (t)) (s) − s w 0+ − w 0+
(10.2.18)
Proprietà 9 (teorema del valore iniziale)
lim w (t) = lim sL (w (t)) (s) = w (0)
s→+∞
t→0
(10.2.19)
Proprietà 10 (teorema del valore nale)
lim w (t) = lim sL (w (t)) (s)
t→+∞
s→0
Proprietà 11 (trasformata di Laplace della convoluzione)
340
(10.2.20)
10 Reti elettriche nel dominio di Laplace
Convoluzione.
f (t) , g (t) ∈ L1loc ([0, +∞[) due funzioni nulle in ]−∞, 0[.
f (t) e g (t) la funzione denita ponendo:
(
0
se t ≤ 0
{f (t) ∗ g (t)} (t) = ´ t
se t > 0
0 f (τ ) g (t − τ ) dτ
Sia
convoluzione tra
Si dimostra che la convoluzione risulta localmente sommabile in
Si chiama
(10.2.21)
[0, +∞[
f (t) assolutamente L-trasformabile per Re {s} > %∗ e g (t) L-trasformabile
per Re {s} > %, allora la convoluzione {f (t) ∗ g (t)} (t) risulta L-trasformabile per Re {s} >
max (%∗ , %) e sussiste la formula:
Se risulta
L ({f (t) ∗ g (t)} (t)) (s) = L (f (t)) (s) L (g (t)) (s)
(10.2.22)
10.2.3 Trasformata di Laplace di alcune forme d'onda
10.2.3.1 Trasformata di Laplace del gradino
(
1 se t ≥ 0
u (t) =
0 se t < 0
u (t)
La funzione gradino
(10.2.23)
[0, +∞[, cioè è a segno
L-trasformabile o assolutamente L-
è sempre positiva nell'intervallo
denitivamente costante, quindi dire che
trasformabile è la stessa cosa.
u (t)
è
In altri termini il raggio di convergenza coincide con
il raggio di assoluta convergenza:
% = %∗ .
Troviamo i numeri reali s per i quali succede
che:
ˆ
∗
+∞
L (u (t)) (s) =
u (t) e−st dt < +∞
0
Poichè per s=0 si ha che
∗
ˆ
+∞
∗
u (t) e
−s0
ˆ
1 dt = +∞
0
la funzione
u (t)
+∞
dt =
0
non risulta trasformabile secondo Laplace in s=0 e quindi neanche per
% = %∗ = 0. Per i numeri reali s>0 si ha:
∗ ˆ +∞
∗ ˆ +∞
−st
L (u (t)) (s) =
u (t) e dt =
1e−st dt =
s<0; pertanto si ha che
0
=
Se
s∈C
0
e−st
−s
+∞
=
0
1
< +∞
s
si ha che
L (u (t)) (s) =
purchè sia
Re {s} > 0.
341
1
s
(10.2.24)
10 Reti elettriche nel dominio di Laplace
10.2.3.1.1 Trasformata di Laplace del gradino traslato.
Utilizzando la formula di
traslazione data in (10.2.13) e la (10.2.24) si trova la trasformata di Laplace del gradino
traslato:
L (u (t − a)) (s) = e−as
purchè sia
1
s
(10.2.25)
Re {s} > 0.
10.2.3.2 Trasformata di Laplace della funzione sinusoidale
Si vuole determinare la trasformata di Laplace della funzione sinusoidale:
w (t) = u (t) sin ωt
con
ω ∈ C.
Utilizzando la formula di Eulero per il seno si ha:
eiωt − e−jωt
1
1
L (u (t) sin ωt) (s) = L u (t)
(s) = L u (t) ejωt (s)− L u (t) e−jωt (s)
2j
2j
2j
Applicando la formula di traslazione rispetto ad s, data in (10.2.12), quest'ultima espressione si scrive:
1
1
L u (t) ejωt (s) − L u (t) e−jωt (s) =
2j
2j
1
1
1
1
1
s + jω − s + jω
1 j2ω
−
=
=
2j s − jω 2j s + jω
2j (s − jω) (s + jω)
2j s2 + ω 2
L (u (t) sin ωt) (s) =
Cioè
L (u (t) sin ωt) (s) =
s2
ω
+ ω2
(10.2.26)
La formula trovata vale se vengono rispettate le condizioni (vedi formula di traslazione
rispetto ad s):
(
Re {s} > Re {jω} = Re {j (Re {ω} + jIm {ω})} = −Im {ω}
Re {s} > Re {−jω} = Re {−j (Re {ω} + Im {ω})} = Im {ω}
che sono equivalenti alla condizione:
Re {s} > |Im {ω}|
342
10 Reti elettriche nel dominio di Laplace
10.2.3.3 Trasformata di Laplace della funzione cosinusoidale
Allo stesso modo si trova la trasformata di Laplace della funzione cosinusoidale:
w (t) = u (t) cos ωt
con
ω∈C
vale:
L (u (t) cos ωt) (s) =
s2
s
+ ω2
(10.2.27)
per
Re {s} > |Im {ω}|
10.2.3.4 Tabella delle trasformate di Laplace di alcune funzioni
Qui di seguito viene mostrata una tabella iin cui sono riportate alcune funzioni con le
corrispondenti trasformate di Laplace.
w (t) =
(
1 t≥0
u (t) =
0 t<0
ku (t)
t
n
t con n ∈ N
e−at
tn e−at
W (s) = L (w (t)) (s) =
1
s
k
s
1
s2
n!
sn+1
1
s+a
n!
(s+a)n+1
ω
s2 +ω 2
s
s2 +ω 2
ω
(s+a)2 +ω 2
s+a
(s+a)2 +ω 2
2ωs
(s2 +ω 2 )2
s2 −ω 2
(s2 +ω 2 )2
sin ωt
cos ωt
e−at sin ωt
e−at cos ωt
t sin ωt
t cos ωt
δ (t)
1
sn
dn
dtn δ (t)
Tabella 10.1: tabella delle trasformate di Laplace di alcune funzioni
Le ultime due trasforformate si ricavano inquadrando la trasformata di Laplace nell'ambito delle distribuzioni.
343
10 Reti elettriche nel dominio di Laplace
10.2.4 L.K nel dominio di Laplace
10.2.4.1 L.K.T. nel dominio di Laplace
La LKT nel dominio del tempo
X
vk (t) = 0
k
nel dominio di Laplace, si scrive:
X
Vk (s) = 0
(10.2.28)
k
essendo:
ˆ
∗
+∞
Vk (s) =
vk (t) e−st dt
(10.2.29)
0
Dimostrazione. Basta applicare la (10.1.4) alla (10.1.23):
!
L
X
k
vk (t) (s) =
Xˆ
+∞
vk (t) e−st dt =
X
0
k
L (vk (t)) (s) =
k
X
X
Vk (s) = 0
k
Vk (s) = 0
k
10.2.4.2 L.K.I. nel dominio di Laplace
La LKI nel dominio del tempo
X
ik (t) = 0
(10.2.30)
Ik (s) = 0
(10.2.31)
k
nel dominio di Laplace, si scrive:
X
k
essendo:
∗
ˆ
+∞
Ik (s) =
ik (t) e−st dt
(10.2.32)
0
10.2.5 L.L. nel dominio di Laplace
10.2.5.1 Resistore lineare tempo-invariante
v (t) = R i (t) ⇐⇒ V (s) = R I (s)
344
(10.2.33)
10 Reti elettriche nel dominio di Laplace
Figura 10.2.3: resistore nel dominio di Laplace
10.2.5.2 Capacitore lineare tempo-invariante
Applicando la Trasformata di Laplace all'equazione costitutiva del capacitore:
i (t) = C
d
v (t)
dt
si ottiene:
I (s) = sCV (s) − Cv 0+
Quest'ultima si può scrivere come segue:
V (s) =
v (0+ )
1
I (s) +
sC
s
(10.2.34)
Secondo (10.2.32), il capacitore (carico) nel dominio di Laplace risulta essere equivalente alla serie tra un capacitore scarico di impedenza:
Zc (s) =
1
sC
(10.2.35)
ed un generatore di tensione equivalente:
v (0+ )
s
(10.2.36)
Figura 10.2.4: capacitore nel dominio di Laplace
La formula in (10.2.32) suggerisce di trasformare la condizione iniziale sullo stato energetico del capacitore in generatore di tensione equivalente e poi applicare la trasformata
di Laplace.
345
10 Reti elettriche nel dominio di Laplace
10.2.5.3 Induttore lineare tempo-invariante
Applicando la Trasformata di Laplace all'equazione costitutiva dell'induttore :
v (t) = L
d
i (t)
dt
si ottiene:
V (s) = sLI (s) − Li 0+
Quest'ultima si può scrivere come segue:
I (s) =
1
i (0+ )
I (s) +
sL
s
(10.2.37)
Secondo (10.2.33), l'induttore (carico) nel dominio di Laplace risulta essere equivalente
al parallelo tra un induttore scarico di ammettenza:
YL (s) =
1
sL
(10.2.38)
ed un generatore di corrente equivalente:
i (0+ )
s
(10.2.39)
Figura 10.2.5: induttore nel dominio di Laplace
La formula in (10.2.35) suggerisce di trasformare la condizione iniziale sullo stato energetico dell'induttore in generatore di corrente equivalente e poi applicare la trasformata
di Laplace.
10.2.5.4 Impedenza del bipolo elementare
Per un bipolo elemetare si può denire nel dominio di Laplace, l'impedenza come segue:
Z (s) =


R
1
 sC
= Xc

sL = XL
(resistenza)
(reattanza capacitiva)
(reattanza induttiva)
346
(10.2.40)
10 Reti elettriche nel dominio di Laplace
Figura 10.2.6: impedenza
In Figura 10.2.6 viene mostrato il simbolo circuitale per rappresentare l'impedenza per
un bipolo.
Oppure l'ammettenza:

1

R = G
1
Y (s) =
= sC = BC
Z (s) 
1
sL == BL
conduttanza
sucettanza capacitiva
suscettanza induttiva
(10.2.41)
10.2.5.5 Coppia di induttori mutuamente accoppiati
Le equazioni costitutive che regolano il funzionamento della coppia di induttori mutuamente accoppiati mostrata in Figura 10.2.7 sono:
(
d
d
i1 (t) + M dt
i2 (t)
v1 (t) = L1 dt
d
d
v2 (t) = M dt i1 (t) + L2 dt i2 (t)
Figura 10.2.7: coppia di induttori mutuamente accoppiati
Applicando la trasformata di Laplace a tali equazioni si ottengono le sguenti equazioni
(
V1 (s) = sL1 I1 (s) − L1 i1 (0+ ) + sM I2 (s) − M i2 (0+ )
V2 (s) = sM I1 (s) − M i1 (0+ ) + sL2 I2 (s) − L2 i2 (0+ )
(10.2.42)
che suggeriscono il circuito mostrato in Figura 10.2.8
Scrivendo le equazioni in (10.2.40) esplicitando le correnti
I1 (s)
es
I2 (s)
si ottengono
le equazioni

I (s) =
1
I (s) =
2
1
sL1 V1 (s)
1
sL2 V2 (s)
+
+
i1 (0+ )
M i2 (0+ )
+ sL1
s
M i1 (0+ )
i2 (0+ )
+ s
sL2
347
−
−
M I2 (s)
L1
M I2 (s)
L2
(10.2.43)
10 Reti elettriche nel dominio di Laplace
Figura 10.2.8: coppia di induttori mutuamente accoppiati nel dominio di Laplace
che conducono al circuito equivalente mostrato in Figura 10.2.9
Figura 10.2.9: coppia di induttori mutuamente accoppiati nel dominio di Laplace
10.2.5.6 Trasformatore ideale
(
v1 (t) = t v2 (t)
i1 (t) = − 1t i2 (t)
(
V1 (s) = t V2 (s)
⇐⇒
I1 (s) = − 1t I2 (s)
(10.2.44)
Figura 10.2.10: trasformatore ideale
10.2.5.7 Generatore ideale di tensione
v (t) = vg (t) ⇐⇒ V (s) = Vg (s)
348
(10.2.45)
10 Reti elettriche nel dominio di Laplace
10.2.5.8 Generatore ideale di corrente
i (t) = ig (t) ⇐⇒ I (s) = Ig (s)
(10.2.46)
10.3 Antitrasformata di Laplace
10.3.1 Il problema dell'antitrasformabilità
Un problema molto importante dal punto di vista sia puramente matematico che applica-
antitrasformazione ; cioè data una funzione W (s) derivabile in un
Re {s} > %, dire se esite ed eventualmente determinarla, una funzione
w (t) localmente sommabile in [0, +∞[ nulla in ]−∞, 0[ tale che L (w (t)) (s) = W (s). Se
ciò accade la funzione w (t) prende il nome di antitrasormata della funzione W(s) e verrà
−1 (W (s)) (t):
indicata con il simbolo L
tivo, è il problema dell'
semipiano del tipo
w (t) = L−1 (W (s)) (t)
(10.3.1)
Esisto delle condizioni necessarie ma non sucienti per l'antitrasformabilità.
Condizione 1
%.
w (t) ∈ L1loc ([0, +∞[) nulla in ]−∞, 0[ L-trasformabile per Re {s} >
s0 ∈ C e α ∈ R tali che Re {s0 } > % e 0 < α < π2 . Considerato l'insieme:
Sia
Siano inoltre
Sα = {s ∈ C : |arg (s − s0 ) ≤ α|}
si ha che:
lim W (s) |Sα = 0
(10.3.2)
s→+∞
essendo
W (s) = L (w (t)) (s)
Con il simbolo
W (s) |Sα
viene indicata la restrizione della funzione
W (s)
al semipiano
Sα .
Si osservi che in particolare si ha che
lim W (s) = 0
(10.3.3)
s→+∞
Condizione 2
%.
Sia inoltre
w (t) ∈ L1loc ([0, +∞[) nulla in ]−∞, 0[ L-trasformabile
δ > %. Detto Πδ il semipiano denito da Re {s} ≥ δ , cioè:
Sia
per
Re {s} >
Πδ = {s ∈ C : Re {s} ≥ δ}
si ha che:
W (s)
|Πδ = 0
s→+∞
s
lim
349
(10.3.4)
10 Reti elettriche nel dominio di Laplace
essendo
W (s) = L (w (t)) (s)
Se
W (s)
non soddisfa le condizioni 1 e 2 allora certamente non risulta antitrasforma-
bile. Se vengono rispettate tali condizioni, potrebbe pure succedere che
W (s)
non sia
antitrasformabile.
Esempio 1.
Si consideri la funzione
W (s) = 1.
Chiaramente tale funzione non soddisfa
le condizoni necessarie 1 e 2 e pertanto non risulta antitrasformabile
Si consideri pure la funzione
W (s) = sn
con
n ∈ N.
Anche questa funzione non è
antitrasformabile perche non soddisfa le condizioni necessarie 1 e 2 .
Tuttavia va detto che tali funzioni ammettono antitrasformata di Laplace se vengono
inquadrate nell'ambito della teoria delle distribuzioni.
Esempio 2.
Si consideri la funzione
W (s) = e−s denita per Re {s} > 0.
Tale funzione
soddisfa le condizioni necesssarie, infatti
e−s
=0
s→+∞ s
lim e−s = 0
lim
s→+∞
Tuttavia non esiste una funzione
tale che
L (w (t)) (s) = W (s).
w (t) localmente sommabile in [0, +∞[ nulla in ]−∞, 0[
Ciò si prova facilmente per assurdo.
Supponiamo esista una funzione
w (t) localmente sommabile in [0, +∞[ nulla in ]−∞, 0[
tale che
L (w (t)) (s) = W (s) = e−s
Se così è allora, derivando rispetto ad s si ottiene:
D [L (w (t)) (s)] = D e−s
(−1) L (t w (t)) (s) = (−1) e−s
ovvero:
L (t w (t)) (s) = e−s
Con ciò è stato trovato che le funzioni
Laplace e ciò vuol dire che
w (t) = t w (t)
w (t)
e
t w (t)
hanno la stessa trasformata di
quasi ovunque in
R,
cioè
w (t) (1 − t) = 0 quasi ovunque in R
A questo punto per la legge di annullamento del prodotto dovrebbe essere
ciò è assurdo altrimenti si avrebbe:
L (w (t)) (s) = W (s) = 0
Si dimostra che vale la relazione:
350
w (t) = 0
e
10 Reti elettriche nel dominio di Laplace
w (t) = L−1 (W (s)) (t) =
d 1
=
V.P.
dt 2πj
per
Re {s} > %,
essendo
ˆ
x+j∞
x−j∞
e−st
L (w (t)) (s)
ds q.o. in R
s
(10.3.5)
s = x + jy∈ C.
10.3.2 Proprietà dell'antitrasformata di Laplace
Siano
F (s) e G (s) due funzioni derivabili in un semipiano Re {s} > %, valgono le seguenti
proprietà.
Proprietà 1.
L−1 (λ1 F (s) + λ2 G (s)) (t) = λ1 L−1 (F (s)) (t) + λ2 L−1 (G (s)) (t)
(10.3.6)
Proprietà 1.
L
−1
1
(W (as)) (t) = L−1 (W (s))
a
t
a
a>0
(10.3.7)
Proprietà 2.
L−1 (W (s − α)) (t) = eαt L−1 (W (s)) (t)
α∈C
(10.3.8)
Proprietà 3.
L−1 e−as W (s) (t) = L−1 (W (s)) (t − a) u (t − a)
(10.3.9)
Proprietà 4.
L−1 (F (s) G (s)) (t) = L−1 (F (s)) (t) ∗ L−1 (G (s)) (t)
(10.3.10)
10.3.3 Antitrasformata di Laplace delle funzioni razionali fratte
Un'importante famiglia di funzioni antitrasformabili è quella delle funzioni razionali fratte
del tipo:
N (s)
a0 sm + a1 sm−1 + ...... + am
=
D (s)
b0 sn + b1 sn−1 + ...... + bn
(10.3.11)
Si stinguono 2 casi:
ˆ
caso 1: funzione razionale fratta impropria o irregolare (m
351
≥ n)
10 Reti elettriche nel dominio di Laplace
In questo caso la frazione risulta essere propria e si procede eseguendo la divisione tra i
polinomi ottenendo così l'uguaglianza:
N (s)
R (s)
= Q (s) +
D (s)
D (s)
A questo punto
Q (s)
(10.3.12)
risulta essere un polinomio del tipo:
Q (s) = c0 sp + c1 sp−1 + ...... + cp
che è facilmente antitrasformabile facendo uso della tabella delle trasformate di Laplace:
L−1 (Q (s)) (t) = c0 L−1 (sp ) (t) + c1 L−1 sp−1 (t) + ...... + cp L−1 (1) (t) =
= c0 δ (p) (t) + c1 δ (p−1) (t) + ...... + cp δ (t)
Mentre
(10.3.13)
R(s)
D(s) risulta essere una frazione propria, cioè una frazione in cui il grado del
polinomio al numeratore risulta minore del grado del polinomio al denominatore.
Se si decide di studiare una rete elettrica nel dominio di Laplace, per ritornare nel
dominio del tempo, occorre sempre antitrasformare una funzione razionale fratta impropria.
ˆ
caso 2: funzione razionale fratta impropria (m
< n)
Si dimostra che un funzione razionale fratta propria si può scrivere come somma di
frazioni fratte proprie elementari, conosciute come
fratti semplici,
mediante il principio
di identità dei polinomi.
I fratti semplici sono le seguenti funzioni razionali fratte:
A
s+a
A
(s + a)n
s2
(10.3.14)
n intero positivo ≥ 2
as + b
+ ps + q
(10.3.15)
con p2 − 4q < 0
(10.3.16)
L'antitrasformata di Laplace della (10.3.14), secondo la tabella delle trasformate di
Laplace vale:
−1
L
A
s+a
−1
(t) = AL
1
s+a
(t) = Ae−at
(10.3.17)
L'antitrasformata di Laplace della (10.3.15), secondo la tabella delle trasformate di
Laplace vale:
−1
L
A
(s + a)n
−1
(t) = AL
352
1
(s + a)n
(t) =
10 Reti elettriche nel dominio di Laplace
=
A
L−1
(n − 1)!
(n − 1)!
(s + a)n
A
tn−1 e−at
(n − 1)!
(t) =
(10.3.18)
Per antitrasformare la (10.3.16) occorre prima scriverla in una forma più appropriata.
Tenendo conto che
√
4q−p2
s2 + ps + q = s2 + ps +
2
p2
4
+q−
p2
4
= s+
p 2
2
4q−p2
4
+
= s+
p 2
2
+
la (10.3.16) si scrive:
2
as + b
=
s2 + ps + q
a s + ab
a s + p2 + ab − p2
2 =
2 =
√
√
4q−p2
4q−p2
p 2
p 2
s+ 2 +
s+ 2 +
2
2
p
2
b
a
√
4q−p2
2
a −
a s + p2
1
=
2 + √
2
√
√
4q−p2
4q−p2
4q−p2
p 2
p 2
s+ 2 +
s+ 2 +
2
2
2
A questo punto utilizzando la tabella delle trasformate di Laplace è chiaro che:

−1
L
as + b
2
s + ps + q


s + p2

√
2  (t) +

2
4q−p2
s + p2 +
2


(t) = aL−1 


+
= ae
Esempio.
− p2 t
a
b
−p
√a 2
4q−p2
2
p
cos



√
−1 
L
4q − p2
t
2
!
s+
p 2
2

4q−p2
2
√
+


2  (t) =

4q−p2
2
2b − ap − p
+p
e 2 sin
4q − p2
p
4q − p2
t
2
!
(10.3.19)
Si vuole antitrasformara la funzione:
s2 + s + 1 (s + 2)
W (s) = 6
s + 4s5 + 8s4 + 10s3 + 8s2 + 4s + 1
Innanziutto occorre scomporre il denominatore:
D (s) = s6 + 4s5 + 8s4 + 10s3 + 8s2 + 4s + 1 = (s + 1)2 s2 + s + 1
Quindi si ha:
W (s) =
s+2
(s + 1) (s2 + s + 1)
2
Applicando il principio di identità dei polinomi
353
2
10 Reti elettriche nel dominio di Laplace
W (s) =
Cs + D
s+2
A
B
+ 2
=
+
2
(s + 1) (s + 1)
s +s+1
(s + 1) (s2 + s + 1)
2
(10.3.20)
restano da determinare le costanti A, B, C e D come segue:
A (s + 1) s2 + s + 1 + B s2 + s + 1 + (Cs + D) (s + 1)2
s+2
=
=
(s + 1)2 (s2 + s + 1)
(s + 1)2 (s2 + s + 1)
A s3 + 2s2 + 2s + 1 + B s2 + s + 1 + Cs3 + (2C + D) s2 + (C + 2D) s + D
=
(s + 1)2 (s2 + s + 1)
=
=
(A + C) s3 + (2A + B + 2C + D) s2 + (2A + B + C + 2D) s + A + B + D
(s + 1)2 (s2 + s + 1)
Anchè la prima frazione sia identica all'ultima frazione presente in quest'ultima espressione, deve essere:


A+C =0



2A + B + 2C + D = 0

2A + B + C + 2D = 1



A + B + D = 2
Risolvendo quest'utlimo sistema si trova:


A =


B =

C=



D =
2
1
−2
−1
(10.3.21)
1
2s + 1
2
+
− 2
2
(s + 1) (s + 1)
s +s+1
(10.3.22)
Sostituendo (10.3.21) in (10.3.20) si ottiene:
W (s) =
Attraverso l'applicazione del principio di identità dei polinomi è stata scomposta la
funzione
W (s)
nella combinazione lineare di fratti semplici.
Applicando l'antitrasformata di Laplace all'espressione in (10.3.22) si ha:
−1
L
(W (s)) (t) = 2L
−1
1
(s + 1)
(t) + L
−1
1
(s + 1)2
(t) − L
−1
2s + 1
2
s +s+1
(t)
(10.3.23)
Utilizzando la tabella delle trasformate di Laplace si ottiene:
354
10 Reti elettriche nel dominio di Laplace
L−1
L
L−1
2s + 1
2
s +s+1
−1
2 s+ 2
2
s + 21 +
3
4
1
(s + 1)
1
(s + 1)2
(t) = L−1
!
1
= L−1
(t) = e−t
(10.3.24)
(t) = t e−t
(10.3.25)
2 s + 12
s2 + s + 14 −

!
1
4
+1
(t) =

1
s+ 2

√ 2  (t) =
2
s + 12 + 23
√ !
3
t
2

(t) = 2L−1 
1
= 2e− 2 t cos
(10.3.26)
Sostituendo inne (10.3.24), (10.3.25) e (10.3.24) in (10.3.23) si ha:
−1
L
(W (s)) (t) = 2 e
−t
−t
+ te
− 12 t
− 2e
cos
√ !
3
t
2
(10.3.27)
10.4 Risoluzione reti elettriche mediante trasformata di
Laplace
Consideriamo la rete elettrica mostrata in
Figura 10.1.1. Si vuole determinare la tensione ai capi del capacitore
vc (t) per t > 0
applicando la trasformata di Laplace.
Quando si vuole studiare una rete elettrica mediante la trasformata di Laplace,
la prima cosa che si fà è trasformare le
condizioni iniziali relative ai dispositivi a
memoria in generatori equivalenti come
mostrato in Figura 10.1.2.
Figura 10.4.1: rete elettica
Applicando la trasformata di Laplace si ottiene il circuito nel dominio di Laplace
mostrato in Figura 10.4.3.
Avendo sostituito le condizioni iniziali relative ai dispositivi a memoria con generatori equivalenti, per determinare una qualunque variabile di rete non serve passare dalla
conoscenza delle equazioni di stato perchè non serve trovare le condizioni iniziali sulle
355
10 Reti elettriche nel dominio di Laplace
Figura 10.4.2: rete elettrica
Figura 10.4.3: rete elettrica
derivate delle variabili di rete di interesse. Si otterrà dunque una risposta che è combinazione lineare dei generatori ideali e dei generatori equivalenti; ossia nel caso della rete
mostrata in Figura 10.1.3 si troverà come risposta la somma tra 2 risposte con ingresso
zero e 2 risposte con stato zero.
A questo punto per studiare la rete elettrica di Figura 10.1.3 si può applicare uno dei
metodi di analisi noti. Anche se confrontando i numeri N-1 ed L-N+1 si scopre che il
metodo dei potenziali ai nodi e il metodo delle correnti di maglia sono equivalenti, conviene utilizzare il metodo dei potenziali ai nodi visto che siamo interessati a determinare
una tensione anzichè una corrente.
Denendo i potenziali ai nodi
E1 (s) ed E2 (s), come mostrato in Figura 10.1.3, si scrive
di getto il sistema risolvente:
1
R1
+ sC +
1
− sL
1
sL
1
− sL
1
1
R2 + sL
E1 (s)
E2 (s)
=
Vg (s) + V0 −
Ig (s) + Is0
I0
s
R1 ,R2 , L, C quest'ultimo si scrive:
− 1s
E1 (s)
Vg (s) + V0 − Is0
=
1 + 1s
E2 (s)
Ig (s) + Is0
Sostituendo i valori numerici per
1+s+
− 1s
1
s
356
(10.4.1)
10 Reti elettriche nel dominio di Laplace
Basta determinare dal sistema risolvente
E1 (s),
visto che quest'iltimo coincide con la
trasformata di Laplace della tensione ai capi del capacitore:
E1 (s) = Vc (s)
Risolvendo utilizzando il metodo di Cramer si ha:
∆=
∆E1 =
1
1+s+
s
1
1
s2 + 2s + 2
1+
− 2 =
s
s
s
(1 + s)
1
(1 + s)
1
Vg (s) + Ig (s) +
V0 − I0
s
s
s
s
Vc (s) = E1 (s) =
=
s2
∆E1
=
∆
(1 + s)
1
(1 + s)
1
Vg (s) + 2
Ig (s) + 2
V0 − 2
I0
+ 2s + 2
s + 2s + 2
s + 2s + 2
s + 2s + 2
E' chiaro che la tensione
Vc (s)
(10.4.2)
e la somma tra 2 risposte con ingresso zero e 2 risposte
con stato zero come accennato prima. Sostituendo le espressioni analitiche dei generatori
ideali e dei generatori equivalenti si ottiene:
Vc (s) =
(1 + s) 9
1
1
(1 + s)
1
+
+
−
s2 + 2s + 2 s s2 + 2s + 2 s s2 + 2s + 2 s2 + 2s + 2
ossia:
Vc (s) =
s2 + 9s + 10
s (s2 + 2s + 2)
(10.4.3)
Per determinare dalla (10.1.3) l'espressione della tensione nel dominio del tempo, occorre applicare l'anti-trasformata di Laplace.
Bisogna però scomporre la frazione nel-
la variabile s in fratti che si possono antitrasformare in maniera immediata.
Quindi
innanzitutto occorre scomporre in fratti semplici la funzione razionale fratta:
s2 + 9s + 10
A
Bs + C
= + 2
s (s2 + 2s + 2)
s
s + 2s + 2
(10.4.4)
Applicando il principio di identità dei polinomi si ha:
A s2 + 2s + 2 + (Bs + C) s
A
Bs + C
s2 + 9s + 10
= + 2
=
=
s (s2 + 2s + 2)
s
s + 2s + 2
s (s2 + 2s + 2)
=
(A + B) s2 + (2A + C) s + +2A
s (s2 + 2s + 2)
(10.4.5)
Confrontando il primo e il quarto membro dell'espressione in (10.1.5), per avere l'dentità
dei polinomi, deve essere:
357
10 Reti elettriche nel dominio di Laplace


A + B = 1
2A + C = 9


2A = 10
(10.4.6)
Risolvendo il sistema in (10.1.6) si ottiene facilmente:


A = 5
B = −4


C = −1
(10.4.7)
Utilizzando i valori in (10.1.7) la (10.1.4) ossia la (10.1.3) si scrive:
Vc (s) =
−4s − 1
5
+
s s2 + 2s + 2
Quest'ultima relazione si può scrivere pure come segue:
Vc (s) =
=
=
s
1
5
−4 2
− 2
=
s
s + 2s + 2 s + 2s + 2
5
s+1−1
1
−4 2
−
=
s
s + 2s + 2 s2 + 2s + 2
5
s+1
4
1
−4 2
+
−
=
s
s + 2s + 1 + 1 s2 + 2s + 1 + 1 s2 + 2s + 1 + 1
=
5
s+1
1
−4
+3
2
s
(s + 1) + 1
(s + 1)2 + 1
ovvero:
Vc (s) =
s+1
1
5
−4
+3
2
s
(s + 1) + 1
(s + 1)2 + 1
(10.4.8)
A questo punto si può dire che la (10.1.8) si può antitrasformare in maniera immediata:
vc (t) = L (Vc (s)) (t) = 5 u (t) − 4 e−t cos t + 3 e−t sin t
Posto
(
K cos ϕ = −4
−K sin ϕ = 3
(10.4.9)
(10.4.10)
la (10.1.9) si scrive:
vc (t) = L (Vc (s)) (t) = 5 u (t) + e−t (k cos ϕ cos t − k sin ϕ sin t) =
= 5 u (t) + e−t k cos (t + ϕ)
358
(10.4.11)
10 Reti elettriche nel dominio di Laplace
Resta da determinare le quantità
k
e
ϕ
dal sistema in (10.1.10); si ha facilmente che:
(
√
K = 16 + 9 = 5
ϕ = π + arctan 34 = 3, 78509
(10.4.12)
Sostituendo (10.1.12) in (10.1.11) si ottiene inne:
vc (t) = 5 u (t) + 5 e−t k cos (t + 3, 78509) V
(10.4.13)
esattamente come in (4.3.46). La trasformata di Laplace permette di risolvere problemi
in transitorio che iniziano al tempo t=0 s.. Questa trasformata non va confusa con la
trasformata di Fourier che si applica invece a quelle reti o a quei sistemi che si studiano
a partire dal tempo t=-∞.
Per esempio la teoria delle telecomunicazioni si basa tutta sulla trasformata di Fourier;
infatti per un sistema di telecomunicazioni i transitori non sono di interesse; per essi si
studia il regime per segnali non periodici.
359
11 La teoria dei doppi bipoli
11.1 Il doppio bipolo
Il doppio bipolo è un dispositivo a 4 morsetti a due a due intteressati da una stessa
corrente. In Figura 11.1.1 viene mostrato un doppio bipolo chiuso attraverso due bipoli.
Figura 11.1.1: doppio bipolo
Il doppio bipolo è quindi un dispositivo a due porte. Come indicato in Figura 11.1.1
la porta 1 è interessata dalla corrente i1
i2 (t).
(t)
mentre la porta 2 è interessata dalla corrente
Si dice che il doppio bipolo mostrato in alto in Figura 11.1.1 è un doppio bipolo
per ragioni esterne; cioè qualunque insieme di taglio si considera, la corrente entrante
dall'insieme di taglio è uguale a quella uscente (Figura 11.1.2).
Figura 11.1.2: doppio bipolo per ragioni interne
Π1
morsetti Π2
Se il dispositivo a quattro morsetti
un altro dispositivo a quattro
mostrato in Figura 11.1.3 viene collegato ad
è impossibile dire che tali dispositivi sono dei
doppi bipoli per ragioni esterne.
Consideriamo per esempio il dispositivo
Π2 .
La somma delle correnti, all'insieme di
taglio I è chiaramente zero per la LKC, ma non esiste alcuna ragione esterna per cui le
quattro correnti interessate all'insieme di taglio si annullino a due a due. Pertanto
non è un doppio bipolo per ragioni esterne.
360
Π2
11 La teoria dei doppi bipoli
Figura 11.1.3: dispositivi a quattro morsetti
Tuttavia un dispositivo a quattro morsetti può essere un doppio bipolo per
interne.
Se per esempio all'interno del dispositivo
Π2
ragioni
vi è una coppia di induttori mutu-
amente accoppiati, come mostrato in Figura 11.1.4, allora esso risulta essere un doppio
bipolo per ragioni interne.
Figura 11.1.4:
Π2
è un doppio bipolo per ragioni interne
Si studiano i doppi bipoli perchè la struttura tipica di un sistema di telecomunicazioni
è fatta da doppi bipoli tutti in cascata come mostrato in Figura 11.1.5. Ogni dispositivo
è un doppio bipolo per costruzione: solo la sorgente e la destinazione sono dei semplici
bipolo.
Gli studi che si eettuano sui doppi bipoli, prevedono che al loro interno non ci siano
sorgenti.
Quindi all'interno del doppio bipolo possono esserci resistori, capacitori, in-
duttori, induttori mutuamente accoppiati e generatori pilotati:
ovviamente induttori
mutuamente accoppiati e generatori pilotati devono essere necessariamente accoppiati
361
11 La teoria dei doppi bipoli
Figura 11.1.5:
Π2
è un doppio bipolo per ragioni interne
solo con grandezze interne al doppio bipolo.
Siccome tutti i dispositivi all'interno del
doppio bipolo sono lineari tempo-invariante, l'analisi può essere arontata nel dominio
del tempo, nel dominio dei fasori o nel dominio di Laplace.
Nel dominio dei fasori, il doppio bipolo si rappresenta come mostrato in Figura 11.1.6.
Figura 11.1.6: rappresentazione del doppio bipolo nel dominio dei fasori
Si osservi come per ciascuna porta viene utilizzata la convenzione dell'utilizzatore. Il
doppio bipolo lega le grandezze
V̇1 , I˙1 , V̇2 , I˙2
in maniera duplice; ci si aspetta pertanto
delle relazioni del tipo:
(
ȧ11 V̇1 + ȧ12 V̇2 + ḃ11 I˙1 + ḃ12 I˙2 = 0̇
ȧ21 V̇1 + ȧ22 V̇2 + ḃ21 I˙1 + ḃ22 I˙2 = 0̇
(11.1.1)
Le equazioni scritte sono omogenee (manca il termine noto), in quanto nel doppio
bipolo non sono previsti generatori ideali. Le equazioni in (11.1.1) si possono scrivere in
forma matriciale compatta:
h ih i h ih i Ȧ V̇ + Ḃ I˙ = 0̇
(11.1.2)
essendo:
h i ȧ
11
Ȧ =
ȧ21
h i ḃ
11
Ḃ =
ḃ21
ȧ12
ȧ22
ḃ12
ḃ22
h i V̇ 1
V̇ =
V̇2
h i I˙ I˙ = ˙1
I2
La relazione in (11.1.2) è lapiù generale che può caratterizzare un doppio bipolo. ovviamente gli otto coecienti
ȧ11 , ȧ12 , ȧ21 , ȧ22 , ḃ11 , ḃ12 , ḃ21 , ḃ22
il doppio bipolo.
362
li determina chi hastudiato
11 La teoria dei doppi bipoli
Le matrici
h i
Ȧ
e
h i
Ḃ
specicano completamente il funzionamento del doppio bipolo.
Supponiamo di chiudere il doppio bipolo attraverso due bipoli di Thevenin come mostrato
in Figura 11.1.7.
Figura 11.1.7: doppio bipolo chiuso mediante bipoli Thevenin
Le porte del doppio bipolo sono legati ai corrispondenti bipoli di chiusura mediante le
relazioni:
Se le
h i
Ȧ
e
h i
Ḃ
del doppio bipolo
V̇1 = V̇g1 − Ż1 I˙1
(11.1.3)
V̇2 = V̇g2 − Ż2 I˙2
(11.1.4)
Π
sono note, il circuito mostrato in Figura 11.1.7 si
risolve completamente tramite il seguente sistema di 4 equazioni in 4 incognite:
h i h i h i h i 
˙

 Ȧ V̇ + Ḃ I = 0̇
V̇1 = V̇g1 − Ż1 I˙1


V̇ = V̇ − Ż I˙
2
g
2 2
(11.1.5)
2
Si tenga presente che un circuito come quello mostrato in Figura 11.1.7 potrebbe
essere una rete molto compliata; per convincersi di ciò basti pensare che il doppio bipolo potrebbe pure essere una rete con 1000 incognite, pertanto rappresentare una rete
elettrica mediante un doppio bipolo risulta essere una vera e propria semplicazione.
Esistono 7 diversi modi per rappresentare un doppio bipolo.
11.1.1 Rappresentazione del doppio bipolo mediante la matrice delle
impedenze e la matrice delle ammettenze
11.1.1.1 Matrice delle impedenze
Supponiamo che la matrice
la sua inversa
h i−1
Ȧ
.
(11.1.2) per la matrice
h i
Ȧ sia invertibile.
Se la matrice
h i
Ȧ è invertibile allora esiste
Premoltiplicando entrambi i membri dell'equazione matriciale in
h i−1
Ȧ
si ricava:
h i−1 h i h i h i−1 h i h i h i−1 Ȧ
Ȧ V̇ + Ȧ
Ḃ I˙ = Ȧ
0̇
363
11 La teoria dei doppi bipoli
ovvero:
h i−1 h i h i
h i
Ḃ I˙
V̇ = − Ȧ
Denendo la
(11.1.6)
matrice dele impedenze :
h i
h i−1 h i Ż
11 Ż12
Ż = − Ȧ
Ḃ =
Ż21 Ż22
(11.1.7)
h i h ih i
V̇ = Ż I˙
(11.1.8)
la (11.1.6) si scrive:
La (11.1.8) è l'equazione matriciale rappresentativa del doppio bipolo che in forma
scalare si scrive:
(
V̇1 = Ż11 I˙1 + Ż12 I˙2
V̇2 = Ż21 I˙1 + Ż22 I˙2
Ponendo
I˙2 = 0̇,
si dice che il doppio bipolo ha la porta 2 a vuoto. Sotto questa ipotesi
le equazioni in (11.1.9) forniscono i valori di
Ż11
si chiama
(11.1.9)
Ż11
e
Ż21 :
Ż11 =
V̇1 ˙
I˙1 I2 =0̇
(11.1.10)
Ż21 =
V̇2 ˙
I˙1 I2 =0̇
(11.1.11)
auto-impedenza della porta 1, Ż21 si chiama trans-impedenza;
queste due
impedenze si ricavano dallo schema di calcolo mostrato in Figura 11.1.8.
Figura 11.1.8: schema di calcolo per determinare
I˙1 = 0̇, si dice che il doppio bipolo ha la porta 1 a vuoto.
equazioni in (11.1.9) forniscono i valori di Ż12 e Ż22 :
Ponendo
le
Ż11
V̇1 ˙
I˙2 I1 =0̇
V̇2 =
˙
I˙2 I1 =0̇
e
Ż21
Sotto questa ipotesi
Ż12 =
(11.1.12)
Ż22
(11.1.13)
364
11 La teoria dei doppi bipoli
Ż12
si chiama
trans-impedenza, Ż22 si chiama auto-impedenza della porta 2;
queste due
impedenze si ricavano dallo schema di calcolo mostrato in Figura 11.1.9.
Figura 11.1.9: schema di calcolo per determinare
11.1.1.1.1 Esempio.
Ż12
e
Ż22
Si consideri il doppio bipolo mostrato in Figura 11.1.10.
Figura 11.1.10: doppio bipolo
Il doppio bipolo è descrivibile mediante la matrice delle impedenze. La relazione in
(11.18) suggerisce di utilizzare il metodo delle correnti di maglia; possiamo quindi eccitare
le due porte attraverso due generatori ideali di tensione come mostrato in Figura 11.1.11
Figura 11.1.11: doppio bipolo
Con riferimento alle maglie indicate nel circuito è facile scrive di getto il corrispondente
sistema risolvente:
365
11 La teoria dei doppi bipoli
1
R1 + jωC

0
1
− jωC
1
0
− jωC
R2
R2
R2 R2 + jωL +

1
jωC

 ˙  
I1
V̇1
  I˙2  =  V̇2 
0̇
J˙
Quest'ultimo in forma scalare si scrive:

1
1 ˙
˙

R
+
1

jωC I1 − jωC J = V̇1

R2 I˙2 + R2 J˙ = V̇2 

− 1 I˙ + R I˙ + R + jωL +
2
1
2 2
jωC
Ricavando
J˙
(11.1.14.1)
(11.1.14.2)
1
jωC
(11.1.14)
J˙ = 0̇ (11.1.14.3)
da (11.1.14.3) e sostituendo in (11.1.14.1) e (11.1.14.2) si ottiene il sistema
nelle incognite
I˙1
e
I˙2 :

 R1 +

R2 +jωL
2
1+jωCR2 +(jω)
LC
R2
I˙1 +
1+jωCR2 +(jω)2 LC
2
I˙1 + 1+jωCRR+(jω)
I˙2 = V̇1
2
LC
2
1+(jω)2 LC
R2 1+jωCR
I˙2 = V̇2
+(jω)2 LC
(11.1.14.1)
(11.1.14.2)
(11.1.15)
2
Quest'ultimo sistema conduce alla matrice delle impedenze:

h i
R1 +
Ż = 
R2 +jωL
1+jωCR2 +(jω)2 LC
R2
1+jωCR2 +(jω)2 LC
I termini della matrice delle impedenze
R2
1+jωCR2 +(jω)2 LC (jω)2 LC
R2 1+jωCR
2
2 +(jω) LC
h i
Ż


(11.1.16)
si possono ricavare facilmente utilizzando le
denizioni date in (11.1.10), (11.1.11), (11.1.12) e (11.1.13).
Con riferimento al circuito mostrato in Figura 11.1.12 si possono determinare i termini
Ż11
e
Ż21 .
Si tenga presente che tale circuito non deriva da quello mostrato in Figura
11.1.1 applicando il teorema di sovrapposizione degli eetti. Esso è il caso particolare
dello schema di calcolo mostrato in Figura 11.1.8
Figura 11.1.12: doppio bipolo
L'auto-impedenza della porta 1,
Ż11 ,
si ricava in modo molto semplice applicando le
regole delle impedenze in parallelo e delle impdenze in serie:
366
11 La teoria dei doppi bipoli
1
V̇1
jωC (R2 + jωL)
= R1 +
1 =
R1 + jωL + jωC
I˙1
Ż11 =
= R1 +
La trans-impedenza
Ż21
R2 + jωL
1 + jωCR1 + (jω)2 LC
(11.1.17)
si ricava scrivendo la legge di lato per il resistore di resistenzaR2
ed esplicitando la corrente che lo attraversa mediante la legge del partitore di corrente:
V̇2 = R2 I˙2 = R2
1
jωC
1
jωC
+ jωL + R2
I˙1 = R2
1
I˙1
1 + jωCR2 + (jω)2 LC
Da quest'ultima relazione segue:
Ż21 =
R2
V̇2
=
˙
I1
1 + jωCR2 + (jω)2 LC
(11.1.18)
Con riferimento al circuito mostrato in Figura 11.1.13 si possono determinare inne i
termini
Ż22
e
Ż12 .
Anche questo circuito non deriva da quello mostrato in Figura 11.1.1
applicando il teorema di sovrapposizione degli eetti.
Esso è il caso particolare dello
schema di calcolo mostrato in Figura 11.1.9
Figura 11.1.13: doppio bipolo
L'auto-impedenza della porta 2,
Ż22 ,
si ricava in modo molto semplice applicando le
regole delle impedenze in parallelo e delle impdenze in serie:
R2
Ż22 =
= R2
La trans-impedenza
1
jωC
+ jωL
V̇2
=
R2 + jωL +
I˙2
1
jωC
=
1 + (jω)2 LC
1 + jωCR1 + (jω)2 LC
!
(11.1.19)
Ż12 si ricava scrivendo la legge di lato per il capacitore ed esplicitando
la corrente che lo attraversa mediante la legge del partitore di corrente:
367
11 La teoria dei doppi bipoli
V̇1 =
1 ˙
1
Ic =
jωC
jωC
1
jωC
R2
R2
I˙2 =
I˙2
+ jωL + R2
1 + jωCR2 + (jω)2 LC
Da quest'ultima relazione segue:
Ż12 =
V̇1
R2
=
I˙2
1 + jωCR2 + (jω)2 LC
(11.1.20)
Si osservi che il doppio bipolo in esame soddisfa la tesi del teorema di reciprocità data
in (9.5.9):
Ż12 = Ż21
(11.1.21)
Questo fatto era del tutto prevedibile visto che nel doppio bipolo non gurano generatori
pilotati.
Le trans.ammettenze per un doppio bipolo privo di generatori pilotati si possono quindi
ricavare applicando il teorema di reciprocità.
Visto che i nodi 1-1' e 2-2' del doppio bipolo mostrato in Figura 11.1.10 sono coppie di
nodi distinti del circuito, le porte si possono alimentare soltanto in corrente. Alimentando
la porta 1 mediante il generatore ideale di corrente
I˙1
si ha il circuito mostrato in Figura
11.1.14.1. Alimentando la porta 2 mediante il generatore ideale di corrente
I˙2
si ha il
circuito mostrato in Figura 11.1.14.2.
1
2
Figura 11.1.14: doppio bipolo
Eseguendo gli stessi passaggi visti in precedenza si scopre che i circuiti mostrati in
Figura 11.1.14 conducono alla relazione in 11.1.21.
11.1.1.2 Matrice delle ammettenze
Supponiamo che la matrice
la sua inversa
h i−1
Ḃ
.
(11.1.2) per la matrice
h i
Ḃ sia invertibile.
Se la matrice
h i
Ḃ è invertibile allora esiste
Premoltiplicando entrambi i membri dell'equazione matriciale in
h i−1
Ḃ
si ricava:
h i−1 h i h i h i−1 h i h i h i−1 Ḃ
Ȧ V̇ + Ḃ
Ḃ I˙ = Ḃ
0̇
368
11 La teoria dei doppi bipoli
ovvero:
h i−1 h i h i
h i
Ȧ V̇
I˙ = − Ḃ
Denendo la
matrice dele
(11.1.22)
ammettenze:
h i
h i−1 h i Ẏ
11 Ẏ12
Ẏ = − Ḃ
Ȧ =
Ẏ21 Ẏ22
(11.1.23)
h i h ih i
I˙ = Ẏ V̇
(11.1.24)
la (11.1.22) si scrive:
La (11.1.24) è l'equazione matriciale rappresentativa del doppio bipolo che in forma
scalare si scrive:
(
I˙1 = Ẏ11 V̇1 + Ẏ12 V̇2
I˙2 = Ẏ21 V̇1 + Ẏ22 V̇2
Ponendo
V̇2 = 0̇,
si dice che il doppio bipolo ha la porta 2 in cortocircuito. Sotto questa
ipotesi le equazioni in (11.1.25) forniscono i valori di
Ẏ11
si chiama
(11.1.25)
Ẏ11
e
Ẏ21 :
I˙1 V̇1 V̇2 =0̇
I˙2 =
V̇1 V̇2 =0̇
Ẏ11 =
(11.1.26)
Ẏ21
(11.1.27)
auto-ammettenza della porta 1, Ẏ21
si chiama
trans-ammettenza;
queste
due ammettenze si ricavano dallo schema di calcolo mostrato in Figura 11.1.15.
Figura 11.1.15: schema di calcolo per determinare
Ponendo
V̇1 = 0̇,
Ẏ11
e
Ẏ21
si dice che il doppio bipolo ha la porta 1 in cortocircuito.
questa ipotesi le equazioni in (11.1.25) forniscono i valori di
I˙1 V̇2 V̇1 =0̇
I˙2 =
V̇2 V̇1 =0̇
Ẏ12
e
Sotto
Ẏ22 :
Ẏ12 =
(11.1.28)
Ẏ22
(11.1.29)
369
11 La teoria dei doppi bipoli
Ẏ12
si chiama
trans-ammettenza, Ẏ22 si chiama auto-ammettenza della porta 2;
queste
due ammettenze si ricavano dallo schema di calcolo mostrato in Figura 11.1.16.
Figura 11.1.16: schema di calcolo per determinare
Ẏ12
e
Ẏ22
h i
Ż allora esiste
h i h i
matrici Ȧ e Ḃ sono
In generale non è detto che se esiste la matrice delle impedenze
pure la matrice delle ammettenze
h i
Ẏ
e viceversa. Solo se le
entrambe invertibili allora esistono entrambe le rappresentazioni. Se esistono entrambe
le rappresentazioni allora si ha che:
h i
1
Ẏ = h i
Ż
h i
1
Ż = h i
Ẏ
(11.1.30)
Si pensi per esempio alla coppia di induttori mutuamente accoppiati mostrata in Figura
11.1.17
Figura 11.1.17: coppia di induttori mutuamente accoppiati
Le equazioni che ne descrivono il funzionamento
(
V̇1 = jωL1 I˙1 ± jωM I˙2
V̇2 = ±jωM I˙1 + jωL2 I˙2
(11.1.31)
conducono immediatamente alla matrie delle impedenze:
h i jωL
1
Ż =
±jωM
±jωM
jωL2
(11.1.32)
La matrice delle impedenze per il doppio bipolo mostrato in Figura 11.1.7 esiste sempre;
anche quando tra gli induttori c'è accoppiamento perfetto. La sua inversa, ossia la matrice
370
11 La teoria dei doppi bipoli
delle ammettenze
h i
Ẏ
non è detto che esista sempre. Basta ricavarne la corrispondente
espressione per determinare la condizione che garantisce la sua esistenza. Si ha:
h i
1
1
L2
Ẏ = h i =
2)
∓M
(jω)
(L
L
−
M
1 2
Ż
∓M
L1
Da (11.1.33) si capisce facilmente che la matrice delle ammettenze
L1 L2 − M 2 6= 0
(11.1.33)
h i
Ẏ
esiste solo sè
(11.1.34)
ovvero se non c'è accoppiamento perfetto tra gli induttori. Pertanto stiamo vericando
che l'esistenza della matrice delle impedenze non implica in generale l'esistenza della
matrice delle ammettenze.
11.1.1.2.1 Esempio.
Si consideri il doppio bipolo mostrato in Figura 11.1.10 che per
comodità riportiamo in Figura 11.1.18.
Figura 11.1.18: doppio bipolo
Il doppio bipolo è descrivibile mediante la matrice delle ammettenze. La relazione in
(11.1.24) suggerisce di utilizzare il metodo dei potenziali ai nodi; possiamo quindi eccitare
le due porte attraverso due generatori ideali di corrente come mostrato in Figura 11.1.19.
Figura 11.1.19: doppio bipolo
371
11 La teoria dei doppi bipoli
Con riferimento ai potenziali ai nodi indicati nel circuito è facile scrive di getto il
corrispondente sistema risolvente:

1
R1


0
− R11
0
1
1
R2 + jωL
1
− jωL
1
R1

− R11
1
− jωL
+ jωC +
1
jωL
 
V̇1

 V̇2  = 
Ė

I˙1
I˙2 
0̇
Quest'ultimo in forma scalare si scrive:

1
V̇ − 1 Ė = I˙1


R1 1 R1 1
1
1
Ė = I˙2
R2 + jωL V̇2 − jωL


− 1 V̇ − 1 V̇ + 1 + jωC +
R1
Ricavando
Ė
1
jωL 2
R1
(11.1.35.1)
(11.1.35.2)
1
jωL
(11.1.35)
Ė = 0̇ (11.1.35.3)
da (11.1.35.3) e sostituendo in (11.1.35.1) e (11.1.35.2) si ottiene il sistema
nelle incognite
V̇1
e
V̇2 :
1+(jω)2 LC
1
V̇1 − R +jωL+(jω)
V̇ = I˙1
2
R1 +jωL+(jω)2 LCR1
LCR1 2
1
R1 +R2 +jω(CR1 R2 +L)+(jω)2 LCR1
1
−
V̇
+
V̇2
1
2
R1 +jωL+(jω) LCR1
R2 (R1 +jωL+(jω)2 LCR1 )


= I˙2
Quest'ultimo sistema conduce alla matrice delle ammettenze:

h i
Ẏ = 
1+(jω)2 LC
R1 +jωL+(jω)2 LCR1
1
R1 +jωL+(jω)2 LCR1
1
R1 +jωL+(jω)2 LCR1
R1 +R2+ jω(CR1 R2 +L)+(jω)2 LCR1
R2 (R1 +jωL+(jω)2 LCR1 )

(11.1.36)

Visto che non ci sono generatori pilotati, il doppio bipolo risulta simmetrico e quando il
doppio bipolo è espresso mediante la matrice delle ammettenze ciò equivale a dire:
Ẏ12 = Ẏ21
(11.1.37)
h i
I termini della matrice delle ammettenze Ẏ si possono ricavare facilmente utilizzando
le denizioni date in (11.1.26), (11.1.27), (11.1.28) e (11.1.29).
Con riferimento al circuito mostrato in Figura 11.1.20 si possono determinare i termini
Ẏ11
e
Ẏ21 .
Si tenga presente che tale circuito non deriva da quello mostrato in Figura
11.1.19 applicando il teorema di sovrapposizione degli eetti. Esso è il caso particolare
dello schema di calcolo mostrato in Figura 11.1.15.
L'auto-ammettenza della porta 1,
Ẏ11 ,
si ricava in modo molto semplice applicando
le regole delle ammettenze in parallelo e delle ammettenze in serie.
L'induttore e il
capacitore risultano disposti in parallelo e sono caratterizzati dall'impedenza
1
ẎL = jωC + jωL
del resistore R1 :
=
Ẏp = Ẏc +
1+(jω)2 LC
. Quest'ultima risulta in serie con l'ammettenza
jωL
Ẏ11 =
I˙1
=
V̇1
1
Ẏ1
1
+
1
Ẏp
=
372
1
R1 +
jωL
1+(jω)2 LC
Ẏ1 =
1
R1
11 La teoria dei doppi bipoli
Figura 11.1.20: doppio bipolo
=
1 + (jω)2 LC
R1 + jωL + (jω)2 LCR1
(11.1.38)
In modo analogo si possono trovare gli altri termini della matrice delle ammettenze.
11.1.2 Relazioni tra le matrice
h i
Ż
e
h i
Ẏ
11.1.2.1 Passaggio dalla matrice delle impedenze
ammettenze
h i
Ż
alla matrice delle
h i
Ẏ
Supponiamo che per un doppio bipolo esista sia la matrice delle impedenze
matrice delle ammettenze
Allora si ha che
h i
Ẏ =
h i
Ż
che la
h i
Ẏ .
1
[Ż ]
h i−1
= Ż
.
Esplicitando quest'ultima espressione si ha che:
−1
h i h i−1 Ż
1
Ż22 −Ż12
11 Ż12
Ẏ = Ż
=
=
Ż21 Ż22
Ż11 Ż22 − Ż12 Ż21 −Ż21 Ż11
(11.1.39)
Dall'espressione in (11.1.39) si deducono i termini della matrice delle ammettenze in
funzione dei termini della matrice delle impedenze:
Ẏ11 =
Ż22
Ż11 Ż22 −Ż12 Ż21
Ẏ21 =
−Ż21
Ż11 Ż22 −Ż12 Ż21
Ẏ12 =
−Ż12
Ż11 Ż22 −Ż12 Ż21
Ẏ22 =
Ż11
Ż11 Ż22 −Ż12 Ż21
(11.1.40)
Le relazioni in (11.1.40) valgono purchè sia
Ż11 Ż22 − Ż12 Ż21 6= 0̇.
373
11 La teoria dei doppi bipoli
11.1.2.2 Passaggio dalla matrice delle ammettenze
impedenze
h i
Ẏ
alla matrice delle
h i
Ż
Supponiamo che per un doppio bipolo esista sia la matrice delle impedenze
matrice delle ammettenze
Allora si ha che
h i
Ż =
h i
Ż
che la
h i
Ẏ .
1
[Ẏ ]
h i−1
.
= Ẏ
Esplicitando quest'ultima espressione si ha che:
−1
h i h i−1 Ẏ
1
Ẏ22 −Ẏ12
11 Ẏ12
Ż = Ẏ
=
=
Ẏ21 Ẏ22
Ẏ11 Ẏ22 − Ẏ12 Ẏ21 −Ẏ21 Ẏ11
(11.1.41)
Dall'espressione in (11.1.41) si deducono i termini della matrice delle impedenze in
funzione dei termini della matrice delle ammettenze:
Ż11 =
Ẏ22
Ẏ11 Ẏ22 −Ẏ12 Ẏ21
Ż21 =
−Ẏ21
Ẏ11 Ẏ22 −Ẏ12 Ẏ21
Ż12 =
−Ẏ12
Ẏ11 Ẏ22 −Ẏ12 Ẏ21
Ż22 =
Ẏ11
Ẏ11 Ẏ22 −Ẏ12 Ẏ21
(11.1.42)
Le relazioni in (11.1.42) valgono purchè sia
Ẏ11 Ẏ22 − Ẏ12 Ẏ21 6= 0̇.
11.1.3 Rappresentazione del doppio bipolo mediante la matrice ibrida e la
matrice ibrida inversa
11.1.3.1 matrice ibrida
h i
Ȧ
Consideriamo come al solito la rappresentazione del doppio bipolo mediante le matrici
e
h i
Ḃ :
h ih i h ih i Ȧ V̇ + Ḃ I˙ = 0̇
(11.1.43)
Quest'ultima in forma scalare si scrive:
(
ȧ11 V̇1 + ȧ12 V̇2 + ḃ11 I˙1 + ḃ12 I˙2 = 0̇
ȧ21 V̇1 + ȧ22 V̇2 + ḃ21 I˙1 + ḃ22 I˙2 = 0̇
(11.1.44)
Scrivendo prima la tensione alla porta1 e la corrente alla porta 2 e poi la tensione alla
porta 2 e la corrente alla porta 1 si ottiene:
(
ȧ11 V̇1 + ḃ12 I˙2 + ȧ12 V̇2 + ḃ11 I˙1 = 0̇
ȧ21 V̇1 + ḃ22 I˙2 + ȧ22 V̇2 + ḃ21 I˙1 = 0̇
(11.1.45)
Il sistema di equazioni in (11.1.45) si può scrivere in forma matriciale come segue:
ȧ11 ḃ12
ȧ21 ḃ22
V̇1
I˙2
+
ȧ12 ḃ11
ȧ22 ḃ21
374
V̇2
I˙1
=
0̇
0̇
(11.1.46)
11 La teoria dei doppi bipoli
Supponiamo che la matrice:
ȧ11 ḃ12
ȧ21 ḃ22
sia invertibile. Se così è allora è pure dotata di inversa:
ȧ11 ḃ12
ȧ21 ḃ22
−1
(11.1.47)
Premoltiplicando entrambi i membri dell'equazione matriciale in (11.1.46) per la matrice inversa data in (11.1.47) si ottiene:
V̇1
I˙2
V̇1
I˙2
+
ȧ11 ḃ12
ȧ21 ḃ22
−1 ovvero:
Denendo la
=−
ȧ11 ḃ12
ȧ21 ḃ22
ȧ12 ḃ11
ȧ22 ḃ21
−1 V̇2
I˙1
ȧ12 ḃ11
ȧ22 ḃ21
=
0̇
0̇
V̇2
I˙1
(11.1.48)
matrice ibrida:
−1 h i ḣ
ȧ11 ḃ12
ȧ12 ḃ11
11 ḣ12
Ḣ =
=−
ḣ21 ḣ22
ȧ21 ḃ22
ȧ22 ḃ21
(11.1.49)
la rappresentazione data in (11.1.48) si scrive:
V̇1
I˙2
=
ḣ11 ḣ12
ḣ21 ḣ22
V̇2
I˙1
(11.1.50)
In forma scalare si ha ovviamente:
(
V̇1 = ḣ11 V̇2 + ḣ12 I˙1
I˙2 = ḣ21 V̇2 + ḣ22 I˙1
Ponendo
V̇2 = 0̇,
(11.1.51)
si dice che il doppio bipolo ha la porta 2 in cortocircuito.
questa ipotesi le equazioni in (11.1.51) forniscono i valori di
ḣ12
e
Sotto
ḣ22 :
ḣ12 =
V̇1 I˙1 V̇2 =0̇
(11.1.52)
ḣ22 =
I˙2 I˙1 V̇2 =0̇
(11.1.53)
auto-impedenza della porta 1 con la porta 2 cortocircuitata, mentre
la quantità ḣ22 è il guadagno di corrente di cortocircuito; queste due quantità si ricavano
La quantità
ḣ12
è l'
dallo schema di calcolo mostrato in Figura 11.1.21.
375
11 La teoria dei doppi bipoli
Figura 11.1.21: schema di calcolo per determinare
I˙1 = 0̇, si dice che il doppio bipolo ha la porta 1 a vuoto.
equazioni in (11.1.25) forniscono i valori di ḣ11 e ḣ21 :
Ponendo
le
ḣ12
ḣ22
Sotto questa ipotesi
V̇1 ˙
V̇2 I1 =0̇
(11.1.54)
I˙2 =
˙
V̇2 I1 =0̇
(11.1.55)
ḣ11 =
ḣ21
e
ḣ11 è il guadagno di tensione a vuoto, mentre la quantità ḣ21 è l'autoammettenza della porta 2 con la porta 1 a vuoto; queste due quantità si ricavano dallo
La quantità
schema di calcolo mostrato in Figura 11.1.22.
Figura 11.1.22: schema di calcolo per
376
determinare ḣ11 e ḣ21
11 La teoria dei doppi bipoli
11.1.3.1.1 Proposizione.
izzato dalla matrice ibrida
hSiai Π un doppio bipolo privo di generatori pilotati,
Ḣ . Allora per il teorema di reciprocità si ha che:
− ḣ11 = ḣ22
caratter-
(11.1.56)
Dimostrazione.
La proposizione si dimostra applicando il teorema di reciprocità al bipolo
due cortocircuiti della rete
Π
Π.
Isoliamo
come mostrato in Figura 11.1.23. Restano così denite 2
porte che si possono eccitare solamente in corrente.
Figura 11.1.23: rete elettrica
Eccitando la porta 1 del circuito mostrato in Figura 11.1.23 attraverso un generatore
ideale di tensione
v̇1
si ha:
Figura 11.1.24: rete elettrica
Dallo schema di calcolo di Figura 11.1.24 si può denire la
Ẏ21 (jω) =
I˙2
V̇1
trans-ammettenza:
(11.1.57)
Visto che il doppio bipolo è rappresentato mediante la matrice ibrida, valgono le relazioni
in (11.1.51) che nel caso specico dello schema di Figura 11.1.24, si scrivono ponendo
V̇2 = 0̇:
(
V̇1 = ḣ12 I˙1
I˙2 = ḣ22 I˙1
(11.1.58)
Eseguendo il rapporto tra la seconda e la prima equazione in (11.1.58), si ricava
l'espressione della trans-ammettemza
Ẏ21
in funzione dei termini della matrice ibrida:
377
11 La teoria dei doppi bipoli
Ẏ21 (jω) =
ḣ22
I˙2
=
V̇1
ḣ12
(11.1.59)
Eccitando la porta 2 del circuito mostrato in Figura 11.1.23 attraverso un generatore
ideale di tensione
V̇2
si ha:
Figura 11.1.25: rete elettrica
Dallo schema di calcolo di Figura 11.1.25 si può denire la
Ẏ12 (jω) =
I˙1
V̇2
trans-ammettenza:
(11.1.60)
Visto che il doppio bipolo è rappresentato mediante la matrice ibrida, valgono le relazioni in (11.1.51) che nel caso specico dello schema di Figura 11.1.24, si scrivono
ponendo
V̇1 = 0̇.
(
0̇ = ḣ11 V̇2 + ḣ12 I˙1
I˙2 = ḣ21 V̇2 + ḣ22 I˙1
(11.1.61)
Dalla prima delle equazione in (11.1.61), si ricava l'espressione della trans-ammettemza
Ẏ12
in funzione dei termini della matrice ibrida:
ḣ11
I˙1
=−
V̇2
ḣ12
(11.1.62)
I˙1
I˙2
=
= Ẏ12 (jω)
V̇1
V̇2
(11.1.63)
Ẏ21 (jω) =
Per il teorema di reciprocità si ha che:
Ẏ21 (jω) =
Sostitundo (11.1.59) e (11.1.62) in (11.1.63) si ottiene la tesi:
− ḣ11 = ḣ22
(11.1.64)
11.1.3.2 matrice ibrida inversa
h i
Ȧ
Consideriamo nuovamente la rappresentazione del doppio bipolo mediante le matrici
e
h i
Ḃ
378
11 La teoria dei doppi bipoli
h ih i h ih i Ȧ V̇ + Ḃ I˙ = 0̇
(11.1.65)
Quest'ultima in forma scalare si scrive:
(
ȧ11 V̇1 + ȧ12 V̇2 + ḃ11 I˙1 + ḃ12 I˙2 = 0̇
ȧ21 V̇1 + ȧ22 V̇2 + ḃ21 I˙1 + ḃ22 I˙2 = 0̇
(11.1.66)
Scrivendo prima la tensione alla porta 2 e la corrente alla porta 1 e poi la tensione alla
porta 1 e la corrente alla porta 2 si ottiene:
(
ȧ12 V̇2 + ḃ11 I˙1 + ȧ11 V̇1 + ḃ12 I˙2 = 0̇
ȧ22 V̇2 + ḃ21 I˙1 + ȧ21 V̇1 + ḃ22 I˙2 = 0̇
(11.1.67)
Il sistema di equazioni in (11.1.67) si può scrivere in forma matriciale come segue:
ȧ12 ḃ11
ȧ22 ḃ21
V̇2
I˙1
ȧ11 ḃ12
ȧ21 ḃ22
+
V̇1
I˙2
=
0̇
0̇
(11.1.68)
Supponiamo che la matrice:
ȧ12 ḃ11
ȧ22 ḃ21
sia invertibile. Se così è allora è pure dotata di inversa:
ȧ12 ḃ11
ȧ22 ḃ21
−1
(11.1.69)
Premoltiplicando entrambi i membri dell'equazione matriciale in (11.1.68) per la matrice inversa data in (11.1.69) si ottiene:
V̇2
I˙1
V̇2
I˙1
+
ȧ12 ḃ11
ȧ22 ḃ21
−1 ovvero:
Denendo la
=−
ȧ12 ḃ11
ȧ22 ḃ21
ȧ11 ḃ12
ȧ21 ḃ22
−1 V̇1
I˙2
ȧ11 ḃ12
ȧ21 ḃ22
0̇
0̇
=
V̇1
I˙2
(11.1.70)
matrice ibrida inversa:
−1 0
h 0 i ḣ0
ḣ12
ȧ12 ḃ11
ȧ11 ḃ12
11
Ḣ =
=−
0
0
ḣ21 ḣ22
ȧ22 ḃ21
ȧ21 ḃ22
(11.1.71)
la rappresentazione data in (11.1.70) si scrive:
V̇2
I˙1
=
0
0
ḣ11 ḣ12
0
0
ḣ21 ḣ22
In forma scalare si ha ovviamente:
379
V̇1
I˙2
(11.1.72)
11 La teoria dei doppi bipoli
(
0
0
V̇2 = ḣ11 V̇1 + ḣ12 I˙2
0
0
I˙1 = ḣ V̇1 + ḣ I˙2
21
Ponendo
V̇1 = 0̇,
(11.1.73)
22
si dice che il doppio bipolo ha la porta 1 in cortocircuito.
questa ipotesi le equazioni in (11.1.73) forniscono i valori di
0
ḣ12 =
0
ḣ22 =
0
ḣ12
e
0
Sotto
ḣ22 :
V̇2 I˙2 V̇1 =0̇
(11.1.74)
I˙1 I˙2 V̇1 =0̇
(11.1.75)
auto-impedenza della porta 2 con la porta 1 cortocircuitata, mentre
la quantità ḣ22 è il guadagno di corrente di cortocircuito; queste due quantità si ricavano
La quantità
0
0
ḣ12
è l'
dallo schema di calcolo mostrato in Figura 11.1.26.
Figura 11.1.26: schema di calcolo per determinare
I˙2 = 0̇, si dice che il doppio bipolo ha la porta 2 a vuoto.
equazioni in (11.1.73) forniscono i valori di ḣ11 e ḣ21 :
Ponendo
le
ḣ12
0
ḣ11 =
0
ḣ21 =
e
ḣ22
Sotto questa ipotesi
V̇2 ˙
V̇1 I2 =0̇
(11.1.76)
I˙1 ˙
V̇1 I2 =0̇
(11.1.77)
ḣ11 è il guadagno di tensione a vuoto, mentre la quantità ḣ21 è l'autoammettenza della porta 1 con la porta 2 a vuoto; queste due quantità si ricavano dallo
La quantità
schema di calcolo mostrato in Figura 11.1.27.
11.1.3.2.1 Proposizione.
Sia
Π
un doppio
h i bipolo privo di generatori pilotati, carat-
terizzato dalla matrice ibrida inversa
Ḣ
0
.
che:
380
Allora per il teorema di reciprocità si ha
11 La teoria dei doppi bipoli
Figura 11.1.27: schema di calcolo per
0
determinare ḣ11 e ḣ21
0
0
0
ḣ11 = −ḣ22
(11.1.78)
Dimostrazione.
La proposizione si dimostra applicando il teorema di reciprocità al bipolo
un cortocircuito e un circuito aperto della rete
Restano così denite 2 porte:
Π
Π.
Isoliamo
come mostrato in Figura 11.1.28.
la porta 1 si può eccitare soltanto in tensione mentre
la porta 2 si può eccitare solamente inn corrente.
Figura 11.1.28: rete elettrica
Eccitando la porta 1 del circuito mostrato in Figura 11.1.28 attraverso un generatore
ideale di tensione
v̇1
si ha:
Figura 11.1.29: rete elettrica
Dallo schema di calcolo di Figura 11.1.29 si può denire il
ĠV (jω) =
V2
V̇1
guadagno di tensione:
(11.1.79)
Visto che il doppio bipolo è rappresentato mediante la matrice ibrida inversa, valgono
le relazioni in (11.1.73) che nel caso specico dello schema di Figura 11.1.29, si scrivono
ponendo
I˙2 = 0̇.
381
11 La teoria dei doppi bipoli
(
0
V̇2 = ḣ11 V̇1
0
I˙1 = ḣ V̇1
(11.1.80)
21
Dalla prima delle equazione in (11.1.80), si ricava l'espressione del guadagno di tensione
ĠV
in funzione dei termini della matrice ibrida inversa:
ĠV (jω) =
V̇2
0
= ḣ11
V̇1
(11.1.81)
Eccitando la porta 2 del circuito mostrato in Figura 11.1.28 attraverso un generatore
ideale di corrente
I˙2
si ha:
Figura 11.1.30: rete elettrica
Dallo schema di calcolo di Figura 11.1.30 si può il
ĠI (jω) = −
guadagno di corrente:
I˙1
I˙2
N.B. Il segno - è dovuto al fatto che la corrente
(11.1.82)
I˙1
è opposta nello schema di calcolo
usato per dimostrare il teorema di reciprocità.
Visto che il doppio bipolo è rappresentato mediante la matrice ibrida inversa, valgono
le relazioni in (11.1.73) che nel caso specico dello schema di Figura 11.1.24, si scrivono
ponendo
V̇1 = 0̇.
(
0
V̇2 = ḣ12 I˙2
0
I˙1 = ḣ22 I˙2
(11.1.83)
Dalla seconda delle equazione in (11.1.83), si ricava l'espressione del guadagno dio corrente
ĠI
in funzione dei termini della matrice ibrida inversa:
I˙1
0
= −ḣ22
˙
I2
(11.1.84)
V̇2
I˙1
=
= ĠV (jω)
˙
I2
V̇1
(11.1.85)
ĠI (jω) = −
Per il teorema di reciprocità si ha che:
ĠI (jω) = −
Sostitundo (11.1.81) e (11.1.83) in (11.1.85) si ottiene la tesi:
382
11 La teoria dei doppi bipoli
0
0
ḣ11 = −ḣ22
11.1.4 Relazioni tra le matrice
h i
Ḣ
11.1.4.1 Passaggio dalla matrice ibrida
e
h
Ḣ
h i
Ḣ
0
(11.1.86)
i
alla matrice ibrida inversa
Supponiamo che per un doppio bipolo esista sia la matrice ibrida
h 0i
ibrida inversa Ḣ .
h 0i
Allora si ha che Ḣ
=
h
Ḣ
0
i
1
[Ḣ ]
h i−1
.
= Ḣ
h i
Ḣ
h
Ḣ
0
i
che la matrice
Esplicitando quest'ultima espressione si ha che:
−1
h i−1 ḣ
1
ḣ22 −ḣ12
11 ḣ12
=
=
= Ḣ
ḣ21 ḣ22
ḣ11 ḣ22 − ḣ12 ḣ21 −ḣ21 ḣ11
(11.1.87)
Dall'espressione in (11.1.87) si deducono i termini della matrice ibrida inversa in funzione
dei termini della matrice ibrida:
0
ḣ22
ḣ11 ḣ22 −ḣ12 ḣ21
0
−ḣ21
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ11 =
0
−ḣ12
ḣ11 ḣ22 −ḣ12 ḣ21
0
ḣ11
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ12 =
(11.1.88)
ḣ21 =
ḣ22 =
Le relazioni in (11.1.88) valgono purchè sia
ḣ11 ḣ22 − ḣ12 ḣ21 6= 0̇.
11.1.4.2 Passaggio dalla matrice ibrida inversa
h
Ḣ
0
i
alla matrice ibrida
Supponiamo che per un doppio bipolo esista sia la matrice ibrida
h 0i
ibrida inversa Ḣ .
h i
Allora si ha che Ḣ =
1
[Ḣ 0 ]
h 0 i−1
.
= Ḣ
h i
Ḣ
h i
Ḣ
che la matrice
Esplicitando quest'ultima espressione si ha
che:
−1
0
0
0
h i h 0 i−1 ḣ0
1
ḣ12
ḣ22 −ḣ12
11
Ḣ = Ḣ
=
= 0 0
0
0
0
0
0
0
ḣ21 h22
ḣ11 ḣ22 − ḣ12 ḣ21 −ḣ21 ḣ11
(11.1.89)
Dall'espressione in (11.1.89) si deducono i termini della matrice ibrida in funzione dei
termini della matrice ibrida inversa:
ḣ11 =
0
ḣ22
0
0
0
0
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ21 =
−ḣ21
0
0
0
0
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ12 =
0
−ḣ12
0
0
0
0
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ22 =
ḣ11
0
0
0
0
ḣ11 ḣ22 −ḣ12 ḣ21
(11.1.90)
0
0
383
11 La teoria dei doppi bipoli
Le relazioni in (11.1.42) valgono purchè sia
11.1.5 Relazioni tra le matrici
0
0
0
0
ḣ11 ḣ22 − ḣ12 ḣ21 6= 0̇.
h i h i
Ḣ , Ż
e
h i
Ẏ
11.1.5.1 Passaggio dalla matrice delle impedenze
h i
Ż
alla matrice ibrida
h i
Ḣ
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.54)
per
I˙2
si ottiene:
ḣ11 =
V̇1
I˙2
V̇2
I˙2
V˙1
I˙1 =0̇ =
I˙2
V̇2
I˙2
I˙1 =0̇
I˙1 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.12) e (11.1.13), si scrive:
ḣ11 =
Ż12
Ż22
(11.1.91)
Tenendo conto della relazione in (11.1.26), la (11.1.52) si scrive:
ḣ12 =
Utilizzando l'espressione di
Ẏ11
1
Ẏ11
(11.1.92)
data in (11.1.40) è ovvio che la (11.1.92) conduce alla
relazione:
ḣ12 =
Ż11 Ż22 − Ż12 Ż21
Ż12 Ż21
= Ż11 −
Ż22
Ż22
(11.1.93)
Tenendo conto della relazione in (11.1.13), la (11.1.55) si scrive:
ḣ21 =
1
Ż22
(11.1.94)
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.53)
per
V̇1
si ottiene:
ḣ22 =
I˙2
V̇1
I˙1
V̇1
V̇2 =0̇ =
I˙2 V̇1 V̇2 =0̇
I˙1 V̇1 V̇2 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.26) e (11.1.27), si scrive:
ḣ22 =
Inne utilizzando le espressioni di
Ẏ21
e
Ẏ21
Ẏ11
Ẏ11
conduce alla relazione:
384
(11.1.95)
date in (11.1.40) è ovvio che la (11.1.95)
11 La teoria dei doppi bipoli
ḣ22 = −
Ż21
Ż22
(11.1.96)
Riassumendo sono state ricavate le formule di passaggio:
ḣ11 =
Ż12
Ż22
ḣ21 =
1
Ż22
ḣ12 =
Ż11 Ż22 −Ż12 Ż21
Ż22
(11.1.97)
ḣ22 =
Ż21
− Ż
22
11.1.5.2 Passaggio dalla matrice delle ammettenze
Utilizzando le espressioni di
Ż12
e
Ż22
h i
Ẏ
alla matrice ibrida
h i
Ḣ
date in (11.1.42) è ovvio che la (11.1.91) conduce
alla relazione:
ḣ11 = −
Utilizzando l'espressione di
Ż22
ḣ21 =
Ẏ12
Ẏ11
(11.1.98)
data in (11.1.42), la (11.1.94) si scrive:
Ẏ11 Ẏ22 − Ẏ12 Ẏ21
Ẏ12 Ẏ21
= Ẏ22 −
Ẏ11
Ẏ11
(11.1.99)
Riassumendo sono state ricavate le formule di passaggio:
ḣ11 = − ẎẎ12
11
ḣ12 =
1
Ẏ11
ḣ22 =
Ẏ21
Ẏ11
(11.1.100)
ḣ21 =
Ẏ11 Ẏ22 −Ẏ12 Ẏ21
Ẏ11
11.1.5.3 Passaggio dalla matrice ibrida
h i
Ḣ
alla matrice delle impedenze
h i
Ż
Invertendo (11.1.94) si trova immediatamente che:
Ż22 =
1
ḣ21
(11.1.101)
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.12)
per
V̇2
si ottiene:
Ż12 =
V̇1
V̇2
I˙2
V̇2
I˙1 =0̇ =
V̇1 V̇2 I˙1 =0̇
I˙2 V̇2 I˙1 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.54) e (11.1.55), si scrive:
Ż12 =
ḣ11
ḣ21
385
(11.1.102)
11 La teoria dei doppi bipoli
Dalla (11.1.96) si ricava:
Ż21 = −Ż22 ḣ22
(11.1.103)
Sostituendo (11.1.101) in (11.1.103) si ottiene:
Ż21 = −
ḣ22
ḣ21
(11.1.104)
Ż12 Ż21
Ż22
(11.1.105)
Invertendo la (11.1.93) si ha:
Ż11 = ḣ12 +
Inne sostituendo (1.11.101), (1.11.102), (1.11.104) in (11.1.105) si ha:
Ż11 = ḣ12 − ḣ21
ḣ12 ḣ21 − ḣ11 ḣ22
ḣ11 ḣ22
=
ḣ21 ḣ21
ḣ21
ovvero:
Ż11 = −
ḣ11 ḣ22 − ḣ12 ḣ21
ḣ21
(11.1.106)
Riassumendo sono state ricavate le formule di passaggio:
Ż11 = − ḣ11 ḣ22ḣ−ḣ12 ḣ21
21
Ż12 =
ḣ11
ḣ21
Ż22 =
1
ḣ21
(11.1.107)
Ż21 =
− ḣḣ22
21
11.1.5.4 Passaggio dalla matrice ibrida
h i
Ḣ
alla matrice delle ammettenze
h i
Ẏ
Invertendo (11.1.92) si trova immediatamente che:
Ẏ11 =
1
ḣ12
(11.1.108)
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.27)
per
I˙1
si ottiene:
Ẏ21 =
I˙2
I˙1
V̇1
I˙1
V̇2 =0̇ =
I˙2 I˙1 V̇2 =0̇
V̇1 I˙1 I˙2 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.52) e (11.1.53), si scrive:
Ẏ21 =
ḣ22
ḣ12
Dalla (11.1.98) si ricava:
386
(11.1.109)
11 La teoria dei doppi bipoli
Ẏ12 = −Ẏ11 ḣ11
(11.1.110)
Sostituendo (11.1.108) in (11.1.110) si ottiene:
Ẏ12 = −
ḣ11
ḣ12
(11.1.111)
Invertendo la (11.1.99) si ha:
Ẏ22 = ḣ21 +
Ẏ12 Ẏ21
Ẏ11
(11.1.112)
Inne sostituendo (1.11.108), (1.11.109), (1.11.111) in (11.1.112) si ha:
Ẏ22 = ḣ21 − ḣ12
ḣ11 ḣ22
ḣ12 ḣ21 − ḣ11 ḣ22
=
ḣ12 ḣ12
ḣ12
ovvero:
Ẏ22 = −
ḣ11 ḣ22 − ḣ12 ḣ21
ḣ12
(11.1.113)
Riassumendo sono state ricavate le formule di passaggio:
Ẏ11 =
1
ḣ12
Ẏ21 =
ḣ22
ḣ12
Ẏ12 = − ḣḣ11
12
(11.1.114)
Ẏ22 =
− ḣ11 ḣ22ḣ−ḣ12 ḣ21
12
11.1.6 Rappresentazione del doppio bipolo mediante la matrice di
trasmissione e la matrice di trasmissione inversa
11.1.6.1 matrice di trasmissione diretta
Fino ad ora abbiamo rappresentato il doppio bipolo utilizzando per ciascuna porta la
convenzione dell'utilizzatore:
Figura 11.1.31: doppio bipolo con porte che utilizzano la convenzione dell'utilizzatore
I doppi bipoli descritti attraverso la matrice di trasmissione, che essa sia diretta o
inversa, prevedono che la corrente uisca da sinistra verso destra come mostrato in Figura
11.1.32:
387
11 La teoria dei doppi bipoli
Figura 11.1.32: doppio bipolo con corrente che scorre da sinistra verso destra
La
matrice di trasmissione diretta, lega tensione e corrente alla porta 1 con tensione e
corrente alla porta 2; in altri termini permette di scrivere la tensione e la corrente alla
porta 1 in funzione della tensione e della corrente alla porta 2 per un doppio bipolo come
quello mostrato in Figura 1.11.32.
Per determinare la matrice di trasmissione diretta
nuovamente la rappresenh i hscriviamo
i
Ȧ e Ḃ
h ih i h ih i Ȧ V̇ + Ḃ I˙ = 0̇
tazione del doppio bipolo mediante le matrici
(11.1.115)
Quest'ultima in forma scalare si scrive:
(
ȧ11 V̇1 + ȧ12 V̇2 + ḃ11 I˙1 + ḃ12 I˙2 = 0̇
ȧ21 V̇1 + ȧ22 V̇2 + ḃ21 I˙1 + ḃ22 I˙2 = 0̇
(11.1.116)
Scrivendo prima tensione e corrente alla porta 1 e poi tensione e corrente alla porta 2 si
ottiene:
(
ȧ11 V̇1 + ḃ11 I˙1 + ȧ12 V̇2 + ḃ12 I˙2 = 0̇
ȧ21 V̇1 + ḃ21 I˙1 + ȧ22 V̇2 + ḃ22 I˙2 = 0̇
(11.1.117)
Il sistema di equazioni in (11.1.67) si può scrivere in forma matriciale come segue:
ȧ11 ḃ11
ȧ21 ḃ21
V̇1
I˙1
+
ȧ12 ḃ12
ȧ22 ḃ22
V̇2
I˙2
=
0̇
0̇
(11.1.118)
L'espressione trovata in (11.1.118) rappresenta il doppio bipolo mostrato in Figura 11.1.31.
Il sistema di equazioni che rappresenta il doppio bipolo mostrato in Figura 11.1.32, si
I˙2
ottiene da (11.1.118) sostituendo semplicemente
ȧ11 ḃ11
ȧ21 ḃ21
V̇1
I˙1
+
ȧ12 ḃ12
ȧ22 ḃ22
−I˙2 :
V̇2
0̇
=
0̇
−I˙2
con
Supponiamo che la matrice:
ȧ11 ḃ11
ȧ21 ḃ21
sia invertibile. Se così è allora è pure dotata di inversa:
388
(11.1.119)
11 La teoria dei doppi bipoli
ȧ11 ḃ11
ȧ21 ḃ21
−1
(11.1.120)
Premoltiplicando entrambi i membri dell'equazione matriciale in (11.1.119) per la
matrice inversa data in (11.1.120) si ottiene:
V̇1
I˙1
+
−1 ȧ11 ḃ11
ȧ21 ḃ21
ovvero:
Denendo la
V̇1
I˙1
=−
ȧ11 ḃ11
ȧ21 ḃ21
−1 ȧ12 ḃ12
ȧ22 ḃ22
ȧ12 ḃ12
ȧ22 ḃ22
V̇2
−I˙2
V̇2
−I˙2
=
0̇
0̇
(11.1.121)
matrice di trasmissione diretta:
−1 h i Ȧ Ḃ ȧ12 ḃ12
ȧ11 ḃ11
=−
Ṫ =
Ċ Ḋ
ȧ22 ḃ22
ȧ21 ḃ21
(11.1.122)
la rappresentazione data in (11.1.121) si scrive:
V̇1
I˙1
=
Ȧ Ḃ
Ċ Ḋ
V̇2
−I˙2
(11.1.123)
Quest'ultimo in forma scalare si scrive:
(
V̇1 = ȦV̇2 − Ḃ I˙2
I˙1 = Ċ V̇2 − ḊI˙2
Ponendo
V̇2 = 0̇,
(11.1.124)
si dice che il doppio bipolo ha la porta 2 in cortocircuito.
questa ipotesi le equazioni in (11.1.124) forniscono i valori di
Ḃ
e
Sotto
Ḋ:
V̇1 −I˙2 V̇2 =0̇
I˙1 Ḋ =
−I˙2 V̇2 =0̇
Ḃ =
(11.1.125)
(11.1.126)
La quantità Ḃ è la trans-impedenza di cortocircuito, mentre la quantità Ḋ è l'attenuazione
di corrente in cortocircuito; queste due quantità si ricavano dallo schema di calcolo
mostrato in Figura 11.1.33.
Ponendo
−I˙2 = 0̇,
si dice che il doppio bipolo ha la porta 2 a vuoto.
ipotesi le equazioni in (11.1.73) forniscono i valori di
Ȧ =
V̇1 ˙
V̇2 −I2 =0̇
389
Ȧ
e
Sotto questa
Ċ :
(11.1.127)
11 La teoria dei doppi bipoli
Figura 11.1.33: schema di calcolo per determinare
Ċ =
Ḃ
e
Ḋ
I˙1 ˙
V̇2 −I2 =0̇
(11.1.128)
'attenuazione di tensione a vuoto, mentre la quantità Ċ è la transammettenza a vuoto; queste due quantità si ricavano dallo schema di calcolo mostrato in
La quantità
Ȧ
è l
Figura 11.1.34.
Figura 11.1.34: schema di calcolo per
390
determinare Ȧ e Ċ
11 La teoria dei doppi bipoli
11.1.6.1.1 Proposizione.
izzato dalla matrice di
Π un doppio hbipolo
privo di generatori pilotati, caratteri
trasmissione diretta Ṫ . Allora per il teorema di reciprocità si
Sia
ha che:
h i
det Ṫ = ȦḊ − Ḃ Ċ = 1
(11.1.129)
Dimostrazione.
La proposizione si dimostra applicando il teorema di reciprocità al bipolo
due cortocircuiti della rete
Π
Π.
Isoliamo
come mostrato in Figura 11.1.35. Restano così denite 2
porte che si possono eccitare solamente in corrente.
Figura 11.1.35: rete elettrica
Eccitando la porta 1 del circuito mostrato in Figura 11.1.35 attraverso un generatore
ideale di tensione
v̇1
si ha:
Figura 11.1.36: rete elettrica
Dallo schema di calcolo di Figura 11.1.24 si può denire la
Ẏ21 (jω) =
−I˙2
V̇1
trans-ammettenza:
(11.1.130)
Visto che il doppio bipolo è rappresentato mediante la matrice di trasmissione diretta,
valgono le relazioni in (11.1.124) che nel caso specico dello schema di Figura 11.1.36, si
scrivono ponendo
V̇2 = 0̇:
(
V̇1 = −Ḃ I˙2
I˙1 = −ḊI˙2
(11.1.131)
Dalla prima delle equazioni in (11.1.131), si ricava l'espressione della trans-ammettemza
Ẏ21
in funzione dei termini di trasmissione diretta:
391
11 La teoria dei doppi bipoli
Ẏ21 (jω) =
1
−I˙2
=
V̇1
Ḃ
(11.1.132)
Eccitando la porta 2 del circuito mostrato in Figura 11.1.35 attraverso un generatore
ideale di tensione
V̇2
si ha:
Figura 11.1.37: rete elettrica
Dallo schema di calcolo di Figura 11.1.25 si può denire la
Ẏ12 (jω) = −
trans-ammettenza:
I˙1
V̇2
(11.1.133)
Visto che il doppio bipolo è rappresentato mediante la matrice di trasmissione diretta,
valgono le relazioni in (11.1.124) che nel caso specico dello schema di Figura 11.1.37, si
scrivono ponendo
V̇1 = 0̇.
(
0̇ = ȦV̇2 − Ḃ I˙2
I˙1 = Ċ V̇2 − ḊI˙2
Ricavando
I˙2
(11.1.134)
dalla prima equazione e sostituendo nella seconda, si ricava l'espressione
della trans-ammettemza
Ẏ12
in funzione dei termini della matrice di trasmissione diretta:
I˙1
ȦḊ − Ḃ Ċ
=
V̇2
Ḃ
(11.1.135)
I˙2
I˙1
=−
= Ẏ12 (jω)
V̇1
V̇2
(11.1.136)
Ẏ21 (jω) = −
Per il teorema di reciprocità si ha che:
Ẏ21 (jω) = −
Sostitundo (11.1.132) e (11.1.135) in (11.1.136) si ottiene la tesi:
ȦḊ − Ḃ Ċ = 1
11.1.6.2 matrice di trasmissione inversa
Per il doppio bipolo mostrato in Figura 11.1.38
sappiamo che le equazioni che ne descrivono il funzionamento sono:
392
11 La teoria dei doppi bipoli
Figura 11.1.38: doppio bipolo con corrente che scorre da sinistra verso destra
ȧ11 ḃ11
ȧ21 ḃ21
V̇1
I˙1
ȧ12 ḃ12
ȧ22 ḃ22
+
V̇2
−I˙2
0̇
0̇
=
(11.1.137)
Supponiamo che la matrice:
ȧ12 ḃ12
ȧ22 ḃ22
sia invertibile. Se così è allora è pure dotata di inversa:
−1
ȧ12 ḃ12
ȧ22 ḃ22
(11.1.138)
Premoltiplicando entrambi i membri dell'equazione matriciale in (11.1.137) per la
matrice inversa data in (11.1.138) si ottiene:
ȧ12 ḃ12
ȧ22 ḃ22
−1 ȧ11 ḃ11
ȧ21 ḃ21
ȧ12 ḃ12
ȧ22 ḃ22
−1 ovvero:
Denendo la
V̇2
−I˙2
=
V̇1
I˙1
+
V̇2
−I˙2
ȧ11 ḃ11
ȧ21 ḃ21
=
V̇1
I˙1
0̇
0̇
(11.1.139)
matrice di trasmissione inversa:
h i Ȧ0
Ṫ =
0
Ċ
0
Ḃ
0
Ḋ
=−
ȧ12 ḃ12
ȧ22 ḃ22
−1 ȧ11 ḃ11
ȧ21 ḃ21
(11.1.140)
la rappresentazione data in (11.1.140) si scrive:
V̇2
−I˙2
=
0
Ȧ
0
Ċ
0
Ḃ
0
Ḋ
V̇1
I˙1
(11.1.141)
Quest'ultimo in forma scalare si scrive:
(
0
0
V̇2 = Ȧ V̇1 + Ḃ I˙1
0
0
−I˙2 = Ċ V̇1 + Ḋ I˙1
393
(11.1.142)
11 La teoria dei doppi bipoli
Ponendo
V̇1 = 0̇,
si dice che il doppio bipolo ha la porta 1 in cortocircuito.
questa ipotesi le equazioni in (11.1.142) forniscono i valori di
0
Ḃ =
0
Ḋ =
Ḃ
0
e
Ḋ
0
Sotto
:
V̇2 I˙1 V̇1 =0̇
(11.1.143)
−I˙2 I˙1 V̇1 =0̇
(11.1.144)
a trans-impedenza di cortocircuito, mentre la quantità Ḋ è l'attenuazione
di corrente in cortocircuito; queste due quantità si ricavano dallo schema di calcolo
La quantità
Ḃ
0
èl
mostrato in Figura 11.1.39.
Figura 11.1.39: schema di calcolo per determinare
0
I˙1 = 0̇, si dice che il doppio bipolo ha la porta 1 a vuoto.
0
0
equazioni in (11.1.142) forniscono i valori di Ȧ e Ċ :
(
0
0
V̇2 = Ȧ V̇1 + Ḃ I˙1
0
0
−I˙2 = Ċ V̇1 + Ḋ I˙1
Ponendo
le
Ḃ
0
Ḋ
0
Sotto questa ipotesi
(11.1.145)
V̇2 ˙
V̇1 I1 =0̇
(11.1.146)
−I˙2 ˙
V̇1 I1 =0̇
(11.1.147)
Ȧ =
Ċ =
e
'attenuazione di tensione a vuoto, mentre la quantità Ċ è la transammettenza a vuoto; queste due quantità si ricavano dallo schema di calcolo mostrato in
La quantità
Ȧ
è l
Figura 11.1.40.
394
11 La teoria dei doppi bipoli
Figura 11.1.40: schema di calcolo per
11.1.6.2.1 Proposizione.
izzato dalla matrice di
determinare Ȧ e Ċ
Π un doppio hbipolo
i privo di generatori pilotati, carattertrasmissione inversa Ṫ . Allora per il teorema di reciprocità si
Sia
ha che:
h 0i
0
0
0
0
det Ṫ = Ȧ Ḋ − Ḃ Ċ = 1
(11.1.148)
La (11.1.148) si dimostra come nel caso della matrice di trasmissione diretta.
11.1.7 Relazioni tra le matrice
h i
Ṫ
e
h i
0
Ṫ
11.1.7.1 Passaggio dalla matrice di trasmissione diretta
trasmissione inversa
h i
Ṫ
alla matrice di
h 0i
Ṫ
Supponiamo che per un doppio bipolo esista sia la matrice di trasmissione diretta
che la matrice di trasmissione inversa
Allora si ha che
h
Ṫ
i
0
=
h 0 i h i−1
Ṫ = Ṫ
1
h
Ṫ
h i−1
= Ṫ
.
0
i
h i
Ṫ
.
Esplicitando quest'ultima espressione si ha che:
[Ṫ ]
−1
1
Ḋ −Ḃ
Ȧ Ḃ
=
=
Ċ Ḋ
ȦḊ − Ḃ Ċ −Ċ Ȧ
(11.1.149)
Dall'espressione in (11.1.149) si deducono i termini della matrice di trasmissione inversa
in funzione dei termini della matrice di trasmissione diretta:
0
Ḋ
ȦḊ−Ḃ Ċ
Ḃ =
0
−Ḃ
ȦḊ−Ḃ Ċ
0
−Ċ
ȦḊ−Ḃ Ċ
Ḋ =
0
Ȧ
ȦḊ−Ḃ Ċ
Ȧ =
(11.1.150)
Ċ =
Le relazioni in (11.1.150) valgono purchè sia
ȦḊ − Ḃ Ċ 6= 0̇.
395
11 La teoria dei doppi bipoli
11.1.7.2 Passaggio dalla matrice di trasmissione inversa
h 0i
Ṫ
alla matrice diretta
h i
Ṫ
Supponiamo che per un doppio bipolo esista sia la matrice di trasmissione diretta
h
che la matrice di trasmissione inversa
Allora si ha che
h i
Ṫ =
h i h 0 i−1
Ṫ = Ṫ
1
[Ṫ 0 ]
0
Ȧ
=
0
Ċ
Ṫ
h 0 i−1
.
= Ṫ
0
Ḃ
0
Ḋ
−1
0
i
h i
Ṫ
.
Esplicitando quest'ultima espressione si ha che:
1
= 0 0
Ȧ Ḋ − Ḃ 0 Ċ 0
0
Ḋ
0
−Ċ
−Ḃ
0
Ȧ
0
(11.1.151)
Dall'espressione in (11.1.151) si deducono i termini della matrice di trasmissione diretta
in funzione dei termini della matrice di trasmissione inversa:
0
Ȧ =
Ḋ
Ȧ0 Ḋ0 −Ḃ 0 Ċ 0
Ċ =
−Ċ
Ȧ0 Ḋ0 −Ḃ 0 Ċ 0
0
Ḃ =
−Ḃ
Ȧ0 Ḋ0 −Ḃ 0 Ċ 0
Ḋ =
Ȧ
Ȧ0 Ḋ0 −Ḃ 0 Ċ 0
(11.1.152)
0
0
Le relazioni in (11.1.152) valgono purchè sia
11.1.8 Relazioni tra le matrici
0
0
0
h i h i
Ṫ , Ż
e
h i
Ẏ
11.1.8.1 Passaggio dalla matrice delle impedenze
diretta
0
Ȧ Ḋ − Ḃ Ċ 6= 0̇.
h i
Ż
alla matrice di trasmissione
h i
Ṫ
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.146)
per
I˙2
si ottiene:
Ȧ =
V̇2
I˙2
V̇1
I˙2
V˙2
I˙1 =0̇ =
I˙2
V̇1
I˙2
I˙1 =0̇
I˙1 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.12) e (11.1.13), si scrive:
Ȧ =
Ż22
Ż12
(11.1.153)
Tenendo conto della relazione in (11.1.28), la (11.1.143) si scrive:
Ḃ =
Utilizzando l'espressione di
Ẏ12
1
Ẏ12
(11.1.154)
data in (11.1.40) è ovvio che la (11.1.154) conduce alla
relazione:
396
11 La teoria dei doppi bipoli
Ḃ = −
Ż11 Ż22
Ż11 Ż22 − Ż12 Ż21
= Ż21 −
Ż12
Ż12
(11.1.155)
Tenendo conto della relazione in (11.1.12), la (11.1.147) si scrive:
Ċ = −
1
Ż12
(11.1.156)
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.144)
per
V̇2
si ottiene:
−I˙2
V̇2
I˙1
V̇2
Ḋ =
V̇1 =0̇ =
−I˙2 V̇2 V̇1 =0̇
I˙1 V̇2 V̇1 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.28) e (11.1.29), si scrive:
Ḋ =
Inne utilizzando le espressioni di
Ẏ22
e
−Ẏ22
Ẏ12
Ẏ12
(11.1.157)
date in (11.1.40) è ovvio che la (11.1.157)
conduce alla relazione:
Ḋ =
Ż11
Ż12
(11.1.158)
Riassumendo sono state ricavate le formule di passaggio:
Ȧ =
Ż22
Ż12
Ḃ = − Ż11 Ż22Ż−Ż12 Ż21
12
(11.1.159)
− Ż1
12
C=
Ḋ =
Ż11
− Ż
12
11.1.8.2 Passaggio dalla matrice delle ammettenze
alla matrice di
h i
Ṫ
trasmissione diretta
Utilizzando le espressioni di
h i
Ẏ
Ż22
e
Ż12
date in (11.1.42) è ovvio che la (11.1.153) conduce
alla relazione:
Ȧ = −
Utilizzando l'espressione di
Ż12
Ċ =
Ẏ11
Ẏ12
(11.1.160)
data in (11.1.42), la (11.1.156) si scrive:
Ẏ11 Ẏ22 − Ẏ12 Ẏ21
Ẏ11 Ẏ22
=
− Ẏ21
Ẏ12
Ẏ12
Riassumendo sono state ricavate le formule di passaggio:
397
(11.1.161)
11 La teoria dei doppi bipoli
Ȧ = − ẎẎ11
Ḃ =
12
1
Ẏ12
(11.1.162)
C=
Ẏ11 Ẏ22 −Ẏ12 Ẏ21
Ẏ12
Ḋ =
− ẎẎ22
12
11.1.8.3 Passaggio dalla matrice di trasmissione diretta
impedenze
h i
Ṫ
alla matrice delle
h i
Ż
Invertendo (11.1.156) si trova immediatamente che:
Ż12 = −
1
Ċ
(11.1.163)
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.13)
per
V̇1
si ottiene:
Ż22 =
V̇2
V̇1
I˙2
V̇1
V̇2 V̇1 I˙1 =0̇
I˙2 V̇1 I˙1 =0̇
I˙1 =0̇ =
Quest'ultima, tenendo conto delle relazioni in (11.1.146) e (11.1.147), si scrive:
Ż22 = −
Ȧ
Ċ
(11.1.164)
Dalla (11.1.158) si ricava:
Ż11 = Ż12 Ḋ
(11.1.165)
Sostituendo (11.1.163) in (11.1.165) si ottiene:
Ż11 = −
Ḋ
C
(11.1.166)
Invertendo la (11.1.155) si ha:
Ż21 = Ḃ +
Ż11 Ż22
Ż12
(11.1.167)
Inne sostituendo (1.11.163), (1.11.164), (1.11.166) in (11.1.167) si ha:
Ż21 =
Ḃ Ċ − ȦḊ
Ċ
(11.1.168)
Riassumendo sono state ricavate le formule di passaggio:
Ż11 = − Ḋ
Ċ
Ż12 = − Ċ1
(11.1.169)
Ż21 =
Ḃ Ċ
− ȦḊ−
Ċ
398
Ż22 =
Ȧ
− Ċ
11 La teoria dei doppi bipoli
11.1.8.4 Passaggio dalla matrice di trasmissione diretta
ammettenze
h i
Ṫ
alla matrice delle
h i
Ẏ
Invertendo (11.1.154) si trova immediatamente che:
Ẏ12 =
1
Ḃ
(11.1.170)
Dividendo numeratore e denominatore del secondo membro dell'equazione in (11.1.29)
per
I˙1
si ottiene:
Ẏ22 =
I˙2
I˙1
V̇2
I˙1
I˙2 I˙1 V̇1 =0̇
V̇1 =0̇ =
V̇2 I˙1 V̇1 =0̇
Quest'ultima, tenendo conto delle relazioni in (11.1.143) e (11.1.144), si scrive:
Ẏ22 =
−Ḋ
Ḃ
(11.1.171)
Dalla (11.1.160) si ricava:
Ẏ11 = −Ẏ12 Ȧ
(11.1.172)
Sostituendo (11.1.170) in (11.1.172) si ottiene:
Ẏ11 = −
Ȧ
Ḃ
(11.1.173)
Invertendo la (11.1.161) si ha:
Ẏ11 Ẏ22
− Ċ
Ẏ12
Ẏ21 =
(11.1.174)
Inne sostituendo (1.11.170), (1.11.171), (1.11.173) in (11.1.112) si ha:
Ẏ21 =
ȦḊ − Ḃ Ċ
=
Ċ
(11.1.175)
Riassumendo sono state ricavate le formule di passaggio:
Ȧ
Ẏ11 = − Ḃ
Ẏ12 =
1
Ḃ
(11.1.176)
Ẏ21 =
ȦḊ−Ḃ Ċ
Ċ
399
Ẏ22 =
− Ḋ
Ḃ
11 La teoria dei doppi bipoli
11.1.9 Simmetria di un doppio bipolo
Un doppio bipolo si dice
simmetrico
se scambiando la porta 1 con la porta 2 rimane
inalterato
Per vedere cosa implica la proprietà di simmetria nelle varie matrici che caratterizzano
il doppio bipolo basta scambiare 1 con 2 ed imporre un'uguaglianza tra relazioni
11.1.9.1 Matrice delle impedenze
Un bipolo caratterizzato dalla matrice delle impedenze
h i
Ż è descritto mediante il sistema
di equazioni:
V̇1
V̇2
=
Ż11 Ż12
Ż21 Ż22
I˙1
I˙2
I˙2
I˙1
(11.1.177)
Scambiando 1 con 2 il sistema in (11.1.177) si scrive:
V̇2
V̇1
=
Ż22 Ż21
Ż12 Ż11
(11.1.178)
Anchè il doppio bipolo sia simmetrico deve risultare:
(
Ż11 = Ż22
Ż12 = Ż21
⇐ condizione di reciprocità
(11.1.179)
Secondo (11.1.179) è evidente che un doppio bipolo simmetrico è un doppio bipolo
reciproco per cui vale la relazione
Ż11 = Ż22 .
Quindi se un doppio bipolo è simmettrico allora è senz'altro reciproco. Ciò vuol dire che
se il doppio bipolo è simmetrico, anche se contiene generatori pilotati, risulta reciproco.
11.1.9.2 Matrice delle ammettenze
Un bipolo caratterizzato dalla matrice delle ammettenze
h i
Ẏ
è descritto mediante il
sistema di equazioni:
I˙1
I˙2
=
Ẏ11 Ẏ12
Ẏ21 Ẏ22
V̇1
V̇2
V̇2
V̇1
(11.1.180)
Scambiando 1 con 2 il sistema in (11.1.180) si scrive:
I˙2
I˙1
=
Ẏ22 Ẏ21
Ẏ12 Ẏ11
(11.1.181)
Anchè il doppio bipolo sia simmetrico deve risultare:
(
Ẏ11 = Ẏ22
Ẏ12 = Ẏ21
⇐ condizione di reciprocità
400
(11.1.182)
11 La teoria dei doppi bipoli
Secondo (11.1.182) è evidente che un doppio bipolo simmetrico è un doppio bipolo
reciproco per cui vale la relazione
Ẏ11 = Ẏ22 .
11.1.9.3 Matrice ibrida
Un bipolo caratterizzato dalla matrice ibrida
h i
Ḣ
è descritto mediante il sistema di
equazioni:
V̇1
I˙2
=
ḣ11 ḣ12
ḣ21 ḣ22
V̇2
I˙1
(11.1.183)
Scambiando 1 con 2 il sistema in (11.1.183) conduce alle equazioni che descrivono il
doppio bipolo mediante la matrice ibrida inversa
V̇2
I˙1
=
h
0
0
ḣ11 ḣ12
0
0
ḣ21 ḣ22
i
0
Ḣ :
V̇1
I˙2
(11.1.184)
Anchè il doppio bipolo sia simmetrico deve risultare:
0
h i
0
h i ḣ
0
ḣ11 ḣ12
11 ḣ12
Ḣ =
=
= Ḣ
0
0
ḣ21 ḣ22
ḣ21 ḣ22
(11.1.185)
Tenendo conto che valgono le relazioni, in 11.1.88 che per comodità riportiamo qui di
seguito,
0
ḣ22
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ12 =
0
−ḣ21
ḣ11 ḣ22 −ḣ12 ḣ21
ḣ22 =
ḣ11 =
ḣ21 =
0
−ḣ12
ḣ11 ḣ22 −ḣ12 ḣ21
0
ḣ11
ḣ11 ḣ22 −ḣ12 ḣ21
è chiaro che il sistema in (11.1.185) conduce alle seguenti uguaglianze:
ḣ11 =
ḣ22
ḣ11 ḣ22 −ḣ12 ḣ21
(11.1.190) ḣ12 =
−ḣ12
ḣ11 ḣ22 −ḣ12 ḣ21
(11.1.191)
ḣ21 =
−ḣ21
ḣ11 ḣ22 −ḣ12 ḣ21
(11.1.192) ḣ22 =
ḣ11
ḣ11 ḣ22 −ḣ12 ḣ21
(11.1.193)
Imponendo la condizione
ḣ11 ḣ22 − ḣ12 ḣ21 = −1
le equazioni in (11.1.191) e (11.1.192)
diventano delle identità mentre le equazioni in (11.1.190) e (11.1.193) conducono alla
condizione di reciprocità
ḣ11 = −ḣ22 .
Quindi un doppio bipolo è simmetrico se risulta:
ḣ11 ḣ22 − ḣ12 ḣ21 = −1
(11.1.186)
e se è simmetrico è anche reciproco:
ḣ11 = −ḣ22
401
(11.1.187)
11 La teoria dei doppi bipoli
11.1.9.4 Rappresentazione mediante la matrice di trasmissione diretta
Un bipolo caratterizzato dalla matrice di trasmissione diretta
h i
Ṫ
è descritto mediante
il sistema di equazioni:
V̇1
I˙1
=
Ȧ Ḃ
Ċ Ḋ
V̇2
−I˙2
(11.1.188)
Scambiando 1 con 2 il sistema in (11.1.192) conduce alle equazioni che descrivono il
doppio bipolo mediante la matrice di trasmissione inversa
V̇2
−I˙2
=
0
Ȧ
0
Ċ
0
Ḃ
0
Ḋ
V̇1
I˙1
h
Ṫ
0
i
:
(11.1.189)
Tenendo conto che valgono le relazioni, in 11.1.150 che per comodità riportiamo qui di
seguito,
0
Ḋ
ȦḊ−Ḃ Ċ
Ḃ =
0
−Ḃ
ȦḊ−Ḃ Ċ
0
−Ċ
ȦḊ−Ḃ Ċ
0
Ȧ
ȦḊ−Ḃ Ċ
Ȧ =
(11.1.190)
Ċ =
Ḋ =
è chiaro che il sistema in (11.1.193) si scrive:
(
Ḋ
Ḃ
V̇2 = ȦḊ−
V̇ − ȦḊ−
I˙
Ḃ Ċ 1
Ḃ Ċ 1
Ȧ
Ċ
V̇ + ȦḊ−
I˙
−I˙2 = − ȦḊ−
Ḃ Ċ 1
Ḃ Ċ 1
(11.1.195.1)
(11.1.195.2)
(11.1.191)
Le equazioni in (11.1.195) descrivono il doppio bipolo mostrato in Figura 11.1.41 dove
si vede che la corrente scorre da sinistra verso destra. Per imporre la simmetria occorre
però che la corrente uisca da destra verso sinistra; pertanto serve invertire i sensi delle
correnti
I˙1 e I˙2 .
Figura 11.1.41: doppio bipolo con corrente che scorre da destra verso sinistra
Invertendo la corrente
I˙2
(ciò equivale a moltiplicare la (11.1.195.2) per -1) il sistema
in (11.1.195) si scrive:
(
V̇2 =
I˙2 =
Ḋ
Ḃ
V̇ − ȦḊ−
I˙
ȦḊ−Ḃ Ċ 1
Ḃ Ċ 1
Ċ
Ȧ
V̇ − ȦḊ−
I˙
ȦḊ−Ḃ Ċ 1
Ḃ Ċ 1
402
(11.1.192)
11 La teoria dei doppi bipoli
Invertendo la corrente
I˙1
(ciò equivale a sostituire
I˙1
con
−I˙1 ),
il sistema di equazioni in
(11.1.196) si scrive:
(
V̇2 =
I˙2 =
Ḋ
Ḃ
V̇ + ȦḊ−
I˙
ȦḊ−Ḃ Ċ 1
Ḃ Ċ 1
Ċ
Ȧ
V̇ + ȦḊ−
I˙
ȦḊ−Ḃ Ċ 1
Ḃ Ċ 1
(11.1.193)
Le equazioni in (11.1.196) descrivono il doppio bipolo mostrato in Figura 11.1.42 dove
le correnti vanno da destra verso sinistra.
Figura 11.1.42: doppio bipolo con corrente che scorre da sinistra verso destra
Il sistema in (11.1.197) in forma matriciale si scrive:
V̇2
I˙2
"
=
Ḋ
ḊȦ−Ḃ Ċ
Ċ
ḊȦ−Ḃ Ċ
Ḃ
ḊȦ−Ḃ Ċ
Ȧ
ḊȦ−Ḃ Ċ
#
V̇1
I˙1
(11.1.194)
La simmetria diventa una proprietà per il doppio bipolo descritto mediante la matrice di
trasmissione se viene imposta l'uguaglianza tra le matrici contenute nelle rappresentazioni
date in (11.1.192) e (11.1.198):
Ȧ Ḃ
Ċ Ḋ
"
=
Ḋ
ḊȦ−Ḃ Ċ
Ċ
ḊȦ−Ḃ Ċ
Ḃ
ḊȦ−Ḃ Ċ
Ȧ
ḊȦ−Ḃ Ċ
#
(11.1.195)
L'uguaglianza matriciale in (11.1.195) è garantita soltanto se:
(
ȦḊ − Ḃ Ċ = 1 ⇐ condizione di reciprocità
Ȧ = Ḋ
Ancora una volta è stato vericato che la simmetria implica la reciprocità.
403
(11.1.196)
11 La teoria dei doppi bipoli
11.2 Impedenza in un doppio bipolo
11.2.1 Impedenza a vuoto
Si denisce
impedenza a vuoto primaria Ż01
l'impedenza vista dalla porta 1 quando la
porta 2 non è connessa ad alcun carico come mostrato in Figura 11.2.1:
Figura 11.2.1: impedenza a vuoto primaria
Essa coincide con il termine
Ż11
della matrice delle impedenze:
Ż01 = Ż11
Si denisce
(11.2.1)
impedenza a vuoto secondaria Ż02 l'impedenza vista dalla porta 2 quando la
porta 1 non è connessa ad alcun carico come mostrato in Figura 11.2.2:
Figura 11.2.2: impedenza a vuoto secondaria
Essa coincide con il termine
Ż22
della matrice delle impedenze:
Ż02 = Ż22
404
(11.2.2)
11 La teoria dei doppi bipoli
11.2.2 Impedenza iterativa
Si denisce
impedenza iterativa primaria Żit.1 l'impedenza vista dalla porta 1 quando la
porta 2 è chiusa attraverso il carico
Żit.1
come mostrato in Figura 11.2.3:
Figura 11.2.3: impedenza iterativa primaria
Si denisce
impedenza iterativa secondariaŻit.2 l'impedenza vista dalla porta 2 quando
la porta 1 è chiusa attraverso il carico
Żit.2
come mostrato in Figura 11.2.4
Figura 11.2.4: impedenza iterativa secondaria
11.2.3 Impedenza di cortocircuito
Si denisce
impedenza di cortocircuito primaria Żcc1
l'impedenza vista dalla porta 1
quando la porta 2 è chisa attraverso un cortocircuito come mostrato in Figura 11.2.5:
Figura 11.2.5: impedenza a vuoto primaria
Essa coincide con l'inverso del termine
Ẏ11
della matrice delle ammettenze:
Żcc1 =
Si denisce
1
Ẏ11
impedenza di cortocircuito secondaria Żcc2
(11.2.3)
l'impedenza vista dalla porta 2
quando la porta 1 è chisa attraverso un cortocircuito come mostrato in Figura 11.2.6:
405
11 La teoria dei doppi bipoli
Figura 11.2.6: impedenza a vuoto primaria
Essa coincide con l'inverso del termine
Ẏ22
della matrice delle ammettenze:
Żcc2 =
1
Ẏ22
(11.2.4)
11.2.4 Impedenza immagine
Le
impedenze immagine vanno denite a coppia.
Żim.1 , Żim.2
sono denite nella seguente maniera:
1 quando la porta 2 è chiusa attraverso il carico
La coppia di impedenze immagine
Żim.1
Żim.2 ,
è l'impedenza vista dalla porta
mentre
dalla porta 2 quando la porta 1 è chiusa attraverso il carico
Żim.2
è l'impedenza vista
Żim.1 .
L'immagine mostrata in Figura 11.2.7 chiarisce il signicato delle impedenze immagine.
Figura 11.2.7: impedenze immagine
11.2.5 Impedenza caratteristica
Se il doppio bipolo è simmetrico allora
Żit.1 = Żit.2 = Żim.1 = Żim.2 = Ż0
si chiama
impedenza caratteristica
(11.2.5)
del doppio bipolo.
11.2.6 Espressioni analitiche delle impedenze del doppio bipolo
In questa sezione si vuole determinare l'espressione analitica per ciascuna impedenza
denita precedentemente. Tutte le impedenze del doppio bipolo si possono ricavare da
una qualunque delle rappresentazioni del doppio bipolo (matrice delle impedenze, matrice
delle ammettenze..).
406
11 La teoria dei doppi bipoli
Qui si determiano le espressioni delle impedenze del doppio bipolo attraverso la matrice
delle impedenze.
In maniera immediata si hanno le espressioni delle impedenze a vuoto:
Ż01 = Ż11
(11.2.6)
Ż02 = Ż22
(11.2.7)
come osservato in precedenza.
Per determinare le altre impedenze si consideri lo schema di calcolo mostrato in Figura
11.2.8:
Figura 11.2.8: schema di calcolo
Per esso valgono le relazioni:

˙
˙

V̇1 = Ż11 I1 + Ż12 I2
V̇2 = Ż21 I˙1 + Ż22 I˙2


V̇2 = −Ż2 I˙2
Risolvedo il sistema in (11.2.8) rispetto a
V̇1 =
V̇1 ,
(11.2.8)
si trova la relazione:
Ż11 Ż22 + Ż11 Ż2 − Ż12 Ż21 ˙
I1
Ż22 + Ż2
da cui si ricava l'espressione dell'impedenza vista dalla porta 1:
Ż1 =
essendo
h i
det Ż
V̇1
=
I˙1
h i
det Ż + Ż11 Ż2
(11.2.9)
Ż22 + Ż2
il determinate della matrice delle impedenze
h i
Ż .
E' facile controllare l'esattezza della (11.2.9): passando al limite per
+∞(porta
Ż2
che tente a
2 a vuoto) si ha che:
Ż1 = Ż11 = Ż01
In modo analogo, si trova per lo schema di calcolo mostrato in Figura 11.2.9:
una relazione simile alla (11.2.9) per l'impedenza vista dalla porta 2:
407
(11.2.10)
11 La teoria dei doppi bipoli
Figura 11.2.9: schema di calcolo
Ż2 =
V̇2
=
I˙2
h i
det Ż + Ż22 Ż1
Ż11 + Ż1
(11.2.11)
Si osservi che la (11.2.11) si può ricavare a partire dalla (11.2.9) scambiando semplicemente 1 con 2.
passando al limite per
Ż1
che tente a
+∞(porta
1 a vuoto) si ha che:
Ż2 = Ż22 = Ż02
Se
Ż2 = 0̇,
allora vuol dire che la porta 2 è chiusa attraverso un cortocircuito e la
(11.2.9) fornisce l'
impedenza di cortocircuito primaria :
h i
det Ż
Żcc1 =
Se
Ż1 = 0̇,
(11.2.12)
=
Ż22
1
Ẏ11
(11.2.13)
allora vuol dire che la porta 1 è chiusa attraverso un cortocircuito e la
(11.2.11) fornisce l'
impedenze di cortocircuito
secondaria:
h i
det Ż
Żcc2 =
Ż11
=
1
Ẏ22
(11.2.14)
Tenendo conto delle relazioni in (11.2.6) e (11.2.7), le relazioni in (11.2.12) e (11.2.13)
permettono di scrivere la relazione
h i
det Ż = Ż01 Żcc2 = Ż02 Żcc1
che conduce all'espressione:
Ż01
Żcc1
=
Ż02
Żcc2
Posto:
Ż1 = Ż2 = Żit.1 ,
la (11.2.9) si scrive:
h i
det Ż + Ż11 Żit.1
Żit.1 =
Ż22 + Żit.1
408
(11.2.15)
11 La teoria dei doppi bipoli
Manipolando quest'ultima espressione si ricava la relazione:
h i
2
Żit.1
+ Ż22 − Ż11 Żit.1 − det Ż = 0
(11.2.16)
impedenza iterativa
La radice con parte reale positiva dell'equazione in (11.2.16) è l'
primaria.Posto: Ż1 = Ż2 = Żit.2 , la (11.2.9) si scrive:
h i
det Ż + Ż22 Żit.2
Żit.2 =
Ż11 + Żit.2
Manipolando quest'ultima espressione si ricava la relazione:
h i
2
Żit.2
+ Ż11 − Ż22 Żit.2 − det Ż = 0
(11.2.17)
impedenza iterativa
La radice con parte reale positiva dell'equazione in (11.2.16) è l'
secondaria. Ponendo
Ż1 , Ż2 = Żim.1 , Żim.2 le relazioni

Żim.1 = det[Ż ]+Ż11 Żim.2
Ż22 +Żim.2
det[Ż ]+Ż22 Żim.1
Ż
=
im.2
Ż11 +Żim.1
in (11.2.9) e(11.2.11) scrivono:
(11.2.18.1)
(11.2.18)
(11.2.18.2)
Żim.1 , Żim.2 il sistema in (11.2.18) si ottiene

h i
Żim.1 Ż22 + Żim.1 Ż2 = det Ż + Ż11 Żim.2
h i
⇒
Żim.2 Ż11 + Żim.2 Żim.1 = det Ż + Ż22 Żim.1
Risolvendo rispetto a
⇒ Żim.1 Ż22 − Żim.2 Ż11 = Ż11 Żim.2 − Ż22 Żim.1 ⇒
⇒ 2Żim.1 Ż22 = 2Ż11 Żim.2
ovvero:
Żim.1
Ż11
=
Żim.2
Ż22
Tenendo conto anche delle relazioni precedenti è ovvio che quest'ultima relazione si può
completare come segue:
Ż11
Ż01
Żcc1
Żim.1
=
=
=
Żim.2
Ż22
Ż02
Żcc2
(11.2.19)
Da quest'ultima relazione si ricava facilmente che:
Żim.1 =
Ż11
Żim.2
Ż22
409
(11.2.20)
11 La teoria dei doppi bipoli
Sostituendo (11.2.20) in (11.2.18.1) si ottine inne l'espressione analitica dell'impedenza immagine
Żim.2 :
Ż11
Żim.2 =
Ż22
⇒
h i
det Ż + Ż11 Żim.2
Ż22 + Żim.2
⇒
h i
Ż11 2
Żim.2 + Ż11 Żim.2 = det Ż + Ż11 Żim.2 ⇒
Ż22
⇒
h i
Ż11 2
Żim.2 = det Ż
Ż22
ovvero:
s
h i Ż
22
det Ż
Ż11
Żim.2 =
La (11.2.21) si può scrivere in altre forme, infatti tenendo conto che
Ż22 = Ż02
(11.2.21)
det[Ż ]
Ż11
= Żcc2
e che
si ha:
q
Żim.2 =
Żcc2 Ż02
(11.2.22)
L'altra impedenza immegine si ricava inne scambiando 1 con 2 in (11.2.22):
q
Żim.1 =
Żcc1 Ż01
(11.2.23)
11.3 Il quadripo composito e il doppio bipolo composito
Due doppi bipoli si possono connettere tra di loro in 5 dierenti modi:
1. interconnessione serie-serie;
2. interconnessione parallelo-parallelo;
3. interconnessione serie-parallelo;
4. interconnessione parallelo-serie;
5. interconnessione a cascata.
La strutttura che si realizza collegando 2 doppi bipoli è in generale un quadripolo
composito.
11.3.1 Interconnessione serie-serie
Due doppi bipoli sono in interconnessione serie-serie se collegati come mostrato in Figura
11.3.1:
410
11 La teoria dei doppi bipoli
Figura 11.3.1: interconnessione serie-serie
11.3.2 interconnessione parallelo-parallelo
Due doppi bipoli sono in interconnessione parallelo-parallelo se collegati come mostrato
in Figura 11.3.2:
Figura 11.3.2: interconnessione parallelo-parallelo
11.3.3 Interconnessione serie-parallelo
Due doppi bipoli sono in interconnessione serie-parallelo se collegati come mostrato in
Figura 11.3.3:
411
11 La teoria dei doppi bipoli
Figura 11.3.3: interconnessione serie-parallelo
11.3.4 Interconnessione parallelo-serie
Due doppi bipoli sono in interconnessione parallelo-serie se collegati come mostrato in
Figura 11.3.4:
Figura 11.3.4: interconnessione serie-parallelo
11.3.5 Interconnessione cascata
Due doppi bipoli sono in interconnessione a cascata se collegati come mostrato in Figura
11.3.5:
Figura 11.3.5: interconnessione a cascata
11.3.6 Il doppio bipolo composito
Per un quadripolo del tipo1 o del tipo 2 o del tipo 3 o del tipo 4, non è possibile dare
in generale una rappresentazione analitica.
412
In altri termini un quadripolo composito
11 La teoria dei doppi bipoli
non è detto che sia un doppio bipolo composito.
Si può dare una rappresentazione
analitica per il quadripolo composito se dopo l'interconnessione dei due doppi bipoli,
questi continuano ad essere dei doppi bipoli e in tal caso la struttura complissiva è un
doppio bipolo composito.
Consideriamo il doppio bipolo composito serie-serie mostrato in Figura 11.3.6.
Figura 11.3.6: interconnessione serie-serie
Scrivendo la LKC all'insieme di taglio si ha ovviamente che
0
0
− I˙1R − I˙2R + I˙1R + I˙2R = 0̇
(11.3.1)
Ma la (11.3.1) non implica che le correnti si annullano a 2 a 2 come segue:
(
0
−I˙1R + I˙1R = 0̇
−I˙2R + I˙2R = 0̇
(11.3.2)
ovvero non implica che R ed S siano dei doppi bipoli dopo la loro connessione.
Tuttavia potrebbe succedere che uno tra R ed S sia un doppio bipolo per ragioni interne.
In tal caso lo è anche l'altro. In questa circostanza i doppi bipoli R ed S realizzano un
doppio bipolo composito.
Per un doppio bipolo composito serie-serie si trova che:
h i h i h i
Ż = ŻR + ŻS
(11.3.3)
Per un doppio bipolo composito parallelo-parallelo si trova che:
h i h i h i
Ẏ = ẎR + ẎS
(11.3.4)
Per un doppio bipolo composito serie-parallelo si trova che:
h i h i h i
Ḣ = ḢR + ḢS
(11.3.5)
Per un doppio bipolo composito parallelo-serie si trova che:
h 0i h 0 i h 0 i
Ḣ = ḢR + ḢS
413
(11.3.6)
11 La teoria dei doppi bipoli
Contrariamente ai casi precedenti se due doppi bipoli sono connessi in cascata, allora il
quadripolo composito è un doppio bipolo composito. In questo caso si trova che:
h i h i h i
Ṫ = ṪR · ṪS
(11.3.7)
Visto che le interconnessioni a cascata sono molto importanti nell'ambito delle telecomunicazioni dimostriamo la 11.3.7.
Consideriamo l'interconnessione a cascata mostrata in Figura 11.3.7 dove vengono
esplicitate tensioni e correnti alle porte.
Figura 11.3.7: interconnessione a cascata
Il doppio bipolo R è caratterizzato dalla rappresentazione analitica:
V̇1R
I˙1R
i V̇
2R
= ṪR
−I˙2R
h
(11.3.8)
mentre il doppio bipolo S è caratterizzato dalla rappresentazione analitica:
V̇1S
I˙1
S
h i V̇
2S
= ṪS
−I˙2S
(11.3.9)
Dallo schema mostrato in Figura 11.3.7 risulta che:
V̇2R
−I˙2R
=
V̇1S
I˙1S
(11.3.10)
La (11.3.10) consente di sostituire (11.3.9) in (11.3.8), ottenendo così la tesi:
V̇1R
I˙1
R
h i h i V̇
2S
= ṪR ṪS
−I˙2S
ovvero:
h i h i h i
Ṫ = ṪR · ṪS
(11.3.11)
11.3.7 Trasformazione stella-triangolo
I circuiti elettrici possono presentare impedenze connesse in serie oppure connesse in
parallelo. In realtà esisto altre possibilità; esistono delle situszioni in cui le impedenze
414
11 La teoria dei doppi bipoli
non risultano connesse nè in serie nè in parallelo; in questi casi le impedenze possono
formare una
stella
oppure un
triangolo.
Tre impedenze costituiscono una stella se tutte e tre hanno solo un morsetto a comune
come mostrato in Figura 11.3.8.1. Il morsetto a comune si chiama centro stella O. Si noti
che in Figura 11.3.8.1 viene mostrato il simbolo di stella.
Tre impedenze costituiscono una triangolo se prese a due a due hanno solo un morsetto
a come mostrato in Figura 11.3.8.2. I morsetti a comune sono i tre vertici di un triangolo
i cui lati sono le impedenze. Si noti che in Figura 11.3.8.2 viene mostrato il simbolo di
stella.
Figura 11.3.8: 1 stella; 2 triangolo
Una stella oppure un triangolo si può rappresentare usando la sintassi sei doppi bipoli;
in Figura 11.3.9.1 viene mostrata una stella di impedenze, mentre in Figura 11.3.9.2 viene
mostrato un triangolo di impedenze.
Esistono delle formule di passaggio stella-triangolo e triangolo-stella. Queste formule
si possono ricavare uguagliando la matrice delle impedenze del doppio bipolo a stella e
del doppio bipolo a triangolo.
Chiudendo le porte del doppio bipolo a stella mediante i generatori ideali di tensione
si ottiene il circuito mostrato in Figura 11.3.10:
Applicando il metodo delle correnti alle maglie è facile scrivere di getto il sistema
I˙1 e I˙2 :
Ż1 + Ż3
Ż3
I˙1
V̇1
=
Ż3
Ż2 + Ż3
I˙2
V̇2
risolvente nelle incognite
(11.3.12)
Da quest'ultimo sistema è evidente che la matrice delle impedenze del doppio bipolo a
stella è data da:
415
11 La teoria dei doppi bipoli
Figura 11.3.9: 1 doppio bipolo a stella; 2 doppio bipolo a triangolo
Figura 11.3.10: 1 doppio bipolo a stella
h i Ż + Ż
Ż3
1
3
Żf =
Ż3
Ż2 + Ż3
(11.3.13)
Chiudendo le porte del doppio bipolo a triangolo mediante i generatori ideali di tensione
si ottiene il circuito mostrato in Figura 11.3.11:
Applicando il metodo delle correnti alle maglie è facile scrivere di getto il sistema
risolvente nelle incognite
I˙1
e
I˙2 :


Ż31
0̇
−Ż31
 0̇

Ż32
Ż23
−Ż31 Ż23 Ż31 + Ż12 + Ż23
Ricavando
J˙
 

I˙1
V̇1
I˙2  =  V̇2 
0̇
J˙
(11.3.14)
dalal terza equazione e sostituendo nelle prime due equazioni si ricava il
sistema risolvente nelle incognite
I˙1
e
I˙2 :
416
11 La teoria dei doppi bipoli
Figura 11.3.11: 1 doppio bipolo a triangolo

1

Ż12 + Ż23 + Ż31
Ż31 Ż12 + Ż23
Ż31 Ż23

Ż31 Ż23

Ż23 Ż12 + Ż31
I˙1
I˙2
=
V̇1
V̇2
(11.3.15)
Da quest'ultimo sistema è evidente che la matrice delle impedenze del doppio bipolo a
triangolo è data da:

h i
Ż4 =
1

Ż12 + Ż23 + Ż31
Ż31 Ż12 + Ż23
Ż31 Ż23

Ż31 Ż23

Ż23 Ż12 + Ż31
(11.3.16)
Uguagliando la matrice delle impedenze del doppio bipolo a stella con la matrice delle
impedenze del doppio bipolo a triangolo:
h
Ż4
i


Ż31 Ż12 + Ż23
Ż31 Ż23
1

=
=
Ż12 + Ż23 + Ż31
Ż31 Ż23
Ż23 Ż12 + Ż31
=
si ottegono le
Ż1 + Ż3
Ż3
Ż3
Ż2 + Ż3
h i
= Żf
formule di passaggio triangolo stella (4 −→ f).
(4 −→ f)

Ż12 Ż31

Ż =

 1 Ż12 +Ż23 +Ż31





12 Ż23
Ż2 = Ż Ż
12 +Ż23 +Ż31







Ż =
Ż31 Ż23
3
Ż +Ż +Ż
Formule di passaggio stella-triangolo
12
23
31
Utilizzando le relazioni in (11.3.17), è facile vericare che:
417
(11.3.17)
11 La teoria dei doppi bipoli
Ż1 Ż2 + Ż2 Ż3 + Ż3 Ż1 = Ż1 Ż23
da cui si ricava che:
Ż23 = Ż2 + Ż3 +
Utilizzando le permutazioni cicliche
Ż2 Ż3
Ż1
1 −→ 2 −→ 3 −→ 1,
(11.3.18)
dalla (11.3.18) si ricavano le
altre espressioni delle impedenze del triangolo:
Ż31 = Ż3 + Ż1 +
Ż3 Ż1
Ż2
(11.3.19)
Ż12 = Ż1 + Ż2 +
Ż1 Ż2
Ż3
(11.3.20)
Formule di passaggio stella-triangolo
Quindi le le
(f −→ 4)
formule di passaggio stella-triangolo (f −→ 4) sono :


Ż12 = Ż1 + Ż2 +







Ż23 = Ż2 + Ż3 +







Ż = Ż + Ż +
31
3
1
Ż1 Ż2
Ż3
Ż2 Ż3
Ż1
(11.3.21)
Ż3 Ż1
Ż2
Formule di passaggio nel caso di stella equilibrata e triangolo equilibrato
Una stella si dice
equilibrata
se risulta:
Ż1 = Ż2 = Ż3 = Żf
Un triangolo si dice
equilibrato
(11.3.22)
se risulta:
Ż12 = Ż23 = Ż31 = Ż4
(11.3.23)
Utilizzando (11.3.22) e (11.3.23) le formule date in (11.3.17) e (11.3.21) forniscono le
espressioni:
Ż4 = 3 Żf
(11.3.24)
1
Żf
3
(11.3.25)
Żf =
418
11 La teoria dei doppi bipoli
Esempio
Si vuole determinare la resistenza equivalente vista dai nodi A e B del circuito mostrato
in Figura 11.3.12
Figura 11.3.12: circuito elettrico:
Ż1 = Ż2 = 10Ω, Ż3 = Ż4 = Ż5 = Ż4 = j 12Ω
Guardando il circuito dai nodi A e B non si riesce ad individuare nè resistenze in serie
nè in parallelo; tuttavia è possibile notare 2 triangoli di cui uno equilibrato.
Trasformando il triangolo equilibrato di vertici B, C e D in stella equilibrata di impedenze
Żf =
Ż4
3
= j 4Ω
si ottiene il circuito equivalente mostrato in Figura 11.3.13:
Figura 11.3.13: circuito elettrico:
Ż1 = Ż2 = 10Ω, Żf = j 4Ω
A questo punto l'impedenza equivalente vista dai nodi A e B si può determinare facilmente in quando è evidente che risulta essere la combinazione di impedenze in serie e in
parallelo:
419
11 La teoria dei doppi bipoli
Żeq. =
Ż1 + Żf
Ż2 + Żf
Ż1 + Ż2 + 2 Żf
+ Żf
(11.3.26)
Sostituendo i valori numerici, l'espressione in (11.3.26) fornisce:
Żeq. =
=
(10 + j 4Ω)2
84 + 80 j
21 + 21 j
+j4=
+j4=
+j4=
20 + j 8
20 + j 8
5+j2
21 + 20 j 5 − j 2
145 + 58 j
+j4=
+ j 4 = 5 + j6 Ω
5+j2 5−j2
29
(11.3.27)
Possiamo vericare l'esattezza dell'espressione trovata applicando uno dei metodi di analisi studiati. Chiudendo il bipolo mostrato in Figura 11.3.12 attraverso un generatore di
prova
V̇p
si ottiene il circuito mostrato in Figura 11.3.14; è chiato che:
Żeq. =
Figura 11.3.14: circuito elettrico:
V̇p
I˙p
(11.3.28)
Ż1 = Ż2 = Ż = 10Ω, Ż3 = Ż4 = Ż5 = Ż4 = j 12Ω
Applicando il metodo delle correnti di maglia si trova di getto il sistema risolvente:


Ż + Ż4
Ż
Ż4

Ż
2 Ż + Ż4 −Ż4  
Ż4
−Ż4
3 Ż4
In forma scalare si ha:
420
 

i̇p
V̇p
J˙1  =  0̇ 
0̇
J˙2
(11.3.29)
11 La teoria dei doppi bipoli


Ż
+
Ż
I˙p + Ż J˙1 + Ż4 J˙2 = V̇p (11.3.30.1)
4


˙p + 2 Ż + Ż4 J˙1 − Ż4 J˙2 = 0̇ (11.3.30.2)
Ż
I



Ż4 I˙p − Ż4 J˙1 − Ż4 J˙2 = 0̇
(11.3.30.3)
(11.3.30)
Dalla (11.3.30.3) si ricava immediatamente che:
J˙1 = I˙p + 3 J˙2
(11.3.31)
Sostituendo (11.3.31) in (11.3.30.1) e (11.3.30.2) si ricava:
(
2 Ż + Ż4 I˙p + 3 Ż + Ż4 J˙2 = V̇p
I˙p + 2 J˙2 = 0̇
(11.3.32.1)
(11.3.32)
(11.3.32.2)
Dalla (11.3.32.2) si ricava che:
1
J˙2 = − I˙p
2
(11.3.33)
Sostituendo inne (11.3.33) in (11.3.33.2) si ha:
1
1
Ż + Ż4 I˙p = V̇p
2
2
ovvero:
Żeq. =
V̇p
1
1
= Ż + Ż4 = 5 + j6 Ω
2
2
I˙p
Esattamente come in (11.3.27).
421
(11.3.34)
12 Linee di trasmissione
12.1 Introduzione
Una
linea di trasmissione è un sistema di conduttori molto estesi, idealmente di lunghezza
innita, paralleli tra di loro, interposti in un materiale isolante. La linea di trasmissione
collega una sorgente ad un carico molto lontano dalla sorgente al ne di trasportare
energia oppure informazione.
Essa può essere
biconduttore
oppure
multiconduttore ;
si dice biconduttore se risulta
costituita da due soli conduttori, si dice multiconduttore se risulta costituita da più
di due conduttori.
uniforme :
Una linea di trasmissione può anche essere
uniforme
oppure
non
si dice uniforme se il materiale interposto tra i conduttori risulta omogeneo,
cioè se i suoi parametri costitutivi
ε (costante dielettrica), µ (permeabilità magnetica), σ
(conducibilità elettrica) sono costanti per tutta la lunghezza della linea di trasmissione;
si dice non uniforme se i parametri costitutivi
ε, µ
e
σ
variano da punto a punto lungo
la linea di trasmissione. Per semplicità ci occuperemo soltanto delle linee di trasmissione
uniformi biconduttori e uniformi multiconduttori.
12.2 Linea di trasmissione biconduttore
Come mostrato in Figura 12.1.1 una linea di trasmissione uniforme biconduttore (d'ora
in avanti semplicemente linea di trasmissione) viene indicata con due segmenti paralleli
ed in grassetto in modo da collegare una sorgente ad un carico.
Figura 12.2.1: simbolo circuitale linea di trasmissione biconduttore
In Figura 12.2.1 vengono mostrati alcuni esempi di linea di trasmissione uniforme
biconduttore.
Vogliamo determinare un
modello matematico
zare la linea di trasmissione.
attraverso cui sia possibile caratteriz-
Questo modello deve essere, nei limiti consentiti, il più
SEMPLICE, ACCURATO e GENERALE possibile. Per determinare il modello matematico della linea di trasmissione possiamo pensare di utilizzare le equazioni di Maxwell
422
12 Linee di trasmissione
Figura 12.2.2: esempi di linee di trasmissione
che sono le più generali e accurate che regolano i sistemi dal punto di vista elettromagnetico. Se utilizzassimo le equazioni di Maxwell, il modello matematico non risulterebbe
aatto semplice. Possiamo pensare allora di utilizzare le leggi di Kirchho (LK) che sono
le approssimazioni delle equazioni di Maxwell. Utilizzando le LK il modello matematico
risulterebbe più semplice, ma allo stesso tempo meno accurato e generale; inoltre non è
detto che si possano applicare le LK. Bisogna vedere se le linee di trasmissione soddisfano
la condizione di validità delle L K.
Σ un sistema elettrico di dimensione d come mostrato in Figura. 12.2.3, interessato
un segnale elettrico w (t) (che può essere un segnale di tensione o di corrente).
Sia
da
Condizione
cente,
necessaria
ma
NON su-
anché si possano applicare le LK
al sistema
Σ
è che la dimensione
d
sia
molto minore della lunghezza d'oda minima
ν
λmin
associata alla più alta frequenza
del segnale
w (t):
d << λmin
Nel caso più semplice di segnale
frequenza dalla relazione:
(12.2.1)
w (t)
monocromatico la lunghezza d'onda è legata alla
Figura 12.2.3: sistema di dimensione d
l
v= ν
essendo v la velocità di propagazione del segnale
(12.2.2)
w (t).
ν.
Si ricordi che un segnale
monocromatico è caratterizzato da un'unica frequenza
Nel caso generale la (12.2.2) non vale perchè in generale il segnale
da uno spettro che si estende da una frequenza minima
νM AX .
νmin
w (t) è caratterizzato
a una frequenza massima
Facendo riferimento alla linea di trasmissione mostrata in Figura. 12.2.1 è chiaro
dimensione trsversale dt soddisfa la condizione (12.2.1) mentre la dimensione
longitudinale dl non soddisfa la condizione (12.2.1), essendo per ipotesi dl >> dt .
che la
423
12 Linee di trasmissione
Si deduce quindi che NON è POSSIBILE applicare le LK alla linea di trasmissione nel
suo complesso. Si deduce pure che è POSSIBILE applicare le LK ad un tratto nito, al
limite innitesimo, di linea di trasmissione. Quello che faremo adesso è quindi denire
∆x,
un modello circuitale per un tratto di linea di linea di lunghezza nita
con
∆x
tendente a zero, da cui, applicando le LK si ricava il modello matematico del tratto di
linea innitesimo.
Visto che l'analisi di un circuito si può arontare sia nel dominio
del tempo che nel dominio dei fasori, condurremo l'
frequenza
per il
tratto di linea innitesimo
analisi in transitorio
e l'
analisi in
della linea di trasmissione.
12.3 Linea di trasmissione in regime transitorio
12.3.1 Equazioni dei telegrasti
modello circuitale
In Figura 12.2.3 è riportato il
trasmissione di lunghezza nita
Passando al limite per
rappresenta il
∆x
che caratterizza un tratto di linea di
∆x.
che tende a zero, il circuito mostrato in Figura 12.3.1
tratto di linea innitesimo
della linea di trasmissione.
Figura 12.3.1: modello circuitale della linea di trasmissione biconduttore
Dove
linea :
v = v (x, t)
ed
i = i (x, t)
si chiamano rispettivamente
dipendono oltre che dal tempo t, anche dalla posizione
tensione
e
corrente
di
x che descrive la lunghezza
della linea.
Le quantità
r , l, c
e
g
si chiamano
parametri primari e sono grandezze per
unità di lunghezza. I parametri r ed l
si chiamano pure parametri longitudinali
perché sentono la corrente di linea
mentre i parametri
c
parametri trasversali
tensione di linea
v.
r
e
g
Unità di misura
r
l
c
g
Ω m−1
H m−1
F m−1
s m−1
i,
si chiamano pure
perché sentono la
resistenza
lineica, l si chiama induttanza lineica, c si
chiama capacità lineica, ed inne g si chiaIn particolare,
Parametro primario
Tabella 12.1: parametri
si chiama
trasmissione
424
della
linea
di
12 Linee di trasmissione
ma
conduttanza lineica.
In Tabella 12.1 sono riportate le unità di misura dei parametri
primari.
ˆ r 4x
linea
ˆ l 4x
è la resistenza che descrive tutto l'eetto Joule prodotto dalla corrente di
i
nei due conduttori di lunghezza
è l'induttanza che descrive l'energia immagazzinata dovuta al campo mag-
netico prodotto dalla corrente di linea
ˆ c 4x
4x
i
è la capacità che descrive l'energia immagazzinata dovuta al campo elettrico
che si viene a creare a seguito della d.d.p. tra i due conduttori
ˆ g 4x è la conduttanza che descrive i passaggi di corrente da un conduttore all'altro
dovuti al non perfetto funzionamento dell'isolante interposto tra i conduttori
ˆ vg (x + 4x) 4x
e
ig (x + 4x) 4x
sono generatori ideali che stanno a indicare le
interferenze dovute a sorgenti di campo elettromagnetico quali potrebbero essere
per esempio, le linee di trasmissione circostanti alla linea di trasmissione considerata. E' ovvio che
vg (x + 4x)
si misura in
V m−1
mentre
ig (x + 4x)
si misura in
Am−1 .
Facendo riferimento al circuito mostrato in Figura 12.3.1 si scrivono facilmente le equazioni
all'insieme di taglio e alla maglia.
Equazione all'insieme di taglio (LKC)
Con riferimento al circuito mostrato in Figura 12.3.2, si ha:
i (x, t) + ig (x + ∆x, t) 4x =
= g∆x (−vg (x + ∆x, t) ∆x + v (x + ∆x, t)) +
+i (x + ∆x, t) + c∆x
∂
(−vg (x + ∆x, t) ∆x + v (x + ∆x, t))
∂t
Attraverso semplici operazioni di manipolazione algebrica, da quest'ultima espressione si
ricava la relazione:
i (x + ∆x, t) − i (x, t)
= ig (x + ∆x, t) + g∆xvg (x + ∆x, t) − gv (x + ∆x, t) +
∆x
+ c∆x
Passando al limite per
4x
∂
∂
vg (x + ∆x, t) − c v (x + ∆x, t)
∂x
∂t
(12.3.1)
che tende a zero la (12.3.1), fornisce:
∂
∂
i (x, t) = −g v (x, t) − c v (x, t) + ig (x, t)
∂x
∂t
425
(12.3.2)
12 Linee di trasmissione
Equazione alla maglia (LKT)
Con riferimento al circuito mostrato in Figura 12.3.2, si ha:
−v (x, t) + r ∆x i (x, t) + l ∆x
∂
i (x, t) − vg (x + ∆x, t) ∆x + v (x + ∆x, t) = 0
∂t
Attraverso semplici operazioni di manipolazione algebrica, da quest'ultima espressione si
ricava la relazione:
v (x + ∆x, t) − v (x, t)
∂
= −r i (x, t) − l i (x, t) + vg (x + ∆x, t)
∆x
∂t
Passando al limite per 4x che tende a zero la (12.3.3), fornisce:
(12.3.3)
∂
∂
v (x, t) = −r i (x, t) − l i (x, t) + vg (x, t)
∂x
∂t
Le espressioni in (12.3.2) e (12.3.4) prendono il nome di
(12.3.4)
equazioni dei telegrasti.
Si dimostra che le equazioni dei telegrasti non dipendono dal modello circuitale adottato per rappresentare il tratto innitesimo di linea di trasmissione.
Per esempio si
trovano le stesse equazioni se si utilizza il modello circuitale mostrato in Figura. 12.3.2.
Figura 12.3.2: modello circuitale della linea di trasmissione biconduttore
purchè si pone:

0
00
000

r =r +r +r



l = l0 + l00 + l000
0
00

c=c +c



g = g 0 + g 00
(12.3.5)
Le equazioni dei telegrasti costituiscono un sistema di due equazioni dierenziali alle
condizioni inizilali e
le condizioni al contorno (se la linea di trasmissione è nita) o le condizioni di regolarità
all'innito (se la linea di trasmissione è seminita o innita ).
derivate parziali. Per risolvere tale problema bisogna specicare le
D'ora in avanti supporremo la linea di trasmissione di lunghezza nita L, quindi si
tratta di risolvere il problema:
426
12 Linee di trasmissione

∂
∂


∂x i (x, t) = −g v (x, t) − c ∂t v (x, t) + ig (x, t) (12.3.6.1)


 ∂ v (x, t) = −r i (x, t) − I ∂ i (x, t) + v (t)
(12.3.6.2)
g
∂x
∂t

condizioni iniziali t = t0



condizioni al contorno Γ
(12.3.6)
Al ne di rendere più semplice il problema in (21.3.4), supponiamo nulle le interferenze
modellizzate con i generatori indipendenti:

∂
∂


∂x i (x, t) = −g v (x, t) − c ∂t v (x, t) (12.3.7.1)


 ∂ v (x, t) = −r i (x, t) − I ∂ i (x, t) (12.3.7.2)
∂x
∂t

condizioni
iniziali
t
=
t
0



condizioni al contorno Γ
Il problema in (12.3.5) è molto dicile da risolvere in quanto le variabili
v(x, t)
risultano
accoppiare
accoppiate.
(12.3.7)
i(x, t)
Per rendere più semplice il problema bisogna cercare di
e
dis-
le variabili, ovvero bisogna cercare di determinare una equazione dierenziale
alle derivate parziali che contiene la sola variabile
i(x, t)
oppure la sola variabile
v(x, t).
Vediamo un modo per disaccoppiare le variabili: derivando parzialmente rispetto a x
l'equazione in (12.3.7.1), si ricava:
∂2
∂
∂ ∂
i (x, t) = −g
v (x, t) − c
v (x, t)
2
∂x
∂x
∂x ∂t
(12.3.8)
Derivando parzialmente rispetto a t l'equazione (12.3.7.2), si ricava:
∂
∂2
∂ ∂
v (x, t) = −r i (x, t) − I 2 i (x, t)
∂t ∂x
∂t
∂t
Per il teorema di Schwartz quest'ultima espressione si scrive pure:
∂ ∂
∂
∂2
v (x, t) = −r i (x, t) − I 2 i (x, t)
∂x ∂t
∂t
∂t
(12.3.9)
Inserendo (12.3.7.2) e (12.3.9) in (12.3.8), si ricava:
∂2
∂2
∂
i
(x,
t)
=
−l
c
i (x, t) − (g l + c r)
i (x, t) − g r i (x, t)
2
2
∂x
∂t
∂t
(12.3.10)
Analogamente derivando parzialmente rispetto a t l'equazione in (12.3.7.1) e rispetto
a x l'equazione (12.3.7.2) e apportando le dovute sostituzioni, si ricava:
∂2
∂2
∂
v
(x,
t)
=
−l
c
v (x, t) − (g l + c r)
v (x, t) − g r v (x, t)
2
2
∂x
∂t
∂t
(12.3.11)
Visto che le equazioni in (12.3.10) e (12.3.11) sono formalmente identiche, si possono
compattare in un'unica equazione:
∂2
∂2
∂
f
(x,
t)
=
−l
c
f (x, t) − (g l + c r)
f (x, t) − g r f (x, t)
∂x2
∂t2
∂t
427
(12.3.12)
12 Linee di trasmissione
essendo:
f (x, t) = i(x, t)
oppure
f (x, t) = v(x, t).
Nota l'equazione in (12.3.12) è chiaro che il problema in (12.3.7) diventa:
 2
∂
∂2

 ∂x2 f (x, t) = −l c ∂t2 f (x, t) − (g l + c r)
condizioni iniziali t = t0


condizioni al contorno Γ
∂
∂t f
In conseguenza del disaccoppiamento delle variabili
in (12.3.13).
(x, t) − g r f (x, t)
(12.3.13)
i(x, t) e v(x, t) si ottiene il problema
In realtà questo problema non è equivalente al problema in (12.3.7) in
quanto non hanno lo stesso insieme di soluzioni. E' facile capire che tutte le soluzioni del
problema in (12.3.13) sono soluzioni del problema in (12.3.7), mentre tutte le soluzioni
del problema in (12.3.7) non è detto che siano anche soluzioni del problema (12.3.13). In
altre parole per garantire il disaccoppiamento delle variabili è stato necessario aumentare
l'ordine di derivazione delle equazioni dei telegrasti e ciò ha inevitabilmente ampliato
l'insieme delle soluzioni.
Lo stesso discorso si ripete per esempio, se pensiamo di derivare l'equazione dierenziale
di ordine minimo del circuito RC:
RC
RC
d
vc (t) + vc (t) = vg (t)
dt
d2
d
d
vc (t) + vc (t) = vg (t)
dt2
dt
dt
Un'equazione dierenziale del secondo ordine ha sempre un insieme delle soluzioni più
ampio rispetto ad una equazione dierenziale del primo ordine.
Sono di interesse alcuni casi notevoli di linee di trasmissione:
ˆ
LINEA DI TRASMISSIONE IDEALE O SENZA PERDITE
Una linea di trasmissione si dice ideale o senza perdite se risulta
r=g=0
(12.3.14)
In tal caso l'equazione in (12.3.12) si scrive:
1 ∂2
∂2
f
(x,
t)
+
f (x, t) = 0
∂x2
u2 ∂t2
(12.3.15)
avendo posto:
u2 =
Essendo
u
1
lc
(12.3.16)
un termine di velocità che indica la velocità di propagazione del segnale
lungo la linea di trasmissione.
La (12.3.5) è nota con il nome di
equazione di D'Alambert.
428
12 Linee di trasmissione
ˆ
LINEA DITRASMISSIONE NON DISTORCENTE O ANTIDISTORCENTE
Una linea di trasmissione si dice non distorcente se viene vericata la
Heaveside :
condizione di
r
g
= =σ
l
c
Posto
σ = 0
(12.3.17)
si ricava la linea di trasmissione ideale; quest'ultima quindi è un caso
particolare di linea non distorcente.
ˆ
LINEA DI TRASMISSIONE IN CAVO INTERRATO
Una linea di trasmissione si dice in cavo interrato se risulta:
l=g=0
(12.3.18)
In tal caso l'equazione in (12.3.12) si scrive:
∂2
∂
f (x, t) − c r f (x, t) = 0
2
∂x
∂t
ˆ
(12.3.19)
LINEA DI TRASMISSIONE NEL CASO RESISTIVO
Una linea di trasmissione si dice resistiva se risulta:
l=c=0
(12.3.20)
In tal caso l'equazione in (2.1.10) si scrive:
∂2
f (x, t) − g r f (x, t) = 0
∂x2
(12.3.21)
12.3.2 Linea di trasmissione non distorcente
Una linea di trasmissione si dice non distorcente se viene vericata la
Heaveside :
Condizione di
r
g
= =σ
l
c
(12.3.22)
Vogliamo esprimere l'equazione caratteristica di una linea di trasmissione:
∂2
∂2
∂
f
(x,
t)
=
−l
c
f (x, t) − (g l + c r)
f (x, t) − g r f (x, t)
∂x2
∂t2
∂t
nell'ipotesi di
linea di trasmissione non distorcente.
(12.3.23)
Per far ciò consideriamo le equazioni
dei telegrasti in cui sono nulli i generatori indipendenti che modellizzano le interferenze
elettromagnetiche:
∂
∂
v (x, t) = −r i (x, t) − l i (x, t)
∂x
∂t
429
(12.3.24)
12 Linee di trasmissione
Mettendo in evidenza
∂
∂
i (x, t) = −g v (x, t) − c v (x, t)
∂x
∂t
il termine −l i(x, t) , l'equazione in (12.3.24)
r
∂
∂
i (x, t)
v (x, t) = −l
+
∂x
l
∂t
(12.3.25)
si scrive:
(12.3.26)
Utilizzando (12.3.22), l'espressione in (12.3.26) si scrive:
∂
∂
i (x, t)
v (x, t) = −l σ +
∂x
∂t
Si osservi come
di linea
i(x, t).
σ+
∂
∂t
(12.3.27)
sia semplicemente un operatore simbolico applicato alla corrente
Mettendo in evidenza il termine
−c v(x, t)
, l'equazione in (12.3.25) si
scrive:
∂
i (x, t) = −c
∂x
g
∂
+
c ∂t
v (x, t)
(12.3.28)
Utilizzando (12.3.22), l'espressione in (12.3.28) si scrive:
∂
∂
i (x, t) = −c σ +
v (x, t)
∂x
∂t
(12.3.29)
Derivando parzialmente rispetto a x l'equazione in (12.3.27) si scrive:
∂2
∂
∂
v
(x,
t)
=
−l
σ
+
i (x, t)
∂x2
∂t ∂x
(12.3.30)
Inserendo (12.3.29) in (12.3.30) si ricava:
∂2
∂ 2
v (x, t) = l c σ +
v (x, t)
∂x2
∂t
Tenendo conto che
u2 =
(12.3.31)
1
l c , la (12.3.31) si scrive:
∂2
1
v (x, t) − 2
2
∂x
u
∂ 2
σ+
v (x, t) = 0
∂t
(12.3.32)
Denendo l'operatore simbolico:
"
∂2
1
−
∂x2 u2
# ∂
∂ 2
1
∂
∂
1
∂
σ+
=
−
σ+
+
σ+
∂t
∂x u
∂t
∂x u
∂t
(12.3.33)
L'espressione in (12.3.32) si scrive:
∂
1
−
∂x u
∂
∂
1
∂
σ+
+
σ+
v (x, t) = 0
∂t
∂x u
∂t
430
(12.3.34)
12 Linee di trasmissione
In modo analogo si ricava facilmente pure l'equazione:
∂
∂
∂
1
σ+
σ+
i (x, t) = 0
+
∂t
∂x u
∂t
∂
1
−
∂x u
(12.3.35)
Visto che le equazioni in (12.3.34) e (12.3.35) sono formalmente identiche, si possono
compattare in una unica equazione:
essendo:
∂
1
−
∂x u
∂
∂
∂
1
σ+
σ+
f (x, t) = 0
+
∂t
∂x u
∂t
f (x, t) = i(x, t)
oppure
f (x, t) = v(x, t).
(12.3.36)
L'equazione in (12.3.36) è l'equazione
in (12.3.23) nell'ipotesi di linea di trasmissione non distorcente. L'equazione in (12.3.36)
è equivalente alle due seguenti equazioni:
∂
1
+
∂x u
∂
1
−
∂x u
∂
σ+
∂t
∂
∂t
σ+
Ciò vuol dire che l'integrale generale
tra l'integrale generale
f+ (x, t)
f (x, t)
f+ (x, t) = 0
(12.3.37)
f− (x, t) = 0
(12.3.38)
dell'equazione in (12.3.36) è la somma
dell'equazione in (12.3.37) e l'integrale generale
f− (x, t)
dell'equazione in (12.3.38):
f (x, t) = f+ (x, t) + f− (x, t)
Determiniamo l'INTEGRALE GENERALE
f+ (x, t)
(12.3.39)
dell'equazione in (12.3.37): espan-
dendola si ha:
∂
σ
1 ∂
f+ (x, t) + f+ (x, t) +
f+ (x, t) = 0
∂x
u
u ∂t
L'equazione in (12.3.40) si integra facilmente imponendo il
D'Alambert :
(12.3.40)
cambiamento di variabili di
(
ξ = x − ut
η = x + ut
(12.3.41)
Sommando membro a membro le relazioni in (12.3.41) si ha:
x=
ξ+η
2
(12.3.42)
Sottraendo membro a membro, invece si ha:
t=
η−ξ
2u
(12.3.43)
Note le relazioni in (12.3.42) e (12.3.43) l'integralef+ (x, t) si può esprimere in termini di
ξ eη :
431
12 Linee di trasmissione
f+ (x, t) = f+
ξ+η η−ξ
,
2
2u
= h+ (ξ, η)
(12.3.44)
Derivando parzialmente rispetto a x, le posizioni in (12.3.41) forniscono le relazioni:
(
∂
∂x ξ
∂
∂x η
=1
=1
(12.3.45)
Derivando parzialmente rispetto a t, le posizioni in (12.3.41) forniscono le relazioni:
(
∂
∂t ξ
∂
∂t η
= −u
=u
(12.3.46)
Per il teorema di derivazione di funzione composta, e con l'ausilio dei risultati in (12.3.45)
e (12.3.46) si trovano le relazioni:
∂
∂
∂ξ
∂
∂η
f+ (x, t) =
h+ (ξ, η)
+
h+ (ξ, η)
=
∂x
∂ξ
∂x ∂η
∂x
=
∂
∂
h+ (ξ, η) +
h+ (ξ, η)
∂ξ
∂η
(12.3.47)
∂
∂
∂
∂ξ
∂η
f+ (x, t) =
h+ (ξ, η)
+
h+ (ξ, η)
=
∂t
∂ξ
∂t
∂η
∂t
= −u
∂
∂
h+ (ξ, η) + u
h+ (ξ, η)
∂ξ
∂η
(12.3.48)
Sostituendo (12.3.44), (12.3.47) e (12.3.48) in (12.3.40) si ricava:
∂
σ
h+ (ξ, η) +
h+ (ξ, η) = 0
∂η
2u
(12.3.49)
L'integrale dell'equazione in (12.3.49) si determina applicando il
delle variabili,
secondo cui l'integrale generale
funzioni di cui una dipende solo da
ξ
h+ (ξ, η)
metodo delle separazioni
risulta essere il prodotto di due
e l'altra dipende solo da
η:
h+ (ξ, η) = a− (ξ) b+ (η)
(12.3.50)
Inserendo (12.3.50) in (12.3.49) si ricava:
a− (ξ)
∂
σ
b+ (η) +
a− (ξ) b+ (ξ) = 0
∂η
2u
(12.3.51)
σ
d
b+ (η) +
b+ (ξ) = 0
dη
2u
(12.3.52)
ovvero:
Si osservi come la derivata parziale diventa totale per eetto della separazione delle
variabili.
432
12 Linee di trasmissione
La (12.3.52) è una equazione dierenziale del primo ordine, il cui integrale generale è:
σ
b+ (ξ) = k+ e− 2 u η
(12.3.53)
Sostituendo (12.3.53) in (12.3.50) si ricava l'integrale generale dell'equazione in (12.3.49):
σ
h+ (ξ, η) = a− (ξ) k+ e− 2 u η
Inglobando la costantek+ all'interno della funzione arbitraria
(12.3.54)
a− (ξ),
l'integrale generale
in (12.3.54) si scrive:
σ
h+ (ξ, η) = a− (ξ) e− 2 u η
(12.3.55)
Imponendo il cambiamento di variabile (12.3.41), l'espressione in (12.3.55) porta all'integrale generale
f+ (x, t):
σ
f+ (x, t) = a− (x − u t) e− 2 u (x+u t)
Determiniamo l'INTEGRALE GENERALE
f− (x, t)
(12.3.56)
dell'equazione in (12.3.38):
l'equazione in (12.3.38) si scrive:
∂
σ
1 ∂
f− (x, t) − f− (x, t) −
f− (x, t) = 0
∂x
u
u ∂t
(12.3.57)
l'equazione in (12.3.57) si integra imponendo il cambiamento di variabili di D'Alambert
dato in (12.3.41)
Note le relazioni in (12.3.42) e (12.3.43) l'integrale
di
ξ
e
f− (x, t) si
può esprimere in termini
η:
f− (x, t) = f−
ξ+η η−ξ
,
2
2u
= h− (ξ, η)
(12.3.58)
Per il teorema di derivazione di funzione composta, e con l'ausilio dei risultati in (12.3.45)
e (12.3.46) si trovano le relazioni:
∂
∂
∂
f− (x, t) =
h− (ξ, η) +
h− (ξ, η)
∂x
∂ξ
∂η
(12.3.59)
∂
∂
∂
f− (x, t) = −u h− (ξ, η) + u
h+ (ξ, η)
∂t
∂ξ
∂η
(12.3.60)
Sostituendo (12.3.58), (12.3.59) e (12.3.60) in (12.3.57) si ricava:
∂
σ
h− (ξ, η) −
h− (ξ, η) = 0
∂η
2u
(12.3.61)
L'integrale dell'equazione in (12.3.61) si determina applicando il
delle variabili,
secondo cui l'integrale generale
funzioni di cui una dipende solo da
ξ
h− (ξ, η)
e l'altra dipende solo da
433
metodo della separazione
risulta essere il prodotto di due
η:
12 Linee di trasmissione
h− (ξ, η) = a+ (ξ) b− (η)
(12.3.62)
Inserendo (12.3.62) in (12.3.61) si ricava:
a+ (ξ)
σ
∂
b− (η) −
a+ (ξ) b− (ξ) = 0
∂η
2u
(12.3.63)
d
σ
b− (ξ) −
b− (ξ) = 0
dη
2u
(12.3.64)
ovvero:
Si osservi come anche in questo caso, la derivata parziale diventa totale per eetto della
separazione delle variabili. La (12.3.64) è una equazione dierenziale del primo ordine,
il cui integrale generale è:
σ
b− (ξ) = k− e 2 u ξ
(12.3.65)
Sostituendo (12.3.65) in (12.3.62) si ricava l'integrale generale dell'equazione in (12.3.61):
σ
h− (ξ) = k− a+ (η) e 2 u ξ
Inglobando la costante
k−
(12.3.66)
all'interno della funzione arbitraria
a+ (η) , l'integrale generale
in (12.3.66) si scrive:
σ
h− (ξ) = a+ (η) e 2 u ξ
(12.3.67)
Imponendo il cambiamento di variabile (12.3.41), l'espressione in (12.3.67) porta all'integrale generale
f− (x, t)
:
σ
f− (x, t) = a+ (x + u t) e 2 u (x−u t)
(12.3.68)
Inserendo in ne (12.3.56) e (12.3.68) in (12.3.39) si ricava l'integrale generale dell'equazione in (12.3.36):
f (x, t) = f+ (x, t) + f− (x, t) =
σ
σ
= a− (x − u t) e− 2 u (x+u t) + a+ (x + u t) e 2 u (x−u t)
(12.3.69)
Osserviamo che in virtù della relazione
−
σ
σ
σ
σ
(x + u t) = −
(x + u t + x − x) =
(x − u t) −
2x
2u
2u
2u
2u
si ha:
σ
σ
σ
e− 2 u (x+u t) = e 2 u (x−u t) e− u x
Analogamente, in virtù della relazione
434
(12.3.70)
12 Linee di trasmissione
σ
σ
σ
σ
(x − u t) =
(x − u t + x − x) = −
(x + u t) +
2x
2u
2u
2u
2u
si ha:
σ
σ
σ
e 2 u (x−u t) = e− 2 u (x+u t) e u x
(12.3.71)
Quindi sostituendo (12.3.70) e (12.3.71) in (12.3.69) si ha:
f (x, t) = f+ (x, t) + f− (x, t) =
σ
σ
σ
σ
= a− (x − u t) e 2 u (x−u t) e− u x + a+ (x + u t) e− 2 u (x+u t) e u
(12.3.72)
Denendo le funzioni arbitrarie:
σ
0
a− (x − u t) = a− (x − u t) e 2 u (x−u t)
σ
0
a−+ (x + u t) = a+ (x + u t) e− 2 u (x+u t)
l'integrale
f (x, t)
(12.3.73)
(12.3.74)
in (12.3.72) si scrive:
f (x, t) = f+ (x, t) + f− (x, t) =
σ
0
0
σ
= a− (x − u t) e− u x + a+ (x + u t) e u
La funzione arbitraria
(12.3.75)
0
a− (x − u t)
si chiama
onda progressiva
in quanto rappresenta una propagazione ondosa lungo l'asse
Per vericare ciò supponiamo che all'istante di tempo t = t1 la
0
a− (x − u t) assuma massimo in corrispondenza dell'ascissex = x1 . Supponiamo
inoltre che assuma massimo pure all'istante di tempo t = t2 > t1 e in corrispondenza
dell'ascisse x = x2 .
0
Anchè la funzione a− (x − u t) rappresenti un'onda che si propaga lungo la direzione
delle ascisse positive deve succedere chex2 > x1 . Visto che:
positivo delle ascisse.
funzione
0
0
a− (x1 − u t1 ) = a− (x2 − u t2 )
deve essere:
x1 − u t1 = x2 − u t2
da cui si ricava:
x2 = x1 + u (t2 − t1 ) > x1
435
12 Linee di trasmissione
La funzione arbitraria
0
a− (x + u t)
onda regressiva
si chiama
in quanto rappresenta una propagazione ondosa lungo l'asse
σ
e− u x appresenta un fattore di decadimento spaziale
σ
x
l'esponenziale e u rappresenta un fattore di decadimento
negativo delle ascisse. L'esponenziale
per l'onda progressiva mentre
spaziale per l'onda regressiva .
Osserviamo che in virtù della relazione
−
σ
σ
σ
σ
(x + u t) = −
(x + u t + u t − u t) = −
(x − u t) −
2u t
2u
2u
2u
2u
si ha:
σ
σ
e− 2 u (x+u t) = e− 2 u (x−u t) e−σ t
(12.3.76)
Analogamente, in virtù della relazione
σ
σ
σ
σ
(x − u t) =
(x − u t + u t − u t) =
(x + u t) −
2u t
2u
2u
2u
2u
si ha:
σ
σ
e 2 u (x−u t) = e 2 u (x+u t) e−σ t
(12.3.77)
Quindi sostituendo (12.3.76) e (12.3.77) in (12.3.69) si ha:
f (x, t) = f+ (x, t) + f− (x, t) =
σ
σ
= a− (x − u t) e− 2 u (x−u t) e−σ t + a+ (x + u t) e 2 u (x+u t) e−σ t
(12.3.78)
Denendo le funzioni arbitrarie:
00
σ
00
σ
a− (x − u t) = a− (x − u t) e− 2 u (x−u t)
a−+ (x + u t) = a+ (x + u t) e 2 u (x+u t)
l'integrale
f (x, t)
(12.3.79)
(12.3.80)
in (12.3.78) si scrive:
f (x, t) = f+ (x, t) + f− (x, t) =
00
00
= a− (x − u t) e−σ t + a+ (x + u t) e−σ t
La funzione arbitraria
(12.3.81)
00
a− (x − u t)
si chiama
onda progressiva
in quanto rappresenta una propagazione ondosa lungo l'asse
positivo delle ascisse, mentre la funzione
436
12 Linee di trasmissione
00
a+ (x + u t)
si chiama
onda progressiva
in quanto rappresenta una propagazione ondosa lungo l'asse
positivo delle ascisse.
Con questa rappresentazione i termini esponenziali rappresentano fattori di decadimento temporale per l'onda progressiva e per l'onda regressiva .
Per semplicare la
notazione indichiamo con il simbolo:
ϕ = ϕ(x − u t)
(12.3.82)
l'onda progressiva , mentre con il simbolo:
ψ = ψ(x + u t)
(12.3.83)
l'onda regressiva .
Pertanto l'espressine in (12.3.75) si scrive:
σ
σ
f (x, t) = ϕ e− u x + ψ e u
(12.3.84)
mentre l'espressione in (12.3.81) si scrive :
f (x, t) = ϕ e−σ t + ψ e−σ t
Ricordando che
f (x, t) = v(x, t)
oppure
f (x, t) = i(x, t)
(12.3.85)
l'equazione in (12.3.84)
fornisce:
(
σ
σ
v (x, t) = ϕv e− u x + ψv e u x
σ
σ
i (x, t) = ϕi e− u x + ψi e u x
(12.3.86)
mentre l'equazione in (12.3.85) fornisce:
(
v (x, t) = ϕv e−σ y + ψv eσ t
i (x, t) = ϕi e−σ t + ψi eσ t
(12.3.87)
Non è dicile dimostrare che tra le funzioni arbitrarie sussistono le relazioni :
(
ϕi = R1c ϕv
ψi = − R1c ψv
(12.3.88)
essendo :
1
1
= cu =
= Gc
Rc
lu
(12.3.89)
Rc si chiama resistenza caratteristica della linea di trasmissione non distorcente, mentre
Gc si chiama conduttanza caratteristica della linea di trasmissione non distorcente.
Facendo uso delle relazioni in (12.3.88) le espressioni in (12.3.86) e (12.3.87) si riscrivono
come segue:
437
12 Linee di trasmissione
Per una
(
σ
σ
v (x, t) = ϕv e− u x + ψv e u x
ψv σ
ϕv − σ
e ux − R
eux
i (x, t) = R
c
c
(12.3.90)
(
v (x, t) = ϕv e−σ t + ψv eσ t
ϕv −σ t
ψv σ t
i (x, t) = R
e
−R
e
c
c
(12.3.91)
linea di trasmissione ideale
vale
σ = 0.
In questo caso le equazioni in (12.3.90)
e (12.3.91) diventano:
(
v (x, t) = ϕv + ψv
ϕv
ψv
−R
i (x, t) = R
c
c
(12.3.92.1)
(12.3.92.2)
(12.3.92)
Solo abbinando le condizioni iniziale e le condizioni al contorno si determinano le
funzioni arbitrarie
ϕv
e
ψv .
Vedremo in seguito attraverso delle applicazioni come
determinarle in casi particolarmente semplici .
12.3.2.1 Esercizio
Consideriamo due linee di trasmissione semi-innite ideali caratterizzate dalle resistenze
caratteristicheRc1 ed
Rc2 congiunte
all'ascisse
x=0
come mostrato in Figura 12.3.3.
Figura 12.3.3: linea di tramissione di lunghezza innita
Supponiamo di trasmettere un'onda di tensione progressiva
(I)
ϕv
. All'ascisse x=0 suc-
cede che parte di questa onda continua a propagarsi nella direzione positiva delle ascisse:
(II)
ϕv
e parte torna indietro:
ψv .
Ovviamente nella Linea II non c'è onda regressiva per-
ché essa è di lunghezza innita in direzione delle ascisse positive. Secondo (12.3.92.1), la
tensione nella Linea I vale:
v (I) (x, t) = ϕ(I)
v + ψv
(12.3.93)
v (II) (x, t) = ϕ(II)
v
(12.3.94)
mentre nella Linea II vale:
All'ascisse
x=0
si ha l'uguaglianza tra le relazioni in (12.3.93) e (12.3.94):
438
12 Linee di trasmissione
(II)
ϕ(I)
v + ψv = ϕv
(12.3.95)
Analogamente, utilizzando l'equazione in (12.3.92.2), si determina la corrente nella Linea
I:
1
1 (I)
ϕv −
ψv
Rc1
Rc1
i(I) (x, t) =
(12.3.96)
e la corrente nella Linea II:
v (II) (x, t) =
All'ascisse
x=0
1 (II)
ϕ
Rc2 v
(12.3.97)
si ha l'uguaglianza tra le relazioni in (12.3.96) e (12.3.97):
1 (I)
1
1 (II)
ϕ −
ψv =
ϕ
Rc1 v
Rc1
Rc2 v
(12.3.98)
Le equazioni in (12.3.95) e (12.3.98) costituiscono un sistema di due equazioni nelle
incognite
(II)
ϕv
e
ψv
(I)
ϕv è l'onda di tensione
( (I)
(II)
ϕv + ψv = ϕv
in quanto
1 (I)
Rc ϕv
−
1
Rc ψ v
=
nota:
(12.3.99)
1 (II)
Rc ϕv
Risolvendo il sistema in (12.3.99) si trova:
ϕ(II)
=
v
ψv =
2Rc2
ϕ(I)
Rc1 + Rc2 v
Rc2 − Rc1 (I)
ϕ
Rc1 + Rc2 v
12.3.3 Bilancio energetico per una linea di trasmissione
Consideriamo un tratto di linea di trasmissione di lunghezza nita
∆x
con
∆x
sucien-
temente piccolo, al limite innitesimo. Possiamo rappresentare questo tratto di linea di
trasmissione attraverso un doppio bipolo come mostrato in Figura 12.3.4.
La
potenza
che
viene
immessa
nel
doppio bipolo risulta :
p = v1 i 1 + v2 i 2
(12.3.100)
Visto che:
(
v1 = v (x, t)
i1 = i (x, t)
v2 = v (x + ∆x, t) i2 = −i (x + ∆x, t)
Figura 12.3.4: tratto di linea di lunghezza
∆x
(12.3.101)
439
12 Linee di trasmissione
l'espressione in (12.3.100) si scrive:
p = v (x, t) i (x, t) + v (x + ∆x, t) [−i (x + ∆x, t)]
Sviluppando in serie di Taylor i termini
v(x + ∆x, t)
e
−i(x + ∆x, t)
(12.3.102)
attorno al punto
x
l'espressione in (12.3.102) si scrive:
p = v (x, t) i (x, t) +
∂
∂
+ v (x, t) +
v (x, t) ∆x + ...
−i (x, t) −
i (x, t) ∆x + ... =
∂x
∂x
= v (x, t) i (x, t) − v (x, t) i (x, t) − v (x, t)
− i (x, t)
∂
i (x, t) ∆x+
∂x
∂
∂
∂
v (x, t) ∆x −
v (x, t)
i (x, t) (∆x)2 + .....
∂x
∂x
∂x
(12.3.103)
Tracurando i termini innitesimi di ordine superiore, quest'ultima espressione si scrive:
p = −v (x, t)
∂
∂
i (x, t) ∆x − i (x, t)
v (x, t) ∆x =
∂x
∂x
= −∆x
∂
{v (x, t) i (x, t)}
∂x
(12.3.104)
Per spiegare il signicato dell'equazione in (12.3.104) basta combinare opportunamente
le equazioni dei telegrasti. In questo ambito è opportuno considerare le equazioni che
tengono conto dei generatori indipendenti date in (12.3.6).
Moltiplicando ambo i membri dell'equazione in (12.3.6.2) per i(x, t)∆x si ricava:
∂
∂
−∆x i (x, t)
v (x, t) = −∆x i (x, t) −r i (x, t) − l i (x, t) + vg (x, t)
∂x
∂t
ovvero:
∂
− ∆x i (x, t)
v (x, t) = ∆x
∂x
∂ 1 2
2
r i (x, t) +
l i (x, t) − i (x, t) vg (x, t)
∂t 2
(12.3.105)
Moltiplicando ambo i membri dell'equazione in (23.3.6.1) per v(x, t)∆x si ricava:
−∆x v (x, t)
∂
∂
i (x, t) = −∆x v (x, t) −g v (x, t) − c v (x, t) + ig (x, t)
∂x
∂t
ovvero:
∂
− ∆x v (x, t)
v (x, t) = ∆x
∂x
∂
g v (x, t) +
∂t
2
1 2
c v (x, t) − v (x, t) ig (x, t)
2
(12.3.106)
440
12 Linee di trasmissione
Sommando membro a membro le equazioni in (12.3.105) e (12.3.106) si ricava:
p = −∆x
∂
+
∂t
∂
{v (x, t) i (x, t)} = ∆x r i2 (x, t) + g v 2 (x, t) +
∂x
l 2
c 2
i (x, t) + v (x, t) + (−i (x, t) vg (x, t) − v (x, t) ig (x, t))
2
2
(12.3.107)
Confrontando (12.3.104) con (12.3.107) è ovvio che la (12.3.107) rappresenta la potenza
istantanea
p
immessa nel tratto di linea di trasmissione di lunghezza
∆x.
La quantità
pd = r i2 (x, t) + g v 2 (x, t) +
è la
potenza per unità di lunghezza dissipata
(12.3.108)
dalla linea di trasmissione.
La quantità
l
c
Ei = i2 (x, t) + v 2 (x, t)
2
2
energia per unità di lunghezza mmagazzinata
è l'
(12.3.109)
dalla linea di trasmissione.
Inne la quantità
pg = −i (x, t) vg (x, t) − v (x, t) ig (x, t)
è la
(12.3.110)
potenza per unità di lunghezza dei generatori ideali.
Utilizzando i simboli in (12.3.108) (12.3.109) e (12.3.110) l'espressione della potenza
istantane data in (12.3.107) si scrive:
∂
p == ∆x pd + Ei + pg
∂t
(12.3.111)
Nel caso in cui risultano nulli i generatori indipendenti , la potenza istantanea immessa
nel tratto di linea di lunghezza
Dx vale:
∂
p == ∆x pd + Ei
∂t
(12.3.112)
Denizione: bipolo passivo
Sia
bk
un bipolo facente parte di una rete complicata come mostrato in Figura 12.3.5
Tale bipolo si dice
passivo
se risulta:
u (t0 ) + Le (t0 , t) ≥ 0
essendo
il bipolo
u(t0 )
bk e
l'energia del bipolo
bk
all'istante
t0
ed
il resto della rete elettrica dall'istante
denizione:
441
(12.3.113)
Le lavoro elettrico scambiato tra
t0 all'istante t; quest'ultimo è per
12 Linee di trasmissione
Figura 12.3.5: bipolo in un rete complicata
ˆ
t
p (τ ) dτ
Le (t0 , t) =
(12.3.114)
t0
essendo
p(t)
la potenza istantanea del bipolo
bk .
Alternativamente possiamo dire che il bipolo
bk
risulta
passivo
scambiato tra esso e il resto della rete elettrica, dall'istante
l'energia posseduta all'istante
t0
se il lavoro elettrico
all'istante
t
, non supera
t0 :
Le (t0 , t) ≥ −u (t0 )
(12.3.115)
Denizione: doppi bipolo passivo
Un doppio bipolo si dice passivo se viene vericata la condizione in (12.3.113) o in
(12.3.115), a patto che per
Le (t0 , t)
il
lavoro elettrico
u(t0 )
si intenda l'
enenrgia del doppio bipolo
all'stante
t0 e
scambiato tra il doppio bipolo e il resto della rete elettrica.
Quest'ultimo risulta denito come in (12.3.115) a patto che
istantanea del doppio bipolo. Assumendo
t0 = −∞,
p
rappresenti la potenza
è ragionevole supporre:
u(−∞) = 0
in quanto si presume che all'alba dei tempi l'energia dell'universo fosse nulla.
Sotto questa ipotesi, il doppio bipolo si dice passivo se risulta:
Le (t0 , t) ≥ 0
essendo
p
(12.3.116)
la potenza istantanea del doppio bipolo.
Proposizione
Un tratto di linea di trasmissione, privo di generatori indipendenti, è un doppio bipolo
passivo.
Dimostrazione. Per vericare quanto detto basta inserire (12.3.112) in (12.3.116) :
ˆ
t
ˆ
t
∂
Le (−∞, t) =
p (τ ) dτ =
∆x pd + Ei dτ =
∂t
−∞
−∞
ˆ t
2
= ∆x
r i (x, τ ) + g v 2 (x, τ ) dτ +
−∞
442
12 Linee di trasmissione
ˆ
t
+∆x
−∞
ˆ
∂
∂τ
l 2
c 2
i (x, τ ) + v (x, τ ) dτ =
2
2
t
∆x
2
2
r i (x, τ ) + g v (x, τ ) dτ + ∆x
−∞
Si ha chiaramente che
c 2
l 2
i (x, τ ) + v (x, τ ) dτ ≥ 0
2
2
Le (−∞, t) ≥ 0 in quanto
l 2
c 2
∆x
i (x, t) + v (x, t) > 0
2
2
e
ˆ
t
2
r i (x, t) + g v 2 (x, t) dτ
∆x
−∞
2
essendo r i (x, t)
+
g v 2 (x, t) una funzione non negativa.
Denizione: doppio bipolo conservativo
Un doppio bipolo si dice conservativo se risulta:
ˆ
+∞
p (τ ) dτ = 0
(12.3.117)
−∞
Proposizione
Un tratto di linea di trasmissione privo di generatori indipendenti è un doppio bipolo
conservativo.
Ciò risulta ovvio in quanto è ragionevole supporre che per
t = +∞
risultano nulle la
tensione e la corrente.
12.4 Linea di trasmissione in regime sinusoidale
12.4.1 Rappresentazione fasoriale
A regime sinusoidale la tensione di linea e la corrente di linea sono i segnali sinusoidali:
Ai segnali sinusoidali
v (x, t) = V (x) cos (ωt + ϕV (x))
(12.4.1)
i (x, t) = I (x) cos (ωt + ϕI (x))
(12.4.2)
v(x, t)
e
i(x, t)
si fanno corrispondere i numeri complessi o
V̇ (x) = V (x) ejϕV (x)
443
fasori :
(12.4.3)
12 Linee di trasmissione
I˙ (x) = I (x) ejϕI (x)
Noti i fasori
˙ ,
V̇ (x)e I(x)
(12.4.4)
è possibile risalire alla tensione e alla corrente di linea, tramite
le formule:
n
o
v (x, t) = Re V̇ (x) ejωt
(12.4.5)
o
n
i (x, t) = Re I˙ (x) ejωt
(12.4.6)
Dimostrazione. Proviamo la relazione in (12.4.5).
Sostituendo (12.4.3) in (12.4.5) si ha:
n
o
n
o
v (x, t) = Re V (x) ejϕV (x) ejωt = Re V (x) ej(ϕV (x)+ωt) =
= Re {V (x) (cos (ωt + ϕV (x))) + V (x) sin (ωt + ϕV (x))} =
= V (x) cos (ωt + ϕV (x))
Allo stesso modo si prova la (12.4.6).
12.4.2 Equazioni dei telegrasti nel dominio dei fasori e parametri
secondari della linea di trasmissione
Visto che
v(x, t)
e
i(x, t)
sono segnali sinusoidali, possiamo scrivere le equazioni dei
telegrasti:
(
nel
∂
∂x i (x, t) = −g v (x, t) − c
∂
∂x v (x, t) = −r i (x, t) − I
dominio dei fasori.
∂
∂t v (x, t)
∂
∂t i (x, t)
(12.4.7.1)
(12.4.7.2)
(12.4.7)
Scriviamo l'equazione in (12.4.7.2) nel dominio dei fasori. Utiliz-
zando (12.4.5) il primo membro della (12.4.7.2) si scrive:
n
o
∂
∂
v (x, t) =
Re V̇ (x) ejωt = Re
∂x
∂x
∂
V̇ (x) ejωt
∂x
jωt
= Re e
d
V̇ (x)
dx
(12.4.8)
Utilizzando (12.4.6) il secondo membro della (12.4.7.2) si scrive:
n
o
n
o
∂
∂
i (x, t) = −r Re I˙ (x) ejωt − l Re I˙ (x) ejωt =
∂t
∂t
n
o
∂
jωt
jωt
= Re −r I˙ (x) e
+ Re −l I˙ (x) e
=
∂t
n
o
n
o
= Re −r I˙ (x) ejωt + Re −jω l I˙ (x) ejωt
−r i (x, t) − I
444
(12.4.9)
12 Linee di trasmissione
Sostituendo (12.4.8) e (12.4.9) in (12.4.7.2) si ricava l'uguaglianza:
jωt
Re e
n
o
n
o
d
V̇ (x) = Re −r I˙ (x) ejωt + Re −jω l I˙ (x) ejωt
dx
(12.4.10)
L'uguaglianza in (12.4.10) deve essere garantita per ogni x e per ogni t .
Quindi per
t=0
si scrive:
Re
Mentre per
n
o
n
o
d
V̇ (x) = Re −r I˙ (x) + Re −jω l I˙ (x)
dx
(12.4.11)
π
2ω si scrive:
t=
n
o
n
o
π
π
j π2 d
Re e
V̇ (x) = Re −r I˙ (x) ej 2 + Re −jω l I˙ (x) ej 2
dx
ovvero:
n
o
n o
d
Re j
V̇ (x) = Re −j r I˙ (x) + Re j −jω l I˙ (x)
dx
(12.4.12)
Ricordando la nota proprietà:
n o
n o
Re j Ȧ = Re {j (Ar + jAi )} + Re {−Ai + jAr } = −Ai = −Im Ȧ
(12.4.13)
l'equazione in (12.4.12) si scrive:
d
V̇ (x)
dx
n
o
n
o
= −Im −r I˙ (x) − Im −jω l I˙ (x)
d
V̇ (x)
dx
n
o
n
o
= Im −r I˙ (x) + Im −jω l I˙ (x)
−Im
ovvero:
Im
Moltiplicando ambo i membri di quest'ultima espressione per l'unità immaginaria
j
si
ricava:
j Im
n
o
n
o
d
V̇ (x) = j Im −r I˙ (x) + j Im −jω l I˙ (x)
dx
(12.4.14)
Sommando membro a membro le equazioni in (12.4.12) e (12.4.14) si ricava:
Re
d
d
V̇ (x) + j Im
V̇ (x) =
dx
dx
n n
o
n
oo n n
o
n
oo
= Re −r I˙ (x) + j Im −r I˙ (x)
+ Re −jω l I˙ (x) + j Im −jω l I˙ (x)
ovvero:
445
12 Linee di trasmissione
d
V̇ (x) = −r I˙ (x) − jω l I˙ (x)
dx
(12.4.15)
Allo stesso modo si ricava l'equazione in (12.4.7.1) nel dominio dei fasori:
d ˙
I (x) = −g V̇ (x) − jω c V̇ (x)
dx
(12.4.16)
Le espressioni in (12.4.15) e (12.4.16) sono le equazioni dei telegrasti nel dominio dei
fasori.
Si osservi come nel dominio dei fasori, le equazioni dei telegrasti perdono la
dipendenza dal tempo t: ciò d'altra parte, era prevedibile dato che un numero complesso
è per denizione indipendente dal tempo t. Le espressioni in (12.4.15) e (12.4.16) possono
essere riscritte come segue:
d
V̇ (x) = −Z̄l I˙ (x)
dx
(12.4.17)
d ˙
I (x) = −Ȳt V̇ (x)
dx
(12.4.18)
Z̄l = r + jω l
(12.4.19)
Ȳt = g + jω c
(12.4.20)
essendo:
l'
l'
impedenza longitudinale
ammettenza trasversale
unità di lunghezza.
e
della linea di trasmissione.
E' ovvio che sono grandezze per
Le equazioni in (12.4.17) e (12.4.18) costituiscono un sistema di
equazioni dierenziali e fasoriali.
Per determinare una soluzione di tale sistema bisogna specicare le
condizioni al con-
torno, note anche come condizioni di chiusura della linea di trasmissione.
Si tratta quindi
di risolvere il problema:

d
˙

(12.4.21.1)
 dx V̇ (x) = −Z̄l I (x)
d ˙
(12.4.21.2)
dx I (x) = −Ȳt V̇ (u)


condizioni al contorno
Le incognite
(12.4.21)
˙
V̇ (x) e I(x)
sono accoppiate, il ché rende il problema di dicile risoluzione.
Il modo per rendere più semplice il problema è quello di disaccoppiare le incognite: ciò
è possibile incrementando l'ordine di derivazione delle equazioni in (12.4.21).
A seguito dell'incremento dell'ordine di derivazione si allarga inevitabilmente l'insieme
delle soluzioni del problema. Derivando rispetto a x l'equazione in (12.4.21.1) si ricava:
d ˙
d2
V̇ (x) = −Z̄l
I (x)
dx2
dx
Sostituendo (12.4.21.2) in (12.4.22) si ricava:
446
(12.4.22)
12 Linee di trasmissione
d
d2
V̇ (x) = Z̄l Ȳt
V̇ (x)
2
dx
dx
(12.4.23)
Derivando rispetto a x l'equazione in (12.4.21.2) si ricava:
d2 ˙
d
I (x) = −Ȳt
V̇ (x)
2
dx
dx
(12.4.24)
Sostituendo (12.4.21.1) in (12.4.24) si ricava:
d2 ˙
d ˙
I (x) = Z̄l Ȳt
I (x)
2
dx
dx
(12.4.25)
γ̇ 2 = Z̄l Ȳt
(12.4.26)
Ponendo:
le equazioni in (12.4.23) e (12.4.25) si scrivono:
d
d2
V̇ (x) = γ̇ 2
V̇ (x)
2
dx
dx
(12.4.27)
d2 ˙
d ˙
I (x) = γ̇ 2
I (x)
2
dx
dx
(12.4.28)
Note queste ultime due equazioni il problema in (12.4.21) diventa:
 2
d
2

(12.4.29.1)
 dx2 V̇ (x) = γ̇ V̇ (x)
2
d ˙
2
˙
I (x) = γ̇ I (x)
(12.4.29.2)
dx2


condizioni al contorno
(12.4.29)
Integrando le equazioni, il problema in (12.4.29) si scrive:

−γ̇ x + V̇ eγ̇ x

−
V̇ (x) = V̇+ e
I˙ (x) = I˙+ e−γ x + I˙− eγ̇x


condizioni al contorno
(12.4.30.1)
(12.4.30.2)
(12.4.30)
La quantità:
γ̇ =
si chiama
p
γ̇ 2 =
parametro di propagazione.
−1 . Visto che
misura in m
γ̇
p
(r + jω l) (g + jω c)
Come suggeriscono le equazioni in (12.4.30) esso si
è una funzione complessa della pulsazione
γ̇ = α (ω) + j β (ω)
essendo
α (ω)
il
(12.4.31)
parametro di attenuazione e β (ω) il parametro di fase.
Il termine
447
ω
si può scrivere:
(12.4.32)
12 Linee di trasmissione
V̇+ e−γ̇ x
si chiama
onda progressiva di tensione, mentre il termine
V̇− eγ̇ x
si chiama
onda regressiva di tensione.
(12.4.33)
Analogamente il termine
I˙+ e−γ̇ x
si chiama
onda progressiva di corrente, mentre il termine
I˙− eγ̇ x
si chiama
onda regressiva di corrente.
I termini
V̇+ , V̇− , I˙+ , I˙−
sono costanti complesse
da determinare se si conoscono le condizioni al contorno.
I risultati in (12.4.30.1) e (12.4.30.2) sono soluzioni delle equazioni in (12.4.29.1) e
(12.4.29.2). In realtà visto che l'insieme delle soluzioni del problema in (12.4.29) è più
ampio dell'insieme delle soluzioni del problema in (12.4.21), non è detto che risultati in
(12.4.30.1) e (12.4.30.2) sono anche soluzioni delle equazioni in (12.4.21.1) e (12.4.21.2).
Sostituendo (12.4.30.1) e (12.4.30.2) in (12.4.21.1) o (12.4.21.2) si ricavano le condizioni
per cui ciò avviene; sostituendo (12.4.30.1) e (12.4.30.2) in (14.4.21.1) si ricava:
d
V̇ (x) = −Z̄l I˙ (x)
dx
⇓
d V̇+ e−γ̇ x + V̇− eγ̇ x = −Z̄l I˙+ e−γ̇ x + I˙− e−γ̇ x
dx
⇓
−γ̇ V̇+ e−γ̇ x + γ̇ V̇− eγ̇ x = −Z̄l I˙+ e−γ̇ x − Z̄l I˙− e−γ̇ x
⇓
Visto che
e−γ̇ x ,
e
−γ̇ V̇+ + Z̄l I˙+ eγ̇ x + γ̇ V̇− + Z̄l I˙− e−γ̇ x = 0̇
eγ̇ x
sono positivi per ogni
x,
anchè venga fericata l'equazione in
(12.4.34) occorre che valgono le condizioni:
−γ̇ V̇+ + Z̄l I˙+ = 0̇
γ̇ V̇− + Z̄l I˙− = 0̇
448
(12.4.34)
12 Linee di trasmissione
Queste ultime due relazioni si posssono scrivere meglio come segue:
γ̇
I˙+ = V̇+
Z̄l
(12.4.35)
γ̇
I˙− = − V̇−
Z̄l
(12.4.36)
Attraverso le relazioni in (12.4.35) e (12.4.36) stiamo trovando che in realtà le costanti
da determinare non sono quattro (V̇+ ,
V̇− ,
le costanti
I˙+ , I˙−
V̇− , I˙+ , I˙− ),
bensì due: conoscendo lecostanti
V̇+ ,
sono univocamente determinate. La quantità:
γ̇
Z̄l
Essa si indica con il simboloȲc e si chiama
ha la dimensione di una ammettenza.
ammettenza caratteristica
della linea di trasmissione.
Si ha facilemente che essa vale:
γ̇
Ȳc =
=
Z̄l
s
s
s
p
Z̄l Ȳt
Z̄l Ȳt
Ȳt
g + jω c
=
=
=
2
r + jω l
Z̄l
Z̄l
Z̄l
(12.4.37)
L'inverso dell'ammettenza caratteristica della linea di trasmissione si chiama
caratteristica Z̄c
Z̄l
Z̄l
Z̄c =
=
=p
γ̇
Z̄l Ȳt
Le quantità
impedenza
della linea di trasmissione:
γ̇ , Z̄c
e
Ȳc
si chiamano
lizzando il parametro secondario
Z̄c
s
Z̄l2
=
Z̄l Ȳt
s
Z̄l
=
Ȳt
parametri secondari
s
r + jω l
g + jω c
(12.4.38)
della lineadi trasmissione. Uti-
, le relazioni in (12.4.35) e (12.4.36) si scrivono:
1
V̇+
I˙+ =
Z̄c
1
I˙− = − V̇−
Z̄c
(12.4.39)
(12.4.40)
Utilizzando i risultati in (12.4.39) e (12.4.40) è chiaro che il problema in (12.4.30) diventa:

−γ̇ x + V̇ eγ̇ x

−
V̇ (x) = V̇+ e
1
−γ
x
˙
− Z̄1 V̇− eγ̇x
I (x) = Z̄ V̇+ e
c
c


condizioni al contorno
(12.4.41.1)
(12.4.41.2)
Per risolvere il problema in (12.4.41) basta determinare le costanti
minare le costanti
V̇+
e
V̇−
(12.4.41)
V̇+
e
V̇− .
Per deter-
occorre specicare le condizioni al contorno ossia le condizioni
di chiusura della linea di trasmissione.
Nell'ipotesi che la linea di trasmissione sia di lunghezza nita
x = L,
queste relazioni
si ricavano banalmente se teniamo conto del fatto che la linea di trasmissione viene
449
12 Linee di trasmissione
Figura 12.4.1: linea di trasmissione di lunghezza nita L
alimentata da un bipolo Thevenin (serie tra il generatore ideale
mentre risulta chiuso da un carico
Z̄u
V̇g
e l'impedenza
Żg
),
come mostrato in Figura 12.4.1
Facendo riferimento al circuito mostrato in Figura 12.4.1 è evidente che le condizioni
al contorno sono:
V̇g − Z̄g I˙ (0) = V̇ (0)
(12.4.42)
− Z̄u I˙ (L) = V̇ (L)
(12.4.43)
Note queste ultime relazioni è chiaro che il problema in (12.4.41) si riscrive come segue:


V̇ (x) = V̇+ e−γ̇ x + V̇− eγ̇ x



I˙ (x) = 1 V̇ e−γ x − 1 V̇ eγ̇x
Z̄c +
Z̄c −
¯

V̇g − Z̄g I (0) = V̄ (0)


−Z̄ I˙ (L) = V̇ (L)
u
Prima di determinare le costanti complesse
azioni.
V̇+
e
(12.4.44.1)
(12.4.44.2)
V̇−
(12.4.44)
doverose sono alcune consider-
Sappiamo già che il parametro di propagazione è una funzione complessa del-
la pulsazione
ω
che si pèuò esprimere in termini del parametro di attenuazione e del
parametro di fase:
γ̇ = α (ω) + j β (ω)
(12.4.45)
Le costanti complesse si possono esprimere utilizzando la notazione polare:
V̇+ = V+ ejϕ+
(12.4.46)
V̇− = V− ejϕ−
(12.4.47)
Inserendo (12.4.45), (12.4..46) e (12.4.47) in (12.4.41.1) si ricava:
V̇ (x) = V+ ejϕ− e−(α(ω)+jβ(ω)) x + V− ejϕ− e(α(ω)+jβ(ω)) x
450
12 Linee di trasmissione
⇓
V̇ (x) = V+ e−α(ω)x ej (−β(ω)x+ϕ+ ) + V− eα(ω)x ej (β(ω)x+ϕ− )
(12.4.48)
La (12.4.48) nel dominio del tempo conduce all'espressione della tensione di linea
v (x, t)
nel caso di regime sinusoidale:
n
o
v (x, t) = Re V̇ (x) ejωt =
= Re
n
o
V+ e−α(ω)x ej (−β(ω)x+ϕ+ ) + V− eα(ω)x ej (β(ω)x+ϕ− ) ejωt =
n
o
n
o
= V+ e−α(ω)x Re ej (ωt−β(ω)x+ϕ+ ) + V− eα(ω)x Re ej (ωt+β(ω)x+ϕ− ) =
= V+ e−α(ω)x cos ωt − β (ω) x + ϕ+ + V− eα(ω)x cos ωt + β (ω) x + ϕ−
(12.4.49)
Osservando che si può scrivere:
ωt − β (ω) x = −β (x) x −
ω
t = −β (ω) (x − u t)
β (ω)
ω
ωt + β (ω) x = β (x) x +
t = β (ω) (x + u t)
β (ω)
(12.4.50)
(12.4.51)
essendo:
u=
la
ω
β (ω)
(12.4.52)
velocità di fase, la (12.4.49) si può porre come segue:
o
n
v (x, t) = Re V̇ (x) ejωt =
= V+ e−α(ω)x cos −β (ω) (x − u t) + ϕ+ +V− eα(ω)x cos β (ω) (x + u t) + ϕ−
(12.4.53)
E' evidente a questo punto che
V+ e−α(ω)x cos −β (ω) (x − u t) + ϕ+
è un'onda progressiva di tensione, mentre
V− eα(ω)x cos β (ω) (x + u t) + ϕ−
è un'onda regressiva di tensione.
451
(12.4.54)
12 Linee di trasmissione
Analogamente si trova l'espressione della corrente di linea nel caso di regime sinusoidale:
n
o
i (x, t) = Re I˙ (x) ejωt =
=
V
V+ −α(ω)x
e
cos −β (ω) (x − u t) + ϕ+ − − eα(ω)x cos β (ω) (x + u t) + ϕ−
Z̄c
Z̄c
(12.4.55)
12.4.3 I parametri secondari nel caso di linea di trasmissione non
distorcente
Il parametro di propagazione nel caso di linea di trasmissione non distorcente si scrive:
p
p
γ̇ = γ̇ 2 = (r + jω l) (g + jω c) =
r g
r
l
+ jω c
+ jω =
l
c
q
p
= l c (σ + jω) c (σ + jω) = l c (σ + jω)2
ovvero:
√
γ̇ =
l c (σ + jω)
(12.4.56)
Dalla (12.4.56) risulta evidente che il parametro di attenuazione nel caso di linea non
distorcente è
√
α (ω) =
lcσ
(12.4.57)
mentre il parametro di fase è:
√
β (ω) =
lcω =
ω
u
(12.4.58)
Attraverso (11.4.57) stiamo trovando che il parametro di attenuazione non dipende dalla
pulsazione
ω
e ciò vuol dire che una linea di trasmissione non distorcente attenua i
segnali tutti allo stesso modo ; in altri termini ciò vuol dire che non introduce distorsione
di ampiezza.
Dalla (11.4.58) risulta evidente che il parametro di fase risulta proporzioale alla pulsazione
ω
e ciò equivale a dire che la linea non introduce distorsione di fase.
L'impedenza caratteristica per una linea di trasmissione non distorcente si scrive:
s
Z̄c =
r + jω l
=
g + jω c
s
l
c
r
l
g
c
r
+ jω
l
=
= Rc
c
+ jω
(12.4.59)
Secondo (12.4.59) l'impedenza caratteristica per una linea di trasmissione non distorcente
risulta puramente reale, cioè una resistenza
Rc .
452
12 Linee di trasmissione
12.4.4 Impedenza di linea e coecienti di riessione
Il rapporto tra la tensione di linea data in (12.4.44.1) e la corrente di linea data in
(12.4.44.2), denisce l'
impedenza di linea Z̄ (x) nel punto della linea di ascissa x:
Z̄ (x) =
V̇ e−γ̇ x + V̇− eγ̇ x
V̇ (x)
= +
V̇+ −γ̇ x
V̄
I˙ (x)
e
− Z̄− eγ̇ x
Z̄
c
Il reciproco di
Z̄ (x)
c
ammettenza di linea Ȳ (x) nel punto di ascissa x:
è ovviamente l'
Ȳ (x) =
Si chiama
(12.4.60)
coeciente di riessione Γ̄V
1
Z̄ (x)
(12.4.61)
della tensione all'ascissa
x,
il rapporto tra
l'onda regressiva di tensione e l'onda progressiva di tensione:
Γ̄V (x) =
Si chiama
V̇− eγ̇ x
=
V̇+ e−γ̇ x
V̇−
V̇+
e2γ̇ x
(12.4.62)
coeciente di riessione Γ̄I della corrente all'ascissa x, il rapporto tra l'onda
regressiva di corrente e l'onda progressiva di corrente:
V̇
Γ̄I (x) =
− Z̄− eγ̇ x
C
V̇+ −γ̇ x
e
Z̄c
=−
V̇−
V̇+
e2γ̇ x
(12.4.63)
Confrontando (12.4.62) con (12.4.63) è chiaro che vale la relazione:
Γ̄I (x) = −Γ̄V (x)
Osservazione.
Valurtando (12.4.62) in
x = x1
Γ̄V (x1 ) =
Analogamente per
x = x2
V̇−
V̇+
(12.4.64)
si ottiene:
e2γ̇ x1
(12.4.65)
e2γ̇ x2
(12.4.66)
si ottiene:
Γ̄V (x2 ) =
V̇−
V̇+
Dalla (11.4.66) si trova facilmete che:
V̇−
V̇+
= Γ̄V (x2 ) e−2γ̇ x2
(12.4.67)
Sostituendo (12.4.67) in (12.4.65) si ricava la relazione:
Γ̄V (x1 ) = Γ̄V (x2 ) e2γ̇ (x2 −x1 )
453
(12.4.68)
12 Linee di trasmissione
Essendo
e2γ̇ (x2 −x1 ) 6= 0
∀ (x1 , x2 ) con x1 6= x2
risulta ovvio che se risulta:
Γ̄V (x1 ) = 0
Z̄ (x)deve
necessariamente essere:
Γ̄V (x2 ) = 0
Moltiplicando numeratore e denominatore dell'impedenza di linea
eγ̇ x
si riesce ad esprimere
V̇+
Z̄ (x)
in termini di
Z̄ (x) =
eγ̇ x
V̇+
eγ˙x
V̇+
Z̄ (x)
per il termine
Γ̄V (x) = 0:
V̇+ e−γ̇ x + V̇− eγ̇ x
V̇+ −γ̇ x
e
Z̄c
−
V̄− γ̇ x
e
Z̄c
=
V̇− 2γ̇ x
1 + V̇ e
1 + Γ̄V (x)
+
= Z̄c
=
V̄
1 − Γ̄V (x)
1
1 − V̇− e2γ̇ x
Z̄
c
+
ovvero:
Z̄ (x) = Z̄c
Si chiama
1 + Γ̄V (x)
1 − Γ̄V (x)
(12.4.69)
impedenza normalizzata Z̄n (x) rispetto all'impedenza caratteristica, l'espres-
sione:
Z̄n (x) =
Si osservi che se
Γ̄V (x) = 0,
Z̄ (x)
1 + Γ̄V (x)
=
Z̄c
1 − Γ̄V (x)
(12.4.70)
Z̄ (x)
=1
Z̄c
(12.4.71)
allora:
Z̄n (x) =
Ciò vuol dire che in qualunque ascissa x della linea, l'impedenza della linea
Z̄ (x),
risulta pari all'impedenza caratteristica della linea:
Z̄n (x) = Z̄c
Dalla denizione in (12.4.62), è evidente che
(12.4.72)
Γ̄V (x) = 0
se e solo se l'onda regressiva
risulta nulla
V̇− = 0̇
In tal caso la linea di trasmissione si dice
adattata.
(12.4.73)
Nella prossima sezione ci occuper-
emo nel dettaglio della linea di trasmissione adattata.
454
12 Linee di trasmissione
12.4.5 Linea di trasmissione adattata
Una linea di trasmissione di lunghezza nita L come quella mostrata in Figura 12.4.2 è
denita dal sistema di equazioni:


V̇ (x) = V̇+ e−γ̇ x + V̇− eγ̇ x



I˙ (x) = 1 V̇ e−γ x − 1 V̇ eγ̇x
+
−
(12.4.74.1)
(12.4.74.2)

V̇g − Z̄g I¯ (0) = V̄ (0)



Z̄ I˙ (L) = V̇ (L)
(12.4.74.3)
(12.4.74.4)
Z̄c
Z̄c
u
(12.4.74)
Figura 12.4.2: linea di trasmissione di lunghezza nita L.
La linea di trasmissione si dice adattata, sel'onda regressiva di tensione o equivalentemente di corrente risulta identicamente nulla.
Come suggeriscono le equazioni in
V̇− = 0.
carico Z̄u anchè
(12.4.74.1) e (12.4.74.2) ciò avviene se risulta
Possiamo ottenere una condizione sul
avvenga
V̇− = 0.
Per
x=L
l'equazione in (12.4.74.1) si scrive:
V̇ (L) = V̇+ e−γ̇ L + V̇− eγ̇ L
(12.4.75)
mentre l'equazione in (12.4.74.2) si scrive:
1
1
I˙ (L) =
V̇+ e−γ L −
V̇− eγ̇L
Z̄c
Z̄c
quest'ultima si può scrive pure come segue:
Z̄c I˙ (L) = V̇+ e−γ L − V̇− eγ̇L
Sottraendo alla (12.4.75) la (12.4.76) si ricava:
V̇ (L) − Z̄c I˙ (L) = 2 V̇− eγ̇ L
da cui si ottiene l'espressione di
V̇− :
V̇− =
1
V̇ (L) − Z̄c I˙ (L) e−γ̇L
2
455
(12.4.76)
12 Linee di trasmissione
Anchè possa essere
V̇− = 0
occorre che sia:
V̇ (L) − Z̄c I˙ (L) = 0
Da cui si ricava facilmente che
Z̄u =
V̇ (L)
= Żc
I˙ (L)
(12.4.77)
La (12.4.77) è nota con il nome di adattamento del carico.
trasmissione adattata l'impedenza della linea
Z̄ (x)
Nel caso di linea di
denita in (12.4.60) diventa:
Z̄ (x) = Z̄c
(12.4.78)
Ciò vuol dire che per qualunque ascissa x della linea, l'impedenza vista tra i due conduttori della linea è sempre pari a
Z̄c .
Se vale l'espressione in (12.4.78) è chiaro che
l'impedenza normalizzata data in (12.4.70) diventa:
Z̄n (x) = 1
(12.4.79)
L'equazione in (12.4.70) fornisce pure la relazione:
1 + Γ̄V (x)
=1
1 − Γ̄V (x)
Quest'ultima equazione implica che il coeciente di riessione della tensione deve è nullo:
Γ̄V (x) = 0
(12.4.80)
12.4.6 Rappresentazione della linea mediante la sintassi dei doppi bipoli
12.4.6.1 Rappresentazione attraverso la matrice di trasmissione diretta
La linea di trasmissione mostrata in Figura 12.4.2 è equivalante al doppio bipolo mostrato
in Figura 11.1.32 purchè si pone:


V̇1 = V̇ (0)



I˙ = I˙ (0)
1
V̇2 = V̇ (L)



−I˙ = I˙ (L)
2
(12.4.81)
Sotto queste ipotesi allora è possibile fare rifermento al circuito mostrato in Figura
12.4.3.
Utilizzando le posizioni in (12.4.81), il sistema di equazioni dato in (12.4.74) si scrive:


V̇ (x) = V̇+ e−γ̇ x + V̇− eγ̇ x



I˙ (x) = 1 V̇ e−γ x − 1 V̇ eγ̇x
Z̄c +
Z̄c −
˙
V̇g − Z̄g I1 = V̇1



−Z̄ I˙ = V̇
u 2
2
456
(12.4.82.1)
(12.4.82.2)
(12.4.82.3)
(12.4.82.4)
(12.4.82)
12 Linee di trasmissione
Figura 12.4.3: linea di trasmissione di lunghezza nita L.
Per
x=L
le equazioni in (12.4.82.1) e (12.4.82.2) si scrivono:
V̇2 = V̇+ e−γ̇ L + V̇− eγ̇
(12.4.83)
− I˙2 Z̄c = V̇+ e−γ L − V̇− eγ̇L
(12.4.84)
Sommando membro a membro le equazioni in (12.4.83) e (12.4.84) si ottiene l'espressione
della costante complessa
V̇+ :
V̇2 − I˙2 Z̄C = 2 V̇+ e−γ̇ L =⇒
=⇒ V̇+ =
1
V̇2 − I˙2 Z̄C eγ̇ L
2
(12.4.85)
Sottraendo membro a membro le equazioni in (12.4.83) e (12.4.84) si ottiene l'espressione
della costante complessa
V̇− :
V̇2 + I˙2 Z̄C = 2 V̇− eγ̇ L =⇒
=⇒ V̇− =
1
V̇2 + I˙2 Z̄C e−γ̇ L
2
(12.4.86)
Sostituendo (12.4.85) e (12.4.86) in (12.4.82.1) e (12.4.82.2) si ottiene:

V̇ (x) =
I˙ (x) =
γ̇ (L−x) −e−γ̇(L−x)
eγ̇ (L−x) +e−γ̇ (L−x)
V̇2 + e
Z̄c −I˙2
2
2
γ̇
(L−x)
−
γ̇
(L−x)
γ̇
(L−x)
−
γ̇
(L−x)
1 e
−e
e
+e
˙
V̇
+
−
I
2
2
2
2
Z̄c
ossia:

V̇ (x) = cosh [γ̇ (L − x)] V̇2 + Z̄c sinh [γ̇ (L − x)] −I˙2
I˙ (x) = 1 sinh [γ̇ (L − x)] V̇2 + cosh [γ̇ (L − x)] −I˙2
Z̄c
457
12 Linee di trasmissione
In forma matriciale ovviamente si ha:
Ponendo
V̇ (x)
I˙ (x)
x=0
dal sistema in (12.4.87) si ottiene:
=
cosh [γ̇ (L − x)] Z̄c sinh [γ̇ (L − x)]
1
sinh [γ̇ (L − x)] cosh [γ̇ (L − x)]
Z̄
c
V̇1
I˙1
=
cosh [γ̇ L] Z̄c sinh [γ̇ L]
1
sinh [γ̇ L] cosh [γ̇ L]
Z̄
c
V̇2
−I˙2
V̇2
−I˙2
(12.4.87)
(12.4.88)
essendo
h i Ȧ Ḃ Ṫ =
=
Ċ Ḋ
cosh [γ̇ L] Z̄c sinh [γ̇ L]
1
sinh [γ̇ L] cosh [γ̇ L]
Z̄
(12.4.89)
c
la matrice di trasmissione diretta della linea di trasmissione di lunghezza nita L.
E' intuitivo pensare che la linea di trasmissione rappresenta un doppio bipolo simmetrico. Questo fatto si prova subito poichè la matrice di trasmissione diretta data in
(12.4.89) soddisfa le condizioni di simmetria:
(
ȦḊ − Ḃ Ċ = 1
Ȧ = Ḋ
(12.4.90)
Risolvendo il sistema:
"
# "

V̇1


=

 I˙
1
cosh [γ̇ L] Z̄c sinh [γ̇ L]
1
sinh [γ̇ L] cosh [γ̇ L]
Z̄
#"
c
V̇2
−I˙2
#

V̇g − Z̄g I˙1 = V̇1



−Z̄ I˙ = V̇
u 2
(12.4.91)
2
si determinano univocamente tensione e corrente a inizio linea e a ne linea.
12.4.6.2 Rappresentazione attraverso la matrice di trasmissione inversa
Per
x=0
le equazioni in (12.4.82.1) e (12.4.82.2) si scrivono:
V̇1 = V̇+ + V̇−
(12.4.92)
I˙1 Z̄c = V̇+ − V̇−
(12.4.93)
Sommando membro a membro le equazioni in (12.4.92) e (12.4.93) si ottiene l'espressione
della costante complessa
V̇+ :
V̇1 + I˙1 Z̄C = 2 V̇+ =⇒
=⇒ V̇+ =
1
V̇1 + I˙1 Z̄C
2
458
(12.4.94)
12 Linee di trasmissione
Sottraendo membro a membro le equazioni in (12.4.92) e (12.4.93) si ottiene l'espressione
della costante complessa
V̇− :
V̇1 − I˙1 Z̄C = 2 V̇− =⇒
=⇒ V̇− =
1
V̇1 − I˙1 Z̄C
2
(12.4.95)
Sostituendo (12.4.94) e (12.4.95) in (12.4.82.1) e (12.4.82.2) si ottiene:
(
γ̇ x
−γ̇ x
γ̇ x
−γ̇ x
V̇ (x) = e +e
V̇1 − e −e
Z̄c I˙1
2
2
γ̇
x
−
γ̇
x
γ̇
x
−γ̇ x
I˙ (x) = − Z̄1 e −e
V̇1 + e +e
I˙1
2
2
c
ossia:
(
V̇ (x) = cosh [γ̇ x] V̇1 − Z̄c sinh [γ̇ x] I˙1
I˙ (x) = − Z̄1 sinh [γ̇ x] V̇1 + cosh [γ̇ x] I˙1
c
In forma matriciale ovviamente si ha:
Ponendo
V̇ (x)
I˙ (x)
x=L
=
− Z̄1
c
cosh [γ̇ x]
−Z̄c sinh [γ̇ x]
sinh [γ̇ (L − x)]
cosh [γ̇ x]
V̇1
I˙1
(12.4.96)
dal sistema in (12.4.96) si ottiene:
V̇2
−I˙2
=
cosh [γ̇ L]
−Z̄c sinh [γ̇ L]
1
− Z̄ sinh [γ̇ L]
cosh [γ̇ L]
c
V̇1
I˙1
(12.4.97)
essendo
h 0 i Ȧ0
Ṫ =
0
Ċ
0
Ḃ
0
Ḋ
=
cosh [γ̇ L]
−Z̄c sinh [γ̇ L]
1
− Z̄ sinh [γ̇ L]
cosh [γ̇ L]
(12.4.98)
c
la matrice di trasmissione inversa della linea di trasmissione di lunghezza nita L.
Visto che la linea di trasmissione è un doppio bipolo simmetrico, ammette sia la rappresentazione che fa uso della matrice di trasmissione diretta che quella che fa su della
matrice di trasmissione inversa. Si prova immediatamente che
h i h 0 i−1
Ṫ = Ṫ
Infatti:
−1
cosh [γ̇ L]
−Z̄c sinh [γ̇ L]
=
− Z̄1 sinh [γ̇ L]
cosh [γ̇ L]
c
t
1
cosh [γ̇ L]
sinh [γ̇ L]
1
Z̄
c
=
=
cosh2 [γ̇ L] − sinh2 [γ̇ L] Z̄c sinh [γ̇ L] cosh [γ̇ L]
h i
cosh [γ̇ L] Z̄c sinh [γ̇ L]
=
= Ṫ
1
sinh [γ̇ L] cosh [γ̇ L]
Z̄
h 0 i−1 =
Ṫ
c
459
(12.4.99)
12 Linee di trasmissione
12.4.6.3 Rappresentazione attraverso la matrice delle impedenze
E' possibile determinare la rappresentazione attraverso la matrice delle impedenze a
partire dalla rappresentazione attraverso la matrice di trasmissione inversa. Le equazioni
in (12.4.97) in forma scalare si scrivono come segue:
(
˙
V̇2 = cosh [γ̇ L] V̇1 − Z̄c sinh [γ̇ L]
h I1 i
−I˙2 = − 1 sinh [γ̇ L] V̇1 + cosh γ ˙L I˙1
(12.4.100)
Z̄c
Vistoche la matrice delleimpedenzeprevede la orrente
bisogna moltiplicare per
−1
I˙2
entrante nel doppio bipolo,
la seconda equazione del sistema in (12.4.100):
(
V̇2 = cosh [γ̇ L] V̇1 − Z̄c sinh h[γ̇ L]iI˙1
I˙2 = 1 sinh [γ̇ L] V̇1 − cosh γ ˙L I˙1
(12.4.101.1)
(12.4.101)
(12.4.101.2)
Z̄c
Dal sistema in (12.4.101) si ricava la rappresentazione attraverso la matrice delle impedenze purchè si espimano le tensioni
(12.4.101.2) si ricava la tensione
V̇1
V̇1
e
V̇2
in funzione delle correnti
in funzione delle correnti
V̇1 = Z̄c coth [γ̇ L] I˙1 + Z̄c
e
e
I˙1
e
I˙2 .
Dalla
I˙2 :
1
I˙2
sinh [γ̇ L]
(12.4.102)
V̇1
in funzione delle correnti
Inserendo (12.4.102) in (12.4.101.1) si ricava la tensione
I˙1
I˙1
I˙2 :
V̇2 = Z̄c
1
[γ̇ L] I˙1 + Z̄c coth [γ̇ L] I˙2
sinh [γ̇ L]
(12.4.103)
Le equazioni in (12.4.102) e (12.4.103) si possono compattare come segue:
V̇1
V̇2
"
= Z̄c
coth [γ̇ L]
1
sinh[γ̇ L]
1
sinh[γ̇ L]
coth [γ̇ L]
#
I˙1
I˙2
(12.4.104)
L'espressione in (12..4.104) è la rappresentazione della linea di trasmissione attraverso
la matrice delle impedenze:
"
#
h i Ż
coth [γ̇ L] sinh[1γ̇ L]
I˙1
11 Ż12
Ż =
= Z̄c
1
coth [γ̇ L]
Ż21 Z˙22
I˙2
sinh[γ̇ L]
(12.4.105)
12.4.6.4 Rappresentazione attraverso la matrice delle ammettenze
Invertendo la (12.4.105) si determina in maniera immediata la matrice delle ammettenze:
h i h i−1
Ẏ = Ż
=
"
1
n
Z̄c2 coth2 [γ̇ L] −
1
sinh [γ̇ L]
2
460
o Z̄c
coth [γ̇ L] − sinh[1γ̇ L]
− sinh[1γ̇ L] coth [γ̇ L]
#t
=
12 Linee di trasmissione
"
1
=
Z̄c
n
cosh2 [γ̇ L]−1
sinh2 [γ̇ L]
1
=
Z̄c
"
o
coth [γ̇ L] − sinh[1γ̇ L]
− sinh[1γ̇ L] coth [γ̇ L]
coth [γ̇ L] − sinh[1γ̇ L]
− sinh[1γ̇ L] coth [γ̇ L]
#
=
#
(12.4.106)
Quindi la rappresentazione della linea di trasmissione attraverso la matrice delle ammettenze è la seguente:
I˙1
I˙2
"
1
=
Z̄c
coth [γ̇ L] − sinh[1γ̇ L]
− sinh[1γ̇ L] coth [γ̇ L]
#
V̇1
V̇2
(12.4.107)
Le rappresentazioni in (12.4.104) e (12.4.107) permettono di desrivere la linea di
trasmissione mostrata in Figura 12.4.3 con due circuiti equivalenti. In particolare la rap-
circuito equivalente a T
circuito equivalente a Π.
presentazione in (12.4.104) porta al
in (12.4.107) porta al
12.4.6.5 Circuito equivalente a
mentre la rappresentazione
T
La rappresentazione in (12.4.104) in forma scalare si scrive:
(
V̇1 = Z̄c coth [γ̇ L] I˙1 + Z̄c sinh[1γ̇ L] I˙2
V̇2 = Z̄c 1 I˙1 + Z̄c coth [γ̇ L] I˙2
(12.4.108)
sinh[γ̇ L]
Le equazioni in (12.4.108) si possono scrivere pure come segue:
(
V̇1 = Z̄c coth [γ̇ L] I˙1 −
V̇2 = Z̄c I˙1 + Z̄c
sinh[γ̇ L]
Z̄c
˙
sinh[γ̇ L] I1
+
Z̄c
˙
sinh[γ̇ L] I2
+
˙ + Z̄c coth [γ̇ L] I˙2 −
sinh[γ̇ L] I2
Z̄c
˙
sinh[γ̇ L] I1
Z̄c
˙
sinh[γ̇ L] I2
ossia:

n
o
n
o
Z̄c
1
˙
˙
˙
V̇1 = Z̄c coth [γ̇ L] −
I1 + sinh[γ̇ L] I1 + I2
n
osinh[γ̇ L]n
o
Z̄
1
c
V̇2 =
I˙1 + I˙2 + Z̄c coth [γ̇ L] −
I˙2
sinh[γ̇ L]
(12.4.109)
sinh[γ̇ L]
Tenendo conto che vale l'identità:
coth δ −
1
δ
= tanh
sinh δ
2
le equazioni in (12.4.109) si scrivono:

h i
n
o
˙1 + I˙2
V̇1 = Z̄c tanh γ̇ L I˙1 + Z̄c
I
n2
o sinh[γ̇ L] h i
γ̇ L ˙
˙
˙
V̇2 = Z̄c
I2
2
sinh[γ̇ L] I1 + I2 + Z̄c tanh
Denendo le impedenze:
461
(12.4.110)
12 Linee di trasmissione
Z̄a = Z̄c tanh
Z̄b = Z̄c
γ̇ L
2
(12.4.111)
1
sinh [γ̇ L]
(12.4.112)
le equazioni in (12.4.110) si scrivono:

o
n
V̇1 = Z̄a I˙1 + Z̄b I˙1 + I˙2
n
o
V̇2 = Z̄b I˙1 + I˙2 + Z̄a I˙2
(12.4.113)
Le equazioni in (12.4.113) conducono al circuito equivalente a
T
mostrato in Figura
12.4.4:
Figura 12.4.4: circuito equivalente a
12.4.6.6 Circuito equivalente a
T
Π
La rappresentazione in (12.4.107) in forma scalare si scrive:
(
I˙1 = Z̄1 coth [γ̇ L] V̇1 − Z̄1 sinh[1γ̇ L] V̇2
c
C
I˙2 = − Z̄1 sinh[1γ̇ L] V̇1 + Z̄1 coth [γ̇ L] V̇2
c
(12.4.114)
c
Le equazioni in (12.4.114) si possono scrivere pure come segue:
(
I˙1 = Z̄1 coth [γ̇ L] V̇1 − Z̄1 sinh[1γ̇ L] V̇1 − Z̄1 sinh[1γ̇ L] V̇2 + Z̄1 sinh[1γ̇ L] V̇1
c
c
c
c
I˙2 = − Z̄1 sinh[1γ̇ L] V̇1 + Z̄1 sinh[1γ̇ L] V̇2 + Z̄1 coth [γ̇ L] V̇2 − Z̄1 sinh[1γ̇ L] V2
c
c
c
c
ossia:

I˙1 =
n
o
n
o
coth [γ̇ L] − sinh[1γ̇ L] V̇1 + Z̄1 sinh[1γ̇ L] V̇1 − V̇2
n
o
n c
o
1
1
1
I˙2 = − 1
V̇
−
V̇
+
coth
[
γ̇
L]
−
1
2
sinh[γ̇ L] V̇2
Z̄ sinh[γ̇ L]
Z̄
1
Z̄c
c
c
Tenendo conto che vale l'identità:
462
(12.4.115)
12 Linee di trasmissione
coth δ −
1
δ
= tanh
sinh δ
2
le equazioni in (12.4.115) si scrivono:

I˙1 =
1
Z̄c
tanh
I˙2 = − 1
Z̄
c
h
i
γ̇ L
2 nV̇1
1
sinh[γ̇ L]
+
V̇1 −
n
o
1
1
V̇2
sinh[γ̇ L] V̇1 −
Z̄c o
h i
γ̇
V̇2 + Z̄1 tanh 2L V̇2
c
(12.4.116)
Denendo le ammettenze:
1
γ̇ L
Ȳa =
tanh
2
Z̄c
Ȳb =
(12.4.117)
1
1
Z̄c sinh [γ̇ L]
(12.4.118)
le equazioni in (12.4.116) si scrivono:

n
o
I˙1 = Ȳa V̇1 + Ȳb V̇1 − V̇2
n
o
I˙2 = −Ȳb V̇1 − V̇2 + Ȳa V̇2
(12.4.119)
Le equazioni in (12.4.113) conducono al circuito equivalente a
Π
mostrato in Figura
12.4.5:
Figura 12.4.5: circuito equivalente a
T
12.4.6.7 Linea di trasmissione corta
I circuiti equivalenti a
T
e a
Π
sono di dicile realizzazione nel caso generale di linea di
trasmissione in quanto non risulta possibile realizzare le impedenze denite in (12.4.111) e
(12.4.112) ( o le ammettenze denite in (12.4.117) e (12.4.118)) utilizzando solo elementi
a parametri concentrati, perchè questi presentano fattori iperbolici.
I circuiti equivalenti a
T
e a
Π
sono molto utili nel caso di
Per una linea di trasmissione corta infatti le impedenze
linea di trasmissione corta.
Z̄a , Z̄b
o le ammettenze
possono realizzare utilizzando elementi a parametri concentrati.
463
Ȳa , Ȳb
si
12 Linee di trasmissione
Una linea di trasmissione di lunghezza nita Lcome quella mostrata in Figura 12.4.3
si dice
corta
se risulta:
|γ̇ L| << 1
Nel caso di linea di trasmissione corta, limpedenza
(12.4.120)
Z̄a
denita in (12.4.111) si scrive:
Z̄l γ̇ L
L
γ̇ L
γ̇ L
' Z̄c
=
= Z̄l
Z̄a = Z̄c tanh
2
2
γ̇ 2
2
mentre l'impedenza
Z̄b
(12.4.121)
denita in (12.4.112) si scrive:
Z̄b = Z̄c
=
Analogamente le ammettenze
1
1
' Z̄c
=
sinh [γ̇ L]
γ̇ L
Z̄l
Z̄l 1
1
=
=
γ̇ γ̇ L
Z̄l Ȳt L
Ȳt L
Ȳa
e
Ȳb
(12.4.122)
nel caso di linea di trasmissione corta si scrivono:
Ȳa =
L
Ȳt
2
(12.4.123)
Ȳb =
1
Z̄l L
(12.4.124)
12.4.6.8 Impedenza di ingresso di una linea di trasmissione
Consideriamo la linea di trasmissione di lunghezza nita L mostrata in Figura 12.4.3 e
supponiamo che questa sia rappresentata dalla matrice delle impedenze. Si può assumere
allora la linea di trasmisssione come un doppio bipolo e ridisegnare il circuito mostrato
in Figura 12.4.3 come mostrato inFigura 12.4.6
Figura 12.4.6: linea di trasmissione di lunghezza nita L.
Si vuole determinare l'impedenza d'ingresso
464
Z̄110 .
12 Linee di trasmissione
Ponendo
Z̄110 = Ż1
e
Z̄u = Ż2
l'espressione in (11.2.9) fornisce l'espressione dell'impe-
denza d'ingresso:
h i
det Ż + Ż11 Z̄u
Ż110 ==
(12.4.125)
Ż22 + Z̄u
Da (12.4.105) si deduce facilmente che:
(
Ż11 h= iŻ22 = Żc coth [γ̇ L]
det Ż = Żc2
(12.4.126)
Note le relazioni in (12.4.126), l'espressione in (12.4.125) si scrive:
Ż110 =
Żc2 + Żc Żu coth [γ̇ L]
Żc coth [γ̇ L] + Z̄u
(12.4.127)
Tenendo conto che:
coth [γ̇ L] =
cosh [γ̇ L]
sinh [γ̇ L]
(12.4.128)
l'espressione in (12.4.128) si scrive:
Ż110 = Żc
Żc sinh [γ̇ L] + Z̄u cosh [γ̇ L]
Żc cosh [γ̇ L] + Z̄u sinh [γ̇ L]
(12.4.129)
Se la linea di trasmissione è di lunghezza x, allora limpedenza d'ingresso vale:
Ż110 = Żc
Żc sinh [γ̇ x] + Z̄u cosh [γ̇ x]
Żc cosh [γ̇ x] + Z̄u sinh [γ̇ x]
(12.4.130)
12.4.7 Linea di trasmisssione ideale
La linea di trasmissione ideale è una linea senza perdite:
r=g=0
Utilizzando (12.4.131) il parametro di propagazione
γ̇ =
(12.4.131)
γ̇
si scrive:
p
p
√
(r + jω l) (g + jω c) = j 2 ω 2 l c = jω l c
(12.4.132)
Dalla relazione in (12.4.132) si deduce che il parametro di attenuazione vale:
α (ω) = 0
(12.4.133)
√
β (ω) = ω l c
(12.4.134)
mentre il parametro di fase vale:
465
12 Linee di trasmissione
Utilizzando (12.4.131) l'impedenza caratteristica vale:
s
Z̄c =
r + jω l
=
g + jω c
r
l
= Rc
c
(12.4.135)
Utilizzando (12.4.132), (12.4.134) e (12.4.135), l'equazione in (12.4.130) si scrive:
Ż110 = Rc
Rc sinh [jβ (ω) x] + Z̄u cosh [jβ (ω) x]
Rc cosh [jβ (ω) x] + Z̄u sinh [jβ (ω) x]
Dividendo numeratore e denominatore per
Ż110 = Rc
cosh [jβ (ω) x],
(12.4.136)
si ha:
Rc tanh [jβ (ω) x] + Z̄u
Rc + Z̄u tanh [jβ (ω) x]
(12.4.137)
Tenendo conto che vale l'identità:
tanh [jδ] = j tan [δ]
si ha:
Ż110 = Rc
j Rc tan [β (ω) x] + Z̄u
Rc + j Z̄u tan [β (ω) x]
(12.4.138)
Si osservi come l'impedenza d'ingresso per una linea di trasmissione ideale dipenda da l,
c,
ω
e x. Fissati i parametri primari l e c e la pulsazione
ω , l'impedenza d'ingresso risulta
essere una funzione della lunghezza x della linea. Due casi particolarmente signicativi si
Z̄
=
0
u
Z̄u = +∞ .
hanno quando la linea di trasmissione ideale viene chiusa con un cortocircuito
oppure quando la linea di trasmissione ideale viene lasciata aperta
Se
Z̄u = 0
la (12.4.138) si scrive:
Ż110 = j Rc tan [β (ω) x]
Dividendo ambo i membri della (12.4.139) per la resistenza caratteristica
(12.4.139)
Rc
si ottiene
l'impedenza d'ingresso normalizzata
Ricordando inne che
β=
Ż110
n
=
Ż110
= j tan [β (ω) x]
Rc
(12.4.140)
2π
λ la (12.4.140) si scrive:
Ż110
n
Ż110
2π
= j tan
x
=
Rc
λ
(12.4.141)
Attraverso (12.4.141) stiamo scoprendo che una linea di trasmissione ideale chiusa in
cortocircuito presenta un'impedenza d'ingresso normalizzata uguale ad una reattanza che
può essere capacitiva o induttiva a seconda della lunghezza x della linea di trasmissione.
In Figura viene mostrato il graco dell'impedenza normalizzata indicata in (12.4.141)
466
12 Linee di trasmissione
Figura 12.4.7: impedenza d'ingresso normalizzata per linea di tramissione chiusa in
cortocircuito
Si osservi come per
0≤x≤
λ
4
essa è induttiva, mentre per
λ
λ
≤x≤
4
2
e una reattanza capacitiva. Questo fenomeno non avviene con i doppi bipoli a parametri
concentrati.
Se
Z̄u = +∞
la (12.4.138) si scrive:
Ż110 = −j Rc cot [β (ω) x]
(12.4.142)
Dividendo ambo i membri della (12.4.139) per la resistenza caratteristica
Rc
si ottiene
l'impedenza d'ingresso normalizzata
Ricordando inne che
β=
Ż110
n
=
Ż110
= −j cot [β (ω) x]
Rc
(12.4.143)
2π
λ la (12.4.143) si scrive:
Ż110
n
Ż110
2π
=
= −j cot
x
Rc
λ
(12.4.144)
Anche in questo caso l'impedenza d'ingresso normalizzata è una reattanza che può
essere capacitiva o induttiva a seconda della lunghezza x della linea di trasmissione.
In Figura viene mostrato il graco dell'impedenza d'ingresso normalizzata indicata in
(12.4.144)
Figura 12.4.8: impedenza d'ingresso normalizzata per linea di tramissione chiusa in
cortocircuito
Rispetto al caso precedente il comportamento d'ingresso normalizzata è completamente
speculare.
Vogliamo adesso determinare la tensione di linea e la corrente di linea per una linea di
trasmissione ideale nel caso in cui questa sia chiusa con un cortocircuito
Z̄u = +∞ .
Z̄u = 0 implica V̇2 = 0
Z̄u = 0
o con
un circuito aperto
La condizione
mentre la condizione
Z̄u = +∞
implica
I˙2 = 0.
Visto che durante l'analisi dobbiamo imporre delle condizioni sulla porta 2 della linea
di trasmissione possiamo rappresentarla attraverso le equazioni date in (12.4.87). Tali
equazioni valgono nel caso generale e specicano i fasori della tensione di linea e della
467
12 Linee di trasmissione
corrente di linea alla generica ascissa x.
equazioni vanno riscritte tenedo conto che
V̇ (x)
I˙ (x)
=
Nel caso di linea di trasmissione ideale tali
√
γ̇ = j β = j ω l c
e
Z̄c =
q
l
c , quindi si ha:
Z̄c sinh [j β (L − x)]
cosh j̇ β (L − x)
V̇2
1
sinh [j β (L − x)] cosh [j β (L − x)]
−I˙2
Z̄c
(12.4.145)
ovvero
(
V̇ (x) = cosh [j β (L − x)] V̇2 − Rc sinh [j β (L − x)] I˙2
I˙ (x) = R1c sinh [j β (L − x)] V̇2 − cosh [j β (L − x)] I˙2
La condizione
Z̄u = 0
implica
V̇2 = 0
e le equazioni in (12.4.146) si scrivono:
(
V̇ (x) = −Rc sinh [j β (L − x)] I˙2
I˙ (x) = − cosh [j β (L − x)] I˙2
Tenendo conto che
(12.4.146)
−I˙2 = I˙ (L) le equazioni in (12.4.147) si scrivono:
(
V̇ (x) = Rc sinh [j β (L − x)] I˙ (L)
I˙ (x) = cosh [j β (L − x)] I˙ (L)
(12.4.147)
(12.4.148)
Ricordando le identità
(
sinh [j δ] = j sin [δ]
cosh [j δ] = cos [δ]
le equazioni in (12.4.148) si scrivono:
(
V̇ (x) = j Rc sin [β (L − x)] I˙ (L)
I˙ (x) = cos [β (L − x)] I˙ (L)
Supponiamo per semplicità che
(12.4.149)
I˙ (L) sia a fase nulla, cioè supponiamo sia I˙ (L) = I (L)
e riscriviamo le equazioni in (12.4.149):
(
V̇ (x) = j Rc sin [β (L − x)] I (L)
I˙ (x) = cos [β (L − x)] I (L)
(12.4.150)
Queste ultime nel dominio del tempo si scrivono:
(
v (x, t) = Rc I (L) sin [β (L − x)] cos ωt + π2
i (x, t) = I (L) cos [β (L − x)] cos (ωt)
(12.4.151)
Si osservi innanzitutto che la tensione di linea e la corrente di linea sono sfasate di
90°. Notiamo pure che sono onde stazionarie, cioè onde che non si propagano al variare
del tempo infatti se osserviamo le relazioni in (12.4.151) la dipendenza dal tempo t serve
solo a modulare l'ampiezza della tensione e della corrente di linea.
468
12 Linee di trasmissione
Figura 12.4.9: onda stazionaria
Se per esempio
t = t1 ,
x = x1
è un punto di massimoperla corrente di linea
lo è anche all'istante
La condizione
Z̄u = +∞
t = t2
implica
i (x, t)
all'istante
come mostrato in Figura 12.4.9
I˙2 = 0
e le equazioni in (12.4.146) si scrivono:
(
V̇ (x) = cosh [j β (L − x)] V̇2
I˙ (x) = 1 sinh [j β (L − x)] V̇2
(12.4.152)
Rc
Tenendo conto che
V̇2 = V̇ (L) le equazioni in (12.4.152) si scrivono:
(
V̇ (x) = cosh [j β (L − x)] V̇ (L)
I˙ (x) = R1c sinh [j β (L − x)] V̇ (L)
(12.4.153)
Ricordando le identità
(
sinh [j δ] = j sin [δ]
cosh [j δ] = cos [δ]
le equazioni in (12.4.153) si scrivono:
(
V̇ (x) = cos [β (L − x)] V̇ (L)
I˙ (x) = j R1c sin [β (L − x)] V̇ (L)
Supponiamo per semplicità che
V (L)
V̇ (L)
(12.4.154)
sia a fase nulla, cioè supponiamo sia
V̇ (L) =
e riscriviamo le equazioni in (12.4.154):
(
V̇ (x) = cos [β (L − x)] V (L)
I˙ (x) = j R1c sin [β (L − x)] V (L)
(12.4.155)
Queste ultime nel dominio del tempo si scrivono:
(
v (x, t) = V (L) cos [β (L − x)] cos (ωt)
i (x, t) = R1c V (L) sin [β (L − x)] cos ωt + π2
(12.4.156)
Anche in questo caso tensione e corrente di linea sono onde stazionarie sfasate di 90°
tra di loro.
12.4.8 Potenze in regime sinusoidale
Una linea di trasmissione di lunghezza nita L come quella mostrata in Figura 12.4.3 è
denita dal sistema di equazioni:
469
12 Linee di trasmissione


V̇ (x) = V̇+ e−γ̇ x + V̇− eγ̇ x



I˙ (x) = 1 V̇ e−γ x − 1 V̇ eγ̇x
+
−
(12.4.157.1)
(12.4.157.2)

V̇g − Z̄g I˙ (0) = V̇ (0)



Z̄ I˙ (L) = V̇ (L)
(12.4.157.3)
(12.4.157.4)
Z̄c
Z̄c
u
(12.4.157)
La potenza complessa è denita dalla relazione:
1
Ȧ = V̇ (x) I˙ (x)∗
2
(12.4.158)
Utilizzando (12.4.157.1) e (12.4.157.2),la (12.4.158) si scrive:
1
Ȧ = V̇ (x) I˙ (x)∗ =
2
1 1
−γ̇ x
γ̇ x
∗ −γ̇ ∗ x
∗ γ̇x
=
V̇+ e
+ V̇− e
V̇+ e
− V̇− e
2
Z̄c∗
(12.4.159)
Tenendo conto delle relazioni:
(
γ̇ = α + jβ
Z̄c = Zc ejϕc
γ̇ ∗ = α − jβ
Z̄c∗ = Zc e−jϕc
(12.4.160)
l'espressione in (12.4.159) si scrive:
Ȧ =
=
1 V̇+ e−α x e−jβ x + V̇− eα x ejβ x + V̇+∗ e−α x ejβ x − V̇−∗ eα x ejβ x ejϕc =
2Zc
1 V̇+ V̇+∗ e−2α x − V̇+ V̇−∗ e−j2β x + V̇− V̇+∗ ej2β x − V̇− V̇−∗ e2α x ejϕc
2Zc
(12.4.161)
Tenedo conto delle relazioni:
(
V̇+ = V+ ejϕ+
V̇− = V− ejϕ−
V̇+∗ = e−jϕ+
V̇−∗ = V̇− e−jϕ−
(12.4.162)
si ha facilmente che:
(
V̇+ V̇+∗ = V+2
V̇− V̇−∗ = V−2
Inoltre i numeri complessi
V̇+ V̇−∗ e−j2β x
e
V̇− V̇+∗ ej2β x
(12.4.163)
sono uno il coniugato dell'altro,
quindi per una nota proprietà dei numeri complessi si può scrivere:
V̇+ V̇−∗ e−j2β x − V̇− V̇+∗ ej2β x = j 2Im V̇− V̇+∗ ej2β x
470
(12.4.164)
12 Linee di trasmissione
Utilizzando le posizioni in (12.4.162), l'espressione in (12.4.164) si scrive:
V̇+ V̇−∗ e−j2β x − V̇− V̇+∗ ej2β x = j 2Im V− V+ e−j(ϕ+ −ϕ− ) ej2β x
Denendo la fase
δ = ϕ+ − ϕ−
, quest'ultima espressione si scrive:
V̇+ V̇−∗ e−j2β x − V̇− V̇+∗ ej2β x = j 2Im V− V+ ej(2β x−δ) =
= j 2V− V+ sin (2β x − δ)
(12.4.165)
Sostituendo i risultati in (12.4.163) e (12.4.165), l'espressione in (12.4.161) si scrive:
Ȧ =
1
V+2 e−2α x − V−2 e2α x + j2V− V+ sin (2β x − δ) (cos ϕc + j sin ϕc )
2Zc
(12.4.166)
Separando la parte reale da quella immaginaria si ricavano le espressioni della potenza
attiva P e della potenza reattiva Q:
n o
1
P = Re Ȧ =
2Zc
V+2 e−2α x − V−2 e2α x cos ϕc − 2V− V+ sin (2β x − δ) sin ϕc
(12.4.167)
n o
1
Q = Im Ȧ =
2Zc
V+2 e−2α x − V−2 e2α x sin ϕc + 2V− V+ sin (2β x − δ) cos ϕc
(12.4.168)
12.4.8.1 Linea di trasmissione non distorcente
Per una linea di trasmissione non distorcente si ha che
sin ϕc = 0
e
cos ϕc = 1,
Z̄c =
q
l
c
= Rc
e ciò implica che
quindi per una linea di trasmissione non distorcente la potenza
attiva e quella reattiva valgono rispettivamente:
Pn.d. =
1
V+2 e−2α x − V−2 e2α x
2Rc
(12.4.169)
1
V+ V− sin (2β x − δ)
Rc
(12.4.170)
Qn.d. =
Il pedice n.d. sta per non distorcente.
La potenza attiva
Pn.d.
conta di due contributi di potenza:
quello dovuto all'onda
progressiva e quello dovuto all'onda regressiva in una certa sezione x della linea.
potenza reattiva
Qn.d.
La
è invece interpretabile come un termine di interferenza.
Se la linea di trasmissione non distorcente è pure adattata (V̇−
= 0),
le relazioni in
(12.4.169) e (12.4.70) si scrivono:
Pn.d. =
1 2 −2α x
V e
2Zc +
Qn.d. = 0
471
(12.4.171)
(12.4.172)
12 Linee di trasmissione
12.4.8.2 Linea di trasmissione adattata
Se la linea di trasmissione è adattata (V̇−
= 0),
le relazioni in (12.4.167) e (12.4.68) si
scrivono:
P =
1 2 −2α x
V e
cos ϕc
2Zc +
(12.4.173)
Q=
1 2 −2α x
sin ϕc
V e
2Zc +
(12.4.174)
Consideriamo una linea di trasmissione generica caratterizzata da una impedenza
Z̄c
e
una linea di trasmissione non distorcente caratterizzata da una resistenza caratteristica
Rc .
Se il modulo dell'impedenza
Z̄c
della linea di trasmissione generica coincide con la
resistenza caratteristica della linea di trasmissione non distorcente:
Zc = R c
12.4.8.3 Linea di trasmissione ideale
12.5 Linee di trasmissione in regime transitorio
12.6 Linee di trasmissione multiconduttori
12.7 Applicazioni
472
(12.4.175)
13 Problema di campo quasi stazionario
473
14 Circuiti trifase
474
15 Cenni sulle macchine elettriche
475
16 Appendice A: Teoria delle
distribuzioni
476
17 Appendice B: Trasformata di Fourier
nel senso delle distribuzioni
477
18 Appendice C: Trasformata di Laplace
nel senso delle distribuzioni
478