Doppi Bipoli - Polinformatici

Doppi Bipoli
I1
I2
V1
V2
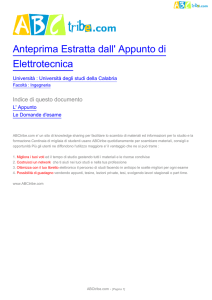
Figura 1: Esempio di un doppio bipolo
Matrice R (Rappresentazione controllata in corrente)
Esempio a pagina 7
Per ricavare R11 ed R21 si deve applicare un generatore di corrente tra i morsetti 1 ed 1', lasciare
aperti i morsetti 2 e 2' (i2 = 0) e calcolare v1 e v2.
Per ricavare R21 ed R22 si deve applicare un generatore di corrente tra 2 e 2', lasciare aperti i morsetti
1 ed 1' (i1 = 0) e calcolare v1 e v2.
{
v 1 = R11 i 1  R12 i 2
v 2 = R21 i 2  R22 i 2
∣
∣
R11 =
v1
i1
R21 =
v2
i1


i2 = 0
i2 =0
  
∣
∣
R11 R12 i 1
v
⋅
= 1
R21 R22 i 2
v2
R12 =
v1
i2
i1 = 0
R22 =
v2
i2
i1 = 0
R11 ed R22 prendono il nome di “Resistenza Propria”, mentre R12 ed R21 di “Resistenza Mutua”.
Matrice G (Rappresentazione controllata in tensione)
Esempio a pagina 8
Per ricavare G11 e G21 si deve applicare un generatore di tensione tra i morsetti 1 ed 1', collegare i
morsetti 2 e 2' tramite un corto circuito (v2 = 0) e calcolare i1 ed i2.
Per ricavare G12 e G22 si deve applicare un generatore di tensione tra i morsetti 2 e 2', collegare i
morsetti 1 ed 1' tramite un corto circuito (v1 = 0) e calcolare i1 ed i2.
{
i 1 = G11 v 1  G12 v 2
i 2 = G21 v 2  G 22 v 2
G11 =
i1
v1
G 21 =
i2
v1

∣
∣
v2 = 0
v2 = 0

  
∣
∣
G11 G12 v 1
i
⋅
= 1
G 21 G22 v 2
i2
G12 =
i1
v2
v1 = 0
G 22 =
i2
v2
v1 = 0
G11 e G22 prendono il nome di “Conduttanza Propria”, mentre G12 e G21 di “Conduttanza Mutua”.
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
1
Matrice H (Rappresentazione ibrida)
Per ricavare H11 ed H21 si deve applicare un generatore di corrente tra i morsetti 1 e 1', collegare i
morsetti 2 e 2' tramite un corto circuito (v2 = 0) e calcolare v1 ed i2.
Per ricavare H12 ed H22 si deve applicare un generatore di tensione tra i morsetti 2 e 2', lasciare
aperti i morsetti 1 ed 1' (i1 = 0) e calcolare v1 ed i2.
{
v 1 = H 11 i 1  H 12 v 2
i 2 = H 21 i 1  H 22 v 2
∣
∣
H 11 =
v1
i1
H 21 =
i2
i1


v2 = 0
v2 = 0
   
∣
∣
H 11 H 12
i
v
⋅ 1 = 1
H 21 H 22 v 2
i2
H 12 =
v1
v2
i1 = 0
H 22 =
i2
v2
i1 = 0
H11 = Resistenza di ingresso
H12 = Guadagno di tensione
H21 = Guadagno di corrente
H22 = Conduttanza di ingresso
Matrice H' (Rappresentazione ibrida inversa)
Per ricavare H'11 ed H'21 si deve applicare un generatore di tensione tra i morsetti 1 ed 1', lasciare
aperti i morsetti 2 e 2' (i2 = 0) e calcolare i1 e v2.
Per ricavare H'12 ed H'22 si deve applicare un generatore di corrente tra i morsetti 2 e 2', collegare i
morsetti 1 ed 1' tramite un corto circuito (v1 = 0) e calcolare i1 e v2.
{
i 1 = H ' 11 v 1  H ' 12 i 2
v 2 = H ' 21 v 1  H ' 22 i 2

∣
∣
H ' 11 =
i1
v1
H ' 21 =
v2
v1
i2 = 0
i2 = 0

   
∣
∣
H ' 11 H ' 12 v 1
i
⋅
= 1
H ' 21 H ' 22 i 2
v2
H ' 12 =
i1
i2
v1 = 0
H ' 22 =
v2
i2
v1 = 0
H11 = Conduttanza di ingresso
H12 = Guadagno di corrente
H21 = Guadagno di tensione
H22 = Resistenza di ingresso
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
2
Matrice T (Rappresentazione con matrice di trasmissione)
Le grandezze della porta (2-2') sono variabili indipendenti, mentre quelle della porta (1-1') sono dipendenti.
Per ricavare A e C, si deve applicare un generatore di tensione tra i morsetti 1 ed 1', lasciare aperti i
morsetti 2 e 2' (i2 = 0) e calcolare v1 ed i1.
Per ricavare B e D, si deve applicare un generatore di corrente tra i morsetti 1 ed 1', collegare i
morsetti 2 e 2' tramite un corto circuito (v2 = 0) e calcolare v1 ed i1.
{
v 1 = A v 2 − B i2
i1 = C v 2 − D i2
A=
C=
v1
v2
i1
v2
∣
∣


A
C
   
B ⋅ v2 = v1
D
− i2
i1
B=
i2 = 0
D=
i2 =0
v1
−i 2
∣
∣
v2 = 0
i1
−i 2
v2 = 0
A = Guadagno di tensione
B = Transresistenza diretta
C = Transconduttanza diretta
D = Guadagno di corrente
Matrice T' (Rappresentazione con matrice di trasmissione inversa)
Le grandezze della porta (1-1') sono variabili indipendenti, mentre quelle della porta (2-2') sono dipendenti.
Per ricavare A' e C', si deve applicare un generatore di tensione tra i morsetti 2 e 2', lasciare aperti i
morsetti 1 ed 1' (i1 = 0) e calcolare v2 ed i2.
Per ricavare B' e D', si deve applicare un generatore di corrente tra i morsetti 2 e 2', collegare i
morsetti 1 ed 1' tramite un corto circuito (v1 = 0) e calcolare v2 ed i2.
{
v 2 = A ' v 1 − B ' i1
i2 = C ' v 1 − D ' i1
A' =
C' =
∣
∣
v2
v1
i2
v1


A'
C'
   
B ' ⋅ v1 = v2
D'
− i1
i2
B' =
i1 = 0
i1 = 0
D' =
v2
−i 1
∣
∣
i2
−i 1
v1 = 0
v1 = 0
A = Guadagno di tensione
B = Transresistenza diretta
C = Transconduttanza diretta
D = Guadagno di corrente
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
3
Trasformazioni tra le rappresentazioni (Δ = Determinante della matrice)
DA
A
R
G
G22
G
− 12
G
G
G 21
G11
−
G
G
R
G
R 12
R 22
1
R 22
H
H'
R
1
− 12
R 11
R 11
R 21  R
R 11 R 11
T'
R 11
R 21
1
R 21
R 22
R 12
1
R 12
H
H 22
H
− 21
H 22
H'
H 12
H 22
1
H 22
H
1
− 12
H 11
H 11
H 21  H
H 11
H 11
R 22
R
− 12
R
R
R 21
R 11
−
R
R
R
R 22
R
− 21
R 22
T
H
G
1
− 12
G 11
G 11
G 21 G
G 11
G11
G
G 22
G
− 21
G 22
G22
G21
G12
G22
1
G22
R
R 21
R 22
R 21
1
G 21
G
G
−
− 11
G21
G 21
R
R 12
R 11
R 12
1
G 12
G
G
−
− 22
G 12
G 12
−
−
G 11
G 12
−
−
T
H'
1
− 12
H ' 11
H ' 11
H ' 21  H '
H ' 11
H ' 11
H'
H ' 22
H'
− 21
H ' 22
H ' 12
H ' 22
1
H ' 22
H ' 22
H ' 12
−
H '
 H'
H ' 21
H ' 11
−
H '
H '
H 22
H
H 21
−
H
H
H 21
H
− 22
H 21
−
1
H 12
H 22
H 12
H 12
H
H 11
H
H 11
H 21
−
1
H 21
H 11
H 12
H
H 12
D
T
−
B
B
1
A
−
B
B
B
D
1
−
D
D'
C'
T '
C'
T
C
D
C
A'
B'
T'
−
B'
T
D
C
D
C
T
−
A
A
1
B
A
A
−
−
A
C
1
C
T'
1
H ' 21
H ' 11
H ' 21
H ' 22
H ' 21
D
T
C
T
1
B'
D'
B'
−
1
A'
C'
A'
C'
1
−
D'
D'
T '
B'
D'
D'
D'
T '
C'
T '
H'
H ' 21
H ' 22
H '
−
H ' 12
H ' 12
H ' 11
1
−
−
H ' 12
H ' 12
−
B'
A'
T'
−
A'
1
C'
A'
C'
B'
T '
A'
T '
B
T
A
T
N.B. : Per poter trasformare una rappresentazione in un' altra è necessario che i denominatori delle
frazioni siano diversi da zero.
Potenza totale assorbita da un doppio bipolo
P totale = V 1 I 1  V 2 I 2
Il bipolo si dice passivo se per ogni insieme di tensioni e correnti che soddisfano le equazioni costitutive si ha: P totale > 0.
Reciprocità e simmetria
Un doppio bipolo è reciproco se date due coppie diverse di tensioni e correnti, che soddisfano le
relazioni costitutive, se inverto le porte di ingresso e di uscita il circuito non cambia.
La simmetria è la proprietà per cui se inverto le porte di ingresso e di uscita il comportamento del
bipolo non cambia. Un bipolo simmetrico è anche reciproco, ma non vale il contrario.
Rappresentazione
Condizione di reciprocità e simmetria
Matrice R
R12 = R21 (simmetrico se anche R11 = R22)
Matrice G
G 12 = G 21 (simmetrico se anche G11 = G22)
Matrice H
H 12 = − H 21 (simmetrico se anche: det(H) = 1)
Matrice H'
H ' 12 = − H ' 21 (simmetrico se anche: det(H') = 1)
Matrice T
determinante di T = 1 (simmetrico se anche A = D)
Matrice T'
determinante di T' = 1 (simmetrico se anche A' = D')
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
4
NOTA BENE
Di seguito si usa la seguente convenzione:
• v1 ed i1 sono la tensione e la corrente entranti al collegamento tra i due bipoli (ovvero i1 è la
corrente che circola in ingresso sulla linea nera più in alto e v1 è la tensione in ingresso tra la
linea nera più in basso e quella più in alto)
• v2 ed i2 sono la tensione e la corrente uscenti dal collegamento tra i due bipoli (ovvero i2 è la
corrente che circola in uscita sulla linea nera più in alto e v2 è la tensione in uscita tra la linea
nera più in basso e quella più in alto)
Collegamento di doppi bipoli in serie
Bipolo 1
Quando i bipoli sono collegati in serie, hanno le stesse correnti ai capi delle
porte.
i 1 = i 1 bipolo1 = i 1 bipolo 2
i 2 = i 2 bipolo 1 = i 2 bipolo 2
Bipolo 2
Bisogna ricavare per ognuno dei bipoli connessi in serie la rappresentazione con la matrice R.
Per trovare le correnti e le tensioni ai capi dei bipoli in serie si farà la somma delle matrici R e si
risolverà il seguente sistema in forma matriciale:
 
v1
R11 bipolo1  R11 bipolo 2
=
v2
R21 bipolo1  R 21bipolo 2

R12 bipolo1  R12 bipolo 2 i 1
⋅
R 22 bipolo1  R22 bipolo 2 i 2
Collegamento di doppi bipoli in parallelo
Bipolo 1
Quando i bipoli sono collegati in parallelo, hanno le stesse tensioni ai capi
delle porte.
v 1 = v 1 bipolo 1 = v 1 bipolo 2
v 2 = v 2 bipolo 1 = v 2 bipolo 2
Bipolo 2
Bisogna ricavare per ognuno dei bipoli connessi in parallelo la rappresentazione con la matrice G.
Per trovare le correnti e le tensioni ai capi dei bipoli in parallelo si farà la somma delle matrici G e
si risolverà il seguente sistema in forma matriciale:
 
i1
G 11 bipolo 1  G 11bipolo 2
=
i2
G 21 bipolo 1  G 21 bipolo2
 
G 12 bipolo 1  G 12 bipolo2
v
⋅ 1
G 22 bipolo 1  G 22 bipolo 2 v 2
Collegamento di doppi bipoli in cascata
Quando i bipoli sono collegati in cascata, la corrente entrante in un bipolo è
la stessa che esce dal bipolo precedente.
Bipolo 1
Bipolo 2
Bisogna ricavare per ognuno dei bipoli connessi in cascata la rappresentazione con la matrice T.
Per trovare le correnti e le tensioni ai capi dei bipoli in cascata si farà la moltiplicazione delle
matrici T e si risolverà il seguente sistema in forma matriciale:
 
v1
A1
=
i1
C1

  
B1
A B2
v
A1 A2  B 1 C 2
⋅ 2
⋅ 2 =
D1 C 2 D 2
− i2
C 1 A2  D 1 C 2
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
 
A1 B 2  B1 D 2
v
⋅ 2
C 1 B2  D 1 D 2
− i2
5
Trasformatore ideale
t
primario
V1
a : b
secondario
V2
oppure
V1
primario
V2
secondario
Un caso particolare di doppio bipolo è il trasformatore ideale, che è in grado di modificare le
tensioni e le correnti che sono poste in ingresso, amplificandole o smorzandole in uscita.
Il circuito posto alla sinistra del trasformatore si chiama “circuito primario”, mentre quello posto a
destra si chiama “circuito secondario”.
Le relazioni di tensioni e correnti tra primario e secondario sono:
v2 = t v1
v
i2 = − 1
t
t é il coefficiente di trasformazione da primario a secondario
Da queste relazioni è possibile ricavare una tabella pratica per le operazioni di trasporto dei
componenti dal primario al secondario e viceversa:
t è il coefficiente di trasformazione da primario a secondario. In caso di coefficiente (a:b) → t = b/a
Da Primario
A Secondario
Da Secondario
A Primario
R  Resistenza
R
t2
A
t
A corrente
A⋅ t
E ⋅t
E tensione 
E
t
R  Resistenza
R⋅ t
A corrente
E tensione 
2
Il trasformatore ideale non assorbe potenza e permette di cambiare il valore della tensione senza
modificare la potenza complessiva del sistema:
i2
P assorbita = v 1 i 1  t v 1 − = 0
t
 
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
6
Esempio di Matrice R (per doppio bipolo a T)
Teoria a pagina 1
1. Ricavo R11 ed R21:
Collego un generatore di corrente a sinistra del doppio bipolo e lascio aperta l'altra coppia di
morsetti. I1 è la corrente imposta dal generatore di corrente ed I2 = 0, per cui tolgo anche R3.
v 1 =  R1  R 2 i 1

Legge di Kircchoff alla maglia
v 2 = R 2 i1

Legge di Ohm
Posso trovare R11 ed R21:
 R  R2 i 1
R11 = 1
=  R 1  R2 
i1
R21 =
R2 i 1
= R2
i1
2. Ricavo R12 ed R22:
Collego un generatore di corrente a destra del doppio bipolo e lascio aperta l'altra coppia di
morsetti. I2 è la corrente imposta dal generatore di corrente ed I1 = 0, per cui tolgo anche R1.
v 1 = R2 i 2

Legge di Ohm
v 2 =  R2  R3 i 2

Posso trovare R12 ed R21:
R i
R12 = 2 2 = R2
i2
Legge di Kircchoff alla maglia
R22 =
 R2  R3 i 2
=  R2  R3 
i2
3. Il sistema finale in forma matriciale è:
 
v1
R  R2
= 1
v2
R2
Aleksandar Gotev – Elettrotecnica – Doppi Bipoli

R2
i
⋅ 1
R2  R3 i 2
7
Esempio di matrice G (Per doppio bipolo a Π)
Teoria a pagina 1
Promemoria
G=1 / R
Serie:
G12 = 1 / (R1 + R2)
1. Ricavo G11 e G21:
Parallelo:
G12 = 1/R1 + 1/R2
Legge di Ohm
I=GV
Collego un generatore di tensione a sinistra del doppio bipolo e un corto circuito a destra. V1 è la
tensione imposta dal generatore E1, mentre V2 = 0. Dato che R2 è in parallelo con un corto circuito,
la tolgo e la corrente I2 sarà quella che scorre in R3.
1
1
v1
1
i1 = v 1 ⋅

oppure
i2 = − v 1 ⋅
R 1 R3
R1
R3
R


Posso trovare G11 e G21:
1
1
v1 ⋅

R1
R3
1
1
G11 =
=

v1
R1
R3


3
R1  R 3

1
R3
V 1⋅

G 21 = −
v1
=−
1
R3
2. Ricavo G12 e G22:
Collego un generatore di tensione a destra del doppio bipolo e un corto circuito a sinistra. V2 è la
tensione imposta dal generatore E2, mentre V1 = 0. Dato che R1 è in parallelo con un corto circuito,
la tolgo e la corrente I1 sarà quella che scorre in R3.
1
1
1
i2 = v 2 ⋅

i1 = − v 2 ⋅
R3
R2
R3

Posso trovare G12 e G22:
v2 ⋅
G12 = −
1
R3
v2
=−
v2 ⋅
1
R3
G 22 =

1
1

R2
R3
v2


=

1
1

R2
R3

3. Il sistema finale in forma matriciale è:

1
1

i1
R
R3
= 1
i2
1
−
R3

Aleksandar Gotev – Elettrotecnica – Doppi Bipoli
 
1
R3
v
⋅ 1
1
1
v2

R2
R3
−
8