Esercizio Convertitore Tensione

Esercizio Convertitore Tensione - Corrente
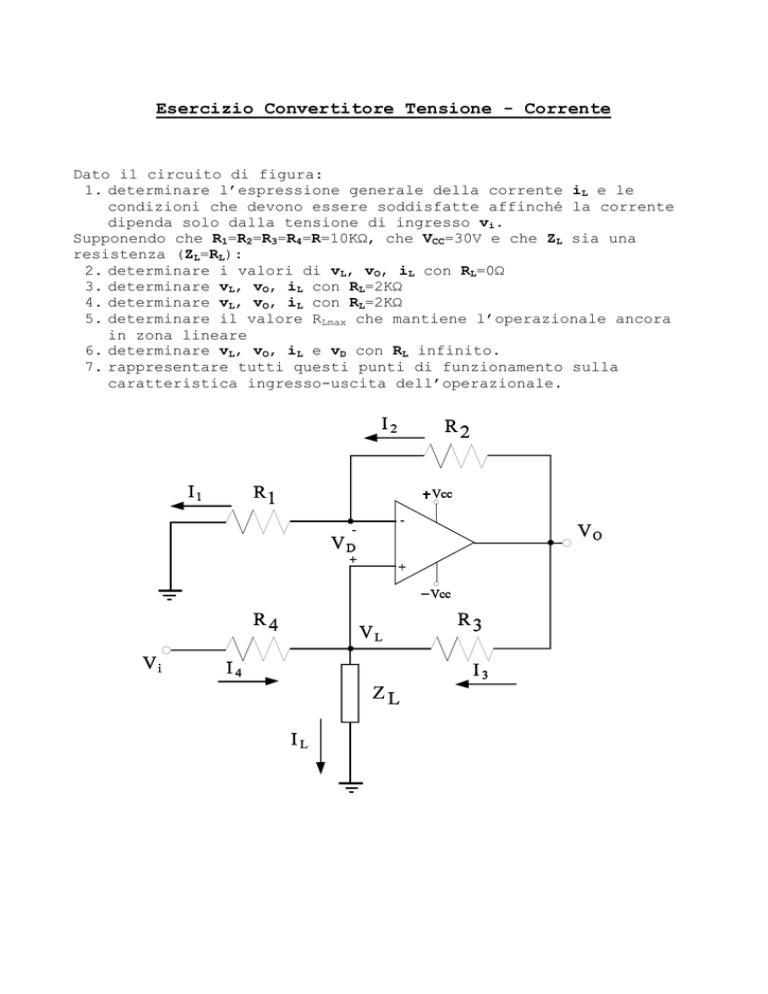
Dato il circuito di figura:
1. determinare l’espressione generale della corrente iL e le
condizioni che devono essere soddisfatte affinché la corrente
dipenda solo dalla tensione di ingresso vi.
Supponendo che R1=R2=R3=R4=R=10KΩ, che VCC=30V e che ZL sia una
resistenza (ZL=RL):
2. determinare i valori di vL, vO, iL con RL=0Ω
3. determinare vL, vO, iL con RL=2KΩ
4. determinare vL, vO, iL con RL=2KΩ
5. determinare il valore RLmax che mantiene l’operazionale ancora
in zona lineare
6. determinare vL, vO, iL e vD con RL infinito.
7. rappresentare tutti questi punti di funzionamento sulla
caratteristica ingresso-uscita dell’operazionale.
Soluzione
1.
applicando il primo p. di K. al nodo con potenziale vL si ha:
iL  i3 i4 
vO v L
v v L
 i
R3
R4
Osservando che vL e vO sono, rispettivamente, ingresso e uscita di
amplificatore con operazionale nella connessione non invertente,
si può eliminare, dalla precedente, la variabile vO;

R 
1  2 v L v L

R1 

v v L
R v
v
v
v
iL  
 i

1  2 L  L  i  L
R3
R4
R3
R4
R4
 R1 R3
iL 
R
vi
1
 2  v L
R4
R4 
R1R3
iL 
R R R1R3 
vi
 2 4
v L
R4
R
R
R
 1 3 4 
Scegliendo le quattro resistenze in modo che risulti R2R4=R1R3 si
ottiene il risultato voluto:
iL 
vi
R4
per cui la corrente iL, fissati vi e R4, risulta indipendente dalla
impedenza ZL che attraversa. Ovviamente iL e vL sono legati dalla
relazione che governa la legge del bipolo ZL.
Nel caso particolare in cui ZL=RL si ha:
iL 
vi
v
 L
R4
RL
che consente di ricavare il legame di proporzionalità tra vL e RL
con iL costante
vL 
vi
RL
R4
Naturalmente anche vO varia proporzionalmente a RL dato il legame,
ancora di proporzionalità, tra vO e vL.
Applicando questi risultati finali si può rispondere alle domande
successive.
2. Con RL=0 si ha la seguente soluzione
Per la legge di Ohm applicata a RL si impone vL=0 quindi anche
vO=0. Con l’operazionale in zona lineare, vD=0 comporta v-=0 e
quindi anche i1=i2=0. L’unica corrente diversa da zero è la:
iL  i4 
vi
5V

 0,5mA
R4
10k 
a conferma della relazione precedente.
3. Con RL=2kΩ si può calcolare ancora
iL 
vi
5V

 0,5mA
R4
10k 
e quindi le correnti su tutti gli altri rami del circuito
vL 
RL
2k 
vi 
5V  1V
R4
10k 

R 
 10k 
vO  
1  2 v L  
1 
v L  2 v L  2V
R1 
 10k 

v
1V
i1  L 
 0,1mA
R1
10k 
v v L
2V 1V
i2  O

 0,1mA
R2
10k 
v v L
2V 1V
i3  O

 0,1mA
R3
10k 
v v L
5V 1V
i1  i

 0,4mA
R4
10k 
Questi valori sono rappresentati nel seguente schema e, applicando
il primo principio di K. ai nodi si nota la perfetta coerenza dei
risultati ottenuti.
4. Con RL=10kΩ si ha ancora
iL 
vi
5V

 0,5mA
R4
10k 
e quindi le correnti su tutti gli altri rami del circuito
vL 
RL
10k 
vi 
5V  5V
R4
10k 

R 
 10k 
vO  
1  2 v L  
1 
v L  2 v L  10V
R
10
k




1 
v
5V
i1  L 
 0,5mA
R1
10k 
v v L
10V 5V
i2  O

 0,5mA
R2
10k 
v v L
10V 5V
i3  O

 0,5mA
R3
10k 
v v L
5V 5V
i4  i

 0mA
R4
10k 
Questi valori sono rappresentati nel seguente schema e, applicando
il primo principio di K. ai nodi si nota la perfetta coerenza dei
risultati ottenuti.
5. Il valore di RLmax si ottiene il valore della resistenza di
carico che produce il massimo valore di uscita, vO=vCC=30V, con
operazionale ancora in zona lineare.
v L max 
vO max
vO max
30


 15V
10k 
2

R2  
1 
1   


10
k



R

1 
RL max  R4
vL
15V
 10k 
 30k 
vi
5V
Con procedimento analogo ai precedenti si ottengono le correnti
sulle resistenze
iL 
vi
5V

 0,5mA
R4
10k 
vL
15V

 1,5mA
R1
10k 
v v L
30V 15V
i2  O

 1,5mA
R2
10k 
v v L
30V 15V
i3  O

 1,5mA
R3
10k 
v v L
5V 15V
i4  i

 1mA
R4
10k 
i1 
Anche in questo caso il primo p. di K. è pienamente soddisfatto.
***
In tutti questi casi il funzionamento in zona lineare
dell’operazionale ha garantito il risultato fondamentale
iL =
vi
5V
=
= 0,5mA = costante
R 4 10kΩ
per cui il circuito analizzato risulta essere un generatore a
corrente costante.
***
6. Con il valore infinito di RL si ottiene il seguente circuito
I valori delle correnti e dei potenziali ai nodi si calcolano
facilmente
iL  0
vO
30V

 1,5mA
R1 R2
20k 
v vi
30V 5V
i3  i4  O

 1,25mA
R3 R4
20k 
v vi
v vi
30V 5V
v L  vi R3i4  vi R3 O
 O

 17,5V
R3 R4
2
2
R1
v
v   vO
 O  15V
R1 R2
2
i1  i2 
v D  v L v   17,5V 15V  2,5V
>0 operazionale in saturazione
In questo ultimo caso non si ha più il funzionamento a corrente
costante (iL=0) infatti loperazionale è uscito decisamente dalla
zona lineare.
7. Il seguente grafico mostra i cinque punti di funzionamento
dell’operazionale sulla sua caratteristica ingresso-uscita.