2. Richiami di calcolo delle probabilità
L’analisi esposta, consistente nell’ipotizzare la crisi in fase plastica, comporta,
indubbiamente, vantaggi rispetto al metodo elastico-lineare, ma non può considerarsi
pienamente accettabile poiché i parametri presi in considerazione sono valutati in forma
deterministica, senza tenere conto delle diverse aleatorietà e delle cause d’incertezza insite
nella loro determinazione.
Ad ogni parametro corrisponde un unico valore: un unico valore della tensione di
snervamento, delle dimensioni geometriche e dei carichi. Nella realtà ad ogni grandezza
corrisponde una gamma di valori: se, ad esempio, si misura su più campioni di identico
materiale la tensione di snervamento, si otterrà un valore diverso in ogni prova; così per le
dimensioni geometriche dei profilati a causa delle inevitabili imperfezioni e tolleranze di
lavorazione; così per i carichi, sia per quelli permanenti ed ancor più per i carichi variabili.
In definitiva si dispone, per ciascuna grandezza, di una gamma di valori e, dunque, di una
gamma di valori della resistenza R e della sollecitazione S.
Non essendo R e S valori deterministici, l’equazione fondamentale simbolica alla base
delle verifiche R > S dipende anch’essa dalla variabilità dei parametri considerati.
Poiché le grandezze in gioco sono aleatorie, il problema non può risolversi che con criteri
probabilistici, passando quindi dalla
Certezza della sicurezza alla Probabilità della sicurezza
Si ammette cioè la possibilità dell’evento negativo (crisi), ma la probabilità che esso si
verifichi deve essere sufficientemente piccola e correlata ai rischi, ossia:
P (R - S < 0) < pr
dove pr è una quantità piccola e correlata al tipo di crisi che si vuole evitare.
In conclusione il problema in termini probabilistici si imposta considerando la possibilità
dell’evento negativo e verificando che la probabilità del suo verificarsi sia minore di un valore
sufficientemente piccolo che dipende dalla pericolosità dell’evento negativo considerato.
Si ritiene quindi indispensabile fornire le basi del calcolo delle probabilità, necessarie per
effettuare le verifiche.
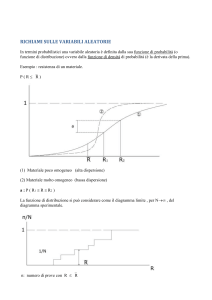
2.1. Variabili aleatorie o casuali
Sia assegnata una variabile x aleatoria o casuale, una variabile cioè i cui valori si
discostano da quello dichiarato per cause solo accidentali e non sistematiche.
Metodo semiprobabilistico agli stati limite
12
Ad esempio la dimensione di un elemento prefabbricato prodotto in serie, se non
intervengono cause sistematiche, quali una errata dimensione del cassero, può assumere
valori sia maggiori che minori rispetto a quello dichiarato. Se ci sono cause sistematiche,
invece lo scostamento da quello dichiarato è sempre dello stesso segno.
Se nell’esempio precedente il cassero è più grande della dimensione nominale, l’elemento
prefabbricato sarà sempre più lungo rispetto alla dimensione dichiarata.
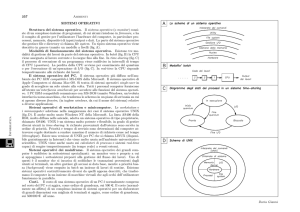
Si consideri quindi una grandezza variabile x e si supponga di avere n misurazioni di essa
(x1, x2, …., xn). Si divida l’asse x in intervalli di ampiezza ∆x; nell’ i-esimo intervallo ∆x siano
comprese ni misurazioni (ni < n) (Fig. 2.1). Si calcoli l’ordinata yi in modo che:
∆x yi = ni /n.
y
xi
yi
x
x
xr
Fig. 2.1
Si ripeta tale operazione per tutti gli intervalli ∆x. Tale operazione porta alla costruzione
dell’istogramma delle frequenze (Fig. 2.1), cioè un diagramma caratterizzato da r rettangoli, il
generico dei quali è individuato dall’ascissa xi e dall’ordinata yi ed ha area pari a:
∆x yi = ni /n
ossia il rapporto tra casi favorevoli ni compresi nell’intervallo ∆x e casi totali n.
Se l’intervallo ∆x è sufficientemente piccolo, non si commette un grosso errore facendo
riferimento al valore medio xi dell’i-esimo rettangolo, come rappresentativo di tutte le
grandezze che ricadono nello stesso intervallo di valori, e assegnando ad esso la
corrispondente frequenza. Si può così esprimere il valore medio dell’istogramma delle
frequenze:
xm =
r
∑x
i =1
i
⋅ y i ⋅ ∆x =
r
∑
i =1
n
xj
x i ⋅ ni
=
n
j =1 n
∑
Metodo semiprobabilistico agli stati limite
13
In questa ipotesi il valore medio dell’istogramma delle frequenze è uguale alla media
aritmetica degli n valori di x misurati.
Si definisce scarto quadratico medio per un numero finito n di osservazioni la grandezza:
n
σx =
∑ (x
j
− x m )2
j =1
n −1
Se il numero delle osservazioni tende ad infinito e gli intervalli ∆x tendono a dx
l’istogramma delle frequenze tende alla curva di densità delle probabilità.
Di una variabile statistica casuale x si definisce infatti curva di distribuzione della
probabilità o curva di densità di probabilità y = f(x) (Fig. 2.2) quella curva tale che si abbia:
dP = f(x0) dx =y(x0) dx
essendo dP la probabilità elementare che la grandezza x cada nell’intervallo x0÷x0+dx.
La probabilità P che x cada nell’intervallo x0÷x1 è data dalla somma delle probabilità
elementari dP (Fig. 2.2):
x1
P=
∫ f ( x )dx
x0
La probabilità P1 che sia x < xk, ossia che x cada nell’intervallo a1÷xk, essendo a1 il limite
inferiore della variabile x, vale (Fig. 2.2):
xk
P1 =
∫ f ( x)dx
a1
La probabilità P2 che sia x > xk, ossia che x cada nell’intervallo xk÷ a2, essendo a2 il limite
superiore della variabile x, vale (Fig. 2.2):
a2
P2 =
∫ f ( x)dx
xk
La somma delle probabilità P1 e P2 è uguale ad uno, ossia la certezza, in quanto a1 e a2
sono i limiti inferiore e superiore della variabile x: P1 + P2 = 1.
Metodo semiprobabilistico agli stati limite
14
y=f(x)
y=f(x)
dP
P2
P1
0
a1
x0
dx
x1
a2
x
0
a1
xk
a2
Fig. 2.2
Assegnata una variabile casuale x e la sua curva di distribuzione di probabilità y=f(x), si
definisce valore medio xm della variabile x la quantità (Fig. 2.3):
a2
xm =
∫ x ⋅ f ( x )dx
a1
dove il secondo membro non è altro che il momento statico dell’area sottesa dalla curva
rispetto all’asse delle y. Poiché:
a2
∫ f ( x)dx = 1
a1
nulla cambia se si divide la xm per tale quantità:
a2
xm =
∫ x ⋅ f ( x)dx
a1
a2
.
∫ f ( x )dx
a1
Per il teorema di Varignon, xm è l’ascissa del baricentro dell’area sottesa dalla curva di
distribuzione di probabilità.
y=f(x)
xm
G
a1
a2
x
Fig. 2.3
Si definisce scarto quadratico medio o varianza σx la quantità:
a2
σx =
∫ (x − x
m)
2
⋅ f ( x )dx
a1
Metodo semiprobabilistico agli stati limite
15
x
La quantità sotto radice non è altro che il momento d’inerzia dell’area sottesa dalla curva
rispetto all’ asse verticale passante per G (Fig. 2.3).
Dividendo l’espressione di σx per:
a2
∫ f ( x)dx = 1
a1
si ottiene:
a2
∫ (x − x
σx =
m)
2
⋅ f ( x )dx
a1
a2
∫ f ( x)dx
a1
Dunque, lo scarto quadratico medio rappresenta il raggio d’inerzia rispetto alla verticale
passante per il baricentro G. Più la curva è stretta, più il momento d’inerzia e,
conseguentemente, il raggio d’inerzia e, quindi, lo scarto quadratico medio è piccolo.
Nei problemi di ingegneria le grandezze aleatorie, ossia le grandezze la cui variabilità è
legata al caso, seguono con buona precisione la curva di distribuzione delle probabilità di De
Moivre - Gauss.
L’adozione di questa legge di distribuzione delle probabilità di una variabile casuale
semplifica notevolmente il calcolo in quanto è possibile il suo tracciamento conoscendo solo
il valore medio xm e lo scarto quadratico medio σx e, quindi, può essere costruita anche con
un numero finito n di valori.
La funzione di Gauss è:
y(x) =
1
σ x 2π
⋅e
⎛ x − xm ⎞
⎟
−⎜
⎜σ 2⎟
⎝ x
⎠
2
Tale curva peraltro si adatta bene ai problemi di ingegneria, in quanto possiede le
seguenti proprietà (Fig. 2.4):
1) il valore medio è il valore più probabile: per x = xm la y(x) è massima;
2) la curva è simmetrica rispetto al valore medio;
3) se diminuisce lo scarto quadratico medio, diminuisce la dispersione;
Metodo semiprobabilistico agli stati limite
16
y=f(x)
x
x
xm
x
Fig. 2.4
4) man mano che ci si allontana dal valore medio, la densità di probabilità di un valore
diverso dal medio si riduce tanto più quanto più piccolo è lo scarto quadratico medio ed è
praticamente nulla per x= ± ∞.
Con n=30 misurazioni della variabile è possibile determinare, con buona rispondenza, il
valore medio e lo scarto quadratico medio della distribuzione di Gauss.
Si può passare così, senza introdurre errori significativi, dal diagramma delle frequenze di
una variabile casuale a quello della densità di probabilità p(x) di Gauss.
Si illustra ora il significato fisico dello scarto quadratico medio.
o
Funzione di Gauss:
p(x) =
o
1
⋅e
σ x 2π
⎛ x − xm ⎞
⎟
−⎜
⎜σ 2⎟
⎝ x
⎠
2
Derivata prima e seconda:
p' (x) =
p" (x ) =
1
σ x 2π
1
σ x 2π
⋅e
⋅e
⎛ x − xm ⎞
⎟
−⎜
⎜σ 2 ⎟
⎝ x
⎠
⎛ x − xm ⎞
⎟
−⎜
⎜σ 2⎟
⎝ x
⎠
2
⎛ x − xm
⋅ ⎜⎜ −
σ 2x
⎝
2
⎧⎪ 1
⎨− 2
⎪⎩ σ x
⎞
⎟
⎟
⎠
⎡ (x − x m )2 ⎤ ⎫⎪
⎢1 −
⎥⎬
σ 2x
⎢⎣
⎥⎦ ⎪⎭
o Annullando la derivata seconda si determinano le ascisse dei due punti di flesso della
curva di Gauss:
p'' (x) = 0 ⇒ 1 −
(x - x m )2
σ 2x
= 0 ; (x - x m ) = σ 2x
2
da cui:
x - xm = ± σx
→
x = xm ± σx
Metodo semiprobabilistico agli stati limite
17
In particolare in x = xm - σx
in x = xm + σx
[ p''' (xm - σx ) > 0 ] si ha un punto di flesso ascendente, mentre
[p''' (xm + σx ) < 0] si ha un punto di flesso discendente.
Lo scarto quadratico medio σx rappresenta quindi la distanza tra il punto di flesso e la
retta passante per xm e parallela all’asse y(x) (vedi Fig. 2.4).
Noti il valore medio e la varianza è possibile determinare altri valori legati alla
statistica del processo, il cui utilizzo in termini di valutazione strutturale sarà più chiaro nel
seguito.
2.2. Valori caratteristici
Si costruisce dapprima la funzione integrale F(x ) = p(x ) dx .
∫
P(x)
-∞
xm
+∞
x
xm
+∞
x
Fig. 2.5
F(x)
1
0.5
-∞
Fig. 2.6
Se ad ogni valore della variabile x (Fig. 2.5) si associa la grandezza F(x) che misura l’area
racchiusa dall’asse x, dalla curva e dalla retta con ascissa x, si ha il diagramma di Fig. 2.6
che ad ogni ascissa x associa la probabilità F(x) di non essere superata e la probabilità [1F(x)] di essere superata. Il limite di F(x) è ovviamente l’unità (Fig. 2.6).
Si definisce valore mediano di x, ossia x m , quel valore a cui corrisponde F( x m ) = 0.5.
Nella distribuzione di Gauss il valore mediano x m coincide con quello medio xm, essendo la
distribuzione simmetrica (Fig. 2.5).
Si definisce frattile inferiore x’ di ordine P1% = F(x’) quel valore di x che ha la probabilità
P1 di non essere superato (Fig. 2.7a):
x'
F(x' ) = P1 (x < x' ) =
∫ p(x)dx.
−∞
Metodo semiprobabilistico agli stati limite
18
Si definisce frattile superiore x” di ordine P2% quel valore di x che ha la probabilità P2 di
essere superato (Fig. 2.7a)
+∞
P2 ( x > x" ) =
∫ p( x)dx
x"
p(x)
p(x)
P
2
P
P
1
1
P
2
x"
x'
x'
x
Fig. 2.7a
x
Fig. 2.7b
Pertanto ad ogni valore della variabile x si possono associare le probabilità corrispondenti
al frattile inferiore di ordine P1 e al frattile superiore di ordine P2 = 1 - P1 (Fig. 2.7b).
Si esegue un’applicazione dei frattili ora definiti alle resistenze ed ai carichi.
Si definisce resistenza caratteristica quel valore della resistenza con un frattile inferiore di
ordine 5% (Fig. 2.8). È necessario definire come valore caratteristico un valore della
resistenza che abbia una piccola probabilità di non essere superato, ossia un valore
sufficientemente piccolo tra quelli misurati sperimentalmente.
Viceversa, si definiscono valori caratteristici dei carichi quei valori con frattile superiore di
ordine 5% (frattile inferiore di ordine 95%), ossia che abbiano una piccola probabilità di
essere superati (ossia una grande probabilità di non essere superati) (Fig. 2.9).
Si osserva che per avere la certezza della sicurezza si dovrebbe considerare il massimo
valore dei carichi, o meglio, delle sollecitazioni generate da questi, ed il minimo valore della
resistenza.
Adottando la distribuzione di Gauss l’ordine di un generico frattile inferiore x (ki) è dato da:
x(i)
k
P(x < x (i)
k ) =
∫ p(x)dx = σ
−∞
x (i)
k
1
x
2π
∫e
⎛ x − xm ⎞
⎟
−⎜
⎜σ 2⎟
⎠
⎝ x
2
dx
−∞
mentre l’ordine di un generico frattile superiore x (ks ) è dato da:
Metodo semiprobabilistico agli stati limite
19
+∞
P(x > x (s)
k ) =
∫ p(x)dx = σ
x(ks )
⎞
⎛
+ ∞ −⎜ x − x m ⎟
⎜σ 2⎟
⎠
⎝ x
1
x
2π
2
∫e
dx
x (ks )
Fissato ad esempio l’ordine del frattile inferiore, noti il valore medio della distribuzione e la
varianza, si può valutare il corrispondente frattile, ossia il valore caratteristico della
grandezza in esame.
Operata la sostituzione di variabile nell’integrale:
(
)
t = (x - x m ) / σ x 2 ⇒ dx = 2σ x dt
e definiti i limiti di integrazione per la nuova variabile t:
(
)
x k ⇒ t k = (x k − x m ) / σ x 2
si ha:
P(x < x k(i) ) =
tk
1
σ x 2π
∫
2
σ x 2 e −t dt =
-∞
tk
1
π
∫e
−t 2
dt
−∞
Risolvendo l’integrale si ha per:
P = 0.05
⇒
tk = − 1.64 / 2
⇒
xk = xm – 1.64 σx;
P = 0.015
⇒
tk = − 2.16 / 2
⇒
xk = xm – 2.16 σx;
P = 0.005
⇒
tk = − 2.58 / 2
⇒
xk = xm – 2.58 σx.
In modo analogo si può operare nei confronti dei carichi e delle sollecitazioni.
Il frattile superiore di ordine 5% (o frattile inferiore di ordine 95%) risulta:
⇒
P = 0.95
tk = + 1.64 / 2
⇒
xk = xm + 1.64 σx.
E’ evidente che al frattile inferiore di ordine P corrisponde il frattile superiore di ordine [1-P].
I valori caratteristici di ordine 5% e di ordine 95% sono simmetrici rispetto al valore medio,
essendo la curva di Gauss simmetrica. Inoltre, si osserva che, a parità di valore medio, il
frattile inferiore di ordine 5% è tanto più piccolo quanto più grande è lo scarto quadratico
medio.
fR
fS
fR
fS
5%
5%
xk(i)
xk(s)
x=R
Fig. 2.8
Metodo semiprobabilistico agli stati limite
x=S
Fig. 2.9
20