La rappresentazione dei numeri
reali: i numeri floating point
Numeri floating point
z
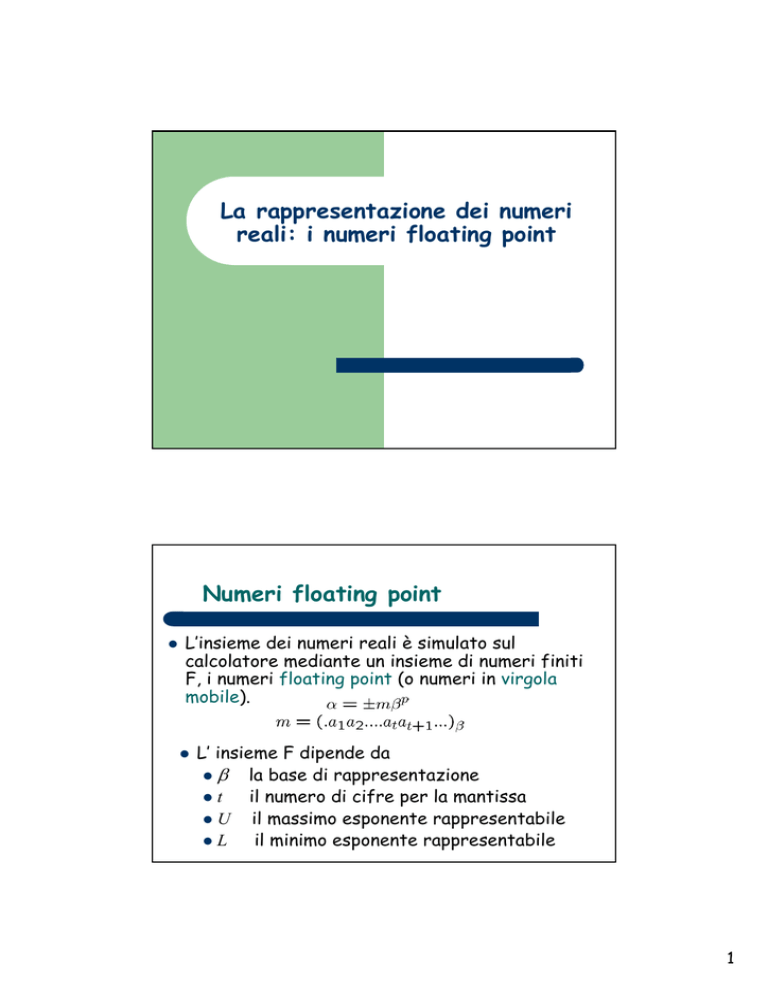
L’insieme dei numeri reali è simulato sul
calcolatore mediante un insieme di numeri finiti
F, i numeri floating point (o numeri in virgola
mobile).
z
L’ insieme F dipende da
zβ
la base di rappresentazione
zt
il numero di cifre per la mantissa
zU
il massimo esponente rappresentabile
zL
il minimo esponente rappresentabile
1
Convenzioni del formato IEEE
(Institute of Electrical and Electronic Engeneerings),
documento 745 dell’ANSI
z
z
z
z
β=2;
1 bit per il segno (0=+, 1=-);
Rappresentazione traslata di una costante
(bias) dell’esponente p+bias
Rappresentazione della mantissa troncata al
t-esimo bit. Il primo è 1 quindi non si
rappresenta, quindi si rappresentano t-1
cifre
Precisione semplice e doppia
2
Rappresentazione floating point di
0.25
z
Conversione da base 10 a base 2
z
Normalizzazione
z
Traslazione dell’esponente
Da floating point a base 10
z
z
Traslazione inversa dell’ esponente:
128-127=1
Mantissa
3
Il più piccolo numero floating point
z
Numeri più piccoli danno l’underflow floating
point e vengono rappresentati come 0
Il più grande numero floating point
z
Numeri più grandi danno l’overflow floating
point e provocano l’arresto dell’elaborazione
4
Rappresentazione dell’esponente
z
z
Per effetto della traslazione, gli esponenti
sono rappresentati come numeri che vanno
da 1 a 254 (precisione semplice).
Esponenti negativi hanno il primo bit=0, quelli
positivi hanno il primo bit=1
Rappresentazioni speciali
5
Numeri denormalizzati
z
Sono numeri più piccoli di
L’insieme dei numeri floating point
z
z
Non è continuo, ma è finito e limitato.
Ha esattamente
elementi (si ottiene contando tutte le
possibili combinazioni tra segno, mantissa ed
esponente).
6
Insieme dei numeri floating point
con β = 2, t = 2, L = -2, U = 1
Osservazioni
z
z
z
Attorno allo 0 c’è un intervallo
di numeri reali che vengono rappresentati
come 0 (underflow)
Per numeri più grandi di
o più piccoli di
si incorre in
overflow
Numeri piccoli sono meglio rappresentati
7
Come si rappresenta un numero
che non appartiene ad F?
z
Arrotondamento o troncamento
Osservazione
8
Troncamento
z
Tutti i numeri in [2,5/2) vengono
rappresentati come “2”
fl
2=
1.00 21
1.001 21
1.0011 21
………
5/2 =1.01 21
1.00 21
fl
1.01 21
Ampiezza dell’intervallo = 1/2
Arrotondamento
z
Tutti i numeri in [15/8,17/8) vengono
rappresentati come “2”
15/8 = 1.111 20
1.1111 20
1.111101 20
1.00 21
1.0001 21
1.00011 21
………
17/8 =1.001 21
fl
1.00 21
fl
1.01 21
Ampiezza dell’intervallo = 1/4
9
Ogni elemento di F rappresenta se
stesso e un intervallo di reali
z
Troncamento
z
Arrotondamento
z
La rappresentazione floating point di un
numero reale α si può definire come
l’elemento di F più prossimo ad α
10
Errori nella rappresentazione dei
numeri reali
Teorema dell’errore di
rappresentazione di un numero reale α
Arrotondamento-> k=1,
Troncamento->k=1/2
Precisione di macchina
Proprietà della precisione di macchina:
11
Algoritmo per determinare la
precisione di macchina
z
z
u=1
while 1+u > 1
–
z
z
u = u/2;
u = u*2;
La precisione di macchina ha lo stesso ordine di
grandezza del valore di u al penultimo passo
12












