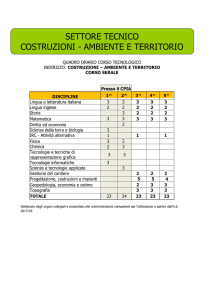
Una nuova geometria:
Un viaggio virtuale
Sulla superficie sferica
Elaborato finale
Laureando: Marco Costanzi
Relatore: prof. Italo Tamanini
Obiettivo
Argomento: GEOMETRIA SFERICA
Destinatari: CLASSI QUARTE E QUINTE SCUOLE MEDIE
SUPERIORI
Luogo:
MUSEO o LABORATORIO DIDATTICO
Modalità:
LABORATORIO INTERATTIVO
Costruzioni sulle SFERE di LÉNÁRT
Presentazioni da proiettare
• Introduzione argomento
• Definizioni ambiente ed elementi
• Costruzioni
1
Presentazioni:
• Introduzione argomento
• Definizioni ambiente ed elementi
• Costruzioni
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
La geometria piana studia le figure geometriche nel
piano: rette, punti, poligoni….
2
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
La GEOMETRIA
SFERICA si
occupa delle figure
sulla sfera:
triangoli, poligoni,
cerchi, rette….
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Tagliando una sfera
con un piano
possiamo ottenere:
INSIEME VUOTO
se la distanza d del
piano da O è
maggiore di R;
3
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Tagliando una sfera
con un piano
possiamo ottenere:
UN PUNTO
quando d=R; in
questo caso il piano
è tangente ad S;
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Tagliando una sfera
con un piano
possiamo ottenere:
UNA
CIRCONFERENZA
di raggio r compreso
tra 0 ed R se 0<d<R.
Esempio sono i paralleli
del mappamondo;
4
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Tagliando una sfera
con un piano
possiamo ottenere:
UNA
CIRCONFERENZA
MASSIMA
di raggio R, se d=0,
ossia il piano secante
passa per il centro O
della sfera.
Chiameremo queste
rette!
Presentazioni:
• Introduzione argomento
• Definizioni ambiente ed elementi
• Costruzioni
5
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Nella geometria
sferica il piano è
costituito da una
sfera S di raggio
R, immersa nello
spazio ordinario.
S è l’insieme dei punti
dello spazio che
distano R>0 da un
punto fissato O detto
centro della sfera.
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Per due punti A, B
di S passa
un’unica retta
(cerchio massimo).
Per trovare tale
cerchio basta
intersecare S con
il piano passante
per A, B, O.
6
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
Le circonferenze
massime sono le
geodetiche della
sfera (linee di
minima lunghezza).
La distanza tra due
punti di S è definita
come la lunghezza
del più breve arco di
cerchio massimo
che li collega.
• Introduzione argomento
Una nuova geometria
• Definizioni ambiente ed elementi
• Costruzioni
L’ampiezza di un
angolo compreso
fra due archi di
cerchio massimo
s0, s1 di origine C,
si misura con
l’angolo piano fra
le tangenti a s0, s1
in C.
7
Presentazioni:
• Introduzione argomento
• Definizioni ambiente ed elementi
• Costruzioni
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
PROBLEMA:
Come possiamo
calcolare l’area di
un triangolo
sferico qualsiasi?
8
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
Disegniamo i cerchi
massimi completi su
cui giacciono i tre
lati. Troviamo così il
triangolo antipodale
A’B’C’ congruente
ad ABC.
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
Osserviamo che il triangolo ABC appartiene sia alla
luna L(A), sia alla luna L(B) che alla luna L(C).
Analogamente A’B’C’ appartiene alla luna L(A’), alla
luna L(B’), alla luna L(C’).
9
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
Calcoliamo l’area delle singole lune:
^
Area ( LA )
Area ( LA ' )
A
Area ( S )
360
^
Area ( LB )
Area ( LB ' )
B
Area ( S )
360
^
Area ( LC )
Area ( LC ' )
C
Area ( S )
360
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
Sommiamo tutte le
lune prima
calcolate ed
otteniamo la
superficie sferica
più quattro volte il
triangolo giallo
(infatti il triangolo è
coperto dalle tre lune,
dunque una copre la
superficie sferica, le altre
due sono in eccesso!)
10
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
• Introduzione argomento
Area di un Triangolo Sferico
Area L A
• Definizioni ambiente ed elementi
• Costruzioni
Area L A '
Area LB
Area LB '
Area LC
Area LC '
Area S
2 Area ABC
2 Area A' B ' C '
ma Area(ABC)=Area(A’B’C’) perché i
triangoli sono congruenti:
Area L A
Area L A '
Area LB
Area LB '
Area LC
Area LC '
Area S
4 Area ABC
11
• Introduzione argomento
Area di un Triangolo Sferico
4 Area ABC
Area L B '
^
4 Area ABC
^
B
Area ( S )
360
A
Area ( S )
360
^
C
Area ( S )
360
• Definizioni ambiente ed elementi
• Costruzioni
Area L A
Area L A '
Area LB
Area LC
Area LC '
Area ( S )
^
^
A
Area ( S )
360
B
Area ( S )
360
^
C
Area ( S )
360
Area ( S )
• Introduzione argomento
Area di un Triangolo Sferico
• Definizioni ambiente ed elementi
• Costruzioni
^
Osservato che:
Area ( LA )
Area ( LA' )
A
Area ( S )
360
Area ( LB )
Area ( LB ' )
B
Area ( S )
360
Area( LC )
Area( LC ' )
C
Area( S )
360
^
^
otteniamo:
^
2A
Area ( S )
360
4 Area ABC
^
quindi:
Area ABC
^
^
2B
360
^
2C
1
360
^
( A B C 180 ) Area ( S )
720
12