Capitolo 1
Il nucleo atomico: generalità
1.1 Struttura e sistematica del nucleo
La Fisica atomica era nata con la scoperta dell’elettrone (J.J.Thomson 1897). A
distanza di poco più di 30 anni, con la scoperta del neutrone (Chadwick 1932) nasce
la fisica nucleare. Nasce così la concezione dell’atomo costituito da una nuvola di
elettroni distribuita in una zona di dimensioni 10-8cm e da un nucleo centrale
costituito da protoni e neutroni con dimensioni di 10-13cm. Una dettagliata teoria
dell’atomo e del nucleo è stata usata per la prima volta da Heisemberg nel 1932.
Precedentemente non era netta la distinzione tra atomo e nucleo: nel modello di
Thomson gli atomi venivano descritti come distribuzioni sferiche di carica positiva,
delle dimensioni di 10-8cm all’interno delle quali erano sistemati gli elettroni in
numero tale da garantire una carica complessivamente nulla all’atomo. Il modello
tuttavia non rendeva conto dei risultati dell’esperimento di diffusione delle
particelle α su atomi pesanti (un sottile foglio di oro dello spessore di 5·10-4mm)
effettuato da Rutherford. Nel modello di Thomson le particelle α interagiscono con
una sfera essenzialmente neutra (teorema di Gauss) e non possono quindi subire
deflessioni a grandi angoli. Sperimentalmente si trovò invece che alcune particelle α
erano deflesse ad angoli anche maggiori di 90°. Rutherford immaginò che l’atomo
fosse composto da un nucleo centrale con carica positiva +Ze delle dimensioni di RN
≈ 10-12cm; gli Z elettroni erano sistemati attorno al nucleo ad una distanza
dell’ordine del raggio atomico Ra ≈ 10-8cm.
V(r) nucle o
V(r) elettro ni
V tot
R
a
r
r
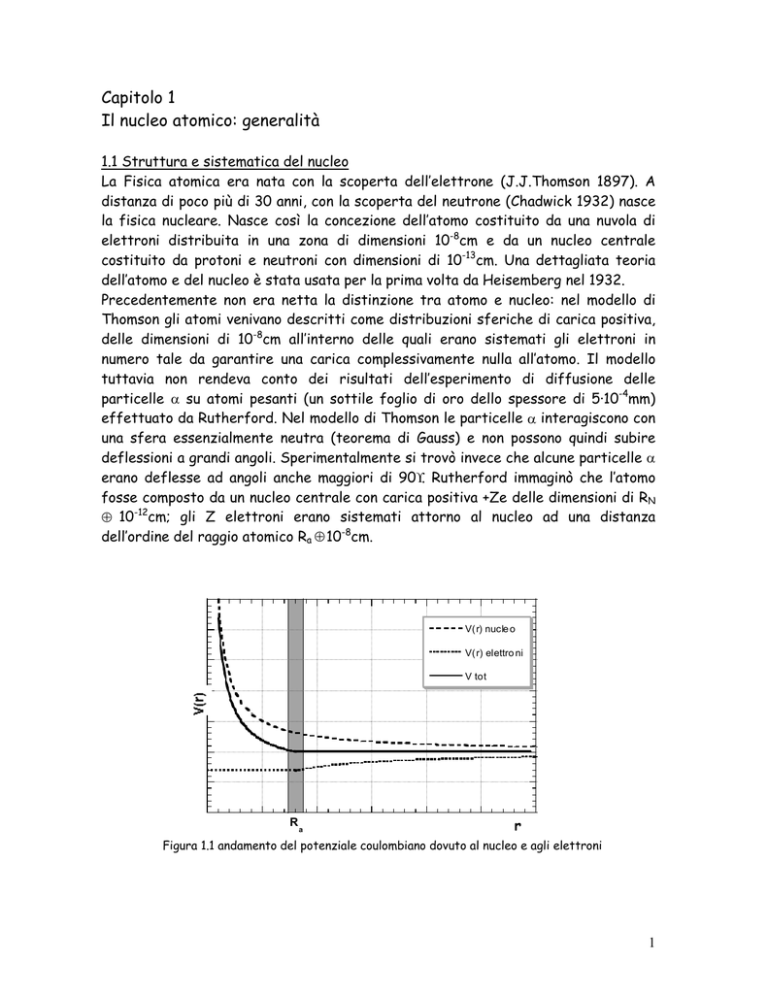
Figura 1.1 andamento del potenziale coulombiano dovuto al nucleo e agli elettroni
1
In questo modo le particelle α che passano ad una distanza inferiore a Ra dal nucleo
centrale “vedono” una carica effettiva +Ze e possono quindi subire deflessioni
considerevoli. Gli elettroni esercitano una sorta di schermo elettrostatico a
distanze maggiori del raggio atomico. In figura 1.1 è riportato il potenziale
elettrostatico dovuto al nucleo centrale e agli elettroni, schematizzati come una
corteccia sferica di raggio Ra e carica -Ze.
Una stima della dimensione del nucleo può essere ricavata dal seguente
ragionamento. Il minimo parametro d’urto è dell’ordine delle dimensioni del nucleo e,
se sono possibili deflessioni delle particelle α a grandi angoli, significa che vi può
essere una quasi totale trasformazione dell’energia cinetica incidente in energia
potenziale (per grandi angoli, nel limite di una retrodiffusione a 180°, la particella si
ferma per un istante alla minima distanza dal centro del potenziale). Quindi:
2Ze 2
2Ze 2
∆Eα = −Eα = V (RN ) = −
RN =
RN
Eα
Poiché e2=1.44 MeV.fm, e per Z ≈ 80 ed Ea ≈ 10 MeV, si ricava appunto che il
raggio nucleare vale RN ≈ 10-12cm. (per una descrizione delle unità usate vedi
paragrafi 1.3 e 1.5)
La scoperta del neutrone effettuata de Chadwick nel 1932 suggellò definitivamente
il modello del nucleo atomico. E’ da notare comunque che già nel 1920 era stata
suggerita da Rutherford la possibilità che un elettrone ed un protone potessero
essere così vicini nel nucleo da formare una particella neutra, e a questa particella
diede appunto il nome di neutrone. Inoltre, poiché la massa dell’elettrone è circa
2000 volte più piccola della massa del protone, questa ipotetica particella avrebbe
avuto la massa praticamente uguale a quella del protone, come di fatto è per il
neutrone.
Il nuclide è un ben definito nucleo costituito da un determinato numero di protoni e
di neutroni. Esso viene indicato come ZA XN o spesso più semplicemente ZAX dove:
- X sta a indicare l’elemento chimico;
- Z è il numero atomico dell’elemento, cioè il numero di protoni nel nucleo (anche
uguale al numero di elettroni atomici);
- A è il numero di massa del nucleo, cioè il numero totale di protoni (Z) e neutroni
(N). I protoni ed i neutroni vengono chiamati genericamente nucleoni
Ne risulta ovviamente che N=A-Z
Tutti i nuclidi con lo stesso numero di protoni Z si chiamano isotopi. Essi hanno lo
stesso numero di elettroni e quindi le stesse proprietà chimiche, e sono indicati
dallo stesso elemento X.
Tutti i nuclidi con lo stesso numero di neutroni N si chiamano isotoni: essi non hanno
in generale lo stesso numero di protoni (e di elettroni) e quindi appartengono ad
elementi chimici diversi.
Tutti i nuclidi con lo stesso numero di massa A si chiamano isobari: anche questa
volta non possono appartenere allo stesso elemento.
2
Esempio di isotopi:
6
7
12
3 Li 3 Li
6C
13
6
C
14
6
Esempio di isotoni:
2
3
14
15
1 H1 2 He1
6 C8 7 N8
16
8
Esempio di isobari:
14
14
6
6
6C 7N
2 He 4 3 Li3
6
4
C
O8
Be2
3
1
H2
3
2
He1
Il nome degli elementi è noto dalla chimica o dalla fisica atomica.
Un quantità importante del nuclide è la massa nucleare, cioè l’esatto valore della
massa del nucleo. Esso non va confuso con la massa atomica, che comprende anche la
massa degli elettroni. Le due quantità comunque sono numericamente molto vicine,
dato che gli elettroni sono molto meno massivi.
La massa di un nucleo costituito da Z protoni e N neutroni M(Z,N) non è uguale alla
somma delle masse dei nucleoni costituenti:
M(Z,A) ≠ Zmp + (A-Z)mn
essendo rispettivamente mp e mn la massa del protone e del neutrone.
Questo deriva dal principio di equivalenza massa-energia, principio fondamentale
della meccanica relativistica di Einstein espresso dalla famosa relazione: E=mc2, ed
ampiamente verificato nella fisica nucleare: “Massa ed energia sono essenzialmente
simili, sono soltanto espressioni differenti dello steso concetto. La massa di un
corpo non è costante, essa varia al variare della sua energia”. Ad una variazione di
energia ∆E di un sistema isolato deve essere associata una variazione di massa ∆m =
∆E/c2 e viceversa. Questo principio si applica anche alla massa a riposo dei nuclei.
L’energia potenziale dei nucleoni dentro il nucleo è negativa (stato legato): occorre
infatti compiere del lavoro per rimuovere protoni e neutroni dal nucleo. La forza
nucleare è infatti attrattiva, dovendo come minimo superare la enorme forza di
repulsione elettrostatica con la quale i protoni si respingono. Alla energia potenziale
negativa corrisponde una diminuzione di massa inerziale. Si definisce difetto di
massa di un nucleo la differenza:
∆m = Zmp + (A-Z)mn – M(Z,A)
Il difetto di massa rappresenta quindi anche l’energia di legame del nucleo, cioè il
lavoro che si deve compiere per portare tutti i nucleoni allo stato libero. Vediamo
ora come si misurano le masse atomiche (da queste si deducono le masse nucleari).
1.2 Lo spettrometro di massa
Lo spettrometro di massa dà informazioni sulla massa atomica caratteristica di un
particolare valore di Z ed A. Da questo valore, sottraendo Z volte la massa
dell’elettrone, si ottiene la massa del nucleo. In effetti, essendo gli elettroni legati,
la loro massa nell’atomo è minore della massa dell’elettrone libero: per il calcolo
esatto (valori riportati nelle tabelle dei nuclidi) va sottratta quindi l’energia di
legame atomica degli elettroni nell’atomo. Tuttavia questa energia di legame
3
elettronico rappresenta una correzione piccola, essendo dell’ordine del centinaio di
eV o al più di qualche keV.
Il funzionamento dello spettrometro è schematizzato in figura 1.2 (spettrometro
tipo Bainbridge)
Figura 1.2 Lo spettrometro di massa
La sorgente produce atomi ionizzati con carica +ne, massa M, ed una certa
distribuzione di velocità. Si noti che la carica ne dello ione non corrisponde alla
carica Ze dell’atomo, in quanto la ionizzazione non è completa: essa è prodotta per
effetto termoionico e quindi, di solito n=1 o al massimo n=2. Gli atomi ionizzati
passano attraverso il foro S1 e raggiungono la zona di campo magnetico B ed
elettrico E. L’insieme di questi due campi agisce come selettore di velocità. Infatti,
oltre la zona di campi B ed E vi è un secondo foro S2, e solo gli ioni che hanno un
ben determinata velocità lo attraversano. La velocità selezionata dai collimatori è
legata al valore di E e di B. Infatti le particelle si muovono di moto rettilineo solo se
le forze elettrica e magnetica si annullano, cioè quando: neE = nevB. Ossia: v = E/B
non dipende dal valore di n (nel seguito assumeremo n=1). Gli ioni di velocità fissata,
oltrepassato il foro S2, sono soggetti solo al campo magnetico costante e quindi
seguono una traiettoria circolare di raggio R, tale che:
RBe RB 2 e
Mv 2
. Da cui si ricava: M =
. La massa atomica può essere
=
evB =
R
v
E
determinata dalla misura assoluta di R, B ed E. In pratica si fa uso di masse note
4
per calibrare l’apparato. Con questo metodo si possono fare misure estremamente
accurate di masse atomiche. Inoltre con lo spettrometro di massa si possono
misurare, in un campione chimico, le percentuali isotopiche.
Un altro tipo di spettrometro di massa (tipo Dempster) è rappresentato in figura
1.3 In questo caso gli atomi ionizzati sono accelerati tra A e C da una d.d.p. V ed
escono dal foro S1 con energia cinetica data da:
eV = ½Mv2
(1)
Incontrano la zona di campo magnetico B e vengono deflessi in un moto circolare
definito dalla solita relazione:
Mv 2
(2)
evB =
R
Figura 1.3
Affinché gli ioni attraversino la fenditura S2 e siano rivelati in P, il raggio della
e
traiettoria deve avere un particolare valore, legato al rapporto
. Infatti:
M
e
eBR
2eV
2V
dalla (1): v 2 =
, e dalla (2): v =
. Eliminando quindi la velocità v:
= 2 2 .
M B R
M
M
2 2
e ⋅B R
Da cui si ricava il valore della massa M =
2V
e
corrisponde ad una data combinazione di V e B:
Per un fissato valore di R ogni
M
variando quindi V, B o entrambi, saranno selezionate dal foro diverse masse M.
5
Anche in questo caso lo strumento è calibrato sulla misura di masse note. Le figure
1.4 e 1.5 che seguono riportano alcuni spettri di massa.
Figura 1.5 spettro di massa del mercurio
6
Figura 1.4 spettro di massa del potassio
Figura 1.5 spettro di massa
7
1.3 Unità di misura per massa ed energia
In fisica nucleare la massa di un nucleo (e di un atomo) è misurata in unità di massa
atomica. L’unità di massa atomia (amu, da: atomic mass unit) è stata scelta come un
dodicesimo della massa atomica di un atomo neutro di 12C. Il valore di 1 amu può
essere facilmente espresso in grammi, ed è pari al reciproco del numero di
Avogadro. Infatti:
1
1 12
1 amu =
=1.66⋅10-24 g
m( 12 C ) =
12
12 NAv
Noi useremo però un’altra unità di misura, molto più pratica specie quando si devono
fare conti numerici che spesso coinvolgono energia e quantità di moto.
Dalla relazione di equivalenza massa-energia E=mc2 si ricava per l’energia a riposo di
una particella: Eo = moc2. Ad esempio, l’energia a riposo di un elettrone vale:
Eoe = moc2 = (9.11⋅10-31)⋅(3⋅108)2 = 8.2⋅10-14 J; per un protone si ha invece: Epe = moc2 =
(1.67⋅10-27)⋅(3⋅108)2 = 1.5⋅10-10 J. Tali unità di misura sono inadeguate per la misura
delle energie in fisica atomica e nucleare. Si ricorre ad un’altra unità di misura:
l’elettronvolt (eV) ed i suoi multipli (keV, MeV). Quando si accelera una carica q
tramite una differenza di potenziale V, il guadagno di energia cinetica vale: ∆T = qV.
Un elettronvolt è l’energia acquistata da un particella avente la carica unitaria (la
carica di un elettrone) attraverso una differenza di potenziale di un Volt:
1 eV =1.602⋅10-19 Coulomb⋅Volt = 1.602⋅10-19 Joule = 1.602⋅10-12 erg
con i rispettivi multipli: 1 keV = 103eV e 1 MeV = 106eV
In queste unità di misura: Eoe=0.511 MeV e EoP 938.21 MeV.
L’unità di misura della massa si ricava dalla solita equivalenza E=mc2. Si esprime m =
E/c2, e si prende come unità di misura della massa il valore espresso in MeV/c2
Così l’energia a riposo dell’elettrone vale 0.511 MeV, la sua massa a riposo vale 0.511
MeV/c2; l’energia a riposo del protone vale 938.21 MeV, la sua massa a riposo vale
938.21 MeV/c2. Possiamo introdurre una ulteriore semplificazione: specie quando si
fanno conti relativistici, è molto più utile usare il cosiddetto “sistema c=1”: come
unità di misura della velocità scegliamo la velocità della luce nel vuoto
(c=2.99796⋅108 m/s ≈ 3⋅108 m/s) e poniamo quindi c=1: lunghezza e tempo hanno le
stesse dimensioni:
1s → 3⋅108m
e
1m → 3.3⋅10-9s
Quindi la velocità, indicata con β (β = v /c appunto), è una grandezza adimensionale.
Inoltre, dalla relazione E=mc2 si vede che energia e massa hanno le stesse
dimensioni: scegliamo come unità di misura per entrambe il MeV. Anche il momento
p=mv ha le stesse dimensioni di m e di E, e sarà misurato anch’esso in MeV.
Vediamo alcune formule relativistiche che ci saranno utili nel seguito. Nel sistema
c=1 la relazione: E = mc2 diviene semplicemente: E = m
Nel caso di una particella in quiete: E = m0 , avendo indicato con m0 la massa a riposo
della particella. Se indichiamo con T l’energia cinetica possiamo scrivere:
E = m = m0 + T
8
D’altra parte, sempre dalla relatività ristretta, sappiamo che m = m0γ, dove
γ = (1 − β 2 )
−1 / 2
T = m – m0 = m0(γ-1)
Nel caso classico, dove β<<1 (ossia: v<<c) si può sviluppare γ in serie ed arrestarsi al
primo termine: γ = (1 − β 2 )
−1 / 2
≈ 1 + 21 β 2 che, sostituito nella espressione di T
fornisce la usuale relazione classica: T = m0(γ-1) = ≈ m0 (1 + 21 β 2 − 1) = 21 m0 β 2
La quantità di moto si scrive: p = mβ = Eβ. Pertanto il valore di β per una particella è
p
dato dal rapporto tra il suo momento p e la sua energia totale: β =
E
La quantità di moto si può anche scrivere: p = mβ = m0βγ. Quadrando: p2 = m02β2γ2
(γ 2 − 1) , β 2 γ 2 = (γ 2 − 1).
1
2
Le relazioni tra β e γ sono: γ 2 =
,
β
=
(1 − β 2 )
γ2
Pertanto: p2 = m02(γ2 –1) = m2 – m02 = E2 - m02 che fornisce le importanti relazioni:
E2 = p2 + m02 , ossia: E = p 2 + m02 , p = E 2 − m02
D’altra parte, poichè E = T + m0, si ha:
E 2 = p 2 + m02 = T 2 + m02 + 2Tm0 , da cui si ricava la relazione relativistica tra p e T:
p = T ⋅ (T + 2m0 )
che nel limite classico di basse velocità, quindi con T<<m0, si riduce a: p = 2m0 T
Vediamo ora alcuni esempi di impiego delle tabelle delle masse ed il loro utilizzo per
il calcolo dei difetti di massa e delle energie di legame. Cominciamo con il nucleo
“composto” più semplice esistente in natura, il deutone (nucleo dell’atomo di
deuterio) 21H1 ≡ d , composto da un protone e da un neutrone, per il quale Z=1 e A=2
Sulle tavole non si trovano le masse “nucleari” (che nel seguito indicheremo con m, in
minuscolo) ma le masse “atomiche” M.
Md = 1876.007 MeV è la massa dell’atomo di deuterio
Mp = 938.72 MeV è la massa dell’atomo di idrogeno
mn = 938.51 MeV è la massa del neutrone
Poiché sia l’atomo di deuterio che quello di idrogeno contengono un solo elettrone, si
ha che:
Md = md + me
Mp = mp + me
Come è facile verificare, a causa dell’energia di legame, risulta: md < mp + mn. Il
difetto di massa è pari a: ∆m = mp + mn - md = Mp + mn - Md = 2.22 MeV. Questa è
appunto l’energia di legame del deutone, e rappresenta il lavoro che bisogna fare per
separare il protone ed il neutrone.
Notare che abbiamo usato la masse atomiche, non quelle nucleari. Ma poiché il
numero degli elettroni che compare nei due termini della differenza è lo stesso, il
loro contributo in massa si cancella automaticamente. Questo è vero in genere, per
tutti i nuclei. In effetti nella massa a riposo bisognerebbe tener presente che gli
9
elettroni sono legati, e quindi sottrarre la loro energia di legame. Questa e’
comunque dell’ordine di 13.5⋅Z eV e quindi almeno 8 ordini di grandezza minore della
energia a riposo del nucleo (≈ A⋅109 eV)
Vediamo qualche altro esempio:
Carbonio 12: M6,12 = 11177.24 MeV
∆M6,12 = 6Mp +6mn –M6,12 = 92 MeV
Alluminio 27:
M13,27 = 25131.57.24 MeV
∆M13,27 = 13Mp +14mn –M13,27 = 229.4 MeV
Calcio 40: M20.40 = 37222.58 MeV
∆M20.40 = 20Mp +20mn –M20.40 = 342.0 MeV
Iodio 127:
M53,127 = 118203.5 MeV
∆M53,127 = 53Mp +74mn –M53,127 = 1072.3 MeV
1.4 Energia di legame. Proprietà generali dei nuclei
Si definisce “Energia di legame media per nucleone” l’energia di legame del nucleo
divisa per il numero di nucleoni che lo costituiscono.
BZ,A = ∆MZ,A
∆MZ,A
B BZ,A
=
=
A
A
A
Dai valori calcolati prima, ricaviamo:
nuclide
2
H
12
C
27
Al
40
Ca
127
I
B (MeV)
2.22
92.1
224.9
342.0
1072.3
B/A (MeV)
1.11
7.68
8.33
8.55
8.44
Possiamo notare che, ad eccezione del deuterio, l’energia di legame per nucleone è
pressoché costante e dell’ordine di 8 MeV.
In tabella 1.1 sono riportate le energie di legame e le caratteristiche di alcuni
nuclei.
10
Nuclide
Z
N=A-Z
B (MeV)
B/A (MeV)
1
1
n
0
1
0
H
1
2
1.113
2.225
1
H
1
4
7.07
28.29
2
He
2
5.61
39.24
4
Li7
3
9
6.46
58.15
5
Be
4
11
6.93
76.19
6
B
5
12
7.68
92.14
6
C
6
13
7.47
97.09
7
C
6
14
7.47
104.63
7
N
7
16
7.97
127.58
8
O
8
17
7.75
131.73
9
O
8
18
7.77
139.80
10
O
8
19
7.78
147.75
10
9
F
20
8.03
160.62
10
10
Ne
27
8.33
224.92
14
13
Al
28
8.45
236.51
14
14
Si
31
8.48
262.88
16
15
P
32
8.49
271.74
16
16
S
8.52
298.13
18
17
Cl35
37
8.57
317.00
20
17
Cl
40
8.59
313.71
22
18
A
40
8.55
341.92
20
20
Ca
56
8.79
493.11
30
26
Fe
63
8.75
551.92
34
29
Cu
75
8.70
652.23
42
33
As
88
8.73
768.13
50
38
Sr
98
8.63
845.73
56
42
Mo
116
8.52
988.14
66
50
Sn
120
8.50
1020.2
76
50
Sn
130
8.44
1096.6
76
54
Xe
136
8.39
1141.5
82
54
Xe
150
8.25
1237.1
90
60
Nd
176
8.06
1419.1
104
72
Hf
184
8.01
1473.5
110
74
W
7.92
1560.0
118
79
Au197
7.88
1623.7
124
82
Pb206
232
7.62
1763.0
142
90
Th
238
7.58
1803.1
146
92
U
La figura 1.6 rappresenta invece l’andamento di B/A in funzione di A.
11
Figura 1.6 andamento di B/A in funzione di A
Esiste inoltre una correlazione tra il numero di protoni Z ed il numero di neutroni N
che compongono un nucleo: se osserviamo infatti come sono disposti i nuclei nel
piano Z-N (fig 1.7), notiamo che questi si addensano in una regione ristretta del
piano e quindi secondo una relazione del tipo Z=Z(N), oppure Z=Z(A). Per i nuclei
A
stabili si ottiene: Z =
2.0 + 0.015 ⋅ A2 / 3
In particolare, per A < 40 si ha che N ≈ Z; per nuclei più pesanti N aumenta più
velocemente di Z. Il motivo, che sarà meglio spiegato nel seguito, è il seguente:
tutti i nucleoni, cioè sia i protoni sia i neutroni, subiscono indistintamente la forza
nucleare attrattiva, mentre solo i protoni subiscono la forza elettrostatica
repulsiva. Quando Z cresce, la stabilità del nucleo tende a diminuire a causa della
repulsione coulombiana, le forze nucleari attrattive devono quindi aumentare ed è
necessario un numero N di neutroni percentualmente maggiore.
1.5 Valori di alcune costanti utili.
Abbiamo introdotto nuove unità di misura per l’energia e la massa.
La lunghezza è spesso misurata in “fermi”, fm)
1 fm = 10-15 m = 10-13 cm
Già che siamo in argomento, apriamo una parentesi riguardante i valori numerici di
alcune costanti espresse in MeV e fermi. E’ utile ricordarli: questo semplificherà di
molto i calcoli che faremo nel seguito del corso.
e2
1
la costante di struttura fine (adimensionale) vale:
α=
=
hc 137
12
la costante di Plank, espressa in MeV·s, vale:
h = 6.58·10-22 MeV·s
la velocità della luce vale invece:
c = 3 1010cm/s =30 cm/ns =3 1023fm/s
Ricaviamo allora due importanti valori numerici, che incontreremo spesso nel
seguito:
hc = 197.4 MeV⋅fm
hc
= 1.44 MeV⋅fm
e2 =
137
Figura 1.7 la rappresentazione dei nuclei stabili nel piano Z-N
13