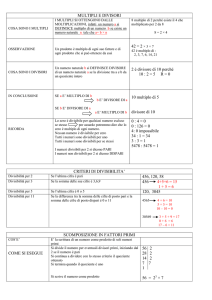
MULTIPLI E DIVISORI
Si dice multiplo
p di un numero “a” diverso da zero,, ogni
g numero
naturale che si ottiene moltiplicando a per ciascun elemento di N.
Poiché N = 0,1,2,3...7....95,..104..
Zero è multiplo di tutti i numeri quindi non lo si considera, inoltre poiché
l’insieme N è infinito anche i multipli di un numero sono infiniti. L’insieme
dei multipli
p di un numero si indica
Es : M4= 0,4,8,12,16,20,...44,....100,..220..
Solo lo zero ha un solo multiplo : 0
Altri esempi : M8 = 0,8,16,24,32,...40,....104,..224..
M7 = 0,7,14,21,35,...49,....105,..217..
DIVISORI
Se una divisione è esatta o propria cioè non ha resto, Es : a:b = c il
divisore dato “b” sarà detto anche divisore di a o sottomultiplo
p di a
a = multiplo di b
a= divisibile per b
b = sottomultiplo di a
b = divisore di a
Se la divisione a : b = c + resto non è esatta si dirà che:
a non è divisibile per b
b non è divisore di a.
I sottomultipli di un numero diverso da zero si dicono fattori di quel numero,
l’insieme dei divisori si indica:
D8= 1,2,4,8
D10= 1,2,5,10
D13= 1,13
OSSERVAZIONI
L’insieme
L
insieme dei divisori di un numero è finito
finito.
1 è divisore di tutti i numeri.
Ogni numero è divisibile per se stesso.
Se un numero a è divisibile per il numero b saranno divisibile per b anche i
sui multipli Es : 21 è divisibile per 3 e per 7, anche 42, 63, 210 …saranno
divisibili per 3 e per 7
CRITERI DI DIVISIBILITA’
DIVISIBILITA
PER 2 : Un numero è divisibile per 2 se l’ultima sua cifra a destra è pari o zero
((0 – 2 – 4 - 6 – 8).
) Es:
Sono divisibili per 2 : 34; 876; 900; 654; 3456….
Non sono divisibili per 2 : 65; 87; 549; 8761,……….
PER 5 : Un numero è divisibile per 5 se l’ultima sua cifra a destra è 5 o zero
(0 – 5). Es:
Sono divisibili p
per 5 : 35; 875; 900; 170; 34585….
Non sono divisibili per 5 : 643; 887; 2549; 80761,……….
PER 10 -100 -1000 : Un numero è divisibile per 10-100-1000… se l’ultima sua
cifra a destra è uno zero, due zeri, tre zeri…….
(0 – 00 – 000 – 0000…….). Es:
Sono divisibili per 10 : 30; 870; 950; 170; 34580….
N sono di
Non
divisibili
i ibili per 10 : 643
643; 887;
887 2549;
2549 80761,……….
80761
Sono divisibili per 100: 400, 5300, 7400, 763 200, …)
Non sono divisibili per 100: 340
340, 5320,
5320 2189,
2189 43876..)
43876 )
PER 3 e per 9 : Un numero è divisibile per 3 se sommando tutte le sue cifre si
ottiene un multiplo di 3. Es:
Sono divisibili per 3 : 36 perché 3+6 =9; 876 perché 8+7+6 = 21;
900 perché 9+0+0 =9 ;
654 perché 6+5+4 = 15
N sono di
Non
divisibili
i ibili per 3 : 65 perché
hé 6
6+5
5 = 11
11;
82 perché
hé 8
8+2
2 =10;
10
841 perché 8+4+1=13;
Un numero è divisibile per 9 se sommando tutte le sue cifre si ottiene un
multiplo di 9. Es:
Sono divisibili per 9 : 405 perché 4+0+5 =9 7317 perché 7+3+1+7 = 18
Non sono divisibili per 9: 329 perché 3+2+9 =14
806 perchè 8+0+6 =14
PER 4: Un numero è divisibile per 4 se le ultime due cifre sono 00 oppure
multipli di 4
(00 – 04 – 20 - 40 – 08 – 80 – 12 – 16 – 32 – 36…) Es :
Sono divisibili per 4 : 340, 520, 7656
Non sono divisibili per 4 : 342, 574, 4321
PER 25: Un numero è divisibile p
per 25 se le ultime due cifre sono 00
oppure multipli di 25
(00 – 25 – 50 – 75) Es :
Sono divisibili per 25 : 350, 2500, 7675
Non sono divisibili per 25 : 340, 5472, 43205
PER 11: Un numero è divisibile per 11 se la differenza tra la somma delle sue cifre
di posto dispari e quella delle sue cifre di posto pari (o viceversa) è zero, 11 o
multiplo
p di 11.
Sono divisibili per 11 : 363 perché (3+3) – 6 =0,
3509 perché (5+9) – (3 + 0) =14-3=11,
7656 perché (7+5) – (6+6) = 12 -12 =0
Non sono divisibili per 11 : 342, 574, 4321 perché …..
NUMERI PRIMI
Un numero si dice primo se ammette solo due divisori : 1 e il numero stesso.
Es:
D7= 1;7
D23= 1;23
D53= 1;53
Tutti
T
tti glili altri
lt i numerii sii di
dicono composti.
ti I numerii parii eccetto
tt il 2 sono
composti.
D27= 1;3;9;27
Es : D14= 1;2;7;14
L’unico numero pari primo è il 2 perché ha solo due divisori: 1 e 2
Esiste un metodo per individuare i numeri primi, si chiama “CRIVELLO DI
ERATOSTENE” consiste nello scrivere i primi 100 o più numeri,
nell’eliminare
nell
eliminare tutti quei numeri pari e quelli che rispondono ai criteri di
divisibilità studiati; i numeri rimanenti saranno numeri primi.
I numeri primi compresi tra 1 e 1000 si trovano anche nelle prime pagine
delle tavole numeriche
numeriche.
CRIVELLO DI ERATOSTENE
SCOMPOSIZIONE DI UN NUMERO IN FATTORI PRIMI
I numeri composti si possono scomporre nel prodotto di due o più fattori
primi .
Es:
Oppure :
7
42
42= 2 x 3 x7
2
6
42
21
7
1
2
3
7
3
2
6
54 = 2 x3 x 3 x3
3
54
3
9
3
54 = 2 x 33
54
27
9
3
1
2
3
3
3
Divisibilità di un numero p
per un altro
Un numero è divisibile per un altro se, scomposti entrambi in fattori primi, il primo
numero contiene tutti i fattori del secondo numero con esponente uguale o
maggiore
Es : 1116; e 93
Scomposti in fattori primi:
1116 = 22 x 32 x 31
93 = 3 x 31
Poiché 1116 scomposto in fattori primi contiene sia il 3 che il 31 si dirà
di i ibil per 93
divisibile
93.
Il quoto della divisione sarà :
1116 : 93 = 22 x 322-11 x 3111-11 = 22 X 3 = 4 x 3 =12
Massimo Comune Divisore (M.C.D.)
(
)
Il Massimo Comune Divisore tra due o più numeri è il divisore maggiore
tra tutti i divisori in comune.
Es : M. C. D. (15; 36)
D15 =
1;3;5;15
D15
D36= 1;3
D36= 1;2;3,4;6;9;12;18;36
Il divisore maggiore in comune è 3
Ricerca del Massimo Comune Divisore con il
metodo della scomposizione in fattori primi
Il M.C.D. di due o più numeri si ottiene scomponendo i numeri dati in fattori primi
e moltiplicando i fattori comuni, presi una sola volta, con l’esponente minore.
E : M.C.D
Es
M C D ( 400
400; 160)
400 22 x 52
4 22
1
400 =
24
x
52
160
16
8
4
2
1
2x5
2
2
2
2
160 = 25 x 5
M.C.D (400;160) = 24 x 5 = 80
Minimo comune multiplo (m
(m.c.m.)
cm)
Il minimo comune multiplo tra due o più numeri è il multiplo minore tra
tra i multipli in comune.
Es : m. c. m. (16; 36)
M16 = 16;32;48;64 : 80;96;112;128;144
M36 = 36;72;108;144
m.c.m (16,36) = 144
Se uno dei due numeri è multiplo del secondo sarà pure il m.c.m.
Es : m.c.m.( 4 ; 12) = 12
Se i due numeri sono primi tra loro il m.c.m. sarà il loro prodotto:
Es : m.c.m.( 4 ; 15) = 4 x 15 =60
Ricerca del minimo comune multiplo
p con il metodo
della scomposizione in fattori primi
Il m.c.m. di due o più numeri si ottiene scomponendo i numeri dati in fattori primi
e moltiplicando i fattori comuni, presi una sola volta, con l’esponente maggiore e i
fattori non comuni.
Es : m.c.m ( 45; 120)
45 3
15 3
5 5
1
45 = 32 x 5
120
12
6
3
1
2 x5
2
2
3
120 = 23 x 3 x 5
m.c.m ( 45; 120) = 32 x 23 x 5 = 9 x 8 x5 = 360