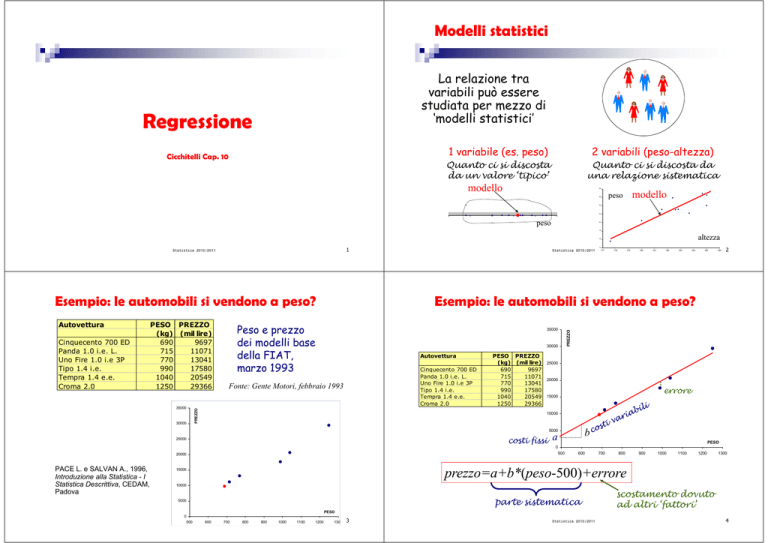
Modelli statistici
La relazione tra
variabili può essere
studiata per mezzo di
‘modelli statistici’
Regressione
Cicchitelli Cap. 10
1 variabile (es. peso)
2 variabili (peso-altezza)
Quanto ci si discosta
da un valore ‘tipico’
Quanto ci si discosta da
una relazione sistematica
modello
88
86
modello
peso
84
82
peso
80
78
altezza
76
1
Statistica 2010/2011
Cinquecento 700 ED
Panda 1.0 i.e. L.
Uno Fire 1.0 i.e 3P
Tipo 1.4 i.e.
Tempra 1.4 e.e.
Croma 2.0
PESO PREZZO
(kg) (mil lire)
690
9697
715
11071
770
13041
990
17580
1040
20549
1250
29366
35000
30000
Peso e prezzo
dei modelli base
della FIAT,
marzo 1993
35000
30000
Autovettura
Cinquecento 700 ED
Panda 1.0 i.e. L.
Uno Fire 1.0 i.e 3P
Tipo 1.4 i.e.
Tempra 1.4 e.e.
Croma 2.0
Fonte: Gente Motori, febbraio 1993
179
180
181
182
183
184
185
186
2
PESO PREZZO
(kg) (mil lire)
690
9697
715
11071
770
13041
990
17580
1040
20549
1250
29366
25000
20000
errore
15000
10000
5000
costi fissi
25000
20000
PACE L. e SALVAN A., 1996,
Introduzione alla Statistica - I
Statistica Descrittiva, CEDAM,
Padova
178
Esempio: le automobili si vendono a peso?
PREZZO
Autovettura
177
PREZZO
Esempio: le automobili si vendono a peso?
Statistica 2010/2011
74
b
a
0
500
PESO
600
700
800
900
1000
1100
1200
1300
prezzo=a+b*(peso-500)+errore
15000
10000
parte sistematica
5000
PESO
0
500
600
700
800
900
1000
1100
1200
130
3
Statistica 2010/2011
scostamento dovuto
ad altri ‘fattori’
4
Esempio di relazione lineare crescente
Sintesi
tramite
funzioni
analitiche
Equazione della retta: Y = β0+β1X
La relazione tra due
variabili numeriche
può essere
sintetizzata con una
funzione matematica
(retta, parabola,
logaritmo …)
La retta è la
funzione più
semplice da
adattare ai dati e da
interpretare
β1 =
β0 è l’intercetta, cioè il punto in cui la retta interseca l’asse
di Y (valore di Y quando X=0)
β1 è la pendenza o coefficiente angolare o rapporto
incrementale (variazione in Y quando X aumenta di 1)
Levine, Krehbiel, Berenson - Statistica II ed.© 2006 Apogeo
5
Regressione lineare semplice
ΔY
ΔX
6
Regressione lineare semplice
REGRESSIONE: metodo per studiare come una
variabile di risposta (detta anche variabile
dipendente) Y dipende da una o più variabili
esplicative (dette anche variabili indipendenti o
regressori)
In
uno studio sui fattori che influenzano la spesa
annuale per consumi di una famiglia, la variabile di
risposta è la spesa annuale per consumi, mentre le
variabili esplicative sono il reddito annuale
complessivo, il tipo di lavoro svolto dal capofamiglia, il
numero di componenti della famiglia, …
Statistica 2010/2011
Statistica 2010/2011
SEMPLICE: è il caso in cui vi è una sola variabile
esplicativa Æ si tratta di un metodo bivariato perché
riguarda due variabili: una variabile di risposta Y e una
variabile esplicativa X
LINEARE: si assume che, nella popolazione, la relazione
tra la variabile di risposta Y e la variabile esplicativa X
sia di tipo lineare (= una retta); più precisamente, si
assume che per ogni valore x appartenente al range di X
il valor medio di Y condizionatamente a x, M(Y |X=x), sia
una funzione lineare di x
La regressione lineare semplice è un metodo per studiare la dipendenza di una
variabile quantitativa Y da una variabile X che può essere sia quantitativa che
qualitativa (anche se in questo corso trattiamo solo il caso di X quantitativa);
quando la risposta Y è qualitativa occorrono modelli di regressione di altro tipo
7
Statistica 2010/2011
8
Regressione lineare semplice
Regressione lineare semplice
Variabile indipendente
(esplicativa)
Variabile dipendente
(risposta)
y = β 0 + β1 x + ε
Parte sistematica
Parte accidentale
(segnale)
(rumore)
L’ipotesi fondamentale del modello è che l’effetto di X
sulla media di Y sia completamente catturato dalla parte
sistematica; in altri termini, che la media della parte
accidentale non dipenda da X
M (ε | X = x) = 0 ∀x
In alternativa
M (Y | X = x) = β 0 + β1 x ∀x
Questo modello ipotizza che la risposta y sia generata dalla somma di
• una parte sistematica (che è funzione lineare di x)
• una parte accidentale (che è puramente casuale e quindi non dipende da x)
Statistica 2010/2011
9
Statistica 2010/2011
Regressione lineare semplice
Interpretazione della pendenza
Il modello assume che la relazione che lega la media di
Y condizionata a X sia una funzione lineare di X (per i
valori x appartenenti al range)
Supponiamo che X assuma un certo valore x* in corrispondenza del
quale la media condizionata di Y è
M (Y | X = x* ) = β 0 + β1 x*
Y = “spesa per consumi” e X = “reddito”
ad ogni valore del reddito x appartenente al range
corrisponde un insieme di famiglie con una certa
distribuzione della spesa per consumi e quindi con una certa
spesa media per consumi M(Y | X=x). La teoria economica
(supportata dall’evidenza empirica) sostiene che al crescere
del reddito cresce la spesa per consumi, cioè M(Y | X=x) è
funzione crescente di x; se si usa la regressione lineare
semplice si assume che tale funzione sia lineare
Statistica 2010/2011
10
Supponiamo poi che X aumenti di 1 e quindi assuma il valore x*+1, in
corrispondenza del quale la media condizionata di Y è
M (Y | X = x* + 1) = β 0 + β1 ( x* + 1)
11
Sottraendo si ottiene
M (Y | X = x* + 1) − M (Y | X = x* ) = β1
Pertanto β1 è la variazione della media condizionata di Y conseguente
all’aumento di 1 di x, qualunque sia il valore x* di partenza
Statistica 2010/2011
12
Interpretazione della pendenza
Dal modello ai dati
L’interpretazione di β1 dipende dall’unità di misura delle
due variabili
Se X è l’altezza in cm e Y è il peso in kg allora β1 è
espresso in kg/cm perché rappresenta la variazione in kg
del peso quando l’altezza aumenta di 1 cm
Popolazione o campione di
n unità statistiche
variabili
i = 1, 2,K , n
Si aggiunge l’indice i
Unità
statistiche
Yi = β0 + β1xi +εi
Statistica 2010/2011
13
⎡ y1 ⎤
⎢M⎥
⎢ ⎥
⎢ yi ⎥
⎢ ⎥
⎢M⎥
⎢⎣ yn ⎥⎦
⎡ x1 ⎤
⎢M⎥
⎢ ⎥
⎢ xi ⎥
⎢ ⎥
⎢M⎥
⎢⎣ xn ⎥⎦
14
Statistica 2010/2011
Dati e retta di regressione stimata
stima
y
Determinare la retta di
regressione:
il metodo dei minimi quadrati
.
yˆi
yi
Statistica 2010/2011
15
.
retta stimata
β 0 ⇒ b0
β1 ⇒ b1
dati
. .
. . .
. . .. .
.
.
.
yˆi = b0 + b1 xi
.
.
b0 + b1x
ei
xi
Statistica 2010/2011
x
16
Retta di regressione stimata
Retta di regressione stimata
In termini geometrici: dato un diagramma di
dispersione (che rappresenta n osservazioni della coppia
di variabili in esame), qual è la retta che si adatta meglio
ai punti, che passa più “vicina” all’insieme dei punti?
Occorre stabilire una misura di
distanza tra retta e insieme di punti (punto di vista geometrico)
errore di previsione complessivo (punto di vista algebrico)
I valori x sono considerati quantità date per cui il problema della
previsione riguarda i valori y
yi = valore osservato di Y per l'unità i
yˆi = b0 + b1 xi = valore previsto di Y per l'unità i
ei = yi − yˆi = errore di previsione (scarto)
In termini algebrici: come si calcolano l’intercetta b0 e
la pendenza b1 della retta di regressione stimata in modo
che l’errore di previsione che si commette con la retta sia
il più piccolo possibile?
Il criterio più usato per definire la distanza tra retta e insieme di punti
o per definire l’errore di previsione complessivo è quello della
somma dei quadrati degli errori (di previsione)
n
Statistica 2010/2011
2
i
i =1
17
Minimi Quadrati (MQ)
n
∑ e = ∑ ( y − yˆ )
Retta di MQ
i =1
i
2
i
18
Statistica 2010/2011
ŷ = b0 + b1 x
n
La retta che rende minimo l’errore di previsione
quadratico è chiamata retta dei minimi quadrati
Le rette del piano sono infinite, ognuna individuata in
modo univoco da una coppia di valori (intercetta,
pendenza): determinare la retta dei minimi quadrati
significa determinare la coppia di valori (intercetta,
pendenza) per cui la somma dei quadrati degli errori è
minima
Da un punto di vista matematico si tratta di un problema
di minimizzazione di una funzione in due variabili; per
fortuna, la soluzione è unica ed è esprimibile con due
semplici formule
Statistica 2010/2011
C
b1 = XY =
DX
∑ ( x − x )( y − y )
i
i =1
i
n
∑ (x − x )
i =1
2
=
Cov( X , Y ) σ XY
= 2
Var ( X )
σX
i
b0 = y − b1 x
CXY è detta CODEVIANZA, σXY è detta COVARIANZA
Per determinare i coefficienti della retta di MQ occorrono
quattro indici: media di Y, media di X, devianza di X,
codevianza tra X e Y
19
Statistica 2010/2011
20
Esempio: come crescono i bambini? /1
Il ritmo di crescita varia da
bambino a bambino, possiamo
capire meglio il modello
generale di crescita
osservando come varia nel
tempo l’altezza media di un
gruppo di bambini
18
19
20
21
22
23
24
25
26
27
28
29
Altezza media per mese di
161 bambini
Es. tratto da Moore (2005)
Y=Altezza media (variabile dipendente)
altezza
media (cm)
76.1
77.0
78.1
78.2
78.8
79.7
79.9
81.1
81.2
81.8
82.8
83.5
Statistica 2010/2011
Scatterplot
dell’altezza media di
161 bambini per età
84.0
83.0
82.0
81.0
altezza (cm)
età (mesi)
Esempio: come crescono i bambini? /2
80.0
79.0
78.0
77.0
X=Età (variabile esplicativa)
76.0
75.0
16
18
20
22
24
26
28
30
3
età (mesi)
I punti sono quasi allineati Æ una linea retta che passa
tra i punti descrive bene il legame tra X e Y
21
Esempio: come crescono i bambini? /3
22
Statistica 2010/2011
Esempio: come crescono i bambini? /4
I coefficienti della retta di MQ sono
Retta di MQ: altezza=64.93+0.635*età
84.0
83.0
82.0
Cov( X , Y )
b1 =
Var ( X )
b0 = y − b1 x
altezza (cm)
81.0
80.0
b0=64.93 cm intercetta:
altezza media alla nascita
(età=0)
79.0
78.0
77.0
76.0
75.0
Nel nostro esempio:
M(x)=23.5 mesi, M(y)=79.85
Var(x)=11.52, Cov(x,y)=7.57
16
18
20
22
24
26
28
30
3
età (mesi)
b1=7.57/11.52=0.635
b0=79.85-23.5*0.635=64.93
Statistica 2010/2011
23
b1=0.635 pendenza: l’altezza dei bambini cresce
ogni mese in media di 0.6 cm Æ la pendenza
della retta è il tasso di variazione Y al variare di X
Statistica 2010/2011
24
Alcune proprietà delle stime di MQ
Alcune proprietà dei MQ
n
b1 =
C XY
=
DX
∑ ( x − x )( y − y )
i
i =1
i
n
∑ (x − x )
i =1
b0 = y − b1 x
2
n
i
b1 =
La retta dei MQ passa per il baricentro
x=x
⇒
i =1
i
∑
i i
i
i
i
y − ∑ i yˆi = 0
i i
yˆi = ∑ i yi
(da cui segue yˆ = y )
∑ yˆ = ∑ ( b + b x ) = ∑ ( ( y − b x ) + b x )
= ∑ y +b ∑ (x − x) = ∑ y
i
i
i
1
Traslazione
1 i
0
i
25
Statistica 2010/2011
i
Infatti :
∑ e = ∑ ( y − yˆ ) = ∑
b0 = y − b1 x
∑ ( xi − x )2
La somma dei valori stimati è uguale alla somma dei
valori osservati
=0
Infatti :
i
n
i =1
La somma dei residui è nulla
∑e
i
i =1
yˆ = y
Infatti : yˆ = b0 + b1 x = ( y − b1 x ) + b1 x = y
n
C XY
=
DX
∑ ( x − x )( y − y )
i
i
1
i
i
1 i
i
Statistica 2010/2011
26
Cambiamento di scala
x ' = dx x
Consideriamo una traslazione a della x
x' = x + a ⇔
x = x '− a
y = β0 + β1x + ε
y = β 0 + β1 x + ε
⎛ x' ⎞
y'
= β0 + β1 ⎜ ⎟ + ε
dy
⎝ dx ⎠
= β 0 + β1 ( x '− a ) + ε
= ( β 0 − β1a ) + β1 x '+ ε
Caso speciale: a = − x , cioè x ' = x − x
⎛d
⎞
y ' = d y β0 + ⎜ y β1 ⎟ x '+ d yε
⎝ dx ⎠
Pendenza invariata
→ Pendenza invariata
• espansione della scala y (dy > 1) Æ aumenta pendenza
→ Nuova intercetta ben interpretabile:
è il valore previsto di y quando x = x
Statistica 2010/2011
y ' = dy y
• espansione della scala x (dx > 1) Æ diminuisce pendenza
27
Statistica 2010/2011
28
Interpolazione
Possiamo utilizzare la retta di regressione per
prevedere il valore di Y per un dato valore di X
non osservato, ma interno al range di X
(nell’esempio 18-29 mesi).
Interpolazione
ed
estrapolazione
Altezza media dei bambini per x=20.5 mesi:
altezza=64.93+0.635*20.5=77.95 cm
Statistica 2010/2011
29
30
Statistica 2010/2011
Estrapolazione
Esempio del tempo TV: dati
Possiamo utilizzare la retta di regressione per prevedere
il valore di Y per un dato valore di X esterno al suo range
(nell’esempio 18-29 mesi).
I dati riportati nella tabella seguente si riferiscono all’età in anni
(X) e al tempo in minuti passato davanti alla televisione
nell’ultima settimana (Y) per un campione di 6 soggetti:
Altezza media dei bambini per x=32 mesi:
altezza=64.93+0.635*32=85.25 cm
L’accuratezza dell’estrapolazione dipende da:
• quanto la retta si adatta bene ai dati
• quanto il valore di X è lontano dai valori osservati
Esempio
X=0 è un valore esterno lontano Æintercetta potrebbe
non essere una buona previsione dell’altezza alla nascita
Statistica 2010/2011
Somma
Media
31
Età
X
34
42
55
59
61
63
314
52.3
Tempo TV
Y
430
365
620
580
800
780
3575
595.8
Statistica 2010/2011
n
∑ (x − x )
i =1
i
2
= 683.333
n
∑ ( x − x )( y − y ) = 9118.333
i =1
i
i
32
Esempio del tempo TV: interpretazione
Esempio del tempo TV: retta di regressione
n
b1 =
∑ ( x − x )( y − y )
i
i =1
i
n
∑ (x − x )
i =1
2
=
9118.333
= 13.344
683.333
i
b0 = y − b1 x = 595.8 − 13.344 × 52.3 = −102.498
tempo TV (Y)
Diagramma di dispersione e retta di regressione
900
800
700
600
500
400
300
200
100
0
yˆ = −102.498 + 13.344 x
0
10
20
30
40
50
60
70
La pendenza b1 = 13.3 è la variazione media del tempo TV settimanale
in minuti corrispondente ad un aumento di 1 anno dell’età
Poiché la pendenza è positiva all’aumentare dell’età tende ad
aumentare il tempo TV:
1 anno in più Æ aumento medio di 13.3 minuti per settimana
2 anni in più Æ aumento medio di 26.6 minuti per settimana
10 anni in più Æ aumento medio di 133 minuti per settimana
1 anno in meno Æ riduzione media di 13.3 minuti per settimana
… ecc.
L’intercetta b0 = –102.5 è il tempo TV settimanale previsto per un
soggetto di età zero (x=0)
In questa applicazione l’intercetta non è interpretabile perché non ha
senso chiedersi qual è il valore previsto del tempo TV per un
neonato!
L’intercetta è un caso speciale di valore previsto (è il valore previsto di Y
quando x=0)
età (X)
Statistica 2010/2011
33
Statistica 2010/2011
Esempio del tempo TV: previsioni
Interpolazione vs estrapolazione
La retta di regressione può essere usata per calcolare il valore previsto
di Y in corrispondenza di un qualunque valore di X, sia un valore
osservato nel campione che un valore non osservato
Usando la retta di regressione precedente yˆ = −102.498 + 13.344 x
si ottengono, ad esempio, i seguenti valori previsti (arrotondati all’intero)
x
-10
0
20
30
55
60
70
100
500
ŷ
-236
-102
164
298
631
698
832
1232
6570
In ogni applicazione si può determinare a priori (cioè
indipendentemente dai dati effettivamente rilevati) un
intervallo di valori di x che ha senso prendere in
considerazione
nell’esempio del tempo TV l’intervallo di x che ha senso
considerare va grosso modo da 3 a 100 anni
A posteriori, alla luce dei dati effettivamente rilevati,
l’intervallo di valori di x che è opportuno utilizzare per
prevedere la Y non dovrebbe essere molto più ampio del
cosiddetto intervallo rilevante, cioè l’intervallo di valori
assunti dalla variabile esplicativa X nel campione osservato
nell’esempio del tempo TV l’intervallo rilevante va da 34 a
63 anni
La retta, come funzione matematica, è definita
sull’intero asse dei reali e quindi qualsiasi valore
x di X può essere usato per fare la previsione di Y
Tuttavia non tutti i valori di x hanno senso nel
contesto applicativo: nell’esempio del tempo TV
x è l’età e quindi non può essere negativa, ma
non ha senso nemmeno prendere in
considerazione valori di x vicini a 0 (perché i
neonati non guardano la TV) e valori di x oltre
100 (perché gli esseri umani raramente superano
tale età)
Statistica 2010/2011
34
35
Statistica 2010/2011
36
Interpolazione vs estrapolazione
I pericoli dell’estrapolazione
Diagramma di dispersione e retta di regressione
Interpolazione: prevedere Y in corrispondenza di un valore x
interno all’intervallo rilevante (come la previsione di 398 per
x=60)
Estrapolazione: prevedere Y in corrispondenza di un valore
x esterno all’intervallo rilevante (come la previsione di 164 per
x=20 o la previsione di 832 per x=70)
Le estrapolazioni vanno evitate o, per lo meno, limitate a
valori x appena fuori dall’intervallo rilevante.
Infatti la retta di regressione è stata determinata usando i valori x
dell’intervallo rilevante e non vi è alcun modo di sapere come la retta si
modificherebbe aggiungendo valori x esterni all’intervallo rilevante;
facendo estrapolazioni si assume implicitamente che aggiungendo
valori x esterni la retta rimarrebbe sostanzialmente invariata, ma tale
ipotesi non è verificabile ed è tanto meno plausibile quanto più i punti
considerati sono lontani dall’intervallo rilevante
Statistica 2010/2011
tem po TV (Y)
Intervallo rilevante
900
800
700
600
500
400
300
200
100
0
0
10
20
30
40
50
60
70
età (X)
La linea rossa rappresenta una possibile relazione tra Y e X nella
popolazione, mentre la retta nera è la retta di regressione determinata
con i dati campionari, in cui l’intervallo rilevante è [34,63]
37
38
Statistica 2010/2011
Misure di variabilità nella regressione
DY (Devianza totale di Y): misura la variabilità dei valori Y
osservati attorno alla loro media
n
DY = ∑ ( yi − y ) 2
i =1
Bontà di adattamento della
retta di regressione:
il coefficiente di
determinazione r2
DSL (Devianza di Y Spiegata della regressione Lineare su X):
misura la variabilità dei valori Y previsti attorno alla loro media
(la quale, per una proprietà del metodo dei minimi quadrati,
coincide con la media dei valori osservati)
n
n
i =1
i =1
DSL = ∑ ( yˆi − yˆ ) 2 = ∑ ( yˆi − y ) 2
DRL (Devianza di Y Residua rispetto alla regressione Lineare
su X): misura la variabilità degli errori di regressione attorno
alla loro media
n
n
n
DRL = ∑ (ei − e ) 2 = ∑ ei 2 = ∑ ( yi − yˆi ) 2
i =1
Statistica 2010/2011
39
i =1
Statistica 2010/2011
i =1
40
Misure di variabilità nella regressione
Misure di variabilità nella regressione
Con alcuni passaggi algebrici si dimostra che
DY = DSL + DRL
n
DRL = ∑( yi − yˆi )2
i =1
n
DY = ∑( yi − y )2
n
DSL = ∑ ( yˆi − y ) 2
i =1
i =1
Statistica 2010/2011
41
Coefficiente di determinazione r2
Il coefficiente di determinazione è la
proporzione di variabilità totale di Y
spiegata dalla relazione lineare con X:
La regressione può essere vista come un metodo per
spiegare la variabilità di una variabile (Y) tramite la
relazione lineare con un’altra variabile (X)
La spesa per consumi (Y) varia molto da famiglia a famiglia e può
essere misurata da SST (che è il numeratore della varianza).
D: perché le famiglie hanno consumi diversi? R: i motivi sono
molti, uno è perché le famiglie hanno redditi diversi e il consumo
cresce al crescere del reddito.
D: quanto è importante il ruolo del reddito nello spiegare la
variabilità dei consumi delle famiglie? R: assumendo una
relazione lineare tra consumi e reddito, la risposta è fornita dalla
scomposizione di SST nelle due parti SSR (variabilità dei
consumi spiegata dalla relazione lineare con il reddito) e SSE
(variabilità residuale dei consumi)
Statistica 2010/2011
42
Statistica 2010/2011
Regressione: spiegare la variabilità
Pertanto la regressione lineare semplice opera una
scomposizione della variabilità totale di Y in due parti,
interpretabili come
DSL: variabilità di Y spiegata da X (più precisamente:
variabilità di Y dovuta alla relazione lineare con X )
DRL: variabilità residuale di Y (cioè non dovuta alla
relazione lineare con X)
43
DSL
DY
Poiché DSL≥0 e DSL≤DY segue che r2 ∈[0,1]. Dunque r2 è un
indice normalizzato: per ogni insieme di dati r2 ha valore min 0 e
max 1
Il coefficiente di determinazione misura la bontà di adattamento
della retta di regressione; infatti per la scomposizione di DY, r2 si
può scrivere anche
r2 = 1−
r2 =
DRL
DY
La retta di regressione si adatta ai dati tanto meglio quanto più
piccola è la somma dei quadrati degli errori, DRL, ovvero quanto
più grande è il coefficiente di determinazione r2 (ma r2 è più
facilmente interpretabile perché è un indice normalizzato)
Statistica 2010/2011
44
Coefficiente di determinazione r2
Coefficiente di determinazione r2
Misurare la bontà di adattamento è cruciale per
l’interpretazione e l’utilizzo dei risultati della regressione
La retta di regressione è la retta che meglio si adatta ai dati,
quella che minimizza l’errore di previsione complessivo
(definito dalla somma dei quadrati degli errori);
Tuttavia la migliore retta potrebbe comunque fare un pessimo
lavoro, cioè la regressione lineare potrebbe spiegare solo una
piccola parte della variabilità di Y (Æ enormi errori di
previsione)
Quando il coefficiente di determinazione r2 è piccolo
l’adattamento della retta è scarso e quindi la regressione
lineare è uno strumento inutile
45
Statistica 2010/2011
Calcolo di r2
Per calcolare r2 occorre calcolare DY e, a scelta, uno dei due
termini della scomposizione della devianza
La via più veloce è quella di calcolare DSL perché
n
n
DSL = ∑ ( yˆi − y ) = ∑ ( (b0 + b1 xi ) − (b0 + b1 x ) )
i =1
2
Nell’esempio del tempo TV si ha
DY = 157220.833
DX = 683.333
b1 = 13.344.
Pertanto, DSL = (13.344)2 × 683.333 = 121675.870
2
i =1
n
n
= ∑ b1 ( xi − x ) 2 = (b1 ) 2 ∑ ( xi − x ) 2 = (b1 ) 2 DX
i =1
46
Statistica 2010/2011
Calcolo di r2
Il metro di giudizio sul valore assunto da r2 dipende dal
contesto applicativo: in alcuni campi r2 è solitamente su
valori tra 0.15 e 0.30, in altri campi (ad es. serie temporali)
r2 è spesso intorno a 0.90 Æ non si può dire in generale
quale sia la soglia al di sotto della quale r2 debba ritenersi
insoddisfacente
Caso limite r2=1: accade quando DRL=0, il che significa
che tutti gli errori di previsione sono nulli e quindi tutti i
punti del diagramma di dispersione giacciono sulla retta di
regressione (che può avere qualunque pendenza, positiva
o negativa)
Caso limite r2=0: accade quando DSL=0, il che significa
che i valori previsti yˆi sono tutti uguali a y e quindi la retta
di regressione è orizzontale (ha pendenza nulla)
i =1
D
121675.870
r = SL =
= 0.7739
DY 157220.833
Pertanto r2 si può scrivere anche
2
⎛ CXY ⎞
⎜
⎟ DX
2
2
DSL (b1 ) DX ⎝ DX ⎠
CXY
2
=
=
=
r =
DY
DY
DY
DX DY
Statistica 2010/2011
2
Questo è il quadrato
del coefficiente di
correlazione lineare
(vedi più avanti)
47
Statistica 2010/2011
Il 77.39% della
variabilità del tempo TV
è spiegata dalla relazione
lineare con l’età
48
Errore medio di previsione
La radice quadrata della varianza residua è interpretabile
come l’errore medio che si commette prevedendo Y tramite il
modello di regressione lineare su X
σ RL =
La simmetria di r2
L’indice è simmetrico: rimane invariato cambiando l’ordine di
X e Y cioè invertendo il ruolo di X e Y nella regressione: la
regressione di Y su X e la regressione di X su Y producono lo
stesso coeff. di determinazione, cioè hanno la stessa bontà di
adattamento
Dunque i risultati della regressione non forniscono alcuna
indicazione in merito alla scelta di quale variabile usare come
risposta e quale come esplicativa: tale scelta è
necessariamente basata sulla conoscenza a priori di quale è
la causa (= l’esplicativa) e quale l’effetto (la risposta); in
mancanza di tale conoscenza la scelta è effettuata
arbitrariamente dall’analista in base al punto di vista che vuole
privilegiare
DRL
1
( yi − yˆi )2
=
∑
n
n i=1
DRL = 157220.833 − 121675.87 = 35544.963
σ RL =
35544.963
= 76.969
6
(minuti)
Statistica 2010/2011
2
CXY
DX DY
Guadiamo l’indice di determinazione nella forma
n
Nell’esempio del tempo TV
r2 =
49
Statistica 2010/2011
50
Relazioni causa-effetto
Regressione e relazioni
causa-effetto
Statistica 2010/2011
51
Si può affermare che X è la causa e Y l’effetto?
La domanda è rilevante sia da un punto di vista
teorico (come funziona il mondo?) che pratico
Infatti, se si interviene nel sistema fissando la X
ad un valore arbitrario, in presenza di una pura
relazione causa-effetto la Y risponde
assumendo il valore medio previsto dal modello,
altrimenti ha un comportamento imprevedibile
Statistica 2010/2011
52
Relazioni causa-effetto: esempio
Relazioni causa-effetto e regressione
Sia X la spesa annuale in pubblicità e Y l’ammontare annuale
di vendite
La pendenza stimata usando i dati degli ultimi anni è 1.2, cioè
ogni euro in più di spesa in pubblicità è associato a 1.2 euro in
più di vendite: se l’anno prossimo l’azienda aumenta la spesa
in pubblicità di 100000 euro si deve attendere un aumento
delle vendite di 120000 euro (e viceversa se riduce la spesa)
Queste previsioni sono attendibili? No!
Il modello di regressione può evidenziare
un’associazione tra X e Y ma non consente di dire niente
sulla relazione causa-effetto
Ad es. non vi è alcun criterio statistico per preferire (1) la
regressione del consumo sul reddito piuttosto che (2) la
regressione del reddito sul consumo (ricorda: entrambe le
regressioni hanno lo stesso r2): è la teoria economica che
suggerisce di usare la versione (1), in quanto asserisce che il
reddito influenza il consumo e non viceversa
Tuttavia per certe finalità può essere utile specificare la
regressione in modo contrario alla relazione causa-effetto:
nell’esempio precedente la versione (2) potrebbe essere
specificata dall’Agenzia delle Entrate qualora disponga di dati sui
consumi dei contribuenti e voglia usarli per inferire il loro reddito
In realtà l’ammontare delle vendite dipende solo in parte dalla
pubblicità, perché è fortemente influenzato da fattori come il ciclo
economico
Inoltre è pure possibile una relazione inversa, cioè che la spesa in
pubblicità sia influenzata dall’andamento delle vendite (se le
vendite aumentano si rendono disponibili risorse aggiuntive che
possono essere destinate alla pubblicità)
Statistica 2010/2011
53
Relazioni causa-effetto e regressione
54
Statistica 2010/2011
Tipi di relazioni causa-effetto
Date due variabili, i due possibili modi di
specificare il modello di regressione
(scambiando i ruoli di risposta ed esplicativa)
sono solo due punti di vista alternativi: scegliere
un punto di vista o l’altro ovviamente non
modifica la realtà, semplicemente si traggono
impressioni diverse dello stesso fenomeno
Date due variabili osservate Z1 e Z2 le possibili relazioni
causali sono:
Z1
Z2
Z1
Z2
Z1 causa Z2
Assenza di relazione
è
come assistere ad un incontro di calcio dalla tribuna
o dalla curva: ciò non modifica l’incontro, anche se si
ottengono impressioni diverse
Z1
Z2
Z1
Z2 causa Z1
Statistica 2010/2011
55
Z2
Z1 causa Z2 e viceversa
Statistica 2010/2011
56
Relazioni causa-effetto e variabili nascoste
Relazioni causa-effetto e variabili nascoste
L’unico modo affidabile di stabilire una relazione causa-effetto
consiste nel raccogliere i dati tramite un esperimento
controllato (assegnare a caso le unità statistiche ai diversi valori
di X, poi osservare la Y)
Al di fuori dei dati sperimentali, vi è sempre un pericolo in
agguato: la relazione tra Z1 e Z2 potrebbe essere in tutto o in
parte dovuta ad una variabile non osservata, o comunque non
inclusa nell’analisi Z0 (variabile nascosta)
Z1
Z2
Associazione tra Z1 e Z2
interamente dovuta a Z0
Z1
Z2 = capacità respiratoria
57
Z2
Associazione tra Z1 e Z2
in parte dovuta a Z0
Z0 = età
Esempio. In una applicazione su bambini di
diverse età: Z1 = lunghezza del piede; Z2 =
numero di vocaboli conosciuti; Z0 = età. La
regressione del numero di vocaboli sulla
lunghezza del piede dà luogo ad una pendenza
positiva significativa, ma ovviamente tra le due
variabili non vi è alcuna relazione causa-effetto
Statistica 2010/2011
Z0
Z1 = numero di sigari fumati al giorno
La regressione della capacità respiratoria sul numero di sigari dà luogo ad una
pendenza significativa (di segno negativo: cioè all’aumentare del numero di sigari la
capacità polmonare tende a diminuire). Tuttavia, entrambe le variabili sono associate
all’età: negli anziani è maggiore la frequenza sia di coloro che fumano il sigaro, sia di
coloro che hanno scarsa capacità polmonare. Gli studi epidemiologici hanno
dimostrato che il fumo (anche quello di sigaro) riduce la capacità polmonare, cioè
esiste una relazione causa-effetto: tuttavia, se nell’analisi si ignora che i soggetti
hanno diverse età, risulta un’associazione più forte di quanto è realmente (la
pendenza della retta di regressione è “troppo” negativa perché incorpora anche
l’effetto dell’età). Una semplice soluzione è di eseguire l’analisi di regressione
separatamente per fasce di età.
58
Statistica 2010/2011
Analisi dei residui
www.causeweb.org
Z0
Esempio. In una applicazione su adulti di
diverse età:
Punti influenti
Variabili nascoste
59
Statistica 2010/2011
60
Analisi dei residui
Residui disposti casualmente
r2 non sempre è sufficiente a verificare la bontà
di adattamento del modello
ei = yi − yˆ i
residui
Plot dei residui vs valori previsti:
La
relazione tra X e Y è lineare?
La variabilità di Y resta costante al variare di X?
Sono presenti valori anomali nei dati?
Statistica 2010/2011
61
Statistica 2010/2011
62
Esempio: relazione non lineare
Analisi dei residui: relazione non lineare
x
6.10
5.91
1.79
2.37
1.66
5.21
4.04
1.95
3.64
2.94
5.38
2.34
2.55
0.91
3.96
y
87.49
83.59
11.71
18.64
9.87
67.96
42.31
12.75
33.63
23.53
68.19
17.60
17.90
4.54
41.09
Y*=-20.25+16.64X
r2=0.9716
Analisi dei residui: relazione
quadratica tra X e Y?
Statistica 2010/2011
63
Statistica 2010/2011
64
Esempio: relazione non lineare (segue)
Analisi dei residui: varianza di Y non costante
Y*=1.49+1.79X+2.03X2
r2=0.9986
Analisi dei residui:
andamento casuale
Statistica 2010/2011
65
Osservazioni particolari
66
Esempio: outlier (residui grandi)
x
-0.73
-0.24
0.41
1.51
2.46
2.71
2.93
3.10
3.37
3.55
4.12
4.26
4.62
6.00
7.92
OUTLIER: osservazione con residuo elevato
(valore anomalo di Y rispetto alla previsione)
LEVERAGE (punto di leva): valore anomalo
della variabile indipendente (X)
PUNTI INFLUENTI: osservazioni con
comportamento anomalo che influenzano
notevolmente i risultati
Non tutti gli outlier e i leverage sono necessariamente
punti influenti
Statistica 2010/2011
Statistica 2010/2011
y
-1.57
2.69
2.67
-1.94
12.54
13.47
14.14
14.89
15.03
15.40
19.46
18.46
20.76
1.95
34.29
Y*=2.11+3.27X
r2=0.5731
Valori anomali!!
67
Statistica 2010/2011
68
Valori anomali e osservazioni influenti
Esempio: outlier (residui grandi) /segue
Cancelliamo i valori anomali
e ristimiamo il modello …
Un valore anomalo è un’osservazione che sta
“lontana” dalle altre osservazioni. I punti che
presentano un valore anomalo per Y (outlier)
hanno residui alti, ma i punti con valori anomali
in X (leverage) non necessariamente
presentano residui alti!
Un’osservazione è influente se la sua rimozione
comporta un cambiamento notevole nelle stime
dei parametri e/o in r2. Punti con valori anomali
in X sono spesso influenti!
Y*=2.06+4.04X
r2=0.9925
Migliore adattamento del
modello!!
69
Statistica 2010/2011
Esempio: parola e abilità
Esempio: parola e abilità /segue
L’età in cui un bimbo inizia a parlare è un buon previsore del punteggio ad
un successivo test di abilità mentali?
x
15
26
10
9
15
20
18
11
8
20
7
y
95
71
83
91
102
87
93
100
104
94
113
x
9
10
11
11
10
12
42
17
11
10
y
96
83
84
102
100
105
57
121
86
100
Il bambino n.18
inizia a parlare
molto più tardi
degli altri: per la
sua posizione
estrema (leverage)
questo punto ha
una forte influenza
sulla posizione
della retta di
regressione!
Per 21 bambini si conosce l’età, in mesi X, in cui
è stata pronunciata la prima parola e il punteggio
ad un test di abilità Y (Moore e McCabe)
n.19 Y grande!
Y*=109.87-1.127X
n.18: x grande!
r2=0.41
Statistica 2010/2011
70
Statistica 2010/2011
outlier
leverage
Attenzione: non tutti i valori anomali sono influenti!!
71
Statistica 2010/2011
72
Esempio: parola e abilità /segue
y = 105.6299 - 0.779221*x
r2= 0.11
www.causeweb.org
Cosa succede se cancelliamo l’osservazione n.18?
La relazione tra X
e Y è debole!
Prima sembrava
alta a causa della
sola osservazione
n. 18! Servono
più dati per
capire meglio la
relazione
studiata!
Statistica 2010/2011
73
Esempio: cambiamento strutturale
anno
1990
1991
1992
1993
1994
1995
1996
1997
x
4595
4827
4427
4258
3995
4330
4265
4351
y
7364
7547
7099
6894
6572
7156
7232
7450
74
Esempio: cambiamento strutturale \segue
I residui mostrano un
andamento differenziato:
da cosa dipende?
Il dipartimento di matematica di una
grande università deve pianificare il
numero di corsi elementari richiesti.
X = studenti iscritti al primo anno
Y = studenti che scelgono il corso di
matematica
Andamento per anno: dal 1995 una %
più elevata di studenti sceglie il corso
di matematica. È questo cambiamento
che spiega l’andamento osservato nei
residui! I dati antecedenti il 1995 non
possono essere usati per previsioni
Y*=2492.69+1.066X
r2=0.694
Statistica 2010/2011
75
Statistica 2010/2011
76
Variabili nascoste: esempio #1
Per le nazioni del mondo rileviamo
Variabili nascoste: esempio #2
X = numero di apparecchi TV per 1000 abitanti
Y = speranza di vita alla nascita
X = indice di sovraffollamento
Y = indice di mancanza di servizi igienici
La regressione di Y su X fornisce un coefficiente
angolare positivo e un elevato indice di determinazione
Possiamo allungare la vita del popolo del Rwanda
inviando loro delle TV? NO!
Le nazioni più ricche hanno più TV di quelle povere e
hanno anche una speranza di vita più elevata perché
hanno una migliore alimentazione, acqua potabile e cure
mediche.
Non c’è un rapporto di causa effetto tra TV e speranza di
vita!!
77
Statistica 2010/2011
Poiché X e Y sono entrambe misure di abitazioni
inadeguate ci aspettiamo una forte relazione; invece la
regressione produce r2=0.006. Come è possibile?
Ulteriori indagini hanno mostrato che in alcuni dei
quartieri più poveri c’è una prevalenza di case pubbliche,
con servizi igienici, mentre in altri non è così
La relazione tra X e Y è diversa in questi due tipi di
quartiere Æ analizzare tutti i quartieri insieme oscura la
relazione tra X e Y.
Due gruppi formati da una variabile categorica
Teorizzazione fenomeno
Y su X | Z=0 Æ r2 = 0.79
Y su X | Z=1 Æ r2 = 0.41
Individuazione variabili
esplicative
Y su X | tutti Æ r2 = 0.12
Formulazione o
identificazione modello
Z=1
Uso dei dati per la stima
del modello
La rappresentazione grafica è importante per capire il
legame tra X e Y nei sottogruppi individuati da Z!
Statistica 2010/2011
78
Statistica 2010/2011
Modello statistico: costruzione e uso
Variabili nascoste: esempio #3
Z=0
Uno studio sulle condizioni di salute nella città di Hull
(GB) ha misurato per i quartieri più poveri della città
Uso del modello:
• Descrizione delle
relazioni
• Inferenza
(conoscenza del
processo
generatore dei dati)
• Previsione dei valori
della variabile di
risposta
verifica modello
79
Utilizzo del modello
Statistica 2010/2011
80
Covarianza /1
Correlazione
Cicchitelli Cap. 11
Consideriamo due variabili quantitative, ad es. SPESE (X) e
RENDIMENTO (Y) nel 2003 per 9 fondi comuni
Esiste una associazione tra SPESE e RENDIMENTO ?
Ovvero: al crescere delle spese il rendimento tende a crescere,
tende a calare o nessuna delle due?
Spese
Rendim.
70.0
1.25
37.3
60.0
0.72
39.2
50.0
1.57
44.2
1.40
44.5
1.33
53.8
1.61
56.6
1.68
59.3
R en d im en to (Y)
40.0
30.0
20.0
10.0
Statistica 2010/2011
81
Covarianza /2
μY= 51.533 e σY= 9.951
66.5
1.50
2.00
82
Statistica 2010/2011
Ma questi indici non dicono nulla sulla associazione tra X e Y
Per questo fine serve un indice calcolato congiuntamente, come la
covarianza
−+
60.0
e σX= 0.271
μX=1.353
1.20
1.00
Spese (X)
70.0
Sia per le SPESE (X) che per il RENDIMENTO (Y) posso calcolare
separatamente media e deviazione std
62.4
0.50
Covarianza /3
Rendimento (Y)
1.42
0.0
0.00
50.0
++
Y
40.0
−−
30.0
20.0
+ + e − − concordanti
10.0
+ − e − + discordanti
0.0
0.00
0.50
+−
X
1.00
1.50
2.00
Spese (X)
Statistica 2010/2011
83
Statistica 2010/2011
84
Covarianza /4
Covarianza /5
Le osservazioni (Xi, Yi) con valori concordanti
hanno scarti dalla media con lo stesso segno (+
+ o − −) e quindi il prodotto degli scarti ha segno
positivo
Le osservazioni (Xi, Yi) con valori discordanti
hanno scarti dalla media con segno opposto (+ −
o − +) e quindi il prodotto degli scarti ha segno
negativo
Per ottenere un indice di associazione basta
sommare i prodotti degli scarti e vedere se il
risultato è positivo (prevalgono i concordanti) o
negativo (prevalgono i discordanti)
Cov ( X , Y ) = σ XY
85
Statistica 2010/2011
Calcolo della covarianza
1.353
spese (X) rendim (Y)
1.25
37.3
0.72
39.2
1.57
44.2
1.40
44.5
1.33
53.8
1.61
56.6
1.68
59.3
1.42
62.4
1.20
66.5
X-M(X)
-0.103
-0.633
0.217
0.047
-0.023
0.257
0.327
0.067
-0.153
Covarianza 9.579 / 9 = 1.064
Statistica 2010/2011
1
=
N
N
∑ (x − μ
i =1
i
X
)( yi − μY )
Se positiva Æ al crescere di X, Y tende a crescere
(notare l’uso della parola tende: infatti, se una unità sta
sopra alla media per X è probabile che vi stia anche per Y,
ma non è detto)
Se negativa Æ al crescere di X, Y tende a diminuire
Se nulla Æ non vi è nessuna tendenza
Statistica 2010/2011
86
Coefficiente di correlazione lineare /1
51.533
Y-M(Y)
-14.233
-12.333
-7.333
-7.033
2.267
5.067
7.767
10.867
14.967
prodotto
1.466
7.807
-1.591
-0.331
-0.052
1.302
2.540
0.728
-2.290
9.579
I valori minimo e massimo assumibili dalla covarianza
dipendono dai dati in esame Æ non si può dire se un
valore (come il 1.064 dell’esempio) sia da considerarsi
grande o piccolo
Per questo si trasforma la covarianza in modo che abbia
sempre lo stesso minimo (−1) e massimo (+1)
ρ XY =
σ XY
σ X σY
Nell’esempio ρXY = 1.064 / (0.271 × 9.951) = 0.395
87
Statistica 2010/2011
88
Coefficiente di correlazione lineare /2
Media del prodotto delle variabili standardizzate:
ρ XY =
Coefficiente di correlazione lineare /3
1
N
N
∑z
i =1
xi
z yi
zx =
xi − μ X
i
zy =
σX
i
yi − μY
σY
Simmetrico: ρ rimane invariato se le due variabili sono
scambiate
Numero puro: ρ non ha unità di misura (es. X altezza in cm, Y
peso in kg Æ SXY è in cm×kg, SX è in cm, SY è in kg, e quindi rXY
è un numero puro)
Invariante per trasformazioni lineari: ρ rimane invariato se le
variabili vengono linearmente trasformate (traslazione e/o
moltiplicazione per una costante) (es. X temperatura in gradi
Celsius, Y raccolto in quintali, ρ non cambia se si esprime la
temperatura in gradi Fahrenheit e il raccolto in tonnellate)
rXY >0 Æ X e Y correlate positivamente
rXY <0 Æ X e Y correlate negativamente
rXY =0 Æ X e Y incorrelate (assenza di correlazione)
rXY = +1 Æ X e Y hanno massima (perfetta) correlazione
positiva = tutte le osservazioni stanno su una retta
crescente
rXY = −1 Æ X e Y hanno massima (perfetta) correlazione
negativa = tutte le osservazioni stanno su una retta
decrescente
89
Statistica 2010/2011
90
Statistica 2010/2011
Diagrammi di dispersione con vari
Coefficienti di Correlazione
Y
Y
Y
X
X
r = -1
r=0
Y
Y
r = +1
X
r = -0.6
Y
r = -0.9
X
X
r = +0.3
Statistica 2010/2011
Diagrammi di
dispersione per
due variabili
utilizzando sei
data set con 100
osservazioni
r = -0.3
r = -0.6
r = +0.3
X
r=0
91
r = +0.6
r = +0.9
92
Correlazione e linearità /1
Correlazione e linearità /2
L’indice rXY fa una sintesi di tutte le osservazioni, ma nei dati vi
potrebbero essere andamenti molto diversi
Il termine “lineare” è spesso sottinteso, ma è importante: infatti rXY
misura l’associazione di tipo lineare (e non parabolico,
esponenziale o altro)
Æ rXY = −1 o +1 significa che vi è relazione lineare perfetta
Æ rXY = 0 significa che, nel complesso, vi è assenza di relazione
lineare, ma vi potrebbe essere una relazione non lineare, anche
forte!
In questo es. vi sono
due sottoinsiemi, uno
con correlazione
negativa e l’altro con
correlazione positiva.
Nel complesso la
correlazione è positiva
(r = 0.612)
Statistica 2010/2011
In questo es. vi è una
relazione di tipo
parabolico, con due
sottoinsiemi. Nel
complesso la
correlazione è quasi nulla
(r = -0.001)
93
Correlazione e causalità /1
94
Correlazione e causalità /2
Se due variabili X e Y sono correlate signfica che tendono
a muoversi insieme (in modo concorde se r >0 o discorde
se r <0)
Es: X = “spesa in pubblicità” e Y = “fatturato”
Ma il valore di r non dice niente su come e perché X e Y
si muovono insieme: può essere che
X è causa di Y
Y è causa di X
X è causa di Y e al tempo stesso Y è causa di X
X e Y non sono in relazione di causa-effetto
(cosiddetta correlazione spuria)
Statistica 2010/2011
Statistica 2010/2011
In una certa regione geografica è stata rilevata una forte
correlazione tra X = “numero di cicogne di passaggio” e Y =
“numero di bambini nati”
è un caso di correlazione spuria, perché tra X e Y non vi è
alcuna relazione!
In alcuni casi la correlazione tra X e Y è generata da una terza
variabile Z nascosta
95
X influenza Y, ma anche Y influenza X
Es. X = “macchie gialle sulle dita” e Y = “tosse”: non vi è
relazione causa-effetto, ma la variabile Z = “fumatore” è
causa di entrambe e provoca la correlazione
Statistica 2010/2011
96
Correlazione e causalità /3
Concordanza
Le serie temporali spesso danno luogo a forti
correlazioni spurie perché vi sono andamenti simili nel
tempo e nello spazio, ad es. in quasi tutti i paesi del
mondo di anno in anno i prezzi crescono, così come gli
studenti che frequentano la scuola superiore, il numero
di donne nel mercato del lavoro …
E’ quindi plausibile trovare una correlazione positiva
elevata tra due fenomeni che tendono a crescere nel
tempo, es. il prezzo delle banane in Italia e il salario
degli operai canadesi, oppure il numero di laureati in
Brasile …
Statistica 2010/2011
Il
coefficiente di correlazione di Bravais-GaltonPearson misura la correlazione lineare (assume i
valori estremi in caso di perfetta relazione lineare)
97
Massima concordanza/discordanza
Tra due variabili X e Y vi è concordanza o
correlazione positiva quando tendono a
crescere insieme
Nel caso contrario si parla di discordanza o
correlazione negativa
Il termine correlazione viene spesso usato nel
senso restrittivo di correlazione lineare, che è
un tipo particolare di concordanza
Indice di Spearman /1
Si elencano le coppie (xi,yi) in ordine crescente
della x:
i valori della y sono crescenti Æ massima
concordanza
Se i valori della y sono decrescenti Æ massima
discordanza
Per ognuna delle due variabili si trasformano i valori in
ranghi (ranks), cioè posizioni in graduatoria (dal più piccolo)
Se
Statistica 2010/2011
98
Statistica 2010/2011
Voto riportato
da 10 studenti
agli esami di
matematica X
e statistica Y
99
id
x
y
g(x)
g(y)
1
25
28
6
8
2
18
21
1
2
3
20
23
2
4
4
27
30
8
10
5
28
24
9
5
6
22
20
4
1
7
21
22
3
3
8
30
29
10
9
9
26
26
7
7
10
24
25
5
6
Statistica 2010/2011
100
Indice di Spearman /2
Indice di Spearman /3
L’indice di Spearman (o coefficiente di
correlazione tra ranghi) rS è il coefficiente di
correlazione lineare tra i ranghi delle due
variabili
Nell’esempio precedente
Coeff.
x
1
5
10
25
y
0.12
0.60
1.20
3.00
x
1
5
10
25
y
0.00
1.61
2.30
3.22
y = 0.12x
y = ln(x)
r=1
rS = 1
3.50
3.00
2.50
2.00
y
di correlazione lineare: r = 0.78
Coeff. di correlazione tra ranghi: rS = 0.76
Perfetta relazione lineare crescente (decrescente)
Æ Massima concordanza (discordanza)
Massima concordanza o discordanza
non implica perfetta relazione lineare
Minimo rS = −1 in caso di massima discordanza
Massimo rS = +1 in caso di massima
concordanza
101
Statistica 2010/2011
Indice di Spearman – caso di parità
In caso di parità (due o più unità con lo stesso valore) si attribuisce il
rango medio
Voto riportato
da 10 studenti
agli esami di
matematica X
e statistica Y
id
x
y
g(x)
g(y)
1
25
28
6
8
2
20
21
1.5
2
3
20
23
1.5
4
4
27
30
8
10
5
28
25
9
6
6
22
20
4
1
7
21
22
3
3
8
30
29
10
9
9
26
25
7
6
10
24
25
5
6
Statistica 2010/2011
rS = 0.78
103
1.50
1.00
r = 0.90
rS = 1
0.50
0.00
0
5
10
15
20
25
30
x
Statistica 2010/2011
102












