itemset

Parallel Frequent Set Counting
Progetto del corso di Calcolo Parallelo
AA 2001-02
Salvatore Orlando
CALCOLO PARALLELO - S. Orlando
1
Cosa significa association mining?
•
Siano dati
– un insieme di item
– un insieme di transazioni, ciascuna contenete un sottoinsieme di item
•
Vogliamo trovare regole/associazioni del tipo:
– if I1 then I2
(sup, conf)
dove:
– I1, I2 sono insieme di item (itemset)
– I1, I2 hanno un sufficiente supporto: P(I1+I2) = sup
– La regola associativa ha sufficiente confidenza: P(I2 | I1) = conf
CALCOLO PARALLELO - S. Orlando
2
Association mining
•
L’utente specifica l’ “interesse” delle regole:
– Minimum support (minsup)
– Minimum confidence (minconf)
1. Frequent Set Countint (FSC):
– Trova tutti gli itemset frequenti (> minsup)
•
•
Spazio di ricerca esponenziale
Molto costoso sia per quanto riguarda
– Computazione e I/O
2. Genera regole
• Solo regole associative forti (> minconf)
• Passo poco costoso
CALCOLO PARALLELO - S. Orlando
3
Esempio
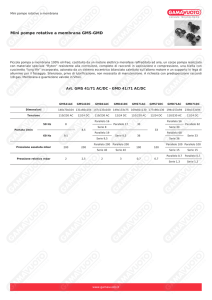
Esempio:
TID
1
2
3
4
5
{Pannolini,Latte} ⇒s,c Birra
Items
Pane, Latte
Birra, Pane, Pannolini, Uova
Birra, Coca, Pannolini, Latte
Birra, Pane, Pannolini, Latte
Coca, Pane, Pannolini, Latte
Association rule: X⇒s,c y
Support: s =σ(X∪y) / |T|
Confidence:
c = σ(X∪y) / σ(X)
s = σ({Pannolini,Latte, Birra}) / Tot_trans =
= 2/5 = 0.4 = 40%
c = σ({Pannolini,Latte, Birra}) /
σ({Pannolini,Latte}) =
= 2/3 = 0.66
Il supporto è la probabilità che un certo
itemset appaia nelle transazioni del dataset.
s=P({Pannolini,Latte, Birra})
La confidenza è una probabilità condizionata
c=P({Pannolini,Latte, Birra} | {Pannolini,Latte})
CALCOLO PARALLELO - S. Orlando
4
Complessità computazionale esponenziale
•
•
•
Dati n transazioni e m differenti item:
– numero di pattern potenzialmente frequenti: O(2m)
– complessità computazionale: O(n2m)
•
Apriori: ricerca di tutti i pattern frequenti, basato su vincoli di
supporto minimo [Agarwal & Srikant]:
– 6HLOSDWWHUQ^$%`KDXQVXSSRUWRGLDOPHQR.DOORUDVLD$HB hanno
XQVXSSRUWRGLDOPHQR.
– 6H$RSSXUH%KDQQRXQVXSSRUWRPLQRUHGL.DOORUD^$%`KDQQRun
VXSSRUWRPLQRUHGL.
⇒ - usa i pattern frequenti di k-1 item per ridurre lo spazio
di ricerca dei pattern lunghi k
- itera il procedimento
CALCOLO PARALLELO - S. Orlando
5
Apriori (Frequent Set Counting)
•
Colleziona i conteggi degli item singoli
– seleziona solo gli item più frequenti
•
Individua le coppie “candidate” ed effettua i conteggi
– seleziona solo le coppie più frequenti
•
Individua le triple “candidate” ed effettua i conteggi
– seleziona solo le triple più frequenti
•
E così via …
•
Principio guida: tutti i sottoinsiemi di un itemset frequente sono anch’essi
frequenti
– Questo principio è usato da Apriori per effettuare il pruning dei
candidati
CALCOLO PARALLELO - S. Orlando
6
Illustriamo il principio di Apriori
 m
Senza pruning |Ci| = 
i
|C1| = 6 |C2| = 15 |C1| = 20
Con pruning:
6+6+2=14
CALCOLO PARALLELO - S. Orlando
7
Contare gli itemset frequenti
•
Gli itemset frequenti sono individuati contando quanti candidati appaiono
in ciascuna delle transazioni del database
•
Per velocizzare il conteggio, bisogna velocizzare la ricerca dei vari
candidati all’interno di ciascuna transazione
– Esistono vari metodi, che fanno affidamento dell’ordinamento degli
item all’interno delle transazioni e degli itemset
– Item rappresentati tramite identificatori numerici
CALCOLO PARALLELO - S. Orlando
8
Prima iterazione di Apriori
•
•
•
•
m:
D:
t:
F1:
gli identificatori numerici associati agli item vanno da 1 a m
file delle transazioni
generica transazione
set dei set frequenti di lunghezza 1
CALCOLO PARALLELO - S. Orlando 9
Loop principale
• Ck:
•
itemset candidati di lunghezza k
L’algoritmo Apriori termina all’iterazione k se non si individuano itemset
frequenti, oppure se non si trovano candidati
CALCOLO PARALLELO - S. Orlando
10
Generazione dei candidati con pruning
•
•
•
Gli itemset in Fk e Ck sono ordinati
c ∈ Ck se e solo se tutti i k-1-itemset c’ ⊂ c appartengono a Fk-1
Condizione necessaria affinché un k-itemset c possa appartenere a Ck
– se esiste una coppia di itemset di Fk-1 che con c condividano un identico
prefisso di k-2 elementi
La condizione diventa sufficiente se tutti i sottoinsiemi di k-1 elementi di c
appartengono a Fk-1
CALCOLO PARALLELO - S. Orlando 11
•
Ordinamento
•
•
Item come numeri
Transazioni a formato variabile
– ciascuna transazione è una lista di interi ordinati in maniera crescente
•
Itemset (itemset sia candidati e sia frequenti) ordinati
• Fk e Ck come vettori di itemset
– Vettori ordinati lessicograficamente
– Ordinamento di Fk-1 utile per rendere più efficiente la costruzione di Ck
• Più semplice individuare prefissi
– Ordinamento di Ck utile per rendere più efficiente la ricerca dei
candidati, e quindi la fase di conteggio
CALCOLO PARALLELO - S. Orlando
12
Ordinamento e conteggio
•
L’ordinamento degli item può essere sfruttata per determinare i candidati
contenuti in una certa transazione
Vengono usate strutture dati complesse per memorizzare i candidati e
velocizzare la ricerca
– Hash-tree o Prefix-tree
•
•
Vogliamo qui suggerire un metodo più semplice da implementare
– Sia data una transazione ordinata
• t={t0, t1, t2, …. ,tz-1 }, z = |t|
– i 2-prefix dei possibili k-itemset ordinati presenti in t
• coppie ordinate (I0,I1), dove I0 ∈ t e I1 ∈ t
• se I1 = tj allora in t esistono al massimo z-j-1 item che possono
essere usati per costruire un k-itemset contenuto in t
• quindi, se z-j-1 < k-2, allora (I0,I1) non può essere un 2-prefix
ammissibile
CALCOLO PARALLELO - S. Orlando
13
Ordinamento e conteggio: subset_and_count(Ck, t)
Tail di t
Ck
Counts
t={t0, t1, t2, t3, …. ,tz-1}
I0
•
I1
Per ogni (I0, I1)
Segmento di Ck
con uno stesso
2-prefix (I0, I1)
– Effettua una ricerca binaria su Ck per
individuare l’inizio del segmento
composto da candidati (k-itemset)
con prefisso: (I0, I1)
– Scorri sequenzialmente il segmento
per controllare se ciascun candidato
è un sottoinsieme di Tail di t, e
aggiorna eventualmente i contatori
associati
CALCOLO PARALLELO - S. Orlando
14
Tecniche di parallelizzazione
•
Consideriamo che
– Il Dataset può essere grande (elaborazione su disco)
– Per valori piccoli di minsup si ottengono molti candidati
•
Data parallelism
– Partiziona il Database di Transazioni
– Partiziona i Candidati
CALCOLO PARALLELO - S. Orlando
15
Count Distribution (CD)
•
Partiziona il Database di Transazioni
– Replica i candidati e conta in maniera distribuita
– Approccio noto come Count Distribution (CD)
•
•
•
Ogni processore ha il completo insieme di candidati Ck
Ogni processore aggiorna i suoi contatori locali
Riduzione globale per determinare il valore dei contatori
•
NOTA: Se Ck è troppo grande rispetto alla memoria, possono essere
necessari scan multipli del database
CALCOLO PARALLELO - S. Orlando
16
Count Distribution (esempio iterazione 2)
CALCOLO PARALLELO - S. Orlando
17
Data Distribution (DD)
•
Partiziona non solo il Database, ma anche i Candidati
•
Ogni partizione dei candidati deve essere confrontata con l’intero Dataset
– Partizioni dei dati comunicati fra tutti i processori
– Comunicazione finale per conoscere l’ Fk globale, necessario per
costruire Ck+1
Alto costo di comunicazione
Approccio utile quando i candidati diventano troppi e non possono essere
mantenuti in memoria
Anello per comunicare le partizioni tra i processori
– Shift sull’anello e ed conteggio rispetto alla partizione remota ricevuta
– Tanti shift quanti sono i processori
– Possibile overlapping tra calcolo e comunicazione
•
•
•
CALCOLO PARALLELO - S. Orlando
18
Data Distribution (DD)
CALCOLO PARALLELO - S. Orlando
19
CALCOLO PARALLELO - S. Orlando
20
Data Distribution (DD)
Cluster di WS
•
•
•
•
Architettura adatta per questo tipo di problema, in quanto le comunicazioni
introdotte da questo algoritmo sono limitate
Dischi multipli, utili per contenere i dati in ingresso / uscita dell’algoritmo di
FSC
Di sotto, abbiamo illustrato due modi di configurare il cluster
– Shared Nothing
– Shared Disk
Considerare anche il load balancing
– Architetture eterogenee, o multiprogrammate
CALCOLO PARALLELO - S. Orlando
21