Progetto di una Unità di Apprendimento flipped
Dati dell’Unità di Apprendimento
Titolo: Strategie in geometria...è un gioco!
Scuola: Scuola Secondaria di primo grado
Materia: Geometria
Classe : 2° (20 alunni)
Argomento curricolare:
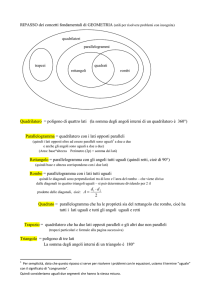
Le proprietà dei quadrilateri
Le aree dei poligoni
La Sfida. Come si attiva l’interesse e la motivazione degli allievi:
Essendo l'inizio dell'anno scolastico voglio far ripassare ai miei alunni il programma di geometria della classe prima: le
proprietà dei quadrilateri. Il mio intento è poi di introdurli alle aree dei poligoni.
Lancio della sfida (½ ora):
Lancio una sfida a tutta la classe alla fine della lezione di geometria: propongo ai miei alunni di fare a casa le figure
note della geometria e poi di ritagliarle seguendo questa descrizione.
Chi trova la figura geometrica “contenitore” del più alto numero di poligoni?
Bisogna anche verificare il rapporto tra le figure e descrivere in modo dettagliato i poligoni in base a lati,
angoli e diagonali.
Il rapporto tra le figure dovrebbe portare all’idea generale di superfici equivalenti ed equiscomponibili.
In questo modo inizio ad anticipare le aree dei poligoni, parlando di “spazio occupato” e non trascuro le proprietà dei
quadrilateri. Infatti, il pomeriggio stesso, dopo aver acceso in mattinata la motivazione verso la sfida, invio a tutti i
miei alunni, tramite casella di posta elettronica, la dispensa di Geometriko (L. Tortorelli, Trento, Erickson-2014/2015)
in pdf. Questo strumento permetterà loro di ripassare in modo individuale tutte le proprietà dei quadrilateri
richiamando le loro preconoscenze e servirà a renderli più sicuri dei loro ragionamenti per individuare la figura
geometrica che riesce a “contenere” il più alto numero di poligoni!
Aumenterò la loro motivazione annunciando tramite mail che la prossima lezione sarà dedicata a svolgere un test di
autovalutazione delle loro conoscenze sulle proprietà dei quadrilateri perché questo ci permetterà di organizzare 4
fasce di livello, per poter creare 5 tavoli, ciascuno composto da quattro alunni: giocheremo a Geometriko!
Lancio della Sfida. Quali attività si svolgono prima o in apertura della lezione:
Prima lezione:
a- Test di autoverifica (1 ora) vedi allegato
In apertura della lezione, prima di sapere chi ha scovato la figura geometrica “contenitore”, propongo il test di
autovalutazione: saranno presenti domande a risposta multipla e alcuni quesiti a risposta aperta presi dal libro
Geometriko (quesiti che i ragazzi non hanno letto poiché possiedono solo la dispensa). Durante la correzione ognuno
di loro conterà quante sono state le domande corrette per poter individuare un voto sul totale grezzo che indicherà la
fascia di livello (fascia: ottima 10-9, buona 8-7, sufficiente 6, non sufficiente 5-4). Dai risultati del test organizzeremo
i 5 tavoli con il metodo di “testa di serie” (un giocatore della prima fascia, uno della seconda e così via). Per
incrementare la spinta motivazionale ciascuna delle 5 “teste di serie” avrà un vantaggio di gioco comunque non
determinante ai fini della vittoria.
b- Domande open-source (1 ora)
Il modello Geometriko prevede anche una fase di elaborazione di ulteriori quesiti in modalità open-source; chiedo
pertanto ai miei alunni, come attività in classe, di pensare e scrivere delle domande che serviranno nel gioco per
sfidare i propri compagni. Tali quesiti, saranno perfezionati in classe attraverso una fase di tutoring. Le domande
possono riguardare tutta la parte di geometria a loro conosciuta, possono aiutarsi con la dispensa di Geometriko,
possono includere alcuni concetti di insiemistica mirati ai quadrilateri e possono anche prendere spunti da prove
Invalsi degli anni passati facilmente reperibili in rete. Le domande con le rispettive risposte, in versione definitiva,
dovranno essere inviate da casa, attraverso una piattaforma moodle. I ragazzi saranno sollecitati ad inviare il loro
lavoro almeno due giorni prima dell'inizio del gioco.
Tutta la loro motivazione alla sfida aumenta per voler essere preparati al gioco e poter vincere. L’attività infatti è
classe-centrica e lo stimolo a studiare per vincere è molto forte.
Condurre la sfida. Quali attività si svolgono per rispondere alla sfida:
I ragazzi ora saranno totalmente coinvolti nel voler imparare il gioco, ma prima dobbiamo provare a verificare se la
sfida a trovare il poligono “contenitore” può partire:
Fase 1 (2 ore): I poligoni contenuti e il poligono contenitore
Primo passaggio: suddivido la classe nei cinque tavoli composti dai quattro alunni, con il metodo di “testa di serie”,
preparati per il gioco. Ogni tavolo, con la tecnica attiva del Jigsaw, sarà impegnato a ripassare in modo ottimale le
proprietà dei quadrilateri, raccogliendo idee, per poter sostenere la loro tesi sul poligono “contenitore”. Ognuno degli
alunni si interesserà di una figura in particolare. Avranno a disposizione le loro figure in carta, per poter verificare con
immediatezza le loro osservazioni.
Secondo passaggio: i tavoli si scompongono per riunire ogni alunno con gli altri della propria fasce di livello e poter
discutere da “esperti”, ogni fascia ha la propria figura geometrica da studiare, componendo una “scheda operativa”
che descrive la loro figura: qui dovranno usare parole chiave come congruenza, figure isoperimetriche, stessa area o
equivalenti, “composti dalle stesse figure geometriche” o equiscomponibili. Ciascun componente insegna, spiega agli
altri alunni e prepara domande per verificare l’apprendimento altrui.
Terzo passaggio: si ricompongono i tavoli iniziali, dove i componenti saranno portatori di un sapere specifico. Si
riorganizzeranno le idee e ogni tavolo proporrà la propria ipotesi riguardo al poligoni “contenitore”.
Nessun indizio sarà dato sulla veridicità delle loro teorie.
Fase 2 (2 ore): Spiegazione delle regole dei gioco attraverso una partita dimostrativa.
Ai quesiti già presenti sul testo – numerati dal 51 al 90 - si selezionano e quindi si aggiungono i quesiti inviati sulla
piattaforma moodle dai ragazzi e si numerano dal numero 91 in poi. Visto che è una partita dimostrativa, ai quattro
giocatori del tavolo si affiancheranno i restanti studenti in modo tale che tutti saranno coinvolti per imparare le regole
del gioco durante la partita simulata.
Regole:
ogni giocatore avrà 4 carte quadrilatero, 8 carte d'attacco e 1 flash card
verrà dato un minuto per attaccare e un minuto per difendersi
si potrà giocare per 50 minuti (quindi vincerà chi rimane l'unico partecipante o chi ha accumulato più
punteggio)
ciascun giocatore non può essere attaccato per più di due volte consecutive (Regola del fair-play)
se all'inizio della partita un giocatore avrà tre carte quadrilatero uguali potrà cambiarne una, se ne riceve
quattro uguali, può cambiarne due (Regola dell’assortimento)
il giocatore che rimane con un solo quadrilatero in mano deve fermare il gioco e chiedere il sorteggio della
speranza che si può richiedere solamente per tre volte. Questo evento si svolge nell'estrarre un numero da un
sacchetto (dal 51 in poi) che corrisponde a uno dei quesiti preparai in precedenza. Se il giocatore risponde in
modo corretto avrà una nuova carta quadrilatero e la possibilità di non essere sfidato nell'immediato, se il
giocatore risponde in modo errato è escluso dal gioco.
Come si gioca:
ogni componente del tavolo tira un dado che ha sulle facce dei quadrilateri. Partirà con il gioco chi avrà ottenuto il
quadrilatero con le ha maggiori caratteristiche.
Il giocatore sfida con una carta d'attacco un altro giocatore, mostrandogli la carta: questa richiede delle
caratteristiche di un quadrilatero e l'attaccato deve difendersi scartando sul tavolo una carta quadrilatero.
Le possibilità a questo punto sono:
1. il giocatore dirà “ Ho vinto!” e metterà sul tavolo una carta quadrilatero che soddisfi le proprietà richieste dalla
carta d’attacco.
2. il giocatore dirà “ Ho perso” e metterà sul tavolo una carta quadrilatero che non soddisfi le proprietà richieste dalla
carta d’attacco.
A verificare l'esattezza delle risposte ci saranno degli studenti in funzione di arbitro supervisionati dal docente.
Se le risposte date sono errate subiranno una “fucilata geometrika” cioè gli verrà tolta una carta quadrilatero scelta a
caso. Se la riposta è corretta e il giocatore ha vinto, potrà attaccare lui un altro giocatore, se invece il giocatore “Ha
perso!” allora il gioco rimane in mano dell'attaccante.
Ogni giocatore ha una flash card che dà un tocco di imprevedibilità al gioco aprendo a diverse possibilità sia positive
sia anche negative per il giocatore (richiedere indietro una carta, far pagare un pegno all'avversario, sostenere una
domanda da fucilata geometrika…).
Fase 2 (2 – 3 ore): Fase eliminatoria e ottavi e quarti di finale
A questa fase si sfidano i 20 partecipanti (in base al metodo di “testa di serie” ) suddivisi in 5 tavoli differenti. I primi
due giocatori classificati di ogni tavolo della fase eliminatoria accedono agli ottavi di finale.
Si suddividono i 10 giocatori vincenti in 2 tavoli da 5. I primi due classificati di ogni tavolo passeranno ai quarti di
finale. Si sfideranno tutti in un unico tavolo per il titolo di campione e vice-campione della classe.
In questo gioco si sviluppa il format del laboratorio, con attivazione di forme di conoscenza alternative rispetto alla
conoscenza tradizionalmente intesa come universale e decontestualizzata. Gli alunni imparano giocando, capiscono
l’insiemistica riconoscendo le figure che hanno più caratteristiche, ricordano le proprietà dei quadrilateri perché alla
domanda della carta d’attacco devono associare uno dei quadrilateri e non imparano a memoria come
tradizionalmente viene intrapreso questo studio.
Il sapere si costruisce attraverso l'azione per rendere la conoscenza esplicita, procedurale e progettuale.
Si esplicitano le tecniche di conduzione:
- di analisi: con il problem solving,
- di simulazione: con le regole -game-,
- di cooperative learning: attraverso il peer tutoring, la non presenza di un leader (perché non è detto che vinca il più
bravo in matematica, ma il più strategico!), la responsabilità di tutti, la qualità dei rapporti, mentre l’insegnante si
muove nel gruppo.
La spinta motivazionale è molto alta, si propone agli alunni un’esperienza sulla quale creare una soluzione per
risolverla, è quindi il processo di apprendimento che stimola la motivazione in quanto analizza situazioni reali, trae
spunti per ulteriori approfondimenti e favorisce la capacità di analisi.
Fase 4 (1 ora): come ricordare le formule per calcolare l'area dei poligoni
A questo punto gli alunni sono pronti per affrontare il passaggio successivo: chi vince anche la sfida? Chi ha trovato il
poligono “contenitore”?
Propongo ai miei alunni di vedere un video https://www.youtube.com/watch?v=CVhka8Gmfj4&feature=youtu.be in
aula con l'uso della LIM. Attraverso il metodo induttivo gli alunni comprendono che tutte le formule per calcolare le
aree dei poligoni possono ricondursi alla formula della superficie del rettangolo, la nostra figura “contenitore”.
Anche in questo format di laboratorio le tecniche attive sono state:
- il problem solving,
- la riproduzione operativa (attraverso le dimostrazioni con la carta),
- il lavoro di cooperazione attraverso i gruppi del Jigsaw.
Tutto questo insieme allo studio personale ha dato modo alle loro conoscenze di amplificarsi e diventare abilità e
competenze. Proprio nella fase 1 e 4 c’è una vera manipolazione del sapere, seguendo una procedura organizzata, si
ottengono dei risultati. In questo tipo di format anche gli alunni con un’intelligenza più pratica possono emergere e si
può avere un approccio trasversale delle conoscenze.
Chiusura della sfida. Quali attività di verifica degli apprendimenti concludono l’attività didattica:
Alla fine del torneo di classe si prevede un valutazione formativa-oggettiva (vedi allegato) dei due argomenti
curricolari proposti: domande a risposta multipla, V/F, completamenti e corrispondenze di difficoltà variabile saranno
utilizzati per verificare per conoscenze/abilità, alcuni quesiti presi dal libro Geometriko (tra questi anche degli Invalsi)
che serviranno per valutare per competenze.
Riflessione finale. In che modo l’approccio proposto differisce dal suo approccio tradizionale:
L'insegnamento della geometria è spesso stato tradotto come insegnamento meccanico di procedure e schemi.
Nel gioco (la sfida di trovare la figura misteriosa attraverso la manipolazione e Geometriko), si sviluppa un aspetto
strategico che fa emergere le competenze che l'alunno ha sviluppato avendo come basi le sue conoscenze e abilità.
Inoltre ad alimentare la riuscita dell'aumento delle competenze ed abilità c'è anche l'importanza del contesto dove si
situano gli alunni che li coinvolge e li rende protagonisti di un sapere che si accresce in una situazione reale di
apprendimento. Gli alunni usano il proprio sapere per agire in un certo contesto sviluppando quindi competenze.
L'utilizzo della presentazione sottolinea nuovamente il distacco dal voler imparare schemi meccanici, ma piuttosto di
comprendere induttivamente le regole della geometria piana.
Nome e Cognome
Test Autoverifica
Classe II
Rispondi alle seguenti domande:
1. Sommando gli angoli interni di un quadrilatero si ottiene un angolo di
A. 180°
B. 270°
C. 360°
D. 400°
2. Un rombo ha un angolo di 35°, quanto misurano gli altri tre angoli?
A. 35°, 145°, 145°
B. 35°, 35°, 35°
C. 35°, 110°, 110°
D. 35°, 55°, 55°
3. Quali dei seguenti gruppi di lati possono appartenere a un quadrilatero?
A. 10cm, 15cm, 3cm, 2cm
B. 10cm, 15cm, 16cm, 17cm
C. 6cm, 12cm, 6cm, 6cm
D. 6cm, 30cm, 6cm, 12cm
4 Quali delle seguenti affermazioni relative a un trapezio isoscele sono vere?
A. ha i lati a due a due paralleli
B. ha gli angoli opposti complementari
C. ha sempre due lati congruenti
D. ha sempre le diagonali uguali
5. Quale delle seguenti figure ha quattro lati di diversa lunghezza e due angoli retti?
A. quadrato
B. trapezio rettangolo
C. rettangolo D. parallelogramma
6. Se in un triangolo si traccia una retta parallela alla base si ottengono
A. un trapezio e un triangolo
B. due triangoli
C. due trapezi
D. un pentagono e un triangolo
7. In un trapezio, l'altezza è
A. la distanza tra le due basi
B. il lato obliquo
C. la proiezione del lato obliquo sulla base
D. la proiezione della diagonale sulla base
8. In un trapezio la somma delle basi misura 100cm, le proiezioni dei lati obliqui sulla base maggiore misurano
rispettivamente 5cm e 15cm. Quanto misurano le due basi?
A. 50cm e 50cm
B. 45cm e 55cm
C. 35cm e 65cm
D. 40cm e 60cm
9. Quali delle seguenti affermazioni relative a un parallelogrammo sono vere?
A. ha le diagonali congruenti
B. ha gli angoli opposti congruenti
C. ha i lati opposti congruenti
D. ha gli angoli adiacenti congruenti
10. Nel seguente parallelogrammo la diagonale è congruente a un lato e forma con esso un angolo di 40°. Quanto
misurano gli angoli del parallelogrammo?
A. 70°, 85°, 90°, 100°
B. 70°, 110°, 70°, 110°
C. 80°,120°, 80°, 120°
D. 80°, 100°, 80°, 100°
11. Quali delle seguenti affermazioni relative a un rettangolo sono vere?
A. le diagonali sono uguali
B. è anche parallelogrammo
C. le diagonali sono perpendicolari
D. i lati sono uguali
12. In un rettangolo la base è 2/3 dell'altezza e il perimetro è di 24cm. Quanto misurano i due lati?
A. 12cm e 12cm
B. 4,8cm e 7,2cm
C. 3,6cm e 8,4cm
D. 4,2cm e 7,8cm
13. Quali delle seguenti affermazioni relative a un rombo sono vere?
A. è un parallelogrammo con tutti i lati congruenti
B. gli angoli adiacenti sono congruenti
C. le diagonali sono perpendicolari
D. tutti gli angoli sono congruenti
14. Un quadrato Q1 ha il lato che è la metà del lato di un quadrato Q2. Il quadrato Q1 ha il perimetro che è
A. la metà del perimetro di Q2
B. doppio del perimetro di Q2
C. il quadruplo del perimetro di Q2
D. stesso perimetro di Q2
15. Un quadrato, un rombo e un rettangolo hanno lo stesso perimetro. Se il lato del quadrato misura 10cm, i lati
delle altre due figure misurano
A. rombo 10cm, rettangolo 10cm e 20cm
B. rombo 20cm, rettangolo non si può calcolare
C. rombo non si può calcolare, rettangolo 40cm
D. rombo 10cm, rettangolo non si può calcolare
16. Quali dei seguenti quadrilateri hanno le diagonali di lunghezza diversa?
A. Il rettangolo
B. Il quadrato
C. Il rombo
D. Il trapezio rettangolo
17. Disegna l’insieme dei quadrilateri per poi rispondere alle seguenti domande
giustifica la tua risposta:_____________________________________________________
giustifica la tua risposta:_____________________________________________________
Nome e Cognome
Verifica formativa-oggettiva
Classe II
1. Rispondi alle seguenti domande
a. Quali dei seguenti quadrilateri hanno le diagonali di lunghezza uguale e perpendicolari?
A. Il rettangolo
B. Il quadrato
C. Il rombo
D. Il trapezio rettangolo
b. Quali delle seguenti affermazioni relative a un rombo non sono vere?
A. è un parallelogrammo con tutti i lati congruenti
B. gli angoli adiacenti sono congruenti
C. le diagonali sono perpendicolari
D. tutti gli angoli sono congruenti
c. Quale delle seguenti figure ha quattro lati di uguale lunghezza?
A. quadrato
B. rombo
C. rettangolo
D. parallelogramma
d. Quali delle seguenti affermazioni relative a un trapezio isoscele non sono vere?
A. ha due lati paralleli
B. ha gli angoli opposti supplementari
C. ha sempre due lati congruenti
D. ha sempre le diagonali uguali
1. Scegli la risposta corretta
a. L’area del rettangolo è
V F
b. Il rombo ha i lati uguali e paralleli a due a due
V F
c. Il triangolo occupa metà area di un rettangolo
V F
d. Per calcolare l’area del rombo uso questa formula
V F
e. Gli angoli del rettangolo sono tutti uguali
V F
f. Nel trapezio le basi sono parallele e gli angoli adiacenti alla base complementari
V F
g. L’area del trapezio si calcola
V F
2. Completa le frasi utilizzando le parole in sovrannumero presenti alla fine del testo
In geometria, il ……………….. è un poligono formato da tre angoli o vertici e da tre lati; rappresenta la figura con il
………………numero di lati, in quanto tre è il numero minimo di segmenti necessari per delimitare
una superficie chiusa, non esistono infatti poligoni aventi due angoli e due lati o un solo angolo e lato.
In geometria,
il quadrato è
un quadrilatero regolare,
cioè
un poligono con
quattro lati ………………..
e
quattro angoli uguali. Il quadrato è un caso particolare di …………….. (in quanto ha tutti e quattro i lati uguali) e
di …………………. (in quanto ha quattro angoli uguali).
In geometria, il rettangolo è un quadrilatero che ha tutti gli angoli interni congruenti tra loro.In un rettangolo
ciascuna delle due coppie di lati opposti è costituita da lati……………………..
Equivalentemente l'insieme dei quadrati è l'intersezione dell'insieme dei ………………… con l'insieme dei……………..
In geometria un trapezio è un quadrilatero con due lati ……………….. Il quadrilatero con meno caratteristiche è il
……………………………. Infatti nell’insieme dei quadrilateri racchiude in sé tutti gli altri.
(triangolo, differenti, minor, congruenti, trapezio, rombo, rettangoli maggior, quadrilatero, rombi, rettangolo, paralleli, deltoide,
congruenti, perpendicolari, paralleli)
3. Collega le figure alla corretta formula dell’area
4. Rispondi giustificando
giustifica la tua risposta:_____________________________________________________
giustifica la tua risposta:_____________________________________________________