Progetto e realizzazione in VLSI analogico di sinapsi e neurone

UNIVERSITÀ DEGLI STUDI DI ROMA
“TOR VERGATA”
FACOLTÀ DI SCIENZE MATEMATICHE FISICHE E NATURALI
TESI DI LAUREA IN FISICA
Progetto e realizzazione in VLSI
analogico di sinapsi e neurone
impulsato per un chip neuromorfo
Relatore:
Laureando:
Dott. Gaetano Salina
Davide Badoni
Relatore esterno:
Dott. Paolo Del Giudice
Anno Accademico 2003/2004
Ad Emanuela, Federico e Luca
Facciamo attenzione che la nostra mente non diventi il nostro oggetto di
culto; ha, certamente, un muscolo poderoso, ma non personalità.
Albert Einstein
Indice
Introduzione
9
1 Reti neuronali e neuroscienze computazionali
1.1 Dal contesto biologico di riferimento ai modelli
1.1.1 L’input-output del neurone . . . . . . .
1.1.2 Modelli . . . . . . . . . . . . . . . . .
1.2 Il modello del neurone . . . . . . . . . . . . .
1.3 Il modello della sinapsi . . . . . . . . . . . . .
.
.
.
.
.
13
14
14
16
17
20
2 Hardware neuromorfo e VLSI in tecnologia CMOS
2.1 Il transistor mosfet . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Effetto Early . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Vincoli tecnologi, flusso di progetto e tecniche di progettazione
2.3.1 Dal disegno di principio alla simulazione post-layout . .
2.3.2 Mismatch dei parametri e simulazione montecarlo . . .
2.4 Il processo di fabbricazione . . . . . . . . . . . . . . . . . . . .
27
28
34
35
37
39
41
3 Realizzazione elettronica
3.1 Topologia della rete . . . . . . . . . . . . . . . . . . . . . . .
3.2 Circuiti base CMOS utilizzati . . . . . . . . . . . . . . . . .
3.2.1 Interruttore . . . . . . . . . . . . . . . . . . . . . . .
3.2.2 Generatore di corrente . . . . . . . . . . . . . . . . .
3.2.3 Invertitore logico . . . . . . . . . . . . . . . . . . . .
3.2.4 Specchio di corrente . . . . . . . . . . . . . . . . . .
3.2.5 Source Follower . . . . . . . . . . . . . . . . . . . . .
3.2.6 Amplificatore a transconduttanza . . . . . . . . . . .
3.2.7 Amplificatore a transconduttanza wide-range . . . . .
3.2.8 Comparatore Open-Loop p a due stadi . . . . . . . .
3.2.9 Comparatori Open-Loop p ed n a due stadi con abilitazione . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 La sinapsi . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
46
48
49
50
51
53
54
54
56
56
7
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. 58
. 59
3.4
3.5
3.6
3.7
3.8
3.9
Il modulo Sinapsi . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1 Circuito di refresh . . . . . . . . . . . . . . . . . . .
3.4.2 Circuito hebbiano . . . . . . . . . . . . . . . . . . . .
3.4.3 Circuito di clipping . . . . . . . . . . . . . . . . . . .
3.4.4 Circuito di selezione . . . . . . . . . . . . . . . . . .
3.4.5 Circuito dendriti . . . . . . . . . . . . . . . . . . . .
Il modulo Calcio-Compara . . . . . . . . . . . . . . . . . . .
Lo shaper . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Il neurone low power adaptive integrate and fire . . . . . . .
3.7.1 Soglia e feedback positivo . . . . . . . . . . . . . . .
3.7.2 Tempo refrattario . . . . . . . . . . . . . . . . . . . .
3.7.3 Meccanismo di adattamento in frequenza . . . . . . .
3.7.4 Simulazioni . . . . . . . . . . . . . . . . . . . . . . .
Una simulazione completa dallo spike pre-sinaptico alla depolarizzazione del soma post-sinaptico . . . . . . . . . . . . . .
I layout FULL-CUSTOM . . . . . . . . . . . . . . . . . . . .
4 Il chip completo e il sistema di test
4.1 Protocollo di comunicazione A.E.R. . . . . . . . . .
4.2 Architettura generale del chip realizzato . . . . . .
4.3 Sistema di test . . . . . . . . . . . . . . . . . . . .
4.3.1 Schede di interfaccia PCI-AER e PCI-GPB
5 Conclusioni e prospettive future
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
61
62
64
66
67
67
69
72
76
78
79
79
79
. 80
. 82
.
.
.
.
87
88
90
95
95
99
Ringraziamenti
101
Bibliografia
103
Introduzione
Per reti neuronali si intende il sistema biologico composto di un elevato numero di cellule nervose connesse tra loro in modo opportuno. L’esempio senz’altro più interessante, che ne rappresenta la massima evoluzione presente
in natura è costituito dalla corteccia cerebrale del cervello dei primati.
Da decenni esse sono oggetto di studio delle più svariate discipline scientifiche: della neurofisiologia che con la biologia molecolare indaga sugli aspetti
della dinamica chimico-fisica delle cellule nervose del tessuto corticale; della psicologia cognitiva che si occupa degli aspetti dell’attività d’insieme del
cervello intesa come manifestazione del comportamento umano; e infine della
matematica, dell’informatica, della scienza dell’informazione e della fisica.
Seppur l’approccio di studio tra le varie discipline sia diverso, si può
identificare un comune intento che è quello di comprendere i meccanismi e le
funzionalità che sono alla base di questa straordinaria manifestazione della
natura: il cervello. La comprensione delle principali funzionalità del cervello, quelle che presiedono alla trasmissione ed alla elaborazione degli stimoli
sensoriali, alla memorizzazione e alla classificazione dell’informazione hanno
molteplici ripercussioni di natura anche pratica ed immediata che vanno dalle discipline in campo medico, come ad esempio lo studio delle disfunzioni
cerebrali, a quelle in campo informatico-tecnologico come ad esempio lo studio dei sistemi automatici di elaborazione, memorizzazione, classificazione e
riconoscimento di informazioni.
Per il fisico l’approccio è quello di costruire ed elaborare modelli matematici che descrivano le funzionalità delle strutture neuronali a partire dai suoi
costituenti base (tipicamente neurone e sinapsi) e procedendo per strutture
più complesse prendendo spunto dai molteplici studi effettuati su esseri viventi, per ottenere la necessaria plausibilità biologica [1]. Il modello potrà essere
una rappresentazione grossolana delle cellule nervose, ma l’aspetto saliente è
il comportamento collettivo d’insieme determinato dall’elevato grado di interazione di tutti gli elementi base. Il modello che si sviluppa viene studiato
sia dal punto di vista teorico che con l’ausilio di simulazioni su calcolatore,
per verificarne la validità nel rappresentare il fenomeno.
9
In questa fase di modellizzazione si inserisce un notevole arricchimento
a questa ricerca con la possibilità di realizzare implementazioni in dispositivi hardware dei modelli stessi. Tale approccio ha tratto motivazione dalle
seguenti considerazioni:
• i vincoli costruttivi e realizzativi che emergono dall’ emulazione hardware, assenti invece nelle simulazioni, sono spesso relazionati a vincoli
reali presenti nella rispettiva controparte biologica. Questo costituisce
uno spunto di riflessione per rivedere il modello matematico atto a rafforzarne la plausibilità biologica con il risultato di ottenere talvolta la
comprensione di fenomeni ancora ignoti
• la velocità di elaborazione di una rete neuronale hardware può essere
estremamente più elevata della corrispettiva simulazione dei modelli in
via teorica permettendo cosı̀ esperimenti con reti di grosse dimensioni
• la stessa realizzazione hardware di dispositivi neuronali può avere scopi
pratici immediati come ad esempio la classificazione ed il riconoscimento di immagini.
Lo sviluppo di dispositivi “neuromorfi” apre la prospettiva di sistemi autonomi (cioè non dipendenti da strumenti di calcolo digitali) in grado di acquisire
ed elaborare in tempo reale stimoli ambientali.
Dal punto di vista dell’approccio teorico, fondamentale è stato il lavoro
di Hopfield del 1982 [2] che di fatto pone questa disciplina nel campo di
interessi della fisica. Hopfield introduce le prime analogie tra le reti neuronali
e i sistemi disordinati a molti gradi di libertà, consentendo di utilizzare un
collaudato e potente strumento quale è la meccanica statistica.
È in questo contesto che trova applicazione il concetto di attrattore e quindi di rete neuronale ad attrattori, (Attractor Neural Network: ANN). La rete
di neuroni interagenti è descritta come un sistema dinamico con feedback
elevato, dotato (in funzione degli accoppiamenti sinaptici) di una molteplicità di stati di equilibrio (attrattori). Data una condizione iniziale per la
dinamica, che viene interpretata come espressione di uno “stimolo” esterno
alla rete, questa evolve verso uno degli attrattori disponibili, stato di equilibrio del sistema, che codifica la “risposta” della rete allo stimolo. L’insieme
delle condizioni iniziali che portano allo stesso attrattore è il bacino di attrazione di questo; l’attrattore fornisce una rappresentazione interna della
“classe” di stimoli definita dal suo bacino di attrazione. Questo tipo di rete
fornisce un modello di memoria associativa. In questo senso una rete neuronale può essere vista come una memoria indirizzabile per contenuto (Content
Addressable Memory: CAM), dove i contenuti di informazione memorizzati
10
sono rappresentati dagli attrattori, e vengono richiamati fornendo delle informazioni anche incomplete o simili, che individuano uno stato iniziale della
rete. La rete sviluppa rappresentazioni delle classi di stimoli modificando
lo schema delle connessioni sinaptiche, ed in particolare la forza di queste
(l’ “efficacia” sinaptica), cioè l’entità dell’effetto che l’impulso emesso da un
neurone produce sul neurone bersaglio. La configurazione sinaptica determinata dinamicamente dalle proprietà degli stimoli, fissa l’insieme di attrattori
accessibili alla dinamica della rete. Sono stati proposti molti modelli di plasticità sinaptica: il principale obiettivo della tesi è la descrizione del progetto
elettronico di un modello di sinapsi plastica, che si modifica in modo probabilistico in funzione del flusso di stimoli, all’interno di un chip VLSI che
realizza una rete neuronale con feedback.
Presentazione del lavoro di tesi
Lo scopo di questo lavoro di tesi è stato la progettazione e la realizzazione
di un dispositivo misto analogico-digitale VLSI che realizza una rete neuronale con 32 neuroni impulsati, con matrice sinaptica configurabile e modulo
di comunicazione A.E.R. (Address Event Rapresentation) necessario per la
comunicazione tra diversi dispositivi neuronali e con il sistema di controllo.
Il principale contributo del mio lavoro a questo progetto è consistito nella
progettazione e simulazione del circuito sinaptico e dell’elettronica di interfaccia con la circuteria digitale responsabile della comunicazione AER ed adattamento del progetto del neurone fornito dall’Istituto di Neuroinformatica di
Zurigo all’architettura del dispositivo, come qui sotto elencato
• Definizione dell’architettura generale del chip
• Progetto della sinapsi
• Simulazione della sinapsi
• Inclusione del circuito neuronale
• Integrazione delle parti analogiche con quelle digitali
• Finalizzazione del layout e sottomissione del progetto alla fonderia
11
Struttura generale della tesi
• Capitolo 1
Fornisce una panoramica introduttiva alle reti neuronali e alle neuroscienze computazionali, nell’ottica di questo lavoro.
Descrive i modelli realizzati in hardware.
• Capitolo 2
Viene descritto il transistor mosfet con le sue equazioni più rappresentative e la tecnologia CMOS che attualmente è la più usata per le
realizzazioni in hardware di reti neuronali.
Vengono descritte le fasi di progettazione, gli strumenti, le tecniche e i
software utilizzati.
• Capitolo 3
Vengono descritti i circuiti analogici di base che costituiscono i mattoni
di tutti i circuiti analogici progettati.
Vengono descritti e si discutono nel dettaglio i circuiti realizzati.
• Capitolo 4
Si presenta l’architettura completa del chip.
Viene descritto il modulo di comunicazione A.E.R., incaricato di codificare e gestire il flusso di informazioni da/e verso altri dispositivi.
Viene descritto il sistema di test.
• Capitolo 5 Conclusioni e prospettive future.
12
Capitolo 1
Reti neuronali e neuroscienze
computazionali
Quando si parla di reti neuronali è inevitabile pensare alle più elevate attività
cognitive del cervello animale, in particolare a quello dei primati. Sebbene
le scienze che si occupano di queste materie siano attualmente diversificate e
non tutte necessariamente legate ad una continua comparazione con il sistema
nervoso, è innegabile che alcune funzioni emergenti del cervello sono state
prese come modello da comprendere, da emulare o almeno da imitare nelle
sue manifestazioni più modellizzabili e riproducibili.
Diverse sono le funzioni tipicamente appetibili e ragionevolmente trattabili del sistema biologico cervello dal punto di vista della modellizzazione ed
emulazione.
Si vogliono qui descrivere brevemente, le attività cognitive tipiche del
cervello che sono più attinenti agli scenari ed al contesto che si sta discutendo.
Volendo tentare di fare un confronto con le funzioni di memoria e di classificazione nei manufatti creati dall’uomo, si può dire che gli stimoli sensoriali
provenienti dall’interazione con l’ambiente rappresentano uno degli input del
sistema cervello, considerato come sistema dinamico. In quest’ottica l’output
viene ad essere identificato con la risposta dinamica del sistema cervello. Il
mondo percepito per tramite delle vie sensoriali, viene ad assumere nel cervello una propria rappresentazione interna. Tra i canali sensoriali più studiati
nel contesto della comprensione del sistema cervello e delle possibili modellizzazioni di alcune funzioni, ci sono ad esempio gli stimoli acustici provenienti
dalla coclea e gli stimoli visivi provenienti dalla retina.
Una evidente e fondamentale manifestazione delle capacità cognitive è
quella della memorizzazione e della classificazione di stimoli. La fase di apprendimento è quella in cui il cervello è sottoposto ad un flusso di stimoli,
che hanno una corrispondenza in diverse rappresentazioni interne. In questa
13
1.1. Dal contesto biologico di riferimento ai modelli
fase non si ha una semplice memorizzazione di tutti o parte degli stimoli ma
piuttosto una classificazione per classi di stimoli con la memorizzazione di
una prototipo rappresentativo per ogni classe di stimoli:
ciascuno di noi ha visto nella vita molti alberi, l’idea di albero non corrisponde alla memoria visiva di tutti i possibili alberi osservati, ma piuttosto
ad una serie di prototipi di immagini di alberi, che corrispondono a specifiche
rappresentazioni interne.
Anche se si hanno ragionevoli argomenti per affermare che l’informazione
o la particolare rappresentazione di essa non è localizzata in uno specifico
punto del cervello, si ha evidenza che alcuni livelli di rappresentazione hanno
sede in zone particolari del cervello, come ad esempio la zona della corteccia
cerebrale in cui vengono rappresentate le immagini dopo la prima elaborazione attuata dalla retina. Moduli corticali diversi reagiscono, manifestando
attività neuronale, ad alcuni tipi e classi di stimoli.
1.1
1.1.1
Dal contesto biologico di riferimento ai
modelli
L’input-output del neurone
Prima di considerare gli argomenti attinenti ai modelli che descrivono gli
elementi di base dei sistemi neuronali, si vuole fornire una breve e sommaria
descrizione della forma delle strutture biologiche e dei meccanismi di base
dell’attività neuronale messi in luce dagli esperimenti di biofisica e biochimica
sulle cellule nervose.
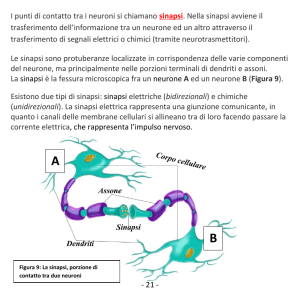
Nella figura 1.1 è rappresentata schematicamente una struttura a due
neuroni interagenti.
La cellula neurone della corteccia cerebrale dei primati (è questa la sede
prevalente in cui si manifestano le attività sopra descritte), è formata da
corpo cellulare chiamato soma delle dimensioni tipiche di 5 − 100 µm.
Da questo si propagano due diversi canali di comunicazione
• l’assone, canale identificabile come uscita, con lunghezze molto variabili
da 0.1 mm a qualche metro
• le dendriti, una serie di ramificazioni che si assottigliano con la distanza
dal corpo cellulare, identificabili come l’ingresso del neurone
La membrana cellulare del neurone separa l’ambiente intracellulare da
quello extracellulare. Nei due ambienti esistono concentrazioni diverse di sostanze in forma ionica. All’interno è presente una concentrazione maggiore
14
Capitolo 1. Reti neuronali e neuroscienze computazionali
Figura 1.1: Rappresentazione di cellule nervose: due neuroni. Il neurone in basso trasmette
la sua attività al neurone più in alto per mezzo del contatto sinaptico sulla dendrite del
neurone ricevente.
di ioni potassio mentre all’esterno di ioni sodio. Le diverse concentrazioni
sono dovute alla semipermeabilità della membrana che, in assenza di perturbazioni elettriche, permette un flusso di potassio verso l’interno ma che
invece costituisce una barriera per il sodio. In condizioni di riposo queste
diverse concentrazioni di forme ioniche creano una differenza di potenziale
tra l’esterno e l’interno del neurone (più negativo), chiamato potenziale di
membrana.
Il neurone subisce l’azione dell’attività degli altri neuroni prevelentemente
attraverso i contatti sinaptici sulle sue dendriti, per mezzo di sostanze chimiche denominate neurotrasmettitori. La comprensione della natura e della
dinamica di questi scambi è attualmente oggetto di studi.
L’effetto sul potenziale di membrana dell’attività degli altri neuroni indu15
1.1. Dal contesto biologico di riferimento ai modelli
ce una variazione del potenziale su di essa. Alcuni tipi di sinapsi favoriscono
una depolarizzazione del potenziale (aumento della differenza di potenziale),
altre una iperpolarizzazione.
Se, per effetto di queste perturbazioni, il potenziale raggiunge una soglia
critica, la permeabilità della membrana cambia drasticamente e rapidamente e quindi si attivano canali ionici dipendenti dal potenziale, favorendo un
passaggio verso l’interno del soma di ioni sodio. Questo crea un potenziale
di azione o spike che ha tipicamente uno sviluppo nel tempo molto rapido
rispetto ai tempi tipici delle variazioni del potenziale di membrana del soma.
Lo spike si propaga lungo l’assone per raggiungere molti neuroni attraverso i
contatti sinaptici. Dopo l’emissione dello spike si osserva il ritorno del neurone in una condizione di riposo. Si osserva altresı̀ che per un periodo di tempo
dopo l’emissione dello spike il neurone rimane inattivato nella possibilità di
emettere un altro spike.
1.1.2
Modelli
Le proprietà emergenti come l’apprendimento e la memoria derivano dall’interazione di un numero elevatissimo di unità elementari fondamentali altamente interagenti, ovvero i neuroni e gli elementi di interconnessioni tra
essi: le sinapsi. Il neurone e la sinapsi possono essere trattate come unità
elementari dotati di ingressi, uscite e di una propria dinamica, ma indipendentemente dalla modellizzazione dei singoli elementi costitutivi, l’approccio
al sistema può essere anche caratterizzato dalle sue proprietà di insieme. Gli
stimoli e le rappresentazioni da essi evocate sono stati del cervello che sono
codificati dall’attività dei neuroni. Attraverso l’attività dei neuroni coinvolti
si definisce lo stato del sistema. Trattando il sistema dal punto di vista dinamico del modello che lo rappresenta, lo stato corrisponde ad un punto nello
spazio delle configurazioni.
In questo senso le proprietà di classificazione sopra descritte si identificano con il fatto che a stimoli differenti possano corrispondere gli stessi stati.
Da qui deriva il concetto di attrattore: punto o zona dello spazio delle configurazioni in cui il sistema evolve dinamicamente a partire da stimoli differenti
ma simili.
È tuttora in discussione il fatto che l’informazione trasmessa dai neuroni
sia rappresentata dalla frequenze medie di emissione.
Un altro aspetto fondamentale abbastanza comune in molti modelli è
che l’apprendimento, nel senso più generico del termine, come ad esempio
la classificazione associativa di insiemi di stimoli, sia dovuto al modificarsi
delle efficacie sinaptiche che rappresentano la forza con cui un neurone presinaptico trasmette la sua attività al post-sinaptico.
16
Capitolo 1. Reti neuronali e neuroscienze computazionali
Recentemente si è affermata una classificazione dei modelli in due categorie, a seconda del tipo di approccio [3], [4]
• TOP-DOWN detti anche connessionistici, che derivano prevalentemente dalla psicologia cognitiva e mirano principalmente a catturare le proprietà cognitive complesse del sistema e a coglierne la logica
computazionale
• BOTTOM-UP in cui si cerca di mantenere un legame tra le parti
del modello e le corrispondenti parti biologiche. In questo tipo di modellizzazioni gli esperimenti di neurofisiologia costituiscono i punti di
riferimento.
Nella seconda categoria ricadono anche i lavori iniziati da Hopfield e sviluppati dai fisici. Questi modelli sono definiti di neuroscienza computazionale.
I modelli di neuroscienza computazionale dinamici prendono spunto, per
la costruzione, dai dati forniti dalla biofisica e biochimica dei neuroni e sinapsi. È evidente che per poter trattare questi modelli dal punto di vista
analitico e delle simulazioni è necessario realizzare delle semplificazioni del
modello stesso.
È questa la categoria di modelli presentati e realizzati in hardware in
questo lavoro.
1.2
Il modello del neurone
Il modello del neurone realizzato è quello del neurone canonico integrate-andfire [5], [6]
È un modello estremamente semplificato del neurone
1. viene trattato come oggetto puntiforme, ovvero non si tiene conto della
sua struttura spaziale, in particolar modo dell’albero dendritico. È
caratterizzato dal solo potenziale di membrana Vsoma . L’intera cellula
è equipotenziale.
2. gli ingressi sinaptici sono dati da una sequenza di impulsi di corrente,
coincidenti con gli spikes in arrivo dagli altri neuroni. Gli impulsi di
corrente si sommano direttamente sul soma, e ciascun impulso determina una variazione istantanea di Vsoma nel verso della depolarizzazione
per sinapsi di tipo eccitatorio e viceversa verso il basso per sinapsi di
tipo inibitorio. L’ampiezza della variazione istantanea è determinata
dall’efficacia sinaptica.
17
1.2. Il modello del neurone
3. è presente un termine di perdita rappresentante la somma di tutti i
contributi delle correnti di perdita, necessario a ristabilire gli equilibri
ionici in assenza di spikes.
4. la generazione dello spike è introdotta come condizione al contorno.
quando il potenziale di soma raggiunge una certa soglia di emissione viene emesso uno spike. Immediatamente dopo, il potenziale
ritorna ad un valore di riposo (potenziale di reset)
per un certo periodo di tempo dopo l’emissione dello spike il neurone
è totalmente inibito e non può emettere spikes (ARP Absolute
Refractory Period).
Rispetto al modello del neurone canonico sopra descritto, altri ingredienti vengono aggiunti per dettagliare e arricchire il modello che è stato poi
realizzato.
• il termine di decadimento sopra descritto nel modello qui esposto è un
termine costante che da luogo quindi ad un decadimento lineare. Da
qui la denominazione neurone I.F. lineare [7].
• viene imposto un valore minimo possibile per la Vsoma indicato con il
termine di barriera riflettente [8]
• viene modellizzato un meccanismo di adattamento in frequenza, le cui
evidenze biologiche vengono qui di seguito accennate [5], [9]
Sperimentalmente (soprattutto in esperimenti in vitro) si osserva che se
un neurone è sottoposto improvvisamente ad un brusco innalzamento della
corrente in ingresso, la frequenza di emissione degli spikes all’inizio sarà molto
alta per poi scendere a valori più bassi. Il neurone reagisce a stress improvvisi
o stimoli troppo forti e persistenti abituandosi tramite un meccanismo di
autoregolazione che impedisce il persistere di elevate frequenze di emissione
per lunghi periodi di tempo. Questo meccanismo rappresenta quindi una
forma di adattamento in frequenza dell’emissione degli spikes.
Le forti evidenze sperimentali suggeriscono che il meccanismo sia dovuto
alla concentrazione degli ioni calcio Ca2+ che modula una corrente di ioni
potassio. Tale corrente è chiamata IAHP (After Hyper Polarization current).
All’emissione dello spike viene attivato un flusso di ioni Ca2+ verso l’interno della cellula. La IAHP è stimolata dall’aumento di concentrazione degli
ioni Ca2+ . L’effetto della presenza di questa corrente è quello di allontanare
il potenziale di membrana dalla soglia di emissione.
18
Capitolo 1. Reti neuronali e neuroscienze computazionali
Il neurone hardware utilizzato realizza un meccanismo di adattamento in
frequenza funzionalmente analogo a quello descritto.
Il modello del neurone I.F. lineare è quindi
1
1
1 Zt
I(t0 )dt0 − Iadapt (t)
Vsoma (t) = Vsoma (0) − Iβ (t) +
C
C t0
C
(1.1)
con le condizioni aggiuntive

emissione dello spike al raggiungimento della soglia con immediato





successivo ritorno al potenziale di reset





tempo refrattario assoluto








limite inferiore a Vsoma
dove I(t) è la somma di tutte le correnti afferenti, Ibeta è il termine di
perdita e Iadapt (t) è la corrente che produce il meccanismo di adattamento in
frequenza ed è una corrente proporzionale (in media, in condizioni stazionarie) alla frequenza media di emissione degli spikes in un intervallo di tempo
impostabile precedente il tempo t.
C in questo contesto rappresenta la capacità del soma.
La corrente afferente al neurone i − esimo è data da
Ii (t) =
N
X
j
Jij
X
δ(t − tj (k) )
k
dove N è il numero di neuroni pre-sinaptici afferenti, Jij è il peso (efficacia
sinaptica) del contributo del neurone pre-sinaptico j e k è l’indice degli istanti
di tempo in cui arrivano gli spikes pre-sinaptici.
Nella teoria entra anche la distribuzione temporale degli spikes in ingresso
al neurone. Gli I.S.I.1 sono molto irregolari. Questa proprietà ha riscontri
negli esperimenti di neurofisiologia ed ha delle implicazioni in taluni importanti aspetti del modello della sinapsi plastica ad apprendimento stocastico.
Poichè i tempi di arrivo gli spikes presinaptici sono un processo stocastico,
lo è anche il potenziale di membrana Vsoma (t).
Una caratterizzazione delle proprietà stazionarie del processo stocastico
accennato è fornita dalla funzione di trasferimento
ν = Φ(µ, σ 2 )
1
Inter Spikes Interval, tempo trascorso tra due spikes
19
1.3. Il modello della sinapsi
che fornisce la frequenza media di emissione del neurone in funzione di una
statistica fissata della corrente afferente in termini di valor medio µ e della
σ 2 . Il neurone I.F. può operare in due ben distinti regimi
• SD (Signal Dominated) regime dominato dal segnale. La σ 2 è piccola o
nulla e µ è costante. Il comportamento è deterministico. L’ ISI fluttua
poco intorno al valore deterministico
• ND (Noise Dominated) regime dominato dal rumore. La σ 2 non è
piccola e µ è sufficentemente piccolo. La soglia viene raggiunta occasionalmente per effetto di fluttuazioni della corrente afferente. L’ ISI
fluttua molto.
Nella figura 1.2 sono rappresentati gli andamenti temporali tipici del neurone
dei due regimi.
Regime dominato dal segnale
Regime dominato dal rumore
Figura 1.2: Potenziale di membrana Vsoma di un neurone I.F. nei due differenti regimi di
Noise Dominated (a destra) e Signal Dominated (a sinistra)
1.3
Il modello della sinapsi
Per la sinapsi non esiste un modello canonico di riferimento. Le conoscenze
fornite dalla biofisica e dalla biochimica non forniscono ancora una spiegazione sufficentemente approfondita dei meccanismi principali, tale da poter
suggerire un modello di riferimento. Sono piuttosto le considerazioni teoriche che giocano un ruolo di stimolo nella costruzione del modello, se mai
confortate da una accettabile plausibilità biologica.
20
Capitolo 1. Reti neuronali e neuroscienze computazionali
Nella maggior parte dei modelli sinaptici cosı̀ come in quello realizzato in
hardware in questo lavoro c’è l’idea che l’efficacia sinaptica venga modificata
dalla attività dei neuroni pre e post-sinaptici.
Il tipo di plasticità che viene qui descritta è quella a lungo termine LTP
(Long Term Potentiation) e LTD (Long Term Depression), che ha una evidenza sperimentale nella biologia (sono stati successivamente introdotti nei
modelli anche effetti di facilitazione e depressione a breve termine).
Uno dei tasselli che sono serviti ad arrivare alle attuali modellizzazioni
dei meccanismi che sono alla base dell’apprendimento, della memoria e della
classificazione per effetto degli stati sinaptici e delle loro dinamiche di modificazione è dato da una serie di esperimenti di neurofisiologia effettuati su
primati.
Fra questi ci sono quelli effettuati dal gruppo di Miyashita [10].
Vengono utilizzate delle scimmie che sono sottoposte ad esperimenti per
registrare le attività dei neuroni di aree corticali visive profonde che manifestano un livello di rappresentazione più complesso delle rappresentazioni
provenienti dagli stimoli sensoriali.
L’area è quella implicata nelle rappresentazioni visive ed è situata nella
zona inferotemporale della corteccia.
Vengono registrati gli spikes emessi da un gruppo campione di neuroni.
Questo tipo di esperimenti, denominati DMS (delayed match to sample,
corrispondenza ritardata sul campione), sono concepiti per mettere in evidenza non solo le relazioni tra attività del modulo corticale e gli stimoli presentati
ma anche le correlazioni temporali tra sequenze di immagini e attività nel
modulo corticale. L’evidenza più immediata è la presenza di attività selettiva
di un gruppo di neuroni a particolari stimoli, distinta dall’attività spontanea
in assenza di stimolo.
L’animale vede sullo schermo, per breve tempo, uno stimolo visivo (non
cognitivamente rilevante); segue un periodo lungo (diversi secondi) di ritardo in cui non viene mostrata alcuna immagine, e quindi un’altra immagina
appare sullo schermo. L’animale deve fornire una risposta diversa a seconda
che il secondo stimolo (match) sia o meno uguale al primo (sample). Ad
ogni stimolo campione corrisponde un insieme diverso di neuroni attivi (ma
un neurone può essere selettivo a più stimoli), con frequenze medie più alte
rispetto all’attività spontanea. Nel tempo di ritardo dopo lo stimolo campione, quando esso è stato rimosso, si registra ancora una particolare attività
selettiva.
L’aspetto notevole che emerge è che, dopo un numero relativamente grande di stimoli presentati, le distribuzioni di frequenze registrate durante i periodi di ritardo corrispondono a rappresentazioni, non di singole immagini
ma di classi di stimoli memorizzati.
21
1.3. Il modello della sinapsi
Questi risultati, oltre a mettere in evidenza la proprietà di classificazione,
suggeriscono un correlato neuronale della memoria di lavoro [11], [12]. Dopo
l’apprendimento, l’applicazione di uno stimolo induce una attività selettiva
che è la rappresentazione interna dello stimolo stesso. Dopo la successiva
rimozione si può osservare una attività riverberante indotta che persiste per
un certo tempo e che rappresenta il prototipo della classe cui lo stimolo
presentato appartiene.
Fu lo psicologo Donald O. Hebb più di cinquanta anni fa [13] a suggerire un meccanismo per questo duplice aspetto della memoria. Da una parte
deve esistere un meccanismo che in qualche modo mantenga la memoria a
lungo termine, che si modifica con l’apprendimento. L’intuizione ed il suggerimento è che questo derivi dalla covarianza delle attività dei neuroni pre
e post-sinaptico, quindi che sia un meccanismo locale. La sinapsi vede solo
la coppia di neuroni pre e post-sinaptico e si potenzia (aumenta l’efficacia)
se entrambi i neuroni sono attivi (diversi meccanismi sono stati poi suggeriti
per il depotenziamento). Questa descrizione è coerente con il meccanismo
LTP indicato precedentemente. Lo stato delle sinapsi modificatosi durante
la fase di apprendimento, rappresenta la memoria a lungo termine delle classi memorizzate. Sebbene il meccanismo di modifica sia locale, la memoria è
distribuita nelle sinapsi di tutta la rete.
L’altro meccanismo è a breve termine ed è rappresentato dalla riverberazione. Uno stimolo presentato per breve tempo e poi rimosso innesca il processo dinamico che si autosostiene per effetto dell’elevato feedback, ponendo
la memoria di quello stimolo in uno stato “attivo”.
Per descrivere la struttura sinaptica di una rete si ricorre spesso alla
metafora di un paesaggio fatto di valli e alture. I punti del paesaggio rappresentano gli stati di attività della rete e la tendenza ad andare verso il basso o
verso l’alto dipendono dalla dinamica neuronale. I fondo valle rappresentano
gli attrattori della rete e sono stati di equilibrio della stessa.
Il modello di Hopfield costituisce un esempio ben trattato dal punto di
vista analitico di rete neuronale ad attrattori [2]. La rete ha N neuroni che
possono assumere solo due stati (attivo e inattivo) identificati con i valori −1
e 1, in questo caso lo stato della rete corrisponde ad una parola binaria di N
bit.
Senza entrare nel dettaglio di questo modello, si vuole evidenziare una
limitazione generale che hanno questi sistemi se non si aggiungono ulteriori
arricchimenti:
la sinapsi del modello di Hopfield può assumere un numero di valori diversi
che dipende dal numero delle classi memorizzate (2p + 1 valori per p classi).
La difficoltà nella realizzazione di un dispositivo reale è evidente, tenendo
conto anche del fatto che il numero di sinapsi è proporzionale a N 2 .
22
Capitolo 1. Reti neuronali e neuroscienze computazionali
Una possibile assunzione realistica consiste nel ridurre la profondità analogica della sinapsi a pochi valori di efficacia stabili a lungo termine. Questo
vincolo (numero discreto e finito di stati stabili di efficacia) limita severamente la memoria della rete: la memorizzazione di nuovi stimoli cancella
rapidamente quella degli stimoli più vecchi. Questa limitazione viene superata assumendo [14] che alla presentazione di ogni stimolo, ogni sinapsi
elegibile per il potenziamento o depotenziamento sulla base delle attività
neuronali pre- e post-sinaptiche, subisca effettivamente queste modificazioni
con una certa probabilità.
Il prezzo che si paga per il recupero per una elevata capacità di memoria assicurata da tale meccanismo stocastico, è la necessità di aumentare il
numero di presentazioni necessarie a memorizzare uno stimolo.
Il meccanismo adottato in [15] è considerare la sinapsi un dispositivo analogico su brevi scale dei tempi e discreto (a due stati nel modello realizzato)
su lunghe scale dei tempi.
Un meccanismo a soglia imposto sulla variabile analogica, determina le
transizioni di potenziamento/depotenziamento tra i due stati di efficacia.
Nel modello adottato, la natura stocastica delle transizioni sinaptiche viene
assicurata dalle fluttuazioni nei tempi di arrivo degli spikes che guidano la
dinamica sinaptica (determinando, nel modello in esame, cambiamenti nella
variabile analogica della sinapsi) [16] [17].
Viene definito un valore istantaneo analogico X(t) della sinapsi che in
assenza di stimoli tende ad un valore stabile che si mantiene indefinitamente.
Questo valore viene discriminato da una soglia per fissare i due valori possibili
di efficacia sinaptica. La stessa soglia discrimina i due versi possibili a cui
tende X(t) in assenza di stimoli. La modificazione del valore analogico deve
avvenire secondo le prescrizioni hebbiane, prendendo come input gli spikes del
neurone pre-sinaptico, e grandezze che rappresentano l’attività del neurone
post-sinaptico. Nei primi modelli proposti e anche realizzati in VLSI dal
nostro gruppo, il modello della sinapsi prevedeva che l’attività del neurone
post-sinaptico potesse essere letta dal potenziale di membrana Vsoma . Si
suddivide il campo di variabilità del potenziale in due zone (con una soglia
discriminatrice): la zona alta rappresenta una alta attività del neurone postsinaptico e quindi in coincidenza dello spike-presinaptico la X(t) deve tendere
verso un potenziamento, viceversa se all’arrivo dello spike pre-sinaptico la
Vsoma si trova nella zona bassa la sinapsi deve tendere alla depressione.
In questo modo la sinapsi pur avendo un comportamento stocastico dovuto all’attività dei neuroni pre e post-sinaptici ha dinamica deterministica.
Tutti gli ingredienti sopra descritti più ulteriori prescrizioni si trovano sul
modello di sinapsi realizzato.
23
1.3. Il modello della sinapsi
Il modello teorico della sinapsi qui di seguito descritto [18], è quello che
è stato realizzato nel presente lavoro.
Le nuove prescrizioni si riferiscono ad un meccanismo in cui l’attività
del post-sinaptico non viene letta soltanto dal potenziale del neurone postsinaptico, ma anche dall’attività pregressa degli spikes post-sinaptici emessi.
Questa regola aggiuntiva prevede che sia il meccanismo di potenziamento
che di depressione possa avvenire se il neurone non ha avuto attività eccessivamente alte o eccessivamente basse (stimate dall’attività pregressa dell’emissione di spikes post-sinaptici) in un tempo recente rispetto all’emissione
dello spike pre-sinaptico. Il meccanismo che ha delle motivazioni teoriche mirate prevalentemente ad una ottimizzazione delle risorse sinaptiche rispetto a
insiemi di stimoli particolari, ha anche delle analogie biologiche con gli effetti
che produce la concentrazione degli ioni calcio, da cui il nome che appare
nelle variabili di seguito utilizzate e nel modulo realizzato.
Qui di seguito viene data la descrizione del modello.
La sinapsi ha due soli stati stabili la cui efficacia vale J+ quando è
potenziata o J− quando è depressa.
Il comportamento dinamico è governato da due variabili interne
• X(t) che rappresenta il valore analogico interno della sinapsi
• C(t) (variabile Calcio) che è la variabile con lunga scala dei tempi che
fornisce una stima dell’attività pregressa del neurone post-sinaptico
Lo stato stabile vale J− se X(t) è inferiore ad una certa soglia θX fissata,
J+ altrimenti.
La dinamica della variabile Calcio si può realizzare con decadimento lineare con la condizione al contorno di un salto definito di ampiezza Jc verso
l’alto all’arrivo dello spike post-sinaptico al tempo t0
C(t) = −Kc t
(1.2)
C(t0+ ) = C(t0− ) + Jc
con Kc > 0 costante di decadimento lineare.
Si può definire il recovery-time come il tempo necessario alla variabile
X(t) per ritornare ad valore X(t0 ) dopo l’arrivo dello spike post-sinaptico
al tempo t0 per effetto del solo decadimento lineare. Il recovery-time, che
dipende in questa rappresentazione dall’ ampiezza del salto e dalla pendenza
del decadimento lineare, dovrà essere maggiore del I.S.I medio tipico della
rete, se si vuole avere memoria dell’attività trascorsa del neurone.
Ad ogni arrivo di uno spike pre-sinaptico al tempo tpre vengono valutate
le variabili C(t) e la depolarizzazione Vp (t) del neurone post-sinaptico. La
24
Capitolo 1. Reti neuronali e neuroscienze computazionali
variabile interna sinaptica X(t) potrà fare, o non fare, un salto con la seguente
regola
X(t)− > X(t) + a se V p (tpre ) > θp
e K1up < C(tpre ) < K2up
X(t)− > X(t) − b se V p (tpre ) ≤ θp
e K1down < C(tpre ) < K2down
(1.3)
dove a, b > 0 e K1up , K2up , K1down , K1down sono soglie fissate sulla variabile
Calcio.
In assenza di spike pre-sinaptici oppure se non sono soddisfatte le condizioni 1.3 la variabile X(t) tende verso i due stati stabili con velocità
dX(t)
= α se X(t) > θX
dt
dX(t)
= −β
dt
se X(t) ≤ θX
con α, β > 0.
25
(1.4)
1.3. Il modello della sinapsi
26
Capitolo 2
Hardware neuromorfo e VLSI
in tecnologia CMOS
L’approccio tipico con cui si implementano modelli di strutture biologiche
che presentano una natura squisitamente analogica non è rappresentata da
circuiti complessi come ad esempio quello di un circuito digitale, ma piuttosto
da circuiti più semplici dove le caratteristiche fisiche implicite di ciascun
dispositivo elementare rappresentato da un unico simbolo nello schematico
costituisce di per sè una parte di modellizzazione.
Il questo contesto il transistor MOSFET (Metal-Oxide-Semiconductor
Field Effect Transistor), risulta attualmente il miglior dispositivo che si presta a questo scopo. Le sue caratteristiche di basso consumo, basso costo,
moderata complessità circuitale e sopratutto la sua versatilità nel realizzare circuiti di memoria a breve-termine o a lungo-termine caratteristici dei
sistemi neuronali lo rende il dispositivo principe delle implementazioni hardware dei circuiti neuronali. Le strutture circuitali elettroniche di base che
realizzano tali sistemi hanno delle affinità, dal punto di vista funzionale, cosı̀
evidenti con i relativi modelli biologici che da qualche anno è stata coniata la parola Hardware neuromorfo per indicare proprio questo tipo di
implementazioni [19], [20].
La tecnologia VLSI (Very Large Scale Integration) usata e piu’ comune
per i transistor MOS è la CMOS (Complementary Metal Oxide Silicon). La
sigla CMOS indica la presenza su uno stesso chip di entrambi i dispositivi
a canale n (n-mos) e a canale n (p-mos). Una ulteriore specificazione della
tecnologia che abbiamo usato per realizzare il chip del presente lavoro, è
n-well che sta ad indicare che i dispositivi p-mos sono situati all’interno
di pozzetti (aree nel substrato) drogate n mentre i dispositivi n-mos sono
impiantati direttamente nel substrato drogato p.
27
2.1. Il transistor mosfet
2.1
Il transistor mosfet
In questo paragrafo viene descritta la struttura fisica del transistor mosfet, e
le relative equazioni caratteristiche sotto soglia con una breve e riassuntiva
discussione della fisica che porta alla loro derivazione. Vengono anche indicate le equazioni sopra soglia. Per approfondimenti si veda [20], [21], [22],
[23], [24].
Nei circuiti neuromorfi gran parte dei mosfet vengono fatti generalmente
lavorare in regime sotto soglia. Tra Le motivazioni principali di questa scelta ci sono i bassi consumi, determinati sostanzialmente dai piccoli valori di
corrente di lavoro e il tipo di dipendenza corrente-tensione che è esponenziale. Una raffigurazione pittorica del dispositivo è visibile in fig. 2.1 dove
Gate (G)
Source (S)
Drain (D)
W
n+
L
n+
p
Substrato (B)
Figura 2.1: Struttura di un Mosfet tipo n nel substrato tipo p
ne è raffigurata una sezione trasversale. Il dispositivo indicato è di tipo n,
l’estensione al caso tipo p è ovvia. Il semiconduttore del substrato è drogato
p mentre le aree poste ai lati sone chiamate aree attive di drain e di source
che sono drogate n+ (drogate pesantemente). Queste due aree identificano i
terminali Drain e Source. Queste sono simmetriche tra loro, ovvero la loro
denominazione è definita solo dal segno del potenziale relativo applicato (il
source è la sorgente di elettroni mentre il drain li rimuove), esse inoltre formano con il substrato due giunzioni a semiconduttore. La parte centrale è la
struttura MOS, costituita da un piatto a bassa resistività di polisilicio (silicio
policristallino), separato dalla parte sottostante da un sottile strato di SiO2
28
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
isolante, il piatto identifica il terminale di Gate. Le cariche maggioritarie
del substrato sono le lacune mentre quelle delle aree attive sono gli elettroni.
A causa del forte drogaggio le aree attive hanno bassa resistività. La zona
sottostante il Gate è caratterizzata da una larghezza W e da una lunghezza
L di canale. Nel normale modo di operazione le tensioni dei 4 terminali G,
B, S, D, sono tali che Vg ≥ Vb , Vs ≥ Vb , Vd ≥ Vb .
Se Vd ≥ Vs e Vg non è troppo bassa una corrente positiva avrà il verso
Drain → Source.
Il parametro che determina la zona di funzionamento del dispositivo è
la tensione di soglia Vt . Questa è funzione delle caratteristiche costruttive
fisiche del dispositivo, tra cui:
• concentrazioni del drogaggio nel substrato
• capacità specifica di gate (dell’ossido di silicio)
Il valore della tensione di soglia, pertanto, è un parametro imposto dalla
tecnologia.
Al variare della Vgs e in funzione dei valori relativi di tensione ai 4
terminali si definiscono differenti regimi di funzionamento.
Si assuma Vd > Vs
• cut-off Vgs = 0 oppure Vgs ¿ Vt : la zona sottostante il gate è piena
di cariche positive (lacune), la corrente tra drain e source è praticamente nulla perche’ i due diodi drain-substrato e substrato-source sono
polarizzati inversamente.
• svuotamento Vgs <' Vt : le lacune vengono allontanate dal gate per
effetto del campo elettrico; si crea una zona di svuotamento di lacune
che permette il passaggio di una piccola corrente.
• debole inversione Vgs ' Vt : la zona di svuotamento è sempre presente,
ma il forte campo elettrico richiama elettroni sotto il gate e si forma
un sottile strato sottostante il gate con accumulo di cariche negative
denominato strato d’inversione. Questo costituisce un percorso di conduzione aggiuntivo tra il drain ed il source, contributo altresı̀ ancora
trascurabile rispetto alla corrente dovuta alle cariche nella regione di
svuotamento.
• forte inversione Vgs > Vt : lo strato d’inversione interposto tra gate e
area di svuotamento diventa considerevole e fornisce il principale contributo alla corrente che assume valori molto più alti rispetto agli altri
regimi.
29
2.1. Il transistor mosfet
Figura 2.2: (tratta da [22]) Regioni di svuotamento e di inversione nel mosfet
ENHANCEMENT
Entrambi i regimi di forte e debole inversione vengono indicati come sottosoglia. La dipendenza Id vs. Vgs nei due regimi sotto e sopra soglia è ben
distinta essendo la prima di tipo esponenziale mentre la seconda di tipo
quadratico.
Questo tipo di dispositivo viene detto MOSFET ENHANCEMENT (arricchimento) per distinguerlo dall’altro MOSFET DEPLETION dove lo strato di inversione è già formato in prossimità del biossido di silicio: con Vgs = 0
si ha passaggio di corrente. Per annullare il passaggio di corrente Vgs deve
essere negativa.
Verranno ora descritte le principali equazioni del dispositivo nel regime
sotto-soglia passando per una sintetica derivazione fisica [20].
In tale regime trascuriamo le cariche presenti nello strato d’inversione.
Si consideri la concentrazione degli elettroni nel canale. Si assuma che il
potenziale nel canale ψs sia costante. La concentrazione nelle zone terminali
del canale adiacenti al source ed al drain dipenderà dalla barriera di energia
che gli elettroni incontrano. Questa dipende dalla differenza di tensione tra
il potenziale superficiale ψs e Vs , Vd per il source e drain rispettivamente.
Indichiamo con Θs e Θd le altezze delle barriere di potenziale.
Θs = Θ0 − q(ψs − Vs ) e Θd = Θ0 − q(ψs − Vs )
(2.1)
dove Θ0 e q sono rispettivamente la barriera di potenziale intrinseca della
giunzione e la carica elettrica elementare. La densità degli elettroni della
parte del source e del drain rispettivamente sono dati da
Ns = N0 eΘs = N0 e
30
−(Θ0 −q(ψs −Vs )
KT
(2.2)
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
Nd = N0 eΘd = N0 e
−(Θ0 −q(ψs −Vd )
KT
(2.3)
dove K è la costante di Boltzmann e N0 è il numero effettivo di stati per
unità di area.
La corrente nel transistor si può ottenere dalla equazione per la densità
di corrente di diffusione dell’elettrone
dN
I = Jdif f W t = − q W t Dn
(2.4)
dz
Dove Jdif f è la densità di corrente di diffusione degli elettroni, W e t sono
la larghezza e la profondità del canale, Dn è il coefficente di diffusione e dN
dz
è il gradiente di concentrazione lungo il canale. Una buona approssimazione
è assumere che la conduzione sia senza perdita e che quindi il gradiente di
concentrazione lungo il canale sia costante. Possiamo allora esprimere il
gradiente come
dN
Nd − Ns
N1 Uψs
=
=
e T
dz
L
L
µ
V
e
− Ud
dove L E la lunghezza di canale, UT =
KT
q
T
− UVs
−e
T
¶
(2.5)
è la tensione termica1 e
−θ0
N1 = N0 e KT
Sostituendo la 2.5 nella 2.4 si ottiene
ψs
I = It0 e UT
µ
e
− UVs
T
V
− Ud
−e
T
¶
(2.6)
con It0 = q W
t D n N1 .
L
ψs è funzione della tensione di gate Vg . In un intorno del suo punto di
lavoro ψ0 possiamo esprimerla come
ψs = ψ0 − kVg
(2.7)
dove k è il rapporto di accoppiamento capacitivo tra gate e canale chiamato
anche fattore di pendenza sotto-soglia 2 , 3 . Sostituendo la 2.7 nella 2.6 si
ottiene
µ −V
¶
kVg
−Vd
s
I = I0 e UT e UT − e UT
(2.8)
ψ0
con I0 = It0 e KT
Nella figura 2.4 è presentato l’andamento della corrente nei due regimi
sopra e sotto soglia.
1
UT ≈ 25.8mV a temperatura ambiente
Cox
Si trova che k = Cox
+Cd dove Cox è la capacità di ossido di silicio per unità di area
mentre Cd è la capacità dello strato di svuotamento per unità di area. Questo fattore si
trova in tutte le equazioni sotto-soglia
3
in questo contesto occorre prestare attenzione a non confondere questo k con K
costante di Boltzmann
2
31
2.1. Il transistor mosfet
Figura 2.3: Corrente in funzione della Vgs in una simulazione Spectre-CADENCE in scala
logaritmica di un mosfet della tecnologia AMS 0.35 µ di dimensioni L = 0.35 µ (minime)
e W = 1 µ. È chiaramente distinguibile la regione esponenziale nel regime sotto-soglia da
quella sopra soglia
In entrambi i regimi di funzionamento sotto e sopra soglia la caratteristica corrente-tensione del MOSFET si suddivide nettamente in due regioni
distinte, riguardo la dipendenza rispetto a Vds , a seconda del valore della
stessa.
• regione lineare o ohmica
nel regime sotto-soglia è definita per valori relativamente bassi di Vds
(Vds ≤ UT ).
I = I0 e
kVg −Vs
UT
µ
1−e
−Vds
UT
¶
(2.9)
Espandendo in serie di Taylor si può osservare che I è approssimativamente lineare con Vds
nel regime sopra soglia si ha quando 0 < Vds < Vgs − Vt
I = β[(Vg − Vt )(Vd − Vs ) −
approssimare con
2
Vds
]
2
che per valori piccoli di Vds si può
I = β(Vg − Vt )(Vd − Vs )
(2.10)
dove β = µCox W
e µ è la mobilità degli elettroni. Anche qui è
L
evidente la relazione lineare di I con Vds con gli altri parametri
fissati.
32
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
In questa zona il Mosfet si comporta come una resistenza tra drain e
source controllata in tensione dalla Vgs .
• regione di saturazione
nel regime sotto-soglia si è in questa regione quando Vds raggiunge o
supera 4UT . La concentrazione degli elettroni in prossimità del
drain è trascurabile rispetto a quella del source, perchè dal drain
essi vengono immediatamente catturati. La corrente di diffusione
non dipende più da Vd ma solo da Vs (oltre che da Vg )
Isat = I0 e
kVg −Vs
UT
(2.11)
nel regime sopra soglia si ha quando 0 < Vgs − Vt < Vds
Isat =
β
(Vg − Vt )2
2
(2.12)
In questa zona il Mosfet si comporta come un generatore di corrente
tra drain e source controllata in tensione dalla Vgs .
Figura 2.4: Caratteristica di uscita (corrente-tensione) di un mosfet della tecnologia AMS
0.35 µ di dimensioni L = 0.5 µ e W = 1 µ in una simulazione Spectre-CADENCE, per
diversi valori della tensione Vgs . Il grafico a sinistra mostra il caso nel regime sotto soglia
mentre quello a destra nel regime sopra soglia.
33
2.2. Effetto Early
2.2
Effetto Early
Tra i principali effetti al secondo ordine, almeno l’effetto Early merita di
essere menzionato essendo la causa dello scostamento dalla condizione di
generatore di corrente ideale che è una caratteristica ampiamente sfruttata
in molti elementi circuitali neuromorfi progettati in questo lavoro.
Le equazioni in regime di saturazione 2.11 e 2.12 mostrano una indipendenza della corrente di saturazione dalla tensione Vds . Il canale reale effettivo
Lef f è sempre un poco più stretto di quello costruttivo L, perchè la tensione
di drain induce un restringimento dello stesso in prossimità del drain; il punto vicino al drain in cui il canale si riduce praticamente a zero è chiamato
pinch-off, questo punto quindi si muove un poco al variare di Vd (si veda fig.
2.5.
Figura 2.5: (tratta da [22]) Effetto Early. Xd corrisponde alla differenza L − Lef f
Finchè la lunghezza L è relativamente grande rispetto a queste variazioni
di posizione del pinch-off ( che hanno l’ordine di grandezza delle dimensioni
sub-micrometriche tipiche delle attuale tecnologie disponibili) la variazione
di lunghezza effettiva è piccola rispetto a L, viceversa per L piccolo questo
effetto non è più trascurabile. Per le ragioni sopra indicate tale effetto è
chiamato anche modulazione di canale.
Poichè l’effetto è quello di una dipendenza funzionale della corrente da
Lef f si può descrivere questa dipendenza valutando la pendenza della curva
corrente-tensione che corrisponde alla conduttanza di uscita gds del transistor
gds =
∂I ∂Lef f
∂I
=
∂Vds
Lef f ∂Vds
34
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
I
Slope = gds
- Ve (tensione Early)
Vds
Figura 2.6: Tensione di Early
Derivando rispetto a L nella 2.6 si può trovare che
∂I
I
=−
∂Lef f
Lef f
e quindi
gds = −
I ∂Lef f
I
=
Lef f ∂Vds
Ve
∂Vds
dove Ve = −Lef f ∂L
è il valore assoluto di tensione dove la retta interseca
ef f
l’ascissa in fig 2.6. Nel dominio sotto-soglia la corrente espressa dall 2.11 si
corregge quindi in
Vds
)
(2.13)
I = Isat + gds = Isat (1 +
Ve
2.3
Vincoli tecnologi, flusso di progetto e tecniche di progettazione
È noto che i sistemi elettronici, sia essi a componenti discreti che in VLSI si
possono suddividere in due categorie: analogici e digitali. Nella progettazione
di circuiti integrati la metodologia e gli strumenti software utilizzati sono
differenti nei due casi.
Gli elementi di base nei sistemi digitali realizzano funzioni sequenziali
e combinatorie e sono in genere molto semplici. Il sistema complesso può
essere descritto come un insieme degli elementi base e dei collegamenti tra
essi: rappresentazione schematica oppure tramite un linguaggio descrittivo
appropriato che descrive in un listato le funzioni utilizzate e le interazioni tra
esse, come ad esempio il VHDL4 .
4
VHDL è un doppio acronimo: V sta per Very High Integrated Circuit e HDL per
Hardware Description Language
35
2.3. Vincoli tecnologi, flusso di progetto e tecniche di progettazione
Tali sistemi possono essere simulati con grande precisione e accuratezza
con l’utilizzo di simulatori digitali. Inoltre, per la loro natura che è quella di
trattare segnali a due soli livelli, essi si prestano bene ad essere sintetizzati
a partire da una descrizione ad alto livello come il VHDL. Moltissimi sono i
software che realizzano simulazione di sorgenti VHDL e che implementano le
funzioni del sistema in un insieme definito di celle base fisiche disponibili. In
questo senso i tools software disponibili per implementare sistemi in un chip
VLSI piuttosto che in un FPGA5 sono molto simili tra loro.
Diverso è il caso dei circuiti analogici che invece richiedono un tipo di
simulazione di segnali continui nel tempo. In generale il livello di complessità
nell’utilizzo dei simulatori analogici è superiore a quello dei simulatori digitali. Una ulteriore sostanziale differenza è che non esistono sintetizzatori ad
uso generale di circuiti analogici. Questo aspetto è ovvia conseguenza della
natura stessa dei segnali trattati.
Un altro aspetto importante da sottolineare è la differenza che si ha in termini di gradi di libertà nella progettazione analogica di circuiti VLSI rispetto
a quelli discreti. Ogni dispositivo elementare (come ad esempio transistor,
resistenza) viene descritto geometricamente con la sua forma fisica e le sue
dimensioni che specificatamente sono per il Mosfet la sua larghezza e lunghezza di canale W e L. Questi due parametri insieme alla forma fisica devono
essere imposti dal progettista in funzione delle caratteristiche che deve avere
quel singolo dispositivo nel contesto del circuito. Da qui viene l’appellativo
di progettazione FULL-CUSTOM.
Come osservato nelle precedenti sezioni le caratteristiche di ogni singolo
dispositivo sono determinati oltre che dalle dimensioni fisiche anche dalle
caratteristiche della tecnologia usata. Queste ultime comprendono, tra gli
altri, gli spessori dei singoli materiali, come ad esempio lo spessore dell’ossido
sottile sottostante il gate che determina la capacità specifica del gate e tutti i
parametri ad essa collegati; il numero di metalli disponibili per le connessioni;
le percentuali di drogaggio nei semiconduttori. Anche la definizione e le
minime dimensioni disponibili sono determinate dalla tecnologia usata. La
dimensione minima in particolare è il comune appellativo con cui si identifica
la tecnologia ed è importante perchè determina il grado di integrazione dei
dispositivi in un chip. Attualmente sono disponibili tecnologie intorno a 0.1µ.
L’insieme delle regole per il disegno e dei parametri per la simulazione
vengono forniti dalla fonderia in un pacchetto software che si integra con i
tools software utilizzati. Questo pacchetto è chiamato Design-Kit.
In questo lavoro è stata usata la tecnologia AMS 0.35 µ 4 metalli, e il
5
FPGA è un acronimo che sta per Field Programmable Gate Array . L’FPGA è un
dispositivo programmabile che riproduce funzioni logiche
36
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
software utilizzato per tutti i tools di progettazione è CADENCE. Il chip
realizzato è di tipo Mixed-Signal ovvero comprende sia circuiti analogici che
digitali. Il lavoro che specificatamente è stato fatto in questa tesi riguarda i moduli analogici, pertanto nel seguito vengono trattati in modo più
approfondito gli aspetti legati alla progettazione analogica.
2.3.1
Dal disegno di principio alla simulazione postlayout
Nella figura 2.7 sono rappresentati schematicamente tutti i passi della progettazione.
In una prima fase vengono analizzati il modello da implementare e le
specifiche di progetto e se ne disegna una possibile implementazione in uno
schematico. Lo schematico è una rappresentazione che non tiene conto di
tutti gli aspetti che intervengono in una realizzazione fisica. I dispositivi
sono trattati come ideali ovvero con tutte le caratteristiche indicate dalla
tecnologia e le dimensioni indicate dal progettista ma senza tener conto degli
elementi parassiti che si introducono nella realizzazione fisica, come le capacità di sovrapposizione dei layer e le resistenze dei conduttori di collegamento
tra gli elementi che nello schematico vengono considerate nulle. Questa limitazione descritta si manifesta nei risultati di simulazione a livello schematico,
che è lo strumento per effettuare le verifiche di progetto in ogni fase di un
progetto VLSI analogico.
Il simulatore usato è Spectre di CADENCE, ed è basato sul noto simulatore analogico Spice6 introdotto negli anni ‘70, di cui ne costituisce una
versione migliorata in termini di accuratezza e velocità di calcolo [25] e [26].
I tipi di analisi che si possono effettuare sono fondamentalmente quattro:
nel dominio della frequenza, del rumore, in continua , nel dominio del tempo.
Di questi solo gli ultimi due sono stati usati in questo contesto. L’analisi in
frequenza non è stata utilizzata perchè i circuiti sono progettati per lavorare a
frequenze molto basse rispetto a quelle massime raggiungibili dalla tecnologia
essendo i tempi caratteristici dei circuiti neuromorfi vicini a quelli biologici.
Anche l’analisi del rumore non è stata eseguita perchè i sistemi neuronali
sono intrinsecamente robusti rispetto al rumore.
La simulazione in continua (in dc) calcola il punto di lavoro del circuito
(op), ossia le correnti e le tensioni di tutti gli elementi presenti nel circuito,
considerando condensatori aperti e induttori cortocircuitati. Utilizza le equazioni lineari e non lineari dei modelli forniti dalla fonderia per i dispositivi
elementari. La ricerca delle soluzioni, quando si è in presenza, di elementi
6
Simulator Program with Integrated Circuit Emphasis
37
2.3. Vincoli tecnologi, flusso di progetto e tecniche di progettazione
non lineari avviene con metodo iterativo, per cui è utile a volte suggerire
al simulatore dei valori di partenza per una o più tensioni. Gli algoritmi di
soluzione sono essenzialmente basati sulla analisi nodale con la matrice delle
conduttanze.
La simulazione nel dominio del tempo è denominata transiente ed è una
analisi per grandi segnali. Si considerano anche le non-linearità presenti nel
circuito, quelle dei dispositivi attivi. Essa calcola, oltre alle tensioni e alle
correnti relative agli elementi tempo invarianti, anche le variazioni di carica
Q associati ai condensatori dei flussi F associati alle induttanze.
Le equazioni costitutive dei singoli elementi circuitali sono più o meno
complesse a seconda del modello utilizzato, che corrisponde ad un livello
descrittivo più o meno dettagliato del dispositivo,
Gli algoritmi per la soluzione delle equazioni descriventi il circuito elettrico riguardano, tra gli altri, le equazioni differenziali ordinarie non lineari. La
soluzione in dc dei circuiti lineari avviene con l’analisi nodale e l’eliminazione
gaussiana, fattorizzazione L.U. ecc.. Per l’analisi in dc nel caso di elementi
non-lineari è usato il metodo iterativo di Newton-Raphson. Per l’analisi nel
dominio del tempo vengono usati algoritmi di integrazione numerica iterativa:
eulero inverso, trapezioidale, Gear che sono di ordine da 1 a 6. Quest’ultima
è l’analisi più completa perchè comprende tutti gli algoritmi a disposizione
di Spice/Spectre.
Quando la simulazione dello schematico dà risultati soddisfacenti in termini dei risultati attesi, si passa alla fase di layout ovvero al disegno fisico
dei dispositivi e dei collegamenti tra essi. Il layout deve essere disegnato
tenendo conto delle regole di disegno fornite dalla fonderia che possono venir controllate con il pacchetto DRC (Design Rule Checker). Disegnato un
modulo di layout a cui corrisponde uno (o più) schematici viene fatto girare
il pacchetto LVS (Layout Versus Schematic) che controlla che il layout abbia
una esatta corrispondenza con lo schematico di riferimento. Un passo successivo è l’estrazione dei parassiti e successiva simulazione post-layout che ne
tiene conto.
Nei circuiti neuromorfi le capacità parassite possono rivelarsi, in taluni
casi, non trascurabili. Una delle regole generali della progettazione VLSI è
il risparmio dell’area di silicio. In quei casi in cui le capacità richieste dalla
funzionalità del circuito siano piccole, è possibile sfruttare questa condizione.
Purtroppo queste stesse capacità possono rivelarsi estremamente dannose se accoppiano segnali digitali rapidamente variabili con zone analogiche
sensibili creando il fenomeno del crosstalk.
Il presente chip realizzato rientra esattamente nella categoria dei circui38
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
&RQFH]LRQHGHOOಫLGHD
'HILQL]LRQHGHOSURJHWWR
'LVHJQR
HOHWWULFR
GHO FLUFXL WR
&RPSDUD]LRQHFRQOH
VSHFLILFKHGLSURJHWWR
,PSOHPHQWD]LRQH
&RPSDUD]LRQHFRQOH
VSHFLILFKHGLSURJHWWR
6LPXOD]LRQH
'HILQL]LRQHILVLFD
'LVHJQR
ILVLFR
GHO FLUFXL WR
9HULILFDILVLFD
(VWUD]LRQHGHLSDUDVVLWL
)DEEULFD]LRQH
6YLOXSSR
7HVW3URGX]LRQH
)DEEULFD]LRQH
7HVW9HULILFKH
3URGX]LRQH
Figura 2.7: Processo di progettazione di circuiti analogici integrati
ti potenzialmente esposti a rischio crosstalk. Basti pensare, ad esempio,
agli spikes generati dai neuroni che in qualche modo devono raggiungere le
sinapsi.
Per tale motivo è stato necessario effettuare prima del disegno dei layout
dei singoli moduli, lo studio e la definizione dei percorsi dei segnali, della loro
distribuzione, e della schermatura con piani di alimentazioni.
2.3.2
Mismatch dei parametri e simulazione montecarlo
Una delle peculiaretà dei circuiti neuromorfi è quella di lavorare in regime di
sotto soglia. Questo si traduce nella necessità di impostare correnti di lavoro
molto basse, tipiche della zona weak-invertion dei transistor mosfet. Se per
un verso questo comporta il vantaggio dei bassi consumi, per contro si deve
affrontare l’inevitabile problema della dispersione dei parametri tecnologici
nel wafer di silicio da cui verrà prodotto il chip.
Molteplici e svariate ne sono le cause, per lo più determinate dai processi di fabbricazione: ad esempio l’inevitabile non perfetta omogeneità dello
spessore dell’ossido di silicio provoca una capacità di gate specifica per unità
39
2.3. Vincoli tecnologi, flusso di progetto e tecniche di progettazione
di superfice del mosfet che può differire da un dispositivo ad un altro; analogamente la frazione di drogaggio del silicio avrà una certa caratteristica
distribuzione sull’area del chip. Tutte queste disomogeneità si traducono,
operativamente, in una varianza non trascurabile nella distribuzione dei valori dei parametri dei dispositivi intrinseca alla tecnologia. Un aspetto importante di cui deve tener conto il progettista, è che alcuni di questi effetti
negativi dipendono dalla dimensione dei dispositivi, in particolare dal rapporto delle dimensioni fisiche del dispositivo con la dimensione minima imposta
dalla tecnologia. Questo fenomeno è dovuto sostanzialmente alla precisione
delle maschere di layout con cui vengono prodotti i dispositivi. La prima
ovvia strategia per ridurre questi effetti indesiderati è quella di disegnare
dispositivi con le dimensioni abbastanza più grandi di quelle minime.
Un grande ausilio per valutare quantitativamente queste problematica
viene dalla possibilità di usare la simulazione montecarlo. Questa permette
di avere un’ idea di come sarà la distribuzione di uno o più segnali prodotti dai
nostri circuiti al variare dei parametri tecnologici. I modelli di simulazione
sono forniti dalla fonderia stessa con il design-Kit.
L’analisi montecarlo consiste in una procedura automatica di esecuzione
di un numero definibile di iterazioni che non sono altro che simulazioni ripetute del tipo desiderato (transiente, dc o altro) con parametri che cambiano
da iterazione ad iterazione. I parametri per la simulazione utilizzati non sono
quelli tipici, ma viene generato un set di parametri diversi in ogni simulazione.
La generazione del valore di ciascun parametro avviene con un meccanismo
pseudorandom che genera valori concordemente alla distribuzione statistica
del parametro tecnologico fornita dalla fonderia.
Sono disponibili due modalità fondamentali di utilizzo
• mismatch tra dispositivi dello stesso chip
La distribuzione statistica si applica a istanze diverse dello stesso tipo di dispositivo. Questa modalità da indicazioni del comportamento
del circuito in cui dispositivi definiti inizialmente identici a livello di
descrizione schematica, hanno invece differenti valori di parametri.
• mismatch tra dispositivi di chip diversi
La distribuzione statistica si applica globalmente e rappresenta variazioni di processo da chip a chip.
Verrà mostrato più avanti nel Cap.3 l’utilizzo di tale strumento di verifica
per la definizione di alcuni parametri di progetto, relativi alla sinapsi.
40
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
2.4
Il processo di fabbricazione
In questa sezione si da cenno dei processi industriali che sono alla base della
fabbricazione dei dispositivi VLSI, con riferimento particolare alla tecnologia
CMOS n-well che è quella con cui è stato realizzato il chip del presente lavoro.
Tutti i processi iniziano con un singolo pezzo di silicio monocristallino. La
maggior parte dei metodi di accrescimento sono basati sul metodo sviluppato
da Czochralski nel 1917.
Il singolo pezzo di silicio (seme) viene immerso in un crogiolo contenente
silicio con impurità che possono essere P, As o Sb per il substrato P oppure
B, Al o Ga per un substrato N . La temperatura nel crogiolo è di poco
superiore a quella di fusione del silicio. Il seme viene contemporaneamente
tirato fuori e ruotato e poichè la temperatura della sua superfice è di poco
inferiore a quella di fusione, il silicio drogato solidifica con la stessa struttura
cristallina del seme. Il livello di drogaggio è in genere approssimativamente
1015 atomi di impurità per cm2 . Il cristallo di forma cilindrica che ne risulta
ha un diametro di 75 − 300 mm ed è lungo circa 1 metro. Viene tagliato in
wafer (fette) dello spessore di circa 0.5 − 0.7 mm.
La creazione dei vari dispositivi attivi e passivi sul substrato richiede
diversi passaggi legati a diverse tecniche di lavorazione per
creare i differenti drogaggi (zone attive) dei MOSFET
depositare i diversi materiali isolanti (come il SiO2 ) e conduttori (come
polisilicio e metalli per le connessioni.
I vari processi sono applicati in maniera selettiva su insiemi di aree ben
definite tramite un processo fotolitografico. Le maschere fotolitografiche vengono prodotte a partire da files generati dal progettista del dispositivo tramite
ogni tipo di software di C.A.D.7 di sviluppo VLSI.
I passi principali e le tecniche di base sono
• ossidazione: è il processo di accrescimento dell’ossido sulla superfice
del wafer.
Serve sia a proteggere i materiali sottostanti da contaminazione che a
fornire l’isolamento tra due layer conduttivi. Due diverse tecniche sono
usate per ottenere spessori diversi:
a secco per ottenere uno spessore molto sottile (100 ÷ 1000 Å)
7
Computer Aid Design
41
2.4. Il processo di fabbricazione
in atmosfera umida per ottenere uno spessore più grande (> 1000Å)
• diffusione termica: è uno dei metodi per drogare il substrato. Consiste
nel movimento per diffusione delle impurità, dall’ambiente ad alta concentrazione al silicio che può avvenire se la temperatura dell’ambiente
e superficiale è intorno a 800 ÷ 1400 ◦ C
• impiantazione ionica : è un altro metodo per drogare il substrato.
Consiste nell’accelerare le impurità in un fascio che viene sparato sul
silicio. Avviene a temperature più basse della tecnica di diffusione.
• deposizione: è la modalità con cui vari materiali possono essere depositati sul wafer di silicio, come ad esempio
Silicon Nitride (Si3 N4 )
biossido di silicio (SiO2 )
alluminio
polisilicio
le tecniche usate per la deposizione sono svariate: dalla deposizione con
vapori chimici (CVD) alla deposizione vapor-chimica a bassa pressione
(LPCVD) e altre ancora
• etching è il processo che rimuove selettivamente un materiale
Come esempio viene riportato il caso della realizzazione di un nmos.
42
Capitolo 2. Hardware neuromorfo e VLSI in tecnologia CMOS
Figura 2.8: (tratta da [24]) Creazione di una maschera di ossido - A partire dall’alto: preparazione del wafer; deposizione dell’ossido e successivamente del fotoresist materiale
sensibile alla luce; posizionamento della maschera fotografica ed esposizione a raggi ultravioletti, la parte esposta polimerizza e può essere successivamente rimossa; rimozione
dell’ossido
43
2.4. Il processo di fabbricazione
Figura 2.9: (tratta da [24]) Creazione di un nmos nel substrato p - A partire dall’alto:
deposizione ossido spesso; deposizione ossido sottile; deposizione polisilicio; drogaggio n+ delle aree attive con tecnica di diffusione oppure impiantazione; deposizione di
ossido; deposizione dell’alluminio dei contatti
44
Capitolo 3
Realizzazione elettronica
L’intero lavoro di progettazione hardware è frutto di una collaborazione
europea nell’ambito del progetto ALAVLSI 1
tra il gruppo di Roma che comprende
il gruppo del dipartimento di Fisica e sezione I.N.F.N. di Roma2
il gruppo afferente al gruppo INFN collegato di Sanità dove tra l’altro
sono stati e vengono sviluppati anche i modelli teorici trattati e tutta la
piattaforma dei sistemi di test.
con l’Istituto di Neuroinformatica dell’ Università di Zurigo (Svizzera).
In particolare il circuito del neurone I.F. utilizzato e parte degli elementi
AER sono stati sviluppati presso quest’ultimo.
Questa realizzazione segue una prima esperienza di studio e realizzazione
di una rete neuronale ricorrente connessa da sinapsi plastiche con memoria
lungo termine, con il chip lann21 precedentemente progettato e realizzato da
questo gruppo [27].
Utilizzando l’esperienza acquisita dal dispositivo lann21 sia in termini
di verifica dei modelli neuronali rappresentati, sia in termini di know-how
nella progettazione VLSI, la presente realizzazione si prefigura come un ulteriore passo in avanti nella modellizzazione delle reti neuronali e della loro
implementazione in hardware.
Diverse sono le caratteristiche innovative introdotte rispetto al precedente
dispositivo. La natura di queste novità è presente sia in termini di arricchimento dei modelli teorici rappresentati che di miglioramento della versatilità
e della funzionalità del dispositivo, come viene illustrato nel dettaglio più
avanti.
1
Attend-to-learn and learn-to-attend with neuromorphic analogue VLSI. Progetto
europeo che si pone come obbiettivo lo sviluppo di architetture per la percezione e
l’apprendimento e la loro implementazione in hardware analogico VLSI
45
3.1. Topologia della rete
3.1
Topologia della rete
Nella figura 3.1 è rappresentata la topologia del core analogico del chip ovvero
della rete ricorrente di Neuroni e Sinapsi. In questa sezione si vuole mettere
in evidenza l’ organizzazione generale della rete ed il fatto che gli elementi
neuronali: neurone, sinapsi, e albero dendritico non hanno una esatta corrispondenza topologica con i moduli di questa implementazione hardware.
Questo a motivo dell’ottimizzazione topologica e funzionale dei layout. I
singoli moduli saranno dettagliatamente illustrati nelle sezioni successive.
Spike riformato
Modulo
Sinapsi
Selezione
Modulo
Calcio-Compara
Syn
Dendriti
Generazione
variabile Calcio
Shaper (i)
Neurone (i)
Sistema
comparatori
Spike riformato
Modulo
Sinapsi (i-j)
Selezione
Modulo
Calcio-Compara
Syn
Dendriti
Generazione
variabile Calcio
Sistema
comparatori
Bus digitale
MATRICE SINAPTICA
Contributo sinaptico
Shaper (j)
Neurone (j)
Spike
Potenziale di soma
COLONNA NEURONI-SHAPER-CALCIO
Figura 3.1: Topologia della rete ricorrente. A destra è rappresentata una porzione della
colonna da 32 Neuroni-Shaper-Calcio-Compara: la riga i e la riga j mentre a sinistra la
riga j della matrice sinaptica 32x32. I segnali sottili sono digitali mentre quelli più spessi
sono analogici.
Nel cap.1 è stata evidenziata la necessità di avere nella matrice di connessione sinaptica un certo numero di sinapsi plastiche e un certo numero di
quelle inibitorio. Un ulteriore grado di libertà dimostrato da studi teorici,
46
Capitolo 3. Realizzazione elettronica
consiste nella percentuale di connettività della rete che può essere ridotta
(diluizione della matrice sinaptica) pur mantenendo sostanzialmente tutte le
caratteristiche peculiari della rete stessa.
La diluizione della matrice sinaptica è stato, ed è, un argomento di
interesse nello studio delle reti neuronali.
In questo scenario si è pensato di fornire questa rete della possibilità
di avere la matrice sinaptica di connessione tra i neuroni completamente
riconfigurabile.
Ciascuna dalle sinapsi della matrice ricorrente Sji che connette il neurone
postsinaptico Nj al presinaptico Ni è definibile per mezzo del sistema di
controllo ogni qual volta prima dell’inizio di un test come
1. eccitatoria (plastica)
2. inibitoria (fissa, non plastica)
3. disconnessa
Un’altra novità introdotta è la possibilità di poter selezionare globalmente
la dinamica di apprendimento presente nella lann21.
L’intero core della matrice ricorrente, è organizzata in due zone
• una colonna di 32 righe composte dal Neurone, dal modulo CalcioCompara e dallo Shaper.
• una matrice quadrata di 32 ∗ 32 sinapsi
Il blocco Syn posto all’interno del modulo Sinapsi insieme ai due blocchi
Generazione della variabile Calcio e Sistema comparatori posti
all’interno del modulo Calcio-Compara, rappresentano la sinapsi del modello
che si vuole implementare.
La sinapsi raffigurata è quella che connette in neurone presinaptico i con
il neurone postsinaptico j.
Il blocco Dendriti posto all’interno del modulo Sinapsi realizza l’iniezione dell’impulso di corrente in coincidenza con l’arrivo del neurone presinapico
i, posto nella i − esima riga.
Il blocco Selezione è l’elemento digitale, programmato da un controller
esterno al chip, che determina il tipo della sinapsi Sji .
47
3.2. Circuiti base CMOS utilizzati
Quando il neurone emette uno spike è il blocco Shaper che si occupa di
produrre un impulso finito di durata definibile adatto a pilotare la dinamica
sinaptica.
Questa scelta topologica rende molto semplice e compatta la distribuzione
dei segnali. Inoltre lo spostamento del modulo di comparazione della sinapsi
fuori della sinapsi stessa, implica un evidente notevole risparmio di silicio
rispetto alla soluzione di replicare il modulo per le N − 1 sinapsi della riga,
visto che i segnali di input sono comuni a tutte le N − 1 sinapsi della riga.
Ciascuno dei 32 segnali spikes viaggia in verticale, sopra la colonna di sinapsi (per chiarezza nella figura lo spike è disegnato sulla sinistra del Modulo
Sinapsi). La connessione del conduttore di spike della riga i − esima con la
colonna i − esima relativa avviene con un collegamento locale nel punto di
incrocio. Lungo la riga j − esima corrono
• lo spike da collegare alla colonna corrispondente
• un bus di due segnali digitali generati dal Modulo Calcio-Compara per
pilotare la dinamica sinaptica di tutte le sinapsi della riga
• la linea analogica che raccoglie tutti i contributi delle sinapsi della riga,
che si può dunque pittoricamente identificare con l’albero dendritico.
La connessione elettrica tra le dendriti è diretta perchè la somma si
effettua in corrente. Questa stessa linea è una estensione di un polo
della capacità soma, ovvero il potenziale sul ramo dendritico è proprio
il potenziale di soma.
3.2
Circuiti base CMOS utilizzati
Si descrivono in primo luogo i sottocircuiti analogici di base che sono stati
ampiamente usati nel ruolo di mattoni per realizzare le funzionalità dei circuiti analogici complessi del chip. In tutti gli schemi presentati la tensione
Vdd si riferisce alla tensione di alimentazione positiva del chip che nella tecnologia usata è di 3.3V . Nella figura 3.2 sono mostrati i simboli utilizzati per
i mosfet di tipo p e di tipo n.
nmos
pmos
Figura 3.2: Simboli schematici del mosfet n e del mosfet p
48
Capitolo 3. Realizzazione elettronica
3.2.1
Interruttore
Vdd
I
carico
Vin=3.3 -> on
Vin=0 -> off
nmos
Figura 3.3: Semplice interruttore
La più semplice funzione realizzabile con un solo mosfet, è l’interruttore
analogico. Nella figura 3.3 è raffigurata la versione a nmos, quella a pmos è
del tutto analoga con il source del mosfet p a Vdd e il carico verso massa.
Questa è una versione particolare in cui il source si trova a potenziale più
basso (o più alto per il pmos); in realtà l’interruttore si può posizionare tra
due carichi qualunque, ma questa versione è quella usata nella stragrande
maggioranza dei circuiti realizzati.
La tensione di gate Vg che determina i due stati possibili ON e OFF
assume rispettivamente i due valori estremi Vdd e zero, tale tensione di
controllo dell’interruttore si può quindi assumere essere digitale.
• Stato ON: Vds è piccola, il mosfet è in zona lineare: Vgs − Vds > Vt
I ' β(Vg − Vt )(Vd − Vs )
Il valore della resistenza equivalente si trova essere
Ron =
Vds
=
I
1
µCox W
(Vgs
L
− Vt )
e puo’ assumere valori relativamente bassi dell’ordine delle decine-centinaia
. Semplificando molto, si può afdi ohm in dipendenza del rapporto W
L
fermare che è il carico che limita (e determina) la corrente che circola
nel ramo se questa assume valori non elevati, come nel caso di circuiti
di carico impostati per lavorare sotto-soglia.
49
3.2. Circuiti base CMOS utilizzati
• Stato OFF: Vg è nulla, il mosfet è in zona di cut-off: la corrente è
praticamente nulla essendo ridotta alla sola corrente di leakage 2 .
Rof f −→ ∞
3.2.2
Generatore di corrente
Vdd
I
carico
Vadj
nmos
Figura 3.4: Semplice generatore di corrente
È identico all’interruttore precedente illustrato, qui però il valore di tensione applicato è un parametro continuo che determina la corrente che scorre
nel carico, se la limitazione imposta dal carico stesso non è prevalente, il
che corrisponde ad affermare che la maggior parte della tensione cade nel
generatore stesso e che quindi il mosfet si trova ad operare in saturazione
(Vds > 4 Ut in regime sottosoglia). In tali condizioni, come già visto, si ha
sotto-soglia
Vds
)
Ve
Il secondo termine tiene conto dell’effetto Early e produce uno scostamento dalla condizione ideale di corrente indipendente da Vds quanto più è
piccola, in valore assoluto, la tensione di Early Ve . Per tenerla ragionevolmente bassa la strategia usata è quella di stabilire per la lunghezza di canale
L un valore sensibilmente superiore alla minima di 0.35µ. Occorre trovare un
compromesso affinchè la lunghezza non sia troppo grande perchè questo implicherebbe uno spreco eccessivo di silicio. Sono state effettuate simulazioni
Spectre e si è trovato che il valore oltre il quale non ci sono miglioramenti apprezzabili è intorno a L = 1 µ. Il valore impostato di norma per la lunghezza
è L = 1 µ e per la larghezza L = 1.4 µ.
I = I0 e
2
kVg −Vs
UT
Leakage current: corrente di perdita
50
(1 +
Capitolo 3. Realizzazione elettronica
3.2.3
Invertitore logico
Vdd
Vin
Vout
Figura 3.5: Semplice invertitore logico
Se si considera la tensione in ingresso come digitale, ovvero circa 0V per
lo stato 0 e circa Vdd per lo stato 1, si vede che questo circuito realizza la
funzione logica N OT . Con un approccio semplificato si osserva che questo
circuito è formato da due interruttori complementari che hanno in comune
l’ingresso e l’uscita. Quindi per quanto visto sopra per l’interruttore:
• Vin = 0 il mosp è in zona lineare e il mosn è in zona cut-off Vout ≈ Vdd
• Vin = 3.3 il mosn è in zona lineare e il mosp è in zona cut-off Vout ≈ 0
Una analisi poco più approfondita richiede di osservare come questo semplice
circuito si comporti durante la fase di commutazione da 1 a 0 o viceversa della
tensione di ingresso. Una analisi statica del circuito, ovvero che non tenga
conto degli effetti dinamici delle variazioni di tensione, porta ad osservare
quanto segue. I due parametri che entrano in gioco sono le due tensioni di
soglia Vtn e Vtp rispettivamente del mosfet n e del mosfet p. Le due tensioni
di soglia non sono in genere uguali in valore assoluto ma sono comunque
inferiori a V2dd , quindi si può considerare 0 < Vtn < V2dd < Vtp < Vdd .
Di conseguenza tutto il campo dei valori di Vin si può suddividere in
cinque regioni interessanti
• 0 ≤ Vin ≤ Vtn il mosp è in zona lineare e il mosn è in zona cut-off
• Vtn ≤ Vin ≤
• Vin =
•
Vdd
2
Vdd
2
il mosp è in zona lineare e il mosn è in saturazione
i mosfet sono entrambi in saturazione
Vdd
2
≤ Vin ≤ Vdd − Vtp il mosp è in zona saturazione e il mosn è in zona
lineare
51
3.2. Circuiti base CMOS utilizzati
• Vin ≥ Vdd − Vtp il mosp è in zona di cut-off e il mosn è in zona lineare
Si può definire una tensione Vcomm di soglia dell’inverter come quel valore
di Vin per cui la tensione Vout vale V2dd . Se si impostano le dimensioni dei
mosfet uguali, la tensione di soglia dell’inverter si discosta dal valore centrale
perchè le tensioni di soglia Vtn e Vtp sono diverse a causa della differente
mobilità delle lacune rispetto a quella degli elettroni. Una regola grossolana,
spesso usata, per raggiungere una maggior simmetria è quella di realizzare il
mosp di larghezza (W ) doppia rispetto al mosn.
Figura 3.6: Funzione di trasferimento di un inverter CMOS in tecnologia AMS 0.35µ, in
una simulazione Spectre-CADENCE. Le dimensioni del mosn sono per la curva a sinistra:
L = 0.35µ , W = 0.4u, del mosp sono L = 0.35µ , W = 0.4u (entrambi minime); e per
la curva a destra: L = 0.35µ , W = 0.8u. La tensione di soglia dell’inverter è intorno a
1.2 V nel primo caso e 1.4 V nel secondo. Nella zona centrale la corrente è dell’ordine dei
20 − 40 µA
Nella figura 3.6 è riportata la funzione di trasferimento in una simulazione
Spectre di un inverter costituito con mosfet della tecnologia usata, con due
valori di larghezza del mosfet p, un primo uguale al mosfet n e un secondo
pari al doppio della larghezza del mosfet n. Si può osservare la migliore
posizione della tensione di soglia dell’inverter nel secondo caso.
Il massimo valore di corrente si ha quando la tensione di ingresso è intorno
a Vcomm per Vtn ≤ Vin ≤ Vdd − Vtp valendo:
Imax =
β
(Vg − Vt )2
2
52
Capitolo 3. Realizzazione elettronica
Questo valore non è trascurabile in quei casi in cui la tensione in ingresso
varia piuttosto lentamente nel passaggio intorno alla soglia, perchè la potenza
media dissipata per unità di tempo aumenta considerevolmente.
3.2.4
Specchio di corrente
Vg=Vd1
Vd2
Iin
Iout
m1
m2
Figura 3.7: Specchio di corrente
Con questa semplice configurazione è possibile, in prima approssimazione
senza tener conto dell’effetto Early, replicare la corrente I1 nella I2 se i mosfet
m1 ed m2 sono perfettamente identici dato che hanno la stessa tensione di
gate.
Tenendo conto dell’effetto Early si può facilmente verificare (vedi 2.13)
che ancora Iin = Iout se Vd1 = Vd2 , quest’ultima però non è sempre una
approssimazione accettabile. Quindi dove è richiesta una limitata deviazione
della corrente specchiata occorre dimensionare i mosfet per ridurre al minimo
la modulazione di canale.
Nel caso che m1 e m2 abbiano dimensioni diverse, nel calcolare la corrente di uscita, senza tener conto dell’effetto Early si attua un semplice
riscalamento.
L1 W 2
Iout
=
Iin
W1 L2
Lo specchio di corrente meglio approssima un generatore ideale di corrente nel regime sotto-soglia piuttosto che in quello sopra soglia perchè in
quest’ultimo si ha il vincolo della dipendenza dalla Vg per stare in saturazione ed inoltre l’effetto Early è più marcato essendo più piccolo il valore
assoluto della tensione Early.
53
3.2. Circuiti base CMOS utilizzati
Vin
m1
Vout
Vb
mb
Vs
Figura 3.8: Source follower
3.2.5
Source Follower
Il source follower ha la caratteristica fondamentale di avere una alta impedenza di ingresso e una bassa di uscita. Si realizza con un generatore di
corrente fissata mb connesso al source del mosfet m1 operante in saturazione.
Nel regime sotto soglia si dimostra che [20]
Vout = kn Vin − kb Vb + Vs
assumendo che i due transistor abbiano le stessa dimensioni.
Degna di nota è la linearità di Vout con Vin con il fattore kn < 1 e l’offset
in uscita regolabile dalla corrente di bias impostabile tramite Vb .
3.2.6
Amplificatore a transconduttanza
Una coppia differenziale m3 m4 è connessa in serie ad uno specchio di corrente. La corrente Ib = I3 + I4 è impostata dal generatore di corrente mb .
Poichè le correnti I1 e I2 sono specchiate si ha Iout = I3 − I4
Nel regime sotto-soglia segue che
Iout = Ib
kV1
kV1
kV1
UT
kV1
UT
e UT − e UT
e
+e
= Ib tanh[
k
(V1 − V2 )]
2UT
(3.1)
Per piccoli valori di tensione differenziale si ha
Iout ≈ gm (V1 − V2 ) dove gm =
Ib k
è al transconduttanza
2UT
Dunque questo circuito amplifica la differenza di potenziale tra i due ingressi
e sotto certe condizioni, l’uscita dipenda poco dal segnale di modo comune 3 .
3
Il segnale di modo-comune corrisponde alla semisomma dei due segnali di ingresso
54
Capitolo 3. Realizzazione elettronica
Vdd
Vdd
I1
I2
m1
m2
Vout
I3
V1
I4
m3
V2
m4
Vs
Ib
Vb
mb
Figura 3.9: Semplice amplificatore a transconduttanza
Come descritto sopra l’amplificatore a transconduttanza è un convertitore
tensione−dif f erenziale ⇒ corrente. Esso può essere anche usato a circuito
aperto come amplificatore differenziale. In questo ambito e nel regime sottosoglia si trova che il guadagno in tensione vale
A≈
kn VE
2UT
dove VE è la tensione di Early dei transistor m3 e m4 . Poichè Vout cresce
all’aumentare di V1 e al diminuire di V2 il primo ingresso è chiamato noninvertente mentre il secondo invertente. I valori tipici di guadagno oscillano
tra 100 e 1000.
Questo semplice circuito non è normalmente usato come amplificatore
invertente a causa del mismatch tra i parametri e il guadagno cosı̀ elevato.
Si presta bene invece all’uso come comparatore.
Una forte limitazione all’uso esteso di questa più semplice versione di
amplificatore a transconduttanza è costituita dal fatto che la tensione di
uscita Vout ha un range limitato. In particolare si può dimostrare che [20] il
valor minimo di Vout è Voutmin ≈ kn V1 − kb Vb + UT ln(2) ovvero la tensione di
uscita è di poco inferiore a V1 .
55
3.2. Circuiti base CMOS utilizzati
Nel presente progetto varianti di questo circuito sono stati usati per la
realizzazione della modulo sinapsi e del modulo Sinapsi e Regola-Calcio.
3.2.7
Amplificatore a transconduttanza wide-range
Una prima variante utilizzata è illustrata nella figura 3.10 Questa non ha le
forti limitazioni sul range di uscita indicate precedentemente. La corrente
del ramo di uscita è specchiata 2 volte cosı̀ il ramo di uscita è simmetrico e
disaccoppiato dallo stadio di uscita Questo circuito è utilizzato come elemento
del circuito di refresh della sinapsi, nella relativa sezione ne verrà illustrata
la funzionalità specifica.
wide
Vdd
Vn
Vp
m5
Vn
m1
m2
m3
m4
Vb
m6
Vout
Vp
m7
m8
Vb
mb
Figura 3.10: Amplificatore a transconduttanza wide-range e suo simbolo
3.2.8
Comparatore Open-Loop p a due stadi
Questo circuito è un’altra configurazione classica [22] che sfrutta l’amplificatore a transconduttanza.
La versione di amplificatore quı̀ rappresentata è quella complementare
(coppia differenziale p), ma nulla cambia se si riferiscono le tensioni a Vdd
piuttosto che a massa. Il secondo stadio è un sostanzialmente un inverter
realizzato con un generatore di corrente mp collegato in configurazione a
56
Capitolo 3. Realizzazione elettronica
drain comune con il mn . Poichè nei due transistor scorre la stessa corrente,
una piccola variazione di ∂Vgn produce una notevole variazione di ∂Vout nella
direzione opposta. Il guadagno An rispetto all’ingresso del mosfet n può
essere stimato dall’effetto Early come segue
An ≡
∂Vout
kp Vne Vpe
=−
V
UT Vne + Vpe
con kn e kp sono i fattori di pendenza sotto soglia e Vne , Vpe le tensioni Early
dei mosfet n e p rispettivamente.
comp_p
Vdd
A
B
m1
B
m2
Vbp
m3
A
m6
Vout
m4
m5
m7
Figura 3.11: Comparatore a due stadi e suo simbolo
Questo circuito viene utilizzato come semplice elemento di comparazione
nei moduli Sinapsi e Calcio-Compara. L’introduzione di due elementi a soglia
in serie rende soddisfacente la risposta del sistema avvicinandola ad una
funzione gradino.
Le dimensioni dei mosfet con funzioni di specchi di corrente e generatori di
corrente, ovvero m1 , m4 , m5 , m6 , hanno dimensioni superiori a quelle minime
per le considerazioni fatte sull’effetto Early. Il mosfet m7 ha dimensioni
minime mentre la coppia differenziale ha dimensioni L minime e W uguale
ai mosfet sottostanti.
Nella figura 3.12 è mostrata, in una simulazione, la funzione di trasferimento del circuito realizzato.
Un ulteriore vantaggio dell’utilizzo di questo secondo stadio inverter è che
la corrente del ramo del secondo stadio è limitata e controllata dalla stessa
tensione di bias dell’amplificatore a transconduttanza.
57
3.2. Circuiti base CMOS utilizzati
Figura 3.12: Funzione di trasferimento del comparatore p a due stadi in una simulazione
Spectre-CADENCE. L’ingresso A (non invertente) è stato fissato a 1.7V , mentre l’ingresso
B (invertente) varia da 0 a 3.3 V , ed è rappresentato dai valori dell’ascissa (mappati anche
sulla retta a 45 gradi). L’ordinata riporta la corrispondente tensione di uscita. L’ampiezza
della zona di transizione della tensione di ingresso per passare dal livello logico basso a
quello alto è di circa 65mV . Fuori dalla zona di transizione i valori alto e basso in uscita
sono sostanzialmente a Vdd e zero
3.2.9
Comparatori Open-Loop p ed n a due stadi con
abilitazione
I due circuiti descritti in questa sezione servono a realizzare la funzione logica
del modulo Calcio-Compara, e sono stati ottenuti modificando opportunamente il comparatore classico Comparatore Open-Loop p a due stadi sopra
descritto ed il suo complementare n.
Consideriamo il comparatore p con abilitazione.
I due mosfet aggiunti m8 e m9 , sono in parallelo tra loro e con m7 . I
segnali En1 e En2 , devono essere segnali digitali, in questo caso i due mosfet
si comportano da interruttori. Quando En1 e En2 sono non-attivi, ovvero
bassi il comportamento è identico a quello descritto nel paragrafo precedente. Viceversa quando almeno uno tra i due segnali è attivo (alto), il gate del
mosfet m7 viene cortocircuitato e quindi va in zona cut-off, di conseguenza
l’uscita è tenuta alta da m6 indipendentemente dal risultato della comparazione. Si noti che la corrente, in m3 dello stadio di ingresso, è limitata dal
generatore di corrente m1 regolato da Vb .
Analogo ragionamento vale per la versione complementare p, tenendo
conto che i due mosfet aggiunti m8 e m9 sono di tipo p e che dunque sono
attivi (accesi) con En1 e En2 bassi.
L’ingresso A è il non-invertente in entrambi i circuiti p ed n.
58
Capitolo 3. Realizzazione elettronica
A
Vdd
B
m1
En1
En2
comp_p_EN
Vbp
B
m2
m4
m3
A
m6
En1
En2
m5
m8
m9
m7
Figura 3.13: Comparatore p a due stadi con abilitazione e suo simbolo
In definitiva si ha
! (En1 # En2 ) VA , VB
1
VA < VB
1
VA > VB
0
/
Vout
0
1
1
Tabella 3.1: Comparatore p. È sufficente che solo uno dei due segnali di abilitazione sia alto per bloccare il comparatore, il controllo per l’attivazione del
comparatore è quindi fornito dalla funzione booleana OR (#) negato (!) tra i
due segnali
3.3
En1 & En2
1
1
0
VA , VB
VA < VB
VA > VB
/
Vout
0
1
0
Tabella 3.2: Comparatore n. È sufficente
che solo uno dei due segnali di abilitazione sia basso per bloccare il comparatore, il controllo per l’attivazione del comparatore è quindi fornito dalla funzione
booleana AND (&) tra i due segnali
La sinapsi
All’inizio di questo capitolo è stata descritta la topologia generale del core
della rete. Si descrive ora nel dettaglio come e dove si mappano le equazioni,
le regole e i vincoli del modello della sinapsi con i rispettivi moduli hardware.
Si parta dalla regola di apprendimento descritta nel cap. 1 per analizzare
nel dettaglio i circuiti che la realizzano.
59
3.3. La sinapsi
Vdd
A
En1
m4
m5
B
En2
m8
m9
En1
En2
comp_n_EN
m7
B
m2
m3
Vout
A
Vbn
m6
m1
Figura 3.14: Comparatore n a due stadi con abilitazione e suo simbolo
La generazione della variabile Calcio C(t) della 1.2 deve leggere solo lo
spike post-sinaptico
⇒ viene realizzata dal blocco Generazione variabile Calcio.
Le disuguaglianze nella 1.3 hanno come ingresso la variabile Calcio C(t)
e il potenziale del neurone postsinaptico Vp
⇒ vengono realizzate dal blocco Comparatori.
I blocchi sopra descritti si trovano all’interno del modulo denominato
Calcio-Compara, accanto al neurone.
Il risultato della comparazione è una informazione a tre possibili stati che
si può cosı̀ convenientemente ridefinire
1. stato a è soddisfatta la prima delle 1.3
2. stato b è soddisfatta la seconda delle 1.3
3. stato null nessuna delle condizioni 1.3 è soddisfatta
Questo stato è mappato in bus digitale a due bit denominati UP e DOWN.
Questo viene trasportato lungo la riga della matrice sinaptica a ciascuno
dei moduli Sinapsi appartenenti all’albero dendritico del relativo neurone.
Ciascuno dei moduli sinaptici riceve il relativo spike da ciascuno degli altri
neuroni pre-sinaptici.
60
Capitolo 3. Realizzazione elettronica
Il modulo Sinaptico contiene il circuito che realizza la dinamica della variabile X(t) ovvero l’azione rappresentata dalla parte sinistra delle 1.3 (circuito hebbiano). Questo è nel blocco Syn, che comprende anche il meccanismo
di refresh della X(t) rappresentato dalle 1.4, ed il circuito di clipping della
variabile X(t) indicato all’inizio del cap 1.
Il blocco Dendrite contiene i due tipi di dendrite, quella plastica eccitatoria e quella inibitoria, selezionabili localmente per ogni sinapsi per mezzo
del blocco Selezione.
3.4
Il modulo Sinapsi
BLOCCO SELEZIONE
Datain
b1
D Q
b0=Dataout
D Q
Q
Vdd
Vdd
BLOCCO DENDRITI
Q
Vdd
NReset
Clockout
NSpike
Clockin
Spike
NSpike
θX
b0
comp_p
J_
A
UP
vu
vd
θX
X(t)
B
wide
Vn
Vp
circuito di clipping
DJ
Uscita
Vb
Jinib
Vb_refr
Csyn
b1
DOWN
circuito di refresh
Spike
circuito hebbiano
elemento di
memoria
BLOCCO SYN
Figura 3.15: Schema del modulo Sinapsi
La variabile analogica sinaptica X(t) è il potenziale ai capi della capacità
Csyn . Tale capacità vale circa 220 f F . La soglia θX è usata per il circuito di
refresh oltre che per il clipping.
61
rami
eccitatori
ramo
inibitorio
3.4. Il modulo Sinapsi
3.4.1
Circuito di refresh
Il termine di refresh indicato nelle 1.4 è realizzato dall’amplificatore widerange. Il terminale invertente è alla soglia fissa θX mentre l’altro è sulla X(t)
che è chiuso in feedback positivo sull’uscita.
Si faccia riferimento alla figura 3.10 del circuito interno del bistabile.
È stato mostrato che nell’amplificatore a transconduttanza è sufficente una
piccola differenza di tensione affinchè la corrente raggiunga il valore di saturazione aumentando poi molto poco all’aumentare della differenza di tensione.
A causa del feedback positivo la tensione X(t) sulla capacità Csyn
• sarà portata verso massa se X(t) < θX
• sarà portata verso Vdd se X(t) > θX .
Nel primo caso la corrente che scarica la capacità scorre attraverso m8 specchiata da m7 ovvero dal ramo di sinistra dell’amplificatore. Nel secondo caso
è il ramo di destra ad essere attivo e la corrente specchiata in m6 da m2
carica la capacità. In entrambi le zone finchè X(t) non approssima i relativi
asintoti, la corrente che entra (o esce) dall’amplificatore è pressochè costante
nei due versi ed è definita dal generatore mb , che determina la corrente Ileak
di bias tramite la tensione di controllo Vb e dal rapporto di specchio Rs di
m2 ⇔ m6 (o m1 ⇔ m5 ), essendo i rami destro e sinistro simmetrici. Si ha
quindi
Ileak Rs
X(t) = X(0) −
t se X(t) < θX
Csyn
X(t) = X(0) +
Ileak Rs
t se X(t) > θX
Csyn
Vicino all’asintoto Vas (0 o Vdd ), ovvero per |X(t) − Vas | < 4UT la X(t)
approssima l’asintoto esponenzialmente, perchè la corrente non è più costante ma invece tende a zero. Questa perturbazione rispetto alle prescrizioni del
modello non è significativa perchè queste due zone sono piccole se paragonate
all’intero range dinamico disponibile di quasi 3.3
V , quindi la si può tratta2
re come un riscalamento efficace dei valori di massimo (minimo) del range,
in considerazione anche del fatto che l’effetto sul neurone post-sinaptico è
ridotto a due soli valori dal clipping.
Nella figura 3.16 è presentato il grafico di una simulazione della X(t)
durante il refresh verso l’alto e verso il basso.
La problematica maggiore legata alla definizione dei parametri per questo
circuito è dovuta per lo più alla necessità di dover impostare correnti molto basse, perchè i tempi caratteristici della dinamica sinaptica devono essere
62
Capitolo 3. Realizzazione elettronica
X(t)
Figura 3.16: Meccanismo di refresh in una simulazione Spectre-CADENCE del circuito
realizzato. Inizialmente X(t) è sopra la soglia (1.7 V ), sale a Vdd con pendenza α, permane
su questo valore finchè non arriva uno spike pre-sinaptico (in corrispondenza del salto
verso il basso), il salto b relativo è regolato appositamente molto elevato cosı̀ da superare
la soglia. da questo istante la variabile tende a zero con pendenza beta.
sensibilmente più lunghi di quelli del neurone. Il tempo da confrontare è quello per cui si ha l’attraversamento di di tutto il range dalla soglia all’asintoto
(tipicamente 1.75 V → 3.3 V e 1.75 V → 0 V ). I tempi sono dell’ordine delle
decine-centinaia di ms. L’aspetto critico che si presenta quando si impostano
correnti molto basse è quello del mismatch dei parametri di processo. Se non
affrontato correttamente, la distribuzione delle pendenze di refresh potrebbe
essere inaccettabile.
I parametri che si possono impostare in modo mirato per ridurre quanto
possibile questo problema sono le dimensioni dei mosfet.
Come accennato nel Cap.2, la simulazione montecarlo ci permette di definire fino a che dimensione è utile aumentare le dimensioni dei mosfet per
ridurre la dispersione dovuta al mismatch dei parametri tecnologici.
Le correnti che è necessario impostare non sono molto più grandi delle
correnti di leakage dei mosfet che sono tenuti nella zona di lavoro sotto soglia.
Qui di seguito si riporta la procedura adottata per stimare le dimensioni.
Si parte da una dimensione convenzionale per i mosfet analogici che
è un fattore 3 almeno più grande della dimensione minima verificato con
simulazione Spectre in condizioni tipiche.
Si eseguono simulazioni montecarlo, successive, aumentando le dimensioni
e valutando di volta in volta il vantaggio ottenuto in termini di distribuzione
più stretta dei tempi di refresh.
Si decide di fissare la dimensione quando non si ottiene più un apprezza63
3.4. Il modulo Sinapsi
bile miglioramento. In tale circostanza questo ha implicato un aumento delle
dimensioni dei mosfet di un fattore 3.
I risultati di tali simulazioni sono presentati nelle figure 3.17- 3.18 e 3.193.20 dove si possono confrontare i risultati relativi alle due diverse configurazioni: una a mosfet “piccoli” e una seconda a mosfet più “grandi”, mantenendo inalterati gli altri parametri, con una simulazione montecarlo di 300
iterazioni.
Sono presentati 2 grafici per ciascuna delle configurazioni, uno rappresenta l’andamento temporale della variabile sinaptica X(t) per le diverse iterazioni montecarlo mentre l’altro rappresenta l’istogramma del valore della
pendenza relativa al tempo trascorso per passare da 1.75V a 1.85V (100mV ).
La tensione Vb ref r in queste simulazioni è pari a 245 mV , valore che ben dentro il regime sotto-soglia e che realizza una corrente di 170 pA nel relativo
mosfet mb e conseguentemente tempi di refresh relativamente lunghi. Questo
valore rappresenta un limite inferiore nelle simulazioni montecarlo in termini
di corretto funzionamento del circuito.
L’istogramma relativo alla configurazione con mosfet piccoli non riporta
tutte le 300 misure perche’ solo 182 di esse sono rese disponibili, infatti le
rimanenti curve di potenziale o non raggiungono i 100 mV nell’intero arco di
tempo simulato di oppure hanno una pendenza negativa.
I risultati mostrano che in un insieme di 300 circuiti replicati costruiti con mosfet piccoli una buona parte di essi mostra un comportamento
comportamento sbagliato.
Il tempo medio di refresh ottenuto dalla simulazione Montecarlo a mosfet
grandi è di 70ms con sd = 4 ms.
3.4.2
Circuito hebbiano
Questo semplice circuito effettua l’azione descritta nella 1.3
• potenziare la variabile sinaptica X(t) quando arriva uno spike dal presinaptico se il neurone ricevente post-sinaptico è in stato di forte attività, ma non troppo o troppo poco
• de-potenziare la variabile sinaptica X(t) quando arriva uno spike dal
pre-sinaptico se il neurone ricevente post-sinaptico è in stato di debole
attività, ma non troppo o troppo poco
Le condizioni sono presenti nei due segnali digitali UP (attivo basso) e DOWN
(attivo alto). Lo spike è un impulso digitale di durata tipica di qualche
decina di µs definita dallo shaper. Il mosfet in alto e in basso nel circuito
realizzano dei semplici interruttori, che si attivano contestualmente all’arrivo
64
Capitolo 3. Realizzazione elettronica
Figura 3.17: Refresh della variabile sinaptica, in una Simulazione in transiente SpectreCADENCE Montecarlo di 300 iterazioni.
Caso mosfet più piccoli.
Figura 3.18: Istogramma del tempo di refresh della variabile sinaptica per passare da
1.75 V a 1.85 V (100 mV ), in una Simulazione Spectre-CADENCE Montecarlo di 300
iterazioni. Caso mosfet più piccoli.
Figura 3.19: Refresh della variabile sinaptica, in una Simulazione in transiente SpectreCADENCE Montecarlo di 300 iterazioni.
Caso mosfet più grandi.
Figura 3.20: Istogramma del tempo di refresh della variabile sinaptica per passare da
1.75 V a 1.85 V (100 mV ), in una Simulazione Spectre-CADENCE Montecarlo di 300
iterazioni. Caso mosfet più grandi.
65
3.4. Il modulo Sinapsi
X(t)
1
21
3
4
5
6 7
8
9
10
Figura 3.21: Dinamica sinaptica in una simulazione Spectre-CADENCE. Per chiarezza
di visualizzazione non sono visibili i segnali UP e DOWN che pilotano la dinamica e il
treno regolare di spike che è presente continuativamente nella simulazione alla frequenza
di 1 KHz. Nella zona 1 X(t) parte sopra soglia e U P / DOW N non sono attivi: refresh
verso l’alto. Nella zona 2: X(t) è al valor massimo Vdd . Zona 3: è attivo solo DOWN : X(t)
fa 12 salti verso il basso. All’inizio della zona 4 i segnali U P / DOW N non sono attivi
e X(t) si trova sotto la soglia e quindi fa refresh verso il basso. Nella zona 5 continua a
perdurare la situazione precedente e X(t) rimane al valor minimo di zero. Nelle zone 6 e 7
è attivo solo UP : sotto la soglia il salto a e il refresh hanno versi opposti, sopra hanno lo
stesso verso. Nella zona 8 U P / DOW N non sono attivi: X(t) è stabile al valore massimo.
Nella successiva zona 9 è attivo solo DOWN : X(t) fa salti verso il basso. Infine nell’ultima
zona U P / DOW N non sono attivi, X(t) parte da un valore sotto soglia e quindi fa refresh
verso il basso.
dello spike e rimangono attivi per tutta la durata dello spike. Il mosfet
UP o DOWN si attivano (mai contemporaneamente) in base alle condizioni
presenti sul neurone post-sinaptico. Durante il tempo in cui permane lo spike
pre-sinaptico una corrente costante impostata da vu (o da vd ) dal relativo
mosfet generatore carica (o scarica) la capacità Csyn . Sulle lunghe scale
dei tempi interessanti della rete determinate dall’ I.S.I. questo intervallo di
tempo è trascurabile e può essere considerato una δ(tpre ). Quindi l’effetto
netto è un salto in alto (o in basso) di un valore a (o b). La relazione che
determina a e b è in prima approssimazione lineare in vu e vd e nel tempo di
durata spike, quindi facilmente regolabile.
Nella figura 3.21 è presentato il risultato della simulazione in cui sono
visibili le diverse fasi della dinamica sinaptica.
3.4.3
Circuito di clipping
Questo circuito è realizzato semplicemente con il Comparatore Open-Loop p
a due stadi precedentemente descritto. La variabile sinaptica X(t) è applicata
66
Capitolo 3. Realizzazione elettronica
all’ingresso invertente mentre sul non-invertente è applicata la soglia θX .
• Se X(t) < θX → Uscita alta
• Se X(t) > θX → Uscita bassa
3.4.4
Circuito di selezione
Questo blocco contiene Standard-Cell digitali 4 della tecnologia usata AMS.
La scelta di includere standard-cell in questo modulo che ha funzionalità
totalmente analogiche in fase di lavoro, non si contraddice con lo stile di fondo
nelle scelte circuitali per i layout full-custom analogici di circuiti neuromorfi,
perchè questo blocco non agisce dinamicamente in fase di test neuronale, ma
viene usato inizialmente per fissare il carattere della sinapsi.
È costituito da due Flip-Flop di tipo D che realizzano gli elementi di
memoria per due bit che vengono caricati serialmente dall’ingresso Datain .
Nel Flip Flop di tipo D Delayed il dato presente all’ingresso D viene
passato all’uscita Q in seguito all’applicazione del fronte di salita del clock,
quando il segnale di reset è disattivato. Il dato permane finchè non arriva il
successivo impulso di clock.
Il segnale di clock determina l’avanzamento del dato dal Flip-Flop di
sinistra a quello di destra.
L’uscita Dataout è resa disponibile per il successivo modulo sinapsi.
Il verso in cui si propaga il segnale di clock è opposto a quello di propagazione del dato perchè in questo modo, utilizzando il ritardo fornito dagli
buffer, sono rispettati correttamente i vincoli sul timing 5 tra i segnali.
I livelli logici dei due bit [b0 ,b1 ] memorizzati determinano il tipo di efficacia
sinaptica.
3.4.5
Circuito dendriti
Questa parte attua l’iniezione (o l’assorbimento) dell’impulso di corrente sul
soma del neurone postsinaptico in coincidenza dello spike del neurone presinaptico con la modalità prescritta dalle condizioni di selezione del tipo di
sinapsi e dal valore stabile di efficacia presente.
4
Le standard Cell sono blocchi funzionali completi forniti dalla fonderia, nelle varie
forme di: schematico, modello di simulazione e layout.
5
Vincoli sulla temporizzazione dei due segnali. Poichè il dato e il segnale di clock
hanno tempi caratteristici di propagazione all’interno della porta logica, per garantire il
corretto funzionamento è necessario che i segnali vengano presentati con la giusta sequenza
e rispettando i tempi limite previsti dalla tecnologia. I riferimenti per questi aspetti sono
forniti dai data-sheet della fonderia.
67
3.4. Il modulo Sinapsi
I rami superiore di eccitazione o inferiore di inibizione sono attivati dai
bit (b1 , b0 ) memorizzati nel blocco di selezione. Questi attivano o meno i
relativi mosfet interruttore secondo la regola già indicata all’inizio di questo
capitolo
b1 b0
Selezione
0 0
Eccitatrice
0 1 Non connessa
1 1
Inibitrice
Il mosfet più in basso (più in alto) è l’interruttore dello Spike,
L’ uscita è connessa insieme a tutte le altre sinapsi alla capacità del soma
del neurone post-sinaptico.
La corrente, quando inibitoria, è IJinib ed è regolata dal potenziale Jinib
per mezzo del relativo mosfet generatore.
La corrente, quando eccitatoria, è definita dalla somma delle correnti impostate dal potenziali DJ e J nei due rami eccitatori dai relativi mosfet
generatori. Con la selezione definita eccitatoria e durante lo spike, se la
sinapsi è depotenziata, il circuito di clipping presenta l’uscita alta che mantiene spento il mosfet interruttore ad esso collegato, e quindi è presente la
sola corrente impostata da J . Viceversa se la sinapsi è potenziata, con le
restanti condizioni identiche a sopra, alla corrente impostata da J si somma
il contributo relativo a DJ proveniente dal ramo di sinistra.
In maniera del tutto analoga al circuito hebbiano, durante il tempo in
cui permane lo spike pre-sinaptico la corrente costante carica (o scarica) la
capacità Csoma del neurone postsinaptico.
Sulle scale dei tempi interessanti della rete questo intervallo è trascurabile
e può essere considerato una δ(tpre ).
Riassumendo: l’effetto netto sul soma del neurone post-sinaptico con capacità Csoma , all’arrivo di uno spike pre-sinaptico è un salto in alto (o in
basso) di valore (efficacia sinaptica non normalizzata):
•
IJ +IDJ
Csoma
•
IJ
Csoma
Tspike se selezionata eccitatoria e potenziata
Tspike se selezionata eccitatoria e depotenziata
I
inib
• − CJsoma
Tspike se selezionata inibitoria indipendentemente dallo stato
potenziato o depotenziato
• 0 se selezionata disconnessa indipendentemente dallo stato potenziato
o depotenziato
dove Tspike è il tempo durata spike.
68
Capitolo 3. Realizzazione elettronica
3.5
Il modulo Calcio-Compara
Vdd
C(t)
NSpike
K2up
θp
vca
C(t)
vca_τ
Vp
Cca
comp_p
A
A
C(t)
B
K1up
comp2
comp1
B
comp_p_EN
En2
A
En1
UP
comp4
P
Sel
B
C(t)
K1down
Generazione
variabile Calcio
comp_p
comp_p
A
B
comp3
K2down
C(t)
A
B
En1
En2
DOWN
comp5
comp_n_EN
Sistema comparatori
Figura 3.22: Modulo Calcio-Compara
Il circuito Generazione variabile Calcio è costituito da soli tre mosfet e
dalla capacità Cca che costituisce l’elemento di memoria della variabile Calcio
C(t). Il mosfet situato più in alto lavora come interruttore. Quando arriva
uno spike post-sinaptico si attiva, in questo caso la corrente Ica che scorre
nel ramo è fissata dal mosfet generatore di corrente intermedio tramite la
tensione vca . Il mosfet generatore di corrente in basso è sempre attivo. La
corrente Ica τ deve essere piccola con Ica τ < Ica . In queste condizioni il
potenziale ai capi della capacità Cca che rappresenta la variabile calcio C(t)
si scarica e quindi decade fin quando non arriva uno spike post-sinaptico, nel
qual caso fa un salto verso l’alto di una quantità proporzionale alla corrente
netta di carica Ica − Ica τ .
La pendenza di scarica è proporzionale al valore di corrente impostato
dal relativo mosfet generatore vca τ .
Le relazioni di disuguaglianza della 1.3 sono risolte dal Sistema comparatori.
In questo circuito è presente anche la logica per selezionare la regola di
apprendimento semplificata alternativa.
Questa regola, sempre coerentemente con l’idea Hebb, prevede di valutare
l’attività del neurone post-sinaptico solo dal valore del potenziale del soma
post-sinaptico.
X(t)− > X(t) + a se V p (tpre ) > θp
69
(3.2)
3.5. Il modulo Calcio-Compara
X(t)− > X(t) − b se V p (tpre ) ≤ θp
La selezione della regola avviene per mezzo dei due Multiplexer digitali a
destra nello schema. Questi insieme ai due buffer collegati sulle loro uscite
sono Standard Cell della fonderia AMS. Il segnale digitale Sel permette la
connessione delle due uscite alla coppia di terminali di ingresso collegati
insieme e all’uscita del comparatore comp1 nel caso della regola semplificata,
ai comparatori comp4 e comp5 nel caso della regola completa.
Regola semplificata
Il comparatore comp1 risolve da solo la disuguaglianza della 3.2. I segnali
UP e DOWN sono identici perchè DOWN è a logica positiva mentre UP a
logica negativa
Nel grafico 3.23 è mostrato il risultato di una simulazione per la verifica
della funzionalità logica del comparatore. Il potenziale che fluttua intorno
alla soglia θp non proviene dal potenziale del neurone post-sinaptico, ma è uno
stimolo aggiuntivo e costruito appositamente per verificare il comparatore
nelle condizioni tipiche di lavoro. Tale scelta di non simulare tutte le parti
circuitali contemporaneamente, si rende spesso necessaria per non rendere le
simulazioni eccessivamente lunghe in durata. Ogni qual volta si opera con
questa metodologia di lavoro, è necessario verificare che gli stimoli emulati
costruiti ben rappresentino gli stimoli originali in termini della risposta da
osservare del circuito.
In questo caso e in quello della regola completa, principalmente due sono
le possibili scelte per la definizione di questo stimolo. Una prima, rigorosa,
in cui vengono forniti al simulatore, in una simulazione in dc tanti valori dei
due potenziali da comparare quante sono le combinazioni di interposizione
delle due tensioni rispetto alle soglie. Una seconda in cui i due potenziali variabili nel tempo sono generati da un algoritmo o circuito simulato stocastico
che produca una variabilità tale da garantire di ottenere in una simulazione transiente uno scenario completo di tutte le possibili posizioni relative
dei potenziali rispetto alle soglie, con pochi tentativi di messa a punto dei
parametri del generatore.
È stata preferita la seconda soluzione in quanto, oltre ad essere più semplice da realizzare della prima, permette di osservare anche il comportamento
dinamico dei comparatori. In prima approssimazione, non ha importanza la
forma con cui queste fluttuazioni vengono presentate all’ingresso dei comparatori, ma piuttosto i tempi tipici con cui queste variazioni avvengono, che
dovono essere paragonabili al processo originale.
È stato quindi utilizzato come circuito emulatore un generatore pseudorandom di sequenza di bit. I valori 0 e 1 del bit corrispondono a due livelli
di tensione fissa impostabile. L’uscita del generatore di bit va ad un circuito
70
Capitolo 3. Realizzazione elettronica
RC che genera le fluttuazioni. Questa soluzione permette di ottenere fluttuazioni che attraversano più volte le soglie e che sono regolabili nei valori
minimo/massimo.
UP
DOWN
Vp(t)
Θ
Figura 3.23: Comparazione per regola semplificata in una simulazione Spectre-CADENCE.
La variabile calcio non è quella proveniente dal circuito di generazione della variabile calcio,
ma è uno stimolo di test.
Regola completa
La figura 3.24 riporta un grafo logico di descrizione della funzione logica
implementata corrispondente al circuito elettrico e costruito con le regole dei
comparatori 3.1 e 3.2. Tale grafo corrisponde alle disuguaglianze delle 3.2.
Nei grafico di fig. 3.25 e 3.26 sono mostrati i risultato di una simulazione
transiente. Come per il caso della dinamica semplificata, gli stimoli non sono
i veri potenziali del neurone postsinaptico della variabile Calcio ma lo stimolo
stocastico sopra descritto.
La prima simulazione ha il solo scopo di verifica della funzionalità logica
del comparatore, mentre nella seconda è riportato anche l’andamento della
variabile sinaptica X(t) della sinapsi.
71
3.6. Lo shaper
Comp1
Vp > θp ?
NO: En2=1
Comp4 bloccato
UP su (spento)
SI: En1=0
Comp5 bloccato
DOWN giu
(spento)
SI
DOWN su
(acceso)
SI: En2=0
Comp5 bloccato
DOWN giu
(spento)
Comp3
C(t)<K1down ?
NO: En1=1
SI: En1=1
Comp5
C(t)<K2down ?
NO
DOWN giu
(spento)
Comp4 bloccato
UP su
(spento)
SI
UP su
(spento)
Comp3
C(t)>K2up ?
NO: En1=0
Comp4
C(t)<K1up ?
NO
UP giu
(acceso)
Figura 3.24: Grafo logico del sistema comparatori
3.6
Lo shaper
L’impulso finito generato dal neurone I.F. ha durata circa 20ns, troppo breve
per pilotare i circuiti della sinapsi, che sono stati progettati per funzionare
al meglio con durate di qualche µs o decine di µs.
Per questo è necessario un circuito che produca un impulso di durata
impostabile la cui partenza è triggerata dallo spike.
Nella figura 3.27 è presentato lo schema del circuito realizzato.
Il cuore del funzionamento è rappresentato dai mosfet m1 , m2 e m3 , dalle
capacità C1 e C2 e dal primo inverter costituito dai mosfet m4 , m5 e m6 .
L’impulso digitale di avvio della dinamica di questo circuito viene presentato all’ingresso Vin e deve essere a logica invertita (attivo basso).
Il mosfet m3 realizza un generatore di corrente il cui valore è impostato
dalla tensione Vtau . I mosfet m1 e m2 lavorano come interruttori.
72
Capitolo 3. Realizzazione elettronica
X(t)
UP
Vp
Θ
DOWN
K1down < K1up < K2down < K2up
Vp
Θ
K2up
K2down
K1up
K1down
Figura 3.25: Comparazione per la regola completa in una simulazione SpectreCADENCE. La variabile calcio non è quella
proveniente dal circuito di generazione della
variabile calcio, ma è uno stimolo di test.
Figura 3.26: Generazione dei segnali UP e
DOWN e loro effetto sulla variabile sinaptica
X(t) della sinapsi in una simulazione SpectreCADENCE. La variabile calcio non è quella
proveniente dal circuito di generazione della
variabile calcio, ma è uno stimolo di test.
A regime, quando l’impulso precedente ha esaurito tutti i suoi effetti
transienti sul circuito, la situazione è la seguente:
• m1 acceso, m2 spento
• il nodo inferiore di C1 è mantenuto a 0 V da m1
• C2 è completamente carico, la tensione sul nodo Vs è pari a Vdd
• Vout si presenta alta
Quando arriva l’impulso su Vin all’istante t = 0, si inverte la situazione
dei mosfet interruttori:
m1 spento e m2 acceso.
m2 mette in condivisione la carica elettrica che si ridistribuisce sulle due
capacità e la tensione pari a Vdd nel circuito serie dei due condensatori, viene
ripartita sul nodo di collegamento dei due condensatori (tensione Vs ).
1
Vs = Vdd C1C+C
.
2
Quindi Vs fa un salto verso il basso. Se il punto di arrivo Vs (0+ ) è inferiore al valore della tensione Vcomm di soglia di commutazione del primo
inverter , questo cambia stato in uscita, dando inizio all’impulso di durata
73
3.6. Lo shaper
finita. Al termine del breve impulso di trigger in Vin , C2 inizia a caricarsi con pendenza determinata dal mosfet generatore di corrente pilotato da
Vtau . Quando Vs , salendo, raggiunge la soglia di commutazione dell’inverter,
l’inverter commuta di nuovo e quindi termina l’impulso generato.
La pendenza con cui Vs approccia la soglia salendo è relativamente bassa,
e poichè la funzione di trasferimento dell’inverter è solo una approssimazione
della funzione Θ(t), essendo invece una tangente iperbolica, il risultato è che
per avere commutazioni non troppo lente è necessario aggiungere almeno un
altro inverter in serie al primo. Il terzo inverter, realizzato da una standard
cell AMS assolve al duplice scopo di riportare la logica nel verso corretto necessario al circuito di ingresso delle sinapsi e contemporaneamente di fornire
la necessaria bufferizzazione alla linea di uscita che rappresenta l’ingresso per
32 moduli sinaptici.
A ragione della bassa rapidità di salita della tensione in ingresso all’inverter, la potenza media dissipata può raggiungere valori troppo elevati a
causa della permanenza per molto tempo della tensione di ingresso intorno
a Vcomm , come spiegato nel paragrafo invertitore logico. Per questo motivo
sono presenti nel ramo di ciascun inverter i mosfet m6 e m7 come limitatori
di corrente.
La tensione Vcomm vale tipicamente circa V2dd con le dimensioni del mosn di
W = 0.4 µ , L = 0.35 µ e del mosp di W = 0.8 µ , L = 0.35 µ. Per realizzare
la condizione che Vs (0+ ) < Vcomm si può agire sul rapporto tra le capacità,
oppure sul valore della Vcomm modificando i rapporti delle dimensioni dei
mosfet.
Si è scelto di percorrere anche questa seconda strada perchè il controllo
sulla capacità effettiva dei condensatori non è estremamente preciso, dato
che occorre tener conto sia le capacità parassite che le capacità intrinseche
Vdd
Vdd
Vtau
Vdd
m3
C1
m2
Vdd
limp
m4
m8 V
out
m5
m9
Vs
C2
m1
limn
m6
Vin
Figura 3.27: Circuito dello Shaper.
74
m7
Capitolo 3. Realizzazione elettronica
Figura 3.28: Andamento dei segnali nel circuito dello Shaper in una simulazione SpectreCADENCE
dei gate dei mosfet collegati ad esse.
Le capacità sono state disegnate per avere un valore nominale di 120 f F e
80f F . Le dimensioni dei mosfet del primo inverter sono state fissate per avere
una funzionalità validata dalle simulazioni tenendo conto del mismatch dei
parametri; esse sono di Wn = 0.8 µ Ln = 0.9 µ Wp = 2.65 µ Lp = 0.5 µ.
Nella grafico di figura 3.28 è rappresentata una simulazione funzionale
dello shaper.
75
3.7. Il neurone low power adaptive integrate and fire
3.7
Il neurone low power adaptive integrate
and fire
Il neurone elettronico qui presentato è una particolare realizzazione del neurone I.F. descritto nel Cap. 1, proposto per la prima volta in hardware da
[19] e realizzato dal nostro gruppo nella lann21.
Le novità introdotte dall’utilizzo di questo circuito di neurone I.F. [28]
rispetto a quello della lann21 sono qui elencate
ha basso consumo di corrente nei regimi di funzionamento tipici
comprende le funzionalità
• del tempo refrattario assoluto
• di un meccanismo di adattamento in frequenza
Il neurone integra la corrente totale afferente e quando il potenziale raggiunge una soglia emette uno spike e subito dopo si riporta ad un potenziale
di reset Vreset fissato con Vreset < Θn .
L’elemento che integra la corrente è la capacità del soma C, ed il potenziale su essa Vsoma rappresenta il potenziale di membrana del soma del
neurone.
Nella regione sotto la soglia di emissione Θn l’equazione che governa Vsoma
è
1
1 Zt
1
Vsoma (t) = Vsoma (0) − Iβ (t) +
I(t0 )dt0 − Iadapt (t)
(3.3)
C
C t0
C
dove I(t) è la somma di tutte le correnti eccitatorie, inibitorie ed esterne,
Ibeta è la corrente di leakage, e Iadapt (t) è la corrente che produce il meccanismo
di adattamento in frequenza.
La Iadapt (t) è funzione di una tensione ottenuta integrando lo spike su
una capacità Cadapt , quindi rappresenta una memoria del tempo inter-spike
trascorso precedentemente. Questa variabile è del tutto analoga alla variabile
calcio C(t) generata dal neurone post-sinaptico e usata nella dinamica della
sinapsi. L’utilizzo però è molto diverso: in questo contesto il meccanismo
di adattamento costituisce una dinamica locale al neurone, mentre nel caso
della variabile C(t) viene usata per il meccanismi di memorizzazione a più
lungo termine della sinapsi.
Il valor medio di questa corrente effettuato su un tempo caratteristico
determinato dal valore di Cadapt rappresenta quindi una informazione sulla
frequenza media di emissione degli spikes. La Iadapt (t) viene sottratta dalla
capacità C del soma e quindi il feedback sulla frequenza è negativo.
76
Capitolo 3. Realizzazione elettronica
L’equazione 3.3 và completata con le condizioni al contorno già indicate
nel Cap.1
1. emissione dello spike al raggiungimento della soglia con immediato
successivo ritorno al potenziale di reset
2. tempo refrattario assoluto (ARP Absolute Refractory Period)
3. barriera riflettente
In questa realizzazione la barriera riflettente e il potenziale di reset coincidono, non sono regolabili e corrispondono alla tensione minima di zero
Volt.
La seconda condizione descrive il fatto che per un fissato periodo di tempo
dopo l’emissione dello spike, denominato tempo refrattario, il soma non possa
ricevere alcun contributo di correnti.
Nella figura 3.29 è presentato lo schema del neurone.
Vdd
Vdd
Vdd
m13
V01
m6
m15
Vdd
VinJ
m14
Vadapt
m7
m16
Idiretta
Ifb
Vdd
Vdd
Vdd
m3
m8
m4
m9
m5
m10
dalle dendtriti
m1
Iβ
Iadapt
Vin
Vsoma C
Vsf
Cadapt
Vβ
m21
m19
Vrf
Ireset
Vc
m17
V02
m12
Cref
m18
Vlkc
m2
m20
Figura 3.29: Schema del neurone I.F. Low Power
77
m11
Vspike
3.7. Il neurone low power adaptive integrate and fire
Si possono identificare 6 blocchi principali
• un source follower m1 , m2 - regolazione della soglia
• un inverter m5 , m4 con feedback positivo m3 , m6 , m7 - riduzione delle
correnti medie di cortocircuito in ingresso
• un inverter m9 , m10 con slew-rate6 controllabile m8 , m11 per regolare
arbitrariamente il tempo refrattario assoluto
• un invertitore digitale m13 , m14 per generare lo spike
• un integratore m15 , m16 , m17 , m18 , m19 , m20 per realizzare il meccanismo
di adattamento in frequenza
• m21 per realizzare la corrente di scarica costante Iβ
3.7.1
Soglia e feedback positivo
Finchè Vsoma (t) < Θn (t) in uscita del source follower si ha
Vin = k(Vmem − Vsf )
dove k è il coefficente di pendenza sotto-soglia del mosfet e Vsf è la tensione,
costante che regola il valore della soglia efficace di emissione.
Quando Vsoma (t) sale al punto che Vin (t) si avvicina alla soglia dell’inverter
m5 , m4 , si innesca il feedback positivo: la corrente cresce in m3 , diminuisce
V01 di conseguenza cresce If b e quindi aumenta Vsoma (t). Il risultato è un
innalzamento rapidissimo della Vsoma (t) e successivo ritorno a zero per effetto della accensione del mosfet interruttore m12 attivato dal livello in uscita
dei due inverter interposti tra il suo gate e Vin , che scarica rapidamente e
totalmente C.
Si produce l’emissione di un rapidissimo spike. Il punto critico concernente i consumi di potenza di questo tipo di circuiti è legato all’elevata corrente
che fluisce nelle strutture semplice a mosfet per discriminare una soglia. Tipicamente queste strutture sono varianti di invertitori digitali. Come spiegato
nel paragrafo degli invertitori, per una tensione di ingresso intorno alla soglia
di commutazione scorre la massima corrente, di entità spesso non trascurabile. Quello che conta, nella definizione delle caratteristiche di un circuito VLSI
in termini di potenza consumata e sopportata è la potenza media. Quindi
6
Definisce la rapidità massima di variazione in uscita come risposta di un gradino in
ingresso
78
Capitolo 3. Realizzazione elettronica
una drastica riduzione del tempo di permanenza della tensione di ingresso
nella zona critica può migliorare notevolmente questo aspetto.
La breve durata di questo impulso è il motivo per cui questo neurone ha
un ridotto consumo di potenza.
3.7.2
Tempo refrattario
Durante l’emissione dello spike il ramo dell’inverter m8 m9 , dove m8 è connesso a diodo, ha rapidamente caricato Cref portando V02 a Vdd . Subito dopo
l’emissione la catena degli inverter ha di nuovo cambiato stato. Ora la capacità Cref , si scarica attraverso il percorso m10 m11 , lentamente perchè la
corrente è limitata da m11 . Finchè la tensione V02 è sufficentemente alta la
capacità C è continuamente scaricata da m12 che è acceso e quindi Vsoma
viene mantenuta a zero. Questo determina il tempo refrattario assoluto..
3.7.3
Meccanismo di adattamento in frequenza
Durante lo spike V01 è bassa e quindi m15 è acceso. Una corrente, regolata
da Vadapt scorre in m17 che è connesso a diodo. Il mosfet interruttore m18 è
acceso durante lo spike e quindi la capacità Cadapt si carica, mentre quando è
assente lo spike si scarica attraverso m20 con il parametro di regolazione Vlkc .
La tensione Vc ai capi della capacità induce una corrente di scarica Iadapt sulla
capacità di soma tramite m19 esponenzialmente dipendente da Vc realizzando
il feedback negativo sulla frequenza di emissione, di entità regolabile da Vadapt
e tempi di risposta del feedback proporzionali a Vlkc .
3.7.4
Simulazioni
Nella figura 3.30 è riportato il grafico di una simulazione del neurone con
adattamento in frequenza disattivato e corrente di ingresso Idiretta costante
fissata dalla tensione VinJ
Nella figura 3.31 è riportato il grafico di una simulazione montecarlo
Spectre-CADENCE, in cui è mostrata la distribuzione dei tempi ISI su 300
iterazioni.
79
3.8. Una simulazione completa dallo spike pre-sinaptico alla
depolarizzazione del soma post-sinaptico
Spike
Vsoma
Figura 3.30: Spike emessi e potenziale
di membrana del neurone I.F. Low Power in una simulazione transiente SpectreCADENCE. Vsf = 1.4 V regola la soglia efficace a circa 1.4V , Vβ = 180mV , VinJ = 2.8V ,
Vrf = 180 m V regola il tempo refrattario a
circa 9 m s. La durata spike è di 20 ns, l’ISI
è di 49 m s.
3.8
Figura 3.31:
Simulazione montecarlo
Spectre-CADENCE 300 iterazioni.
Istogramma dell’ I.S.I. La corrente di ingresso è
stata regolata per avere un ISI in simulazione
tipica di 80 ms.
Una simulazione completa dallo spike presinaptico alla depolarizzazione del soma
post-sinaptico
La simulazione (figura 3.32) di cui si presentano qui i risultati, è stata
effettuata sull’intero circuito postsinaptico, ovvero comprende:
• spike presinaptico emulato da un treno di impulsi
• shaper
• intero circuito sinapsi, inteso come modulo Calcio-Compara più modulo Sinapsi
• neurone post-sinaptico
80
Capitolo 3. Realizzazione elettronica
Non sono visibili, per chiarezza di visualizzazione il treno di spikes e la
variabile calcio C(t) che si mantiene sempre sopra K 2 up in tutta la durata
del tempo simulato.
Condizioni al contorno e condizioni iniziali
• la sinapsi è definita eccitatoria
• La dinamica Calcio viene mantenuta attiva fino a 4ms, quindi viene
disattivata e attivata la regola ridotta.
• è iniettata sul soma del post-sinaptico una corrente diretta costante,
all’inizio molto elevata per poi essere ridotta a step successivi ai tempi
2 ms e 4.4 ms.
• X(t)|0 = 800 mV
• Vp (t)|0 = 800 mV (potenziale di depolarizzazione del soma postsinaptico)
Con questo scenario, dopo aver effettuato un tuning di tutti i parametri
è possibile osservare:
• la generazione dei segnali UP e DOWN
• il conseguente andamento della variabile X(t)
• il clipping del valore della sinapsi, riportato nel grafico come stato
digitale sinapsi
• l’effetto dei due pesi della sinapsi sull’efficacia sinaptica visibile come
salti di ben differente ampiezza sul potenziale di depolarizzazione del
soma Vp
Le simulazioni hanno permesso tra l’altro di verificare, nella progettazione
di ogni circuito, che le regolazioni di ogni parametro di modello fossero impostabili in un range sufficentemente ampio di parametri elettrici (tensioni)
effettivamente applicabili dall’esterno al chip.
Per i valori di efficacia sinaptica si considerano salti tipicamente di 15 ∼
1
del valore della soglia di emissione dello spike che nel caso del neurone
15
utilizzato è tipicamente di 900 mV .
I valori di salto a e b della variabile sinaptica invece ha tipicamente una
granularità maggiore. La soglia è regolabile e può essere posta ad esempio
a metà della tensione di alimentazione del chip visto che il range dinamico
disponibile è tutta l’alimentazione.
81
3.9. I layout FULL-CUSTOM
UP
DOWN
Vp
Θ
stato digitale sinapsi
soglia sinapsi
X(t)
Figura 3.32: Simulazione Spectre-CADENCE dell’intero percorso dallo spike presinaptico all’efficacia sul soma del neurone post-sinaptico, con condizioni al contorno che cambiano durante la simulazione. Il segnale stato digitale sinapsi è generato dall’uscita del
comparatore di clipping
Le simulazioni mostrano che il limite inferiore del salto ragionevolmente
impostabile si attesta intorno ad una decina di mV , mentre il limite superiore è molto alto (intorno al mezzo Volt). Per cui, il range di regolazione
che mostrano questi circuiti in simulazione comprende ampiamente il range
richiesto.
3.9
I layout FULL-CUSTOM
Nella figure 3.33, 3.34 e 3.35 sono presentati il layout realizzati con le corrispondenze con i blocchi descritti nello schematico.
82
Capitolo 3. Realizzazione elettronica
Figura 3.33: Layout del modulo Sinapsi. La capacità Csyn è distribuita per tutta la
larghezza del layout tra i blocchi analogici e le 4 Standard Cell AMS ed inoltre a sinistra
del modulo. Riguardo queste ultime, benchè, sia disponibile il layout dettagliato, è stato
necessario nasconderle per motivi di accordi con la fonderia riguardo la riservatezza delle
informazioni tecnologiche fornite.
83
3.9. I layout FULL-CUSTOM
Figura 3.34: Layout del modulo Calcio-Compara. La capacità Cca è distribuita per tutta
la larghezza del layout tra i blocchi analogici le 4 Standard Cell AMS . Riguardo queste
ultime, benchè, sia disponibile il layout dettagliato, è stato necessario nasconderle per
motivi di accordi con la fonderia riguardo la riservatezza delle informazioni tecnologiche
fornite.
84
Capitolo 3. Realizzazione elettronica
AMS
Standard
Cell
Figura 3.35: Layout dello Shaper. Comprende una standard cell AMS (inverter) che si
è dovuto nasconderle per motivi di accordi con la fonderia riguardo la riservatezza delle
informazioni tecnologiche fornite.
85
3.9. I layout FULL-CUSTOM
86
Capitolo 4
Il chip completo e il sistema di
test
Una rete neuronale realizzata in hardware in un chip, è necessariamente una
rete limitata, in quanto a numero di neuroni, se paragonata alle analoghe
reti biologiche, ad esempio dei moduli corticali dei primati. Si è visto che
tra le proprietà più interessanti osservabili di una rete neuronale sono quelle
derivanti dall’attività collettiva. La qualità dell’insegnamento che si trae
dallo studiare queste proprietà sono fortemente dipendenti dal numero di
neuroni della rete. Da qui la necessità di superare il vincolo tecnologico
imposto dal numero massimo di neuroni contenuti in un chip. La strada
ovvia è quella di replicare i chip. Si rende subito evidente una limitazione.
Cosı̀ come non è possibile mettere in un chip un numero arbitrario di neuroni,
altrettanto impossibile, con le attuali tecnologie, assegnare un pin per ogni
linea di comunicazione tra ciascun neurone.
È per questo che è necessario utilizzare un protocollo di comunicazione.
Nel paragrafo seguente è presentato il protocollo utilizzato, la cui implementazione costituisce, insieme alla rete descritta nel precedente capitolo il
core dell’intero chip realizzato.
Il chip completo si compone del core analogico, del core digitale e del
Padframe. Quest’ultimo elemento circonda il core ed è costituito da un
insieme di Pad allineati dove si connettono tutti i segnali del core da una
parte e i fili metallici del contenitore del chip dall’altra.
Tipicamente il layout del padframe viene disegnato utilizzando le standard cell appositamente predisposte dalla fonderia. Nel presente lavoro invece, i pad utilizzati sono stati sviluppati dall’Istituto di Neuroinformatica di
Zurigo, cosı̀ come una parte del sistema di comunicazione.
Il sistema di test per i chip neuronali realizzati con il sistema per il
87
4.1. Protocollo di comunicazione A.E.R.
controllo/comunicazione sono stati sviluppati e realizzati dal nostro gruppo
[29], [30], [31], [32].
4.1
Protocollo di comunicazione A.E.R.
I dispositivi neuromorfi, come il chip realizzato, sono caratterizzati da un
elevato numero di elementi costitutivi. Tipicamente il comportamento dell’intero sistema è determinato dall’ elevato grado di interazione tra gli elementi, come nel caso di una rete neuronale. Come già ampiamente osservato
nei capitoli precedenti, le interazioni in una rete di neuroni hardware sono
rappresentate dall’inviare e dal ricevere spikes tra un neurone e gli altri. La
pecularietà di queste comunicazioni tra neuroni è che gli spike sono eventi
asincroni stereotipati.
La connettività della rete all’interno del chip si risolve con semplici strategie di scelte topologiche. Il problema si pone quando due o più dispositivi neuronali devono comunicare tra loro. È necessario utilizzare un protocollo di comunicazione per codificare, trasportare e gestire il flusso delle
comunicazioni tra neuroni in chip distinti.
Negli ultimi tempi si sta cercando di definire un protocollo comune per i
sistemi neuromorfi. Tra questi, il protocollo A.E.R. (Address Event Rapresentation) [33] qui descritto è considerato particolarmente conveniente ed è
stato usato ed ampliato, negli aspetti hardware, dal nostro gruppo.
L’A.E.R. è un protocollo che nella sua versione più semplice fornisce un
collegamento point-to-point.
La natura asincrona degli spikes e il numero elevato di neuroni in un
chip determina la necessità di una gestione dei conflitti dalla parte A.E.R. −
out (spikes in uscita dal chip). La parte che si occupa di questo aspetto è
chiamata Arbiter.
La struttura di base tipica di un sistema di due dispositivi neuromorfi
(Sender e Receiver ) con BUS di comunicazione A.E.R. è descritta in fig.4.1.
I segnali di Handshaking 1 che gestiscono il bus e quindi il flusso di comunicazione tra il sender ed il receiver sono il Req (richiesta) e l’Ack (risposta).
L’arbitro che si occupa della gestione dei conflitti è organizzato in una
struttura ad albero binario, ad ogni livello c’è una riga di blocchi decisionali
a due ingressi che all’occorrenza selezionano il passaggio di un solo segnale
(quello che arriva per prima). Nello strato più basso si trovano i singoli
blocchi decisionali a cui afferiscono coppie di spike di neuroni.
La definizione di coincidenza temporale tra due spikes può essere vista
come una esatta sovrapposizione dei due impulsi finiti, ma questo è un evento
1
Letteralmente stretta di mano
88
Capitolo 4. Il chip completo e il sistema di test
Sender
Receiver
t2
t1
1
0
OUT
OUT
1
0
OUT
1
1
0
OUT
1
0
1
0
OUT
ENCODER
1
0
OUT
Handshake
/Ack
/Req
0
1
0
0
Decoder
OUT
Figura 4.1: Sistema di comunicazione A.E.R.. Sono evidenziati in colore rosso i percorsi
dei due neuroni trasmittenti concorrenti (del chip di sinistra), in blu il segnale di Ack di
ritorno dal chip ricevente(a destra) ed il percorso di codifica; in verde il segnale indirizzato
al neurone bersaglio.
molto raro a causa del valore piccolo della durata dello spike rispetto all’I.S.I.
medio.
L’altro scenario in cui si può parlare di coincidenza è quello in cui gli
spikes arrivano ad una distanza temporale più piccola del tempo necessario
al segnale in uscita di fare il percorso completo (Req dal sender al receiver e
Ack di ritorno). In questo tipo di coincidenza opera l’ Arbitro.
Si può descrivere una sequenza tipica di eventi in maniera semplificata
nel seguente modo
• all’istante t1 il neurone emette uno spike; viene generato il segnale di
Req nel relativo ingresso del modulo decisionale al livello più basso
dell’albero.
89
4.2. Architettura generale del chip realizzato
• Il Req prodotto dallo spike percorre i vari livelli dell’arbitro perchè non
entra in competizione con altri tentativi di trasmissione
• all’istante t2 un altro neurone emette uno spike; viene generato il
segnale di Req nel relativo ingresso del modulo decisionale
• Il Req prodotto arriva senza competere fino alla cima, e qui viene bloccato dall’arbitro perchè il modulo binario è occupato; il secondo Req
rimane in attesa a questo livello
• Il segnale di Req raggiunge il receiver e quindi viene generato il segnale
di risposta Ack
• Il segnale Ack percorre all’indietro tutto il percorso del segnale selezionato.
• quando arriva nel livello più basso, corrispondente all’ingresso del relativo spike, viene attivata la logica di codifica dall’encoder che genera
l’indirizzo del neurone trasmittente.
• l’indirizzo codificato transita sul BUS e arriva sul decoder del receiver
che si occupa di trasmettere lo spike al relativo neurone
• il segnale Ack viene disattivato sul BUS dal receiver, l’arbitro rilascia
il blocco sui blocchi decisionali e quindi il Req del secondo neurone può
fare il suo percorso
In questa descrizione semplificata, si evince che la mappatura della connettività tra neuroni trasmittenti e riceventi sembra risiedere nel decoder.
Nel sistema reale non è cosı̀. Nella gestione del BUS entra un sofisticato
sistema di controllo che permette non solo una mappatura configurabile tra
neuroni trasmittenti e ricevitori, ma anche la gestione tra più sender, in
questo caso si parla di architettura multi-sender.
4.2
Architettura generale del chip realizzato
Nella figura 4.2 è mostrata l’architettura generale del chip.
Il chip è costituito
• da una rete ricorrente con 32 Neuroni I.F. e matrice sinaptica 32 x
32 riconfigurabile. La rete ricorrente coincide con il core analogico
ampiamente discusso nel precedente capitolo.
90
Capitolo 4. Il chip completo e il sistema di test
INPUT
AER sin
32x32
Sinapsi
32x32
Neu.
32
Arbiter
AER in
Rete ricorrente
El.Mem.
Decoder XY
OUTPUT
AER out
Mux
Correnti
dirette
Spikes in
uscita
Figura 4.2: Core del chip
• da una matrice sinaptica AER sin 32 x 32 riconfigurabile che fornisce
la connettività per i neuroni esterni
• dall’ AER in comprendente il Decoder nella zona di INPUT
• da un elemento di memoria dai multiplexer per le uscite degli spikes e
dall’ AER out comprendente l’Arbitro nella zona di OUTPUT
Caricamento della configurazione delle matrici sinaptiche
Ulteriori due segnali digitali di ingresso, uno di dati e uno di clock permettono di caricare serialmente la catena di Flip-Flop del blocco Selezione
della matrice sinaptica ricorrente e AER (vedi figura 4.3)
Test point
Per i primi test funzionali sono stati portati fuori dal chip un gruppo
di segnali analogici e digitali di neuroni, modulo sinapsi, modulo CalcioCompara e shaper sufficenti a verificare la funzionalità del singolo blocco e di
un insieme minimale di rete a due neuroni pre e post-sinaptico. La convenzione utilizzata per la numerazione degli elementi nelle matrici sinaptiche è
(riga, colonna)=(i, j) e l’elemento (0, 0) è quello in alto a destra della figura
4.2. I neuroni hanno il solo indice di riga i. Sono state scelte le righe 0 e 31
per prelevare i segnali.
91
4.2. Architettura generale del chip realizzato
Neurone
Sinapsi eccitatoria
Blocco Selezione
Sinapsi inibitoria
Bitstream per la
configurazione seriale
Figura 4.3: Caricamento della configurazioni delle matrici sinaptiche. Un parola seriale di
4096 bit è necessaria per configurare ciascuna sinapsi delle due matrici sinaptiche in modo
indipendente.
• Dei moduli sinapsi (0, 0) della matrice ricorrente e (31, 0) della matrice
AER sono disponibili entrambi i segnali digitali di clipping e i valori
analogici X(t).
• U P , DOW N , Spike-neurone, valore analogico neurone Vsoma (0), variabile calcio C(t)(0) sono disponibili per entrambe le righe 0 e 31.
• Spike-Shaper(31) della matrice ricorrente e Spike-Shaper(0,0) della matrice AER
• modulo sinapsi (31, 5) della matrice AER valore analogico X(t)
La rete comunica in uscita attraverso l’Aer out, ma sono disponibili 2
92
Capitolo 4. Il chip completo e il sistema di test
uscite dirette di spike di una coppia di neuroni selezionabile dal sistema
multiplexer costituito da due Mux 16 → 1.
La rete riceve gli stimoli dall’AER in, ma sono disponibili gli ingressi per
le correnti dirette che permettono di iniettare una corrente dall’esterno
del chip su ciascuno dei neuroni in modo indipendente.
Shaper
Shaper
Ack
to synapse
to synapse
Spk
Spk
Ack
Ack
Connettivita`
interna
Neurone
Arbirter
Connettivita`
esterna
(AER)
Mem. El.
Decoder
Req
Req
Figura 4.4: La Connettività esterna - interna. Gli shaper nella matrice ricorrente sono
presenti in numero di uno per ciascun neurone, mentre nella matrice AER ne è presente
uno per sinapsi.
Dalla parte dell’uscita un sistema di Multiplexer permette di selezionare simultaneamente una coppia di neuroni. Al tempo stesso gli spikes
vengono arbitrati e quindi l’informazione passa sul BUS AER out.
È stato interposta tra l’arbitro e la colonna di neuroni un elemento di memoria. Lo scopo di questo elemento è quello di disaccoppiare l’attività della
rete neuronale dal traffico dei dati AER. È stato mostrato che l’informazione
dell’emissione dello spike, deve essere mantenuta dall’istante di emissione da
parte del neurone fino a quando l’AER non ritorna il segnale Ack di avvenuta
trasmissione. In altre realizzazioni dove si usa questo protocollo e lo stesso
neurone qui presente, è il neurone stesso che viene mantenuto bloccato fino
all’arrivo dell’Ack.
Con questo accorgimento, quando un neurone emette un spike, l’elemento
memorizza l’evento e ne mantiene memoria finchè l’AER out non ha completato il suo ciclo di trasmissione al receiver, a quel punto il controller resetta
l’elemento di memoria. Il vantaggio di questa scelta sta nel fatto che in caso
93
4.2. Architettura generale del chip realizzato
di intenso traffico di dati sul BUS AER la trasmissione viene ritardata, la
rete però non subisce l’ indesiderato blocco sul neurone considerato.
Dalla parte dell’ingresso la connettività è realizzata con una matrice
sinaptica AER, del tutto analoga a quella ricorrente per quanto riguarda i
moduli sinapsi, con la differenza che nella matrice ricorrente gli spikes presinaptici provengono dai neuroni interni al chip dopo aver subito l’estensione
temporale della lunghezza per mezzo dello shaper, per contro in quella AER
gli spikes sono generati da un ulteriore shaper, uno per ciascun modulo sinapsi, posto accanto al esso e pilotato dal decoder x, y (riga-colonna). Il decoder
attiva il relativo shaper quando il l’AER in riceve una richiesta di trasmissione al neurone i − esimo. L’indice x della riga del decoder corrisponde
all’indice i della riga della matrice.
Nella figura 4.4 è rappresentata la connessione tra due matrici sinaptiche e
viene messo in evidenza il meccanismo delle iniezioni degli spikes provenienti dall’AER in e il meccanismo di invio dell’attività dei neuroni attraverso
l’AER out.
La presenza di 32 blocchi ripetuti della coppia Shaper-Modulo sinapsi
(colonne y) nella riga del neurone x realizza una estensione a 32 dei canali
completi di comunicazione per ogni neurone:
due chip con questa architettura costituiscono una rete ricorrente completa di 64 neuroni, in cui il traffico degli spikes è gestito dall’AER tra i neuroni
appartenenti ai due distinti moduli neuronali contenuti nei due chip, mentre
è localizzato e diretto tra neuroni dello stesso modulo.
Nella figura 4.5 è presentato il layout del chip completo.
Figura 4.5: Il chip
Attualmente il chip è in fase di fabbricazione e sarà pronto a Giugno 2005.
94
Capitolo 4. Il chip completo e il sistema di test
4.3
Sistema di test
La progettazione e realizzazione VLSI di questo chip si colloca in un più ampio contesto di attività del nostro gruppo che vanno dalle finalità ultime che
sono quelle di ricerca sui sistemi complessi nel panorama nelle neuroscienze
computazionali, alle implicazioni tecnologiche tramite dispositivi neuromorfi.
La realizzazione di questi dispositivi complessi necessita di sofisticati
sistemi di controllo e comunicazione per i test ai vari livelli.
Esiste attualmente una consolidata piattaforma di test sviluppata nel
nostro gruppo che è stata nel passato e fino ad ora ampiamente usata per
i test sui dispositivi neuronali precedenti, per ultimo la lann21, [31], [32],
nell’ambito degli esperimenti MUNES e HAPTIC.
Alla base del sistema di test due sono le caratteristiche fondamentali
richieste
• gestire la comunicazione con un PC host
• controllare tutti i parametri di regolazione necessari
La prima caratteristica indicata comprende la gestione del protocollo di
comunicazione AER, e si è ottenuta con la progettazione e la realizzazione
di una scheda di interfaccia PCI-AER2
La seconda caratteristica ha avuto come soluzione la progettazione e
realizzazione di una scheda PCI-GPB 3
4.3.1
Schede di interfaccia PCI-AER e PCI-GPB
La scheda PCI-AER realizza una interfaccia programmabile tra il bus
AER di dispositivi neuromorfi e il bus PCI di un PC [32], [30] Nella attuale versione è in grado di operare in un contesto di di comunicazione AER
Multi-chip tra più dispositivi [29]. È basata su dispositivi XILINX (FPGA
programmabili).
I blocchi funzionali fondamentali sono riassumibili in
• SEQUENCER permette di generare via software un flusso di spikes da
inviare ai dispositivi neuronali, emulando dispositivo neuronale
• MONITOR permette di assegnare etichette temporali agli eventi che
trafficano nel bus AER
2
3
Peripheral Component Interconnect - Address Event Rapresentation
Peripheral Component Interconnect - General Purpose Bus
95
4.3. Sistema di test
• MAPPER realizza la connettività riprogrammabile tra i diversi chip
fino a 4 senders e fino a 4 receivers
La scheda è stata sviluppata completamente presso l’I.S.S. per quanto
riguarda l’hardware. Il software è frutto della collaborazione tra l’I.S.S. e l’Istituto di NeuroInformatica di Zurigo. Nella sua attuale versione si presenta
come in figura 4.6.
Figura 4.6: Scheda di interfaccia PCI-AER in uno scenario Multi-chip tipico di lavoro
La scheda PCI-GPB è stata progettata e realizzata dal nostro gruppo
presso l’ I.S.S. ed è una scheda con cui è possibile mappare il BUS PCI di un
PC con un BUS definito generico costituito da da 32 linee bidirezionali più
12 linee di ingresso e 12 di uscita.
Figura 4.7: Scheda di interfaccia PCI-GPB
96
Capitolo 4. Il chip completo e il sistema di test
L’utilizzo tipico di questa scheda è nella mappatura dell’insieme dei DAC 4
che permettono la generazione di tutte le tensioni necessarie al chip per il
controllo dei parametri funzionali.
Il sistema di test utilizzato fino alla lann21 è un sistema che comprende
oltre alle due sopra citate schede montate su PC un box integrato modulare
denominato Big-Box-System che ospita schede con le necessarie funzionalità
per
• accogliere il dispositivo neuronale e fornire il front-end dedicato al particolare chip sotto test. L’ampia versatilità di questa parte prevede una
piccola scheda interscambiabile chiamata POD che si adatta a differenti
chip realizzati dal gruppo. Questa scheda comunica con la PCI-AER
• una scheda con tutti i generatori di corrente per i dispositivi che lo
richiedono
• una scheda di comunicazione/controllo che si interfaccia con la PCIGPB e che ospita tutti i DAC delle regolazioni
Nella figura 4.8 è visibile il Big Box System
Figura 4.8: Big Box System
Attualmente si sta progettando un sistema specifico per testare il chip
del presente lavoro. Il progetto del sistema di test in corso non tiene conto
soltanto nelle necessità di test del singolo chip, ma si colloca in un contesto di
realizzazione di un sistema di controllo e test Multi-chip sfruttando appieno
le caratteristiche di comunicazione della scheda PCI-AER.
4
Digital to Analog Converter
97
4.3. Sistema di test
98
Capitolo 5
Conclusioni e prospettive
future
In questo lavoro di tesi sono stati raggiunti i seguenti risultati.
È stato realizzato un chip in tecnologia mista VLSI analogica full-custom
e digitale che realizza una rete neuronale con 32 neuroni impulsati, con matrice sinaptica configurabile e modulo di comunicazione A.E.R. nella tecnologia AMS (Austria Micro Systems) 4 metalli. Il lavoro è stato svolto con
il software CADENCE per lo sviluppo di dispositivi VLSI analogici e misti
analogico-digitali.
Con la realizzazione di questo chip sono state introdotte novità sostanziali
rispetto ai dispositivi precedentemente realizzati dal gruppo
• la possibilità di configurare in modo arbitrario la matrice sinaptica
• l’introduzione del nuovo modello di sinapsi basato sulla dinamica del
calcio nel neurone post-sinaptico.
• l’introduzione del modulo di comunicazione AER all’interno del chip.
È stata messa a frutto la collaborazione europea nell’ambito del progetto
ALAVLSI per gli aspetti dello sviluppo e progettazione hardware di dispositivi neuronali. Questo ha permesso, tra l’altro, di integrare nel chip il circuito
del neurone dell’ Istituto di Neuroinformatica di Zurigo e parte del circuito
digitale di comunicazione.
È stato elevato il know-how di progettazione in particolare per quanto
riguarda le simulazioni statistiche sul mismatch dei parametri tecnologici.
Il numero di neuroni e sinapsi implementate è stato mantenuto basso:
questo non solo per contenere i costi di un chip prototipale, ma anche in base
99
all’obiettivo perseguito nel progetto, di costruire reti complesse mediante
sistemi costituiti da diversi chip semplici connessi su bus AER.
La piattaforma di test multi-chip è in fase di progettazione e sarà pronta
all’arrivo del chip previsto per Giugno.
Il sistema di test è predisposto per una architettura multi-chip. In una
prima fase si eseguiranno i test preliminari per verificare la funzionalità delle
parti elettroniche. In un secondo momento sarà possibile eseguire i test più
ad alto livello relativi sia agli aspetti del modello della sinapsi che dell’attività di insieme della rete. Questo sistema metterà in evidenza anche le
caratteristiche della comunicazione AER tra chip neuromorfi.
Bisogna sottolineare come la fase di test post-produzione di questo tipo
di chip non si riduca a una mera verifica di corrispondenza alle specifiche di
progetto, ma è assimilabile ad una vera e propria “neurofisiologia su silicio”,
in cui le proprietà del chip sono stabilite in termini statistici dalle relazioni
stimolo-risposta.
L’obiettivo finale del progetto in cui si inserisce il presente lavoro è quello
di fornire una piattaforma hardware per studiare la reciproca interazione tra
attenzione selettiva e memoria associativa in presenza di stimoli complessi.
100
Ringraziamenti
Il primo ringraziamento è rivolto a Gaetano Salina, lo ringrazio moltissimo
non solo per avermi dato la possibilità di svolgere questo lavoro di tesi ma
anche perchè fu proprio lui a suggerirmi di intraprendere questa faticosa
quanto entusiasmante avventura di studente universitario e fu sempre lui ad
avvicinarmi, ancor prima di intraprendere gli studi, al meraviglioso mondo
della ricerca. Gaetano è una persona molto capace e ritengo che sia una
fortuna lavorare con lui.
Ringrazio molto Paolo Del Giudice per tutte le interessantissime, numerose e sempre stimolanti discussioni da sempre avute sui temi dell’attività del
gruppo di ricerca e per la sua disponibilità nell’aiutarmi a chiarire molti punti nella fase di stesura della tesi. La grande capacità comunicativa di Paolo
insieme alla grande competenza lo rendono davvero una persona speciale.
Un ringraziamento sentito va ad Andrea Salamon per tutta la disponibilità mostratami in vari momenti della mia vita da studente quando capitava
gli chiedessi consigli per lo studio. I suoi consigli mi sono stati molto preziosi.
Ringrazio Vittorio Dante per il piacere che trasmette lavorare con lui.
Vittorio ha una professionalità cosı̀ elevata ed una tale capacità di realizzare
qualunque cosa con estrema naturalezza e grande dedizione al lavoro che
lascia stupefatti. Ringrazio Vittorio molto anche per l’aiuto fornitomi nel
chiarire diversi aspetti dei sistemi di test.
Ringrazio Maurizio Mattia per avermi aiutato a chiarire alcuni punti
legati alla teoria, l’entusiasmo che trasmette Maurizio per il suo lavoro è
prorompente e piacevolmente contagioso.
Ringrazio Massimiliano Giulioni con cui ho condiviso le fasi finali del
lavoro sul chip, per avermi sopportato durante quelle estenuanti nottate per
arrivare alla conclusione del progetto. Ringrazio Massimiliano per il supporto
datomi nel chiarire punti della parte digitale del progetto.
Ringrazio Stefano Fusi per la sua grande cordialità e disponibilità nello
spiegarmi aspetti dell’attività di ricerca.
Ringrazio Giacomo Indiveri per avermi dato la possibilità di lavorare con
lui. Giacomo oltre ad essere una persona umanamente molto gradevole, è
101
anche un grande esperto nella progettazione di circuiti neuromorfi. È stato
molto stimolante e piacevole lavorare con lui.
Ringrazio il Prof. Daniel J. Amit con cui ho avuto la fortuna di collaborare nel passato e di cui ho potuto apprezzare l’elevato profilo scientifico e
culturale.
Ringrazio Raffaele Bencardino per la sua grande simpatia e per la sua
disponibilità nel darmi consigli nella gestione delle fasi finali della tesi.
Ringrazio Francesco Palma, Gabriella Russo, Marco Pizziol e Maurizio
Sabene per aver piacevolmente condiviso con loro un poco di esperienza come
studenti compagni di corso seppur non di età. Con loro mi sono sentito uno
studente un pò meno anomalo.
Ringrazio mia sorella Rita, mio fratello Marco e mia zia Suor Gilda per
avermi saputo spesso incoraggiare.
Ringrazio mio nipote Stefano per aver garantito il funzionamento del
portatile nella fase critica di stesura della tesi.
Desidero poi ringraziare tutti quei colleghi che mi hanno talvolta moralmente sostenuto in questa mia avventura.
Lascio in ultimo, ma non certo come ultimo, il mio ringraziamento più
grande e più sentito in assoluto a mia moglie Emanuela, che ha saputo in
tutti questi anni sopportarmi e sostenermi in ogni momento, anche a prezzo
di grandi fatiche e sacrifici per la gestione della famiglia e dei nostri due
figli, senza di lei non ce l’avrei fatta. A Federico e Luca ringrazio per la loro
gioiosità di bimbi e prometto di dedicare loro il tempo che meritano.
Ad Emanuela, Federico e Luca dedico la mia tesi.
102
Bibliografia
[1] Daniel J. Amit. Modellizzare le funzioni del cervello. CEDAM, Milano,
1995.
[2] J. J. Hopfield. Neural networks and physical systems with emergent
selective computational activities. Natl. Acad. Sci. USA, 1982.
[3] P. Del Giudice and G.Parisi . Modelli di neuroscienza computazionale.
Enciclopedia del 900. Istituto dell’Enciclopedia Italiana, Roma, 2004.
[4] P. Dayan and L. F. Abbott. Theoretical Neuroscience. MIT Press,
Cambridge, MA, 2001.
[5] Christof Koch. Biophysics of computation. Oxford University Press,
New York, 1999.
[6] Wulfram Gerstner and Werner Kistler.
Spiking Neuron Models.
Cambridge University Press, Cambridge, 2002.
[7] G. Gerstein and B. Mandelbrot. Random walk models for the spike
activity of a single neuron. Biophys. J., 4:41–68, 1964.
[8] Stefano Fusi and Maurizio Mattia. Collective Behavior of Networks with
Linear (VLSI) Integrate-and-Fire Neurons. Neural Comput., 11(3):633–
653, apr 1999.
[9] G. Gigante. Adattamento alla dinamica neuronale dovuto alla corrente
del calcio. Master’s thesis, Università di Roma “La Sapienza“, 2003.
[10] Y. Miyashita. Neural correlate of visual associative long-term memory
in the primate temporal cortex. Nature, (335):817, 1988.
[11] Daniel J. Amit. The Hebbian paradigm reintegrated: local reverberations as internal representations. Behav. Brain. Sci., 18:617–657,
1995.
103
Bibliografia
[12] D.J. Amit, P. Del Giudice and S. Fusi. Apprendimento dinamico della
memoria di lavoro: una realizzazione in elettronica analogica, volume 3
of Frontiere della Vita. Istituto Della Enciclopedia Italiana, Roma, 1999.
[13] Donald O. Hebb. The Organization of Behavior: A Neuropsychological
Theory. John Wiley & Sons, 1949.
[14] Daniel J. Amit and Stefano Fusi. Learning in neural networks with
material synapses. Neural Comput., 6(5):957–982, sep 1994.
[15] S. Fusi et. al. Spike-driven synaptic plasticity: theory, simulation, VLSI
implementation. Neural Computation, 12:2227–2258, 2000.
[16] S. Fusi. Hebbian spike-driven synaptic plasticity for learning patterns
of asynchronous activity. Biol. Cybern., 87(5–6):459–470, 2002.
[17] S. Fusi P. Del Giudice and M. Mattia. Modeling the formation of working
memory with networks of integrate-and-fire neurons connected by plastic
synapses. Journal of Physiology Paris, 97:659–681, 2003.
[18] J.M. Brader, W. Senn, S. Fusi. Learning real world stimuli in a neural network with spike-driven synaptic dynamics. Neural Comput.,
submitted.
[19] C. Mead. Analog VLSI and Neural System. Addison-Wesley, 1989.
[20] S.Liu, J. Kramer, G. Indiveri, T. Delbruk and R. Douglas. Analog VLSI: Circuits and Principles. MIT Press, Cambridge, Massachusetts London, England, 2002.
[21] J.P.Uyemura. Fundamentals of MOS Digital Integrated Circuits.
[22] P.E. Allen, D. R. Holberg. CMOS Analog Circuit Design. Oxford
University Press, New York, Oxford, second edition.
[23] R.L.Geiger, P.E.Allen, N.R.Straden. VLSI design for analog and digital
circuits.
[24] N.H.E. Weste K. Eshraghian. Principles of CMOS VLSI design.
[25] Ketteth S. Kundert. The Designer’s Guide to SPICE & SPECTRE.
Kluwer Academic Publishers, Boston - Dordrecht , London, 1996.
[26] Andrei Vladimirescu. Guida a Spice. McGraw-Hill, Milano, 1995.
104
Bibliografia
[27] E. Chicca, D. Badoni, V. Dante, M. D’Andreagiovanni, G. Salina, L. Carota, S. Fusi and P. Del Giudice. A VLSI recurrent network of integrateand-fire neurons connected by plastic synapses with long term memory.
IEEE Transactions on Neural Networks, 14(Issue 5):1297– 1307, Sept.
2003.
[28] Giacomo Indiveri. Low power adaptive integrate and fire. In Proc. IEEE
International Symposium on Circuits and Systems, 2003.
[29] V. Dante and P. Del Giudice. Hardware and software for interfacing
to address-event based neuromorphic systems. In The Neuromorphic
Engineer, 2005.
[30] V. Dante and P. Del Giudice. The PCI-AER interface board.
Workshop on Neuromorphic Engineerig, 2001.
In
[31] Del Giudice V. Dante and M. Mattia. Implementation of Neuromorphic
Systems: from discrete components to analog VLSI chips (testing and
communication issues). Ann. Ist. Super. Sanita, (37 (2)):231–239, 2001.
[32] V. Dante. PCI - AER Adapter board User Manual. In Web site of I.S.S.
neural.iss.infn.it, 2002-2003.
[33] Kwabena A. Boahen. Point-to-Point Connectivity Between Neuromorphic Chips using Address-Events. IEEE transaction on circuits &
systems,, 1999.
105