Modulo18

La macchina universale
Una immediata conseguenza della dimostrazione è la seguente
Corollario
il linguaggio L = {M (w) | M rappresenta una macchina di Turing che si ferma con input w}
H
sull’alfabeto {0,1}* è un linguaggio non ricorsivo [e quindi non decidibilie].
LH in altre parole è costituito dalle stringhe che rappresentano una MT seguita dall’input da
essa accettato ovvero che corrispondono ai valori 1 del vettore caratteristico della MT.
Tuttavia è possibile dimostrare il seguente
Teorema: il linguaggio LH è ricorsivamente enumerabile [e quindi semidecidibile].
Sapendo perciò che un linguaggio ricorsivo è anche ricorsivamente numerabile si avrà l’importante
risultato:
Corollario: la classe dei linguaggi ricorsivi è contenuta in modo proprio nella classe dei linguaggi
ricorsivamente enumerabili ovvero LR & LRE
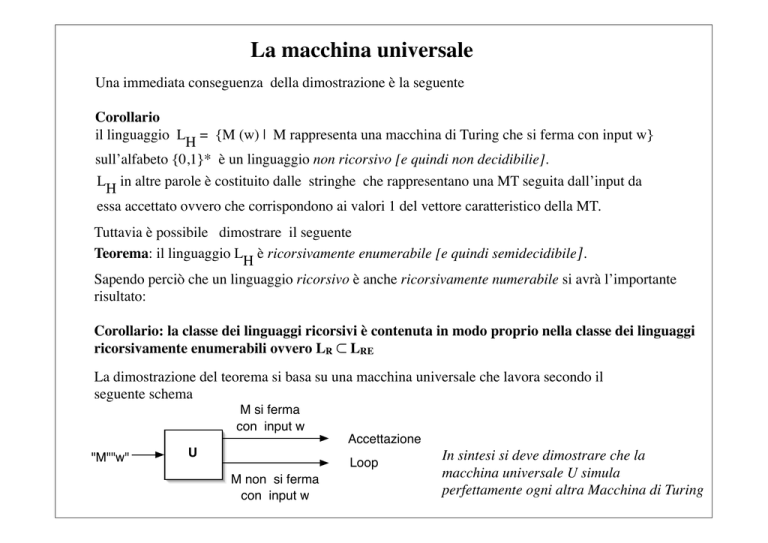
La dimostrazione del teorema si basa su una macchina universale che lavora secondo il
seguente schema
M si ferma
con input w
"M""w"
U
Accettazione
Loop
M non si ferma
con input w
In sintesi si deve dimostrare che la
macchina universale U simula
perfettamente ogni altra Macchina di Turing
Ricorsiva enumerabilità di L
H
La dimostrazione verrà fatta con una macchina a tre nastri. Nel nastro 1 verrà codificato l’input
mentre il nastro 3 verrà usato per effettuare la simulazione dell’esecuzione della macchina M.
Una computazione della macchina U viene ad essere definita nel seguente modo:
1. Se la stringa di input non è della forma “M” “w”, U si muove indefinitivamente verso destra.
2. Viene ricopiata la stringa w sul nastro 3, la testina viene quindi riposizionata a sinistra al primo
carattere, cosicché sul nastro 3 viene ad essere definita la configurazione iniziale di una
computazione di M con input w.
3. viene scritto sul nastro 2 lo stato q0 (il simbolo 1 nella nostra codifica)
4. Passo di simulazione. La transizione di M viene determinata dal simbolo x scandito sul nastro 3
e lo stato qi codificato sul nastro 2.
a) Viene scandito il nastro 1 alla ricerca della coppia EN(qi ) EN (x) se tale transizione non esiste
U si ferma e accetta l’input (configurazione finale).
b) Assunto che il nastro 1 contenga la transizione EN(qi) 0 EN(x) 0 EN(y)0 EN(d) 0 EN(qj)
i) EN(qi) è rimpiazzato da EN(qj) sul nastro 2
ii) il simbolo y è scritto sul nastro 3
iii) la testina del nastro 3 è mossa nella direzione specificata da d
5. si ripete il passo di simulazione (punti 4 e 5)
La simulazione della macchina U accetta stringhe in LH mentre per stringhe in {0,1}* - LH
cicla indefinitivamente. Poiché LH = L(U) LH è ricorsivamente enumerabile essendo
ricorsivamente enumerabile L(U).
Indecidibilità del Linguaggio di diagonalizzazione
Ld = tutte le stringhe wi tali che
wi non è in L(Mi)
Ld = { wi ! "* | wi ! L(Mi}
Teorema il linguaggio Ld è non ricorsivamente enumerabile
w
M
wj
ws
Mi
0 0 0 1 0 0 1 0 . . .
.
Mj
0 0 1 0 1 0 0 1
0 1 0 0 0 1 0 0 . . . .
Supponiamo Ld = L(M) per una macchina M,
allora deve esistere una Macchina di Turing nella
enumerazione ovvero un indice i che individua
la macchina Mi che riconosce wi ! Ld
- se wi ! Ld allora Mi accetta wi pertanto per
definizione di Ld wi non è in Ld poiché Ld contiene
solo stringhe wj tale che Mj non accetta wj
- se wi ! Ld allora Mi non accetta wi pertanto per
definizione di Ld wi è in Ld
Evidentemente si ha contraddizione poiché wi non può essere o non essere in Ld
Riducibilita’
Un problema decisionale P si dice Turing riducibile a un problema P’ se c’è una macchina di
Turing che presa qualsiasi istanza p ! P come input produce un associata istanza p’ ! P’ in cui la
soluzione di p può essere ricavata dalla soluzione di p’.
Risultato
Input
pi ! P
Riduzione di
P a P'
p'i ! P'
Algoritmo
per P'
Yes/not
Teorema
- Se un problema decisionale P è indecidibile, e P è riducibile a P’, allora è indecidibile
! anche il problema P’
- Se un problema decisionale P è non ricorsivamente enumerabile, e P è riducibile a P’,
! allora il problema P’ non è ricorsivamente enumerabile.
Teorema di Rice
TEOREMA (Rice) :Ogni proprietà non banale dei linguaggi ricorsivamente enumerabili è
!!
indecidibile
In altre parole è impossibile riconoscere per mezzo di una MT le stringhe binarie che rappresentano
codici di una MT il cui linguaggio soddisfa la proprietà.
[Una proprietà individua un sottoinsieme dei linguaggi Ricorsivamente enumerabili]
Esempio: “essere un linguaggio Contex-free”.
La proprietà essere liberi dal contesto individua tutti i linguaggi liberi dal contesto all’interno
della classe dei linguaggi ricorsivamente enumerabili. Pertanto il teorema di Rice afferma che
non esiste una MT capace di decidere se una MT’ accetti un linguaggio Contex-free .
Def. Una proprietà si dice banale se appartiene a tutti i linguaggi ricorsivamente enumerabili
oppure a nessuno. Altrimenti si dice non banale.
Se P è una proprietà dei linguaggi ricorsivamente enumerabili il linguaggio LP è l’insieme dei codici di
macchine di Turing Mi tali che L(Mi) è un linguaggio in P, ovvero LP = {Mi : L(Mi ) ! P}
per cui quando parliamo di decidibilità di una proprietà P si intende la decidibilità del linguaggio LP .
[In altre parole si pone attenzione al riconoscimento delle MT che accettano quei linguaggi.]
Il Teorema di Rice dice in sostanza che non è decidibile poter individuare un sottoinsieme proprio
dei linguaggi ricorsivamente enumerabili.
Teorema di Rice
Sia P una proprietà non banale, allora deve esistere un linguaggio L!RE che abbia la
proprietà P. Sia ML la macchina che accetta L.
La dimostrazione verrà fatta riducendo il linguaggio LH , linguaggio della macchina
universale, al linguaggio Lp .
w
M
Accetta
start
x
Accetta
Accetta
ML
M’
L’input della riduzione è la coppia (M,w), l’output è la macchina M’ tale che L(M’) = # se
M non accetta w, L(M’) = L se M accetta w.
- M’ simula M su w comportandosi perciò come la macchina Universale. Si osservi che w
non è l’input alla macchina M’.
- Se M non accetta w allora M’ non fa niente e quindi M’ non accetta nessuna stringa in
input e quindi L(M’)= #. Poiché assumiamo che # $ P ciò significa che il codice di M’ non è in LP
- Se M accetta w allora M’ comincia a simulare ML sul proprio input x per cui siccome L!P
il codice di M’ è in LP
Dato che l’algoritmo di riduzione trasforma l’istanza (M,w) in una macchina M’ che è in LP
se e solo se (M,w) è in LH , dalla indecidibilità di LH segue l’indecidibilità di LP
Alcune Conseguenze del Teorema di Rice
Nell’ambito della programmazione.
E’ indecidibile
-La decidibilità di ogni problema P (halting Problem)
- Dire se un dato programma C va in ciclo infinito su un certo ingresso o termini la sua esecuzine
[quindi l’impossibilità di definire un perfetto sistema di debugging]
- Dire se due programmi C producano lo stesso risultato in corrispondenza degli stessi dati di ingresso.
[quindi l’impossibilità di definire un programma che controlli la correttezza dei programmi, pertanto
siamo costretti ad usare le tecniche di testing per la verifica degli errori in un programma]
Nell’ambito dei linguaggi
E’ indecidibile
- Data una grammatica context-free dire se L(G) = VT*
- Date due grammatiche context-free G1 e G2 dire se L(G1) = L(G2)
- Dati due automi Pushdown dire se accettano precisamente lo stesso linguaggio.
- Il linguaggio accettato da una MT contiene la stringa aabb?
- Il linguaggio accettato da una MT contiene tutti i numeri pari?
.............. .
Perché ci sono tanti problemi indecidibili?
Abbiamo fatto l’assunto che risolvere un problema significhi verificare l’appartenenza di una
stringa ad un linguaggio.
L’insieme dei linguaggi non è enumerabile (Teorema di Cantor)
L’insieme dei programmi è enumerabile (data l’enumerabilità delle Macchine di Turing)
Se ne deduce che ci sono infinitamente meno programmi che problemi.
Il motivo per cui sembra che la maggior parte dei problemi sia decidibile è perché focalizziamo
l’attenzione su problemi semplici e strutturati.
Complessità computazionale di una MT
Data una Macchina di Turing deterministica M si definisce complessità in tempo di M la
funzione tM : N % N tale che tM (n) è il massimo numero di transizioni processate da una
computazione di M su una stringa di dimensione n.
Data una Macchina di Turing non deterministica si definisce la complessità di una
computazione tM (n) come il massimo numero di transizioni effettuate per ogni possibile scelta
di transizioni su una stringa di ingresso di lunghezza n.