CRISI DELLA FISICA CLASSICA
Sono sostanzialmente fenomeni sperimentali di interazione radiazione - materia che mettono in
crisi l'apparato teorico classico non solo rimanendo senza spiegazione, ma a volte anche
contraddicendo le certezze della fisica prequantistica.
Analizzeremo dettagliatamente i seguenti fenomeni:
•
Emissione di corpo nero
•
Effetto fotoelettrico
Emissione di corpo nero
Per definizione, un corpo nero ideale è un corpo in grado di assorbire tutta la radiazione su di esso
incidente. Buoni corpi neri sono per esempio il velluto nero o il nerofumo, ma la realizzazione
sperimentale più efficace per riprodurre tale proprietà, è
quella di una cavità con un piccolo foro.
Infatti, quando la radiazione luminosa entra dal foro,
verrà riflessa moltissime volte dalle pareti essendo
parzialmente assorbita ad ogni riflessione. La probabilità
che il raggio possa uscire di nuovo dal foro prima che la
radiazione sia tutta assorbita, è molto bassa; si dirà quindi
che la radiazione è intrappolata entro la cavità e che tale
dispositivo realizza un corpo nero ideale. In condizioni di
equilibrio, le pareti della cavità emettono radiazione in
quantità pari a quella assorbita; analizzando allora la
radiazione emessa dal foro si ottengono i seguenti
risultati:
2.1
la potenza per unità di area R irraggiata da un corpo nero è proporzionale alla temperatura
attraverso la relazione:
R = σ ⋅T 4
2.2
con σ = 5,6703 ⋅ 10 −8
W
m2K 4
(legge di Stefan - Boltzmann 1879)
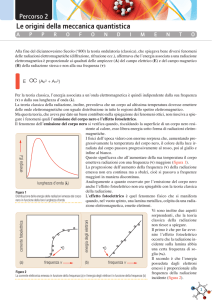
Detta R (λ ) la potenza per unità di area emessa sulla lunghezza d'onda λ , otteniamo
la distribuzione spettrale della radiazione di corpo nero alle varie temperature, riportando su
un grafico l'andamento di
R (λ
)
in
funzione di λ . Osserviamo che il
massimo della curva è funzione della
temperatura. Precisamente, se λm é la
lunghezza
d'onda
d'irraggiamento
massimo, avremo:
λ m ⋅ T = cos tan te = 2,898 ⋅ 10 −3 m ⋅ K
(legge dello spostamento di Wien)
Il limite della fisica classica:
Secondo le leggi della fisica classica doveva essere possibile dedurre le curve della figura sopra
ipotizzando che gli atomi della superficie interna della cavità si comportassero come piccole
antenne capaci di assorbire e riemettere la radiazione elettromagnetica. Il problema non
presentava, tra l’altro, nessuna particolare difficoltà di ordine matematico. Una volta eseguiti i
calcoli, si raggiunse il risultato che al diminuire della lunghezza d’onda λ
la potenza di radiazione R (λ ) aumentava e tale previsione era rappresentabile con una linea
come quella nella figura sottostante
Siccome l’area racchiusa tra le curve e l’asse delle ascisse rappresenta l’energia totale emessa
dalla cavità, nel caso della previsione classica (linea rossa) l’area racchiusa, e quindi l’energia
emessa, è infinita.
Superamento della difficoltà grazie al contributo di Planck
Max Planck rifece il calcolo ipotizzando che lo scambio di energia tra la radiazione e gli atomi della
cavità avvenisse non in modo continuo ma attraverso “pacchetti” di energia, da lui stesso chiamati
quanti . In tal modo l’energia scambiabile era in quantità multiple di hf dove h è una costante detta
di Planck e f è la frequenza della radiazione. In altre parole si poteva scambiare energia solo se
questa era nelle quantità E= nhf, con n numero intero positivo. In base a queste ipotesi Planck
trasse delle deduzioni teoriche che erano perfettamente in linea con i dati sperimentali.
Effetto fotoelettrico
Viene scoperto casualmente da Hertz nel 1887 e consiste in pratica nell'emissione di elettroni
da parte di una superficie metallica quando è illuminata con radiazione monocromatica di una certa
frequenza. Ben presto si dispone dì una notevole quantità di dati che devono essere interpretati
secondo la teoria classica dell'elettromagnetismo: La disposizione sperimentale per osservare
l'effetto fotoelettrico è molto semplice:
I due piatti metallici sono posti entro un tubo in cui è stato fatto il vuoto. Senza differenza di
potenziale, illuminando uno dei due piatti, si osserva passaggio di corrente. Questo significa che la
radiazione elettromagnetica scalza gli elettroni dal metallo (gli elettroni assorbono la radiazione e
quindi acquisiscono energia fino a liberarsi dai legami con il nucleo). Mettendo poi una differenza
di potenziale V si ottiene una accelerazione degli elettroni. Vediamo in dettaglio le caratteristiche di
questa emissione in una situazione sperimentale:
∆VA
A. Aumentando l'intensità della radiazione luminosa aumenta l’emissione degli elettroni e
quindi la corrente misurata dall’amperometro (galvanometro) dove E0 2E0 sono le intensità
della radiazione (irradiamento) incidente.
B. Se aumentiamo la differenza di potenziale aumenta l’intensità di corrente fino ad arrivare
ad una corrente di saturazione (l'aumento ulteriore della differenza di potenziale non
produce più sensibili variazioni di corrente). Se la differenza di potenziale viene invertita gli
elettroni vengono decelerati e regolando opportunamente tale differenza di potenziale si
può raggiungere l’arresto del flusso di elettroni. Tale valore di d.d.p. viene detto potenziale
di arresto ∆VA. Come si vede dalla figura il potenziale di arresto ∆VA non dipende
dall’irradiamento. Esso è lo stesso sia che con intensità di radiazione E0 che 2E0.
C. Gli esperimenti mostrano poi che utilizzando luce (radiazione) con diversa lunghezza
d’onda varia il potenziale di arresto ∆VA e che al di sopra di una certa lunghezza d’onda
λmax l’effetto fotoelettrico di estrazione degli elettroni non si verifica affatto: cioè gli
elettroni pur essendo colpiti dalla luce non si liberano dal nucleo.
L'effetto fotoelettrico é allora spiegato ammettendo che la radiazione elettromagnetica ceda
energia agli elettroni del metallo che colpisce. Quando questi elettroni. accumulano energia
sufficiente ad uguagliare il lavoro di estrazione del metallo, lasciano la targhetta generando la
corrente fotoelettrica.
1
2
m ⋅ v max
= e ⋅VA
2
Il limite della fisica classica:
La fisica classica manifesta le seguenti difficoltà:
A. Se una luce debole (cioè con grande lunghezza d’onda e quindi scarsa energia) investe gli
elettroni, basterebbe soltanto aspettare un tempo sufficientemente lungo per consentire
all’elettrone di fare il “pieno” di energia sufficiente per liberarsi dal nucleo. Nella realtà ciò
non avviene: se la lunghezza d’onda è superiore a λmax nessun elettrone viene rilasciato
pur aspettando un tempo lunghissimo.
B. In secondo luogo il valore dell’energia cinetica massima (e quindi del potenziale di arresto
∆VA) dovrebbe crescere in modo lineare all’aumentare dell’irradiamento, ma ciò non accade.
Nel 1905 A. Einstein risolse il problema dell’effetto fotoelettrico ribaltando radicalmente
l’interpretazione della luce che si era affermata con Maxwell: in sostanza egli adottò l’idea dei
quanti di Planck e la estese fino alle estreme conseguenze: Planck aveva parlato di pacchetti di
energia soltanto riferendosi allo scambio di questa tra la radiazione e gli atomi della cavità nota
come corpo nero, continuando a considerare, invece, nel seno classico, la radiazione
elettromagnetica. Einstein riteneva che è necessario supporre che la luce stessa (la radiazione
elettromagnetica) sia composta da singoli pacchetti di energia, i quanti del campo
elettromagnetico, che successivamente furono chiamati fotoni. Ogni fotone ha massa nulla e
porta una energia E che è direttamente proporzionale alla sua frequenza f e la costante di
proporzionalità è ancora la costante di Planck. Si ha così che l’energia di un fotone di frequenza
f vale E=hf.
L’effetto fotoelettrico si spiega se si ammette l’interazione tra un singolo fotone e un singolo
elettrone. In tal caso l’elettrone potrà uscire dal metallo solo se l’energia del fotone che lo
“colpisce” è almeno uguale al lavoro di “estrazione” We cioè uguale all’energia che occorre
spendere per estrarre l’elettrone. Ma essendo E=hf deve essere hf ≥ We da cui
f ≥ We/h ecco allora che esiste una frequenza minima fmin= We/h a cui corrisponde una
lunghezza d’onda λmax al di sotto della quale non si ha l’effetto fotoelettrico (la frequenza f =
velocità/lunghezza d’onda, quindi f=c/λ
λ). Ecco superata la difficoltà A della fisica classica
Un elettrone che assorbe un fotone di energia E=hf non è costretto a dissipare energia come
farebbe urtando invece un’altra particella (il fotone ha massa ZERO) ed esce dal metallo con
energia cinetica massima
Kmax = hf - We
L’energia con cui l’elettrone emerge dal metallo è pari alla differenza tra l’energia assorbita dal
fotone e l’energia spesa per vincere il legame con il nucleo. Rileggendo la formula appena ora
scritta si deduce che Kmax dipende dalla frequenza, ma non dall’irradiamento cioè non dipende
dal numero di fotoni che nell’unità di tempo colpiscono il metallo