SECONDA PROVA IN ITINERE DI “MATEMATICA DISCRETA E LOGICA”
appello unico del 27.5.2016
SOLUZIONI
FILA “B”
Esercizio 1
Fra i dieci miliardi di numeri naturali compresi fra " e "! !!! !!! !!! quanti sono quelli nella
cui scrittura (in base dieci) non appare né la cifra “"” né la cifra “#”?
Si motivi la risposta.
Soluzione Consideriamo in primo luogo, anziché quelli proposti, i dieci miliardi di
numeri naturali compresi fra ! ( œ ! !!! !!! !!!) e * *** *** *** . Fra essi, quelli in cui non
appare né la cifra “"” né la cifra “#” si formano scegliendo ciascuna delle dieci cifre (incluse
eventuali cifre “!” iniziali per quelli minori di un miliardo) nell’insieme
{!, $, %, &, ', (, ), *}
e quindi sono in tutto )"! (disposizioni con ripetizione di ) oggetti a dieci a dieci) . Nel
problema proposto si considera un diverso insieme di numeri naturali, che però differisce dal
precedente soltanto perché ha in più il numero "! !!! !!! !!! (ma esso non soddisfa le
condizioni del problema) ed ha in meno il numero ! (che invece soddisfa le condizioni del
problema. Dunque la risposta al problema proposto è
)"! " .
(Si noti che le cifre “!” iniziali, che noi abbiamo considerato ma non esistono
nell’usuale scrittura decimale dei numeri naturali, risultano irrilevanti perché diverse sia dalla
cifra “"” che dalla cifra “#”).
Esercizio 2
Una compagnia ferroviaria vende viaggi in modalità “ticketless”, cioè all’atto del pagamento
consegna al viaggiatore un codice alfanumerico che gli permetterà di percorrere la tratta
desiderata partendo il giorno e all’ora concordati.
Si dica, motivando la risposta, quanti sono i possibili codici alfanumerici sapendo che
ciascuno di essi deve rispettare tutte le seguenti condizioni:
deve consistere di "# caratteri;
esattamente ( caratteri devono essere lettere scelte fra le #' dell’alfabeto inglese,
anche ripetute ma disposte in ordine alfabetico;
i restanti & caratteri devono essere cifre scelte fra le usuali dieci (da “!” a “*”) tutte
distinte fra loro.
"#†""†"!†*†)
‰
Soluzione La posizione delle ( lettere può essere scelta in ˆ "#
œ (*#
( œ
&†%†$†#
#'("
$#†$"†$!†#*†#)†#(†#'
modi. Le ( lettere possono essere scelte in ˆ ( ‰ œ
œ $ $'& )&' modi. Le
(†'†&†%†$†#
& cifre (la cui posizione è determinata da quella delle ( lettere) possono essere scelte in
"! † * † ) † ( † ' œ $! #%! modi. Applicando il principio di moltiplicazione, si trova dunque che
i possibili codici alfanumerici che rispettano le condizioni date sono in tutto
(*# † $ $'& )&' † $! #%! œ )! '"# &#! %') %8! .
Esercizio 3
Si dimostri che: comunque si scelgano #" numeri interi positivi non superiori a %!, esistono
due fra i numeri scelti che sono uno multiplo dell’altro.
Si scelgano poi #! numeri interi positivi non superiori a %! in modo che comunque presi due
di essi nessuno dei due sia multiplo dell’altro.
Soluzione Per il teorema fondamentale dell’aritmetica, ogni numero intero positivo
si scrive in uno e un solo modo nella forma #5 . con . dispari. Se il numero non è superiore a
4!, . è uno fra i #! numeri interi positivi dispari minori di %!; se predisponiamo #! “scatole”
etichettate con quei #! possibili valori di . e vi distribuiamo i #" numeri scelti secondo il
valore di . , per il principio dei buchi di piccionaia almeno una scatola contiene almeno due
numeri; essi sono della forma #5 .! e #2 .! per lo stesso numero dispari .! . Se 5 2 , #5 .!
divide #2 .! ; se invece 2 5 , #2 .! divide #5 .! (non può essere 2 œ 5 perché i due numeri
sono diversi fra loro).
Infine, i #! numeri interi positivi compresi tra #" e %! sono tali che comunque presi
due di essi nessuno dei due è multiplo dell’altro.
Esercizio 4
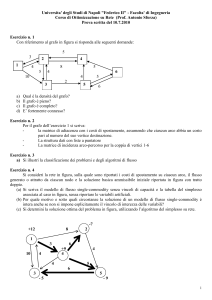
Si dica, motivando la risposta, se il grafo
disegnato qui a fianco (che ha ") lati e *
vertici) è un grafo piano.
Soluzione Si vede subito che il grafo è una suddivisione (ottenuta “inserendo” i tre
vertici di grado #) del grafo ^6 , che contiene un sottografo isomorfo a ^& . Dunque il grafo
non è piano per il teorema di Kuratowski.
Esercizio 5
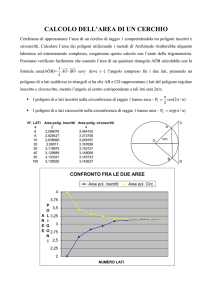
Sia Z il grafo disegnato qui di seguito, che ha 18 lati e "3 vertici. Si dica, motivando la
risposta,
( 3)
se Z è un grafo euleriano;
(33)
se in Z esiste un cammino euleriano;
(333) se Z è hamiltoniano.
Soluzione Poiché Z ha "! vertici di grado $, Z non è euleriano e nemmeno possiede
un cammino euleriano.
Per verificare se Z è hamiltoniano, poiché è disegnato nel piano senza sovrapposizione
di lati possiamo cercare di applicare il teorema di Grinberg. Supponiamo che in Z esista un
ciclo hamiltoniano V! Þ Z ha $ facce col bordo formato da % lati e % facce col bordo formato da
' lati. Detti
/% il numero delle facce di Z esterne a V! col bordo formato da % lati;
/' il numero delle facce di Z esterne a V! col bordo formato da ' lati;
3% il numero delle facce di Z esterne a V! col bordo formato da % lati;
3' il numero delle facce di Z esterne a V! col bordo formato da ' lati
per il teorema di Grinberg dovrebbe essere
#(/% 3% ) %(/' 3' ) œ !
ossia (poiché /% œ $ 3% e /' œ % 3' )
#($ #3% ) %(% #3' ) œ !
da cui
$ #3% 2(% #3' ) œ !
e infine
$ œ #( 3 % 3 ' % )
assurdo perché il primo membro è dispari mentre il secondo membro è pari. Dunque in Z non
può esistere un ciclo hamiltoniano, e quindi Z non è hamiltoniano.
Esercizio 6
Si stabilisca, motivando la risposta, se
(bB)(P(B) ” Q(B)) • (aB)(Q(B) Ä P(B)) } (bC )P(C ) .
Soluzione La formula (bC )P(C ) è conseguenza logica della formula
(bB)(P(B) ” Q(B)) • (aB)(Q(B) Ä P(B))
se e soltanto se la formula
(bB)(P(B) ” Q(B)) • (aB)(Q(B) Ä P(B)) • c(bC )P(C )
non è soddisfacibile. Scriviamo dunque quest’ultima in forma normale prenessa (in modo che
la parte senza quantificatori sia in forma normale congiuntiva), trasformiamola poi in forma di
Skolem e infine riduciamola in un insieme di clausole.
Ricordando che
(bB)(P(B) ” Q(B)) ´ (bC )(P(C ) ” Q(C ))
che
Q(B) Ä P(B) ´ cQ(B) ” P(B)
e che
c(bC )P(C ) ´ (aC )cP(C ) ´ (aB)cP(B)
si trova che
(bB)(P(B) ” Q(B)) • (aB)(Q(B) Ä P(B)) • c(bC )P(C ) ´
´ (bC )(P(C) ” Q(C )) • (aB)(cQ(B) ” P(B)) • (aB)cP(B) ´
´ (bC )a(P(C ) ” Q(C )) • (aB)(cQ(B) ” P(B)) • (aB)cP(B)b ´
´ (bC )(aB)a(P(C ) ” Q(C )) • (cQ(B) ” P(B)) • cP(B)b
che si skolemizza introducendo una costante - per la quale diviene
(aB)a(P(- ) ” Q(- )) • (cQ(B) ” P(B)) • cP(B)b .
Questa formula ha un universo di Herbrandt che consiste nel solo simbolo di costante - , e
quindi è insoddisfacibile se e soltanto se lo è il seguente insieme di clausole:
{{P(- ), Q(- )}, {cQ(- ), P(- )}, {cP(- )}} .
Possiamo applicare l’algoritmo di Davis e Putnam!
Con pivot P(- ) si trova l’insieme di clausole
{{Q(- )}, {cQ(- )}}
e con pivot Q(- ) si trova l’insieme che consiste della sola clausola vuota. Dunque l’insieme di
clausole considerato è insoddisfacibile, cosicché la formula
(bB)(P(B) ” Q(B)) • (aB)(Q(B) Ä P(B)) • c(bC )P(C )
è insoddisfacibile e la formula (bC )P(C ) è effettivamenteconseguenza logica della formula
(bB)(P(B) ” Q(B)) • (aB)(Q(B) Ä P(B)) .
Esercizio 7
Si stabilisca se dalle premesse
( 3)
(33)
(333)
Ogni maschio è castano;
ogni castano è balbuziente;
non ogni balbuziente è maschio;
si può dedurre logicamente che
(3@)
c’è almeno un balbuziente che non è castano.
Soluzione Scegliamo un linguaggio della logica dei predicati con opportuni simboli
di predicato:
M(B) traduce “B è un maschio”;
C(B) traduce “B è castano”;
B(B) traduce “B è balbuziente”.
Posto
! ³ (aB)(M(B) Ä C(B)) ;
" ³ (aB)(C(B) Ä B(B) ;
# ³ c(aB)(B(B) Ä M(B)) ;
$ ³ (bB)(B(B) • cC(B)) ;
dobbiamo dimostrare che
{! , " , # } } $
ossia che
! • " • # • (c$ )
non è soddisfacibile.
Scriviamo dunque quest’ultima formula in forma normale prenessa (in modo che la parte
senza quantificatori sia in forma normale congiuntiva), trasformiamola poi in forma di Skolem
e infine riduciamola in un insieme di clausole.
Ricordando che
M(B) Ä C(B) ´ cM(B) ” C(B)
che analogamente
C(B) Ä B(B) ´ cC(B) ” B(B)
mentre
c(aB)(B(B) Ä M(B)) ´ (bB)c(B(B) Ä M(B)) ´ (bB)(B(B) • cM(B)) ´ (bC )(B(C ) • cM(C ))
e che infine
c(bB)(B(B) • cC(B)) ´ (aB)c(B(B) • cC(B)) ´ (aB)(cB(B) ” C(B))
si trova che
! • " • # • (c$ ) ´
´ (aB)(cM(B) ” C(B)) • (aB)(cC(B) ” B(B)) • (bC )(B(C ) • cM(C )) • (aB)(cB(B) ” C(B)) ´
´ (bC )a(aB)(cM(B) ” C(B)) • (aB)(cC(B) ” B(B)) • B(C ) • cM(C ) • (aB)(cB(B) ” C(B))b ´
´ (bC )(aB)a(cM(B) ” C(B)) • (cC(B) ” B(B)) • B(C ) • cM(C ) • (cB(B) ” C(B))b
che si skolemizza introducendo una costante - per la quale diviene
(aB)a(cM(B) ” C(B)) • (cC(B) ” B(B)) • B(c) • cM(c) • (cB(B) ” C(B))b .
Questa formula ha un universo di Herbrandt che consiste nel solo simbolo di costante - , e
quindi è insoddisfacibile se e soltanto se lo è il seguente insieme di clausole:
{{cM(- ), C(- )}, {cC(- ), B(- )}, {B(- )}, {cM(- )}, {cB(- ), C(- )}} .
Possiamo applicare l’algoritmo di Davis e Putnam!
Con pivot B(- ) si trova l’insieme di clausole
{{cM(- ), C(- )}, {C(- )}, {cM(- )}}
che è soddisfacibile se C(- ) è vera, e M(- ) è falsa.
Ad esempio, nell’universo h ³ {7, 0 } nel quale 7 è un maschio castano balbuziente e 0 è
una femmina ( œ non maschioÑ castana balbuziente sono vere le (3), (33) e (333) ma è falsa la
(3@) .