Altri_appunti_sul_piegamento_della_carta File

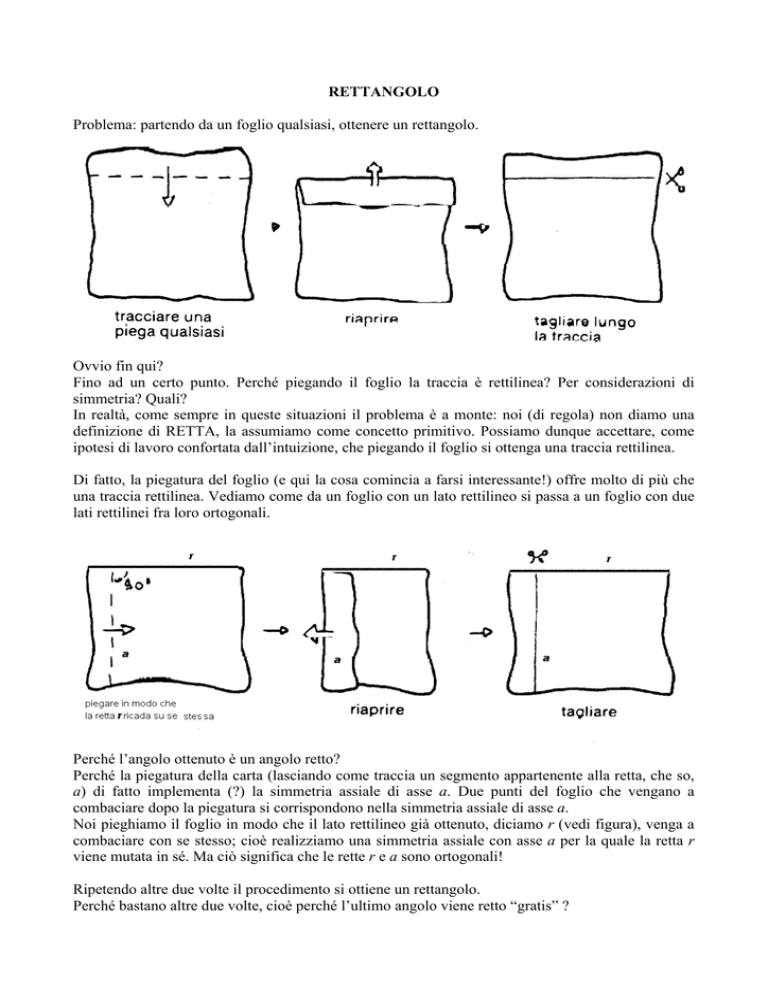
RETTANGOLO
Problema: partendo da un foglio qualsiasi, ottenere un rettangolo.
Ovvio fin qui?
Fino ad un certo punto. Perché piegando il foglio la traccia è rettilinea? Per considerazioni di
simmetria? Quali?
In realtà, come sempre in queste situazioni il problema è a monte: noi (di regola) non diamo una
definizione di RETTA, la assumiamo come concetto primitivo. Possiamo dunque accettare, come
ipotesi di lavoro confortata dall’intuizione, che piegando il foglio si ottenga una traccia rettilinea.
Di fatto, la piegatura del foglio (e qui la cosa comincia a farsi interessante!) offre molto di più che
una traccia rettilinea. Vediamo come da un foglio con un lato rettilineo si passa a un foglio con due
lati rettilinei fra loro ortogonali.
Perché l’angolo ottenuto è un angolo retto?
Perché la piegatura della carta (lasciando come traccia un segmento appartenente alla retta, che so,
a) di fatto implementa (?) la simmetria assiale di asse a. Due punti del foglio che vengano a
combaciare dopo la piegatura si corrispondono nella simmetria assiale di asse a.
Noi pieghiamo il foglio in modo che il lato rettilineo già ottenuto, diciamo r (vedi figura), venga a
combaciare con se stesso; cioè realizziamo una simmetria assiale con asse a per la quale la retta r
viene mutata in sé. Ma ciò significa che le rette r e a sono ortogonali!
Ripetendo altre due volte il procedimento si ottiene un rettangolo.
Perché bastano altre due volte, cioè perché l’ultimo angolo viene retto “gratis” ?
QUADRATO
Problema: partendo da un foglio rettangolare, ottenere un quadrato.
La piegatura, come si è già osservato, realizza una simmetria assiale. Qui sfruttiamo il fatto che
ogni simmetria assiale è una isometria, quindi conserva le misure sia dei segmenti sia degli angoli.
La piegatura porta il segmento PQ nel segmento tratteggiato, il quale
(1) è ortogonale al lato b (perché l’angolo retto con vertice in P viene trasformato dalla nostra
simmetria assiale in un angolo retto!) e dunque
(2) è parallelo al lato a, e pertanto
(3) divide il rettangolo di partenza in due rettangoli, cosicché
(4) ha la stessa lunghezza del lato a. Infatti in un rettangolo lati opposti hanno la stessa lunghezza.
Ma allora PQ, che nella simmetria assiale realizzata dalla piegatura viene trasformato nel segmento
tratteggiato, ha anch’esso la stessa lunghezza del lato a. Pertanto il rettangolo superiore ottenuto
tagliando lungo il segmento tratteggiato ha due lati consecutivi uguali, e dunque è un quadrato
(perché?).
Vale la pena di soffermarsi a notare come si individua in pratica quello che ho chiamato “segmento
tratteggiato”. Esso è individuato chiaramente al momento della piegatura, ma dopo aver riaperto il
foglio resta traccia soltanto del punto Q. Quel che si fa adesso è piegare nel punto Q in modo da
portare il lato opposto al lato b a ricadere su se stesso; si realizza cioè una simmetria assiale che
muta in se quel lato; l’asse di simmetria pertanto è (la retta passante per Q e) ortogonale a quel lato.
Siccome avevamo osservato che il “segmento tratteggiato” (passa per Q ed) è ortogonale al lato b (e
quindi al suo opposto), l’asse di questa simmetria individua proprio il “segmento tratteggiato”.
TRIANGOLO EQUILATERO
Problema: partendo da un foglio quadrato, ottenere un triangolo equilatero.
Per la simmetria della costruzione, basta far vedere che l’angolo SOT (cioè SOK) è di 60°. Ossia
che l’angolo KOP è di 30°. Ossia che l’angolo QOP è di 60°: infatti la simmetria assiale realizzata
dalla piega per O porta l’angolo POK nell’angolo QOK, cioè OK è la bisettrice dell’angolo QOP.
Dunque basta far vedere che l’angolo QOP, cioè QOM, è di 60°.
Consideriamo il triangolo QOM. Esso è rettangolo perché QM è per costruzione ortogonale a OP.
Inoltre l’ipotenusa OQ è uguale al lato del quadrato di partenza, quindi è il doppio (sempre per
costruzione di M) del cateto OM. E dunque l’angolo QOM è di 60°.
Questa costruzione, vista così, non è soddisfacente. Infatti prima si fanno le pieghe senza capire
perché, poi si spiega che tutto funziona.
Bisognerebbe trovare un approccio più intuitivo…
DIVIDERE UN SEGMENTO IN n PARTI UGUALI
Problema: partendo da un foglio rettangolare, dividere uno dei suoi lati in n parti uguali.
Osservazione: sappiamo farlo se n=2:
Infatti la piegatura realizza una simmetria assiale, che è una isometria, che porta A in B e lascia
fermo M. Dunque AM viene trasformato in MB e quindi i due segmenti sono uguali.
Ma allora sappiamo farlo anche se n = 4, se n = 8, se n è qualsiasi potenza di 2: basta ripetere il
procedimento per ciascuno dei sottorettangoli ottenuti.
OSSERVAZIONE IMPORTANTE: le rette che si tracciano con queste piegature sono tutte
ortogonali al lato AB, perché sono assi di simmetrie assiali che mutano in sé il lato AB; e dunque
sono tutte parallele fra loro.
Supponiamo ora che n NON sia una potenza di 2. C’è però certamente una potenza di 2 più grande
di n. (Perché?)
Sia 2k questa potenza di 2. Prendiamo il nostro foglio rettangolare, e dividiamo in 2k parti uguali il
lato che NON ci interessa.
Possiamo “tagliar via” (o trascurare in altro modo, ad esempio ripiegando opportunamente il foglio)
le parti in eccesso rispetto a n, che sono 2k-n. Adesso abbiamo un foglio rettangolare in cui
- uno dei lati è quello che vogliamo dividere in n parti uguali
- il lato adiacente è diviso già in n parti uguali
Il nostro foglio rettangolare, per capirsi, è dunque più corto di quello di partenza. Il nostro problema
adesso è: come “trasferire” la suddivisione in n parti uguali del lato che NON ci interessa sul lato
che invece ci interessa?
Si usa il teorema di Talete.
Pieghiamo il foglio secondo la retta che unisce due vertici opposti (AB nel disegno qua sotto). La
traccia della piegatura individua i punti di intersezione con le rette già tracciate, che dividono in n
parti uguali il lato NON interessante. Per il teorema di Talete, questi n-1 punti dividono anche il
segmento AB in n parti uguali.
Ora, per ciascuno di questi n-1 punti pieghiamo la carta in modo da portare su se stesso il lato che
vogliamo dividere: si ottengono le n-1 rette tratteggiate che si vedono in figura.
Queste rette “tratteggiate” sono tutte ortogonali al lato che vogliamo dividere, e quindi sono tutte
parallele fra loro.
Ancora per il teorema di Talete, il lato che ci interessa viene diviso in n parti uguali.
Osservazione: anche questa costruzione viene “offerta”, ma mi sembra meno brutale di quella del
triangolo equilatero...
Marco Barlotti

appunti sulla geometria del piegamento della carta

vers. 0.1
2.5 - La trisezione dell’angolo.
Mostriamo (e giustifichiamo) un semplice algoritmo (attribuito a H. Abe) per trisecare
un angolo acuto. Osserviamo subito che il requisito che l’angolo sia acuto non è una effettiva
limitazione, perché ogni angolo ottuso è il doppio di un angolo acuto (e ogni angolo concavo è
il doppio di un angolo ottuso), e sono ben noti gli algoritmi per bisecare e raddoppiare un
angolo.
Sia ! l’angolo da trisecare, individuato da due semirette < e = che hanno in comune
l’origine B. Supporremo che il segmento iniziale del primo lato dell’angolo coincida con un
lato di un foglio di carta rettangolare (del quale dunque B è un vertice). “Prepariamo” il nostro
foglio di carta effettuando due pieghe parallele alla semiretta < equidistanti fra loro e dalla
retta di <: ciò significa che i punti B, D, E in cui il primo lato del foglio e le due pieghe
effettuate incontrano l’altro lato del foglio passante per B sono tali che BD œ BE, come nella
figura:
Pieghiamo il foglio lungo una retta ON scelta in modo che la piegatura porti il punto B
sulla retta j" (indichiamo con B" l’immagine di B per effetto della piegatura) e porti anche il
punto E sul secondo lato dell’angolo da trisecare (cioè sulla semiretta = ; indichiamo con E"
l’immagine di E per effetto della piegatura). Nel seguito indicheremo con 5 la simmetria
assiale (di asse ON) indotta da questa piegatura.
Sia K œ ON  j" il punto in cui la piega incontra la retta j" .
Marco Barlotti

appunti sulla geometria del piegamento della carta

vers. 0.1
w
Pieghiamo ancora il foglio lungo l’immagine (che nel disegno è indicata con j" ) della
retta j" per effetto della piegatura: si ottiene la semiretta (di origine K) che nel disegno è
indicata con >. Riapriamo l’ultima piega e pieghiamo adesso lungo la retta KB" (in modo da
evidenziare, una volta riaperto completamente il foglio, il segmento KB). Riapriamo infine
tutte le pieghe. Vogliamo dimostrare che:
( 3)
i punti B, K, D" sono allineati sulla retta di > ;
(33)
la semiretta BK divide l’angolo ! in due angoli E" BK e KBN tali che
E" BK œ "# KBN e quindi E" BK è un terzo dell’angolo !.
Per provare la (3), osserviamo che 5 porta B in B" , D in D" e lascia fermi H e K:
dunque 5 porta l’angolo BKD nell’angolo B" KD" e porta l’angolo DKH nell’angolo D" KH,
cosicché
BKD" œ BKD  DKD" œ B" KD"  DKD" œ DKB" œ +81969 :3+>>9
e dunque i punti B, K, D" sono allineati, come si voleva dimostrare.
Per provare la (33), osserviamo che 5 porta D in D" e lascia fermo K: poiché (per
costruzione) la retta KD è ortogonale alla retta OB, ne segue che la retta KD" è ortogonale alla
retta OB" , cosicché BD" è l’altezza del triangolo BB" E. Inoltre 5 porta ED in E" D" e BD in
B" D" ; poiché ED œ BD, è anche E" D" œ B" D" , dunque BD" è anche mediana del triangolo
BB" E" . Ne segue che il triangolo BB" E" è isoscele sulla base B" E" e quindi BD" è bisettrice
dell’angolo al vertice, ossia
E" BD" œ D" BB" .
D’altro lato, D" BB" œ BB" N (perché sono angoli alterni interni rispetto alle parallele
KD" e NB" (1) tagliate dalla trasversale BB" ) e BB" N œ B" BN perché 5 porta B in B" e lascia
fermi M e N.
Quindi E" BD" œ D" BB" œ B" BN come si voleva dimostrare.
1Le
rette KD" e NB" sono parallele perché immagine mediante 5 delle rette parallele j" e < .
Marco Barlotti

appunti sulla geometria del piegamento della carta

vers. 0.1
2.6 - La duplicazione del cubo.
Questo algoritmo (dovuto a Peter Messer nel 1986) determina un punto P! su un lato
AB del foglio quadrato di carta ABCD in modo che il rapporto tra AP! e P! B sia la radice
terza di #.
“Prepariamo” il nostro foglio quadrato effettuando due pieghe j" e j# che dividano il
lato AB in tre parti uguali. Detto C" il punto in cui la piega j# più vicina al vertice C incontra
il lato CD del foglio, effettuiamo la piega che porta C sul lato AB e C" sulla piega j" : sia P!
l’immagine di C per effetto di questa piega. Vogliamo dimostrare che il rapporto tra AP! e
P! B è la radice terza di #.
Per semplificare i calcoli, scegliamo P! B come unità di misura e indichiamo con B la
lunghezza di AP! . Dobbiamo provare che B$ œ # .

Marco Barlotti
appunti sulla geometria del piegamento della carta
Ognuna delle tre parti in cui è diviso il lato del quadrato misura

B"
$
vers. 0.1
.
Gli angoli BHP! e SP! T sono congruenti perché entrambi complementari dell’angolo
BP! H, dunque i triangoli rettangoli SP! T e BP! H sono simili. Indichiamo con C la lunghezza
del segmento BH. Allora P! H œ B  "  C .
Si ha
P! H
P! T
œ
BH
P! S
ossia
B"C
B"
$
œ
C
B
cioè
B"
$
B"C
B"
œ
C
2B1
.
Ciò equivale a
(#B  ")(B  "  C) œ C (B  ")
ovvero
#B#  #B  #BC  B  "  C œ BC  C
cioè
#B#  B  " œ $BC
ossia
Cœ
#B# B"
$B
D’altro lato C può essere ricavato applicando il teorema di Pitagora al triangolo
rettangolo BP! H . Si trova che deve essere
"  C # œ (B  "  C )#
ossia
"  C# œ B#  1  C #  #B  #BC  #C
cioè
! œ B#  #B  #BC  #C
da cui
Cœ
B# #B
#B#
.
Allora
#B# B"
$B
œ
B# #B
#B#
ovvero
(#B  #)(#B#  B  ") œ $B(B#  #B)
cioè
%B$  #B#  #B  %B#  #B  # œ $B$  'B#
e infine
B$ œ #
come si voleva.