Dispensa di STATISTICA DESCRITTIVA

UNIVERSITÀ DEGLI STUDI DI BARI
FACOLTÀ DI SCIENZE MM.FF.NN
Dispensa di
STATISTICA DESCRITTIVA
Modulo di Probabilità e Statistica (corsi A-B)
Laurea Triennale in SCIENZE BIOLOGICHE
Anno Accademico 2010/2011
docente: Prof.ssa Rosa Maria Mininni
1
La statistica descrittiva consiste di una serie di tecniche e metodi per riorganizzare e
manipolare dati al fine di estrapolarne delle informazioni.
1
Tipi di dati e scale di misurazione
Vale la pena fare qualche precisazione circa la natura dell’insieme di osservazioni,
di dati, che si ottengono in seguito ad un campionamento, un censimento o come
risultato di un esperimento.
Per popolazione si intende un collettivo di elementi di qualsiasi tipo (individui, animali, piante, ecc...) che presentino almeno una caratteristica comune e a cui siamo
interessati nella discussione di un determinato problema. In biologia una popolazione
può essere costituita da una specie, un genere; in economia da una classe sociale;
in medicina da un gruppo di sintomi che costituiscono una sindrome o dai pazienti
ricoverati in un reparto ospedaliero.
Generalmente una popolazione è di dimensione finita.
Per variabile si intende una caratteristica della popolazione in studio che può assumere
diversi valori. Schematicamente, esistono due tipi di variabili alle quali sono associati
i dati qualitativi o i dati quantitativi:
- si parla di variabile qualitativa o categoriale quando le osservazioni possono essere
classificate in base a come essa si presenta. Ad esempio, il colore del mantello di
un animale, la forma della foglia di una pianta, la presenza o assenza di una certa
proprietà. In questi casi la variabile non viene misurata quantitativamente, ma
suddivisa in categorie o modalità come, ad esempio, il gruppo sanguigno, lo stato
sociale;
- si parla di variabile quantitativa quando le osservazioni sono valori numerici. Se
la variabile assume solo valori isolati, si definisce variabile discreta come, ad
esempio, il numero di colonie batteriche su una piastra, il numero di piante
germogliate in un terreno coltivato. Anche in questo caso la variabile viene
suddivisa in categorie o modalità. Se invece puó assumere tutti i possibili valori
reali entro un certo intervallo, è detta variabile continua come, ad esempio, il
peso, l’altezza. La suddivisione di una variabile continua avviene per classi.
Per convenzione una variabile viene indicata con le lettere X, Y ,..., mentre i valori
assunti da una singola variabile X vengono indicati con x1 , x2 ,...
La distribuzione di una variabile indica quali valori questa assume e quanto spesso li
assume.
Un campione è una n-pla (n ≥ 1), (x1 , x2 , . . . , xn ), di valori assunti da una data
variabile e misurati su un campione di elementi estratti casualmente dalla popolazione
in studio.
Quando si raccolgono dati su una popolazione, i valori ottenuti si presentano come
un insieme di dati disordinati; perciò sono chiamati dati grezzi. Se non vengono
ordinati in qualche modo, è difficile che possano fornire qualche informazione sulla
distribuzione della variabile di interesse.
2
Esempio 1.1 Si sono rilevate le variabili altezza (X,in cm), peso (Y , in kg), sesso
(U , codificato f=femmina e m=maschio) ed età (Z) per un gruppo di 18 studenti di
un college americano, ottenendo i seguenti dati:
X : 167 158 160 171 176 171 171 173 165
179 170 183 170 171 160 165 189 169
Y :
64
94
62
64
49
95
58
56
85
53
65
63
78
61
62
73
56
65
U:
f
m
f
f
f
m
f
m
m
f
m
f
f
f
f
m
f
m
Z:
19
24
27
27
27
20
22
22
22
19
28
20
22
19
22
23
22
23
Per effettuare una sintesi dei dati, supponiamo di osservare una variabile (qualitativa
o quantitativa discreta) X con un numero finito M di modalità su una popolazione:
convenzionalmente indicheremo le M modalità con i numeri interi v1 , v2 , . . . , vM . Se
(x1 , x2 , . . . , xn ) è un campione associato alla variabile X, i dati saranno n numeri
interi con valori v1 , v2 , . . . , vM .
Per ogni k = 1, . . . , M , indichiamo con
{j : xj = vk }
l’insieme dei dati osservati che assumono il valore vk , e con
nk = #{j : xj = vk }
(1)
il numero di dati che appartengono all’insieme {j : xj = vk } (il simbolo # indica
la cardinalità di un insieme), cioè il numero di volte che il valore vk si ripete nel
campione (x1 , x2 , . . . , xn ).
Il numero nk è detto frequenza assoluta della k-esima modalità. Si noti che nk =
0, 1, . . . , n e che vale la seguente relazione:
M
X
nk = n.
(2)
k=1
Può essere utile a volte conoscere anche la proporzione di osservazioni xj che assumono
il valore k. In tal caso si definisce il numero
pk =
nk
,
n
k = 1, . . . , M,
(3)
che è detto frequenza relativa della k-esima modalità. Si noti che 0 ≤ pk ≤ 1 e che
vale la seguente relazione:
M
X
pk = 1.
(4)
k=1
Se moltiplichiamo pk per 100 otteniamo la percentuale di dati osservati che assumono
il valore vk .
3
Sia per le frequenze assolute che per quelle relative si introduce il concetto di
frequenze cumulate:
Fk =
k
X
ni = #{j : xj ≤ vk },
fk =
i=1
k
X
i=1
pi =
#{j : xj ≤ vk }
,
n
k = 1, . . . , M.
(5)
La quantità Fk è detta frequenza assoluta cumulata e indica il numero delle osservazioni xj con valore minore o uguale a vk , mentre fk è detta frequenza relativa
cumulata e indica la proporzione del numero delle osservazioni xj con valore minore o
uguale a vk . È evidente che per le frequenze cumulate le relazioni (2) e (4) diventano:
FM = n,
fm = 1.
(6)
Se invece X è una variabile quantitativa discreta con un numero molto grande di
modalità oppure X è continua, possiamo sintetizzare i dati osservati (x1 , x2 , . . . , xn )
raggruppandoli in classi. Tali classi sono intervalli adiacenti, non sovrapponentesi,
tali che ciascun xj possa essere collocato in uno solo degli intervalli. Per suddividere i
dati in classi bisogna innanzitutto ordinare i dati stessi dal più piccolo al più grande.
Si chiama statistica ordinale il campione (x(1) , x(2) , . . . , x(n) ) tale che
x(1) ≤ x(2) ≤ · · · ≤ x(n) .
Con il termine statistica si intende una grandezza calcolata a partire dai dati.
Si chiamano minimo e massimo e si indicano, rispettivamente, con xmin e xmax , il
valore più piccolo e il valore più grande nel campione (x1 , x2 , . . . , xn ). Evidentemente:
xmin = x(1) ,
xmax = x(n) .
Supponiamo che [xmin , xmax ] ⊂ [a, b]. Si suddivide l’intervallo [a, b] in M sottointervalli (non necessariamente tutti della stessa ampiezza) Jk = [dk , dk+1 ), k = 1, . . . , M ,
dove
a = d1 < d2 < · · · < dM +1 = b.
Ciascun sottointervallo Jk è detto classe.
Domanda 1: Quante classi Jk si devono considerare?
• il numero delle classi non deve essere troppo piccolo perchè i dati risulterebbero
troppo sintetizzati e le informazioni contenute in essi verrebbero in parte perse;
• il numero delle classi non deve essere troppo grande perchè i dati non verrebbero
sufficientemente sintetizzati.
Abitualmente il numero di classi varia da un minimo di 4-5 (con n = 10−15) ad un
massimo di 15-20 (con n ≥ 100). Comunque, la migliore guida per la scelta di un
opportuno numero di classi è la nostra conoscenza delle osservazioni effettuate sulla
popolazione. Può essere che le classi siano state già fissate in rilevazioni precedenti.
Domanda 2: Quale deve essere l’ampiezza |Jk | delle classi?
4
• La determinazione delle ampiezze |Jk | delle classi può rivelarsi cruciale per mettere in evidenza alcune caratteristiche dei dati. In genere si cerca di determinare
classi aventi la stessa ampiezza. Tale ampiezza può essere determinata dalla
seguente formula:
b−a
|Jk | =
.
(7)
M
Ovviamente si può scegliere un’ampiezza diversa secondo il proprio giudizio.
Anche in questo caso possiamo definire la frequenza assoluta e relativa del campione
(x1 , x2 , . . . , xn ) nelle classi Jk :
nk = #{j : x(j) ∈ Jk },
pk =
nk
,
n
k = 1, . . . , M,
che soddisfano ovviamente le relazioni (2) e (4). Inoltre, è possibile parlare di frequenze cumulate adottando le definizioni (5):
Fk =
fk =
k
X
i=1
k
X
i=1
ni = #{j : x(j) ∈
k
[
Ji } = #{j : x(j) < dk+1 }
i=1
pi =
#{j : x(j) < dk+1 }
,
n
k = 1, . . . , M,
che soddisfano le relazioni (6).
Una certa importanza riveste anche il concetto di valore centrale della classe Jk =
[dk , dk+1 ):
dk+1 − dk
ck =
,
k = 1, . . . , M.
(8)
2
I valori delle variabili vengono espressi in termini di misure; le misure possono essere
raggruppate in 4 tipi di scale di misurazione in relazione alla natura delle osservazioni:
• nominale o classificatoria;
• ordinale;
• per intervalli;
• per rapporti.
La scala nominale: è il livello più basso di misurazione e si utilizza quando i dati
possono essere raggruppati in categorie qualitative, eventualmente identificate con
simboli. Queste categorie sono mutuamente esclusive, cioè nessun dato si può collocare in più di una categoria. In una popolazione animale si possono distinguere gli
individui in maschi e femmine, per valutare gli effetti di un tossico si distingue tra
cavie morte e cavie sopravvissute, per testare l’efficacia di un farmaco si distingue tra
pazienti guariti e quelli che restano ammalati. Spesso ci sono più di due categorie
qualitative, ad esempio i gruppi sanguigni: A, B, AB, 0.
L’operazione ammessa è il conteggio dei presenti in ogni categoria. La descrizione
dei dati avviene tramite le frequenze assolute e le frequenze relative.
5
Esempio 1.2 Gruppi sangugni del sistema AB0 in un campione (n = 149) di
una popolazione caucasica.
Gruppi sanguigni
A
B
AB
0
nk
60
16
7
66
pk
40.3
10.7
4.7
44.3
NOTA BENE: nella scala nominale esiste la relazione di equivalenza, cioè gli elementi del campione appartenenti a classi diverse sono differenti, mentre tutti quelli
della stessa classe sono tra loro equivalenti.
La scala ordinale: si riferisce ancora a variabili qualitative e conserva la proprietà della
scala nominale di classificare ciascun dato all’interno di una sola categoria, ma è possibile assegnare ad ogni osservazione un valore numerico, un punteggio arbitrario; esso,
pur non rappresentando la vera grandezza della caratteristica studiata, rispetta un
ordine nella classificazione. Quindi la scala ordinale rappresenta una misurazione che
contiene una quantità di informazione immediatamente superiore a quella nominale:
alla relazione di equivalenza tra elementi di una stessa classe si aggiunge
la relazione di ordinamento tra le varie classi.
Esempio 1.3 Valutazione della risposta all’applicazione di un farmaco a n = 100
pazienti.
Criterio di classificazione
peggioramento
nessuna variazione
lieve miglioramento
miglioramento
guarigione
punteggio
-1
0
1
2
3
freq. assoluta (nk ) freq. relativa (pk )
3
0.03
4
0.04
15
0.15
52
0.52
26
0.26
La scala ad intervalli: include le proprietà di quella nominale e di quella ordinale
e in più ha un’unità di misura. È quindi una scala graduata con intervalli costanti
ed uguali, dove la posizione dell’origine dell’unità di misura, cioè il punto zero, è
convenzionale, cioè scelta arbitrariamente. Il punto zero scelto non è uno zero “vero”
nel senso che non indica un’assenza totale della quantità che si sta misurando.
Esempio classico di scala ad intervalli è la temperatura misurata in gradi Celsius (o
centigradi) o Fahrenheit, dove l’unità di misura è il grado e il punto di confronto
è il grado “zero” che non indica una mancanza di calore. Sulla scala Celsius la
temperatura zero (0o C) è stata definita per convenzione come il punto di congelamento
dell’acqua e si è quindi definita l’unità (o C) come 1/100 della distanza sulla scala
dal punto di ebollizione (100o C). Sulla scala Fahrenheit il punto di congelamento
dell’acqua è stato fissato a 32o F e lo zero (0o F ) è fissato a 32o F sotto il punto
di congelamento, mentre il punto di ebollizione è stato fissato a 212o F , cioè a una
distanza di 180o F dal punto di congelamento.
6
Altri esempi di scale a intervalli sono le varie scale per misurare il tempo, come il
calendario annuale con la suddivisione del giorno in 24 ore che per convenzione ha il
suo punto zero a mezzanotte.
Esempio 1.4 Temperatura corporea di un campione di n = 10 soggetti espressa
in gradi Celsius e Fahrenheit.
Soggetto
1
2
3
4
5
6
7
8
9
10
o
C
36.2
36.5
36.8
36.4
36.7
36.8
36.5
36.4
37.0
36.1
o
F
97.16
97.70
98.24
97.50
98.06
98.24
97.70
97.52
98.60
97.00
NOTA BENE: la scala a intervalli è una scala più sofisticata di quelle precedenti
perchè non solo è possibile ordinare le misure, ma è anche nota la distanza tra due
misure qualsiasi. Ha senso fare la differenza di temperature e confrontarle tra loro.
Ad esempio, la differenza di temperatura tra i soggetti 3 e 4 è il doppio di quella tra
i soggetti 9 e 3 per entrambe le scale.
La scala di rapporti: è invece adatta a descrivere fenomeni che presentano un’origine
naturale, cioè in cui lo zero significa quantità nulla. Sono tipiche scale di rapporti
l’altezza, il peso, la velocità, l’età, il reddito, la temperatura in gradi Kelvin, ecc...
Essa è caratterizzata dal fatto che per questa scala è possibile determinare non solo
le differenze ma anche i rapporti tra coppie di valori.
Esempio 1.5 Valori di glicemia in un campione di n = 10 soggetti sani espressi in
mg di glucosio per 100ml di sangue.
Soggetto
1
2
3
4
5
6
7
8
9
10
7
mg/ml
65.5
80.0
92.8
90.2
100.5
95.0
98.0
70.3
80.0
105.5
2
Tabelle e grafici
L’informazione contenuta nelle frequenze assolute e relative può essere messa meglio
in evidenza organizzando i dati in tabelle o anche rappresentandoli in grafici.
La tabella di frequenza è una tabella numerica in cui i dati sono organizzati in
opportune classi o modalità e sono riportati i valori numerici della varie frequenze,
ottenendo cosı̀ la distribuzione di frequenza delle osservazioni.
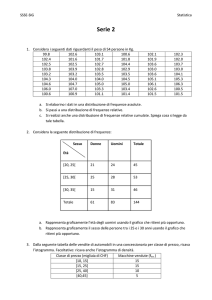
Esempio 2.1 Supponiamo di aver raccolto le seguenti n = 50 misure di una
variabile X, per esempio, di aver esaminato 50 famiglie con 5 figli e di aver registrato
per ciascuna il numero dei figli maschi:
3 0 3 1 1 1 2 4 1 3 2 1 0 2 1 3 3 0 2 1
3 4 3 1 3 4 1 5 0 2 0 4 1 4 2 2 2 1 2 3
2 3 2 2 3 3 2 1 2 1
In questo caso, quindi, la variabile X conta il numero di figli maschi presenti in famiglie
con 5 figli. Il numero di modalità di X è M = 6, tante quanti sono i valori che essa può
assumere, vk = 0, 1, . . . , 5. Le informazioni ottenute dal campione osservato possono
essere sintetizzate nella seguente tabella di frequenza:
Tabella 2.1
Modalità
Freq. ass.
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
vk
0
1
2
3
4
5
5
13
14
12
5
1
5
18
32
44
49
50
0.10
0.26
0.28
0.24
0.10
0.02
0.10
0.36
0.64
0.88
0.98
1.00
Esempio 2.2 Le seguenti osservazioni rappresentano i tempi (in minuti) dei primi
n = 30 corridori maschi in una maratona:
129 130 130 133 134 135 136 136 138 138 138 141 141 141 142
142 142 142 143 143 143 143 143 144 144 145 145 145 145 145
La variabile di interesse è il tempo misurato in minuti. La coincidenza di alcuni
valori dipende dagli arrotondamenti fatti. Supponiamo inizialmente che il numero di
modalità sia M = 12, tante quanti sono i valori che essa assume. Le informazioni
ottenute dal campione osservato possono essere sintetizzate nella seguente tabella di
frequenza:
8
Tabella 2.2
Modalità
Freq. ass.
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
vk
129
130
133
134
135
136
138
141
142
143
144
145
1
2
1
1
1
2
3
3
4
5
2
5
1
3
4
5
6
8
11
14
18
23
25
30
0.033
0.067
0.033
0.033
0.033
0.067
0.100
0.100
0.133
0.167
0.067
0.167
0.033
0.100
0.133
0.166
0.199
0.266
0.366
0.466
0.599
0.766
0.833
1.00
La tabella di frequenza ottenuta non sintetizza in modo ottimale i dati raccolti poichè
ci sono più modalità a cui corrisponde un solo dato. È più opportuno raggruppare i dati in classi. Osserviamo che xmin = 129 e xmax = 145. Allora possiamo
considerare l’intervallo [127.5, 145.5] e suddividerlo in M = 6 classi di ampiezza
145.5 − 127.5
18
|Jk | =
=
= 3, ottenendo la seguente tabella di frequenza:
6
6
Tabella 2.3
Classi
Jk
[127.5,
[130.5,
[133.5,
[136.5,
[139.5,
[142.5,
130.5)
133.5)
136.5)
139.5)
142.5)
145.5)
Valore centrale
delle classi
ck
Freq. ass.
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
129
132
135
138
141
144
3
1
4
3
7
12
3
4
8
11
18
30
0.1000
0.0333
0.1333
0.1000
0.2333
0.4000
0.100
0.133
0.266
0.366
0.600
1.000
Esempio 2.3: Supponiamo di aver raccolto le seguenti n = 100 misure di una
variabile continua X:
0.30 1.03 1.08 1.22 1.46 1.62 2.01 2.17 2.27 2.31
2.33 2.41 2.49 2.49 2.57 2.58 2.59 2.63 2.75 2.75
2.84 2.93 2.95 3.08 3.09 3.23 3.27 3.27 3.28 3.37
9
3.39
3.91
4.31
5.34
5.73
6.44
7.01
3.42
3.91
4.35
5.37
5.94
6.44
7.08
3.47
3.95
4.58
5.40
6.10
6.55
7.11
3.49
3.95
4.69
5.46
6.19
6.56
7.15
3.56
3.96
4.76
5.54
6.24
6.63
7.26
3.60
4.02
4.89
5.62
6.28
6.68
7.44
3.78
4.11
5.12
5.64
6.31
6.73
7.47
3.78
4.12
5.18
5.64
6.33
6.75
7.93
3.79
4.12
5.20
5.68
6.35
6.89
8.21
3.87
4.22
5.34
5.71
6.40
6.99
8.44
Si può pensare, ad esempio, a misure (in una opportuna unità di misura) relative
ad una dimensione fisica di un gruppo di insetti oppure a misure della massa delle
particelle elementari presenti in un determinato esperimento. Per comodità, i dati
sono stati ordinati in senso crescente e la presenza di misure ripetute è dovuta agli
arrotondamenti effettuati. In questo caso xmin = 0.30 e xmax = 8.44. Per poter effettuare una migliore suddivisione in classi, consideriamo l’intervallo [0, 10]. Abbiamo
scelto due differenti raggruppamenti dei dati in classi: il primo in M = 5 classi di
ampiezza |Jk | = 2 e il secondo in M = 20 classi di ampiezza |Jk | = 0.5. I risultati
sono riportati nelle Tabelle 2.4 e 2.5, rispettivamente.
Tabella 2.4
Classi
Freq. ass.
Jk
Valore centrale
delle classi
ck
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
[0.0, 2.0)
[2.0, 4.0)
[4.0, 6.0)
[6.0, 8.0)
[8.0, 10.0)
1.0
3.0
5.0
7.0
9.0
6
39
27
26
2
6
45
72
98
100
0.06
0.39
0.27
0.26
0.02
0.06
0.45
0.72
0.98
1.00
Per rappresentare graficamente la distribuzione delle frequenze di un campione di
dati si usano, tra gli altri, due tipi di grafici. In tutti i casi, sull’asse delle ascisse sono
indicati i valori della variabile in studio, mentre sull’asse delle ordinate vi è invece la
frequenza di ciascun valore.
Un diagramma a barre è un grafico a barre usato per osservazioni di variabili qualitative o quantitative discrete, che mostra le frequenze assolute o relative mediante
l’altezza dei rettangoli. In Figura 2.1 sono riportati i diagrammi a barre per la Tabella
2.1. Come si può notare i due diagrammi sono identici poichè le frequenze assolute e
quelle relative sono tra loro proporzionali.
10
Tabella 2.5
Classi
Freq. ass.
Jk
Valore centrale
delle classi
ck
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
[0.0, 0.5)
[0.5, 1.0)
[1.0, 1.5)
[1.5, 2.0)
[2.0, 2.5)
[2.5, 3.0)
[3.0, 3.5)
[3.5, 4.0)
[4.0, 4.5)
[4.5, 5.0)
[5.0, 5.5)
[5.5, 6.0)
[6.0, 6.5)
[6.5, 7.0)
[7.0, 7.5)
[7.5, 8.0)
[8.0, 8.5)
[8.5, 9.0)
[9.0, 9.5)
[9.5, 10.0)
0.25
0.75
1.25
1.75
2.25
2.75
3.25
3.75
4.25
4.75
5.25
5.75
6.25
6.75
7.25
7.75
8.25
8.75
9.25
9.75
1
0
4
1
8
9
11
11
7
4
8
8
10
8
7
1
2
0
0
0
1
1
5
6
14
23
34
45
52
56
64
72
82
90
97
98
100
100
100
100
0.01
0.00
0.04
0.01
0.08
0.09
0.11
0.11
0.07
0.04
0.08
0.08
0.10
0.08
0.07
0.01
0.02
0.00
0.00
0.00
0.01
0.01
0.05
0.06
0.14
0.23
0.34
0.45
0.52
0.56
0.64
0.72
0.82
0.90
0.97
0.98
1.00
1.00
1.00
1.00
0.25
Freq. relative
Freq. assolute
12
8
0.20
0.15
0.10
4
0.05
0
0.00
0
1
2
3
4
5
0
1
2
3
4
5
Figura 2.1: Diagramma a barre dei dati in Tabella 2.1
11
Un istogramma delle frequenze relative è un grafico utilizzato per dati di variabli
quantitative raggruppati in classi. È costruito disegnando un rettangolo per ciascuna
classe, la cui base corrisponde all’intervallo che definisce la classe (ha quindi ampiezza
pari all’ampiezza della classe), con area uguale alla frequenza relativa della classe. I
rettangoli sono adiacenti perchè le classi sono adiacenti. Inoltre l’altezza di ciascun
rettangolo è data da
hk (x) =
pk
,
|Jk |
per ognix ∈ Jk , k = 1, . . . , M.
(9)
Si noti che se le classi sono tutte della stessa ampiezza, l’istogramma delle frequenze
relative è proporzionale all’istogramma delle frequenze assolute. In questo caso, è del
tutto equivalente disegnare l’uno o l’altro istogramma.
Quindi, un’istogramma è diverso da un diagramma a barre perchè l’istogramma
mostra le frequenze relative o assolute mediante l’area dei rettangoli e non sempre
tramite la loro altezza (questo è vero solo quando la base dei rettangoli è di ampiezza
pari a 1).
Gli istogrammi delle frequenze relative ottenute in Tabella 2.4 ed in Tabella 2.5 sono
rappresentati in Figura 2.2.
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0.00
0
2
4
6
8
10
0.00
12
0 1 2 3 4 5 6 7 8 9 10
Figura 2.2: Istogramma delle frequenze relative dei dati in Tabella 2.4 (grafico a
sinistra) e Tabella 2.5 (grafico a destra)
Si noterà che l’aspetto dei due istogrammi è diverso: quello relativo alla Tabella
2.4 è piuttosto grossolano. Su di esso è stata disegnata la curva densità, che è una
regolarizzazione dell’istogramma e dà un’indicazione sulla distribuzione teorica del
campione di dati. Tale curva presenta due massimi in corrispondenza degli intervalli
[3.0, 4.0] e [5.5, 6.5], e mette in evidenza una caratteristica importante della popolazione: indica che la popolazione è in realtà composta della sovrapposizione di due
12
popolazioni, l’una con valori della variabile prevalentemente compresi tra 3 e 4, e
l’altra con valori vicino a 6. In tal caso si dice che la distribuzione della popolazione
è bimodale. L’istogramma delle frequenze relative ottenuto con classi di ampiezza 0.5
ha un aspetto più equilibrato e mostra chiaramente la distribuzione bimodale della
popolazione.
Si vede quindi come la scelta delle classi modifichi l’aspetto dell’istogramma.
In alcuni casi è preferibile raggruppare i dati in classi di ampiezze diverse. Questo è
particolarmente vero quando le misure relative ad una caratteristica presentano una
forte asimmetria a destra o a sinistra cioè, una coda di valori che si allontanano di
molto dagli altri, come nel seguente esempio.
Esempio 2.4 Si considerino le seguenti n = 40 misure di una variabile quantitativa X:
2 2 2 2 2 2 2 2 2 2
2 2 3 3 3 3 4 4 4 5
5 5 5 6 6 6 6 8 8 9
15 17 22 23 24 24 25 27 32 43
Anche in questo caso i dati sono già stati ordinati in senso crescente e alcune misure
ripetute nel campione sono conseguenza degli arrotondamenti effettuati. Dal campione si deduce immediatamente che xmin = 2 e xmax = 43. La scelta degli intervalli
che definiscono le classi è in questo caso piuttosto soggettiva. Per comodità abbiamo
scelto l’intervallo [1.5, 43.5]. La Tabella 2.6 riporta i risultati ottenuti da una possibile
suddivisione in classi:
Tabella 2.6
Classi
Freq. ass.
Jk
Valore centrale
delle classi
ck
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
[1.5, 6.5)
[6.5, 19.5)
[19.5, 27.5)
[27.5, 43.5)
4
13
23.5
35.5
27
5
6
2
27
32
38
40
0.675
0.125
0.15
0.05
0.675
0.800
0.950
1.000
L’istogramma delle frequenze relative è rappresentato in Figura 2.3. Si noti che
le altezze dei rettangoli sono state calcolate utilizzando la formula (9). È importante
notare che nel caso di classi con ampiezze diverse le aree, e non le altezze, dei rettangoli
sono proporzionali alle frequenze relative.
13
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
1.5
6.5
19.5
27.5
43.5
50
Figura 2.3: Istogramma delle frequenze relative dei dati in Tabella 2.6
3
Misure di tendenza centrale e misure di variabilità
Tabelle di frequenza ed istogrammi o diagrammi a barre sono descrittori grafici del
campione di dati e non esauriscono l’analisi statistica. Per ricavare ulteriori informazioni dal campione si utilizzano dei descrittori numerici o statistiche che permettono di sintetizzare in pochi numeri le caratteristiche più rilevanti dei dati. Tali
descrittori sono le misure di tendenza centrale o indici di centralità e le misure di
variabilià o indici di dispersione.
3.1
Misure di tendenza centrale
Le misure di tendenza centrale forniscono un’idea dei valori attorno ai quali sono
prevalentemente concentrati i dati di un campione. Tali misure sono: moda, media e
mediana campionarie.
Definizione 3.1.1 Sia nota la distribuzione di frequenze di una caratteristica X.
Se X è una variabile qualitatitiva o quantitativa discreta, si definisce moda campionaria la modalità corrispondente alla frequenza massima. Se X è una variabile
quantitativa continua, la moda è la classe (o il suo valore centrale) corrispondente al
rettangolo più alto dell’istogramma.
Ad esempio, nel diagramma a barre di Figura 2.1 la moda è 2 e nell’istogramma
di Figura 2.3 la moda è la classe [1.5, 6.5]. Nel caso dei dati dell’Esempio 2.3
l’identificazione della moda è un pò più delicata. I grafici in Figura 2.2 evidenziano
che può capitare di avere istogrammi (o anche diagrammi a barre) con più di un massimo locale. In realtà il concetto di moda coincide piuttosto con quello di massimo
locale che con quello di massimo assoluto.
Ne consegue che la distribuzione di frequenze di un campione di dati può avere
più di una moda e che, comunque, la moda dipende dalla scelta delle classi.
Supponiamo sia noto un campione (x1 , x2 , . . . , xn ) di dati relativi ad una variabile X.
14
Definizione 3.1.2 Si dice media campionaria di (x1 , x2 , . . . , xn ) il numero reale
x̄ definito da
n
x 1 + x2 + · · · + xn
1X
xi
x̄ =
=
n
n i=1
OSSERVAZIONE: La media campionaria è la media aritmetica degli n dati. A
differenza della moda, essa è unica per un dato campione di dati ed è la misura
più usata per calcolare il centro di una distribuzione. Purtroppo la media è molto
sensibile ai valori estremi (per rendersene conto si calcoli la media di (2,2,2,8)) e
ciò spesso rappresenta un limite per il suo uso. Naturalmente valori estremi in un
campione potrebbero non essere misure corrette della variabile in studio (outlier), ma
una distribuzione asimmetrica (con una lunga coda a sinistra o a destra) della variabile
spingerà il valore della media in direzione della coda più lunga. Di conseguenza, la
media non è una misura robusta del valore centrale di una distribuzione.
Esempio 3.1.1 in riferimento ai dati dell’Esempio 2.2 si ricava x̄ = 139.87,
mentre per i dati dell’Esempio 2.4 si ottiene x̄ = 9.225.
Se il campione di dati è noto solo tramite una tabella di frequenza, vale il seguente
Teorema 3.1.1 Sia X una variabile quantitativa discreta con modalità v1 , v2 , . . . , vM
e siano p1 , p2 , . . . , pM le corrispondenti frequenze relative. Allora
x̄ =
M
X
pk vk .
(10)
k=1
Dimostrazione: Basta osservare che da (3) nk = npk è il numero dei dati che assume
il valore vk , e che quindi
n
M
X
1X
n1 v1 + · · · + nM vM
np1 v1 + · · · + npM vM
x̄ =
p k vk
xi =
=
=
n i=1
n
n
k=1
come volevasi dimostrare.
Dal suddetto Teorema si può notare come la media campionaria non sia altro che una
media pesata dei valori assunti dai dati. Ogni valore usa come peso la sua frequenza
relativa. Se i dati hanno tutti valori distinti allora la media campionaria è proprio la
media aritmetica. Per questo motivo la media campionaria è una misura del baricentro
di una distribuzione.
Esempio 3.1.2 Applicando il Teorema 3.1.1 alla Tabella 2.1 si ricava x̄ = 2.04.
Nel caso di variabili quantitative continue, quando i dati sono raggruppati in classi,
il Teorema 3.1.1 non è applicabile. In questi casi non si potrebbe calcolare la media
campionaria. Però si può calcolare un valore approssimato identificando tutti valori
xi del campione che cadono nella classe Jk con il valore centrale della classe, ck . Si
ottiene cosı̀ una media per dati raggruppati:
x̄f =
M
X
k=1
15
pk ck ,
(11)
dove pk è la frequenza relativa di Jk . Si osservi che in generale x̄ 6= x̄f ; solitamente
però si identificano poichè la loro differenza è poco significativa.
Esempio 3.1.3 Applicando la formula della media per dati raggruppati all’Esempio 2.2, tramite la Tabella 2.3, si ottiene approssimativamente x̄f = 139.59, mentre
per i dati dell’Esempio 2.4, utilizzando la Tabella 2.6, si ottiene approssimativamente
x̄f = 9.625. In entrambi i casi, le medie per dati raggruppati differiscono di molto
poco dalle corrispondenti medie campionarie calcolate nell’Esempio 3.1.1.
Calcolare la media campionaria per i dati dell’Esempio 2.3 e confrontarla con la media
per dati raggruppati calcolata utilizzando la Tabella 2.5.
La media campionaria gode delle seguenti due proprietà.
Teorema 3.1.2 Assegnati due numeri reali a, b e costruito il nuovo campione di dati
(y1 , y2 , . . . , yn ), dove yi = axi + b, i = 1, . . . , n, si ha
ȳ = ax̄ + b.
Dimostrazione: Si ha infatti
n
n
1X
1X
ȳ =
yi =
(axi + b) = a
n i=1
n i=1
Ã
(12)
n
1X
xi
n i=1
!
n
1X
+
b = ax̄ + b,
n i=1
come volevasi dimostrare.
Il Teorema appena enunciato mostra la proprietà di linearità della media campionaria, in quanto ci dice che la media campionaria del nuovo insieme di dati ottenuto
come combinazione lineare del campione assegnato, è legata alla media x̄ dalla stessa
relazione lineare. La suddetta proprietà è utile quando si vogliono modificare i dati
iniziali tramite trasformazioni lineari per renderli più maneggevoli per il calcolo. I
dati cosı̀ trasformati sono detti dati codificati.
Esempio 3.1.4 Consideriamo il campione (x1 , x2 , . . . , x10 ) di misure della temperatura corporea in gradi Fahrenheit riportato nella tabella dell’Esempio 1.4. La
media campionaria è x̄ = 97.772o F . Se volessimo conoscere la media campionaria
delle misure della temperatura corporea in o C, dovremmo prima trasformare queste
misure da gradi Fahrenheit a gradi Centigradi tramite la seguente relazione:
yi =
100
(xi − 32),
180
i = 1, . . . , 10,
ottenendo le temperature in o C riportate in tabella. La media campionaria è quindi
ȳ = 36.54o C. Questo procedimento è piuttosto lungo. Se invece usiamo la formula
(12), si ottiene velocemente
ȳ =
100
(97.772 − 32) = 36.54o C.
180
Teorema 3.1.3 Sia assegnato un altro campione (y1 , y2 , . . . , ym ) di dati relativi alla
variabile X e si consideri il campione (z1 , z2 , . . . , zk ) = (x1 , . . . , xn , y1 , . . . , ym ), di
dimensione k = n + m, ottenuto unificando i primi due. Allora
z̄ =
nx̄ + mȳ
n
m
= x̄ + ȳ.
k
k
k
16
Dimostrazione: Applicando la definizione di media campionaria
Ã n
!
k
m
X
1X
1 X
nx̄ + mȳ
z̄ =
zi =
xi +
yi =
,
k i=1
k i=1
k
i=1
come volevasi dimostrare.
Il suddetto Teorema esprime la proprietà che la media di campioni combinati è
la media pesata delle medie dei singoli campioni : in questo caso i pesi rispettivi sono
n m
e .
k k
Definizione 3.1.3 Si dice mediana campionaria quel numero reale, che denoteremo con xM , che divide il campione di dati in due parti uguali, cioè tale che il
numero di osservazioni nel campione sono per metà più piccole e per metà più grandi
di esso.
Per calcolare la mediana si procede nel seguente modo:
1. si determina la statistica ordinale (x(1) , x(2) , . . . , x(n) );
2. se la dimensione del campione n è dispari, la mediana è : xM = x(k) , dove
n+1
k=
è un intero, cioè xM è il valore intermedio nel campione;
2
n+1
1
n
3. se n è pari,
= r + , dove r =
è un intero. In tal caso la mediana è :
2
2
2
x(r) + x(r+1)
, cioè xM è la media aritmetica dei due valori intermedi nel
xM =
2
campione.
Esempio 3.1.5 Per i dati dell’Esempio 2.2 si ricava xM = 142 che differisce di
poco da x̄ = 139.87, calcolato nell’Esempio 3.1.1, mentre per i dati dell’Esempio 2.4
si ha xM = 5 che differisce di molto da x̄ = 9, 225.
Dall’Esempio 3.1.5 si deduce che la mediana è più robusta della media poichè, a
differenza della media, essa non è calcolata utilizzando i valori delle osservazioni e,
quindi, non è influenzata da valori estremi presenti nel campione di dati.
3.2
Misure di variabilità
Le misure di variabilità forniscono informazioni su come i dati siano concentrati o,
viceversa, dispersi attorno ai valori centrali calcolati nel paragrafo precedente. Tali
misure sono: varianza campionaria, deviazione standard campionaria, coefficiente di
variazione.
Si osservi che, assegnato un campione di dati (x1 , x2 , . . . , xn ) relativo ad una variabile
X, una prima misura di dispersione è ottenuta calcolando il campo di variazione (o
range) del campione, cosı̀ definito
R = xmax − xmin ,
17
dove xmin e xmax sono rispettivamente la prima e l’ultima osservazione nella statistica
ordinale. Questo numero però identifica solo i limiti esterni della distribuzione dei
dati, ma non dà informazioni su che cosa succeda entro questi limti. Il campo di
variazione è inoltre inattendibile poichè è molto sensibile ai valori estremi che tendono
a variare da campione a campione.
Poichè delle tre misure di tendenza centrale presentate nel paragrafo precedente la
più importante è la media campionaria, è necessario avere una misura di dispersione
rispetto alla media. La misura di dispersione più naturale per un campione sarebbe
la media aritmetica delle deviazioni, cioè delle distanze (xi − x̄) dei dati da x̄:
n
1X
(xi − x̄).
n i=1
Purtroppo questa misura è sempre uguale a zero poichè
n
X
(xi − x̄) = n x̄ − n x̄ = 0,
i=1
essendo x̄ il baricentro di una distribuzione. Un modo per risolvere questo problema
è quello di considerare nella formula precedente il quadrato delle deviazioni, (xi − x̄)2 .
Si arriva cosı̀ alla seguente definizione:
Definizione 3.2.1 Si chiama varianza campionaria e si denota con s2X la quantità
n
s2X
1 X
(xi − x̄)2 .
=
n − 1 i=1
La deviazione standard (o scarto quadratico medio) è la radice quadrata della
varianza campionaria:
v
u
n
u 1 X
t
sX =
(xi − x̄)2 .
n − 1 i=1
OSSERVAZIONE: Si noti che nel calcolare la media aritmetica delle deviazioni al
quadrato abbiamo diviso la loro somma per n − 1 anziché per n. La ragione è che
n
X
la somma
(xi − x̄) = 0, cosicché le prime n − 1 deviazioni determinano quella
i=1
restante. Soltanto n − 1 delle deviazioni al quadrato variano liberamente e si calcola
la media dividendo il totale per n − 1.
La varianza campionaria è sempre un numero s2X ≥ 0. In particolare, grandi valori di
s2X indicano che ci sono delle osservazioni xi anche molto lontane da x̄, mentre piccoli
valori di s2X indicano che le osservazioni sono concentrate attorno a x̄. Il caso s2X = 0
si verifica se e solo se tutte le osservazioni hanno valore uguale a x̄.
Come la media x̄, anche s2X non è una misura di dispersione robusta; una forte asimmetria della distribuzione della variabile X o pochi outlier nel campione possono far
aumentare s2X di molto.
La deviazione standard sX è espressa in termini della stessa unità di misura delle
osservazioni iniziali. Questo é un motivo per preferire sX rispetto a s2X , che invece è
espressa in termini di unità al quadrato.
La seguente formula è usata spesso per velocizzare il calcolo manuale della varianza
campionaria.
18
Teorema 3.2.1 Sia assegnato un campione di dati (x1 , x2 , . . . , xn ) associato ad una
variabile X con media x̄, allora
Ã n
!
X
1
s2X =
x2 − nx̄2
(13)
n − 1 i=1 i
Dimostrazione: Infatti si ha
s2X
n
n
1 X
1 X 2
2
=
(xi − x̄) =
(x − 2xi x̄ + x̄2 )
n − 1 i=1
n − 1 i=1 i
!
!
Ã n
Ã n
n
n
X
X
X
X
1
1
xi +
x̄2 =
=
x2 − 2x̄
x2i − 2nx̄2 + nx̄2
n − 1 i=1 i
n
−
1
i=1
i=1
i=1
Ã n
!
X
1
=
x2 − nx̄2
n − 1 i=1 i
come volevasi dimostrare.
Esempio 3.2.1 Riprendendo i dati dell’Esempio 2.2 si ricava s2X = 23.02 min2 e
sX = 4.8 min. Dai dati dell’Esempio 2.4 si ottiene s2X = 104.79 e sX = 10.24.
Se il campione di dati è noto solo tramite una tabella di frequenza, vale il seguente
Teorema 3.2.2 Sia X una variabile quantitativa discreta con modalità v1 , v2 , . . . , vM
e siano p1 , p2 , . . . , pM le corrispondenti frequenze relative. Allora
!
ÃM
M
X
n X
n
2
2
2
2
sX =
pk (vk − x̄) =
pk vk − x̄ ,
(14)
n − 1 k=1
n − 1 k=1
dove x̄ é calcolata tramite la formula (10).
Dimostrazione: Si procede in modo analogo alla dimostrazione del Teorema 3.1.1.
Infatti applicando la (3) e la (4) si ottiene
Ã n
!
n
n
n
X
X
X
X
1
1
s2X =
(xi − x̄)2 =
x2 − 2x̄
xi +
x̄2
n − 1 i=1
n − 1 i=1 i
i=1
i=1
!
ÃM
M
X
X
1
nk vk2 − 2x̄
nk vk + nx̄2
=
n − 1 k=1
k=1
!
ÃM
M
M
X
X
X
n
=
pk vk + x̄2
pk
pk vk2 − 2x̄
n − 1 k=1
k=1
k=1
M
=
M
n X
n X
pk (vk2 − 2x̄vk + x̄2 ) =
pk (vk − x̄)2 .
n − 1 k=1
n − 1 k=1
La seconda uguaglianza consegue immediatamente da (13), applicando la (3).
Esempio 3.2.2 Applicando il Teorema 3.2.2 alla Tabella 2.1 si ricava s2X = 1.51
e sX = 1.23.
19
Nel caso di variabili quantitative continue, quando i dati sono raggruppati in classi, il
Teorema 3.2.2 non è applicabile. Anche per la varianza, cosı̀ come per la media, si può
calcolare un valore approssimato, ottenendo cosı̀ una varianza per dati raggruppati:
ÃM
!
M
X
X
n
n
s2f =
pk (ck − x̄f )2 =
pk c2k − x̄2f ,
(15)
n − 1 k=1
n − 1 k=1
dove ck é il valore centrale della classe Jk e x̄f é la media per dati raggruppati calcolata
tramite la formula (11).
Esempio 3.2.3 Applicando la formula (15) alla Tabella 2.3 si ottiene approssimativamente s2f = 26.25 min2 e sf = 5.12 min, mentre utilizzando la Tabella 2.6, si
ottiene approssimativamente s2f = 87.31 e sf = 9.34.
Calcolare la varianza campionaria per i dati dell’Esempio 2.3 e confrontarla con la
varianza per dati raggruppati calcolata utilizzando la Tabella 2.5.
La varianza campionaria gode della seguente proprietà.
Teorema 3.2.3 Assegnati due numeri reali a, b e costruito il nuovo campione di dati
(y1 , y2 , . . . , yn ) relativo ad una variabile Y , dove yi = axi + b, i = 1, . . . , n, si ha
s2Y = a2 s2X .
Dimostrazione: Dalle definizioni e dal Teorema 3.1.2 si ha
n
s2Y
n
n
1 X
1 X
a2 X
=
(yi − ȳ)2 =
(axi + b − ax̄ − b)2 =
(xi − x̄)2 = a2 s2X ,
n − 1 i=1
n − 1 i=1
n − 1 i=1
come volevasi dimostrare.
Il Teorema appena enunciato mostra che, a differenza della media campionaria, la
varianza campionaria non gode della proprietà di linearità. In ogni caso, la suddetta
proprietà è utile nel caso di dati codificati perchè permette di calcolare la varianza
del campione dei dati trasformati direttamente dalla varianza del campione iniziale.
Definizione 3.2.2 Si dice che (x1 , x2 , . . . , xn ) è un campione standardizzato se
x̄ = 0 e s2X = 1.
Teorema 3.2.4 Assegnato il campione (x1 , x2 , . . . , xn ) con media x̄ e varianza s2X ,
il campione (y1 , y2 , . . . , yn ) cosı̀ definito
yi =
xi − x̄
,
sX
i = 1, . . . , n,
é standardizzato.
Dimostrazione: Infatti dai Teoremi 3.1.2 e 3.2.3 con a =
ȳ =
s2Y =
x̄
x̄
−
= 0,
sX
sX
s2X
= 1,
s2X
20
1
x̄
eb=−
si ha
sX
sX
come volevasi dimostrare.
Le misure di dispersione trattate fino ad ora si chiamano misure di dispersione assoluta
poichè sono calcolate direttamente dai dati e hanno le unità di misura originali o quelle
unità elevate al quadrato.
Quando si vuole confrontare la variabilità di due campioni di dati tramite le corrispettive deviazioni standard, si possono avere risultati ingannevoli, o perchè cambia
l’unità di misura, o perchè, pur essendo l’unità di misura la stessa, una deviazione
standard può essere più grande dell’altra senza che effettivamente il campione corrispondente presenti una maggiore variabilità. È allora più opportuno usare una
misura di dispersione relativa, anzichè una assoluta come la deviazione standard.
Definizione 3.2.3 Sia (x1 , x2 , . . . , xn ) un campione di dati relativo ad una variabile
X, con media campionaria x̄ e deviazione standard sX . Si chiama coefficiente di
variazione la quantità definita da entrambe le equazioni
sX
CV =
,
(16)
x̄
e
sX
CV =
100.
(17)
x̄
OSSERVAZIONE: L’equazione (16) esprime la misura di dispersione assoluta sX
come una proporzione della sua media e l’equazione (17), che è più comune, come
una percentuale della sua media. Per questa ragione il coefficiente di variazione è
detto misura di dispersione relativa. Poichè il numeratore e il denominatore di questo
rapporto hanno la stessa unità di misura, il coefficiente di variazione è un numero
puro, cioè è svincolato da ogni unità di misura, ed è quindi un indice diretto della
variabilità. Esso consente di dare un giudizio sulla “grandezza” della deviazione
standard di un campione indipendentenmente dalla scala di misura con cui essa è
stata misurata. Questo indice ha significato solo se calcolato per variabili espresse in
scale di misura per rapporti.
Esempio 3.2.4 si sta studiando la variazione di peso in ragazzi di età 11 anni e
in ragazzi di età 25 anni. Per un campione di ragazzi di età 11 si è ottenuto x̄ = 36kg
e sX = 4.5kg, mentre per un campione di ragazzi di età 25 si è ottenuto ȳ = 66kg
e sY = 4.5kg. Apparentemente, confrontando le deviazioni standard, sembra che la
variabilità nei due gruppi sia la stessa, ma i due coefficienti di variazione
4.5
4.5
CVX =
100 = 12.5
CVY =
100 = 6.8,
36
66
indicano che c’è una maggiore variabilità nel peso dei ragazzi di età 11.
Esempio 3.2.5 sia A = (0.5, 0.8, 1.1, 1.5, 1.2, 0.9) un campione relativo ad una
variabile X e B = (500, 520, 515, 520, 523, 508) un campione relativo ad una variabile
Y . Per il campione A si ottiene x̄ = 1.00 e sX = 0.3162 e per il campione B si
ottiene ȳ = 514.33 e sY = 8.01. Le osservazioni nei due campioni sono espresse
in scale di misura molto diverse. Confrontando le due deviazioni standard, sembra
che la variabiltà in B sia molto maggiore della variabilità in A, ma il confronto dei
coefficienti di variazione
8.01
0.3162
100 = 31.62
CVY =
100 = 1.56,
CVX =
1.00
514.33
dimostra che in realtà la variabilità è molto maggiore nel campione A.
21
3.3
Quantili di un campione e box plot
Come già osservato in precedenza, quando la distribuzione della variabile in studio
presenta una forte asimmetria a destra o a sinistra, la media campionaria e, quindi, la
varianza campionaria o la deviazione standard possono non essere i migliori descrittori
rispettivamente del valore centrale della distribuzione e della dispersione rispetto ad
esso. Si preferisce, in questo caso, utilizzare misure alternative.
Definizione 3.3.1 Sia 0 < α < 1. Si chiama quantile di ordine α di un campione
(x1 , x2 , . . . , xn ), quel numero reale, che denoteremo con qα , che è a destra di una
frazione α di dati nella statistica ordinale (x(1) , x(2) , . . . , x(n) ).
Per esempio, se α = 13 allora 13 dei dati nel campione ordinato è a sinistra di q1/3 , se
α = 41 allora 14 dei dati è a sinistra di q1/4 .
Dalla definizione di qα consegue che
#{x(j) ≤ qα } ' nα (non deve superare (n + 1)α),
#{x(j) > qα } ' n(1 − α).
Generalmente si considerano tre tipi di quantili: quartili, decili e percentili.
Ci sono tre quartili:
Q1 = q1/4 , Q2 = q1/2 , Q3 = q3/4 .
Q1 è detto primo quartile, Q2 è detto secondo quartile e Q3 è detto terzo quartile. Si
noti che Q2 = xM , cioè il secondo quartile è la mediana campionaria. I tre quartili
dividono il campione di dati in quattro parti uguali.
Ci sono nove decili:
D1 = q1/10 ,
D2 = q2/10 ,
...
D9 = q9/10 .
D1 è detto primo decile, D2 è detto secondo decile e cosı̀ via fino al nono decile D9 .
I nove decili dividono il campione di dati in dieci parti uguali.
Infine ci sono 99 percentili:
P1 = q1/100 ,
P2 = q2/100 ,
...
P99 = q99/100 .
P1 è detto primo percentile, P2 è detto secondo percentile e cosı̀ via fino al novantanovesimo percentile P99 . I novantanove percentili dividono il campione di dati in
100 parti uguali.
OSSERVAZIONE: Q1 corrisponde al 25o percentile, Q2 corrisponde al 50o percentile e Q3 corrisponde al 75o percentile, mentre D1 corrisponde al 10o percentile,
D2 corrisponde al 20o percentile e cosı̀ via D9 corrisponde al 90o percentile.
Per calcolare i quantili di un campione si segue lo stesso procedimento usato per
calcolare la mediana:
assegnato un campione di dati (x1 , x2 , . . . , xn ) e fissato 0 < α < 1,
1. si determina la statistica ordinale (x(1) , x(2) , . . . , x(n) );
2. se (n + 1)α è un intero, il quantile di ordine α è : qα = x(k) , dove k = (n + 1)α;
22
a
a
3. se (n + 1)α non è un intero, si avrà (n + 1)α = r + , dove r è un intero e è
b
b
x(r) + x(r+1)
una frazione. In tal caso il quantile di ordine α è : qα =
.
2
Esempio 3.3.1 Consideriamo il seguente campione di n = 15 dati già ordinati
in senso crescente:
7 7 8 14 14 14 19 25 26 27 31 39 40 45 109
Vogliamo determinare il primo, secondo e terzo quartile.
Posto α = 14 , si ottiene (n + 1)α = 16
= 4 e quindi Q1 = x(4) = 14.
4
1
Posto, invece, α = 2 , si ottiene (n + 1)α = 16
= 8 e quindi Q2 = xM = x(8) = 25.
2
48
3
Se si pone α = 4 , si ottiene (n + 1)α = 4 = 12 e quindi Q3 = x(12) = 39.
Esempio 3.3.2 Consideriamo il seguente campione di n = 16 dati già ordinati
in senso crescente:
4 5 5 7 10 12 20 20 | 24 26 27 28 32 34 41 43
Vogliamo determinare il primo, secondo e terzo quartile.
Posto α = 14 , si ottiene (n + 1)α = 17
= 4 + 14 e quindi
4
Q1 =
Se α = 12 , si ottiene (n + 1)α =
x(4) + x(5)
7 + 10
=
= 8.5.
2
2
17
2
Q 2 = xM =
=8+
e quindi
x(8) + x(9)
20 + 24
=
= 22.
2
2
Infine, se α = 34 , si ottiene (n + 1)α =
Q3 =
1
2
51
4
= 12 +
3
4
e quindi
x(12) + x(13)
28 + 32
=
= 30.
2
2
OSSERVAZIONE: Da entrambi gli esempi si deduce che Q1 è la mediana delle
osservazioni a sinistra di xM , mentre Q3 è la mediana delle osservazioni a destra di
xM .
Per ottenere un rapido ma completo sommario del centro e della dispersione della distribuzione di una variabile X sulla base di un campione di osservazioni (x1 , x2 , . . . , xn ),
possiamo combinare insieme i seguenti cinque numeri:
xmin
Q1
xM
Q3
xmax
I sommari a cinque numeri degli Esempi 3.3.1 e 3.3.2 sono:
7 14 25 39 109
e
4 8.5 22 30 43
Questi cinque numeri possono essere rappresentati su un grafico detto boxplot (grafico
a scatola). Esso è composto da
23
• un rettangolo centrale o scatola (box), i cui lati inferiore e superiore sono rispettivamente Q1 e Q3 ;
• una linea orizzontale nella scatola in corrispondenza della mediana xM ;
• due linee verticali (baffi o whiskers) che partono dai lati inferiore e superiore
della scatola e terminano con due segmenti orizzontali.
OSSERVAZIONE: L’altezza della scatola è l’ampiezza dell’intervallo [Q1 , Q3 ], cioè
è il numero Q3 − Q1 detto differenza interquartile (I.Q. range). Nella scatola cade il
50% delle osservazioni del campione. I baffi mostrano come i rimanenti dati si distribuiscono rispetto alla scatola. Il baffo inferiore si allunga fino al più piccolo valore
nel campione la cui distanza da Q1 deve essere minore o uguale di una distanza pari
a 1.5 volte la differenza interquartile, mentre il baffo superiore si allunga fino al più
grande valore nel campione la cui distanza da Q3 deve essere minore o uguale di una
distanza pari a 1.5 volte la differenza interquartile. Si dice outlier ogni valore nel
campione la cui distanza dalla scatola è maggiore di 1.5 volte la differenza interquartile. Gli outlier, quindi, sono i valori estremi nel campione e, in generale, sono dovuti
a errori di misurazione. Questi vengono indicati nel box plot con un simbolo, tipo
“∗”, o con una linea orizzontale. Se non ci sono outlier, il baffo inferiore si allunga
fino a xmin e il baffo superiore fino a xmax . In questo caso, la distanza tra i due baffi
corrisponde al range del campione.
La Figura 3.3.1 riporta i grafici a scatola per i dati degli Esempi 3.3.1 e 3.3.2. Confrontando i due boxplot si può notare che il primo quartile per il primo campione
(X1) è più alto del primo quartile relativo al secondo campione (X2). Inoltre si nota
la presenza di un outlier nel primo campione, che è il valore 109. La lunghezza della
scatola (la differenza interquartile) è all’incirca la stessa per entrambi i gruppi.
100
80
60
40
20
0
X1
X2
Figura 3.3.1: Boxplot relativi all’Esempio 3.3.1 (X1) e all’Esempio 3.3.2 (X2)
Un grafico a scatola fornisce inoltre indicazioni anche sulla simmetria o asimmetria
di una distribuzione. In una distribuzione simmetrica, la mediana taglia la scatola in
due parti uguali, cioè il primo e il terzo quartile si trovano alla stessa distanza dalla
mediana. Generalmente, in una distibuzione asimmetrica a destra il terzo quartile
sarà più lontano dalla mediana di quanto non lo sia il primo (vedi campione X1),
24
mentre in una distibuzione asimmetrica a sinistra sarà il primo quartile a essere più
lontano dalla mediana rispetto al terzo (vedi campione X2).
3.4
Campioni normali
Osservando gli istogrammi dei campioni numerici forniti da esperimenti reali, si può
notare come vi sia una forma caratteristica che compare molto spesso. Questi grafici
hanno un solo massimo, in corrispondenza della media campionaria (che coincide con
la moda e la mediana campionaria), e decrescono da entrambi i lati simmetricamente,
secondo una curva a campana. Un campione di dati che rispetta questi requisiti si
dice normale.
In realtà pur mantenendo un aspetto simile a quello descritto, non capita mai che
un istogramma reale rispetti perfettamente la simmetria e la monotonia. Si può
parlare allora di campione approssimativamente normale, e l’istogramma in Figura
3.4.1 ne costituisce un esempio. Se un insieme di dati presenta un istogramma che
è sensibilmente asimmetrico rispetto alla media si parla di campione sbilanciato (o
skewed) a sinistra, come in Figura 3.4.2, o a destra come in Figura 3.4.3, a seconda
del lato in cui ha la coda più lunga.
250
200
150
100
50
0
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
Figura 3.4.1: Istogramma di un campione approssimativamente normale
200
180
160
140
120
100
80
60
40
20
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Figura 3.4.2: Istogramma di un campione sbilanciato a sinistra
25
300
250
200
150
100
50
0
0
1
2
3
4
5
6
7
8
9
Figura 3.4.3: Istogramma di un campione sbilanciato a destra
Dalla simmetria degli istogrammi normali segue che un campione approssimativamente normale avrà media e mediana circa uguali. Supponiamo che x̄ e sX siano media e deviazione standard di un campione approssimativamente normale. La seguente
regola empirica specifica che percentuale dei dati ci si aspetta di trovare entro una
distanza pari a sX , 2sX , 3sX dalla media campionaria.
Regola Empirica. Se un campione di dati (x1 , x2 , . . . , xn ) è approssimativamente
normale, ha media campionaria x̄ e deviazione standard campionaria sX > 0, allora
1. circa il 68% dei dati cade nell’intervallo [x̄ − sX , x̄ + sX ];
2. circa il 95% dei dati cade nell’intervallo [x̄ − 2sX , x̄ + 2sX ];
3. circa il 99.7% dei dati cade nell’intervallo [x̄ − 3sX , x̄ + 3sX ];
La regola empirica è illustrata nella Figura 3.4.4.
0.35
0.3
0.25
68% dei dati
0.2
0.15
0.1
95% dei dati
0.05
−3
−2
−1
99.7% dei dati
0
1
2
3
Figura 3.4.4: Distribuzione normale con media 0 e deviazione standard 1
Un insieme di dati ottenuto campionando da una popolazione non omogenea, costituita da sottogruppi eterogenei, di solito non risulta normale. Piuttosto, l’istogramma
26
di un tale campione presenta spesso l’aspetto di una sovrapposizione di istogrammi
normali, e in particolare può avere due o più massimi locali. Siccome questi picchi sono
analoghi alla moda, l’istogramma di un campione di questo tipo si dice bimodale se ne
possiede due e multimodale in generale. L’istogramma relativo ai dati dell’Esempio
2.3 rappresentato in Figura 2.2 è appunto bimodale.
Per stabilire la percentuale di dati che cadono in ciascuno degli intervalli x̄±ksX (k =
1, 2, 3) si usa la seguente disuguaglianza:
Proposizione 3.4.1 (Disuguaglianza di Chebyshev) Sia assegnato un campione
di dati (x1 , x2 , . . . , xn ) con media campionaria x̄ e deviazione standard campionaria
sX > 0. Denotiamo con Dk l’insieme degli indici i = 1, . . . , n corrispondenti ai dati
xi che cadono nell’intervallo [x̄ − ksX , x̄ + ksX ]:
Dk = {i = 1, . . . , n | |xi − x̄| < ksX }.
Allora, per ogni k ≥ 1
#Dk
1
> 1 − 2,
n
k
dove #Dk indica la cardinalità dell’insieme Dk .
(18)
OSSERVAZIONE: Poichè la disuguaglianza (18) vale per ogni valore dell’intero k,
in realtà la percentuale di dati che cadono nell’intervallo x̄ ± ksX è di gran lunga
superiore del confine inferiore stabilito dalla disuguaglianza di Chebyshev.
Esempio 3.4.1 Consideriamo il seguente campione di n = 28 dati già ordinati
in senso crescente:
43 46 52 55 55 56 58 60 62 63 64 66 66 72
74 74 75 77 77 78 83 85 85 87 88 90 91 94
Si trova che x̄ = 70.6 e sX = 14.4.
Applicando la regola empirica, per k = 1 il campione è approssimativamente normale
se il 68% dai dati cade nell’intervallo [x̄ − sX , x̄ + sX ] = [56.2, 85.0]. Dai dati si deduce
che:
#D1
17
=
= 0.6071,
28
28
cioè il 60,71% cade nell’intervallo considerato.
Per k = 2 il campione è approssimativamente normale se il 95% dai dati cade
nell’intervallo [x̄ − 2sX , x̄ + 2sX ] = [41.8, 99.4]. Dai dati si deduce che:
28
#D2
=
= 1,
28
28
cioè il 100% cade nell’intervallo richiesto. Ne consegue che il campione è approssimativamente normale.
27
3.5
Momenti e indici di forma
L’uso degli indici di forma è limitato alla semplice descrizione della forma della distribuzione e riguarda due caratteristiche: la simmetria e la curtosi.
Nelle distibuzioni unimodali si ha simmetria quando media, moda e mediana coincidono; se la distribuzione è bimodale possono essere coincidenti solamente la media
e la mediana. Di norma, le distribuzioni dei dati sono unimodali; pertanto, concentreremo l’analisi della simmetria su di esse.
Si noti che quando media, mediana e moda coincidono non sempre la distribuzione
è simmetrica. Ne consegue che la perfetta coincidenza delle tre misure di
tendenza centrale è condizione solo necessaria, ma non sufficiente per la
simmetria.
Quando media, mediana e moda non coincidono, la distribuzione è asimmetrica. In
una distribuzione unimodale:
a) l’asimmetria destra si ha quando i valori che si allontanano maggiormente dalla
media sono quelli più elevati, collocati a detra dei valori centrali (vedi Figura
3.4.3); in questo caso la successione delle 3 misure di tendenza centrale da
sinistra a destra è: moda, mediana, media;
b) l’asimmetria sinistra si ha quando i valori più distanti dalla media sono quelli
minori, collocati a sinistra dei valori centrali (vedi Figura 3.4.2); in questo caso
la successione delle 3 misure di tendenza centrale da sinistra a destra è invertita
rispetto alla precedente: media, mediana, moda.
Gli indici di forma di una distribuzione attualmente più diffusi sono derivati dei
momenti.
Definizione 3.5.1 Si chiamano rispettivamente momento di ordine h e momento
centrato di ordine h le quantità
n
mh =
1X h
x ,
n j=1 j
n
µh =
1X
(xj − x̄)h ,
n j=1
per un campione (x1 , . . . , xn ), e
mh =
k
X
pj xhj ,
µh =
j=1
k
X
pj (xj − x̄)h ,
j=1
per una distribuzione di frequenza suddivisa in k classi con frequenze relative p1 , . . . , pk .
Per h = 1 risulta m1 = x̄, µ1 = 0 e per h = 2 si ha µ2 = s2X . I momenti centrali di
ordine dispari (µ3 , µ5 , µ7 , . . . ) sono nulli per distribuzioni simmetriche. Inoltre,
in distribuzioni con asimmetria destra hanno valore positivo ed in quelle con
asimmetria sinistra hanno valore negativo.
Per queste caratteristiche, il momento centrale µ3 è adeguato per valutare la simmetria
o asimmetria di una distribuzione, ma esiste il limite che il suo valore dipende dalla
scala di misura utilizzata.
Per ottenere una misura relativa, adimensionale che permetta i confronti tra più
distribuzioni si definisce il seguente indice di forma.
28
Definizione 3.5.2 Si chiama indice di asimmetria la quantità
γ1 =
µ3
.
s3X
L’indice di asimmetria γ1 conserva le proprietà precedentemente descritte per µ3 .
Quindi γ1 assumerà valore prossimo a zero se i dati si distribuiscono in maniera
simmetrica attorno alla media, assumerà valore positivo in presenza di code a destra
e valore negativo in presenza di code a sinistra.
Per valutare il grado di asimmetria è convenzione che si abbia una distribuzione ad
asimmetria
• forte, quando |γ1 | > 1;
• moderata quando
1
2
< |γ1 | < 1;
• trascurabile quando 0 < |γ1 | < 12 .
Quando si descrive la forma di istogrammi che presentano una forma simmetrica, con
il termine curtosi si intende il grado di appiattimento rispetto all’istogramma di campioni normali. Si definisce quindi il seguente indice di misura relativa, adimensionale.
Definizione 3.5.3 Si chiama indice di curtosi la quantità
γ2 =
µ4
.
s4X
Si osservi che l’indice γ2 può assumere solo valori positivi perchè è definito in funzione
di un momento centrale di ordine pari. In particolare se:
• γ2 = 3, l’istogramma coincide con quello di un campione normale;
• γ2 > 3, l’istogramma risulta più alto al centro e agli estremi (code lunghe),
rispetto a quello di un campione normale. Ciò indica un eccesso di frequenza
nelle classi centrali, una frequenza minore nelle classi intermedie ed una presenza
maggiore delle classi estreme;
• 0 < γ2 < 3, l’istogramma risulta più basso al centro e agli estremi (code corte)
rispetto a quello di un campione normale. Ciò indica una frequenza minore
delle classi centrali e di quelle estreme e una frequenza maggiore nelle classi
intermedie.
Esempio 3.5.1 Si consideri la tabella di frequenza 3.5.1 relativa all’altezza (misurata in cm) di n = 50 individui:
Dalla tabella di frequenza si ottiene
m1 = x̄ = 171.44,
µ3 =
5
X
µ2 = s2X = 41.1264,
pj (cj − x̄)3 = −25.13,
µ4 =
j=1
sX = 6.4130,
5
X
j=1
29
pj (cj − x̄)4 = 4294.3818,
Tabella 3.5.1
Classi
Freq. ass.
Jk
Valore centrale
delle classi
ck
Freq. rel.
nk
Freq. ass.
cumulata
Fk
pk
Freq. rel.
cumulata
fk
[155, 161)
[161, 167)
[167, 173)
[173, 179)
[179, 185]
158
164
170
176
182
3
8
20
12
7
3
11
31
43
50
0.06
0.16
0.40
0.24
0.14
0.06
0.22
0.62
0.86
1.00
e quindi
γ1 =
−25.13
1
=
−0.0953
=⇒
|γ
|
=
0.0953
<
1
6.41303
2
γ2 =
4294.3818
= 2.5390 < 3.
41.12642
Si può quindi concludere che la distribuzione del campione presenta una trascurabile asimmetria sinistra e l’istogramma delle frequenze relative risulta più appiattito
rispetto a quello di un campione normale (vedi Figura 3.5.1).
0.06
0.04
0.02
0.00
155
161
167
173
179
185
Figura 3.5.1: Istogramma delle frequenze relative dei dati in Tabella 3.5.1
4
Medie generalizzate
A volte può risultare interessante calcolare la media di variabili trasformate, del tipo
1
g(x) = xh , h ∈ R (x2 , x3 , x 2 , ...).
30
Dato un campione (x1 , . . . , xn ), tali medie sono definite da
"
n
1X h
Mh =
x
n i=1 i
o, in generale, da
Mh =
" k
X
#1/h
,
#1/h
xhi pi
.
i=1
per dati raggruppati in k classi con frequenze relative p1 . . . pk .
Consideriamo alcuni casi particolari. Per h = 2, si ha la media quadratica:
v
u n
u1 X
x2 ,
M2 = t
n i=1 i
cioè la radice quadrata della media campionaria delle osservazioni al quadrato.
OSSERVAZIONE: Di solito si fa ricorso alla media quadratica quando alcuni dati
nel campione sono positivi e altri negativi e quindi si vuole eliminare l’influenza del
segno.
Esempio 4.1 Due piastre quadrate hanno lato x1 = 3 ed x2 = 5. Si desidera
sostituirle con due piastre uguali che mantengano invariata la superficie totale.
Soluzione: dobbiamo quindi imporre che
x21 + x22 = 2l2
Il lato della piastra cercata è quindi dato da:
r
r
x21 + x22
34
l=
=
= 4.123
2
2
Si noti che la media quadratica è maggiore della media campionaria:
x1 + x2
= 4.
2
Per h = −1 si ottiene la media armonica:
#−1
" n
1 X −1
n
xi
M−1 =
= n
.
X1
n i=1
xi
i=1
La media armonica è quindi il reciproco della media campionaria del reciproco delle
osservazioni.
Esempio 4.2 Una certa proteina viene studiata mediante elettroforesi: si vuol conoscerne
la velocità di migrazione media. La proteina viene fatta correre su gel in un campo
elettrico per 20 mm e viene misurato il tempo necessario a percorrere questa distanza
in 5 prove diverse. I dati sono riportati nella seguente tabella:
31
Prova tempo (s)
1
40
2
60
3
30
4
50
5
70
velocità (mm/s)
20/40 = 0.500
20/60 = 0.333
20/30 = 0.667
20/50 = 0.400
20/70 = 0.286
Soluzione: si noti che il tempo totale (su tutte le 5 prove) necessario a percorrere la
distanza totale di 100 mm (20mm per 5 prove)è 250 s. La media aritmetica della
velocità è:
2.186
= 0.4372 mm/s,
5
che però non è la velocità media; infatti risulta
0.4372 mm/s × 250 s = 109.3 mm,
mentre il totale del cammino percorso nelle 5 prove è 20 mm × 5 = 100 mm.
La velocità media è invece calcolata utilizzando la media armonica:
M−1 =
5
5
=
= 0.4 mm
1/0.5 + 1/0.33 + 1/0.66 + 1/0.4 + 1/0.29
12.49
e infatti 0.4 mm × 250 s = 100 mm.
La cosa è evidente in quanto la velocità media generale è:
v=
spazio
100
=
,
20
20
20
20
20
tempo
+
+
+
+
0.5 0.333 0.667 0.4 0.286
da cui dividendo numeratore e denominatore per 20 si ottiene v = M−1 .
Un’altra media utilizzata in alcuni campi particolari, come ad esempio in microbiologia o sierologia, è la media geometrica cosı̀ definita:
1
M0 = (x1 · x2 · .... · xn ) n .
Si può facilmente notare che
log M0 =
n
1 X
log xi ,
n i=1
cioè il logaritmo della media geometrica è la media aritmetica del logaritmo delle
osservazioni.
OSSERVAZIONE: Di solito si fa ricorso alla media geometrica nei problemi in cui
si vogliono calcolare indici statistici come tassi o rendimenti.
Esempio 4.3 Il numero di mosche presenti in una popolazione di laboratorio costituita originariamente da 100 elementi, viene rilevato in tre periodi successivi. Al
primo conteggio risultano 112 mosche, al secondo 196 e al terzo 369. Qual è il tasso
di incremento medio della popolazione?
32
Soluzione: gli incrementi osservati nei tre periodi sono:
112
196
369
= 1.12,
= 1.75,
= 1.88
100
112
196
Allora:
1
M0 = (1.12 · 1.75 · 1.88) 3 = 1.54,
da cui 100 × 1.54 = 154, quindi la popolazione ha subito un incremento medio del
54%.
OSSERVAZIONE: Tra la media campionaria (M ), la media armonica, la media
geometrica e la media quadratica vale la seguente relazione:
M2 > M > M0 > M−1
Le medie introdotte in precedenza godono di alcune proprietà che ne determinano
anche l’utilizzazione.
Si supponga che le osservazioni del campione (x1 , . . . , xn ) sono generate da un modello
additivo del tipo:
xi = a + ²i , i = 1, ..., n,
dove la costante incognita a rappresenta la parte sistematica ed ²i l’errore di misurazione. Allora a può essere determinata imponendo che l’errore che si commette
sia minimo, cioè tale che la funzione
n
X
Q(a) =
(xi − a)2
i=1
assuma valore minimo. Si dimostra che il valore che minimizza Q(a) è la media
campionaria M .
Si può allora concludere che se si ricorre alla media campionaria, si interpretano
implicitamente le osservazioni con un modello additivo e, viceversa, se si interpretano
le osservazioni con un modello additivo, allora la media dei dati deve essere quella
campionaria.
In modo analogo si ottiene la stessa dualità tra:
1. il modello additivo dei quadrati delle osservazioni:
x2i = a2 + ²i
e la media quadratica;
2. il modello additivo dei reciproci delle osservazioni:
1
1
= + ²i
xi
a
e la media armonica;
3. il modello moltiplicativo:
xi = a ² i
e la media geometrica. In quest’ultimo caso si osservi che
log xi = log a + log ²i ,
cioè il logaritmo delle osservazioni soddisfa il modello additivo e quindi, per
quanto detto prima, la media del logaritmo delle osservazioni è la media campionaria.
33
5
Statistica multivariata
5.1
Dati multidimensionali
Sugli individui di una popolazione possono essere eseguite osservazioni e misure di
due o più variabili con lo scopo di metterne anche in evidenza gli eventuali legami
statistici. Ad esempio possiamo misurare altezza e peso dei cittadini di una determinata comunità per mettere in evidenza una relazione tra le due misure. In questa
sezione ci limiteremo ad esaminare il caso di due variabili (X, Y ), sicchè il nostro
campione sarà del tipo (x1 , y1 ), . . . , (xn , yn ).
Se le variabili sono qualitative o quantitative discrete con modalità A1 , . . . , AM della
variabile X e B1 , . . . , BR della variabile Y , una prima maniera di rappresentare il
campione sarà quella di costruire una tabella di contingenza di frequenze assolute
come quella riportata in Tabella 5.1. In essa si riportano:
• le frequenze assolute congiunte nj,k , cioè il numero delle volte in cui si presenta
la coppia di modalità (Aj , Bk );
• le frequenze assolute marginali nj,· e n·,k , cioè il numero di volte in cui si presentano separatamente le modalità Aj e Bk ;
• la numerosità totale n del campione.
Tabella 5.1
A1
..
.
AM
Si noti che
nj,· =
n·,k =
B1
n1,1
..
.
nM,1
n·,1
R
X
k=1
M
X
...
...
···
...
...
BR
n1,R
..
.
n1,·
..
.
nM,R
n·,R
nM,·
n
nj,k ,
j = 1, . . . , M
nj,k ,
k = 1, . . . , R
j=1
n=
R
X
n·,k =
M
X
nj,·
j=1
k=1
In maniera del tutto analoga si costruisce anche la tabella di contingenza delle frequenze relative congiunte e marginali
pj,k =
nj,k
,
n
pj,· =
34
nj,·
,
n
p·,k =
n·,k
n
Si noti che in questo caso, a causa della normalizzazione (4) delle frequenze relative,
nell’angolo destro in basso della corrispondente tabella di contingenza comparirà 1
invece di n.
A1
..
.
AM
B1
p1,1
..
.
pM,1
p·,1
...
...
···
...
...
BR
p1,R
..
.
p1,·
..
.
pM,R
p·,R
pM,·
1
Esempio 5.1. Nella Tabella 5.2 sono riportati in forma di tabella di contingenza i dati
relativi alla scelta della facoltà universitaria di n = 10000 studenti secondo l’attività
lavorativa del padre. I marginali verticali in tabella indicano la composizione sociale
degli studenti universitari, i marginali orizzontali indicano il gradimento delle diverse
facoltà universitarie e infine le frequenze congiunte indicano l’eventuale relazione che
intercorre tra l’estrazione socio-professionale della famiglia degli studenti e la scelta
della facoltà universitaria.
Tabella 5.2
Proprietario
Contadino
Imprenditore
Professionista
Dirigente
Impiegato
Operaio
Altro
5.2
GIU ECO LET SCI MED FAR
80
36
134
99
65
28
6
2
15
6
4
1
168
74
312 137
208
53
470
191
806 400
876
164
236
99
493 264
281
56
145
52
281 133
135
30
166
64
401 193
127
23
321
121
651 258
309
49
1592
639 3093 1490 2005
404
ALTRO
69
511
5
39
89 1035
124 3031
123 1552
74
850
157 1131
142 1851
777 10000
Covarianza, correlazione
Nel caso in cui le variabili osservate (X, Y ) siano quantitative continue è utile rappresentare graficamente nel piano cartesiano x, y i punti di coordinate (x1 , y1 ), . . . , (xn , yn ).
Il grafico che descrive come i punti si distribuiscono nel piano cartesiano è detto diagramma di dispersione. La conformazione della nuvola di punti disegnata fornisce
una prima indicazione sulla eventuale relazione intercorrente tra le due variabili.
Per misurare quantitativamente la tendenza delle due variabili X ed Y a “covariare”, cioè a variare insieme, un parametro molto importante e utile in biologia
è il coefficiente di correlazione lineare. Per introdurre la formula che permette di
calcolare tale parametro, sulla base di un campione di punti delle variabili (X, Y ),
dobbiamo premettere la seguente definizione.
35
Definizione 5.2.1 Dato un campione (x1 , y1 ), . . . , (xn , yn ) di due variabili quantitative continue X e Y , si chiama covarianza campionaria di X e Y la quantità
n
sXY
1 X
=
(xi − x̄)(yi − ȳ),
n − 1 i=1
(19)
dove x̄ e ȳ sono le medie campionarie di (x1 , . . . , xn ) e di (y1 , . . . , yn ), rispettivamente.
OSSERVAZIONE: La covarianza campionaria è detta anche somma dei prodotti
delle deviazioni (xi − x̄) e (yi − ȳ). Se la maggior parte dei prodotti è positiva allora
sXY > 0 , mentre se è negativa si avrà sXY < 0. Se invece vi è un numero quasi uguale
di prodotti positivi e di prodotti negativi allora la covarianza sarà molto vicina allo
zero.
Si prova il seguente risultato che permette di calcolare la covarianza sXY con una
formula semplificata.
Teorema 5.2.1 Sia assegnato un campione (x1 , y1 ), . . . , (xn , yn ) con medie x̄ e ȳ,allora
" n
#
X
1
sXY =
xi yi − n x̄ ȳ .
(20)
n − 1 i=1
Dimostrazione: Infatti da (19), sviluppando i prodotti si ha
n
sXY
1 X
=
(xi yi − xi ȳ − x̄ yi + x̄ ȳ)
n − 1 i=1
" n
#
X
1
=
xi yi − n x̄ ȳ − n x̄ ȳ + n x̄ ȳ
n − 1 i=1
" n
#
X
1
=
xi yi − n x̄ ȳ .
n − 1 i=1
Definizione 5.2.2 Dato un campione (x1 , y1 ), . . . , (xn , yn ) di due variabili quantitative continue X e Y , si chiama coeffciente di correlazione campionario di X e
Y la quantità
sXY
rXY =
,
(21)
sX sY
dove sX e sY sono le deviazioni standard di (x1 , . . . , xn ) e di (y1 , . . . , yn ), rispettivamente.
OSSERVAZIONE: Il coefficiente di correlazione è un parametro adimensionale (cioè
privo di unità di misura). Può essere quindi interpretato facilmente qualunque siano
le variabili prese in esame.
Si prova che −1 ≤ rXY ≤ 1. Una correlazione negativa significa che quando una delle
due variabili decresce, l’altra cresce, mentre una correlazione positiva significa che le
due variabili crescono o decrescono insieme (vedi Figura 5.2.1).
La correlazione massima (rXY = 1) o minima (rXY = −1) si ha quando tutti i punti
giacciono su una retta (vedi Figura 5.2.1): è questo il motivo per cui il coefficiente
36
r=0.5
Y
0
-4
2
-2
Y
0
4
2
6
4
r=-0.8
8
10
12
1
3
4
X
r=-0.2
r=1
6
2
5
Y
-1
0
1
7
6
4
-2
5
Y
2
X
8
6
-1
0
1
2
3
4
5
-4
X
-3
-2
-1
0
X
Figura 5.2.1: Esempi di diagramma di dispersione
di correlazione è detto lineare. Quindi il coefficiente di correlazione lineare
misura l’intensità e la direzione dell’associazione lineare tra due variabili
quantitative numeriche.
Se rXY = 0 allora si dice che le variabili X e Y sono non correlate linearmente, il
che accade o quando le due variabili sono indipendenti (vedi Figura 5.2.2 a)) oppure
quando la relazione che le lega è di tipo non lineare (vedi Figura 5.2.2 b)).
5.3
Regressione lineare
La regressione lineare è il metodo più usato per prevedere il valore di una variabile
quantitativa continua Y sulla base del valore assunto da un’altra variabile numerica
X, supponendo che la relazione tra le due variabili esista e sia realmente lineare.
La variabile Y è detta variabile risposta ed è rappresentata sull’asse delle ordinate,
mentre la varibile X è detta variabile esplicativa ed è rappresentata sull’asse delle
ascisse.
Definizione 5.3.1 Dato un campione (x1 , y1 ), . . . , (xn , yn ), si chiama retta di regressione la retta Y = a X + b che passa attraverso i punti del diagramma di dispersione.
OSSERVAZIONE: Il coefficiente b rappresenta l’intersezione della retta di regressione con l’asse delle ordinate ed è detto intercetta, mentre a è la pendenza o coeffi37
3
2
1
0
-1
-2
-2
-1
0
1
2
3
10
15
20
a)
2
4
6
8
b)
Figura 5.2.2: a) caso di variabili indipendenti, b) caso di variabili dipendenti ma
non linearmente correlate.
ciente angolare della retta ed è una misura della variazione della variabile Y per unità
di variazione di X.
OSSERVAZIONE: In un diagramma di dispersione possiamo tracciare molte rette:
come facciamo a scegliere la migliore? In generale sarà impossibile trovare una retta
che passi per tutti i punti della nuvola, cioè trovare due numeri a e b tale che yi =
a xi + b per ogni i = 1, . . . , n. Una buona idea è trovare una retta che approssimi
nel modo migliore l’andamento della nuvola di punti. Matematicamente questo si
traduce nel determinare quella retta che renda più piccole possibili le distanze (gli
scarti verticali) tra i punti dei dati e i punti sulla retta stessa. Più specificatamente,
vogliamo deteminare i coefficienti a e b della retta di regressione che rendono minimo
l’errore quadratico, cioè la quantità
ε(a, b) =
n
X
[yi − (a xi + b)]2
(22)
i=1
Il metodo sopra descritto, utilizzato per determinare la retta di regressione lineare, è
detto metodo ai minimi quadrati. Vale il seguente teorema
38
Teorema 5.3.1 Dato un campione (x1 , y1 ), . . . , (xn , yn ), le stime campionarie dei
coefficienti a e b sono
sX Y
â = 2 ,
b̂ = ȳ − â x̄
(23)
sX
Dimostrazione: Per determinare i coefficienti a e b che rendono minimo l’errore
quadratico calcoliamo le derivate di ε(a, b)
n
n
X
∂ε
= −2
xi [yi − (a xi + b)],
∂a
i=1
X
∂ε
= −2
[yi − (a xi + b)]
∂b
i=1
e poniamole uguali a 0 ottenendo il sistema di due equazioni nelle incognite a e b
n
X
xi [yi − (a xi + b)] = 0
i=1
n
X
[yi − (a xi + b)] = 0.
i=1
La seconda equazione del sistema si scrive anche come
n
X
(yi − a xi ) − nb = 0,
i=1
da cui si ricava subito
b̂ =
n
n
1 X
aX
yi −
xi = ȳ − â x̄.
n i=1
n i=1
(24)
Sostituendo nella prima equazione si ottiene
n
X
xi [yi − (a xi + b)] =
i=1
=
n
X
xi yi − a
n
X
i=1
i=1
n
X
n
X
xi yi − a
i=1
x2i
− (ȳ − â x̄)
n
X
xi
i=1
x2i − n x̄ ȳ + a n x̄2 = 0.
i=1
Dividendo per n − 1 e applicando i risultati dei Teoremi 3.2.1 e 5.2.1 si ha
1
n−1
" n
X
xi y i − a
n
X
i=1
#
x2i
− n x̄ ȳ + a n x̄
i=1
=
1
n−1
" n
X
= sXY −
i=1
a s2X
2
#
xi yi − n x̄ ȳ − a
1
n−1
" n
X
#
x2i − n x̄2
i=1
= 0,
da cui si ricava immediatamente
â =
sXY
.
s2X
39
(25)
OSSERVAZIONE: La retta di regressione stimata ha equazione:
Ŷ = âX + b̂ = âX + ȳ − â x̄ = â(X − x̄) + ȳ,
e passa per il punto (x̄, ȳ). Inoltre, utilizzando la (21) si può scrivere la covarianza
nella forma
sXY = rXY sX sY ,
che sostituita in (25) permette di esprimere il coefficiente angolare della retta di
regressione stimata in funzione del coefficiente di correlazione lineare
â = rXY
sY
.
sX
Da qui si deduce che quando 0 < rXY < 1, allora â > 0, mentre quando −1 < rXY < 0,
allora â < 0.
Esempio 5.3.1 Nella seguente tabella si riporta la frequenza cardiaca a riposo (misurata in battiti al minuto) e gli anni complessivi di istruzione di 10 individui:
Anni di istruzione(X) : 12 16 13 18 19 12 18 19 12 14
Frequenza cardiaca(Y ) : 73 67 74 63 73 84 60 62 76 71
Soluzione: Calcoliamo le medie campionarie
x̄ =
153
= 15.3,
10
ȳ =
703
= 70.3,
10
e le varianze campionarie usando la formula (13)
82.1
1
= 9.122,
s2X = (2423−2340.9) =
9
9
1
488.1
s2Y = (49909−49420.9) =
= 54.233,
9
9
da cui si ricavano le deviazioni standard camponarie
sX = 3.020,
sY = 7.364.
Calcoliamo inoltre la covarianza campionaria applicando la formula (20)
1
152.9
SXY = (10603 − 10755.9) = −
= −16.99,
9
9
e quindi il coefficiente di correlazione lineare
rXY =
−16.99
= −0.76396,
(3.020) (7.364)
da cui si deduce che esiste una correlazione lineare negativa tra le variabili X e
Y , cioè ad una scolarizazione lunga corrisponde una bassa frequenza cardiaca, il che
equivale a dire una maggiore attenzione alla propria salute (più attività fisica, migliore
alimentazione, ecc...).
Siamo ora in grado di calcolare le stime campionarie â e b̂ dei coefficienti di regressione
e la retta di regressione stimata (vedi Figura 5.3.1):
â = −1.8625,
b̂ = 98.7962
Ŷ = −1.8625 X + 98.7962
40
85
Frequenza cardiaca
80
75
70
65
60
12
14
16
18
Anni di istruzione
Figura 5.3.1: Diagramma di dispersione e retta di regressione per l’Esempio 5.3.1
La retta di regressione può essere utilizzata per effettuare delle previsioni su
possibili valori della Y in corrispondenza di fissati valori della X. Per esempio, relativamente all’Esempio 5.3.1, si vuole prevedere la frequenza cardiaca di un indiviudo
sapendo che il numero di anni di istruzione è x0 = 15. Sostituendo il valore di x0
nell’equazione della retta di regressione sopra determinata, si ottiene:
ŷ0 = −1.8625 (15) + 98.7962 = 70.86 ' 71 battiti al minuto.
L’errore di previsione è l’errore che si commette approssimando i valori osservati,
yi , della Y con i corrispondenti valori ŷi sulla retta di regressione. In altre parole, vi
è una quota di variabilità della Y che non viene spiegata dalla relazione lineare con
la X. Tale errore è detto residuo e si indica con ei = yi − ŷi . Si noti che
n
n
n
n
1X
1X
1X
1X
ei =
(yi − ŷi ) =
yi −
(â xi + b̂)
n i=1
n i=1
n i=1
n i=1
n
= ȳ − â
1X
xi − b̂ = (ȳ − â x̄) − b̂ = b̂ − b̂ = 0.
n i=1
Questo risultato, valido nella teoria, nella pratica non si realizza mai a causa degli
errori di arrotondamento. È chiaro comunque che quanto più i residui sono piccoli
tanto migliore è l’adattamento della retta di regressione ai dati sperimentali, cioè la
maggior parte della variabilità della Y è spiegata tramite la relazione lineare con la
X.
Ritornando all’Esempio 5.3.1, vogliamo calcolare quanto vale il residuo e4 = y4 − ŷ4 .
Dai dati risulta che (x4 , y4 ) = (18, 63), mentre dalla retta di regressione risulta che
ŷ4 = −1.8625 (18) + 98.7962 = 65.27 ' 65,
da cui si deduce che e4 = 63 − 65 = −2.
41
Esempio 5.3.2 Nella seguente tabella si riporta la dose di fertilizzante usato (misurato in g) e il peso della granella (misurato in Kg) di 10 parcelle di mais:
Dose di fertilizzante (X) : 171 169 181 173 178 180 185 183 170 174
Peso della granella (Y ) : 60 57 71 66 65 78 82 78 62 70
Soluzione: Il coefficiente di correlazione lineare è rXY = 0.91. Esiste quindi una
correlazione lineare positiva tra Y e X, cioè all’aumentare della dose di fertilizzante
aumenta il peso della granella di mais.
La retta di regressione stimata è (vedi Figura 5.3.2):
Ŷ = 1.3374 X − 167.0136
80
Peso granella
75
70
65
60
55
169
174
179
184
Fertilizzante
Figura 5.3.2: Diagramma di dispersione e retta di regressione per l’Esempio 5.3.2
42