L`area del trapezio - Campus

L’area del trapezio: un altro modo
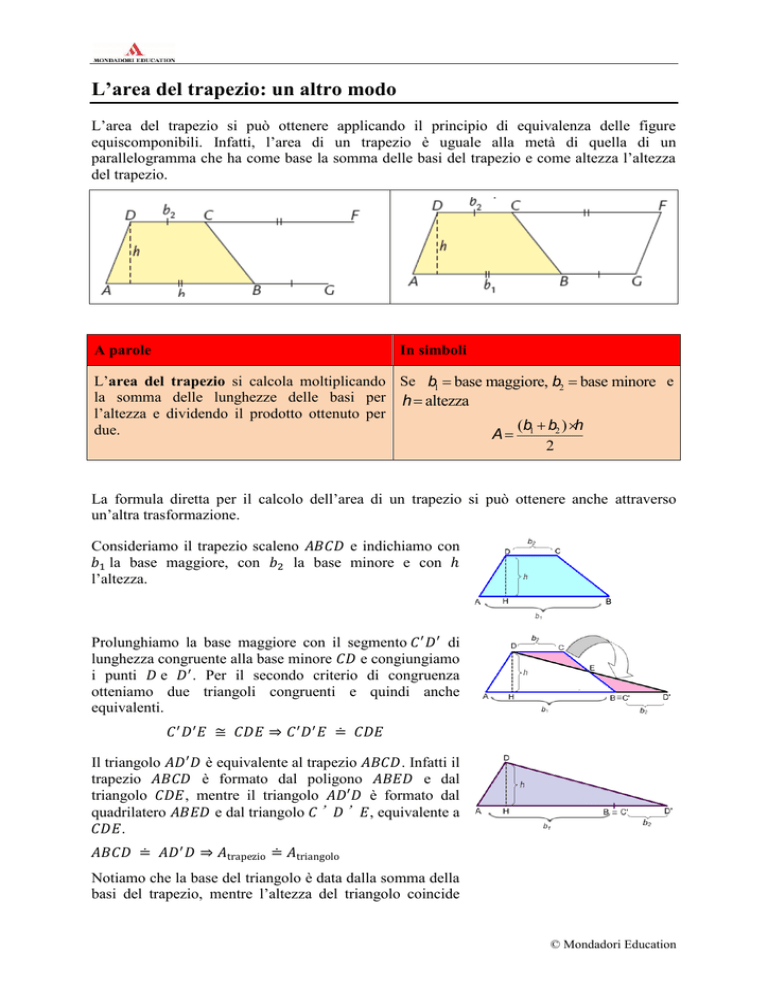
L’area del trapezio si può ottenere applicando il principio di equivalenza delle figure
equiscomponibili. Infatti, l’area di un trapezio è uguale alla metà di quella di un
parallelogramma che ha come base la somma delle basi del trapezio e come altezza l’altezza
del trapezio.
A parole
In simboli
L’area del trapezio si calcola moltiplicando Se b1 = base maggiore, b2 = base minore e
la somma delle lunghezze delle basi per h = altezza
l’altezza e dividendo il prodotto ottenuto per
(b + b )× h
due.
A= 1 2
2
La formula diretta per il calcolo dell’area di un trapezio si può ottenere anche attraverso
un’altra trasformazione.
Consideriamo il trapezio scaleno 𝐴𝐵𝐶𝐷 e indichiamo con
𝑏1 la base maggiore, con 𝑏2 la base minore e con ℎ
l’altezza.
Prolunghiamo la base maggiore con il segmento 𝐶 ′ 𝐷′ di
lunghezza congruente alla base minore 𝐶𝐷 e congiungiamo
i punti 𝐷 e 𝐷′ . Per il secondo criterio di congruenza
otteniamo due triangoli congruenti e quindi anche
equivalenti.
𝐶 ′ 𝐷′ 𝐸 ≅ 𝐶𝐷𝐸 ⇒ 𝐶 ′ 𝐷′ 𝐸 ≐ 𝐶𝐷𝐸
Il triangolo 𝐴𝐷′ 𝐷 è equivalente al trapezio 𝐴𝐵𝐶𝐷. Infatti il
trapezio 𝐴𝐵𝐶𝐷 è formato dal poligono 𝐴𝐵𝐸𝐷 e dal
triangolo 𝐶𝐷𝐸, mentre il triangolo 𝐴𝐷′𝐷 è formato dal
quadrilatero 𝐴𝐵𝐸𝐷 e dal triangolo 𝐶’𝐷’𝐸, equivalente a
𝐶𝐷𝐸.
𝐴𝐵𝐶𝐷 ≐ 𝐴𝐷′ 𝐷 ⇒ 𝐴trapezio ≐ 𝐴triangolo
Notiamo che la base del triangolo è data dalla somma della
basi del trapezio, mentre l’altezza del triangolo coincide
© Mondadori Education
con quella del trapezio.
𝑏triangolo = 𝑏1 + 𝑏2
ℎtriangolo = ℎtrapezio
In generale l’area di un trapezio è equivalente a quella di un triangolo che ha come base la
somma delle basi del trapezio e come altezza l’altezza del trapezio.
© Mondadori Education
Mettiti alla prova
1. Realizza un modello cartaceo della costruzione descritta in precedenza. Verifica che una
volta tagliato il triangolo 𝐶𝐷𝐸 è possibile costruire un triangolo che ha come base la
somma delle basi del trapezio e come altezza l’altezza del trapezio.
2. Esegui in scala 1: 1 il disegno di un trapezio isoscele che abbia la base maggiore di 6 cm,
la base minore di 4 cm e un’altezza di 3 cm. Esegui sempre in scala 1: 1 il disegno di un
triangolo che abbia per base maggiore la somma delle basi del trapezio precedente e per
altezza l’altezza del trapezio. Calcola le aree delle due figure geometriche e verifica che il
trapezio e il triangolo sono equivalenti.
[15 cm2 ]
3. Seguendo le istruzioni, realizza con un programma per la geometria dinamica un modello
che illustri la costruzione descritta in precedenza.
Per costruire un trapezio abbiamo bisogno
di due rette parallele. Realizza una prima
retta per due punti 𝐴 e 𝐵 con lo strumento
idoneo ( ).
Costruisci una retta parallela alla
precedente ( ) e individua un suo punto
𝐶.
Costruisci un trapezio utilizzando lo
strumento poligono ( ) prendendo il
punto 𝐷 sulla seconda retta creata.
Rinomina il quadrilatero in “trapezio”.
Rinomina le basi in 𝑏1 e 𝑏2 .
Crea con lo strumento circonferenza dati
centro e raggio (
) un cerchio con
centro in 𝐵 e raggio pari alla base minore
(𝑏2 ).
Con lo strumento intersezione (
)
individua il punto 𝐸 esterno al segmento
𝐴𝐵 dove la circonferenza interseca la retta
passante per 𝐴 e per 𝐵.
Nascondi le
costruzione.
Costruisci
rette
e
il segmento
il
cerchio
𝐷𝐸
(
di
) e
individua l’intersezione (
) tra il lato
obliquo 𝐶𝐷 e il segmento 𝐷𝐸.
Costruisci i triangoli 𝐵𝐸𝐹 e 𝐶𝐷𝐹.
Con lo strumento relazioni tra due oggetti (
) è possibile ora verificare che i triangoli
𝐵𝐸𝐹 e 𝐶𝐷𝐹 sono uguali, come ci mostra le relazione.
© Mondadori Education
𝐵𝐸𝐹 ≅ 𝐶𝐷𝐹 ⇒ 𝐵𝐸𝐹 ≐ 𝐶𝐷𝐹
𝐴𝐵𝐶𝐷 ≐ 𝐴𝐸𝐷
Costruisci il triangolo 𝐴𝐸𝐷 e rinominalo in modo opportuno. Ora è possibile verificare
che il triangolo 𝐴𝐸𝐷 è equivalente al trapezio 𝐴𝐵𝐶𝐷.
Se si muove uno dei vertici del trapezio questo mantiene, per costruzione, le sue proprietà
e l’equivalenza trovata rimane valida.
© Mondadori Education