2
Domanda individuale e domanda di
mercato
Che cosa vedremo in questo capitolo?
• La determinazione dell’insieme delle alternative all’interno del quale sceglie il consumatore.
• La descrizione e la rappresentazione delle sue preferenze.
• Come si determina la scelta ottima del consumatore e come varia questa scelta al variare dei prezzi e
del reddito.
• Il passaggio dalla domanda individuale alla domanda di mercato.
Dopo avere introdotto la domanda e l’offerta e averne studiato l’interazione, in questo capitolo
approfondiremo l’analisi dell’economia dal lato della domanda. Studieremo la disponibilità dei
soggetti
economici,
siano
essi
considerati
individualmente o in aggregato, a domandare e acquistare un bene o servizio dati alcuni parametri
rilevanti tra cui il prezzo. In altri termini, richiamandoci a quanto affermato nel capitolo precedente,
ci concentriamo sugli elementi che ci consentono di rispondere al quesito «in che quantità verrà
acquistato un bene?» e dunque «quali beni e servizi devono essere prodotti e in quali quantità?». Per
il momento lasciamo invece da parte i quesiti relativi alle modalità di produzione di beni e servizi e
alla loro distribuzione una volta prodotti.
Per non appesantire troppo l’esposizione, useremo il termine «beni» per riferirci all ‘insieme di beni
e servizi, distinguendoli solo nel caso in cui ciò si renda necessario. Ci concentreremo sullo studio
della domanda di beni destinati al consumo individuale, vale a dire utilizzati direttamente da chi li
domanda per soddisfare le proprie esigenze e realizzare i propri desideri. L’analisi può tuttavia
essere estesa, sotto certe condizioni, allo studio della domanda di beni non destinati direttamente al
consumo, ma, ad esempio, utilizzati come input intermedi nel processo di produzione di beni di
consumo.
L’analisi sarà di tipo microeconomico: partiremo dallo studio del singolo individuo e della sua
domanda. Quest’ultima, una volta effettuata un’opportuna aggregazione, darà origine alla domanda
di mercato di un determinato bene e servizio o addirittura alla domanda dell’intera economia.
Chiameremo l’individuo oggetto della nostra trattazione «consumatore», ma la quasi totalità
dell’analisi proposta rimarrebbe inalterata se considerassimo quale soggetto individuale di scelta la
famiglia (ipotizzando che esistano modalità di sintesi di eventuali divergenze di opinione al suo
interno) e non il suo singolo componente.
Scopo di questo capitolo è capire quale sia il processo decisionale dell’individuo nello scegliere
quali beni domandare e in quali quantità, cioè quali siano le determinanti della domanda
individuale. Vedremo poi come, sommando le domande individuali di tutti i soggetti economici che
domandano un certo bene, si ricavi la domanda di mercato ditale bene.
28
1. ECONOMIA E SCELTA RAZIONALE
Come è descritto in microeconomia il problema di scelta del consumatore?
Come abbiamo visto, adottare un approccio microeconomico significa studiare il comportamento
degli agenti individuali. In particolare l’agente, nel caso dello studio della domanda individuale di
beni destinati al consumo, è il consumatore, cioè colui che prende decisioni circa quali e quanti beni
consumare e, dunque, domandare. Per studiare il comportamento degli individui, l’analisi
microeconomica non si sofferma sulle loro azioni, ma sulle conseguenze ditali azioni, descrivendo
queste ultime come variazioni nell’insieme delle risorse disponibili di un individuo. In questo
modo, ad esempio, l’azione di acquistare un’automobile a un prezzo di 10 mila euro può essere
descritta come una variazione nelle disponibilità dell’acquirente caratterizzata dall’aumento di
un’unità nella sua disponibilità di automobili e dalla diminuzione di 10 mila euro nella sua
disponibilità di denaro1.
Il comportamento degli individui viene descritto in un’ottica che si dice consequenzialista. Secondo
tale ottica si considera la scelta tra diverse azioni soltanto come una che da esse deriva no il
comportamento del consumatore è dunque descritto come scelta tra stati alternativi della sua
disponibilità di beni. Nell’esempio precedente uno dei beni a disposizione del consumatore era il
denaro, che però è ovviamente un bene molto particolare. Esso infatti è mezzo di scambio e unità di
conto, ma non ha caratteristiche che lo rendano idoneo al consumo finale, se non per eccezioni del
tutto trascurabili2.
Generalmente, per rappresentare l’insieme delle allocazioni tra le quali il consumatore sceglie, non
si considera esplicitamente la moneta, riconoscendo implicitamente ad essa solo valore di unità di
conto, e si esprime il valore di mercato dei diversi beni in termini relativi, come se ci si trovasse in
un’economia di puro baratto. Ad esempio, l’insieme delle alternative a disposizione di un agente
dotato di una ricchezza pari a 20 mila euro sarà costituito da tutte le possibili combinazioni dei beni
disponibili nel mercato che è possibile acquistare spendendo al massimo quella cifra; se i beni
disponibili sono solo automobili che hanno un prezzo unitario pari a 10 mila euro e crociere che
hanno un prezzo unitario per persona pari a 2.500 euro, le alternative a disposizione saranno: 2
automobili e nessuna crociera, 1 automobile e un numero di crociere non superiore a 4, nessuna
automobile e un numero di crociere non superiore a 8. Se indichiamo con C le crociere e con A le
automobili, l’insieme delle alternative disponibili sarà: (2A, OC), (lA, 4C), (lA, 3C), (lA, 2C), (lA,
1C), (lA, OC), (OA, 8C), (OA, 7C), (OA, 6C), (0A, 5C), (OA, 4C), (OA, 3C), (OA, 2C), (OA, 1C),
(OA, OC).
Il comportamento del consumatore è descritto dalla scelta tra queste alternative, cioè tra le dotazioni
di cui è in grado di disporre a seconda dei piani di acquisto che realizza. In genere si ipotizza che un
agente economico sia razionale e, quindi, che tenga un comportamento, o effettui una scelta, solo se
esso è idoneo a raggiungere i suoi obiettivi individuali, comunque essi siano specificati. Dunque
un consumatore che abbia un comportamento razionale sceglierà quell’alternativa di acquisto che
rende massima la sua soddisfazione. L’analisi microeconomica e, in particolare, il problema del
consumatore possono dunque essere descritti come un’applicazione ai problemi economici della
teoria della scelta razionale in un’ottica consequenzialista. Questo approccio può essere interpretato
in due modi: a) positivo o descrittivo; b) normativo o prescrittivo.
1.1. Interpretazione positiva o descrittiva
Consideriamo la teoria come una descrizione di ciò che farebbe un consumatore perfettamente
razionale preoccupato solo delle conseguenze delle proprie azioni. Secondo questa interpretazione
1
Una descrizione più particolareggiata della medesima azione, sempre nella stessa ottica, terrebbe conto anche del
consumo di energia necessario a raggiungere il concessionario, del tempo impiegato, ecc.
2
Se si esclude il piacere perverso di chi trovi opportuno accendere il sigaro con le banconote.
29
la nostra teoria vale solo se l’agente economico considerato è perfettamente razionale (nel modo
definito in precedenza) e non consente dunque di rappresentare e analizzare comportamenti
irrazionali o dettati da una razionalità non consequenzialista.
1.2. Interpretazione normativa o prescrittiva
In alternativa possiamo dare alla teoria un’interpretazione prescrittiva e affermare, ad esempio, che
le conclusioni alle quali arriva la teoria del consumatore ci dicono come si dovrebbe comportare,
cioè come dovrebbe scegliere, un consumatore che abbia come unico obiettivo la massimizzazione
della soddisfazione derivante dalle conseguenze delle sue azioni, quali che siano le sue preferenze
individuali.
Anche l’analisi del comportamento del consumatore è dunque soggetta a queste due interpretazioni
alternative. In seguito, nel tentativo di delineare una prima approssimazione della realtà e sapendo
di poter fornire in questo modo un costrutto organico e coerente che descriva il funzionamento del
sistema di domanda di un’economia, ipotizzeremo che i consumatori siano razionali (nel senso
sopra esposto) e ci riferiremo dunque a un’interpretazione descrittiva della teoria della scelta
razionale.
30
2. L’INSIEME DELLE ALTERNATIVE E IL VINCOLO DI BILANCIO
Come è descritto l’insieme delle alternative tra le quali sceglie il consumatore?
Se la teoria microeconomica, e in particolare quella del consumatore, costituisce un’applicazione
della teoria della scelta razionale dobbiamo innanzitutto definire l’insieme delle alternative al quale
si applica la razionalità del consumatore. Come abbiamo ricordato nell’introduzione al capitolo
l’analisi della domanda tenta di dare una risposta al quesito: «quali beni devono essere prodotti e in
quali quantità?». Questa domanda, riferita all’approccio individualista e consequenzialista e alla
scelta razionale, diventa: «di quali beni e servizi il consumatore vuole la disponibilità? In che
quantità?». Dalla risposta a questo quesito si ottengono la domanda individuale per un dato bene e,
per aggregazione, la domanda di mercato e quella dell’intera economia. Se invece che il consumo
considerassimo la produzione, il quesito analogo riguarderebbe i mezzi di produzione e le quantità
di questi ultimi che il produttore desidera avere a disposizione. Otterremo la domanda, individuale e
di mercato, dei mezzi di produzione.
L’insieme delle alternative tra le quali il consumatore sceglie è costituito dall’insieme di beni e
servizi almeno potenzialmente a sua disposizione. Tale insieme è necessariamente finito sia nel
numero delle componenti, che è un dato dipendente dalla natura e dallo stato delle conoscenze
tecnologiche, sia nella loro quantità, che dipende direttamente o indirettamente, attraverso la
produzione, dalla dotazione di risorse naturali. L’insieme delle alternative a disposizione del
consumatore è finito: a) sia caso in Cui egli si trovi in condizioni di Completa autarchia e
isolamento, cioè non possa avere alcuna relazione economica con altri agenti, come Robinson
Crusoe sopravvissuto al naufragio e sbarcato su un’isola deserta; 1’) sia nel caso in cui egli possa
invece scambiare con altri agenti o, più impersonalmente, vendere e acquistare beni sul mercato.
Nel primo caso il numero e la quantità di beni a disposizione del consumatore dipenderanno dalla
dotazione di risorse (naturali e personali) di cui egli sia in grado di appropriarsi e dai suoi piani di
produzione o trasformazione di parte ditali risorse. Nel caso invece in cui il consumatore possa
acquistare o vendere sul mercato, le alternative a sua disposizione dipenderanno dalla dotazione
iniziale di risorse possedute o, alternativamente, dal suo reddito (che non è altro che la valutazione
in termini monetari della sua dotazione di risorse), oltre che dalle caratteristiche del mercato in cui
si trova a scambiare e in particolare dai prezzi in esso prevalenti. In quel che segue considereremo
questo secondo caso e ipotizzeremo che la domanda espressa dal consumatore sia trascurabile
relativamente alle dimensioni del mercato così che egli non ha alcun potere sulla determinazione dei
prezzi dei beni scambiati, che per lui costituiscono un dato.
Partiamo dal caso più semplice e consideriamo un insieme di alternative al quale appartengano
quantità diverse di due soli beni. (Si noti che ci concentreremo sul caso di due soli beni per
semplicità espositiva; la quasi totalità dell’analisi si estende a situazioni con un numero maggiore,
ancorché finito, di beni.) Ciascuna alternativa a disposizione del consumatore è costituita da una
particolare combinazione dei due beni, che è normalmente chiamata paniere. Ad esempio se i due
beni a disposizione del consumatore sono latte e libri, i panieri a disposizione del consumatore
potrebbero essere quelli costituiti da I litro di latte e i libro (paniere A), da 2 litri di latte e 3 libri
(paniere B), da 3 litri di latte e nessun libro (paniere 0. Illustriamo questi tre panieri in un grafico
che rappresenta il quadrante positivo di un sistema di assi cartesiani (fig. 2.1). Se i tre panieri
considerati esauriscono le alternative a disposizione del consumatore, questi si troverà a scegliere
tra i punti A, B, e C nel grafico.
31
Il problema della scelta di consumo di latte e libri potrebbe naturalmente essere molto più articolato
e prevedere più di tre alternative a disposizione del consumatore. Potremmo avere panieri che
combinano diversamente le quantità già considerate di ciascuno dei beni; ad esempio un paniere con
I litro di latte e nessun libro, un altro con 3 litri di latte e 3 libri, ecc. Inoltre, potremmo avere
panieri caratterizzati da quantità diverse da quelle già considerate. Notiamo però un’importante
differenza tra i due beni in esame: mentre quantità di libri diverse da quelle considerate
corrispondono a numeri interi (oltre a nessun libro, I libro e 3 libri, possiamo avere 2 libri, 04, o 13,
ecc.), le alternative a disposizione per il latte sono molto più numerose, dal momento che includono
anche infinite frazioni di litro (possiamo avere 4 litri e mezzo di latte, 3,2 litri, 10,03452 litri, ecc.)3.
Distinguiamo dunque tra beni indivisibili, come i libri, ma anche le automobili, le crociere, e beni
divisibili, come tutti quelli che sono in genere misurati non in unità ma con misure di peso o
capacità4. Nella figura 2.2 rappresentiamo l’insieme di tutti i panieri caratterizzati da un numero non
superiore a 4 libri e da non più di 4 litri di latte. Come si vede l’insieme dei panieri è composto da
cinque segmenti rettilinei, uno per ciascun numero di libri potenzialmente a disposizione del
3
il lettore più attento alle questioni matematiche sulle prime potrebbe essere preoccupato per la correttezza di questa
affermazione; si rammenti tuttavia che stiamo considerando un insieme finito di alternative.
4
Naturalmente si potrebbe obiettare che il latte è in genere venduto solo in confezioni con una capacità data e
predefinita, ad esempio un litro oppure mezzo litro, ecc. In linea di principio comunque è possibile concepire
transazioni per quantità di latte diverse da quelle normalmente utilizzate e ci sono ancora luoghi nei quali è possibile
acquistare il latte direttamente dal produttore in qualunque quantità si desideri.
32
consumatore, incluso il caso in cui il consumatore non abbia alcun libro. In corrispondenza di
ciascun numero di libri, la quantità di latte può invece variare in maniera continua, data la perfetta
divisibilità ditale bene. Per semplicità e comodità espositiva considereremo beni perfettamente
divisibili. Ciò non costituisce in sé un limite fondamentale per la nostra analisi,
poiché i principi che guidano le scelte del consumatore nel caso di beni divisibili valgono anche nel
caso di beni indivisibili. Tuttavia considerare beni indivisibili impedisce l’utilizzo del calcolo
differenziale, il che può costituire un limite quando si voglia dare prova rigorosa dei risultati
ottenuti.
Consideriamo ora la rappresentazione grafica dei vincoli fisici ed economici cui è soggetto
l’insieme dei panieri a disposizione del consumatore. I vincoli fisici sono determinati direttamente
dalla dotazione delle risorse, mentre quelli economici dipendono non solo dall’entità di tale
dotazione ma anche dal mercato, vale a dire dalle possibilità del consumatore di scambiare con altri
agenti economici.
2.1. Vincoli fisici
Si pensi alla scelta del menù quotidiano di un navigatore solitario, vincolato dalla provvista che ha
caricato all’inizio del viaggio, o al caso di Robinson Crusoe al quale si è fatto cenno in precedenza.
In realtà, tuttavia, i vincoli fisici alle possibilità di consumo sono molto comuni e per proporre
esempi non è affatto necessario ricorrere a situazioni così estreme. Un esempio di vincolo fisico
all’insieme dei panieri a disposizione del consumatore con il quale ciascuno di noi si confronta
quotidianamente è quello dato dal tempo a disposizione. Se si considera un insieme di beni
composto da ore di tempo libero e litri di latte consumabili in un giorno, è ovvio che la quantità di
ore di tempo libero non potrà eccedere le 24, come mostra la figura 2.3.
2.2. Vincoli economici
Accanto a quelli fisici ci sono poi i vincoli economici al consumo individuale. Il consumatore potrà
consumare solo quanto già possiede o è in grado di acquistare dato quanto già possiede, cioè dato il
suo reddito. Consideriamo ad esempio il caso in cui un consumatore abbia un reddito di 10 euro e
abbia una dotazione costituita esclusivamente da latte e pasta. I prezzi di mercato di latte e pasta, sui
quali il consumatore non può influire giacché la sua dimensione è trascurabile rispetto al mercato,
sono rispettivamente di 1 euro al litro (PL = 1) e 0,5 euro al chilo (pp = 1/2). Se il consumatore
decide di consumare solo latte, ne ottiene 10 litri; se sceglie di domandare solo pasta, ottiene 20
chili di pasta; se sceglie di dividere equamente le sue disponibilità di reddito tra i due beni, avrà 5
litri di latte e 10 chili di pasta, e così via. I tre punti descritti sono rappresentati nella figura 2.4
come punti A, B e C.
33
Se uniamo tutti i punti che identificano nel grafico le alternative disponibili che risultano da un
impiego completo del reddito a disposizione del consumatore otteniamo il segmento rettilineo AB
nella figura 2.5, che divide il quadrante positivo del sistema di assi cartesiani in due sottoinsiemi.
Se utilizza tutto il suo reddito, il consumatore potrà scegliere un punto di tale segmento rettilineo.
Tutti i punti che stanno al di sotto del segmento corrispondono a panieri di cui il consumatore può
disporre senza utilizzare completamente il suo reddito, e quindi caratterizzati da quantità di almeno
uno dei beni disponibili inferiore a quella ottenibile con un pieno impiego del reddito; tutti i punti
che si trovano al di sopra del segmento AB corrispondono invece a panieri di cui il consumatore
non può disporre, dato il suo reddito e dati i prezzi. Se indichiamo con m il reddito monetario e S la
spesa del consumatore, x1 la quantità di latte e x2 quella di pasta, possiamo scrivere il vincolo di
bilancio:
[1] S = x1p1 + x2p2 ≤ m
34
Questa espressione ci dice, dati i prezzi di pasta (p2) e latte (p1), quali coppie di quantità dei due
beni possono essere acquistate dal consumatore dato il vincolo che la spesa non può eccedere il
reddito monetario. Il segmento AB nella figura 2.5 rappresenta la cosiddetta retta di bilancio che
esprime il vincolo di bilancio del consumatore come uguaglianza:
[1 .a] S = x1p1 + x2p2 = m
Questa equazione ci dice quali coppie di quantità dei due beni il consumatore può acquistare
utilizzando completamente il suo reddito m. Una semplice trasformazione algebrica dell’equazione
[1.a] ci consente di evidenziare la relazione tra le quantità dei due beni, espressa implicitamente dal
vincolo di bilancio:
[2] x1 =
m p2
−
⋅ x2
p1 p1
L’equazione [2] evidenzia alcune caratteristiche del vincolo di bilancio espresso come uguaglianza.
Come abbiamo notato sopra, esso ha forma rettilinea ed è espresso algebricamente dall’equazione di
una retta. L’intercetta della retta con ciascuno degli assi esprime il reddito del consumatore in
termini reali, e in particolare in termini del bene la cui quantità è misurata su tale asse. Si noti infatti
che per x1 = 0 il vincolo di bilancio interseca l’asse che misura la quantità di pasta (x2) ad un valore
pari a m/p2, mentre per x2 = 0 l’intercetta è pari a m/p1.
In altri termini, le intercette della retta di bilancio esprimono la quantità massima dei due beni che è
possibile acquistare, dati i prezzi e il reddito monetario. Dato che le intercette esprimono il reddito
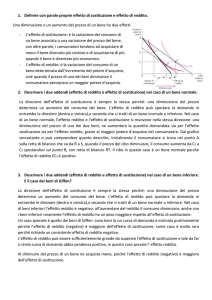
del consumatore in termini reali, un aumento del reddito monetario, a prezzi costanti, sposta il
vincolo di bilancio verso l’alto, come mostrato in figura 2.6, nella quale è rappresentata una
variazione di reddito da m¯ a m_ per m¯ < m_ .
La retta di bilancio, espressa dall’equazione [2], ha pendenza pari al rapporto tra i prezzi dei due
beni preso con segno negativo: il rapporto tra i prezzi, ovvero il prezzo relativo del bene 2 rispetto
al bene 1 (p2/p1), ci dice, per ciascuna variazione unitaria nel consumo di pasta, di quanto deve
variare il consumo di latte per mantenere costante la spesa (che nell’equazione [2] è pari all’intero
reddito). Se vogliamo che il nostro consumatore utilizzi completamente il suo reddito, a ogni
variazione unitaria di x1 deve corrispondere una variazione di segno opposto di x2 pari a p1/p2. In
altri termini il prezzo relativo esprime quante unità del bene i posso acquistare rinunciando a (o
«spendendo») un’unità del bene 2.
35
Se il prezzo del bene 2 aumenta, dato il prezzo del bene 1, aumenta anche l’inclinazione del vincolo
di bilancio, mentre, se diminuisce, si riduce anche l’inclinazione. L’opposto naturalmente vale per
variazioni del prezzo del bene 1 dato il prezzo del bene 2. Nella figura 2.7a mostriamo l’effetto sul
vincolo di bilancio di un aumento del prezzo del bene 2 da p2_ a p2¯ con p2¯ > p2_ ; nella figura
2.7b mostriamo invece l’effetto di una variazione del prezzo del bene 1 da p1_ a p1¯, con p1¯ > p1_.
Notiamo che la variazione del prezzo di un bene determina una modifica dell’intercetta della retta di
bilancio con l’asse sul quale è misurata la quantità di quel bene. In altri termini in seguito a una
variazione del prezzo di uno dei due beni la retta di bilancio ruota su se stessa avendo come fulcro
l’intercetta con l’asse che misura la quantità del bene il cui prezzo non è cambiato.
L’interpretazione di questo spostamento è abbastanza ovvia. Al crescere del prezzo di un bene la
quantità massima ditale bene che può essere acquistata dal consumatore, a reddito invariato,
diminuisce.
Notiamo che fa apparentemente eccezione il caso in cui il bene il cui prezzo varia è prodotto dal
consumatore. Tuttavia non si tratta di una reale eccezione: a un aumento del prezzo corrisponde
infatti anche un aumento del reddito del consumatore, dal momento che i suoi prodotti sono valutati
sul mercato per un importo maggiore. L’esempio è illustrato nella figura 2.8, nella quale si mostra
l’effetto di un incremento del prezzo del latte sulla retta di bilancio di un produttore di latte a parità
di quantità prodotta.
Alla variazione del prezzo da pL_ a pL¯ corrisponde una rotazione del vincolo di bilancio verso
l’esterno attorno all’intercetta con l’asse sul quale è misurata la quantità di latte. Se il consumatore
decide di tenere per sé tutto il latte che produce la sua situazione non cambia qualunque sia il prezzo
del latte; se invece decide di vendere parte del latte prodotto, la sua capacità di acquisto di pasta
aumenta all’aumentare del prezzo del latte, dal momento che può ricavare di più dalla vendita del
latte. Dunque, a eccezione del caso in cui consumi solo latte, il nostro produttore di latte può
consumare una quantità maggiore di pasta. Questo spiega la rotazione del vincolo di bilancio.
36
3. PREFERENZE E LORO RAPPRESENTAZIONE: LE CURVE DI INDIFFERENZA
Come si rappresentano le preferenze del consumatore? Quali condizioni devono essere soddisfatte
da tale rappresentazione?
Una volta descritto l’insieme delle alternative a disposizione del consumato- re, delimitato dal suo
vincolo di bilancio, dobbiamo ora studiare come egli scelga tra le alternative disponibili. La teoria
propone almeno due diversi approcci a questo problema. Il primo si basa direttamente sul
comportamento, cioè sull’osservazione delle scelte del consumatore, imponendo il rispetto di
vincoli di coerenza come presupposto della sua razionalità: il consumatore è razionale e quindi non
farà scelte incoerenti, cioè in contraddizione tra di loro. Secondo questo approccio le motivazioni
delle scelte compiute non hanno rilevanza; ci si limita a considerare ciò che è osservabile, cioè le
scelte degli individui, in un’ottica comportamentalista che, secondo alcuni, in realtà non richiede
nemmeno che l’individuo abbia obiettivi propri e li persegua deliberatamente e nella quale, alla
fine, sembra addirittura dissolversi il concetto stesso di scelta individuale.
Il secondo approccio si basa invece sull’analisi delle prefrenze del consumatore. Si ipotizza che il
consumatore abbia obiettivi propri che si riassumono in una relazione di preferenza, la quale
costituisce I oggetto primitivo dell’ analisi. Si impongono poi alcune restrizioni alle caratteristiche
ditale relazione di preferenza, che riflettono l’ipotesi fondamentale di razionalità degli agenti.
Questo secondo approccio ha il limite di avere come oggetto di indagine qualcosa di non
osservabile, cioè gli obiettivi, le preferenze individuali (mentre l’approccio precedente aveva il
pregio di avere come oggetto di osservazione il comportamento del consumatore); tuttavia, esso
sembra descrivere in modo più efficace la sovranità e l’autodeterminazione del soggetto che sceglie.
Nella presentazione che segue si privilegia, non solo per ragioni di comodità espositiva, questo
secondo approccio, più tradizionale. Partiamo dunque considerando una relazione di preferenza che
consenta al consumatore di ordinare i panieri di beni a sua disposizione, cioè di dire, per ciascuna
coppia di panieri, se ne preferisce uno all’altro o se è indifferente tra i due. Ad esempio, prendiamo
in esame le preferenze di un consumatore che abbia a disposizione i panieri A e B. Se il
consumatore preferisce strettamente A a B, scriviamo A > B; se invece il consumatore è
indifferente tra i due panieri scriviamo A ~ B; se infine il consumatore preferisce debolmente A a B,
cioè se per lui A è almeno tanto buono quanto B, scriviamo A≥ B. Queste tre relazioni di preferenza
sono tra loro correlate, giacché se è contemporaneamente vero che A≤ B e B ≥ A, ciò implica che
A~B; d’altra parte se A≥B ma sappiamo che non è vero che A~B, allora sarà vero che A>B. Per
rappresentare in modo adeguato i criteri di scelta di un consumatore razionale, queste relazioni di
preferenza devono soddisfare i due seguenti assiomi.
3.1. Completezza
Innanzitutto si richiede che il consumatore sia in grado di ordinare tutte le alternative a sua
disposizione, cioè che per ogni coppia di panieri disponibili A e B, o A è debolmente preferito a B,
o B è debolmente preferito ad A o entrambe, vale a dire che il consumatore è indifferente tra A e B.
Formalmente, o A≤B o B≥A o entrambe e dunque A~B. Questo assioma, apparentemente
abbastanza ragionevole, è in realtà molto forte se preso alla lettera, giacché richiede una capacità di
ordinamento sulla generalità delle alternative disponibili. Nei fatti esistono numerose situazioni in
cui è difficile poter ordinare le alternative a disposizione; più in generale, la scoperta delle proprie
preferenze individuali sembra essere un esercizio esistenziale di ampio respiro che per certi oggetti
richiede molto tempo. L’assioma diventa più facilmente accettabile se se ne restringe il campo di
applicazione a insiemi di alternative semplici come molte di quelle considerate negli esempi
proposti. In ogni caso l’assioma di completezza ha un fondamentale ruolo di semplificazione
dell’analisi e viene quindi in genere imposto anche per ragioni di comodità.
37
3.2. Transitività
Si richiede poi che se il consumatore considera un’alternativa almeno tanto buona quanto un’altra e
quest’ultima almeno tanto buona quanto una terza, allora considererà anche la prima almeno tanto
buona quanto la terza. Formalmente, considerando tre alternative a disposizione A, B e C, se A≥ B
e B ≥ C allora anche A ≥C. Abbiamo formulato l’assioma di transitività in termini di preferenza
debole; tuttavia, completezza e transitività insieme implicano che anche le relazioni di preferenza
forte e di indifferenza siano transitive. Questo assioma sostanzialmente impone coerenza alle
preferenze del consumatore: una sua violazione implicherebbe infatti preferenze cicliche, per cui A
è preferito a B che è preferito a C, che è preferito ad A, e così via. Come per il precedente, anche
questo assioma sembra dare una rappresentazione realistica delle preferenze individuali in molte
circostanze, ma la sua validità generale sembra opinabile, soprattutto se si considerano alternative
molto distanti dall’esperienza quotidiana del decisore. Tuttavia in mancanza di questo assioma,
ancor più che del precedente, gran parte della costruzione analitica che ci consente di
studiare il problema del consumatore verrebbe meno e dunque accettarne la validità generale è
comunque necessario per semplificare l’analisi. Come abbiamo notato i due assiomi precedenti
rappresentano le fondamenta per la costruzione analitica della teoria del consumatore. Oltre ad essi,
per comodità espositiva, è utile ipotizzare che le preferenze individuali soddisfino almeno un’altra
proprietà, che, pur essendo del tutto ragionevole nel contenuto, non è però altrettanto necessaria dal
punto di vista analitico. Si tratta dell’ipotesi di monotonicità.
3.3. Monotonicità
L’ipotesi di monotonicità richiede che tra due panieri A e B, che contengano la stessa quantità di
alcuni beni e una quantità diversa di altri beni, in modo tale che A contiene una quantità maggiore
di ciascuno di questi ultimi, il consumatore preferisca sempre A a B. Questa ipotesi implica che il
consumatore preferisce avere a disposizione una maggiore quantità di beni. Ad esempio, tra due
panieri che contengano ciascuno 20 fragole, ma dei quali il primo contenga 10 grammi e il secondo
50 grammi di panna, se vale l’ipotesi di monotonicità, il consumatore preferirà il secondo
al primo. In altri termini è come dire che ciascun bene è un «bene», cioè è
desiderabile; quindi, maggiore è la quantità di esso disponibile meglio è.
Questa ipotesi non vale nel caso in cui i panieri contengano anche elementi che abbiano una natura
che li rende sgradevoli al consumatore, cioè che siano in realtà «mali» e non beni. Tuttavia,
riformulando il problema in modo equivalente e ridefinendo tali componenti del paniere come
assenza del male considerato, l’ipotesi di monotonicità torna a valere.
38
Se valgono completezza, transitività e monotonicità è abbastanza semplice (almeno nel caso di due
beni, fin qui considerato) costruire una rappresentazione grafica delle preferenze del consumatore,
che, insieme al vincolo di bilancio, che rappresenta l’insieme delle alternative disponibili per il
consumatore, consente di individuarne la scelta ottima e dunque di illustrarne il comportamento
razionale.
Consideriamo il paniere A nella figura 2.9, che contiene una quantità lA, ad esempio 4 litri, di latte e
una quantità rA, ad esempio 3 chili, di riso. Data l’ipotesi di monotonicità tutti i panieri che si
trovano a nord-est di A sono preferiti ad A, giacché contengono una quantità maggiore di entrambi i
beni. Per la stessa ipotesi sono preferiti ad A anche tutti i panieri che contengono la stessa quantità
di uno dei beni e una quantità maggiore dell’altro bene. L’insieme di questi panieri è rappresentato
dall’area ombreggiata nel grafico, comprese le due semirette che ne costituiscono i margini. Dunque
ad esempio i panieri B, con 7 chili di riso e 5 litri di latte, e C, con la stessa quantità di riso di A e
10 litri di latte, sono preferiti ad A.
Sempre come conseguenza della monotonicità, A è preferito a tutti i panieri che sono a sud-ovest di
A e a tutti quelli che contengono la stessa quantità di uno dei due beni e una quantità minore
dell’altro (area tratteggiata nel grafico). Ad esempio il consumatore preferisce A sia a D sia a E.
Tutti gli altri panieri che si trovano nel quadrante positivo non sono immediatamente ordinabili
rispetto ad A, dal momento che contengono una quantità maggiore di uno dei due beni, ma una
quantità minore dell’altro. Consideriamo ad esempio F: contiene poco più riso rispetto ad A, ma
molto meno latte. E probabile che l’aumento nella disponibilità di riso non riesca a compensare la
riduzione nella disponibilità di latte. Consideriamo poi G. Sembra probabile che tale paniere risulti
preferito ad A, giacché a una modesta riduzione della quantità di latte corrisponde, rispetto ad A, un
notevole aumento nella disponibilità di riso.
Muovendo da F verso G, cioè per incrementi via via maggiori di riso e decrementi via via minori di
latte, incontriamo prima o poi un paniere che risulta indifferente rispetto ad A. Un paniere
indifferente rispetto ad A potrebbe verosimilmente essere il paniere H, che contiene circa 2 litri di
latte e circa 6 chili di riso. E possibile individuare moltissimi altri panieri con composizione diversa
da A rispetto ai quali il consumatore è indifferente, per esempio L o M.
Se congiungiamo tutti i punti che corrispondono ai panieri che per il consumatore sono indifferenti
rispetto ad A, otteniamo una curva che viene chiamata curva di indifferenza (fig. 2.10). Tale curva
sarà decrescente, poiché sia il riso che il latte sono desiderati dal consumatore, cioè sono «beni». In
presenza di una riduzione nella dotazione di riso del consumatore, è necessario che aumenti in
qualche misura la dotazione di latte, e viceversa, affinché egli rimanga indifferente tra i due panieri.
Tutti i panieri che corrispondono ai punti in alto e a destra della curva sono preferiti dal
consumatore rispetto a quelli che si trovano sulla curva di indifferenza, mentre tutti i panieri
corrispondenti ai punti sotto e a sinistra della curva di indifferenza sono considerati peggiori.
39
L’esercizio che abbiamo appena concluso può essere ripetuto per ogni paniere a disposizione del
consumatore: ciascun paniere, dunque, appartiene a una curva di indifferenza e le preferenze del
consumatore possono essere rappresentate da un’intera famiglia di curve di indifferenza come nella
figura 2.11. Dato un paniere, in linea di principio siamo in grado di individuare la curva di
indifferenza alla quale appartiene. Per l’ipotesi di monotonicità, dunque, dal momento che sia il
latte che il riso sono «beni», a curve di indifferenza più a nord-est corrispondono allocazioni
preferite dal consumatore. La curva di indifferenza che abbiamo denominato 14 di conseguenza,
corrisponderà ad allocazioni preferite a quelle che corrispondono a 13; lo stesso vale per 13 rispetto
a 12, e così via.
Una proprietà fondamentale delle curve di indifferenza è che esse non si intersecano mai. Infatti, se
consideriamo una situazione nella quale due curve di indifferenza si intersecano (fig. 2.12),
otteniamo un risultato contraddittorio. Per l’ipotesi di monotonicità A dovrebbe risultare
strettamente preferito a B, dal momento che contiene una quantità maggiore di entrambi i beni.
Tuttavia, se vale la rappresentazione proposta delle curve di indifferenza, sia A che B risultano
indifferenti rispetto a C, poiché ciascuno ditali panieri appartiene ad una curva di indifferenza alla
quale appartiene anche C, e dunque, per l’assioma di transitività, A e B dovrebbero essere
indifferenti tra loro (infatti se A ~ C e B ~ C allora deve essere vero che A~B). Tuttavia, A ~ B
contraddice la preferenza forte di A su B ottenuta prima. Dunque se valgono transitività e
monotonicità le curve di indifferenza non possono intersecarsi.
40
3.4. Saggio marginale di sostituzione
La curva di indifferenza ci dice in che misura uno dei beni deve essere rimpiazzato dall’altro
affinché il consumatore sia indifferente tra i due panieri. Essa ci dice quale quantità di uno dei beni
compensa esattamente il consumatore per la rinuncia a una data quantità dell’altro, cioè l’entità
della sostituzione necessaria a compensarlo nel caso rinunci, ad esempio, a un’unità di un bene,
mantenendo allo stesso tempo invariato il suo benessere o, simmetricamente, a quante unità di un
bene è disposto a rinunciare per ottenere un’unità dell’altro.
Cerchiamo di comprenderne meglio il significato sulla base della rappresentazione grafica delle
preferenze, considerando innanzitutto l’esempio più semplice, anche se nella maggior parte dei casi
irrealistico, di curve di indifferenza lineari, cioè Costituite da rette, Nella figura 2.13 è rappresentata
una curva di indifferenza lineare per due generici beni x1 e x2.
Consideriamo il paniere A, appartenente a tale curva di indifferenza, che contiene 8 unità del bene 1
e 2 unità del bene 2. Misuriamo di quanto deve aumentare la dotazione del consumatore del bene 2
a fronte di una riduzione unitaria del bene 1, affinché egli resti indifferente rispetto alla situazione
di partenza: identifichiamo cioè il paniere appartenente alla curva di indifferenza rappresentata
contenente 7 unità di x1. Chiamiamo tale paniere B. Le variazioni nelle quantità dei due beni ∆x1 e
∆x2 sono rappresentate in figura dai cateti del triangolo rettangolo che ha come estremi
dell’ipotenusa A e B. Notiamo che il rapporto tra le due variazioni ∆x1/ ∆x2, cioè il saggio al quale
il consumatore è disposto a sostituire x2 a x1 per una variazione unitaria di x1 avendo come
dotazione iniziale il paniere A, dal punto di vista geometrico corrisponde alla pendenza della retta di
indifferenza. Tale rapporto è negativo giacché le variazioni nella disponibilità dei due beni debbono
essere di segno opposto affinché si possano compensare tra loro. Dato che la pendenza di una retta è
costante in ogni suo punto, il rapporto ∆x1/ ∆x2 sarà costante qualunque sia l’ampiezza della
variazione considerata e qualunque sia il suo punto di partenza. Dunque, per compensare il
consumatore di una qualsiasi riduzione data nella sua dotazione di uno dei due beni dovremo
mettere a sua disposizione sempre la stessa quantità dell’altro bene, qualunque sia la sua dotazione
iniziale, mentre la proporzione tra le due variazioni rimarrà invariata qualunque sia la loro
dimensione.
Due beni per i quali valga questo tipo di relazione sono detti perfetti sostituti. Tali beni sono in
grado di soddisfare il medesimo bisogno, tanto che il consumatore è disposto a privarsi
completamente di uno di essi a condizione di avere una sufficiente disponibilità di quell’altro. Si
noti che, affinché due beni siano perfetti sostituti, non è necessario che il consumatore sia disposto a
sostituirli «uno a uno», cioè che ∆x1/ ∆x2 = -1; è sufficiente che tale rapporto sia costante.
Ad esempio, ipotizzando che un consumatore sia assolutamente indifferente tra pasta e riso egli sarà
disposto a rinunciare al consumo di uno dei due per l’altro a un saggio costante; tuttavia la diversità
nella resa dei due determinerà un rapporto ∆x1/ ∆x2 diverso dall’unità. Come detto, tuttavia, il caso
41
di curve di indifferenza lineari è molto particolare. Per la maggior parte dei beni, infatti, sembra
improbabile che la rinuncia a una data quantità possa essere compensata sempre da variazioni di
ugual misura nella dotazione di un altro bene. Per fare solo un esempio, se possiedo 2 chili di
ciliegie, rinunciare a una ciliegia è indubbiamente molto meno oneroso rispetto al caso in cui ne
possieda una soltanto: dunque le variazioni compensative per lasciarmi indifferente dovranno essere
di entità ben diversa nei due casi. L’intuizione che ci viene suggerita da questo esempio
(compatibile con il buon senso) è che l’ipotesi più naturale sia che le necessità di compensazione
aumentino al diminuire della dotazione iniziale. Quanto più ridotta è la dotazione di un certo bene,
tanto più questo diventa prezioso agli occhi del consumatore, il quale richiederà dunque quantità
crescenti di un altro bene se gli si chiede di rinunciare al primo. Ciò si traduce in termini grafici in
curve di indifferenza effettivamente curvilinee con la convessità rivolta verso l’origine come nella
figura 2.14.
Si noti che con curve di indifferenza di questo tipo il rapporto ∆x1/∆x2 è molto sensibile al punto di
∆x11
∆x12
partenza e dunque
; infatti ∆x12 = ∆x22 ma ∆x11 > ∆x12 5, cioè l’aumento nella dotazione
>
1
2
∆x2
∆x2
di x1 che il consumatore richiede per essere compensato del tutto per una riduzione unitaria di x2 è
molto maggiore quando la disponibilità iniziale di x2 è più bassa. Inoltre, a differenza del caso
lineare, il valore del rapporto ∆x1/ ∆x2 varia in questo caso anche al variare dell’ampiezza di ∆x2
rispetto a un medesimo punto di partenza, come mostra la figura 2.15.
Si noti come i due triangoli corrispondenti a due diverse variazioni in x2 e dunque in x1, a partire
dallo stesso paniere A abbiano forma diversa e dunque il rapporto tra i loro cateti sia differente.
Dunque, con curve di indifferenza non rettilinee, da un lato il rapporto ∆x1/ ∆x2 varia al variare del
punto corrispondente al paniere di partenza, dall’altro anche con uno stesso punto di partenza le
differenze possono essere notevoli a seconda dell’ampiezza delle variazioni considerate.
La soluzione a entrambi questi problemi è data dall’uso di una misura puntuale: rilevare cioè il
valore di ∆x1/ ∆x2 in ogni punto appartenente alla curva di indifferenza, calcolandone il valore per
variazioni infinitesime, cioè piccolissime, di x2. Tale valore è noto come saggio marginale di
sostituzione (SMS), che è dunque il valore di ∆x1/ ∆x2 per ∆x2 tendente a 0.
5
Per il lettore che non abbia familiarità con la notazione matematica, ricordiamo che una grandezza riportata tra due barre verticali
viene considerata in valore assoluto, ignorandone cioè il segno (positivo o negativo).
42
Lo stesso concetto può essere espresso con una notazione matematica:
∆x1 dx1
=
∆x 2 → 0 ∆x
dx2
2
SMS = lim
Dal punto di vista geometrico il valore del SMS è la pendenza della curva di indifferenza nel punto
in cui viene calcolato. Dunque, muovendoci lungo curve di indifferenza non rettilinee, così come
varia la pendenza varia anche il SMS. L’analisi del saggio marginale di sostituzione è giustificata
nel caso in cui i beni considerati abbiano tra loro almeno un certo grado di sostituibilità e le curve di
indifferenza corrispondenti abbiano dunque un andamento regolare, senza punti angolosi. Ipotizzare
tale regolarità sembra una buona approssimazione della realtà in moltissimi casi. Un’importante
eccezione è tuttavia quella di beni la cui natura impone che siano consumati insieme come ad
esempio sci e attacchi o computer e mouse. Questi beni sono detti perfetti complementi.
Il consumatore può trarre beneficio dal loro consumo solo se ne ha disponibilità contemporanea in
una proporzione data: avere più di un paio di attacchi è inutile se si possiede solo un paio di sci, così
come avere molti mouse e un solo computer.
Le curve di indifferenza per beni di questo , tipo sono rappresentate nella figura 2.16. Esse sono
caratterizzate dalla presenza di un punto angoloso che corrisponde all’unica proporzione tra le
disponibilità dei due beni che ne consente un consumo proficuo. Muovendo da uno dei punti
angolosi verso destra o verso l’alto si modifica la quantità di uno dei beni senza che cambi quella
dell’altro. Tali variazioni lasciano indifferente il consumatore e infatti si resta sulla stessa curva di
indifferenza. Beni perfetti complementi violano dunque l’ipotesi di monotonicità stretta. Affinché
un incremento nel consumo di uno dei due beni consenta al consumatore di raggiungere un paniere
da lui preferito a quello originario, è necessario che tale incremento sia accompagnato da un
aumento in proporzione data della disponibilità dell’altro bene: preferisco avere due paia di attacchi
anziché uno solo se la mia disponibilità di sci aumenta da un paio a due paia; in presenza di un
incremento unitario nella mia disponibilità di paia di sci sono invece indifferente tra tutte le
variazioni positive nella mia disponibilità di attacchi, incluso l’incremento unitario. Una variazione
in proporzione data della disponibilità di entrambi i beni corrisponde nel grafico a uno spostamento
su una curva di indifferenza più elevata.
43
44
4. L’OTTIMO DEL CONSUMATORE
Come si determina e che caratteristiche ha la scelta ottima del consumatore?
In questo paragrafo raccoglieremo i frutti dall’apparato analitico costruito nei due paragrafi
precedenti, in cui abbiamo definito l’insieme delle alternative e le preferenze del consumatore.
Studieremo quale sia la scelta ottima del consumatore e come questa si caratterizzi. L’insieme delle
alternative ci dice tra quali panieri il consumatore debba scegliere, le preferenze e la loro
rappresentazione attraverso le curve di indifferenza forniscono il criterio di scelta. Consideriamo un
insieme di scelta delimitato da un vincolo di bilancio del tipo di quello rappresentato nella figura
2.5 e sovrapponiamo ad esso la più comune mappa di curve di indifferenza simile a quella
rappresentata nella figura 2.11. Otteniamo così la figura 2.17.
Innanzitutto notiamo che la scelta ottima del consumatore si collocherà sulla retta di bilancio e non
al di sotto di essa. Infatti, a qualunque paniere appartenente all’area delimitata dal vincolo di
bilancio corrisponde almeno un paniere rappresentato da un punto sulla retta di bilancio che
contiene quantità maggiori di entrambi i beni e quindi, per l’ipotesi di monotonicità, sarà preferito
dal consumatore. In altri termini, il consumatore allo scopo di massimizzare il proprio benessere,
avendo a disposizione un determinato reddito rappresentato dal vincolo di bilancio, lo utilizzerà
tutto. Tra tutti i panieri che si trovano sul suo vincolo di bilancio quale verrà scelto?
Abbiamo visto che nella formulazione standard del problema del consumatore il benessere aumenta
se ci spostiamo su curve di indifferenza via via più a nord-est, cioè più lontane dall’origine. Il
consumatore cercherà dunque di scegliere il paniere a sua disposizione che gli consenta di
raggiungere la curva di indifferenza più lontana possibile dall’origine. Questo elimina dalla rosa dei
candidati all’ottimo punti come B o C nella figura 2.17. Trattandosi di punti appartenenti alla retta
di bilancio, a nord-est di B e C non ci sono panieri raggiungibili dal consumatore; tuttavia B e C
sono indifferenti a moltissimi panieri, tutti quelli appartenenti alla curva di indifferenza di cui essi
fanno parte, che hanno invece a nord-est panieri raggiungibili e dunque preferiti dal consumatore.
Questi ultimi, per l’assioma di transitività, saranno preferiti anche a B e C che non risultano dunque
ottimi.
L’ottimo corrisponderà al punto A nella figura 2.17, cioè al punto della retta di bilancio che
appartiene contemporaneamente anche alla curva di indifferenza più a nord-est. Nessun paniere
ottenibile dal consumatore, infatti, si trova a nord-est di A né di alcun paniere appartenente alla
curva di indifferenza alla quale appartiene A. A è l’unico paniere ottenibile dal consumatore tra
quelli appartenenti alla sua curva di indifferenza.
La curva di indifferenza che passa per il punto di ottimo, A, è tangente alla retta di bilancio, cioè ha
in comune con essa solo un punto, che è appunto quello di ottimo. L’analisi matematica ci insegna
che due funzioni tangenti hanno la stessa pendenza nel punto di tangenza, dunque la curva di
45
indifferenza passante per A ha la stessa pendenza in quel punto della retta di bilancio.
L’inclinazione della retta di bilancio è data dal rapporto costante tra i prezzi dei due beni preso con
segno negativo (par. 2.2), l’inclinazione delle curve di indifferenza è data dal saggio marginale di
sostituzione, che per le curve di indifferenza più comuni, cioè quelle convesse verso l’origine, varia
se ci muoviamo lungo la curva (par. 3.4). Dunque possiamo esprimere la condizione di tangenza per
l’ottimo, in precedenza descritta graficamente, nella seguente equazione
[3] SMS =
dx1
p
=− 2
dx2
p1
In corrispondenza dell’ottimo del consumatore il saggio marginale di sostituzione è uguale al
rapporto tra i prezzi. Questa condizione ha una semplice interpretazione che ne evidenzia il
significato economico, al di là del contenuto analitico appena illustrato.
In corrispondenza della scelta ottima del consumatore, saggio marginale di sostituzione e prezzo
relativo dei beni non possono essere diversi tra loro, cioè la valutazione soggettiva del consumatore
circa la desiderabilità dei beni, che corrisponde al SMS, non può discostarsi da quella «oggettiva»
del mercato, rappresentata dal prezzo relativo. Infatti, se il SMS eccedesse in valore assoluto il
rapporto tra i prezzi, ciò significherebbe che il consumatore sarebbe disposto a cedere una certa
quantità del bene i per averne una maggiore del bene 2 a un saggio maggiore di quanto richiesto dal
prezzo di mercato. In altri termini, per avere una maggiore quantità del bene 2 il consumatore
sarebbe disposto a spendere, in termini del bene 1, più del prezzo del bene 2 prevalente sul mercato.
Non c’è dunque ragione per cui il consumatore non si approvvigioni sul mercato di una maggiore
quantità del bene 2 cedendo il bene 1; dato che il SMS tende a ridursi in valore assoluto man mano
che la dotazione del bene 2 aumenta, a un certo punto di questo approvvigionamento SMS e
rapporto tra i prezzi si uguagliano e la condizione viene ad essere soddisfatta.
Un ragionamento del tutto simile si applica al caso in cui il SMS sia inferiore in valore assoluto al
rapporto tra i prezzi, anche se, in quel caso, nello scambio che il consumatore realizzerebbe con il
mercato i ruoli di x2 e x1 sarebbero invertiti. L’altra condizione per l’ottimo del consumatore è,
come abbiamo visto, che il paniere scelto si trovi al margine superiore dell’insieme delle alternative
disponibili, cioè sulla retta di bilancio. Dal punto di vista algebrico il problema del consumatore è
dunque caratterizzabile come un sistema di due equazioni, la condizione [3] e la retta di bilancio, in
due incognite, le quantità scelte dei due beni. L’individuazione del punto di ottimo, A nella figura
2.17, corrisponde alla determinazione delle quantità di ciascun bene che il consumatore domanda,
cioè x1* e x2* . La soluzione dipende anche da variabili che sono determinate esogenamente rispetto al
problema del consumatore, quali i prezzi di mercato dei due beni e il reddito del consumatore.
Nei paragrafi 5 e 6 studieremo cosa accade alla scelta del consumatore al variare ditali variabili.
4.1. Saggio marginale di sostituzione e utilità marginale
Consideriamo un semplice esempio di formalizzazione analitica delle preferenze del consumatore
utilizzando una specifica forma funzionale per le curve di indifferenza: quella lineare, illustrata in
precedenza nella figura 2.13. Una sua possibile specificazione è la seguente:
[4] ax1+bx2 = ū
In essa ū è il livello di benessere o di utilità del consumatore per tutti i panieri che appartengono alla
specifica curva di indifferenza considerata. Spostandoci da una curva di indifferenza ad un’altra il
valore di ū cambierà, per cui possiamo scrivere
[5] ax1+bx2= u
46
che ci dice, dati i valori dei parametri a e b e per determinati livelli di consumo di ciascun bene x1 e
x2, su quale curva di indifferenza ci troviamo, cioè qual è il livello di benessere o utilità del
consumatore. Si noti che i parametri a e b esprimono le cosiddette utilità marginali rispettivamente
dei beni 1 e 2, cioè ci dicono di quanto varia l’utilità del consumatore per ogni variazione
unitaria della quantità consumata del bene corrispondente. Infatti, se dalla [5] ricaviamo
un’espressione per la variazione totale dell’utilità al variare delle quantità consumate dei due beni
[6] a∆x1 = b∆x2 = ∆u
considerando poi solo la variazione nel consumo di uno dei beni, ad esempio il bene 1, e
uguagliando a 0 quella dell’altro, otteniamo
[7] a∆x1 = ∆u
Un semplice passaggio algebrico ci consente poi di scrivere:
[8] UMG1 =
∆u
=a
∆x1
Il rapporto tra le variazioni dell’utilità e del consumo del bene 1, cioè l’utilità marginale di
quest’ultimo (UMG1), è pari ad a. Lo stesso naturalmente vale per x2 e b, per cui:
[9] UMG2 =
∆u
=b
∆x2
Fatte queste osservazioni, ci è ora possibile individuare la relazione tra utilità marginali e saggio
marginale di sostituzione, fornendo così un’interpretazione alternativa del SMS. Consideriamo,
infatti, due variazioni simultanee di x1 e x2 che mantengano inalterata l’utilità del consumatore, cioè
che ci facciano muovere da un punto a un altro appartenente alla stessa curva di indifferenza. Tali
variazioni devono soddisfare la seguenti equazione
[10] a∆x1 + b∆x2 = ∆u = 0
Dalla [10] si ricava l’espressione seguente, che individua la relazione che cercavamo tra SMS e
utilità marginali:
[11] SMS =
b
UMG2
∆x1
=− =−
∆x2
a
UMG1
Il SMS tra due beni è dunque uguale al rapporto tra le loro utilità marginali considerato con segno
negativo. Tale segno è spiegato dalle stesse ragioni che spiegano l’inclinazione negativa delle curve
di indifferenza: affinché l’utilità rimanga costante, a una variazione positiva nel consumo di un bene
deve corrispondere una variazione negativa in quello dell’altro. È possibile dimostrare che la
relazione tra SMS e utilità marginali espressa dalla [11] è generale e, dunque, non vale solo in
questo caso specifico.
Utilizzando la [11] possiamo riscrivere la condizione di equilibrio [3] come segue:
47
[12]
UMG2 p2
=
UMG1 p1
Mettendo a sistema questa espressione con l’equazione [l.a] della retta di bilancio,
[l.a] x1p1+x2p2=m
che costituisce l’altra condizione per l’ottimo del consumatore, abbiamo due equazioni in due
incognite, x1 e x2. Risolvendo il sistema possiamo determinare il livello ottimo di consumo dei due
beni
in
funzione
dei
loro
prezzi,
p1
e
*
*
p2, e del reddito m, che indichiamo genericamente come x1 (p1, p2, m) e x2 (p1, p2, m).
In generale l’ottimo del consumatore appartiene alla retta di bilancio e soddisfa la condizione di
uguaglianza tra e rapporto dei prezzi. Tuttavia, mentre la prima ditali condizioni è sempre
soddisfatta, poiché discende direttamente dalle ipotesi sulla razionalità individuale del consumatore,
e in particolare da quella di monotonicità, la seconda non lo è sempre, dal momento che dipende
dalla struttura delle preferenze e dal suo rapporto con i prezzi dei beni. Ricordiamo in particolare tre
principali eccezioni all’applicazione ditale condizione che comportano tutte soluzioni cosiddette
d’angolo per il problema del consumatore.
Il primo esempio è quello di curve di indifferenza che, pur avendo la classica forma con la
convessità verso l’origine, sono caratterizzate da un SMS sempre maggiore o sempre minore del
rapporto dei prezzi.
Questa situazione è descritta nella figura 2.18 per il secondo di tali possibili casi. L’ottimo del
consumatore è rappresentato dal paniere corrispondente al punto A che contiene esclusivamente il
bene x1.
Il consumatore le cui preferenze sono qui rappresentate ha una predilezione talmente forte per il
bene 1, che il suo SMS è sempre inferiore al rapporto tra i prezzi dei due beni. In altri termini, egli
non trova sul mercato nessuno disposto a pagare il prezzo che pretende per cedere x1, anche quando
il bene 1 è l’unico bene da lui posseduto.
Il secondo esempio di ottimo del consumatore che non soddisfa la condizione di uguaglianza tra
SMS e rapporto dei prezzi è quello di beni perfetti sostituti rappresentato nella figura 2.19. Anche in
questo caso l’ottimo è rappresentato dal punto A. Il paniere corrispondente contiene una quantità
positiva solo del bene 2. Ciò dipende dalla natura stessa di perfetti sostituti dei beni considerati, per
cui il consumatore, non avendo nessun vantaggio a consumare quantità positive di entrambi
48
contemporaneamente, si concentrerà su quello dei due che ha un miglior rapporto tra prezzo e
rendimento.
Dal momento che la mappa delle preferenze in questo caso è formata da rette, il SMS sarà, come
abbiamo visto prima, costante e potrà uguagliate il rapporto tra i prezzi solo in un caso fortuito6.
Nell’esempio considerato il SMS è più grande in valore assoluto del rapporto tra i prezzi e il
consumatore per avere x2 è disposto a cedere quantità del bene 1 maggiori di quanto richiesto dal
mercato. Si noti che nel caso in cui la retta di bilancio fosse più inclinata delle rette di indifferenza il
consumatore domanderebbe solo x1.
L’ultimo esempio di ottimo nel quale non vale la condizione [3] è quello di beni perfetti
complementi. Per le curve di indifferenza ditali beni, rappresentate nella figura 2.16 non è possibile
definire e calcolare il SMS. Dal momento che tali beni devono essere consumati in una proporzione
data, il consumatore potrà essere in una di due condizioni possibili: o è già in possesso dei beni
nella proporzione desiderata, e allora non vorrà scambiare, o non ha un paniere che rispecchi tale
proporzione e allora è disposto a cedere tutta la quantità in eccesso del bene che possiede in
abbondanza per ottenere un incremento anche solo infinitesimo nella sua disponibilità dell’altro.
L’ottimo di questo caso è descritto nella figura 2.20.
6
In tale caso fortuito la curva di indifferenza più alta che abbia un punto in comune con la
retta di bilancio coincide con essa e dunque qualunque punto che appartenga alla tetta di bilancio è un punto di ottimo.
49
5. EFFETTI SULLA QUANTITÀ DOMANDATA DI VARIAZIONI DEL REDDITO
Come cambiano le scelte del consumatore al variare del suo reddito?
Nel paragrafo precedente abbiamo studiato la determinazione dell’ottimo del consumatore; abbiamo
visto che esso dipende dal reddito del consumatore e dai prezzi dei beni e abbiamo sottolineato
queste relazioni scrivendo le quantità domandate dei beni 1 e2 come x1* (p1, p2, m) e x2* (p1, p2, m).
in questo paragrafo studiamo come la quantità domandata di un certo bene muti al variare del
reddito a disposizione del consumatore. Questa analisi sarà condotta isolando l’effetto di variazioni
del reddito da altri effetti, e, in particolare, dalle variazioni dei prezzi, che a questo scopo
considereremo costanti. Nel paragrafo 2.2 abbiamo visto che una variazione del reddito del
consumatore si rappresenta con uno spostamento della sua retta di bilancio. In particolare, aumenti
di reddito comportano spostamenti verso nord-est della retta, aumentando le dimensioni
dell’insieme delle alternative disponibili, mentre riduzioni di reddito comportano uno spostamento
opposto, verso l’origine, e una riduzione dell’insieme delle alternative disponibili. Se a fronte di
variazioni nel reddito i prezzi rimangono costanti, tali spostamenti del vincolo di bilancio saranno
paralleli, cioè la sua inclinazione, che corrisponde al prezzo relativo, rimarrà invariata.
Nella figura 2.21 rappresentiamo un esempio dell’effetto di un aumento di reddito sul consumo dei
beni 1 e 2.
A seguito dell’aumento del reddito, l’ottimo del consumatore si sposta dal punto A al punto B.
A un aumento del reddito consegue un aumento nella quantità domandata di entrambi i beni: il
consumatore, diventato più ricco, ha modo di soddisfare i suoi bisogni con quantità maggiori dei
due beni. Il consumo del bene 2 aumenta da x2A a x2B , mentre quello del bene 1 aumenta da x1A a x1B .
Che incrementi di reddito causino aumenti nel consumo dei beni non ci sorprende, sembra del tutto
naturale. I beni per i quali questo vale sono detti beni normali e costituiscono la maggior parte dei
beni tra i quali siamo soliti scegliere.
A questa regola abbastanza generale fa eccezione una tipologia di beni noti come beni inferiori. I
beni inferiori sono beni per i quali a un aumento di reddito del consumatore consegue una riduzione
nel consumo. Un esempio di bene inferiore è il cibo di bassa qualità: se un consumatore ha a
disposizione un reddito basso, si adatta a mangiare cibi che gli garantiscano il necessario apporto
nutritivo anche se sono di qualità scadente. Nei paesi poveri o con distribuzione molto disuguale del
reddito scelte di consumo di questo tipo sono molto comuni. Al crescere del reddito molti degli
alimenti di bassa qualità vengono sostituiti da cibi migliori sia per il gusto che per le loro qualità
fisico-chimiche. Il caso di un bene inferiore è illustrato nella figura 2.22. Il bene 2 è inferiore poiché
a fronte di un aumento di reddito il suo consumo si riduce da x2A a x2B . Notiamo che nel caso in cui
si considerino solo due beni, essi non possono essere entrambi inferiori: se uno è inferiore, l’altro
sarà per forza normale.
Se consideriamo gli effetti di variazioni del reddito sulle scelte di consumo considerando una
sequenza di possibili livelli di reddito del consumatore e quindi congiungiamo tutti i punti di,
ottimo ottenuti, possiamo costruire una curva che ci dice come variano le quantità domandate dal
consumatore al variare del suo reddito. Tale curva è rappresentata nella figura 2.23 ed è nota come
sentiero di espansione del reddito (SER). Per i beni normali il SER è sempre inclinato
positivamente.
Possiamo infine separare le informazioni contenute nel SER per ciascuno dei due beni e
rappresentare l’evoluzione della quantità domandata per ciascun bene al variare del reddito. Tale
rappresentazione, proposta nella figura 2.24, è nota come curva di Engel. La curva di Engel
rappresenta una funzione di domanda del bene x al variare del reddito del consumatore, a fronte di
prezzi costanti del bene x e di tutti gli altri beni. Nel caso di beni normali tale funzione sarà
crescente, giacché al crescere del reddito cresce anche la domanda ditali beni. Per ragioni
simmetriche, nel caso di beni inferiori, essa sarà decrescente.
50
51
6. EFFETTI SULLA QUANTITÀ DOMANDATA DI VARIAZIONI DEI PREZZI
Come cambia la quantità domandata di un bene al variare del suo prezzo?
In questo paragrafo, analogamente a quanto fatto in quello precedente, analizziamo gli effetti di
variazioni dei prezzi dei beni sulla scelta ottima del consumatore. Tuttavia, a differenza di quanto
avviene per le variazioni di reddito, in genere quelle di prezzo non possono essere isolate da effetti
derivanti da variazioni di altre variabili che condizionano la scelta del consumatore, segnatamente,
da variazioni nel reddito disponibile. Infatti, variazioni dei prezzi dei beni modificano l’insieme
delle alternative disponibili, facendo variare il vincolo di bilancio, e dunque agli effetti di prezzo si
accompagnano inevitabilmente effetti di reddito. Consideriamo ad esempio la variazione di prezzo
presentata nella figura 2.25 quando la retta di bilancio del consumatore si sposta da AB ad AC in
conseguenza della riduzione del prezzo del bene 2.
L’effetto della variazione del prezzo di un dato bene (ad esempio il bene 2) sulla quantità
domandata dello stesso bene può essere scomposto in due parti note come effetto di sostituzione ed
effetto di reddito. Tale scomposizione è puramente virtuale, ma ci consente di distinguere la
variazione del comportamento del consumatore attribuibile alla variazione del prezzo in sé (effetto
di sostituzione), da quella causata dalla variazione indotta del reddito disponibile, misurato come
potere di acquisto, anche noto come reddito reale. Si noti che all’aumentare del prezzo di un bene, il
reddito reale del consumato- re si riduce, giacché diminuisce la sua capacità di acquisto del bene
considerato. Viceversa, naturalmente, se il prezzo di un bene si riduce, il reddito reale aumenta.
La variazione del prezzo di un bene, a parità di prezzo dell’altro bene, comporta una rotazione del
vincolo di bilancio, poiché, come abbiamo visto, l’inclinazione di tale retta è data dal rapporto tra i
prezzi. Si avrà una rotazione verso l’esterno in corrispondenza di diminuzioni del prezzo, verso
l’origine viceversa. In entrambi i casi il reddito reale del consumatore cambia, giacché varia la
quantità massima del bene il cui prezzo è variato che il consumatore è in grado di procurarsi.
Se vogliamo isolare il puro effetto della variazione di prezzo abbiamo due possibilità: considerare
cosa avverrebbe alla scelta ottima del consumatore con un rapporto tra i prezzi pari a quello che si
realizza dopo la variazione di prezzo, mantenendo però costante il suo livello di soddisfazione
(utilità costante); considerare cosa farebbe il consumatore una volta mutato il rapporto tra i prezzi se
avesse a disposizione un reddito reale pari a quello che aveva prima della variazione di prezzo
(reddito costante).
Graficamente, nella prima alternativa, rappresentata nella figura 2.25 e nota come compensazione
hicksiana, consideriamo il punto di tangenza (E) tra una retta di bilancio con l’inclinazione data dal
nuovo rapporto tra i prezzi e la curva di indifferenza alla quale apparteneva l’ottimo prima della
variazione (E1’). In altri termini dopo aver fatto variare il prezzo modifichiamo il reddito del
consumatore in modo che quest’ultima variazione compensi perfettamente la prima e quindi,
restando sulla stessa curva di indifferenza, valutiamo il puro effetto della variazione di prezzo, cioè
l’effetto di sostituzione a benessere o utilità costante.
Nel secondo caso, noto come compensazione di Slutsky e rappresentato in figura 2.26, facciamo
invece ruotare il vincolo di bilancio attorno al punto di ottimo originario e determiniamo poi il
nuovo ottimo nella maniera consueta, applicando la condizione di tangenza. In questo modo la pura
variazione di prezzo, cioè l’effetto di sostituzione, viene valutata a potere d’acquisto costante.
In entrambi i grafici abbiamo chiamato E1 l’ottimo prima della variazione di prezzo ed E2 quello
dopo la variazione di prezzo, mentre abbiamo identificato come E1’ la posizione intermedia mai
raggiunta realmente e funzionale solo alla scomposizione dei due effetti. L’effetto di sostituzione è
rappresentato graficamente dallo spostamento dal punto E1 al punto E1’; l’effetto di reddito dallo
spostamento da E1’ a E2.
Qualunque sia la sua rappresentazione, l’effetto di sostituzione ha sempre segno negativo: nel caso
in esame, caratterizzato da una diminuzione del prezzo del bene 2, nella rappresentazione a utilità
costante il nuovo punto di tangenza sarà in corrispondenza di un SMS più basso in valore assoluto,
e, dato che con curve di indifferenza convesse il SMS è decrescente, il nuovo ottimo sarà a sud- est
52
del precedente e dunque ad esso corrisponderà una quantità più elevata del bene 2; nel caso a
reddito costante la rotazione del vincolo di bilancio attorno al punto di ottimo fa sì che il vincolo
diventi secante della curva di indifferenza alla quale apparteneva l’ottimo iniziale e dunque la
variazione indotta dalla diminuzione del prezzo di x1 non può che comportare un aumento nella
quantità domandata del bene 2. Al ridursi del prezzo di un bene, il consumatore, notando che questo
bene è diventato relativamente più economico rispetto ad altri sostituti, decide di sostituire almeno
in parte questi ultimi con il bene divenuto più economico. Di qui l’aumento della domanda. Lo
stesso ragionamento si applica con segno invertito per un aumento di prezzo.
A differenza dell’effetto di sostituzione, il segno dell’effetto di reddito non può essere determinato
in generale. Esso dipenderà dalla natura del bene il cui prezzo varia. Se si tratta di un bene normale,
l’effetto di reddito sarà positivo e quindi una riduzione del prezzo del bene 2, aumentando il reddito
reale del consumatore, porta a un aumento della domanda del consumatore per il bene 2. Dunque
l’effetto di reddito andrà a sommarsi all’effetto di sostituzione. Nel caso invece di beni inferiori,
l’effetto di reddito sarà negativo e dunque avrà segno opposto all’effetto di sostituzione, che tenderà
a controbilanciare.
Anche nell’ipotesi di effetto di reddito negativo, e cioè di un aumento della domanda di un bene a
fronte della riduzione del reddito reale, il caso più frequente è comunque quello di un effetto
complessivo di segno opposto rispetto alla variazione del prezzo per via della prevalenza
dell’effetto di sostituzione sull’effetto di reddito. Fanno eccezione a questa regola — conosciuta
come legge della domanda — i beni cosiddetti di Giffen la cui domanda diminuisce al diminuire del
prezzo. Un esempio di bene di Giffen è il bene 2 nella figura 2.27: al ridursi del suo prezzo la
quantità domandata diminuisce da x2E1 a x2E 2 . Osserviamo che l’effetto di sostituzione (E1 — E1’) ha
il consueto segno negativo: la diminuzione del prezzo del bene x2 comporta un aumento della
quantità domandata di tale bene; l’effetto di reddito (E1’ — E2) ha anch’esso segno negativo e, dal
momento che la variazione del reddito ha segno opposto a quella del prezzo, riduce la quantità
domandata x2. Si noti dunque che un bene per essere un bene di Giffen deve anche essere un bene
inferiore. Infatti, se a reddito reale costante diminuisce il prezzo di un bene, la domanda ditale bene
aumenterà; quindi, per avere un effetto complessivo di diminuzione della domanda causato da una
riduzione del prezzo è necessario che ci sia un effetto di reddito negativo e che questo prevalga,
cioè è necessario che il bene sia inferiore, anzi, che lo sia in misura talmente accentuata da più che
compensare l’effetto di sostituzione.
53
I beni di Giffen sono però più un curiosum teorico che una diffusa tipologia di beni, giacché si
fatica ad immaginarne uno. Di quale bene infatti pensiamo di diminuire il consumo se il suo prezzo
diminuisce?7
Come per le variazioni del reddito anche per le variazioni dei prezzi dei beni si possono costruire
relazioni che ci dicono quale sia la scelta ottima del consumatore in corrispondenza di qualunque
valore ammissibile della variabile da cui questa scelta dipende, cioè in questo caso del prezzo del
bene considerato. La prima di queste che consideriamo è il sentiero di espansione del
prezzo (SEP), rappresentato in figura 2.28.
Il SEP è costituito dall’insieme di punti di ottimo del consumatore al variate del prezzo di uno dei
beni, rappresentato nello spazio che misura i due beni tra i quali il consumatore sceglie. La figura
mostra alcune rette di bilancio caratterizzate da inclinazioni via via inferiori, che corrispondono a
prezzi via via inferiori del bene 2. Al ridursi del prezzo del bene 2, il consumatore aumenta
progressivamente la quantità domandata ditale bene (dunque il bene 2 non è un bene di Giffen).
Le informazioni circa le variazioni della quantità domandata di un bene al variare del suo prezzo
contenute nel grafico della figura 2.28 possono essere isolate da tale rappresentazione e presentate
separatamente in un grafico, riportato nella figura 2.29.
Esso illustra una relazione tra x1 e p1 nota come funzione di domanda. Tale relazione indica appunto
qual è la quantità del bene x1 domandata dal consumatore al variare del suo prezzo, per valori dati
del prezzo di x2 e del reddito del consumatore m. Tale rappresentazione della funzione di domanda
può essere indicata algebricamente sia come x1(p1), che come x1(p1¯, m¯ ): mentre la prima
alternativa è quella più frequentemente utilizzata per la sua sinteticità, la seconda ha il pregio di
sottolineare come la quantità domandata di un bene dipenda, oltre che dal suo prezzo, anche da altre
variabili, come il prezzo di altri beni e il reddito monetario. Al fine di rendere più chiara l’analisi
delle relazioni tra quantità domandata e prezzo del bene, queste variabili sono prese come un dato.
Tuttavia è bene ricordare che la quantità domandata di un bene dipende anche da altre variabili oltre
al prezzo ditale bene e che quando si prescinde dal considerare questi altri effetti ci si concentra
solo su una, pur se importante, delle determinanti della quantità domandata. Come si vede la
funzione di domanda ha un andamento decrescente, cioè al decrescere del prezzo la quantità
domandata del bene aumenta. Questo vale per quasi tutti i beni; unica eccezione sono i beni di
Giffen per i quali la funzione di domanda è invece crescente.
7
Un possibile esempio è quello dei beni di status, la cui capacità di soddisfare il bisogno dell’acquirente di segnalare la
propria condizione di benestante, diminuisce al diminuire del prezzo.
54
Nell’analisi di questo paragrafo ci siamo concentrati sugli effetti diretti di variazioni di prezzo di un
bene sulla domanda dello stesso bene. Tuttavia, dall’analisi delle figure 2.25-2.28 risulta chiaro che
esiste anche un effetto incrociato delle variazioni di prezzo, cioè che a variazioni del prezzo di un
bene corrispondono variazioni anche nella quantità domandata dell’altro bene considerato. Ad
esempio, nel caso della figura 2.25 la diminuzione del prezzo del bene 2 provoca un aumento della
domanda non solo del bene medesimo ma anche del bene x1. In questo caso dunque l’effetto
incrociato è dello stesso segno di quello diretto, ma si danno anche casi in cui l’effetto incrociato è
di segno opposto, come nell’esempio estremo di beni perfetti sostituti rappresentato in figura 2.19.
Anche per gli effetti di prezzo incrociati c’è una compresenza di effetti di sostituzione e di reddito.
L’incertezza circa il segno dell’effetto di reddito vale anche qui come per gli effetti diretti; l’effetto
di sostituzione, al contrario, non ha segno univoco per gli effetti incrociati di prezzo. 11 segno della
variazione della quantità domandata di un bene al variare del prezzo di un altro potrà essere sia
positivo che negativo a seconda della relazione di complementarità o sostituibilità che caratterizza i
due beni. Su tali relazioni si tornerà nel capitolo seguente; tuttavia possiamo anticipare qui che per
beni sostituti l’effetto incrociato di prezzo ha segno positivo, cioè, come è ovvio, all’aumentare del
prezzo di un bene aumenta la domanda di un bene suo sostituto, mentre avrà segno negativo nel
caso di beni complementari, cioè all’aumentare del prezzo di un bene diminuisce la domanda di un
altro bene ad esso complementare (cap. 3, par. 4.2). Nel prossimo paragrafo vedremo come
dall’aggregazione delle funzioni di domanda individuale di ciascun consumatore si ottenga la
funzione di domanda dell’intero mercato di un determinato bene.
55
7. DOMANDA DI MERCATO, DOMANDA INVERSA E SURPLUS DEI CONSUMATORI
Come si passa dalla domanda individuale a quella di mercato?
7.1. Domanda di mercato
Nel paragrafo precedente abbiamo visto come dall’analisi delle scelte del singolo consumatore si
ricavi la curva di domanda individuale, cioè la relazione che ci dice come varia la quantità che il
consumatore domanda di un certo bene al variare del prezzo del bene medesimo e anche di altri
beni a questo complementari odi questo sostituti. Nella figura 2.29 abbiamo poi visto come si
rappresenta la principale relazione contenuta nella funzione di domanda, cioè quella che lega la
quantità domandata di un bene al suo prezzo. L’insieme delle domande individuali di un certo bene
di ciascun consumatore appartenente ad un determinato territorio individua la domanda di mercato
di quel bene8. Quest’ultima può essere ricavata attraverso un semplice processo di aggregazione
come somma delle domande individuali di tutti i consumatori. La domanda individuale ci dice per
ciascun prezzo di un determinato bene qual è la quantità domandata da parte di ciascun
consumatore, la domanda di mercato sintetizza le informazioni contenute in più domande
individuali indicando quale sia la somma delle quantità domandate da tutti i consumatori per
ciascun livello del prezzo del bene considerato. Ad esempio si consideri un mercato del bene i in cui
siano presenti solo due consumatori A e B. Nella seconda e nella terza colonna della tabella 2.1
sono riportate le quantità domandate da ciascun consumatore (rispettivamente x1A e x1B ) in
corrispondenza di tre possibili livelli del prezzo p1 indicati nella prima colonna; nella quarta
colonna sono indicati i rispettivi livelli della domanda di mercato (X1= x1A + x1B ).
Dal punto di vista grafico la domanda di mercato sarà la somma verticale delle domande individuali
dei consumatori. Nella figura 2.30 abbiamo tracciato le curve di domanda individuali e quella di
mercato (in grassetto) alle quali appartengono i valori riportati nella tabella9.
Tab. 2.1. Esempio di aggregazione delle domande individuali
P1
x1A
x1B
X1
1
2
4
8
6
2
4
3
1
12
9
3
Se consideriamo un contesto più generale e indichiamo con ti il numero di consumatori presenti in
un determinato mercato, possiamo dunque scrivere che la domanda di mercato del bene 1 è
n
X1(p1)= ∑ x1i ( px1 ) , cioè appunto la somma delle domande individuali di tutti i consumatori. Ancora
i =1
più in generale, evidenziando la dipendenza della domanda di un bene anche dal reddito monetario
n
e dal prezzo di altri beni, potremmo altresì scrivere X1 (p1, p2, m) =
∑ x ( p , p , m) .
i =1
i
1
1
2
8
Non esiste un criterio unico e generale per stabilire quale sia il territorio di riferimento per la definizione di un mercato
di un determinato bene. Certamente un molo molto importante è svolto dai costi di trasporto che impediscono di
considerare appartenenti allo stesso mercato due consumatori che siano sufficientemente distanti tra loro da rendere per
ciascuno di essi conveniente rivolgersi a un rivenditore/produttore diverso da quello utilizzato dall’altro.
9
Bisogna comunque tenere in conto il vincolo di non-negatività sulle domande individuali e, quindi, per ottenere la
domanda di mercato ha senso sommare domande individuali solo se e quando assumono valori non-negativi.
56
7.2. Funzione di domanda inversa
L’interpretazione che abbiamo fin qui considerato della relazione tra la quantità domandata di un
bene e il suo prezzo ha evidenziato la prima come variabile dipendente e il secondo come variabile
indipendente, cioè abbiamo considerato come varia la quantità domandata al variare del prezzo. La
medesima relazione si può però leggere in senso inverso, dando luogo alla rappresentazione della
funzione di domanda nota appunto come funzione di domanda inversa. Prendendo ancora una volta
ad esempio il bene 1, indichiamo tale funzione come p1(x1), o, più in generale, come p1(x1, p2¯,
m¯). La rappresentazione grafica della funzione di domanda inversa è di fatto la medesima di quella
della funzione di domanda ad assi cartesiani invertiti (fig. 2.3 1). L’interpretazione della funzione di
domanda inversa aggiunge una prospettiva interessante, e complementare alla precedente, al nostro
studio dei fenomeni relativi alla domanda di beni. Essa ci dice per ogni quantità del bene
considerato quale dovrebbe essere il prezzo affinché i consumatori scelgano di domandare tale
quantità; ci dà dunque una misura della disponibilità a pagare del consumatore o del mercato per
una certa quantità del bene considerato. Parallelamente, la funzione di domanda inversa di mercato
ci dice qual è il prezzo che deve prevalere sul mercato affinché sia venduta una certa quantità di
bene, cioè affinché la somma delle domande individuali di tutti i consumatori sia pari a tale
quantità.
Per meglio comprendere la relazione tra domanda e domanda inversa consideriamo un semplice
esempio con una funzione lineare. La funzione di domanda di mercato del bene 1 sia
57
[13] X1 = l.000-20p1
Dalla [13] i ricava facilmente la funzione di domanda inversa:
[14] p1 = 50 −
1
X1
20
La [13] ci dice che se il prezzo del bene 1 è, ad esempio, 2, la quantità domandata di tale bene sarà
960 (infatti: X1 = 1.000-20 x 2 = 960); per converso la [14] esplicita che, affinché siano vendute
1
960 unità del bene 1, il suo prezzo deve essere pari a 2 (infatti: p1 = 50 − × 960 = 20 ).
20
7.3. Surplus dei consumatori
La nozione di funzione di domanda inversa ci consente di introdurre più chiaramente un’importante
misura di benessere dei consumatori, spesso utilizzata per i confronti tra equilibri o assetti
alternativi di un certo mercato, nota come surplus dei consumatori.
Iniziamo considerando un caso particolare nel quale il surplus dei consumatori ha
un’interpretazione immediata: la domanda di mercato di un bene che si consuma solo in quantità
discrete, cioè corrispondenti a numeri interi, e che chiameremo x1. Beni di questo tipo sono ad
esempio le automobili: ad eccezione di casi particolari ha senso domandare 1 automobile o 2 o 3,
ma non 1,36 o 2,54, ecc. Imponiamo poi l’ulteriore restrizione semplificatrice che ciascun
consumatore possa domandare al massimo un’unità del bene in questione. Quindi ciascun
consumatore i dovrà scegliere tra non domandare tale bene o domandarne un’unità e sarà
indifferente tra le due alternative per un certo livello del prezzo p1 = r1i noto come prezzo di riserva.
Ipotizziamo che i consumatori siano eterogenei rispetto al prezzo di riserva e ordiniamoli da quello
con il prezzo di riserva più alto a quello con il prezzo di riserva più basso. Otteniamo così la
rappresentazione nella quale l’altezza di ciascun rettangolo rappresenta il prezzo di riserva di un
determinato consumatore, mentre la base, che è unitaria, rappresenta la quantità domandata (fig.
2.32).
Consideriamo un generico livello del prezzo di mercato p1¯; se le caratteristiche che rendono
eterogenei i consumatori non possono essere osservate da altri oltre che da chi le possiede, o
comunque non è possibile discriminare tra consumatori, tale prezzo varrà per tutti coloro che
partecipano a tale mercato. Esso potrà coincidere con il prezzo di riserva di qualche consumatore,
che risulterà indifferente tra l’alternativa di acquistare un’unità del bene e quella di non acquistarne
alcuno. In genere ci saranno poi alcuni consumatori il cui prezzo di riserva è maggiore di p1¯, che
acquisteranno dunque il bene per tale prezzo, altri il cui prezzo di riserva è minore di p1, che,
quindi, non acquisteranno nulla. Ciascun consumatore che acquista il bene a un prezzo inferiore a
quello di riserva otterrà un surplus dallo scambio, pari alla differenza tra il proprio prezzo di riserva
e il prezzo di mercato, cioè pari a r1i − p1− . Tale surplus corrisponde all’area ombreggiata per
ciascun rettangolo nel grafico. La somma dei surplus individuali di tutti i consumatori e detta
surplus dei consumatori; esso è una misura del vantaggio collettivo che i consumatori ottengono dal
partecipare al mercato acquistando in esso il bene da loro desiderato.
Se nell’esempio sopra descritto facciamo aumentare indefinitamente il numero dei consumatori e
quindi abbiamo un numero sempre maggiore di rettangoli, ci accorgiamo che il margine superiore
del surplus dei consumatori può essere approssimato con una curva continua, che non è altro che
una porzione della funzione di domanda inversa di tale mercato. Infatti, così come la funzione di
domanda inversa, l’altezza dei rettangoli in figura 2.32 ci dice quale prezzo è necessario prevalga
affinché ci sia una certa domanda del bene considerato.
58
In generale il surplus dei consumatori sarà dunque calcolato come l’area che sta sotto la curva di
domanda inversa ed è delimitata dalla curva di domanda stessa e dal prezzo di mercato, cioè l’area
ombreggiata nella figura 2.33, nella quale sono rappresentati una funzione di domanda inversa e un
dato prezzo di mercato. Il surplus dei consumatori è un importante strumento di analisi per
l’economista poiché consente di valutare quale sia il benessere che i consumatori derivano dalla
partecipazione al mercato per un dato prezzo: attraverso di esso si potranno dunque valutare dal
punto di vista dei consumatori gli effetti, ad esempio, di misure di politica economica che
comportino variazioni nell’assetto del mercato e in particolare modifichino il prezzo del bene in
esso scambiato.
59