I MOTI NEL PIANO
Vettore posizione e vettore spostamento
Si parla di moto in un piano quando lo spostamento non avviene lungo una retta, ma in un piano, e
può essere descritto usando un sistema di riferimento cartesiano con due assi coordinati che si
intersecano nell’origine O.
Si definisce traiettoria di un punto materiale che si muove in un piano la linea formata da tutti
i punti occupati dal punto al trascorrere del tempo.
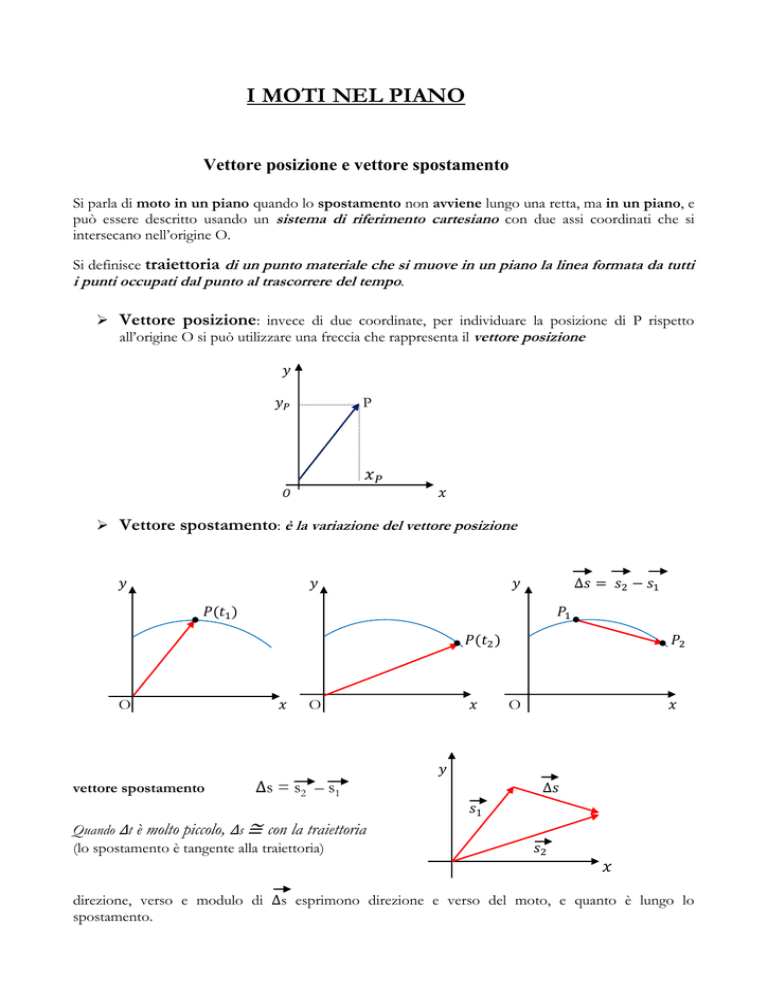
Vettore posizione: invece di due coordinate, per individuare la posizione di P rispetto
all’origine O si può utilizzare una freccia che rappresenta il vettore posizione
P
Vettore spostamento: è la variazione del vettore posizione
O
vettore spostamento
O
O
s = s2 – s 1
Quando t è molto piccolo, s ≅ con la traiettoria
(lo spostamento è tangente alla traiettoria)
direzione, verso e modulo di
spostamento.
s esprimono direzione e verso del moto, e quanto è lungo lo
Il vettore velocità
Nei moti rettilinei la direzione del vettore velocità è fissata, e coincide con la retta su cui avviene il
moto, per cui basta definire la velocità come
Il valore di
ci dice se la velocità è alta o è bassa, mentre il suo segno indica qual è il verso del moto.
Quando ci si muove nel piano, la velocità ha le tre caratteristiche di un vettore: direzione, verso e
valore numerico; nei moti non rettilinei si definisce il vettore velocità come
vettore velocità
vettore spostamento
tempo impiegato
Il vettore velocità ha sempre la direzione ed il verso del vettore
, poiché t è un numero
Se
è un intervallo di tempo finito (ad es. 4 s) la formula rappresenta la velocità vettoriale media in tale
intervallo di tempo; se invece
è un intervallo di tempo piccolissimo, il vettore rappresenta una velocità
vettoriale istantanea, che è tangente alla traiettoria.
Il moto circolare uniforme
Si chiama moto circolare un movimento la cui traiettoria è una circonferenza.
Si chiama moto circolare uniforme un moto circolare in cui il valore del vettore velocità
istantanea rimane costante.
Il moto circolare uniforme è descritto da un sistema di riferimento con l’origine O nel centro della
traiettoria circolare: il vettore posizione di un punto P della circonferenza è rappresentato da una
freccia che va dal centro O a P.
]
P
P
O
Un piccolo spostamento da P , è tangente alla circonferenza e quindi perpendicolare ad ; il vettore
velocità istantanea ha le stesse proprietà.
Periodo e frequenza.
Un punto materiale che si muove di moto circolare uniforme impiega
sempre lo stesso tempo a percorrere un giro completo.
In un moto circolare uniforme la durata di un giro completo di circonferenza è detta periodo
e si indica con il simbolo T.
es.
la lancetta dei secondi ha un periodo di un minuto, la lancetta dei minuti un periodo di un’ora, la
lancetta delle ore un periodo di 12 ore.
Si chiama frequenza del moto circolare uniforme il numero di giri compiuto in un secondo e
si indica con f.
ad es.
Periodo
0,25
0,50
1,00
2,00
4,00
10,00
Frequenza
4,0
2,0
1,00
0,50
0,25
0,10
Nel S.I. la frequenza si misura in giri al secondo, simbolo [1/s] oppure
Tale unità di misura è detta anche Hertz e si indica con il simbolo
.
Valore della velocità istantanea.
.
Il valore della velocità istantanea è dato dal rapporto fra la
distanza
percorsa in un giro e l’intervallo di tempo
impiegato. Nel moto circolare uniforme,
è pari a
,
lunghezza della circonferenza, e
è uguale al periodo .
valore della velocità [m/s]
raggio [m]
periodo [s]
Un punto materiale che si muove di moto circolare uniforme percorre archi di circonferenza che sono
direttamente proporzionali agli intervalli di tempo impiegati.
Si definisce velocità angolare
il rapporto fra l’angolo
l’intervallo di tempo impiegato per percorrerlo
percorso, misurato in
Considerando un giro completo abbiamo che
e
Se ci riferiamo ad una velocità di rotazione espressa in giri/minuto
es.
=
abbiamo che
e
L’accelerazione nel moto circolare uniforme
Nel moto circolare uniforme il vettore velocità istantanea cambia continuamente in direzione e verso,
anche se il suo valore rimane costante.
Il vettore accelerazione
è definito come
variazione del vettore velocità
vettore accelerazione
se
tempo impiegato
è un intervallo di tempo finito, quella sopra definita è l’accelerazione vettoriale media
se t è piccolissimo, il vettore a rappresenta l’accelerazione vettoriale istantanea.
.
O
Il vettore accelerazione ha sempre la direzione e il verso del vettore
valore e unità di misura.
dal quale differisce per
C’è una accelerazione tutte le volte che il vettore velocità cambia: possono
cambiare il valore della velocità, la sua direzione o il suo verso.
L’accelerazione centripeta.
Se un’auto percorre una curva circolare con un valore costante di velocità (NB: è il modulo costante, mentre
la direzione della velocità cambia!) essa subisce una accelerazione vettoriale istantanea detta accelerazione
centripeta: essa è così chiamata perché nel moto circolare uniforme il vettore accelerazione
istantanea è sempre rivolto verso il centro della circonferenza.
Si dimostra che nel moto circolare uniforme il valore dell’accelerazione centripeta è
valore dell’accelerazione [m/s2]
valore della velocità [m/s]
a=
raggio della circonferenza [m]
Poiché vale
La composizione dei moti
s1
P
P
s2
s2
P
stot
s1
Es. una persona cammina in diagonale sul ponte di una nave che intanto si sposta rispetto al molo
s1 è lo spostamento del passeggero rispetto al ponte della nave, partendo dal punto P
Intanto, rispetto al molo, P si è mosso di un tratto rappresentato dal vettore spostamento s2
Lo spostamento del passeggero rispetto al molo è dato dal vettore stot somma di s1 e s2
Se un corpo è soggetto a due spostamenti simultanei s1 e s2 , il suo spostamento
totale stot è dato dalla somma vettoriale degli spostamenti
stot =
s1 +
s2
La composizione delle velocità
Se dividiamo per t tutti i termini della formula sopra si ottiene la relazione fra le velocità vettoriali
Un corpo soggetto a due movimenti simultanei ha una velocità complessiva data dalla
somma delle due velocità












