Applicazioni del calcolo di¤erenziale:
problemi di massimo e minimo
Marco Bramanti
December 1, 2015
Abstract
Vediamo alcuni esempi di come il calcolo di¤erenziale consenta di formalizzare e risolvere problemi geometrici o di altro tipo in cui si cerca di
massimizzare o minimizzare una certa grandezza, sotto opportune condizioni.
1
Problemi di massimo e minimo di tipo geometrico
Esercizio 1 Tra i rettangoli di perimetro assegnato, quello di area massima è
il quadrato.
Sia 2p il perimetro, a; b i lati. a+b = p perciò possiamo porre a = x; b = p x
e l’area
A (x) = x (p x) ;
che ha massimo evidentemente per x = p=2; quindi è un quadrato.
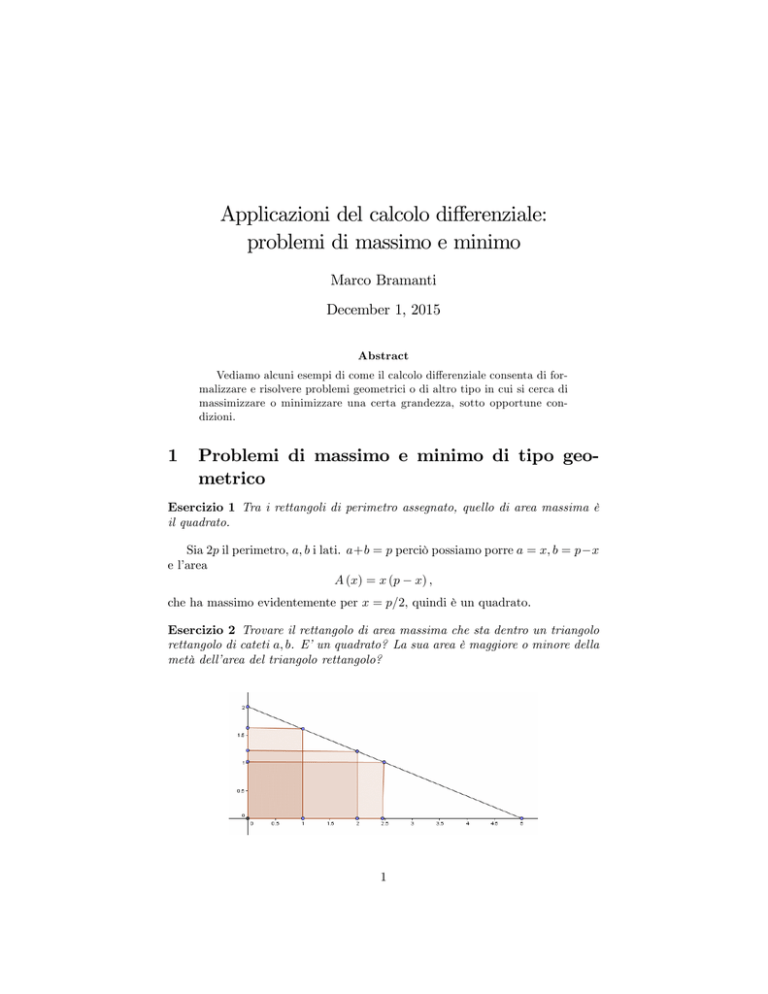
Esercizio 2 Trovare il rettangolo di area massima che sta dentro un triangolo
rettangolo di cateti a; b. E’un quadrato? La sua area è maggiore o minore della
metà dell’area del triangolo rettangolo?
1
Consideriamo il triangolo di vertici1 (a; 0) ; (0; b). L’ipotenusa sta allora sulla
retta y = b ab x. Il rettangolo ha due lati sugli assi, base x, altezza y = b ab x;
area
b 2
b
x =
x + xb;
A (x) = x b
a
a
parabola che ha massimo nel vertice x =
b
b
2a
=
a
2.
Il rettangolo quindi ha
base a=2 e altezza b=2; in generale non è un quadrato. L’area massima è ab=4;
esattamente metà dell’area del triangolo in cui è contenuto. In questo caso
il calcolo di¤erenziale non è servito perché, come nell’esempio precedente, la
funzione da massimizzare è una parabola; questa fortunata coincidenza però
non può continuare a lungo...
Esercizio 3 Trovare il rettangolo di area massima che sta dentro un cerchio di
raggio R. E’un quadrato? La sua area è maggiore o minore della metà dell’area
del cerchio?
Consideriamo la circonferenza x2 + y 2 = R2 e siano a; b i semilati del rettangolo. Per Pitagora si ha
a2 + b2 = R2
quindi possiamo porre
a = x;
p
b = R2
x2
1 Notiamo che, quando utilizziamo la geometria analitica come strumento per a¤rontare un
problema formulato col linguaggio della geometria sintetica, siamo noi a scegliere il sistema
di riferimento nel modo più comodo.
2
e l’area del rettangolo è
p
A (x) = 2a2b = 4x R2
Calcoliamo
A0 (x) = 4
=p
p
x ( 2x)
x2 + p
=4
R2
2 R2 x2
p
R2
4
R2
x2 :
x2
R2
2x2
p
x2
R2
x2
0 per
R2
;x
2
R
p (ricordare che x > 0).
2
q
2
Quindi A (x) è massima per a = pR2 ; b = R2 R2 =
denza del quadrato. L’area massima è
x2
x2
Amax =
R
2p
2
R
p
,
2
perciò in corrispon-
2
= 2R2 .
Per confronto, l’area del cerchio è Acer = R2 , e il rapporto tra le aree è
2
1
Amax
= = 0:63::: > .
Acer
2
Il quadrato inscritto ha area maggiore della metà dell’area del cerchio.
Esercizio 4 Cosa cambia nell’esercizio precedente se al posto del cerchio si
prende il semicerchio o il quarto di cerchio?
Per le simmetrie, la …gura massimizzante è la porzione di quadrato contenuta
rispettivamente nel semicerchio (quindi un rettangolo di proporzioni 2 1) o nel
quarto di cerchio (quindi ancora un quadrato). Anche il rapporto tra area del
rettangolo e area della …gura circoscritta non cambia.
Esercizio 5 (Il problema del fabbricante di lattine) Tra tutti i cilindri di
volume assegnato, determinare quello di super…cie totale minima. Esprimere il
risultato dicendo quanto vale per il cilindro massimizzante il rapporto raggio /
altezza. (Si può pensare a questo problema così: …ssata la capacità che deve
avere una lattina, ad es. 33cl, determinare le sue proporzioni in modo da usare
meno alluminio possibile per fabbricarla).
Siano r; h raggio e altezza del cilindro. Si ha:
Volume = r2 h = V assegnato,
quindi
V
:
r2
h=
3
La super…cie totale è
V
;
r2
S = 2 r2 + 2 rh = 2 r2 + 2 r
perciò dobbiamo massimizzare per r > 0 la funzione
r2 +
S (r) = 2
V
r
:
Calcoliamo
S 0 (r) = 2 2 r
V
r2
0 per
V
;
2
r3
e il volume è massimo per
r=
r
3
V
V
e h = 2 = :::
2
r
Calcoliamo il rapporto
r3
V
1
r
=
=
= ;
h
V
V 2
2
quindi il cilindro massimizzante ha h = 2r: (Altezza pari al diametro di base).
Esercizio 6 Determinare il cilindro di volume massimo inscritto in una sfera
di raggio R. Calcolare il rapporto tra altezza e raggio del cilindro massimizzante.
Il volume del cilindro massimo è maggiore o minore di metà del volume della
sfera?
Siano r; h raggio e altezza del cilindro. Una sezione verticale delle …gure
mostra allora un rettangolo di lati h; 2r inscritto in una circonferenza di raggio
R; e per Pitagora vale:
2
h
r2 +
= R2 ;
2
da cui
r=
r
h2
4
R2
e il volume del cilindro è
V = r2 h =
R2
h2
4
h:
Dobbiamo massimizzare quindi
V (h) =
hR2
h3
4
4
per 0 < h < 2R
Calcoliamo
V 0 (h) =
3 2
h
0 per
4
2
p R.
3
R2
4 2
R ;h
3
h2
Il volume è massimo per
2
h = p R;
3
r
h2
=
4
R2
r=
h p
= 2.
r
r
R2
=
3
R2
r
2
R;
3
Il volume massimizzante è
Vmax =
R2
R2
3
mentre
Vsf era =
e
2
4
p R = p R3
3
3 3
4 3
R
3
Vmax
1
1
= p = 0; 577::: > .
Vsf era
2
3
Il volume del cilindro è (poco) più di metà del volume della sfera circoscritta.
Esercizio 7 Determinare il cilindro di volume massimo che sta dentro un cono
di altezza H e raggio R. Calcolare il rapporto tra altezza e raggio del cilindro
massimizzante. Il volume del cilindro massimo è maggiore o minore di metà del
volume del cono?
Siano r; h raggio e altezza del cilindro. Una sezione verticale delle …gure
mostra allora un rettangolo di lati h; 2r inscritto in un triangolo isoscele di base
2R e altezza H. Se i vertici sono ( R; 0) ; (0; H) ; il lato obliquo di destra è la
retta y = H H
R x e si ha
H
h=H
r:
R
Il volume del cilindro è
V = r2 h = r2 H
H
r :
R
Dobbiamo massimizzare quindi
V (r) = H r2
r3
R
5
per 0 < r < R:
Calcoliamo
V 0 (r) = H 2r
2
3r
R
3r2
R
0 per
2
R.
3
0; r
Il volume è massimo per
2
R;
3
r=
H2
1
R = H;
R3
3
h=H
h
H
=
.
r
2R
Il volume massimizzante è
Vmax = Hr2 1
r
R
4
= H R2 1
9
mentre
Vcono =
e
2
3
=
4
HR2
27
1
HR2
3
4
1
Vmax
= < .
Vcono
9
2
Il volume del cilindro è (poco) meno di metà del volume del cono circoscritto.
Esercizio 8 Determinare il cono di volume massimo inscritto in una sfera di
raggio R. Calcolare il rapporto tra altezza e raggio del cono massimizzante. Il
volume del cono massimo è maggiore o minore di un terzo del volume della
sfera?
Siano r; h raggio e altezza del cono. Una sezione verticale delle …gure mostra
allora un triangolo isoscele inscritto in una circonferenza di raggio R. Indicando
con y la distanza tra la base del cono e il centro della sfera, l’altezza del cono è
h=y+R
e per Pitagora vale:
r 2 + y 2 = R2 ;
da cui ponendo x = r si ha
h=R+
e il volume del cono è
V =
p
R2
x2
p
1 2
1 2
r h=
x R + R2
3
3
6
x2 :
Dobbiamo massimizzare quindi
V (x) =
1
3
x2 R + x2
Calcoliamo
V 0 (x) =
1
3
p
2xR + 2x R2
x2
p
R2
p
x2
per 0 < x < R
x3
R2
x2
p
2 R2 x2
x2
1
x
1
p
=
=
x 2R + 2 R2 x2 p
x 2R +
3
3
R2 x2
R2 x2
p
x
= p
2R R2 x2 + 2R2 3x2
0 per
2
2
3 R
x
p
2R R2 x2 + 2R2 3x2 0
p
2R R2 x2 3x2 2R2 :
2
Occorre risolvere la disequazione irrazionale. Per 3x2
3x2 > 2R2 è equivalente a
4R2 R2
9x4
x2
9x4 + 4R4
8x2 R2
2
9x
2R2 è sempre vera, per
12x2 R2
0
8R2
quindi V (x) cresce …no a x2 = 89 R2 , che dà il punto di massimo
p
2 2
r=x=
R
r3
h=R+
8 2
4
R = R
9
3
R2
h p
= 2
r
Il volume massimizzante è
Vmax
1 8 2
=
R
3 9
R+
r
R2
8 2
R
9
mentre
Vsf era =
e
!
=
1 8 24
8 4 3
R R=
R
3 9 3
27 3
4 3
R
3
Vmax
8
1
< .
=
Vsf era
27
3
Il volume del cono è (poco) meno di un terzo del volume della sfera circoscritta.
7
!
Esercizio 9 Tra tutti i cilindri inscritti in una sfera di raggio R, determinare
quello di super…cie laterale massima. (Il problema fu risolto da Fermat). Calcolare il rapporto h=r per il cilindro massimizzante. La super…cie laterale del
cilindro è maggiore o minore della metà della super…cie della sfera?
Siano r; h raggio e altezza del cilindro. Una sezione verticale delle …gure
mostra allora un rettangolo di lati h; 2r inscritto in una circonferenza di raggio
R; e per Pitagora vale:
2
h
r2 +
= R2 ;
2
da cui
r
h2
r = R2
4
e la super…cie laterale del cilindro è
r
h2
h:
S = 2 rh = 2
R2
4
Dobbiamo massimizzare quindi
r
h2
S (h) = 2
R2
h per 0 < h < 2R
4
Calcoliamo
0r
1
h
2
2
h
h
A
V 0 (h) = 2 @ R2
+ q 4
2
4
2 R2 h4
=q
R2
h2
2R2 ; h
2R2
h2
4
p
h2
0 per
2R.
La super…cie è massima per
h=
r=
p
2R;
r
h2
R
=p ;
4
2
R2
h
= 2.
r
La super…cie massimizzante è
R p
Smax = 2 p 2R = 2 R2
2
mentre
Ssf era = 4 R2 ;
ossia la super…cie laterale del cilindro è esattamente metà di quella della sfera
circoscritta.
8
Esercizio 10 Determinare il parallelepipedo a base quadrata di volume massimo inscritto in una sfera di raggio R. E’un cubo? Il volume del parallelepipedo
massimo è maggiore o minore di metà del volume della sfera? (Il problema fu
risolto da Keplero).
Siano a; a; b i semispigoli del parallelepipedo inscritto. Per il teorema di
Pitagora nello spazio si ha
a2 + a2 + b2 = R2
quindi ponendo
b=x
si ha
a=
r
R2
x2
2
e il volume del parallelepipedo è
2
V = (2a) 2b = R2
x2 4x, da massimizzare per 0 < x < R.
Calcoliamo
V 0 (x) = 4 R2
3x2
2
R
;x
3
x2
R
p
3
R
p
;a
3
quindi il volume è massimo per b = x =
parallelepipedo massimo è un cubo, di volume
Vmax =
e
Vmax
=
Vsf era
3
R
2p
3
8
p
R3
3 3
4
3
3 R
0 per
=
=
q
R2
3
R2
2
=
R
p
,
3
perciò il
8
= p R3 ,
3 3
2
p = 0; 37:::
3
Il volume del cubo è poco più di un terzo del volume della sfera, ma meno della
metà.
Esercizio 11 Tra tutti i cilindri di diagonale …ssata, trovare quello di volume
massimo. Esprimere il risultato dicendo quanto vale il rapporto h=r per il cilindro massimizzante. [Diagonale del cilindro è la diagonale del rettangolo che si
ottiene con una sezione verticale del cilindro passante per il centro].
Per Pitagora si ha:
2
h2 + (2r) = d2
9
dove d è la diagonale …ssata. Perciò poniamo
r=x
p
h = d2
Il volume del cilindro è
4x2
V = r2 h = x2
e dobbiamo massimizzare
V (x) = x2
Calcoliamo
V 0 (x) =
=p
d2
x
p
2x d2
p
d2
p
d2
4x2
4x2 per 0 < x <
d
.
2
p
x2 ( 8x)
4x2 + p
=2 x
d2
2
2
2 d
4x
2 x
d2
4x2
d2
6x2
4x2
p
2x2
d2
4x2
0 per
6x2
d
p :
6
Il volume è massimo per
d
r = x = p ;h =
6
p
h
6 p
= p = 2:
r
3
r
d2
4
d2
d
=p ;
6
3
Si può a questo punto aprire una parentesi sul concetto di diagonale di un
cilindro:
Esercizio 12 Dimostrare che la diagonale di un cilindro (così come è stata
de…nita nell’esercizio precedente) è il segmento più lungo in esso contenuto.
Per inserire un segmento di massima lunghezza in un cilindro “usando bene”
lo spazio a disposizione, è chiaro che i due estremi del segmento dovranno essere
sulla super…cie del cilindro stesso, e dovranno essere sulle due basi opposte.
Scegliamo un riferimento in cui uno dei due punti è P1 ( R; 0; 0) ; e sia l’altro
P2 (x; y; H), con x2 +y 2 = R2 . La lunghezza del segmento al quadrato è (teorema
di Pitagora nello spazio):
2
2
2
(P1 P2 ) = (x + R) + y 2 + H 2 = (x + R) + R2
x2 + H 2 = 2Rx + R2 + H 2 ;
con x 2 [ R; R] ; ed è ovviamente massima per x = R: Quindi P2 (R; 0; H), e
il segmento P1 P2 è proprio quello che abbiamo chiamato diagonale del cilindro.
Qui non è nemmeno servito il calcolo di¤erenziale, visto che si massimizzava
una funzione lineare su un intervallo chiuso e limitato.
10
Esercizio 13 Tra tutti i cilindri di diagonale …ssata, trovare quello di super…cie
totale massima. Esprimere il risultato dicendo quanto vale il rapporto h=r per
il cilindro massimizzante.
Per Pitagora si ha:
2
h2 + (2r) = d2
dove d è la diagonale …ssata. Perciò poniamo
r=x
p
h = d2
4x2
La super…cie totale del cilindro è
p
x2 + x d2
S = 2 r2 + 2 rh = 2
e dobbiamo massimizzare
S (x) = 2
Calcoliamo
S 0 (x) = 2
Se x2
2x +
p
d2
4x2 d2
d2
8
4x2
2x +
d
.
2
p
d2
4x2
x =
p
40
5
si ha
64x4 + d4
20x2 d2 + d4
5
d2
4
< x2
2
crescente …no a x2 =
per 0 < x <
d2
è sempre vera, se
80x4
4x2
x ( 8x)
4x2 + p
=2
2 d2 4x2
8x2
0 per
4x2
d2
=2
2x + p
d2
p
2x d2 4x2 8x2
d2
8
p
x2 + x d2
4x2
d2
0
10d2
x2
p
5+ 5 2
40 d ;
p
16x2 d2
20d4
=
80 p
5+ 5 2
d
40
5
p
40
5
d2
quindi la super…cie è massima per
s
p
1 5+ 5
r=x=
d
2
10
s
s
p
p
5
+
5
5
5
2
2
h= d
d =
d
10
10
s
p
r
1 p
1 5+ 5
p =
5+1 :
=
4
h
2 5
5
11
p
4x2
d2
4x2
Esercizio 14 Tra tutti i coni di super…cie totale …ssata, determinare quello di
volume massimo. Esprimere il risultato mediante il rapporto h=r tra altezza e
raggio del cono.
La super…cie totale è:
1
2 ra
2
S = r2 +
dove a è l’apotema, a =
p
r2 + h2 , quindi
p
S = r 2 + r r 2 + h2
ed S è …ssato. Possiamo ricavare
2
r2
S
h2 =
r2
r
e quindi calcolare il volume
1 2
1 2
V =
r h=
r
3
3
s
r2
S
2
r2 :
r
Occorre quindi massimizzare
s
r
2
1 2
1 2
S2
S
r2
2
V (r) =
r
r =
r
2 r2
3
r
3
r
r
S
S 2
1
2 per 2 r2 < S.
r
=
r2
3
2S
Calcoliamo
2 r
S
S4
2r
r2
r 2 r
1
S4
S
=
2r
3
r2
r
1
V 0 (r) =
3
1
3
=
r
S
4 r2
r
0
r
q
q
S
r2
S
2 r2
2
r2
2+ q
2
2
r
S
r2
2S
r3
S
r2
q
2
2
3
5
S
S
r2
2
3
5
1
3
S =
r
S
4
12
q
q
S
r2
S
S
2
4 r2
0 per
perciò il volume è massimo per
r
r=
S
4
v
u
u S
h=t
S 2
4
2 S
4
S
=
4
r
2S
p
h
= 2 2:
r
2
Altri tipi di problemi di massimo e minimo
I problemi di massimo e minimo facilmente formalizzabili e risolubili col calcolo di¤erenziale scolastico non si limitano ai tipi di problemi geometrici che
abbiamo illustrato nella sezione precedente. Si possono considerare problemi
…sici, economici, o di altro tipo. Nella tradizione didattica dei libri di “Calculus” americani questi problemi occupano ampio spazio. Ad esempio, i seguenti
testi (tradotti in italiano) contengono decine di problemi di questo tipo, alcuni
decisamente interessanti:
Robert A. Adams. Calcolo di¤erenziale 1. Funzione di una variabile reale.
Seconda edizione. Casa Editrice Ambrosiana (v. pagine 190-193).
James Stewart. Calcolo. Funzioni di una variabile. Ed. Apogeo. (v. pagine
312-317).
E’istruttivo rendersi conto di come il calcolo di¤erenziale permetta di risolvere problemi di massimo o minimo anche nel discreto, non solo nel continuo:
Esempio 15 Ci chiediamo per quale n la successione an = n4 e n assume il
suo valore massimo. La domanda è giusti…cata dal fatto che questa successione
è positiva e tende a zero per la gerarchia degli in…niti, ma a0 = 0, perciò deve
avere un elemento massimo. Naturalmente si può facilmente “indovinare” chi
sia questo termine tabulando i primi valori
n
an
0
0
1
0:368
2
2:165
3
4:033
5
4:211
4
4:689
6
3:212
7
1:374
8
0:810
ma noi vorremmo poter dimostrare il risultato congetturato. Consideriamo:
f (x) = x4 e
x
per x 2 [0; +1);
e cerchiamone (in quell’intervallo) il punto di massimo assoluto.
f 0 (x) = e
x
4x3
x4 = x3 e
x
(4
x)
0 per x
4,
quindi f ha il suo massimo per x = 4, ossia f (x)
f (4) per ogni x
0, e
quindi a maggior ragione per ogni x = n
0. Perciò an = f (n) ha il suo
massimo per n = 4:
13
Esempio 16 Dimostrare che per ogni k = 1; 2; 3; :::; la successione an = nk e n
ha massimo per n = k. (Si osservi che la successione dipende dall’indice n,
mentre k è un parametro …ssato). Il procedimento è identico a quello visto.
Si noti che se si fosse a¤ rontato direttamente il problema per la successione
an = n103 e n (ad esempio), non sarebbe stato facile capire per tabulazione che
il valore massimo era assunto per n = 103. Il calcolo di¤ erenziale ci fa scoprire
il risultato, non ce lo fa solo dimostrare.
Esempio 17 Determinare per quale n la successione an = n4 2 n assume il suo
valore massimo. (La ragione per ci aspettiamo che ci sia un valore massimo è
la stessa del primo esempio). Il procedimento è simile ma c’è un fatto tecnico
che rende il problema signi…cativamente diverso. Se poniamo
f (x) = x4 2
x
per x 2 [0; +1)
e calcoliamo
f 0 (x) = 2
x
4x3
x4 log 2 = x4 2
x
(4
x log 2)
0 per x
4
' 5:77
log 2
vediamo che la funzione di variabile reale assume il suo massimo in un punto
non intero. Poiché f cresce prima di 5:77, la successione an è crescente per
n = 1; 2; :::; 5; analogamente, è decrescente per n = 6; 7; 8; ::: La conclusione è
che il valore massimo di an è assunto per n = 5 o per n = 6: solo il calcolo
numerico dei due valori ci può dire quale dei due sia il massimo:
a5 = 19:5313; a6 = 20:25
perciò il valore massimo è a6 .
Un altro tipo ancora di impiego dei problemi di massimo e minimo, di tipo
teorico, è illustrato dal seguente
Esempio 18 Dimostrare che esiste una costante c > 0 per cui si ha:
4
c a4 + b4
(a + b)
per ogni a; b > 0
e determinare la minima costante c per cui questo è vero.
Si tratta qui di dimostrare una disuguaglianza valida per ogni a; b > 0.
Riscriviamo la tesi raccogliendo b4 ad ambo i membri e sempli…cando (b > 0):
a
+1
b
4
c
a
b
4
+1
per ogni a; b > 0
che sarà dimostrata se proveremo che
4
(x + 1)
c x4 + 1 per ogni x > 0:
14
Ci siamo così ricondotti ad un problema in una sola variabile. De…nendo
4
f (x) =
(x + 1)
(x4 + 1)
si vede che il problema è equivalente a trovare il minimo numero c per cui si ha
f (x)
c per ogni x > 0;
ossia determinare il massimo della funzione f (x) per x > 0. Così trasformato,
il problema è ora standard:
3
f 0 (x) =
4 (x + 1)
4
x4 + 1
4x3 (x + 1)
2
(x4 + 1)
3
=
4 (x + 1)
2
(x4 + 1)
x4 + 1
x3 (x + 1)
3
=
4 (x + 1)
(x4
2
+ 1)
1
x3
0 per x
1.
Quindi il massimo di f , ossia la costante c, è:
c = f (1) =
24
= 8:
2
Esempio 19 Determinare la minima costante c per cui si abbia
5
(a + b)
c a5 + b5
per ogni a; b > 0
(oppure si può fare direttamente con esponente k intero positivo qualsiasi).
Esempio 20 Esiste un c > 0 per cui si abbia
5
c a4 + b4
per ogni a; b > 0 ?
4
c a5 + b5
per ogni a; b > 0 ?
(a + b)
E per cui si abbia
(a + b)
Giusti…care le risposte fornendo dimostrazione o contresempio.
[In entrambi i casi c non esiste. Nella prima: porre a = b e far tendere a a
+1; per la seconda: porre a = b e far tendere a a zero].
15