1
Il sistema di numerazione decimale
DEFINIZIONE. Un sistema di numerazione è un insieme di simboli dotato di una o più regole con
cui i simboli vengono raggruppati così da poter rappresentare tutti i numeri.
Il nostro sistema di numerazione viene detto decimale (o base dieci) perché usiamo dieci
simboli diversi che sono:
0
1
2
3
4
5
6
7
8
9
Tali cifre rappresentano i primi dieci numeri e vengono dette unità del primo ordine.
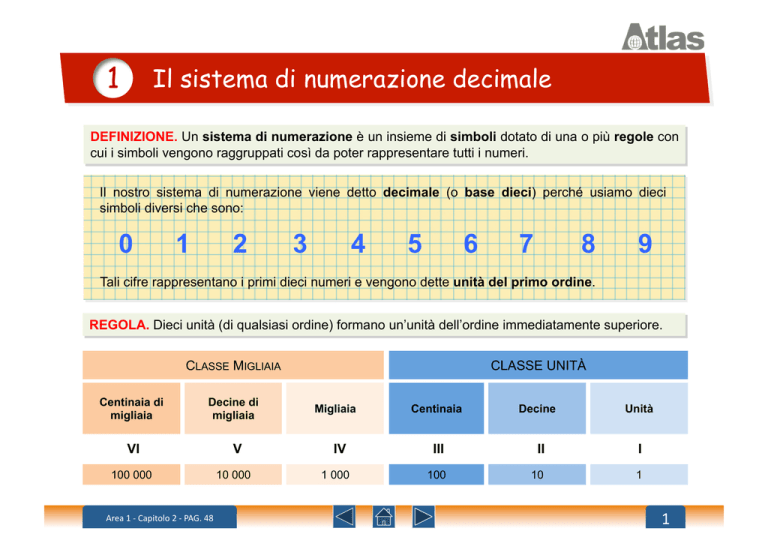
REGOLA. Dieci unità (di qualsiasi ordine) formano un’unità dell’ordine immediatamente superiore.
CLASSE MIGLIAIA
Centinaia di
migliaia
Decine di
migliaia
VI
100 000
Area 1 -­‐ Capitolo 2 -­‐ PAG. 48 V
10 000
CLASSE UNITÀ
Migliaia
Centinaia
Decine
Unità
IV
III
II
I
1 000
100
10
1
1 1
Il sistema di numerazione decimale
DEFINIZIONE. Il nostro sistema di numerazione è decimale (perché utilizza dieci simboli) e
posizionale (in quanto il valore attribuito alle cifre dipende dalla posizione che esse occupano).
ESEMPIO
Valore assoluto
Valore relativo
Area 1 -­‐ Capitolo 2 -­‐ PAG. 49 uno
due
sei
otto
1
2
6
8
un
migliaio
due
centinaia
sei
decine
otto
unità
2 2
L’insieme dei numeri naturali
DEFINIZIONE. Dato un numero naturale, il numero che si ottiene aggiungendo 1 si chiama
consecutivo o successivo.
ESEMPIO
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …
DEFINIZIONE. Ogni numero naturale (escluso lo zero) ha sempre un numero naturale che lo
precede. Tale numero prende il nome di antecedente o precedente.
ESEMPIO
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …
Area 1 -­‐ Capitolo 2 -­‐ PAG. 49 3 2
L’insieme dei numeri naturali
DEFINIZIONE. L’insieme dei numeri naturali è un insieme infinito e ordinato.
ESEMPIO n°1
23
347
La cifra più significativa è
dell’ordine delle decine
La cifra più significativa è
dell’ordine delle centinaia
Quindi
23
< 347
oppure
347 >
Area 1 -­‐ Capitolo 2 -­‐ PAG. 50 23
4 2
L’insieme dei numeri naturali
ESEMPIO n°2
Prime cifre significative sono uguali
Appartengono entrambi
all’ordine delle migliaia
1525
1531
Si devono confrontare le cifre
dell’ordine delle decine
2
<
3
allora
1525
< 1531
oppure
1531
Area 1 -­‐ Capitolo 2 -­‐ PAG. 51 > 1525
5 2
L’insieme dei numeri naturali
Possiamo disporre i numeri naturali partendo dal più piccolo (ordine crescente) o dal più
grande (ordine decrescente):
5
7
13
19
28
37
ORDINE CRESCENTE
45
37
29
18
8
2
ORDINE DECRESCENTE
Utilizzando la rappresentazione dei numeri naturali sulla retta possiamo concludere
PROPRIETÀ. Ogni numero naturale è minore di tutti i numeri naturali che lo seguono ed è maggiore
di tutti i numeri naturali che lo precedono.
Rappresentazione
0
Area 1 -­‐ Capitolo 2 -­‐ PAG. 51 1
2
3
4
5
6
7
8
9
10
6 3
I numeri decimali
DEFINIZIONE. Un decimo (0,1), un centesimo (0,01), un millesimo (0,001), ecc. vengono definiti
unità decimali, rispettivamente di primo, secondo, terzo ordine, ecc.
ESEMPIO
Parte intera
2
decine
23,54
3 , 5
unità
Parte decimale
4
decimi centesimi
si legge <<Ventitré e cinquantaquattro centesimi>>
Area 1 -­‐ Capitolo 2 -­‐ PAG. 52 7 3
I numeri decimali
REGOLA. Il valore di un numero decimale rimane invariato se alla destra della sua ultima cifra
decimale si aggiunge un numero qualsiasi di zeri.
ESEMPIO
32,41
32,410
32,4100
REGOLA. Possiamo pareggiare il numero di cifre decimali di due numeri decimali inserendo, dopo
l’ultima cifra decimale, degli zeri.
ESEMPIO
Area 1 -­‐ Capitolo 2 -­‐ PAG. 52 45,871
12,300
0,670
12,3
0,67
8 3
I numeri decimali
Per rappresentare un numero decimale sulla semiretta orientata bisogna suddividere le unità
intere in unità decimali.
ESEMPIO
1,7
ossia
1
intero
e
7
decimi
Rappresentazione
10 decimi
0
intero
10 decimi
2
1
1
Area 1 -­‐ Capitolo 2 -­‐ PAG. 53 intero
intero
7
decimi
1,7
9












