RICONOSCITORE DI SEQUENZA
Nella seguente relazione si parlerà del riconoscitore di sequenza. Questo circuito è costituito da vari
blocchi i quali sono, circuito antirimbalzo, flip-flop J K, e un circuito oscillatore.
CIRCUITO ANTIRIMBALZO
Una delle applicazioni del latch S - R è quella di un circuito antirimbalzo. Infatti nei circuiti
sequenziali lo stato delle uscite dipende dalla sequenza dei segnali applicati in ingresso. Poiché la
semplice chiusura di un contatto elettromeccanico dà luogo a dei piccoli rimbalzi nella chiusura
dell'interruttore che possono dare luogo a delle variazioni di tensione prima di raggiungere la
tensione finale. Tali variazioni di tensione danno luogo a degli errori di tipo logico. Un circuito
antirimbalzo è il seguente:
Quando il pulsante P si trova verso l'alto si ha S = 0; R = 1; Q = 1. Mentre il pulsante scende verso
il basso il falso contatto nella parte superiore del pulsante non riesce a portare R a 0, anche se S può
oscillare tra 0 e 1; una volta che il pulsante ha toccato la parte inferiore R = 0; S = 1; Q = 0;
successivi falsi contatti nella parte inferiore non riusciranno più a far commutare l'uscita, infatti
perché ciò avvenga, occorre che il pulsante ritorni verso l'alto.
FLIP FLOP J - K
I flip flop sono dei circuiti sequenziali analoghi ai latch S- R, tuttavia si differenziano perché nei
flip flop l'istante in cui avviene la commutazione delle uscite è stabilito con certezza, e si evita il
difetto della trasparenza; dove trasparenza vuol dire che l'uscita si adegua immediatamente allo
stato degli ingressi, non appena variano gli ingressi, ciò è un difetto quando si vogliono circuiti
perfettamente sincronizzati, nei quali gli istanti di commutazione devono essere decisi con
precisione. Lo schema di un flip flop J - K è il seguente:
notiamo che vi è l'ingresso J, che corrisponde a SET del latch S-R; l'ingresso K, che corrisponde al
RESET del latch S-R; l'ingresso di clock CK, che fa commutare il circuito durante il fronte di salita
dell'impulso di clock; il morsetto Pr, che sta per PRESET, cioè pone l'uscita Q = 1
indipendentemente dagli ingressi e dal clock; il morsetto Cl, cioè CLEAR, che pone l'uscita Q = 0,
indipendentemente dagli ingressi e dal clock; infine le due uscite Q e Q negato. La presenza del
clock rende il circuito di tipo sincrono.
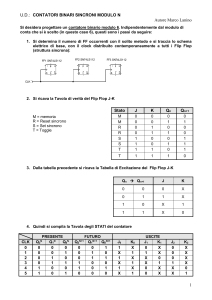
La tabella di verità è la seguente:
CK
J
K
Qn+1
0
X
X
Qn
0
0
Qn
0
1
0
1
0
1
1
1
Qn
Il simbolo indica il fronte di salita dell'impulso di clock. In assenza di clock l'uscita
resta invariata.
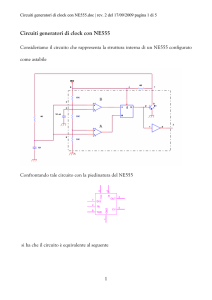
OSCILLATORE CON NE555
L' Ne555 è uno dei circuiti integrati pù utilizzati per la costruzione di timers ed oscillatori. Permette
di generare una tensione che oscilla tra 2 valori di tensione, quindi un'onda quadra di frequenza e
duty cycle desiderato. Il circuito esterno applicato ne permette l'utilizzo in modo astabile, ovvero
come oscillatore (alternanza di 2 stati). Lo shema interno dell' NE555 mostra un partitore di
tensione composto da 3 resistenze che generano le tensioni Vcc* 1/3 e Vcc * 2/3 (dal basso in alto).
Ai capi delle resistenze sono collegati gli ingressi (invertente e non invertente) di 2 amplificatori
operazionali. Gli altri ingressi degli operazionali sono collegati ai piedini dell'integrato e possono
essere connessi a piacimento a seconda della funzione che si vuole realizzare. Le uscite degli
amplificatori operazionali sono collegate al Set ed al Reset di un flip flop S-R. L'uscita Q,
amplificata da uno stadio di potenza che è in grado di fornire una sufficiente corrente viene
trasferita all'esterno dell'integrato tramite il piedino di uscita. L'uscita negata del flip flop è connessa
alla base di un BJT il cui emettitore è a massa, mentre il suo collettore è connesso ad un piedino per
portarlo all'esterno. Si vedrà che questo è utile per poter scaricare la capacità C. Lo schema in
circuitale in figura mostra come devono essere collegati i morsetti dell' NE555 per creare un onda
quadra utilizzandolo in configurazione astabile.
La capacità di 10 nf (nano Farad) è utile per il corretto funzionamento dell' NE555. Le resistenze
R1 ed R2 insieme al valore della capacità C determinano il periodo e il duty cycle dell'onda quadra
in uscita. La relazione che fornisce il valore di frequenza è la seguente: f = 1 / (.693 * C *(R1 + 2 *
R2)) Se consideriamo l'inverso della frequenza, ovvero il periodo, e lo scomponiamo in t1 (quando
il valore di uscita è positivo) e in t2 (quando il valore di uscita è nullo) possiamo calcolare i singoli
periodi t1 e t2.
t1 = .693(R1+R2)C
t2 = .693 x R2 x C
Confrontando le relazioni che forniscono t1 e t2 , è possibile ottenere il duty cycle.
D = t1/t = (R1 + R2) / (R1 + 2R2)
DUTY CYCLE
In elettronica, in presenza di un'onda quadra, si definisce duty cycle il rapporto tra la durata del
segnale "alto" ed il periodo. In base alla definizione, risulterà sempre un numero compreso tra 0 e 1
(estremi teoricamente compresi), ed è per questo che in genere si esprime il duty cicle in
percentuale.
La formula sarà:
La figura alla pagina seguente rappresenta un grafo dal quale sono state ricavate le tabelle e poi il
circuito.
1
JK
0X
1X
X1
X0
0
0
1
1
0
1
0
1
S1
S2
S3
S4
Q2
0
0
1
1
Q1
0
1
1
0
0
S2
S3
S2
S2
1
S1
S1
S4
S1
Q2 Q1
0 0
0 1
1 1
1 0
2
Q2
3
Q2 Q1
0 0
0 1
1 1
1 0
0
0
1
0
0
1
1
1
1
1
0
0
1
0
Q1
0
0
1
0
0
1
0
0
1
0
4
Flip Flop Q2
Q2 Q1
0 0
0 1
1 1
1 0
0
1
1
1
1
1
0
0
0
0
Flip Flop Q1
6
Q2 Q1
0
1
0
0
0
0
5
Q2 Q1
0 0
0 1
1 1
1 0
0
0
1
X
X
0
0
1
1
1
X
X
1
1
0
0
X
X
X
X
o
1
0
1
1
0
J2
7
Q2 Q1
0 0
0 1
1 1
1 0
Q2 Q1
0 0
0 1
1 1
1 0
0
0
1
X
X
1
0
0
X
X
8
0
X
X
1
1
J1 =
K2 = + I * q1
U = Q2 *
Q2 Q1
0 0
0 1
1 1
1 0
0
1
X
X
1
1
0
X
X
0
K1
J2 = * q1
K1 = I
X
0
0
X
J1
K2
9
1
X
X
1
1
X
X
0
1
10
Q2 Q1
0 0
0 1
1 1
1 0
0
X
0
0
X
1
X
1
1
X
0
X
X
0
X
1
1
X
Il circuito sottostante è il riconoscitore di sequenza.