3-tensioni e deformazioni

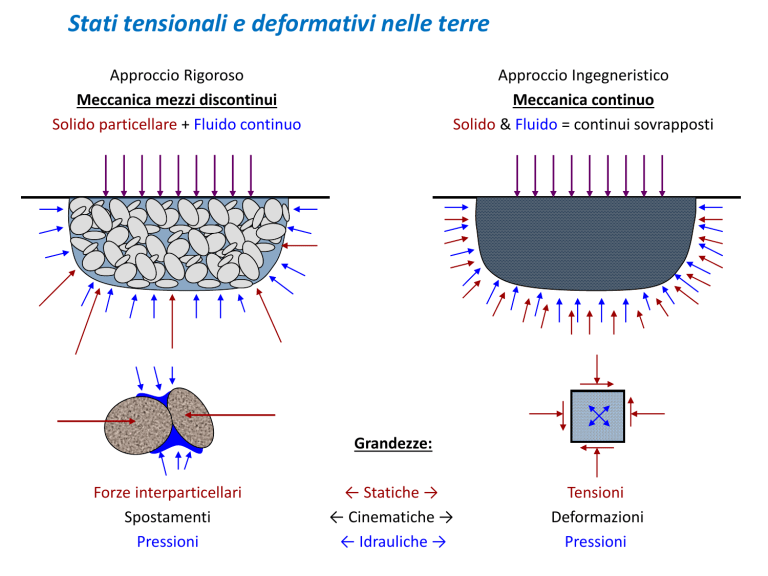
Stati tensionali e deformativi nelle terre
Approccio Rigoroso
Meccanica mezzi discontinui
Solido particellare + Fluido continuo
Approccio Ingegneristico
Meccanica continuo
Solido & Fluido = continui sovrapposti
Grandezze:
Forze interparticellari
Spostamenti
Pressioni
← Statiche →
← Cinematiche →
← Idrauliche →
Tensioni
Deformazioni
Pressioni
Definizione del mezzo continuo
Il continuo è una porzione di spazio occupata da materia in ogni sua parte.
Il continuo è deformabile: può variare la mutua distanza tra due qualsiasi punti del corpo.
Il continuo è soggetto a forze di massa, derivanti dal fatto di essere immersi in un campo di accelerazioni
(ex. gravità), e forze di superficie, agenti sulla frontiera del continuo.
Forze di volume e forze superficiali costituiscono il sistema di forze esterne cui il continuo è soggetto.
Un corpo soggetto ad un sistema di forze esterne resta in quiete, ossia resta in equilibrio sotto tali forze,
se la risultante delle forze esterne e il momento delle forze esterne sono nulli.
Ri=0
Moi=0
i=x,y,z
Gli spostamenti di un corpo continuo devono essere tali che il corpo non cessi di essere continuo, e cioè
tali da non implicare formazione di vuoti. In più occorre che non si verifichino né scorrimenti di materia
tra due piani, né sovrapposizioni di materia.
Tensione e deformazione nel mezzo continuo
Mezzo continuo alla Cauchy
A
l
B
Vettore ( tensore) tensione

F
t  lim
A  0 A
s


s
A
F
A
A
l
B
s
Vettore ( tensore) deformazione

s
d  lim
l  0 l
I vettori t e d sono legati tra loro dal legame costitutivo del mezzo
Se il mezzo è indeformabile (d  0) il legame costitutivo è di tipo rigido
B
Componenti normali e tangenziali
Componenti Normali
Compressione → Contrazione
Componenti Tangenziali
Taglio → Distorsione
u
N
v
w
u
T
w
x
y
z
  lim
A 0
N
A
Tensione
  lim
A 0
T
A
  lim
l0
w
l
Deformazione
  lim
l0
u
l
- In meccanica delle terre prevalgono i fenomeni di compressione
 ad essi si attribuisce segno positivo.
Tensioni normali e tangenziali
p2
p1
m
xS
P7
O
p6
y
S
A
txS
B
x
xS
p4
z
p5
p3
xS
xzS
txS
y
x
S
xyS
z
xS

z
y
z
y
x
z
x
x
z
y
x
y
z
y
z

x
x
y
In meccanica dei terreni è convenzionale considerare positive le tensioni normali di compressione.
Quindi le x, y e x sono positive quando dirette verso l’interno del volume elementare.
Con il simbolo ij si indica la tensione tangenziale agente sulla faccia di normale i ed avente la
direzione dell’asse j. La ij è positiva quando:
• agisce su una faccia di normale uscente di verso concorde all’asse i ed ha verso discorde all’asse j;
• agisce su una faccia di normale uscente di verso discorde all’asse i ed ha verso concorde all’asse j;
Componenti cartesiane
Riferimento: sistema cartesiano (x, y, z)
(1° pedice → direzione normale, 2° pedice → direzione componente)
 x
     yx
  zx

 xz 

 yz 
 z 
 xy
y
 zy
Tensori
 x
    yx
  zx

 xy
y
 zy
 xz 

 yz 
 z 
N. B.: le componenti sono dipendenti dal sistema di riferimento!
Equilibrio statico alla traslazione → Equazioni di continuità (Cauchy)
z
x
y
z
 yz 
 yz
Wz
 xz
  yz
y
 dy
z 
 xz 
  xz
 dx
x
 z
 dz
z
  x  yx  zx


 Wx  0

y
z
 x
  xy  y  zy


 Wy  0

y
z
 x
  xz  yz  z
 x  y  z  Wz  0

(Wx, Wy, Wz = componenti forze di massa lungo x, y, z)
Proprietà di simmetria e reciprocità
Equilibrio statico alla rotazione
Definizione
⇓
⇓
reciprocità tensioni tangenziali
reciprocità deformazioni tangenziali
  yx   xy

  zx   xz
  
zy
 yz
  yx   xy

  zx   xz
  
zy
 yz
Simmetria dei tensori rispetto alla diagonale
⇓
esiste un sistema di riferimento (‘principale’) in cui il tensore è diagonale
Sistema principale delle tensioni ⇔ xy = yz = xz = 0
Componenti principali di tensione e deformazione
1
3
2
3
2
1
Riferimento: sistema principale (1, 2, 3)
[pedice 1/2/3 → tensione (deformazione) principale massima/media/minima]
1 0
0 
2

 0 0
0
0

3 
Tensori
diagonali
1 0
0 
2

 0 0
0
0

 3 
Valori e coseni direttori (n1, n2, n3) di tensioni principali si ottengono imponendo soluzione non
banale al sistema {n}=[]{n}, il che richiede:
 x  
 xy
 xz 


det   yx
y  
 yz   0
  zx
 zy
 z   

Invarianti di tensione e deformazione
L’annullamento del determinante corrisponde alla soluzione dell’equazione di III grado:
 3  I1   2  I 2    I 3  0
(I1, I2, I3 = invarianti* di tensione del 1°, 2°, 3° ordine)
I 1   x   y   z  1   2   3
I 2   x  y   y  z   z  x   2xy   2xz   2yz  1 2  1 3   2  3
I 3   x  y  z   x  2yz   y  2xz   z  2yx  2  xy  zy  xz  1 2  3
Analogamente per le deformazioni:
 3  E1   2  E 2    E 3  0
(E1, E2, E3 = invarianti* di deformazione del 1°, 2°, 3° ordine)
E1   x   y   z  1   2   3


1 2
 xy   2xz   2yz  1 2  1 3   2  3
4
1
1
E 3   x  y  z   x  2yz   y  2xz   z  2yx   xy  zy  xz  1 2  3
4
4
E2   x  y   y  z   z  x 


*invarianti
= non dipendono dal sistema x, y, z
Componenti ottaedrali e invarianti di tensione
Piano ottaedrale = piano ortogonale alla trisettrice del quadrante 1, 2, 3
(coseni direttori n1 =n2 =n3 = √3/3)
Proiettando le 1, 2, 3
(⇔ considerando l’equilibrio del tetraedro):
 o ct 
1   2   3 I 1

3
3
 o ct 
1
3
1   2 2  1   3 2   2   3 2
p = tensione media
q = tensione deviatorica
p
I1
3
p   o ct 
q

2
3
I 12  3 I 2
1   2   3
3
3
1
o ct 
2
2
  1   2 2    1   3 2    2   3 2
 p, q = invarianti di tensione
q  I12  3 I 2
Con queste due sole componenti tensionali, è possibile descrivere
lo stato medio di compressione e di taglio agente sull’elemento
Componenti ottaedrali e invarianti di deformazione
Nel riferimento principale per le deformazioni, proiettando 1, 2, 3:
 o ct 
 o ct
1   2   3 E1

3
3
2

3
1   2 
2
 1   3    2   3 
2
2
2 2

3
v = deformazione volumetrica
 v  3 o ct  1   2   3
s = deformazione distorsionale
s 
 o ct
2

3
2
E12  3 E 2
  1   2 2    1   3 2    2   3 2
 v  E1
2
s 
E12  3E 2
3
 v, s = invarianti di deformazione
Con queste due sole componenti deformative, è possibile descrivere
le variazioni di volume e di forma dell’elemento
Rappresentazione dello stato tensionale in un punto
1.
2.
3.
All’interno di un corpo continuo sollecitato, la tensione varia da punto a punto.
In ogni punto le tensioni che agiscono sui diversi piani sono diverse tra loro.
Per l’analisi dello stato tensionale in un punto è necessario mettere in relazione tra loro le
tensioni che agiscono nelle diverse direzioni.
Il modo più semplice per analizzare lo stato tensionale in un punto è
quello di utilizzare la costruzione dei cerchi di MOHR.
Si può dimostrare che tutte le coppie possibili di n e n devono soddisfare le seguenti diseguaglianze:
n
2  3 2
  3 2
) ( 2
)
2
2
  3 2
  3 2
(b) n2  (n  1
) ( 1
)
2
2
  2 2
  2 2
(c) n2  (n  1
) ( 1
)
2
2
(a) n2  (n 
3
2
1
b
a
c
n
Il cerchio di Mohr
Se si considera ad esempio la faccia del cubetto che si appoggia all’asse principale 2, la tensione su di esso
agente apparterrà al piano principale 1-3, e al variare della sua giacitura, le compoenti n, n apparterranno
al cerchio di Mohr individuato dalle tensioni principali 1, 3.
n
1
3
(1-3)/2
n
n
Noti i valori delle tensioni principali 1 e 3 può essere
tracciato il cerchio di Mohr corrispondente, di centro
(1 +3)/2 e raggio (1 +3)/2.
(1+3)/2
(x,xz)
(x+z)/2
n
(z,zx)
Viceversa, se sono noti i valori delle tensioni
normali e tangen-ziali secondo due assi ortogonali
(x, z) del piano 1-3, il il cerchio di Mohr può essere
tracciato tra i punti (x, xz) e (z, zx), con centro
(x+ z)/2.
Il cerchio di Mohr
z
x
z
xz
x
n
Giaciture di
riferimento per polo
(z,zx)
POLO K
x
zx
z
n
xz
(x+z)/2
(x,xz)
Il polo (K) è quel punto del cerchio di Mohr che gode della proprietà che qualsiasi retta per esso
passante interseca il cerchio in un punto le cui coordinate (n, n) sono rappresentative dello stato
tensionale agente su quella giacitura.
Nella convenzione di Mohr sono positive le n che danno luogo ad una coppia oraria rispetto ad un
osservatore posto sulla normale uscente alla generica faccia del cubetto.
n > 0, dà luogo ad una coppia
oraria rispetto all’osservatore !
zx
xz
n < 0, dà luogo ad una
coppia antioraria
rispetto all’osservatore !
Stati tensionali tipici e cerchi di Mohr
Compressione isotropa

3
1
h  v
1

P
4
Compressione anisotropa
2
5
3

h
3
H

V
H
v

H
5
V
1


3

 h  1
v  3
V
 v  1
V
Taglio puro
1
4

2
Compressione e taglio
h  3
H

Problema tensio deformativo assialsimmetrico
Ipotesi: l’asse verticale (z) è di simmetria radiale
⇓
• ovunque 2 = 3 e 2 = 3
• in asse  = 0  direzioni principali = orizzontale e verticale
(questo non è verificato in generale altrove)
Problemi tipo
prove di compressione
fondazioni circolari
pali
Percorsi di sollecitazione (stress path)
Gli invarianti di tensione media (o sferica) p e deviatorica q
e di deformazione volumetrica v e distorsionale s
sono le variabili più rappresentative per descrivere graficamente
il comportamento di un elemento di terreno
per effetto dei diversi processi e combinazioni di sollecitazione a cui viene sottoposto
q
percorso tensionale
(stress-path)
stato iniziale
p
Per gli invarianti p e q’ analogamente alle componenti  e , vale:
p
q
1
2
 
i,j
2



i
j
1 2 3
3
In condizioni di assialsimmetria
q   1   3 
Percorsi di sollecitazione notevoli
percorso
D1
D2
D3
Dp
Dq
Compressione
isotropa
Schema
q
D
D
0
p
q
Taglio semplice
D
0
D
0
√3D
p
Compressione
cilindrica per carico
q
D
0
0
D/3
3
D
1
Estensione cilindrica
per scarico
q
D
0
0
D/3
D
p
-1
3
p
Problema tensio-deformativo piano
Ipotesi tipica: ogni piano verticale (x, z) è di simmetria
⇓
• stato di deformazione piano  y = yz = xy = 0
• in ipotesi di mezzo elastico  yz = xy = 0
• y = tensione principale 2 (indipendente da y)
Problemi tipo
prove di taglio
muri di sostegno
travi di fondazione
Problema tensio deformativo piano
Cerchi di Mohr di stato piano
deformazioni
tensioni

t
3
s
1   3
2
1 
1   3
2

2

3
 v 1   3

2
2
s (= ascissa del centro) = tensione media nel piano
t (= raggio del cerchio) = tensione deviatorica nel piano
L = lavoro di deformazione per unità di volume = 1∙1 + 2∙2 + 3∙3
2 = 0 ⇒
 L   1   1   3    3  .....  s    v  t    
1
2


1   3
2
Problema tensio deformativo assialsimmetrico
Cerchi di Mohr di stato assialsimmetrico
deformazioni
tensioni

2

3  2
1 
3  2
1
L = lavoro di deformazione per unità di volume = 1∙1 + 2∙2 + 3∙3
2 = 3 , 2 = 3 
 L   1   1  2  3    3  .....  p    v  q    s

Semplificazione legame costitutivo
Azioni di compressione

Idealizzazione
(modello costitutivo)
Realtà
(osservazione sperimentale)



Azioni di taglio
Realtà
(osservazione sperimentale)
Idealizzazione
(modello costitutivo)




Ulteriore idealizzazione legame costitutivo
Analisi
Stati Limite di Esercizio (SLE)
Analisi
Stati Limite Ultimi
(SLU)



Mezzo elastico lineare
• Reversibilità del legame tensio-deformativo

Mezzo rigido - plastico
• Deformazioni non reversibili
• Soluzione dipendente solo dagli incrementi
• Soluzione dipendente dallo stato iniziale
• Applicabilità principio sovrapposizione effetti
• Principio sovrapposizione effetti non valido
• Necessario risolvere equilibrio e congruenza
• Sufficiente soluzione equilibrio (congruenza ok)
Il mezzo solido elastico
Elasticità = relazione biunivoca [s]:[e]
j
i
i
i
Parametro
Modulo di Young
j
Coefficiente di Poisson
Caso generale
Ei 
d i
d i
n ij  
d j
d i
Elasticità lineare
Ei 
n ij  
D i  i

D i  i
D j
D i
Ipotesi di omogeneità  Ei e nij non dipendono da P(x, y, z)
Ipotesi di isotropia  Ei e nij non dipendono dal sistema di assi (x, y, z)

Ei = E ∀ i
nij = n ∀ i,j
Solido continuo elastico ideale = lineare, omogeneo, isotropo

j
i
Il legame costitutivo elastico ideale
Il legame costitutivo è espresso dalle
relazioni di Navier:
esprimibili nella forma matriciale:







1



 x E x  n  y  z

1
 y   y  n z   x 
E

1



z  n x   y
z

E

2( 1  n )
 xy 
 xy
E

2( 1  n )

 yz
 yz 
E

2( 1  n )
 zx 
 zx
E

 1
 E

  x   n
   E
 y  n
  z   E
 
 xy  
  yz  
  
  zx  



n
E
1
E
n

E


n
E
n

E
1
E

2( 1  n )
E
2( 1  n )
E



 x 
 
 y 
   z 
  
  xy 
  yz 
 
  zx 
2( 1  n ) 

E 
Legame elastico ideale in termini di invarianti
È conveniente scrivere le relazioni elastiche in termini di invarianti:


1  2n
3(1  2n)
p
x   y  z 
p
E
E
K
1
2(1  n) 2
2(1  n)
q
s 
E12  3E 2  ... 
I1  3I 2 
q
3E
3G
3 2
3 2E
 v   x   y   z  ... 
avendo posto:
Modulo di rigidezza volumetrica:
K
E
3(1  2n)
(K   per n  0.5)
Modulo di rigidezza tangenziale:
G
E
2(1  n )
(G 
E
per n  0.5)
3
Questa formulazione si traduce nel duplice vantaggio di:
• scrivere la relazione costitutiva in forma matriciale compatta:
• disaccoppiare l’analisi di fenomeni di:
- variazioni di volume (v), causate da variazioni di tensione media p
- variazioni di forma (s), causate da variazioni di tensione deviatorica q
1
 v   K
 
s   0


0  p 
1  q 

3G 
Il terreno come mezzo plastico
Proprietà del mezzo plastico:
• esiste una soglia di sollecitazione (tensione di snervamento, y)
oltre la quale si manifestano deformazioni plastiche permanenti (p)
(non recuperabili  non elastiche)
e indipendenti dalla durata del processo di carico (non viscose)

y
Materiale duttile: ‘strain hardening’ (incrudimento positivo)
Plasticità perfetta
Materiale fragile: ‘strain softening’ (incrudimento negativo)
T
p e

• se il mezzo è perfettamente plastico (non incrudente):
- snervamento e rottura coincidono
- non è necessario imporre condizioni di congruenza
• oltre lo snervamento, l’incremento di deformazione plastica è funzione:
- dello stato tensionale raggiunto (sempre)
- dell’incremento di stato tensionale (se il mezzo è incrudente)
Criterio di resistenza a rottura di un terreno
Modelli meccanici di riferimento
Blocco scorrevole
per attrito
Mezzo granulare
elementare
Mezzo granulare
complesso
F 
(stati impossibili)
curva limite
Il criterio di resistenza a rottura di un terreno
è definibile attraverso una superficie (o curva) limite
= luogo geometrico che separa
gli stati tensionali possibili da quelli impossibili
(stati possibili)
N
Rappresentazione del criterio di resistenza di un terreno
La superficie limite (luogo degli stati tensionali di rottura) è, in genere:
- indipendente dalla giacitura dell’elemento
- ben approssimabile con un andamento lineare
Si può esprimere mediante un legame analitico
tra componenti di tensione totale o efficace:
Criterio di Mohr-Coulomb
Teoria dello Stato Critico
Criterio di Rankine
1


componenti di tensione
tangenziale  e normale 
lungo il piano di rottura
q
3
tensioni principali
massima 1 e minima 3
+ conoscenza del piano di rottura
p
invarianti di tensione
deviatorica q e media p
Il criterio di resistenza di Mohr-Coulomb
Esprimendo il comportamento a rottura in termini di :,
la curva limite generalmente osservabile nel piano di Mohr
è simmetrica rispetto all’asse  (non è così per gli altri due criteri)
e caratterizzabile dall’espressione:
   c   tan 


c
c


Dal punto di vista fenomenologico, si può dire che:
c = coesione = resistenza allo scorrimento in assenza di tensioni normali
tan  = attrito = incremento della resistenza allo scorrimento con 
( = angolo di resistenza al taglio)
Casi tipici di criterio di resistenza
Terreno incoerente (0, c=0)

   tan

Terreno con attrito  e coesione c

Mezzo di Coulomb

  c +  tan

c


  c
c

Terreno coesivo (=0, c0)
Mezzo di Tresca