I POLIGONI
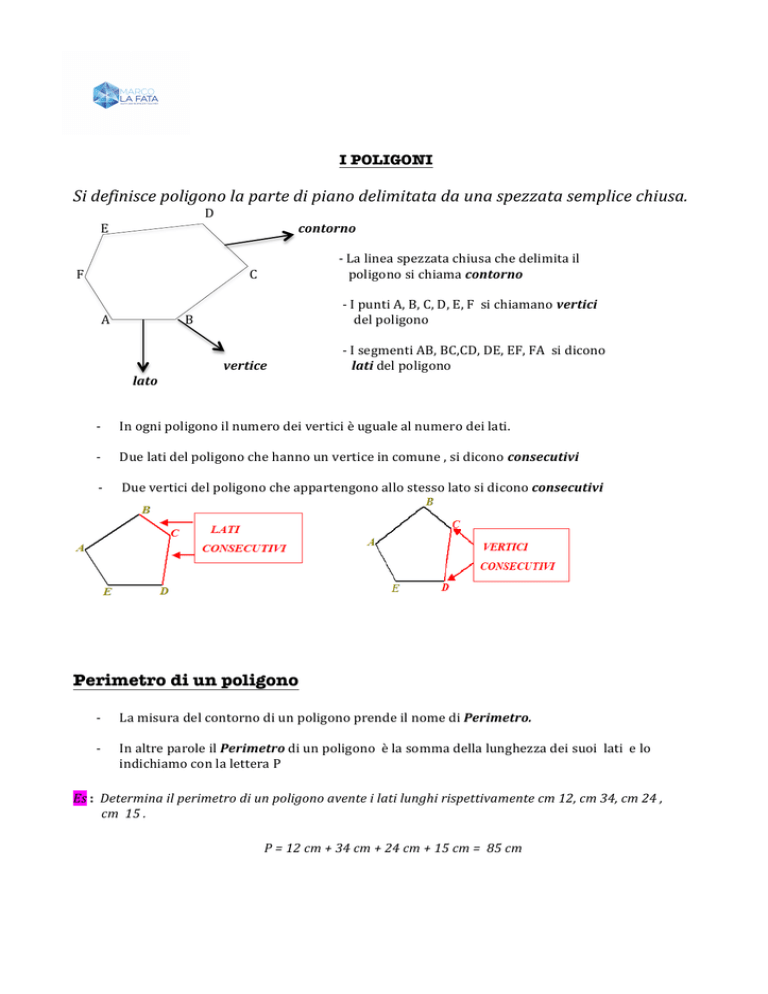
Si definisce poligono la parte di piano delimitata da una spezzata semplice chiusa. D E contorno -­‐ La linea spezzata chiusa che delimita il F C poligono si chiama contorno -­‐ I punti A, B, C, D, E, F si chiamano vertici A B del poligono -­‐ I segmenti AB, BC,CD, DE, EF, FA si dicono vertice lati del poligono lato -­‐ In ogni poligono il numero dei vertici è uguale al numero dei lati. -­‐ Due lati del poligono che hanno un vertice in comune , si dicono consecutivi -­‐ Due vertici del poligono che appartengono allo stesso lato si dicono consecutivi Perimetro di un poligono
-­‐
La misura del contorno di un poligono prende il nome di Perimetro. -­‐
In altre parole il Perimetro di un poligono è la somma della lunghezza dei suoi lati e lo indichiamo con la lettera P Es : Determina il perimetro di un poligono avente i lati lunghi rispettivamente cm 12, cm 34, cm 24 , cm 15 . P = 12 cm + 34 cm + 24 cm + 15 cm = 85 cm Poligoni concavi e convessi
Convesso Concavo -­‐ Un Poligono si dice convesso se, prolungando uno qualsiasi dei suoi lati, esso giace per intero nello stesso semipiano. In caso contrario si dice concavo. Diagonali di un poligono -­‐ Si definisce diagonale di un poligono ogni segmento che unisce due vertici non consecutivi -­‐ L’unico poligono a non avere diagonali è il triangolo poiché i suoi tre vertici sono consecutivi . Tra il numero delle diagonali di un poligono e il numero dei suoi lati sussiste una relazione che viene espressa dalla formula : d = diagonali d =
n × ( n − 3)
n = numero dei lati del poligono 2
Es. Determina il numero delle diagonali di un ottagono n × ( n − 3)
= 2
8 × (8 − 3) 8 × 5 40
=
=
= 20 Sostituendo avremo d =
2
2
2
Applichiamo la formula d =
Classificazione dei poligoni Un poligono può avere un numero variabile di lati. Il nome del poligono varia a seconda del numero dei lati che lo pongono. Numero di lati Nome del Poligono 3 lati Triangolo 4 lati Quadrilatero o Quadrangolo 5 lati Pentagono 6 lati Esagono 7 lati Ettagono 8 lati Ottagono 9 lati Ennagono 10 lati Decagono 12 lati Dodecagono 15 lati Pentadecagono 20 lati Icosagono -­‐ Un Poligono si dice equilatero se ha tutti i lati congruenti; -­‐ Un poligono si dice equiangolo se ha tutti gli angoli congruenti; -­‐ Un poligono si dice regolare se è equilatero ed equiangolo. Relazione tra i lati di un poligono
Supponiamo di voler costruire un poligono di quattro lati che misurano rispettivamente 8 cm, 2 cm, 3 cm, 1 cm 3 cm 2cm 1 cm 8 cm Come possiamo vedere , non è possibile formare il quadrilatero perché il lato maggiore, cioè quello di 8 cm. è maggiore della somma degli altri tre lati e quindi la spezzata rimane aperta. Questo lo possiamo verificare con una tabella Confronto fra il lato e Somma degli altri 3 lato la somma degli altri lati tre 8 2 + 3 + 1 = 6 8 > 6 3 8 +2 + 1 = 11 3 < 11 2 8 + 3 + 1 =12 2 < 12 1 8 + 2 + 3 = 13 1 < 13 Da ciò deduciamo che : In un qualsiasi poligono ogni lato è sempre minore della somma di tutti gli altri lati. Angoli di un Poligono
Come possiamo notare nella figura 1, gli angoli α, β, γ, δ, ε, sono formati da due lati consecutivi essi prendono il nome di angoli interni del poligono. Gli angoli ε e δ appartengono allo stesso lato e pertanto vengono detti adiacenti Fig.1 Fig.2 Nella figura 2, gli angoli sono formati da un lato e dal prolungamento del lato consecutivo e prendono il nome di angoli esterni del poligono Somma degli angoli interni di un poligono
Consideriamo il triangolo ABC e coloriamo gli angoli interni di colore diverso. Ritagliamo i tre angoli e riuniamo i tre vertici in un punto; notiamo che la loro somma è pari ad un angolo piatto cioè 180°. Da questo deduciamo che : In ogni triangolo la somma degli angoli interni è pari ad un angolo piatto ( 180° ) Da queste osservazioni si può determinare la somma degli angoli interni di un poligono qualsiasi: basta scomporre il poligono dato in triangoli tracciando alcune diagonali uscenti da un suo vertice ( Fig. 3 ) . Il quadrilatero, come possiamo notare, è diviso in 2 triangoli, il pentagono in tre e l’esagono in quattro triangoli. Ma abbiamo detto che la somma degli angoli interni di un triangolo è di 180 gradi (1 angolo piatto) e quindi diremo che nel quadrilatero la somma degli angoli interni è pari a 2 angoli piatti, mentre nel pentagono è pari a tre angoli piatti e nell’esagono è pari a 4 angoli piatti . Generalizzando possiamo dire che : In ogni poligono la somma degli angoli interni (Si) è uguale a n-­‐ 2 angoli piatti e cioè: Somma degli angoli esterni di un poligono
Guardando la figura notiamo che ogni angolo esterno è supplementare all’angolo interno a esso adiacente.; ne deriva che la somma degli angoli esterni ed interni di un triangolo è pari a 3 angoli piatti. Se a questi sottraiamo la somma degli angoli interni ,che come sappiamo, è di 180° otteniamo 2 angoli piatti cioè 360°. Se facciamo la prova con un quadrilatero , con un pentagono o con un esagono arriviamo sempre allo stesso risultato per cui : La somma degli angoli esterni di un poligono corrisponde ad un angoli giro, cioè misura 360°.












